2. 中国人民解放军63751部队, 陕西 西安 710043
2. No.63751 Unit of PLA, Xi'an 710043, China
GPS接收机由于其快捷、稳定的定位功能,在现代社会中已经成为重要的组成部分[1, 2, 3]。目前,随着对导航技术的深入研究[4, 5],高灵敏技术已经成为高性能GPS接收机的主要特征之一[6, 7, 8]。国内外研究表明,只有当GPS接收机搜索到至少4颗导航卫星时,才能够成功定位[9]。然而,现实环境中存在各种干扰,致使普通导航接收机无法搜索到所需的卫星[10]。因此,用于复杂环境下的导航接收机,其捕获模块的指标要求相当严格[11]。如果没有良好的弱信号捕获能力,GPS接收机将无法适应复杂的应用环境[12]。
近年来,国内外学者针对GPS弱信号捕获的问题提出了不同的算法。文献[13, 14] 提出了一种遍历码时延和多普勒频移的算法,这种算法硬件简单,但是运算量非常大。文献[15]设计了一种循环相关算法,该算法在同一时间对所有码时延进行处理,可以减少运算量,但是其对弱信号的捕获能力较差。文献 [16, 17]通过延迟-乘积的方式消除了所有多普勒频移仓,同样能够减少运算量,但是该方法更适合捕获码分多址(code division multiple access,CDMA)信号。此外,文献[18]通过与本地多普勒补偿信号进行相关运算,在采用长时间相干累计的同时,减少了处理时间,但是该运算存在功率损失。
以上研究工作表明,在保证较少运算量及较高捕获灵敏度的情况下,设计一种既能够捕获弱信号又能够保证较快运算速度的算法具有极其重要的意义。本文针对GPS弱信号捕获难题,首先简要介绍了DBZP(double block zero padding)算法的原理,通过分析得出该算法具有较好的弱信号捕获能力和快速的运算速度,但是该算法具有相关运算结果利用率低的缺点。针对这一问题,本文在DBZP算法的基础上,提出了一种改进算法。该算法采用延迟累加的方法,不仅能够提高相关运算结果的利用效率,而且能够更好地适应弱信号环境。
1 基于DBZP的改进捕获方法本文介绍的改进算法主要基于DBZP方法,因此有必要介绍DBZP算法的具体实现过程,其流程如图 1所示。根据文献[19]可知,该算法在估计导航数据位的基础上,能够进行长时间的相干累计,这样就保证了其对弱信号的捕获性能。此外,在相关运算之前,对基带信号和本地信号均进行了分块处理,这样进行FFT的点数就很少,导致捕获过程的整体运算量得到极大地减少。相比现有很多弱信号捕获算法捕获时间很长的问题,DBZP算法的优势非常明显。

|
| 图 1 DBZP算法原理图 Fig. 1 The schematic diagram of DBZP algorithm |
在DBZP算法中,每次相关运算结果输出的2N个点,总是只保留前N个点,舍弃后N个点。这种方法进行了2N个点的相关运算,但仅仅将相关运算结果的前N个点视为有用数据,只保留一半的运算结果,降低了运算结果的利用效率。改进算法采用延迟叠加的方法,将初始相关结果的后N个点暂存起来,然后将基带信号进行延迟,重复运算步骤,得到新的相关运算结果,将结果中的前N个点与之前暂存的N个点进行叠加,作为捕获结果输出,算法具体流程如图 2所示。

|
| 图 2 改进算法流程 Fig. 2 The schematic diagram of the improved algorithm |
主要步骤如下。
第1步:采用T-ms接收信号,将其分为m+1块,定义每个子块的大小为N,将相邻的两个子块组合,构成m个2N长度的双块。
第2步:将本地复现的C/A码分为m块,每个子块的大小均为N,用零元素将每个子块拓展成2N长度的双块。
第3步:将对应的双块进行相关运算,得到m个2N点的相关运算结果,将其中第k个相关运算结果前N点和后N点相关序列结果分别保存,记为rk(n)和r′k+1(n)。
第4步:将本地复现的C/A码循环延迟1个子块,重复第2步到第3步,得到m×m个相关运算结果。
第5步:将接收信号延迟1 ms,采用同样长度的信号。重复第1步到第4步,输出的2N个点相关值分别记为rk+1(n)与r′k+2(n)。将叠加结果rk+1(n)+r′k+1(n)作为累加输出存入m×m矩阵中。
第6步:将得到的m×m个相关子块结果对应元素取模值,取其中的最大累积值。将最大累积结果与阈值比较。若有元素模值大于预先设定的阈值即认为信号被捕获,元素对应的位置标定了的C/A码相位与多普勒频率;若没有元素模值大于预先设定的阈值,则重新读取新的T-ms基带信号,重复步骤第1步到第5步。
从算法过程中可以看出,改进算法通过保留相关运算结果的后N个点,提高了相关运算结果的利用率,增加了数据观测量。此外,对于相关运算结果,通过重叠叠加的方法增加了相关累加的过程。因此,根据理论分析,相比DBZP算法,改进算法在增加一次相加运算的前提下,增加了数据观测量和相干累加时间,用很少的运算量换取了较大的处理增益,捕获结果应具有更高的相关峰值,且其捕获性能也应更加优越。
2 仿真结果与分析 2.1 捕获结果分析本文采用的中频数字信号由美国科罗拉多大学利用射频前端采集获得。其参数如下:采样频率为38.192 MHz,中频为9.548 MHz,有符号字符型采样格式(8位)。仿真试验中,通过在接收信号中人工加入随机噪声,构造出载噪比各不相同的中频信号[20]。表 1显示的是在5种载噪比状态下的参数设置方法和捕获结果。由统计结果可以看出,通过设置不同的参数,改进的算法能够捕获载噪比为17 dB-Hz的GPS信号,并且检测概率能够达到91%。
| 载噪比/dB-Hz | 数据长度/ms | 非相干累积次数 | 检测概率 |
| 25 | 80 | 5 | 0.97 |
| 22 | 80 | 5 | 0.80 |
| 22 | 280 | 5 | 0.99 |
| 19 | 80 | 5 | 0.75 |
| 19 | 300 | 5 | 0.95 |
| 17 | 300 | 5 | 0.91 |
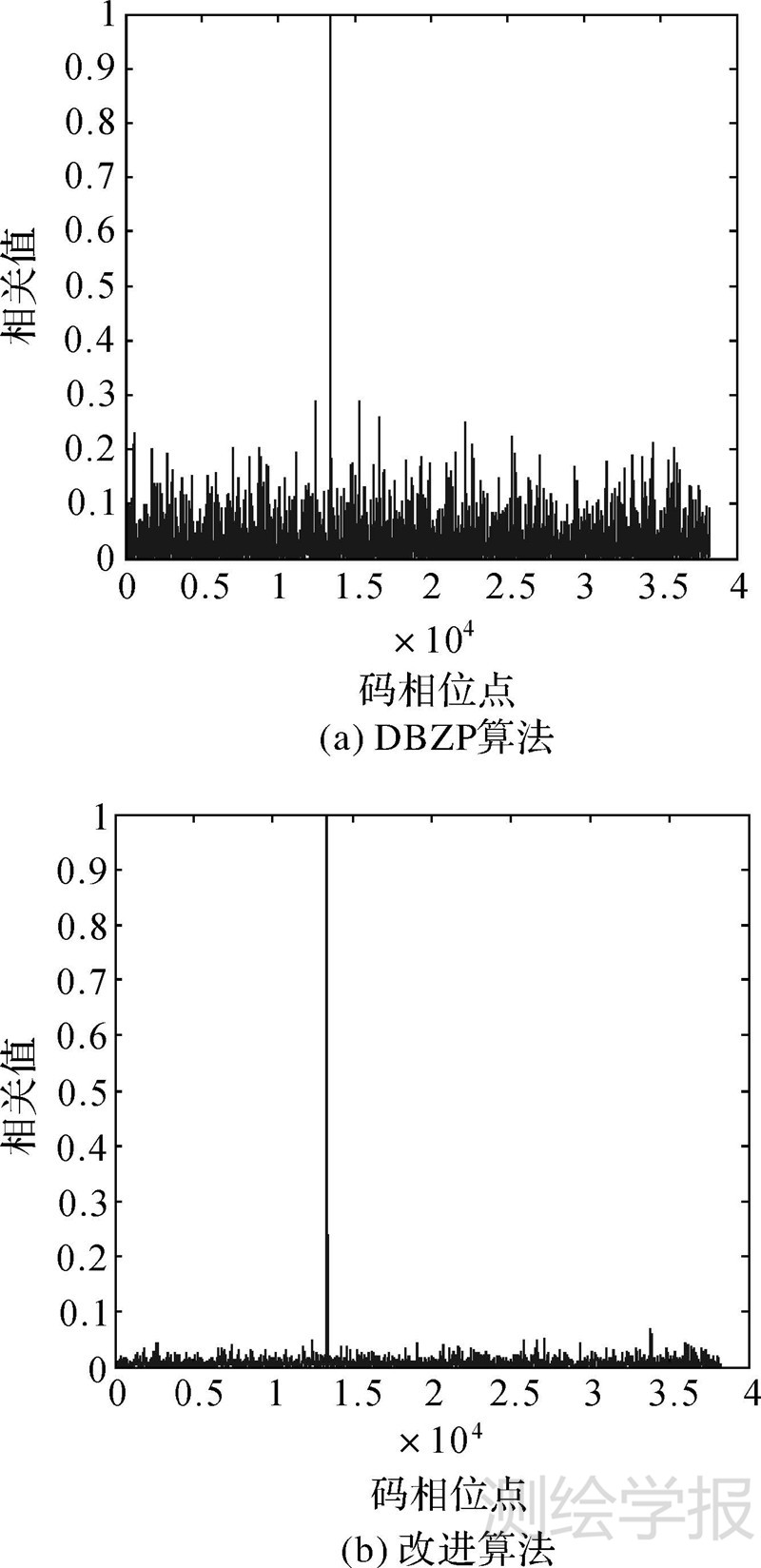
采集载噪比为17 dB-Hz的信号,数据长度设定为300 ms,进行仿真试验,结果如图 3所示(图中横坐标为码相位采样点,纵坐标为归一化相关值)。
|
| 图 3 DBZP算法和改进算法捕获结果对比 Fig. 3 The capture results of DBZP algorithm and the improved algorithm |
从图 3中可以看出,DBZP算法(图 3(a))和改进算法(图 3(b))的捕获结果中都有一个峰值,并且峰值所对应的码相位值准确,说明DBZP算法和改进算法都能够实现这种信号的捕获。但是经过比较可以发现,改进算法的峰值更加明显,而DBZP算法的峰值和次峰值比较小,这就必然会导致较高的虚警概率,从而说明改进算法的检测性能更好。
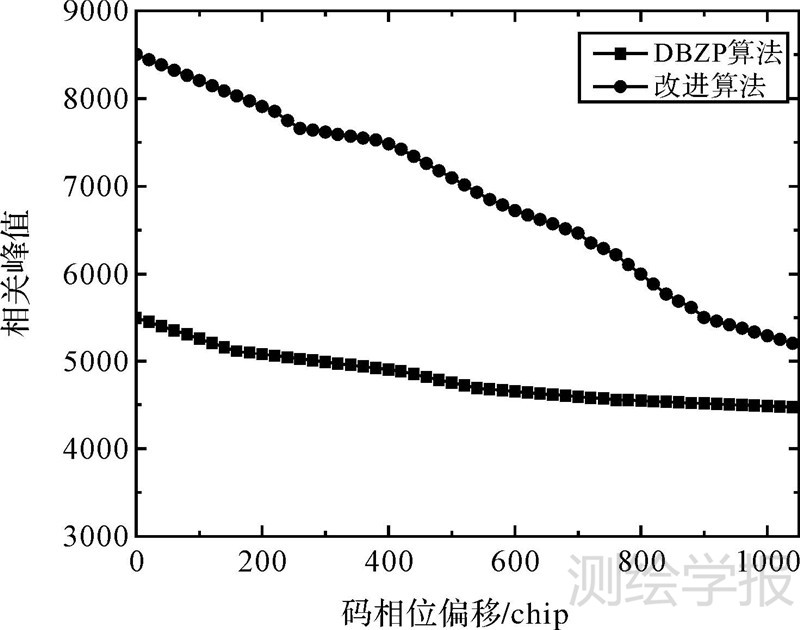
为了进一步测试改进算法的性能,在无噪声、无载波频率偏移的条件下,将码相位偏移由小到大进行调整,设定其变化范围为0~1120 chip,对DBZP算法和改进算法的捕获性能进行仿真,并将在相关运算过程中得到的相关峰值进行统计。图 4为仿真结果得出的DBZP算法和改进算法中相关峰值随码相位偏移的变化曲线。
|
| 图 4 DBZP算法和改进算法的相关峰值随码相位偏移变化曲线 Fig. 4 The relationship between correlation peak and code phase offset of DBZP algorithm and the improved algorithm |
从图 4中可以看出,在接收信号的C/A码相位从0 chip偏移至1024 chip的过程中,DBZP算法和改进算法的相关峰值均随着C/A码相位偏移的增加而逐渐减小,但改进算法的相关峰值始终高于DBZP算法。由此可以说明,改进算法的处理增益比DBZP算法更好。
此外,从图 4中还可以看出,在码相位偏移较少时,改进算法在处理增益上的改善更好,随着码相位偏移的增加,处理增益的改善趋向于零。这主要由于码相位偏移较小时,改进算法引入的噪声较少,对相关结果进行叠加的结果全部体现在处理增益上,因此处理增益改善明显。随着码相位偏移逐渐增大,改进算法引入的噪声也随之增加,叠加相关结果造成处理增益增大的同时,噪声也随之增大,结果导致了处理增益的改善趋向于不明显。
2.2 检测概率分析将接收信号数据长度设定为300 ms,通过仿真,比较改进算法和DBZP算法在不同载噪比状态下的检测性能,得到如图 5所示的曲线。从图中可以看出,两种算法在捕获载噪比为19 dB-Hz的信号时,检测概率均能达到95%,说明两种算法在这种状态下的检测性能相差无几。但是,随着载噪比的继续降低,改进算法的捕获性能优势则会表现得更加明显。在载噪比为17 dB-Hz的状态下,DBZP算法的检测概率仅仅为81%,而此时,改进算法则能达到91%的检测概率,说明改进算法更适合弱信号环境。此外,从图中可以看出,在相同检测概率条件下,改进算法比DBZP算法性能提高约0.6 dB。

|
| 图 5 DBZP算法和改进算法的检测性能分析 Fig. 5 The detection performance analysis of DBZP algorithm and the improved algorithm |
文献[19]针对GPS微弱信号处理算法进行了改进,并对文中提出的针对微弱信号的捕获与跟踪算法进行了比较分析。该课题组捕获的信号源是仿真信号,忽略了空间环境的影响。不同于以上研究工作,本文捕获的信号为射频前端采集获得的真实信号。真实信号由于受到多径、空间环境因素的影响,导致接受过程更加困难,因此会出现数据上的差异。此外,尽管本文与文献[19]捕获过程中采用的算法原理相同,但是实现的方法是在各自独立的环境下进行的,算法实现过程中所加入的滤波器和平滑等处理过程不尽相同,性能各有优劣,也会导致结果不同。因此,相比文献[19]得出的结论,本文捕获程序有2 dB的性能下降。
以上仿真试验,不仅比较了在码相位偏移逐渐增大时,改进算法和DBZP算法在相关运算结果中的最大峰值,而且比较了这两种算法的捕获性能。由此得出的结论为:在捕获弱信号,特别是载噪比为17 dB-Hz的微弱信号,改进算法的检测性能要优于DBZP算法。这主要是由于改进算法是在DBZP算法的基础上,将两个相互延迟1 ms的相关运算结果进行了相干累加,导致了相干累加时间的加长,因此获得了更大的处理增益。所以,在性能检测上表现为改进算法的检测概率高于DBZP算法。
3 结束语本文针对DBZP算法中存在的相关运算结果利用率低的问题,采用延迟累加的方法,对DBZP算法进行了改进。通过保留相关运算结果中丢弃的运算结果,提高了运算结果的利用率。通过叠加相关结果,增加了数据观测量和相干累计时间,提高了捕获的灵敏度。通过理论分析得出,改进算法的捕获结果具有更高的相关峰值,该算法具有更加优越的捕获性能。仿真结果验证,在捕获载噪比为17 dB-Hz的微弱信号时,将处理数据长度增加为300 ms,改进算法的检测概率可以达到91%,因此能够满足捕获的要求。试验结果表明,本文提出的改进算法可以应用于复杂环境下的GPS定位,并且为高灵敏度GPS接收技术的实现提供了保证。
| [1] | OZSOY K, BOZKURT A, TEKIN I. Indoor Positioning Based on Global Positioning System Signals[J]. Microwave and Optical Technology Letters, 2013, 55(5): 1091-1097. |
| [2] | LIU Hui, DARABI H, BANERJEE P, et al. Survey of Wireless Indoor Positioning Techniques and Systems[J]. IEEE Transactions on Systems, Man, and Cybernetics Part C: Applications and Reviews, 2007, 37(6): 1067-1080. |
| [3] | 段举举, 沈云中. GPS/GLONASS组合静态相位相对定位算法[J]. 测绘学报, 2012, 41(6): 825-830. DUAN Juju, SHEN Yunzhong. An Algorithm of Combined GPS/GLONASS Static Relative Positioning[J]. Acta Geodaetica et Cartographica Sinica, 2012, 41(6): 825-830. |
| [4] | 李廷军, 林雪原. 基于多尺度预处理的GPS/SINS组合导航系统[J]. 武汉大学学报(信息科学版), 2011, 36(1): 6-13. LI Tingjun, LIN Xueyuan. GPS/SINS Integrated Navigation System Based on Multi-scale Preprocessing[J]. Geomatics and Information Science of Wuhan University, 2011, 36(1): 6-13. |
| [5] | 杨元喜. 卫星导航的不确定性、不确定度与精度若干注记[J]. 测绘学报, 2012, 41(5): 646-650. YANG Yuanxi. Some Notes on Uncertainty, Uncertainty Measure and Accuracy in Satellite Navigation[J]. Acta Geodaetica et Cartographica Sinica, 2012, 41(5): 646-650. |
| [6] | 莫凡, 王新龙. 高灵敏度GPS捕获技术研究综述[J]. 航空兵器, 2014(2): 19-26. MO Fan, WANG Xinlong. Review of Acquisition Techniques of High Sensitivity GPS[J]. Aero Weaponry, 2014(2): 19-26. |
| [7] | 罗大成, 刘岩, 刘志国, 等. 一种高灵敏度GPS信号快速捕获算法[J]. 电讯技术, 2013, 53(4): 408-414. LUO Dacheng, LIU Yan, LIU Zhiguo, et al. A Novel High Sensitive Fast Acquisition Algorithm of GPS Signals[J]. Telecommunication Engineering, 2013, 53(4): 408-414. |
| [8] | 刘毓, 邹星. 弱GPS信号捕获算法及其仿真研究[J]. 测绘学报, 2013, 38(3): 192-194. LIU Yu, ZOU Xing. Weak GPS Signals Acquisition Algorithm and Simulation[J]. Acta Geodaetica et Cartographica Sinica, 2013, 38(3): 192-194. |
| [9] | ZIEDAN N I. Global Navigation Satellite System (GNSS) Receivers for Weak Signals[M]. Boston: Artech House Publishers, 2006. |
| [10] | 成伟兰, 刘坚强, 谌丽. 干扰条件下接收机减敏机理分析[J]. 舰船科学技术, 2012, 34(3): 122-129. CHENG Weilan, LIU Jianqiang, SHEN Li. Analysis of Receiver Desensitization Mechanism in the Presence of Interference[J]. Ship Science and Technology, 2012, 34(3): 122-129. |
| [11] | 李源明, 张波, 李暑坚, 等. GPS软件接收机中一种新的弱信号捕获算法[J]. 电子测量技术, 2012, 35(11): 13-16. LI Yuanming, ZHANG Bo, LI Shujian, et al. Algorithm for Weak Signal Acquisition in GPS Software Receiver[J]. Electronic Measurement Technology, 2012, 35(11): 13-16. |
| [12] | 李江, 钱富才, 刘丁, 等. 具有未知参数的GPS/DR组合导航系统跟踪与辨识[J]. 电子与信息学报, 2013, 35(4): 921-926. LI Jiang, QIAN Fucai, LIU Ding, et al. Tracking and Identification for GPS/DR Integrated Navigation System with Unknown Parameters[J]. Journal of Electronics & Information Technology, 2013, 35(4): 921-926. |
| [13] | PARKINSON B W, SPILKER J J. Global Positioning System: Theory and Applications[M]. Washington D C: AIAA, 1996. |
| [14] | MISRA P, ENGE P. Global Positioning System: Signal, Measurements and Performance[M]. Lincoln, MA: Ganga-Jumuna Press, 2001. |
| [15] | BORRE K, AKOS D M, BERTELSEN N, et al. A Software-defined GPS and Galileo Receiver: A Single-frequency Approach[M]. Birkhäuser: Springer, 2007: 67-77. |
| [16] | LIN D M, TSUI J B Y. Fundamentals of Global Positioning System Receivers: A Software Approach[M]. New York: John Wiley & Sons, 2000. |
| [17] | LIN D M, TSUI J B Y. Acquisition Schemes for Software GPS Receiver[C]//Proceedings of the 11th International Technical Meeting of the Satellite Division of the Institute of Navigation (ION GPS). Nashville, TN: ION Publications, 1998: 317-325. |
| [18] | LIN D M, TSUI J B Y. Comparison of Acquisition Methods for Software GPS Receiver[C]//Proceedings of the 13th International Technical Meeting of the Satellite Division of the Institute of Navigation (ION GPS). Salt Lake City, UT: ION Publications, 2000: 2385-2390. |
| [19] | 焦瑞祥. 基于FPGA 技术的微弱GPS 信号实时处理的实现[D]. 上海: 上海交通大学, 2008. JIAO Ruixiang. The Implementation of Global Position System Weak Signal Real Time Processing Based on Field Programmable Gate Arrays[D]. Shanghai: Shanghai Jiao Tong University, 2008. |
| [20] | 巴晓辉, 刘海洋, 郑睿, 等. 一种有效的GNSS接收机载噪比估计方法[J]. 武汉大学学报(信息科学版), 2011, 36(4): 457-466. BA Xiaohui, LIU Haiyang, ZHENG Rui, et al. An Effective Carrier-to-noise Ratio Estimation Method for GNSS Receiver[J]. Geomatics and Information Science of Wuhan University, 2011, 36(4): 457-466. |


