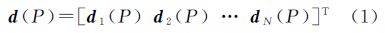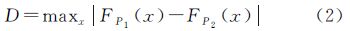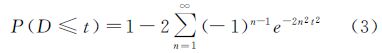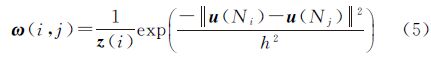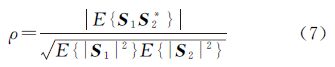2. 中国科学院测量与地球物理研究所, 湖北 武汉 430077
2. Institute of Geodesy and Geophysics, Chinese Academy of Sciences, Wuhan 430077, China
2000年,文献[1—2]首先提出了永久散射体(permanent scatterers,PS)干涉测量技术,通过研究时间序列上雷达反射信号稳定点目标的相位变化,获取高精度的形变监测结果。传统PS-InSAR时序分析技术选取PS点时通常假设点目标雷达幅度特征趋于服从高斯分布,并采用振幅的标准差与均值的比值来衡量点目标强度的时空稳定性,不符合该标准的像元点被舍弃,导致了该技术在实际应用中存在一定的局限性,尤其是在地表植被覆盖区,其雷达散射特性在时间域不符合高斯分布,但是在短时间内具有较好的相干性。
针对上述问题,通过采取降低选取PS点要求的策略和新的时空滤波手段,出现了利用小基线数据集提取地表地形参数和形变速率的新方法。其中,相干目标法(coherent targets,CT)是处理小基线数据集一个重要分支[3, 4, 5, 6]。该方法根据干涉图的平均相干系数识别点目标,并利用多基线干涉条纹图对高相干点目标相位进行时序分析,获取形变量随时间的变化关系。
为了减弱干涉图的相位噪声,该方法通常需要对干涉图进行多视或滤波处理,其中空间均值滤波和Goldstein滤波[7]为常用的干涉图滤波方法,但是上述方法在去噪效果和影像细节保持两个方面仍有不足。针对干涉图的滤波问题,2009年,文献[8—9]将空间非局部滤波(non-local)应用到干涉图滤波中来。该方法在削弱相位噪声和保持干涉图细节方面都取得了较好的效果。针对雷达信号的相干斑噪声和同类型地物雷达散射分布相近的特点,2011年,文献[10]提出了基于同质像元点的相位信息提取方法。该方法基于KS检验算法来提取后向散射特性相近的同质点,之后利用极大似然估计方法获取同质像素点的时序相位。2012年,文献[11]将基于同质点的空间均值滤波方法融入到传统的SBAS方法中,并在油气开采区域取得了较好的监测效果。2013年,文献[12]提出了基于同质像元点的空间非局部滤波方法,即时空同质滤波。该方法首先利用时间序列SAR影像,选取窗口中后向散射系数时间分布相近的像元点作为样本点,然后将这些样本点的相位值进行加权平均计算得到窗口中心点的相位。其中干涉图的滤波效果由参数h决定,但是在该方法中参数是根据经验来选取,具有很大的随机性。2015年,文献[13]提出了一种改进的Nonlocal滤波算法,其基于干涉图的概率分布函数来提取同质像素点,并根据条纹频率高低来自适应设置滤波窗口形状。
相干目标点的选取是雷达干涉时序处理中非常关键的一个步骤,通常是根据干涉图的相干性来选取相干系数稳定的点。在实际计算中,常常假设两个随机平稳序列是各态历经的,并用估计窗口中所有像素的空间平均值来替代期望值来估计相关系数[14]。因此,为了保证相干性估计的平稳性,需要有足够多样本或较大的窗口,但是窗口太大会引入异质像素,导致两个序列不满足随机平稳性。样本点的平稳性条件可体现在两个方面:①散射特性平稳性,即要求估计窗口内样本后向散射特性基本保持一致[15, 16, 17];②相位平稳性,通常情况下,地形相位、大气相位、形变相位等系统性相位的存在,会导致低估干涉图的相干性[14, 17, 18]。针对上述第一方面,部分学者进行了研究,主要是基于时间序列SAR影像,根据地物后向散射特性对窗口内样本进行同分布检验,选择与中心像素点具有相同后向散射强度分布特征的样本点。其中,非参数的KS (Kolmogorov-Smirnov)检验是目前的主流算法[19],该检验方法与样本数大小和数据概率密度函数的形式无关,且容易计算。针对同质点误选的问题,文献[20]提出了一种顾及像素点复数信息的同质点选取算法。该算法通过比较像素点协方差矩阵的相似性来稳健地选取同质像素点。考虑到不同视数条件下振幅序列的概率分布情况,文献[21]提出了一种同质像素点的快速选取算法。该算法能够在少量影像数量下实现同质点的高效提取。为了保证估计窗口的相位平稳性,用户通常采用极大似然条纹频率估计方法去除地表形变、大气、基线误差等因素引起的系统相位[17, 18]。但是系统相位在估计窗口内往往表现为多个频谱信号的叠加,很难通过这种方法分离。针对上述问题,文献[22]提出利用估计多尺度极大似然条纹频率的方法,通过改变估计窗口的大小来获取不同尺度的系统相位。相比较前者而言,该方法能够获取多尺度的、非平稳变化的信号,从而有效去除DEM误差、地表形变、大气相位等影响,保证估计窗口内相位的平稳性。2013年,文献[18]等提出了一种自适应条纹频率估计算法,通过计算相位噪声的程度来确定窗口的大小。
针对传统相干目标法的特点,本文将干涉图时空同质滤波和除去信号非平稳性的相干性估计融入到该框架中来。时空同质滤波具体为利用时序SAR影像提取窗口中后向散射特性相近的同质像素点,并基于同质点对干涉图进行自适应空间非局部滤波,降低干涉图的相位噪声,提高干涉图的质量;而除去信号非平稳性的相干性估计则在可在保证平稳性的条件下提高相干性的估值,增加有效监测点的数量,最后对相干点的相位进行时序分析即可获得可靠监测点的形变信息。
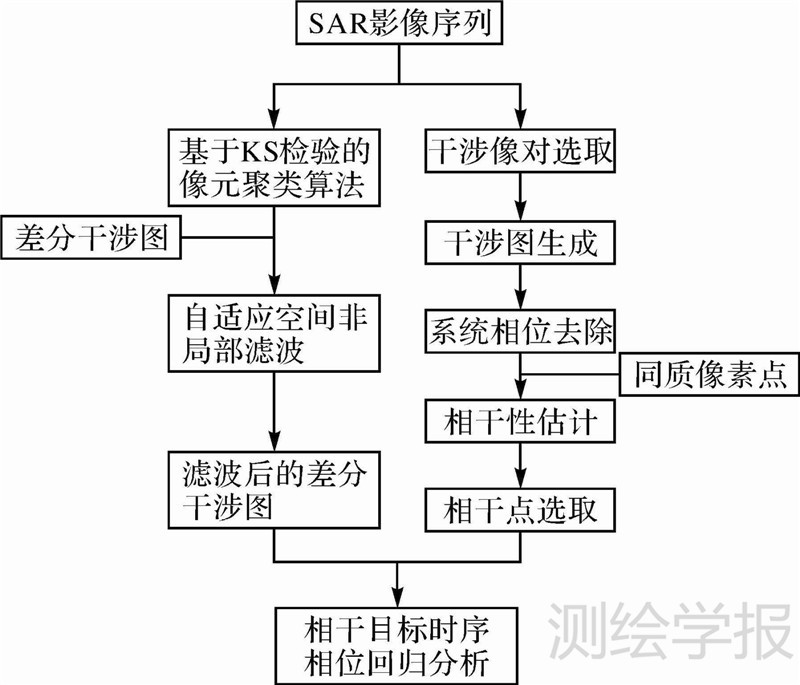
1 改进的相干目标法本文提出改进的相干目标法反演填海区域的地表下沉时序结果,其数据处理流程如图 1所示。时空同质滤波包括基于KS检验的同分布检验算法和自适应空间非局部滤波,可在保持影像空间分辨率的同时有效提高干涉图的质量;相干性的平稳估计则涉及基于KS检验的同分布检验算法、多尺度极大似然频率估计方法去除系统相位和相干性估计3部分内容,可获取空间分辨率和精度都较高的相干图,用于相干目标点的选取。
|
| 图 1 改进后的相干目标法流程图 Fig. 1 The flow chart of the modified version of CT method |
由于受到时间失相关和几何去相关等因素的影响,地表植被区的干涉图随着时间间隔增加,干涉相位噪声也逐渐增大[23]。在相干目标法中,对干涉图进行滤波处理可增加干涉图的相干性,从而可以提取更多的点目标。考虑到窗口内同质像素点的干涉相位所受噪声影响程度相近的特点,本文采用基于同质像素点的空间非局部滤波方法,即首先利用时间序列SAR强度影像进行窗口中心像素点与周围像素点的KS检验,确定与中心像素点后向散射特性一致的同质像素点;然后再利用自适应空间非局部滤波算法对同质点进行加权平均处理,以获取中心像素点的相位值,其中滤波强度由局部相位标准差决定。
1.1.1 基于KS检验的同分布检验算法估计窗口中像素的散射特性发生变化会影响干涉相位的平稳性,影响干涉图滤波的效果。因此,在干涉图滤波之前对窗口内像元点的散射特性进行判断,并选取后向散射特性一致的样本点是非常关键的步骤。在雷达遥感影像中,同地物类型的雷达散射分布相近,而不同地物类型的后向散射特性存在差异,其反映在SAR影像中表现为不同的纹理特征[10]。因此,本文利用雷达回波后向散射的强度序列作为判断同质像素点的依据。
假设所有SAR影像已配准到同一坐标系下。对于SAR影像中任意一点P的后向散射系数序列可表示为
式中,研究两个数据集是否符合相同的概率分布函数可应用KS检验的方法,该检验基于两个数据集分布函数(CDF)差值绝对值的最大值。假设像素点P1和P2的累计分布函数分别表示为FP1(x)和FP1(x)。两个累计分布函数的最大差值D可表示为[19]
D的概率分布函数可用经验KS分布近似,可表示为
KS检验通过度量差值D超过临界值t的概率来确定像素点P1和P2是否符合同一分布。
1.1.2 自适应空间非局部滤波空间非局部滤波可在噪声去除和细节保持方面取得较好的效果,同时保证了仅有同质点参与滤波计算。其核心思想是仅利用同质像素点的相位值进行加权平均来计算中心像素点的相位值[24]。每个像素点所占的权重,可通过计算以该点为中心的图像子块与中心像素点的图像子块的相关性来定义。空间非局部滤波的离散形式可表示为[24]
式中,另外,本文利用估计窗口的相位标准差来自适应调整滤波参数,从而实现低信噪比区域强滤波、高信噪比区域弱滤波的效果,以有效保持影像的细节信息。相位标准差反映了窗口中干涉相位的信噪比情况,干涉相位的信噪比越低,相位标准差就越大。相位标准差可利用窗口中同质像素点的干涉相位求取。另外,文中对相位方差进行了按比例放大,以达到更好的滤波效果,该比例系数通过经验获取。构建的滤波参数模型可表示为
式中,δ为局部相位标准差;k为比例系数。通过计算估计窗口中同质像素点的相位标准差δ即可获得该窗口内的滤波参数h。 1.2 相干性估计
相干目标点的选取是相干目标法中一个至关重要的步骤,通常是利用相干系数图来选取稳定的目标点。两幅影像之间的相干性可用相干系数衡量,两个随机平稳序列
为了保证上式的平稳性,需要有足够的样本点参与计算,然而窗口太大会引入异质像素和系统相位,导致随机序列
另外,DEM误差、大气效应、地表形变等系统相位的存在,同样会引起信号出现非平稳性,需要将其从差分干涉图中去除。差分干涉图可以用正弦函数波模型表示[18]
式中,φs和vs分别为像素点s的系统相位和随机噪声。一般用户通常应用条纹频率估计算法来补偿系统相位的影响,其中极大似然条纹频率估计算法较为简单实用,文献[17]首次将其应用到相干性估计中并取得了较好的效果。具体做法是选取一定大小的窗口对差分干涉图进行二维傅里叶变换,根据极大似然原则选取频谱峰值对应的频率为局部条纹频率,经过傅里叶逆变换即可获得该频率对应的相位趋势面,然后将该相位从差分干涉图中去除。窗口内部的条纹特征与窗口大小有关。窗口越大,系统相位呈现非线性的概率越大,导致窗口内非线性相位不能通过傅里叶变换去除。因此,在傅里叶变换过程中需要窗口足够小以有效地去除非线性的系统相位。但是,较小的估计窗口易引起估计的系统相位包含大量的相位噪声,尤其在失相干严重的情况下。本文采用估计多尺度的极大似然条纹频率的方法[22],即通过选取不同尺度的估计窗口来获取系统相位。该方法能够有效去除DEM误差、地表形变、大气相位等影响,保证估计窗口内相位的平稳性。首先选取较大的窗口进行极大似然条纹频率估计,并将获取的相位趋势面与差分干涉图进行共轭相乘处理以将其去除,然后再依次选用较小的窗口对干涉图的残余相位进行上述处理,以有效地分离系统相位。最后基于同质像素点来计算窗口中心点的相干系数。 2 试验结果与分析 2.1 试验区概况本文共收集了20景方位向和距离向分辨率为3 m的TerraSAR-X影像,拍摄时间为2008年10月至2009年12月,雷达入射波长为3.2 cm,入射角为37.3°,为升轨影像。试验区为香港东部的填海区域,范围约为3 km×3 km。图 2为利用20景SAR影像进行非相干叠加获取的平均强度影像。

|
| 图 2 TerraSAR-X平均强度影像 Fig. 2 The average intensity image of TerraSAR-X |
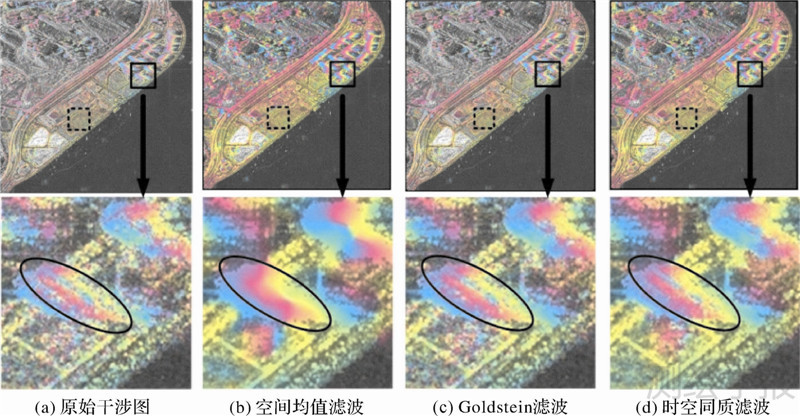
为了评价该滤波方法的滤波性能,选取2009年12月6日和2009年12月17日两景影像进行干涉分析,垂直基线长为103 m。首先基于20景SAR强度影像序列进行KS检验,选取窗口内后向散射特性近似的同质像素点,其中所选用的窗口大小为15×15。然后利用自适应空间非局部滤波方法对干涉图进行滤波处理,局部窗口大小为5×5,比例系数为20。
图 3(见文末)中第1行分别为原始差分干涉图 3(a)、空间均值滤波3(b)、Goldstein滤波3(c)和本文滤波3(d)的结果,其中空间均值滤波和Goldstein滤波所选取的窗口大小分别为15×15和16×16。为了比较3种滤波方法在干涉图细节保持方面的效果,本文将黑色实线所示的特征区域进行了局部放大,如图 3中第2行所示。另外,文中选取图 3中第1行黑色虚线所示区域作为试验区并计算其相位标准差σφ,以客观地衡量3种滤波方法的在相位噪声去除方面的效果,计算结果如表 1所示。由于该区域地势较为平坦且成像时间间隔较短(11 d),其地形相位和形变相位均可忽略不计。比较图 3中滤波后干涉图和表 1中干涉图的相位标准差可知,原始干涉图由于受到各种失相干因素的影响,相位噪声较大,黑色虚线所示区域的相位标准差达到1.37。干涉图经过空间均值滤波后,相位噪声减弱,但是丢失了干涉图的相位细节信息,图中椭圆形实线区域的结构信息损失严重。经Goldstein滤波后,干涉图的相位噪声得到了抑制,细节结构特征同时得到保持。相比前两种滤波方法,本文方法能够更加有效地削弱干涉图的相位噪声,而且该方法的细节保持能力更强,滤波后的结果与原始干涉图更为吻合,这说明时空同质滤波方法在抑制相位噪声和细节特征保持方面都可以取得很好的效果。
|
| 图 3 干涉图 Fig. 3 Interferogram |
| 原始干涉图 | 空间均值滤波 | Goldstein滤波 | 本文方法 | |
| σφ | 1.37 | 0.54 | 1.21 | 0.49 |
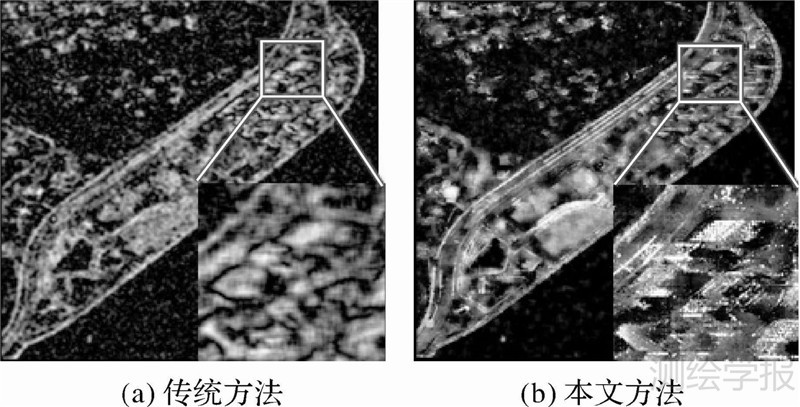
本文应用估计多尺度的极大似然条纹频率方法来去除干涉图中DEM误差、地表形变、大气相位等系统相位。为了去除差分干涉图中多尺度的系统相位,根据经验共选取3种尺度的估计窗口,分别为50×50、30×30、10×10,并依次将利用该窗口进行极大似然条纹频率估计获取的相位趋势面从差分干涉图中去除。之后基于KS检验所获取的同质目标点对已去除系统相位的差分干涉图进行相干性估计。
图 4分别为利用传统方法和本文方法所估计的相干图,其中相干性估计所采用的窗口大小为7×7。为了更好地显示两种方法估计的相干图的差别,文中对白色实框所示区域进行了局部而放大。比较可知,采用传统的固定窗口方法由于引入了异质像素,其获取的相干图细节保持能力很差;而本文方法可以获取更可靠、空间特征更鲜明的相干图。另外,本文方法在相干性估计之前去除了地表形变、地形相位、大气效应等系统相位,保证了窗口中像素点的相位平稳性,提高了相干性估计值。
|
| 图 4 相干系数图 Fig. 4 The coherence map |
本文以垂直基线250 m、时间间隔360 d为限制条件,基于20幅SAR影像共选取了171对干涉对。之后,利用本文所述的时空同质滤波和相干性估计方法对干涉图进行处理,并利用相干图选取平均相干系数大于0.4的点作为高相干候选点。首先选取34幅空间基线较长、时间间隔较短的干涉对初步反演DEM误差,并将其模拟相位从差分干涉图中减去。随后将处理的差分干涉图进行空间低通滤波、空间解缠及SVD分解,以获取差分干涉图的大气相位。最终利用相干性较高的104幅干涉图反演获得线性形变速率和DEM误差。所选取的104幅干涉图的时空基线情况如图 5所示,点号代表SAR影像,实线代表两幅影像形成干涉对,横轴为SAR影像成像时间,纵轴为相对于主影像20090511的垂直基线。
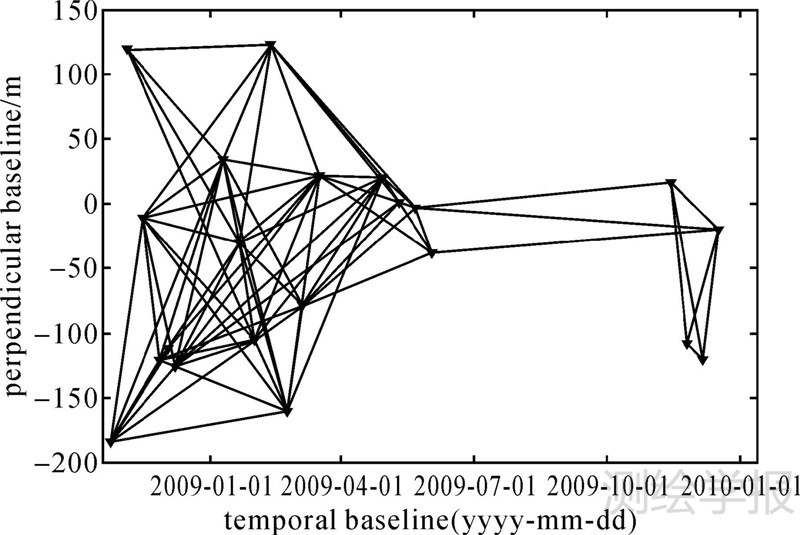
|
| 图 5 所用干涉对的时空基线分布 Fig. 5 Temporal-spatial baselines of the used interferograms |
图 6分别为利用传统相干目标法和本文方法获取的监测期间内LOS方向的线性形变速率,底图为平均强度影像,参考点位于试验区左上角,负值代表下降。选择时间相关系数0.8为阈值,传统相干目标法最终获取了29 868个测量点,而改进后的相干目标法则获取了262 799个测量点,约为传统相干目标法测量点数量的9倍。增加的测量点主要集中于试验区中后向反射强度较低的裸土、沥青路面等同分布目标区域。这主要是因为这些目标点易受基线失相关和时间失相关的影响,其干涉图相干性低于设定的阈值而被舍弃。本文方法首先基于同质目标点对干涉图进行空间非局部滤波,有效地降低了干涉图的相位噪声。同时,基于同质像素点对已去除系统相位的干涉图进行相干性估计,提高了干涉图相干性的估值,可以获取更多的相干目标候选点,最后对相干目标候选点的相位进行时序分析获得了大量的有效监测点。图 6右下角为红色实线所示试验区的局部放大图,基本为裸土区域,易发生失相关现象,这使得传统相干目标法很难在该区域获得有效的结果,而本文方法可有效降低该区域的干涉相位噪声,从而获取更多的有效监测点。

|
| 图 6 LOS方向线性形变速率 Fig. 6 Linear deformation velocity in LOS direction |
从差分干涉图中减去估计的大气相位、模型相位,并对残差相位进行空间低通滤波处理以削弱相位噪声的影响。随后对滤波后的残差相位进行空间相位解缠及SVD分解获取非线性形变时序相位。图 7为相干目标点A在2008年10月至2009年12月期间的形变量时序变化。图 7(a)为利用传统相干目标法获取的时序结果,图 7(b)为利用改进后的相干目标法获取的结果,纵轴为SAR影像获取时间,起始时间为2008年10月,横轴为形变量。黑色十字为SAR影像拍摄时间对应的累计形变量,红色实线代表估计的线性形变速率。比较可知,改进后的相干目标法获取的形变序列具有更高的信噪比,这主要是因为时空同质滤波技术能够有效地减弱干涉图的相位噪声。除此之外,本文方法可以获取更多的目标点,从而更有效地估计和去除大气相位的影响。
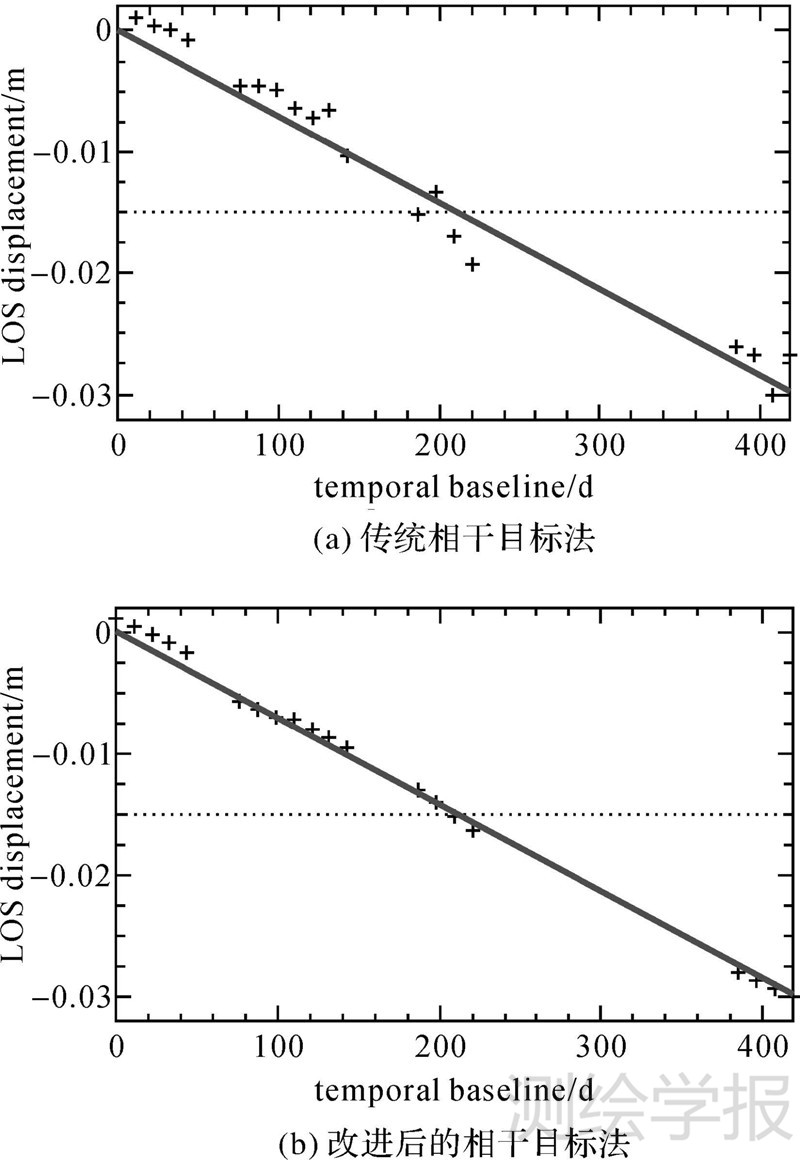
|
| 图 7 相干目标A的形变时序 Fig. 7 The deformation series of coherent point A |
本文提出了一种改进的相干目标算法,将时空同质滤波和除去信号非平稳性的相干性估计应用于小基线集数据处理流程中。时空同质滤波有效地减弱了干涉图的相位噪声,保持了干涉图的细节特征;相干性的平稳估计实现了对干涉图相干性的可靠估计,同时避免了影像空间分辨率的损失。试验结果表明改进后的相干目标法能够充分获取目标点的相位信息,极大地增加了监测点的数量,提高了InSAR监测结果的可靠性和范围,同时有效地降低了干涉图的相位噪声,增加了时序形变结果的信噪比。
| [1] | FERRETTI A, PRATI C, ROCCA F. Nonlinear Subsidence Rate Estimation Using Permanent Scatterers in Differential SAR Interferometry[J]. IEEE Transactions on Geosciences and Remote Sensing, 2000, 38(5): 2202-2212. |
| [2] | FERRETTI A, PRATI C, ROCCA F. Permanent Scatterers in SAR Interferometry[J].IEEE Transactions on Geoscience and Remote Sensing, 2001, 39(1): 8-20. |
| [3] | MORA O, MALLORQUI J J, BROQUETAS A. Linear and Nonlinear Terrain Deformation Maps from a Reduced Set of Interferometric SAR Images[J]. IEEE Transactions on Geoscience and Remote Sensing, 2003, 41(10): 2243-2252. |
| [4] | HOOPER A. A Multi-temporal InSAR Method Incorporating both Persistent Scatterer and Small Baseline Approaches[J]. Geophysical Research Letters, 2008, 35(16): L16302. |
| [5] | PERISSIN D, WANG Teng. Repeat-pass SAR Interferometry with Partially Coherent Targets[J]. IEEE Transactions on Geoscience and Remote Sensing, 2012, 50(1): 271-280. |
| [6] | 张永红, 张继贤, 龚文瑜, 等. 基于SAR干涉点目标分析技术的城市地表形变监测[J]. 测绘学报, 2009, 38(6): 482-487, 493. ZHANG Yonghong,ZHANG Jixian, GONG Wenyu, et al. Monitoring Urban Subsidence Based on SAR Interferometric Point Target Analysis[J]. Acta Geodaetica et Cartographica Sinica, 2009, 38(6): 482-487, 493. |
| [7] | GOLDSTEIN R M, WERNER C L. Radar Interferogram Filtering for Geophysical Application[J]. Geophysical Research Letters, 1998, 25(21), 4035-4038. |
| [8] | DELEDALLE C A, DENIS L, TUPIN F. Iterative Weighted Maximum Likelihood Denoising with Probabilistic Patch-based Weights[J]. IEEE Transactions on Image Processing, 2009, 18(12): 2661-2672. |
| [9] | DELEDALLE C A, DENIS L, TUPIN F. NL-InSAR: Nonlocal Interferogram Estimation[J]. IEEE Transactions on Geoscience and Remote Sensing,2011, 49(4): 1441-1452. |
| [10] | FERRETTI A, FUMAGALLI A, NOVALI F, et al. A New Algorithm for Processing Interferometric Data-stacks: SqueeSAR[J]. IEEE Transactions on Geoscience and Remote Sensing, 2011, 49(9): 3460-3470. |
| [11] | GOELK, ADAMN. An Advanced Algorithm for Deformation Estimation in Non-urban Areas[J]. ISPRS Journal of Photogrammetry and Remote Sensing,2012, 73: 100-110. |
| [12] | 夏耶. 干涉雷达滑坡监测关键技术探讨[C]//中国地球物理学会第29届学术研讨会论文集.昆明: [s.n.], 2013. XIA Y. Study on InSAR Technology Key Methodology for Landslide Monitoring[C]//Proceedings of the 29th Symposium of Chinese Geophysical Society. Kunming:[s.n.],2013. |
| [13] | LI Jinwei, LI Zhenfang, BAO Zheng, et al. Noise Filtering of High-resolution Interferograms over Vegetation and Urban Areas with a Refined Nonlocal Filter[J]. IEEE Geoscience and Remote Sensing Letters, 2015, 12(1): 77-81. |
| [14] | TOUZI R, LOPES A, BRUNIQUEL J, et al. Coherence Estimation for SAR Imagery[J]. IEEE Transactions on Geoscience and Remote Sensing, 1999, 37(1): 135-149. |
| [15] | GUARNIERI A M, PRATI C. SAR Interferometry: A “Quick and Dirty” Coherence Estimator for Data Browsing[J]. IEEE Transactions on Geoscience and Remote Sensing,1997, 35(3): 660-669. |
| [16] | LEE J S, CLOUDE S R,PAPATHANASSIOU K P,et al. Speckle Filtering and Coherence Estimation of Polarimetric SAR Interferometry Data for Forest Applications[J]. IEEE Transactions on Geoscience and Remote Sensing, 2003, 41(10): 2254-2263. |
| [17] | ZEBKER H A,CHEN K.Accurate Estimation of Correlation in InSAR Observations[J]. IEEE Geoscience and Remote Sensing Letters, 2005, 2(2): 124-127. |
| [18] | 蒋弥, 丁晓利, 李志伟, 等.基于时间序列的InSAR相干性量级估计[J]. 地球物理学报, 2013, 56(3): 799-811. JIANG Mi,DING Xiaoli,LI Zhiwei, et al. InSAR Coherence Magnitude Estimation Based on Data Stack[J]. Chinese Journal of Geophysics, 2013, 56(3): 799-811. |
| [19] | STEPHENS M A. Use of the Kolmogorov-Smirnov, Cramér-Von Mises and Related Statistics without Extensive Tables[J]. Journal of the Royal Statistical Society, Series B (Methodological), 1970, 32(1): 115-122. |
| [20] | SCHMITT M, SCHONBERGER J L, STILLA U. Adaptive Covariance Matrix Estimation for Multi-baseline InSAR Data Stacks[J]. IEEE Transactions on Geoscience and Remote Sensing, 2014, 52(11): 6807-6817. |
| [21] | JIANG Mi, DING Xiaoli, HANSSEN R F, et al. Fast Statistically Homogeneous Pixel Selection for Covariance Matrix Estimation for Multitemporal InSAR[J]. IEEE Transactions on Geoscience and Remote Sensing, 2015, 53(3): 1213-1224. |
| [22] | WANG Yuanyuan, ZHU Xiaoxiang, BAMLER R. Retrieval of Phase History Parameters from Distributed Scatterers in Urban Areas Using Very High Resolution SAR Data[J]. ISPRS Journal of Photogrammetry and Remote Sensing, 2012, 73: 89-99. |
| [23] | ZEBKER H A, VILLASENOR J. Decorrelation in Interferometric Radar Echoes[J]. IEEE Transactions on Geoscience and Remote Sensing, 1992, 30(5): 950-959. |
| [24] | BUADES A, COLL B, MOREL J M. A Non-local Algorithm for Image Denoising[C]//Proceedings of IEEE Computer Society Conference on Computer Vision and Pattern Recognition. San Diego, CA:IEEE, 2005, 2: 60-65. |