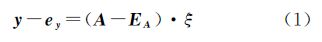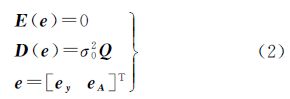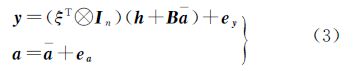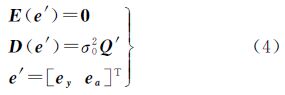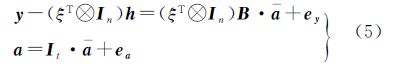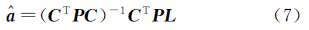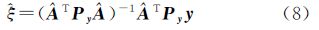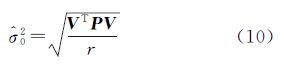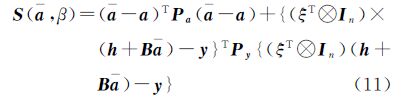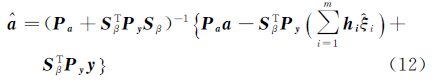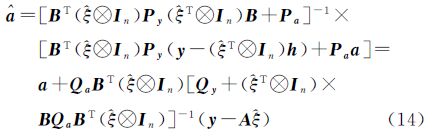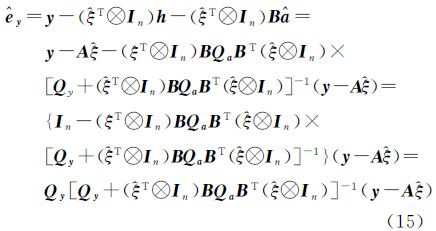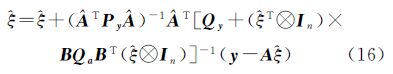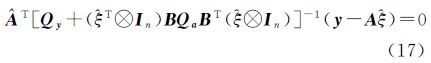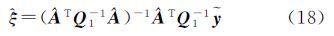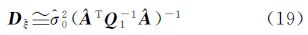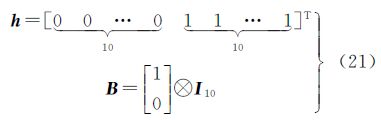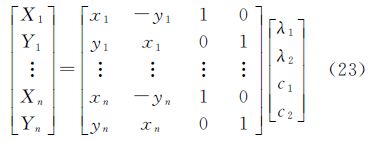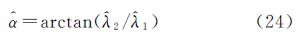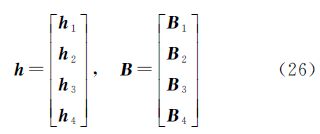2. 流域生态与地理环境监测国家测绘地理信息局重点实验室, 江西 南昌 330013;
3. 江西省数字国土重点实验室, 江西 南昌 330013
2. Key Laboratory of Watershed Ecology and Geographical Environment Monitoring of NASG, Nanchang 330013, China ;
3. Jiangxi Province Key Lab for Digital Land, Nanchang 330013, China
总体最小二乘方法作为errors-in-variables(EIV)模型的严密估计方法,是近30年来发展起来的一种能同时顾及观测向量误差和系数矩阵误差的数学方法[1]。最早可追溯到文献[2]研究的单变量直线拟合问题,之后文献[3, 4, 5],均对其进行了相关研究;文献[6]提出了著名的奇异值分解(singular value decomposition,SVD)算法,随着这一稳健计算方法的引入和应用领域需求的增大,文献[3, 4, 5],[7, 8]先后提出了加权总体最小二乘算法,丰富了总体最小二乘的算法理论。在EIV模型下,针对不同的平差问题,函数模型中系数矩阵的结构也不同,如直线拟合[7, 12, 15, 19]、坐标转换[10, 12, 19]及应变参数反演[17, 18];可见系数矩阵不仅只存在随机元素,而且存在随机元素和非随机元素并存或呈现结构性特征等一般情况[26],其通常的解法是构造特定的权阵,使系数矩阵中常数元素位置的改正数为零,且相同随机元素的改正数相等;因而以上加权总体最小二乘算法均需求解模型参数、观测向量的改正数以及求解系数矩阵中所有元素的改正量,实属含大量带估量的非线性估计问题[20]。文献[21]研究了基于部分变量含误差(partial EIV)模型的总体最小二乘算法,将各种形式的系数矩阵纳入到统一的模型形式下求解[26]。该算法对待估量采用分离的估计方法,将系数矩阵中的不同随机元素一并纳入参数求解,因此partial EIV模型系数矩阵中的待改正量个数要小于或等于对应EIV模型中待改正量的个数,对于海量数据处理,partial EIV模型的总体最小二乘算法能够大大减小计算量[20],试验发现,算法在收敛速度及解算公式的复杂程度方面还有待改善;文献[22]在文献[21]算法的基础上给出了系数矩阵中求解不同随机元素的另一表达形式,一定条件下减小了算法的计算量,同样其解算公式相对复杂需进一步简化。
本文在partial EIV模型的基础上,通过对其部分元素移项,推导了求解partial EIV模型的一种方法,经过适当变换提高了该解法的收敛速度。通过线性回归和平面坐标转换算例,对比分析了本文两种算法与JAZAERI算法[19]、XU算法[21]和最小二乘法;模拟直线,进一步证实本文算法与JAZAERI算法、XU算法能取得相同的结果,表明了本文算法是有效并且可行的。
1 Partial EIV模型的新解法 1.1 平差模型与准则 随机模型 式中,y表示n×1观测向量;ey是y中所包含的n×1随机误差向量;A表示n×m系数矩阵;EA表示系数矩阵A所包含的n×m随机误差矩阵;eA=vec(EA),即eA是将EA列向量化后的nm×1向量;ξ是m×1待估参数向量;而σ0表示单位权中误差;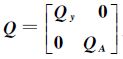 为由观测向量和系数矩阵构成的协因数阵,其中0表示零矩阵。
为由观测向量和系数矩阵构成的协因数阵,其中0表示零矩阵。
然而在实际应用中,系数矩阵A中元素并非全为常数,而是常存在非随机的固定元素或呈现结构性特征等情况[26]。针对上述问题,文献[21]对系数矩阵A作适当处理,提取了A中的不同随机元素,从而将EIV模型改写为partial EIV模型形[21]:
函数模型
随机模型 式中,a是系数矩阵A中不同随机元素组成的t×1列向量,其真值$\bar a$用表示;ea表示a的随机误差;h是由vec(A)中的非随机元素和零构成的nm×1列向量;B是与A中随机元素有关的nm×t固定矩阵;In表示n×n单位矩阵;且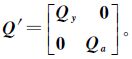
以式(3)为基础,将第一个等式展开并移项
令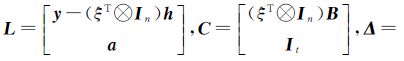
.jpg) ,其中Py=Qy-1、Pa=Qa-1;则式(5)等同于
式中,C为新构建的系数矩阵,并把$\bar a$作为参数平差。
,其中Py=Qy-1、Pa=Qa-1;则式(5)等同于
式中,C为新构建的系数矩阵,并把$\bar a$作为参数平差。
令Δ的估值为V,并在准则VTPV=min下按间接平差原理解算平差参数$\bar a$的估值$\hat a$
进而由$\hat a$重新构造成新系数矩阵$\hat A$,再次按间接平差原理求解模型参数相应的误差方程为
可见由式(6)构成的平差模型就将总体最小二乘平差问题转化为了最小二乘平差问题,可直接按间接平差原理进行平差计算。但与间接平差模型不同,此模型考虑了系数矩阵A中随机元素的影响,且顾及了系数矩阵中的常数项和随机元素具有重复性的问题,是一种新的平差函数模型。新模型中观测数据的总数为n+t,其中t为系数矩阵中不同随机元素的个数;而必要观测数为m个待估参数ξ和t个系数矩阵的待估元素$\bar a$之和,共m+t个。因此,自由度的大小为r=(n+t)-(m+t)=n-m[16],进而得到相应的验后单位权中误差为
1.2 Partial EIV模型的新解法本文算法通过对partial EIV模型的部分元素移项,将总体最小二乘的数据处理问题统一到了最小二乘理论,在模型(6)的求解方面,通过两次运用间接平差原理分别求解平差参数与系数矩阵中的随机元素,经过迭代计算得到合理的参数平差解;数据准备包括系数矩阵A、观测向量y、权阵Py和Pa以及收敛条件ε和δ;现将求解的迭代过程(本文算法1)设计如下:
(1) 初始值:假设A无误差,采用最小二乘法求得模型参数的初值$\hat \xi $(0),并令$\hat a$(0)=a。
(2) 由$\hat \xi $(i)、$\hat a$(i)构造新的观测向量和系数矩阵
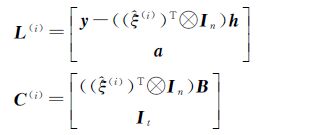
(3) 将步骤(2)求得的L(i)、C(i)代入公式
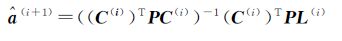
(4) 进而将步骤(3)求得的$\hat a$(i+1)重新构造成改正后的系数矩阵$\hat A$(i+1)。
(5) 按公式$\hat \xi $(i+1)=(($\hat A$(i+1))TPy$\hat A$(i+1))-1($\hat A$(i+1))TPyy平差获取新的参数估值$\hat \xi $(i+1)。
(6)重复步骤(2)至(5),直到满足║$\hat \xi $(i+1)-$\hat \xi $(i)║<ε且║$\hat a$(i+1)-$\hat a$(i)║<δ时迭代终止。
(7) 按式(9)、式(10)分别计算误差向量和验后单位权中误差。
1.3 Partial EIV模型新算法的等价性证明及改进 1.3.1 与XU算法的等价性文献[21]通过考虑partial EIV函数模型式(3)及其对应的随机模型式(4),并构建目标函数<
由目标函数式(11)分别对$\bar a$和ξ求偏导并令其为零,可得XU算法的解算结果为[21] 式中,Sβ=$\sum\limits_{i = 1}^m {{B_i}{\xi _i}} $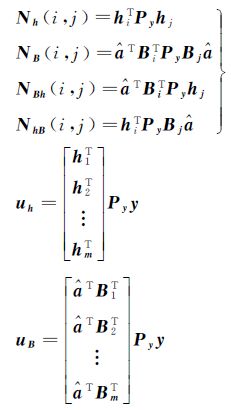
可见XU算法中解算系数矩阵中不同随机元素$\bar a$和模型参数ξ的式(12)和式(13)本质上与本文中式(7)、式(8)是等价的,仅为表现形式不同。然而,按照本文求解思路大大简化了文献[21]的推导,解算公式上本文算法1也更为简洁、紧凑。
1.3.2 与JAZAERI算法的等价性从式(7)出发,将C和L的具体表达式代入式(7),并结合矩阵反演公式(D+ACB)-1=D-1-D-1A(C-1+BD-1A)-1BD-1有[19, 22]
由式(14)并结合式(3),可得$\hat e$y为 由式(15),将y=($\hat \xi $T⊗In)(h+B$\hat a$)+$\hat e$y=$\hat A$$\hat \xi $+$\hat e$y代入式(8),得 顾及($\hat A$TPy$\hat A$)-1正定,则式(16)等价于将式(17)移项,并令Q1=Qy+($\hat \xi $T⊗In)BQaBT(⊗In),经适当处理可得重新构造下参数的具有最小二乘形式的解
式中,$\bar y$=y-$\hat E$A$\hat \xi $。顾及QA=BQaBT,式(18)也与JAZAERI算法求解模型参数的公式等价。
1.3.3 Partial EIV模型新算法改进(本文算法2)数值试验表明,本文算法1求解模型参数估值的收敛速度较慢,现结合1.3.2 中推导,由式(18)可直接求得模型参数的近似精度评定公式[12, 19]
数据准备包括系数矩阵A、观测向量y、权阵Py和Pa以及收敛条件ε和δ,可将本文算法2的具体解算步骤描述如下:
(1) 初始值:假设A无误差,采用最小二乘法求得模型参数的初值$\hat \xi $(0),并令$\hat a$(0)=a。
(2) 由$\hat \xi $(i)、$\hat a$(i)构造新的观测向量和系数矩阵
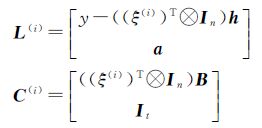
(3) 将步骤(2)求得的L(i)、C(i)代入公式
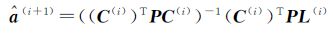
(4) 将$\hat a$(i+1)重新构造成改正后的系数矩阵$\hat A$(i+1),得$\hat E$(i+1)A=A-$\hat A$(i+1)。
(5) 计算:Q(i+1)1=Qy+(($\hat \xi $(i))T⊗In)BQaBT($\hat \xi $(i)⊗In),$\bar y$(i+1)=y-$\hat E$A(i+1)$\hat \xi $(i)。
(6) 由$\hat \xi $(i + 1)=($\hat A$(i + 1)T(Q(i + 1)1)-1$\hat A$(i + 1))-1$\hat A$(i + 1)T(Q(i + 1)1)-1$\bar y$(i + 1)解算新的参数估值$\hat \xi $(i+1)。
(7) 重复步骤(2)至步骤(6),直到满足║$\hat \xi $(i+1)-$\hat \xi $(i)║<ε且║$\hat a$(i+1)-$\hat a$║(i)<δ时迭代终止,进而结合式(10)、式(19)评定模型参数的精度。
2 算例与分析 2.1 算例1为了验证本文算法的效果,引用文献[24]中的试验数据,坐标观测值(xi,yi)及相应的权(pxi,pyi)列于表 1。
直线拟合的EIV模型为
为满足本算法的需求,还需给出向量h和固定矩阵B。对于直线拟合问题,h和B的形式如下
将表 1中的数据分别用本文两种算法、JAZAERI算法、XU算法和最小二乘法进行求解,参数估值结果及迭代次数列于表 2,相应的参数精度估计值及验后单位权中误差见表 3,其中本文两种算法与XU算法的收敛条件分别为ε=10-10和δ=10-12,JAZAERI算法的收敛条件为ε=10-10。
| 结 果 | 本文算法1 | 本文算法2 | JAZAERI算法 | XU算法 | 最小二乘法 |
| $\hat \xi $1 | 5.479 910 224 0 | 5.479 910 224 0 | 5.479 910 224 0 | 5.479 910 224 0 | 6.100 109 316 7 |
| $\hat \xi $2 | -0.480 533 407 4 | -0.480 533 407 4 | -0.480 533 407 4 | -0.480 533 407 4 | -0.610 812 956 6 |
| 迭代次数 | 584 | 7 | 7 | 585 |
| 方案 | $\hat \sigma $ξ12 | $\hat \sigma $ξ22 | $\hat \sigma $0 |
| 本文算法1 | — | — | 1.217 905 640 5 |
| 本文算法2 | 0.129 058 064 | 0.004 987 222 5 | 1.217 905 640 5 |
| JAZAERI算法 | 0.129 058 064 | 0.004 987 222 5 | 1.217 905 640 5 |
| XU算法 | 0.129 058 064 | 0.004 987 222 5 | 1.217 905 640 5 |
平面坐标转换的模型为[19]
式中,s为尺度因子;α为旋转角度参数;c1、c2为纵、横坐标轴上的平移参数;(xi,yi)、(Xi,Yi)分别为原始坐标系和目标坐标系坐标。将式(22)展开,并令λ1=scos α、λ2=ssin α,则式(22)可转化为如下形式
对式(23)采用相应的方法解算可求得模型参数的估值$\hat \lambda $1、$\hat \lambda $2、$\hat c$1和$\hat c$2,进而旋转角度参数和尺度因子可由以下两式求得
对于平面坐标转换问题,向量h和固定矩阵B的形式为 式中,h1、h2为10×1的0向量,h3、h4为10×1的1向量;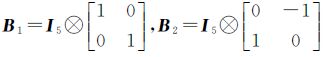 ,
,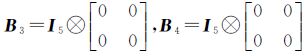 。
。
为验证算法的正确性与可行性,采用与文献[19]中算例2相同的数据进行试验,如表 4,原始坐标和目标坐标的权矩阵分别为:

根据表 4中数据,采用试验1中所述的4种算法求解,相应的估计结果列于表 5、表 6。
| 结 果 | 本文算法1 | 本文算法2 | JAZAERI算法 | XU算法 | 最小二乘法 |
| $\hat \lambda $1 | 0.999 884 750 1 | 0.999 884 750 1 | 0.999 884 750 1 | 0.999 884 750 1 | 0.999 871 705 3 |
| $\hat \lambda $2 | -0.000 066 932 6 | -0.000 066 932 6 | -0.000 066 932 6 | -0.000 066 932 6 | -0.000 072 703 9 |
| $\hat c$1/m | 29.770 065 573 0 | 29.770 065 573 0 | 29.770 065 573 0 | 29.770 065 573 0 | 29.731 573 999 1 |
| $\hat c$2/m | 19.717 128 429 7 | 19.717 128 429 7 | 19.717 128 429 7 | 19.717 128 429 7 | 19.691 680 967 4 |
| 迭代次数 | 43 | 3 | 3 | 43 | — |
| 方 案 | $\hat \sigma $λ12 | $\hat \sigma $λ22 | $\hat \sigma $c12/m2 | $\hat \sigma $2c2/m2 | $\hat \sigma $0/m |
| 本文算法1 | — | — | — | — | 0.389 331 039 2 |
| 本文算法2 | 0.000 000 007 0 | 0.000 000 005 5 | 0.005 440 646 1 | 0.006 942 701 9 | 0.389 331 039 2 |
| JAZAERI算法 | 0.000 000 007 0 | 0.000 000 005 5 | 0.005 440 646 1 | 0.006 942 701 9 | 0.389 331 039 2 |
| XU算法 | 0.000 000 007 0 | 0.000 000 005 5 | 0.005 440 646 1 | 0.006 942 701 9 | 0.389 331 039 2 |
设直线模型为y=kx+d,其中k、d分别为直线的斜率和截距,真值为k=2、d=1.5,将自变量从2至9.2每隔0.8模拟一个自变量x坐标真值,并计算因变量y坐标的值,相应的权阵如下
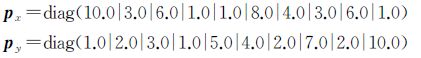
对真值坐标x、y分别模拟一次均值为0,方差为σ02px-1、σ02py-1的随机误差,其中σ0=1.0,分别采用本文两种算法与JAZAERI算法和XU算法对模拟后的数据进行平差计算,估计得到的结果见表 7。
| 结 果 | 本文算法1 | 本文算法2 | JAZAERI算法 | XU算法 | 真 值 |
| $\hat k$ | 1.986 614 450 1 | 1.986 614 450 1 | 1.986 614 450 1 | 1.986 614 450 1 | 2.0 |
| $\hat d$/m | 1.502 062 534 9 | 1.502 062 534 9 | 1.502 062 534 9 | 1.502 062 534 9 | 1.5 |
| $\hat \sigma $k2 | — | 0.025 787 736 7 | 0.025 787 736 7 | 0.025 787 736 7 | — |
| $\hat \sigma $d2/m2 | — | 0.926 630 589 2 | 0.926 630 589 2 | 0.926 630 589 2 | — |
| $\hat \sigma $0/m | 0.904 584 507 7 | 0.904 584 507 7 | 0.904 584 507 7 | 0.904 584 507 7 | 1.0 |
| 迭代次数 | 218 | 7 | 7 | 218 | — |
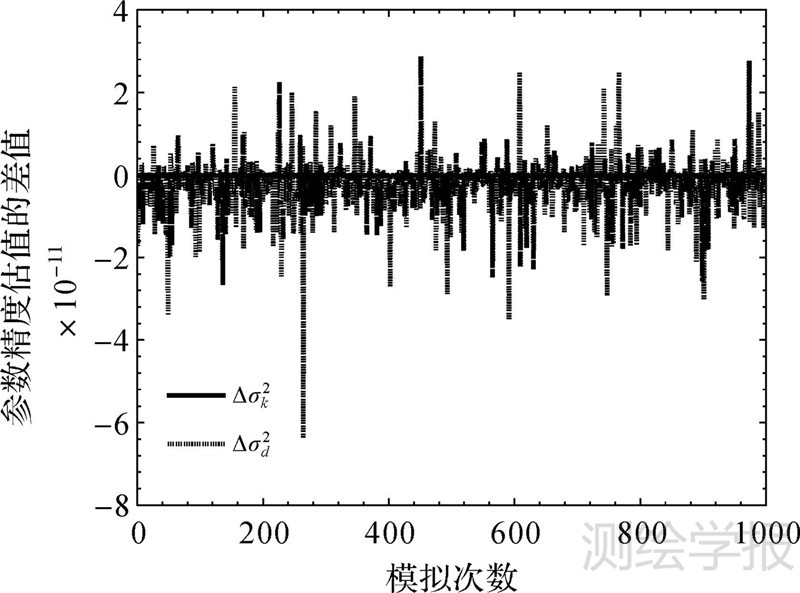
然而上述试验是在模拟一次随机试验下获得的,为进一步讨论,本文在σ0=1.0的条件下模拟试验1000次,并将各算法的平差结果均值列于表 8和表 9,为比较分析,绘制了本文算法2与JAZAERI算法的参数估值之差与精度估计值之差的差值图,如图 1、图 2所示。
| 结果 | 本文算法1 | 本文算法2 | JAZAERI算法 | XU算法 |
| $\hat k$ | 2.010 983 082 3 | 2.010 983 082 3 | 2.010 983 082 3 | 2.010 983 082 3 |
| $\hat k$/m | 1.422 612 006 4 | 1.422 612 006 4 | 1.422 612 006 4 | 1.422 612 006 4 |
| 平均迭代次数 | 228.117 | 8.424 | 8.424 | 228.151 |
| 方案 | $\hat \sigma $k2 | $\hat \sigma $d2/m2 | $\hat \sigma $0/m |
| 本文算法1 | — | — | 0.950 930 020 6 |
| 本文算法2 | 0.031 333 972 6 | 1.104 973 064 5 | 0.950 930 020 6 |
| JAZAERI算法 | 0.031 333 972 6 | 1.104 973 064 5 | 0.950 930 020 6 |
| XU算法 | 0.031 333 972 6 | 1.104 973 064 5 | 0.950 930 020 6 |
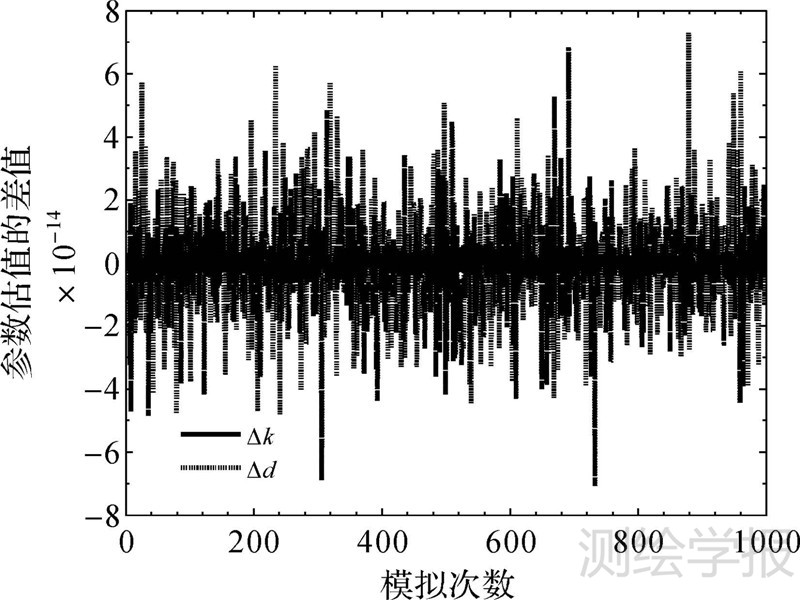
|
| 图 1 本文算法2与JAZAERI算法的参数估值之差 Fig. 1 Parameters difference between proposed method 2 and JAZAERI method |
|
| 图 2 本文算法2与JAZAERI算法的参数精度估值之差 Fig. 2 Accuracies difference between proposed method 2 and JAZAERI method |
(1) 从表 2至表 3和表 5至表 6的结果来看,本文两种算法与JAZAERI算法以及XU算法的参数解算结果和精度评定结果均相同(除本文算法1未给出参数的精度评定外),证明了本文算法是可行的,而最小二乘法的结果与前述3种算法相差较大;这是因为本文算法与JAZAERI算法和XU算法一样,既考虑了系数矩阵中随机元素的影响,又顾及了系数矩阵中包含常数项和随机元素具有重复性的问题,解算结果更为合理,而最小二乘法,由于其只考虑了观测向量中的随机元素,因此解算结果与前述3种方法相差较大。
(2) 在指定的收敛条件下,通过计算不同算法在算例1、2中的迭代次数(见表 2和表 5),可知在收敛速度方面,本文算法1与XU算法相当,而本文算法2与JAZAERI算法的收敛速度相同且较之本文算法1与XU算法,本文算法2的收敛速度有了较大的提高;这是因为本文算法1是从另一思路对partial EIV模型求解,且解算过程中先计算了不同随机元素估值再求解参数估值,这与XU算法的求解过程不同,因而两者的迭代次数相近,但从式(7)和式(8)可知本文算法1解算与公式的实质与XU算法是等价的;同理本文算法2与JAZAERI算法在求解参数估值上等价,因而能取得与JAZAERI算法相同的结果。
(3) 从表 7结果可知,在对真值数据模拟一次随机误差情况下,本文算法两种算法均能获得与JAZAERI算法及XU算法相同的结果;从1000次模拟试验的结果均值表 8和表 9中可知,不同算法参数估值的均值及参数精度估值的均值均相等,且迭代次数的均值结果也与算例1、2及模拟一次随机误差情况下所得的结果一致,进一步表明了本文所提算法的正确性;分析图 1、图 2不难发现,每模拟一次随机误差,本文算法2与JAZAERI算法的差值结果均小于10-11,抛开计算机数值计算所带来的较小扰动,说明了这两种算法的求解结果相同,通过模拟试验发现,本文算法1与XU算法、本文算法1与JAZAERI算法等情况下的差值结果也均小于10-11,表明各算法均能获得相同的平差结果,限于篇幅有限,并未将各差值图一一绘出。
3 结 论本文以partial EIV模型为基础,提出了一种求解总体最小二乘问题的新思路。将系数矩阵中的不同随机元素归为平差参数,直接运用间接平差原理求解,进而将总体最小二乘问题转化为最小二乘问题,因此计算简单易于编程,且新的模型可解算系数矩阵中存在非随机的固定元素或呈现结构性特征等问题;在观测向量与系数矩阵随机元素不相关条件下,算例结果表明partial EIV模型新解法与XU算法、JAZAERI算法等价,证明了本文算法的有效性与可行性;本文方法的估值结果是在观测数据的先验权阵准确已知的情况下得到的,在实际情况下先验信息很难准确给出,更为合理的平差结果还应当结合方差分量估计来求解。
| [1] | 王乐洋. 基于总体最小二乘的大地测量反演理论及应用研究[J]. 测绘学报, 2012, 41(4): 629. WANG Leyang. Research on Theory and Application of Total Least Squares in Geodetic Inversion[J]. Acta Geodaetica et Cartographica Sinica, 2012, 41(4): 629. |
| [2] | ADCOCK R J. Note on the Method of Least Squares[J]. The Analysis, 1877, 4: 183-184. |
| [3] | PEARSON K. On Line and Planes of Closest Fit to Systems of Points in Space[J]. Philosophical Magazine Series 6, 1901, 2(11): 559-572. |
| [4] | MADANSKY A. The Fitting of Straight Lines When Both Variables are Subject to Error[J]. Journal of the American Statistical Association, 1959, 54(285): 173-205. |
| [5] | YORK D. Least-Squares Fitting of a Straight Line[J]. Canadian Journal of Physics, 1966, 44(5): 1079-1086. |
| [6] | GOLUB G H, VAN LOAN C F. An Analysis of the Total Least Squares Problem[J]. SIAM Journal on Numerical Analysis, 1980, 17(6): 883-893. |
| [7] | SCHAFFRIN B, WIESER A. On Weighted Total Least-Squares Adjustment for Linear Regression[J]. Journal of Geodesy, 2008, 82(7): 415-421. |
| [8] | TONG Xiaohua, JIN Yanmin, LI Lingyun. An Improved Weighted Total Least Squares Method with Applications in Linear Fitting and Coordinate Transformation[J]. Journal of Surveying Engineering, 2011, 137(4): 120-128. |
| [9] | 鲁铁定, 宁津生. 总体最小二乘平差理论及其应用[M]. 北京: 中国科学技术出版社, 2011. LU Tieding, NING Jinsheng. Total Least Squares Adjustment Theory and Its Applications[M]. Beijing: China Science and Technology Press, 2011. |
| [10] | MAHBOUB V. On Weighted Total Least Squares for Geodetic Transformations[J]. Journal of Geodesy, 2012, 86(5): 359-367. |
| [11] | FANG Xing. Weighted Total Least Squares: Necessary and Sufficient Conditions, Fixed and Random Parameters[J]. Journal of Geodesy, 2013, 87(8): 733-749. |
| [12] | AMIRI-SIMKOOEI A R, JAZAERI S. Weighted Total Least Squares Formulated by Standard Least Squares Theory[J]. Journal of Geodetic Science, 2012, 2(2): 113-124. |
| [13] | 周拥军, 朱建军, 邓才华. 附参数的条件平差与按行独立的加权总体最小二乘法估计的一致性研究[J]. 测绘学报, 2012, 41(1): 48-53. ZHOU Yongjun, ZHU Jianjun, DENG Caihua. The Consistency between Row-wised Weighted Total Least Squares and Condition Adjustment with Parameters[J]. Acta Geodaetica et Cartographica Sinica, 2012, 41(1): 48-53. |
| [14] | 胡川, 陈义. 非线性整体最小二乘平差迭代算法[J]. 测绘学报, 2014, 43(7): 668-674. HU Chuan, CHEN Yi. An Iterative Algorithm for Nonlinear Total Least Squares Adjustment[J]. Acta Geodaetica et Cartographica Sinica, 2014, 43(7): 668-674. |
| [15] | SHEN Yunzhong, LI Bofeng, CHEN Yi. An Iterative Solution of Weighted Total Least-squares Adjustment[J]. Journal of Geodesy, 2011, 85(4): 229-238. |
| [16] | 姚宜斌, 孔建. 顾及设计矩阵随机误差的最小二乘组合新解法[J]. 武汉大学学报(信息科学版), 2014, 39(9): 1028-1032. YAO Yibin, KONG Jian. A New Combined LS Method Considering Random Errors of Design Matrix[J]. Geomatics and Information Science of Wuhan University, 2014, 39(9): 1028-1032. |
| [17] | 王乐洋. 地壳应变参数反演的总体最小二乘方法[J]. 大地测量与地球动力学, 2013, 33(3): 106-110. WANG Leyang. Inversion of Crustal Strain Parameters Based on Total Least Squares[J]. Journal of Geodesy and Geodynamics, 2013, 33(3): 106-110. |
| [18] | 王乐洋, 许才军, 鲁铁定. 边长变化反演应变参数的总体最小二乘方法[J]. 武汉大学学报(信息科学版), 2010, 35(2): 181-184. WANG Leyang, XU Caijun, LU Tieding. Inversion of Strain Parameter Using Distance Changes Based on Total Least Squares[J]. Geomatics and Information Science of Wuhan University, 2010, 35(2): 181-184. |
| [19] | JAZAERI S, AMIRI-SIMKOOEI A R, Sharifi M A. Iterative Algorithm for Weighted Total Least Squares Adjustment[J]. Survey Review, 2014, 46(334): 19-27. |
| [20] | 刘经南, 曾文宪, 徐培亮. 整体最小二乘估计的研究进展[J]. 武汉大学学报(信息科学版), 2013, 38(5): 505-512. LIU Jingnan, ZENG Wenxian, XU Peiliang. Overview of Total Least Squares Methods[J]. Geomatics and Information Science of Wuhan University, 2013, 38(5): 505-512. |
| [21] | XU Peiliang, LIU Jingnan, SHI Chuang. Total Least Squares Adjustment in Partial Errors-in-Variables Models: Algorithm and Statistical Analysis[J]. Journal of Geodesy, 2012, 86(8): 661-675. |
| [22] | SHI Yun, XU Peiliang, LIU Jingnan, et al. Alternative Formulae for Parameter Estimation in Partial Errors-in-variables Models[J]. Journal of Geodesy, 2015, 89(1): 13-16. |
| [23] | VAN HUFFEL S, VANDEWALLE J. The Total Least Squares Problem: Computational Aspects and Analysis[M]. Philadelphia: SIAM, 1991. |
| [24] | NERI F, SAITTA G, CHIOFALO S. An Accurate and Straightforward Approach to Line Regression Analysis of Error-affected Experimental Data[J]. Journal of Physics E: Scientific Instruments, 1989, 22(4): 215-217. |
| [25] | 曾文宪. 系数矩阵误差对EIV模型平差结果的影响研究[D]. 武汉: 武汉大学, 2013. ZENG Wenxian. Effect of the Random Design Matrix on Adjustment of an EIV Model and Its Reliability Theory[D]. Wuhan: Wuhan University, 2013. |
| [26] | 曾文宪, 方兴, 刘经南, 等. 附有不等式约束的加权整体最小二乘算法[J]. 测绘学报, 2014, 43(10): 1013-1018. ZENG Wenxian, FANG Xing, LIU Jingnan, et al. Weighted Total Least Squares Algorithm with Inequality Constraints[J]. Acta Geodaetica et Cartographica Sinica, 2014, 43(10): 1013-1018. |