2. 武汉大学卫星导航定位技术研究中心, 湖北 武汉 430079
2. Research Center of GNSS, Wuhan University, Wuhan 430079, China
随着各种大型结构体的大量涌现以及滑坡、泥石流等地质灾害的频繁发生,变形监测研究的重要性日益突出,变形监测理论和技术方法也在迅速发展。全球卫星导航系统(GNSS)具有全天候、高精度等优点,早在20世纪80年代中后期,就被作为一种变形监测技术手段。1995年以来,GNSS被用于监测滑坡、大坝等缓慢变形,如在Pacoima、清江隔河岩等大坝建立的GPS变形监测系统,对GPS用于高精度变形监测的可行性进行了分析,精度达毫米级。结果表明,GPS解算所得变形量与水库蓄水量具有高度一致性[1, 2, 3, 4]。为降低变形监测系统的建设成本,文献[5]提出了一机多天线变形监测系统,采用附加的多天线转换开关实现一台接收机与多个天线的时分单通连接。同时,考虑到监测特点(如监测站坐标已知),文献[6—8]提出了“无周跳无模糊度”的变形监测方法。对于桥梁、高大建筑物等结构体的动态变形,适宜采用实时监测系统进行,文献[9]研制了GPS变形监测数据处理软件GPSMON,定位精度为亚厘米级;文献[10]集成GPS、加速度计、伪卫星等技术,建立了桥梁变形实时监测系统。同时,Geo++、Leica、Trimble等测量仪器公司也开发了GPS变形监测系统,并得到了广泛的应用。
中国自20世纪80年代开始研制北斗系统,并实施了系统建设的“三步走”规划[11]。2012年底,北斗卫星导航系统空间信号接口控制文件正式公布,标志着北斗区域导航定位系统的正式建成。目前BDS在轨卫星16颗,其中工作卫星14颗,包括5颗GEO卫星,5颗IGSO卫星及4颗MEO卫星。预计到2020年左右,将建成覆盖全球的北斗卫星导航系统。已有研究表明,北斗二代系统的卫星钟性能、测距精度等与GPS基本处于同一水准[12, 13]。
在变形监测中,尤其对于滑坡、大坝等变形体的监测,受观测环境所限,测站往往遮挡严重,从而影响卫星的几何构型,降低变形监测的精度及可靠性。BDS由于其特殊的星座设计(5颗GEO卫星以及5颗IGSO卫星的存在),即使在目前尚未完成全球构网的情况下,在我国大部分区域其卫星可见数也大于GPS等系统。随着BDS卫星的逐步入轨,这一优势会更加明显。虽然BDS与GPS等类似,但其在信号结构、卫星分布、卫星类型等方面还存在较大的不同[14]。同时,利用多种系统进行监测也可以提高监测结果的精度和可靠性。此外,针对BDS变形监测应用的研究也可以拓展我国北斗系统的应用空间,验证北斗系统在高精度导航定位领域的可用性。因此,研究利用BDS及联合其他系统进行变形监测具有重要的科学和现实意义。
本文首先基于双差模型研究了BDS高精度基线解算方法,并针对变形监测特点,采用可靠的数据处理策略,研制开发了一套基于BDS的变形监测软件平台。同时,本文基于配备了三维精度测试系统的变形监测试验平台,利用在中国中部某地区采集的实测数据,从卫星分布、解算结果的内、外符合精度等多方面对北斗系统在变形监测中的可用性进行了探讨分析,并与GPS解算结果进行了比较。
1 系统算法与实现为探讨利用现有北斗星座进行变形监测的可行性,本文研制了变形监测软件,其数据处理流程如图 1所示。本软件目标为实现BDS变形监测数据的准实时(采用时段解模式)、高精度处理,故软件采用广播星历进行解算。已有研究表明,在短基线条件下,广播星历误差对基线解算结果的影响较小,可忽略不计[15]。软件同时具有BDS-GPS联合解算能力,但已有研究表明目前BDS与GPS高精度解算结果之间存在由于天线相位中心改正等原因引起的系统偏差[16],因此本文仅针对BDS单模结果分析。

|
| 图 1 数据处理流程 Fig. 1 Data processing flow chart |
软件包含了从数据处理到结果输出整个流程,主要包括数据准备、法方程形成与叠加、模糊度固定、时间序列结果分析等4部分。
(1) 数据准备主要包括两方面,一是根据广播星历计算卫星位置;二是将观测数据进行周跳探测与标记。周跳探测采用改进的TurboEdit方法[17, 18],利用MW、LG组合观测值以及LC观测值的双差残差分别探测周跳。结果表明,上述周跳探测策略基本不受电离层活动及观测条件的影响,可以探测到1周的小周跳,从而大幅减小了残差编辑的工作量,缩短了数据解算时间。为避免周跳错误修复而引起的灾难性后果,本文对周跳采取只探测、标记而不修复的策略,对所有周跳引入模糊度参数进行估计。
(2) 形成双差观测方程,进行法方程叠加,并将模糊度映射为双差模糊度[19]。双差观测值选取采用参考站-参考星以及全局搜索相结合的方法。若某历元观测存在参考站或参考星,则采用参考站-参考星法,否则采用全局搜索法,在当前历元所有观测值中最大限度地搜索函数独立的双差观测值。考虑到BDS星座的特殊性,在选择参考星时首选GEO卫星,若由于环境遮挡任何一颗GEO卫星均不为参考星,则依次选择IGSO、MEO卫星为参考星。根据基线长度,解算时既可采用单频观测值,也可利用双频观测值形成无电离层组合以消除电离层误差的一阶影响。形成法方程时需考虑的误差主要有对流层改正、地球自转改正、天线相位中心改正[20]、潮汐负载改正等,其他误差认为在双差过程中得到消除。对流层改正采用Saastamoinen模型,剩余对流层影响采用分段线性模型估计。BDS卫星天线相位中心采用MGEX(multi-GNSS experiment)公布的模型,接收机天线相位中心改正模型未知,在系统中以0代替。求解法方程后得到浮点解,此时需进行残差编辑,对可能存在的周跳和坏值进行标记,然后重新形成法方程,直到残差编辑没有周跳或坏值为止。
(3) 模糊度固定采用决策函数和序贯模糊度固定相结合的方法进行[19]。首先计算每个模糊度可以被固定的概率,并固定对应最大概率的模糊度,再更新法方程,重复上述程序,直到模糊度全部被固定或没有模糊度可以被固定。结果表明,在变形监测应用中,由于基线一般较短,采用此模糊度固定策略基本可将所有的北斗双差模糊度固定。将上述过程得到的整数模糊度回代法方程解算得到模糊度固定解。
(4) 时间序列分析在频域与时域进行。频域分析主要研究原始变形信号中各地球物理效应及GNSS技术类误差的影响,通过设计滤波器从原始结果中提取真正的变形信息。时域分析通过对变形时间序列进行ARIMA建模以分析变形的内在联系,预测变形的发展情况。
2 数据分析 2.1 数据采集为了分析利用北斗系统进行变形监测的精度和可靠性,本文搭建了模拟变形平台,利用实测数据从内、外符合精度等多个角度出发对试验结果进行了讨论。试验采用的仪器为Trimble NetR9型接收机,天线型号为TRM29659.00。此类型接收机可同时接收GPS以及BDS信号,满足系统间的兼容与互操作要求。
本次试验共布设3个测站(JZ01、JC01、JC02),位于中国中部某城市。所有测站均为土层观测墩,高出地面3m。其中JZ01站基座深8m,为钢筋混凝土结构,JC01、JC02站基座深3m,为钢结构。各测站视野开阔,10°高度角以上基本不存在遮挡物。测站间基线长度如表 1所示。3个测站均配置有强制对中标志。另外JC01站装有高程精度测试系统,JC02站装有水平精度测试系统。两套系统均可以通过旋转螺栓使接收天线在水平或垂直方向上精确移动。
本次试验采集了从2014年8月7日至8月10日(年积日219—222)共4d的数据。采样间隔30s,截止高度角10°。数据采集过程中试验平台的位移量如表 2所示。其中JC01、JC02站分别在垂直、水平方向(NS方向)上移动。在此过程中JZ01站保持不动。
与GPS相比,BDS具有自己的独特性,其包含5颗地球静止轨道卫星(GEO)和5颗倾斜地球同步轨道卫星(IGSO)。地球静止轨道卫星与测站相对静止,而倾斜地球同步轨道卫星与测站的相对位置变化也与GPS卫星等不同,因此有必要对各测站能观测到的北斗卫星数及其GDOP值进行分析。
试验中3个测站相距较近,能观测到的卫星数也十分相似,故此处以JZ01站为例分析能观测到的北斗卫星数。分析中选用JZ01站219日GPS时4~24时的观测数据。结果如图 2所示,横坐标是以历元形式表示的观测时间,共2400历元的观测数据。由图 2可知,JZ01站在分析时段内最少可观测到7颗北斗卫星,最多12颗,其数量均多于GPS(最少6颗,最多11颗)。这主要是由北斗卫星导航系统特殊的星座设计引起的。随着BDS星座的逐步完善,其在亚太地区卫星可见性方面的优势会更加明显。
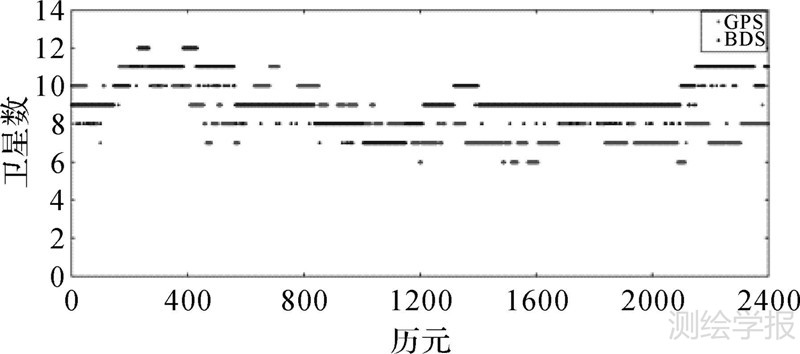
|
| 图 2 JZ01站卫星可见性 Fig. 2 Satellite visibility for site JZ01 |
几何精度因子是衡量定位精度的重要系数,代表GNSS测距误差造成的接收机与卫星间的距离矢量放大因子。图 3为JZ01站BDS与GPS在分析时段内的GDOP值序列。结合图 2可看出,与GPS相比,虽然BDS在卫星可见数方面略占优势,但其GDOP值的平均值在观测时段内大于GPS。与BDS相比,GPS的GDOP值变化更频繁。GDOP值序列的断续表示系统可见星数的变化,由此引入更多的模糊度参数需要解算,增加数据处理负担。

|
| 图 3 JZ01站BDS与GPS GDOP值对比 Fig. 3 Comparison of GDOP at site JZ01 for GPS and BDS respectively |
本文主要从基线解算中误差、基线各分量重复性以及变形监测试验系统调整前后基线分量较差等方面来分析和讨论BDS基线解算精度。为了对比分析,本文将GPS解算的结果作为参考值。GPS数据的解算利用DDMS[4]软件进行。解算时段长度为4h。由于每天9时(北京时间)左右调整变形监测试验系统的位移量,因此舍弃第一个时段(8~12时)的数据,每天只统计5个时段的结果。下述对基线解算中误差、重复性的讨论均基于年积日219日,基线(JZ01-JC02)的结果进行。
GPS与BDS每个测段的基线分量中误差如图 4所示,其中横坐标表示不同系统(BDS与GPS)、不同时段(1~5时段)所对应的解算结果。由图 4可看出,在本试验的基线长度和观测环境条件下,BDS的基线水平分量精度0.7mm左右,高程分量精度1.5mm左右,略低于GPS的结果精度。与GPS类似,利用BDS解算得到的高程分量精度约是水平分量的一半。同时需要注意的是,BDS的N方向精度明显低于E方向,这与文献[21]的结论一致,这可能主要是由BDS的星座结构引起的。
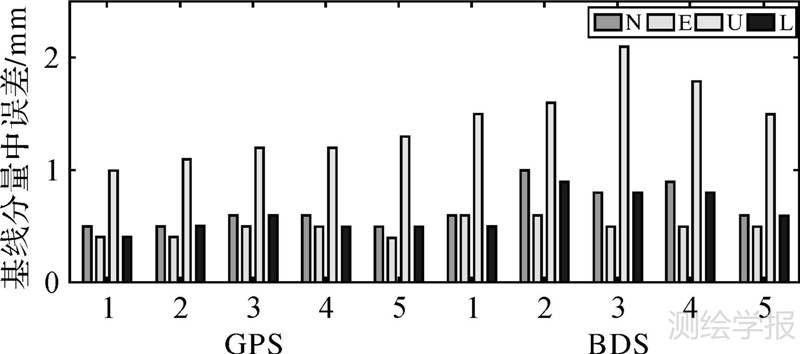
|
| 图 4 基线分量中误差 Fig. 4 Standard deviations of baseline components |
表 3为利用5个测段的结果统计得到的各系统对应基线分量的重复性。由表 3可得到与图 4类似的结果,即BDS的E方向精度最高,N方向次之,高程分量精度最低,约为水平分量的一半。
| 系统 | N分量 | E分量 | U分量 | L分量 |
| GPS | 0.2 | 0.2 | 1.0 | 0.1 |
| BDS | 0.9 | 0.4 | 1.4 | 0.9 |
表 4为各系统所对应的平台实际调整量与解算结果的较差统计。由表 4中较差平均值可看出,解算结果存在明显的系统误差。通过对不同系统、不同调整量所对应的较差平均值取平均后可得此系统误差约为水平方向0.7mm,高程方向0.5mm。后用测微器(可精确至0.01mm)的量测结果证实了上述系统误差的存在,且两种手段所得系统误差值具有较好的一致性。推断此系统误差由试验平台自带的刻度误差引入,是由于试验平台的制造工艺产生的。因此下述对基线分量较差的分析均是根据去除系统误差后的结果进行的。
| 实际调整量 | 最大值 | 最小值 | 平均值 | 标准差 | ||||||||
| 水平 | 垂直 | 水平 | 垂直 | 水平 | 垂直 | 水平 | 垂直 | |||||
| 1 | GPS | 0.9 | 1.4 | 0.1 | -0.4 | 0.5 | 0.4 | 0.3 | 0.7 | |||
| BDS | 1.5 | 1.7 | 0.5 | -0.6 | 0.8 | 0.5 | 0.4 | 0.8 | ||||
| 2 | GPS | 0.9 | 1.0 | 0.6 | -0.5 | 0.7 | 0.3 | 0.2 | 0.6 | |||
| BDS | 0.8 | 0.4 | 0.5 | -1.1 | 0.6 | 0.2 | 0.1 | 0.6 | ||||
| 3 | GPS | 0.9 | 1.1 | 0.6 | -0.2 | 0.7 | 0.6 | 0.1 | 0.6 | |||
| BDS | 1.2 | 1.7 | 0.6 | 0.2 | 0.9 | 0.7 | 0.2 | 0.6 | ||||
图 5为试验平台调整前后各测段基线分量较差。由图 5可以看出,对于3mm的变形,无论此变形发生在水平方向或高程方向,基于目前星座的BDS均可轻易识别。当此变形为2mm时,水平方向仍可轻易识别,但高程方向的较差已不十分明显。进一步,当变形量为1mm时,水平方向仍可以分离出此变形,但高程方向的基线分量较差表现出较大的随机性,已不足以提供明确的变形信息。因此,结合本文上述对基线分量估值中误差以及重复性的讨论,认为基于目前的BDS以及本文所实现的变形监测软件平台可达到水平1mm,高程2mm左右的监测精度。同时由图 5也可以看出,目前的BDS解算精度略低于GPS。结合本文前述对BDS数据质量的分析,认为其由试验区域内BDS较大的GDOP值引起。虽然试验中BDS的可见星数等与GPS基本相当,但不完善的星座结构导致BDS较大的GDOP值,从而造成BDS的解算精度略低于GPS。但可以预测,随着北斗系统星座的逐步构建,这一差距会逐渐缩小,最终接近甚至在某些区域超过GPS精度。
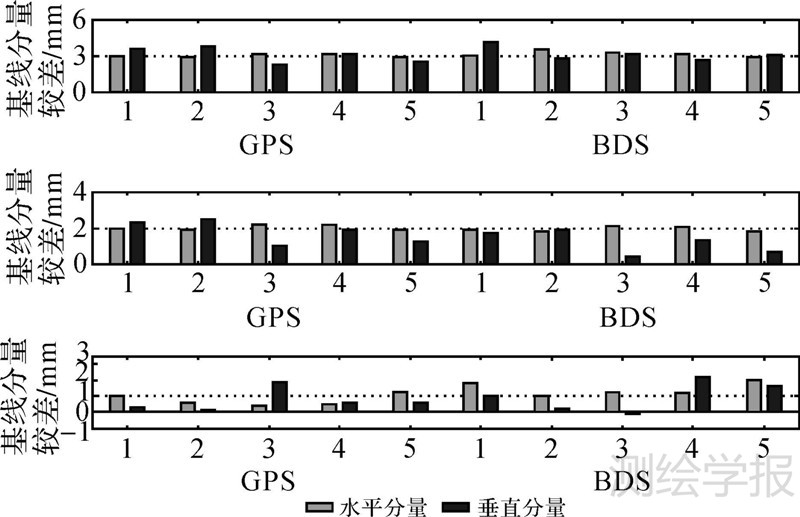
|
| 注:上、中、下图分别对应年积日220、221、222日的结果,虚线表示平台实际位移值。 图 5 试验平台调整前后各测段基线分量较差 Fig. 5 Difference of baseline components before and after adjusting the experimental platform |
本文主要分析了基于目前的北斗星座进行高精度变形监测的可行性。通过实测数据分析与讨论,得到如下结论:①在试验区域(中国中部某城市),目前BDS卫星可见数略大于GPS。但由于BDS星座的特殊设计,其对应的GDOP值略差于GPS;②通过分析变形监测试验平台的实测数据,认为目前BDS在短基线条件下能够达到平面1mm以内,高程2mm以内的精度水平,可满足大部分变形监测工程的需要。总之,目前的北斗卫星导航系统能够满足高精度变形监测工程的需求,可以在生产实践中推广应用。
| [1] | HUDNUT K W, BEHR JA. Continuous GPS Monitoring of Structural Deformation at Pacoima Dam, California[J]. Seismological Research Letters, 1998, 69(4): 299-308. |
| [2] | BEHR J A, HUDNUT K W, KING N E. Monitoring Structural Deformation at Pacoima Dam, California Using Continuous GPS[C]//Proceedings of the 11th International Technical Meeting of the Satellite Division of the Institute of Navigation.Nashville, Tennessee: [s.n.], 1998: 59-68. |
| [3] | 姜卫平, 刘经南. GPS技术在隔河岩大坝监测中的应用研究[J]. 武汉测绘科技大学学报, 1998, 23(S1): 48-49. JIANG Weiping, LIU Jingnan. Study on Application of GPS in the Geheyan Dam Deformation Monitoring[J]. Journal of Wuhan Technical University of Surveying and Mapping, 1998, 23(S1): 48-49. |
| [4] | 姜卫平, 刘鸿飞, 刘万科, 等. 西龙池上水库GPS变形监测系统研究及实现[J]. 武汉大学学报(信息科学版), 2012, 37(8): 949-952. JIANG Weiping, LIU Hongfei, LIU Wanke, et al. CORS Development for Xilongchi Dam Deformation Monitoring[J]. Geomatics and Information Science of Wuhan University, 2012, 37(8): 949-952. |
| [5] | DING X L, CHEN Y Q, HUANG D F, et al. Slope Monitoring Using GPS: A Multi-antenna Approach[J]. GPS World, 2000, 11(3): 52-55. |
| [6] | 李征航, 张小红, 朱智勤. 利用GPS进行高精度变形监测的新模型[J]. 测绘学报, 2002, 31(3): 206-210. LI Zhenghang, ZHANG Xiaohong, ZHU Zhiqin. A New Model of High Accuracy Deformation Monitoring with GPS[J].Acta Geodaetica et Cartographica Sinica, 2002, 31(3): 206-210. |
| [7] | 王新洲, 花向红, 邱蕾. GPS变形监测中整周模糊度解算的新方法[J]. 武汉大学学报(信息科学版), 2007, 32(1): 24-26. WANG Xinzhou, HUA Xianghong, QIU Lei. A New Method for Integer Ambiguity Resolution in GPS Deformation Monitoring[J]. Geomatics and Information Science of Wuhan University, 2007, 32(1): 24-26. |
| [8] | 张小红, 李征航, 徐绍铨. 高精度GPS形变监测的新方法及模型研究[J]. 武汉大学学报(信息科学版), 2001, 26(5): 451-454. ZHANG Xiaohong, LI Zhenghang, XU Shaoquan. A New Model for High Accuracy Deformation Monitor with GPS[J]. Geomatics and Information Science of Wuhan University, 2001, 26(5): 451-454. |
| [9] | 陈永奇, JAMES L. 单历元GPS变形监测数据处理方法的研究[J]. 武汉测绘科技大学学报, 1998, 23(4): 324-328, 363. CHEN Yongqi, JAMES L. Development of the Methodology for Single Epoch GPS Deformation Monitoring[J]. Journal of Wuhan Technical University of Surveying and Mapping, 1998, 23(4): 324-328, 363. |
| [10] | MENG Xiaolin, ROBERTS G W, COSSER E, et al. Real-time Bridge Deflection and Vibration Monitoring Using an Integrated GPS/Accelerometer/Pseudolite System[C]//Proceedings of the 11th International Symposium on Deformation Measurements, International Federation of Surveyors (FIG), Commission 6-Engineering Surveys, Working Group 6.1.Santorini: [s.n.], 2003. |
| [11] | 杨元喜. 北斗卫星导航系统的进展、贡献与挑战[J]. 测绘学报, 2010, 39(1): 1-6. YANG Yuanxi. Progress, Contribution and Challenges of COMPASS/BeiDou Satellite Navigation System[J]. Acta Geodaetica et Cartographica Sinica, 2010, 39(1): 1-6. |
| [12] | SHI Chuang, ZHAO Qile, HU Zhigang, et al. Precise Relative Positioning Using Real Tracking Data from COMPASS GEO and IGSO Satellites[J]. GPS Solutions, 2013, 17(1): 103-119. |
| [13] | STEIGENBERGER P, HUGENTOBLER U, HAUSCHILD A, et al. Orbit and Clock Analysis of COMPASS GEO and IGSO Satellites[J]. Journal of Geodesy, 2013, 87(6): 515-525. |
| [14] | 中国卫星导航系统管理办公室. 北斗卫星导航系统空间信号接口控制文件2.0[EB/OL]. (2013-12-27)[2014-11-15].http://www.beidou.gov.cn. China Satellite Navigation Office. BeiDou Navigation Satellite System Signal in Space Interface Control Document 2.0[EB/OL].(2013-12-27)[2014-11-15]. http://www.beidou.gov.cn. |
| [15] | 姜卫平, 刘经南, 叶世榕. GPS形变监测网基线处理中系统误差的分析[J]. 武汉大学学报(信息科学版), 2001, 26(3): 196-199, 238. JIANG Weiping, LIU Jingnan, YE Shirong. The Systematical Error Analysis of Baseline Processing in GPS Network[J]. Geomatics and Information Science of Wuhan University, 2001, 26(3): 196-199, 238. |
| [16] | 施闯, 赵齐乐, 李敏, 等. 北斗卫星导航系统的精密定轨与定位研究[J]. 中国科学(地球科学), 2012, 42(6): 854-861. SHI Chuang, ZHAO Qile, LI Min, et al. Precise Orbit Determination of BeiDou Satellites with Precise Positioning[J]. Science China(Earth Science), 2012, 55(7): 1079-1086. |
| [17] | BLEWITT G. An Automatic Editing Algorithm for GPS Data[J]. Geophysical Research Letters, 1990, 17(3): 199-202. |
| [18] | 吴继忠, 施闯,方荣新. TurboEdit单站GPS数据周跳探测方法的改进[J]. 武汉大学学报(信息科学版), 2011, 36(1): 29-33. WU Jizhong, SHI Chuang, FANG Rongxin. Improving the Single Station Data Cycle Slip Detection Approach TurboEdit[J]. Geomatics and Information Science of Wuhan University, 2011, 36(1): 29-33. |
| [19] | DONG D N, BOCK Y. Global Positioning System Network Analysis with Phase Ambiguity Resolution Applied to Crustal Deformation Studies in California[J]. Journal of Geophysical Research, 1989, 94(B4): 3949-3966. |
| [20] | 魏子卿, 葛茂荣. GPS相对定位的数学模型[M]. 北京: 测绘出版社, 1998: 56-85. WEI Ziqing, GE Maorong. Relative Positioning Mathematics Model in Global Positioning System[M]. Beijing: Surveying and Mapping Press, 1998: 56-85. |
| [21] | HE H B, LI J L, YANG Y X, et al. Performance Assessment of Single-and Dual-frequency BeiDou-GPS Single-epoch Kinematic Positioning[J]. GPS Solutions, 2014, 18(3): 393-403. |



