2. 中国科学院大学,北京 100049
2. University of Chinese Academy of Sciences, Beijing 100049, China
空间关系查询指的是从空间数据集中查找满足某种空间关系的空间目标的过程,它广泛应用于海量数据集或海量数据库操作中,是地学计算中必不可少且十分常用的一项数据操作。随着空间信息获取技术日趋成熟,所获取的空间数据量急速增加,如何将这些海量、超海量空间数据快速地处理并应用于地学计算,从而获得更有价值的信息,已经成为现今地理信息系统技术创新的热点[1]。
空间关系一般包括拓扑关系、度量关系、方位关系等,而空间拓扑关系是空间关系的主要研究内容[2]。如今,在诸多开源的GIS代码库中,大部分判断空间拓扑关系的算法都是基于Plane Sweep算法及其衍生算法编写的。文献[3]最早提出了Plane Sweep算法,该算法只能检测到是否存在相交的线段,但不能查询到所有相交的线段,文献[4]在此之后对算法进行了完善,解决了这个问题。文献[5, 6, 7]改进了Plane Sweep算法,通过降低算法的时间复杂度来提高计算效率;文献[8]在算法中加入了方位角判断和坐标比较,解决了算法对共线线段及3条以上线段交于一点不适用的情况。但因为该算法本身是一种串行算法,所以在针对海量数据的计算时效率会非常低;文献[9]使用矢量叉积的原理判断两条线段的相交类型,这种方法计算准确,但需要对线段两两逐个比较求交,效率过低;文献[10, 11, 12]基于PRAM并行计算模型,使用不同的方法对一组不相交的线段集并行构建二叉树,然后通过遍历和搜索树,得到最终相交线段的结果。但由于空间关系查询是一项比较常用的操作,而这种并行计算模型在普通计算机上并不适用,所以这种并行模式难以满足需要。
由于计算机硬件系统的不断升级换代,基于异构多核架构的异构计算已经成为各高性能计算领域的主流技术。图形处理单元(GPU)正广泛应用于大型数据集的并行处理中。与传统的CPU多核技术相比较,GPU所拥有的密集型并行构架具有更为强大的并行潜力以及更加显著的加速效果[13, 14]。 针对传统算法在处理海量空间数据时存在的不足,本文打破原有的计算方法,设计了一并行计算方法,该方法先利用CPU+GPU架构并行计算得到两个图层中所有最小外包矩形相交的多边形的线段相交情况,然后根据线段相交情况判断多边形环间拓扑关系,再根据环间的拓扑关系统计多边形间的维度扩展九交模型(DE-9IM)参数值,从而得到多边形间的空间关系。
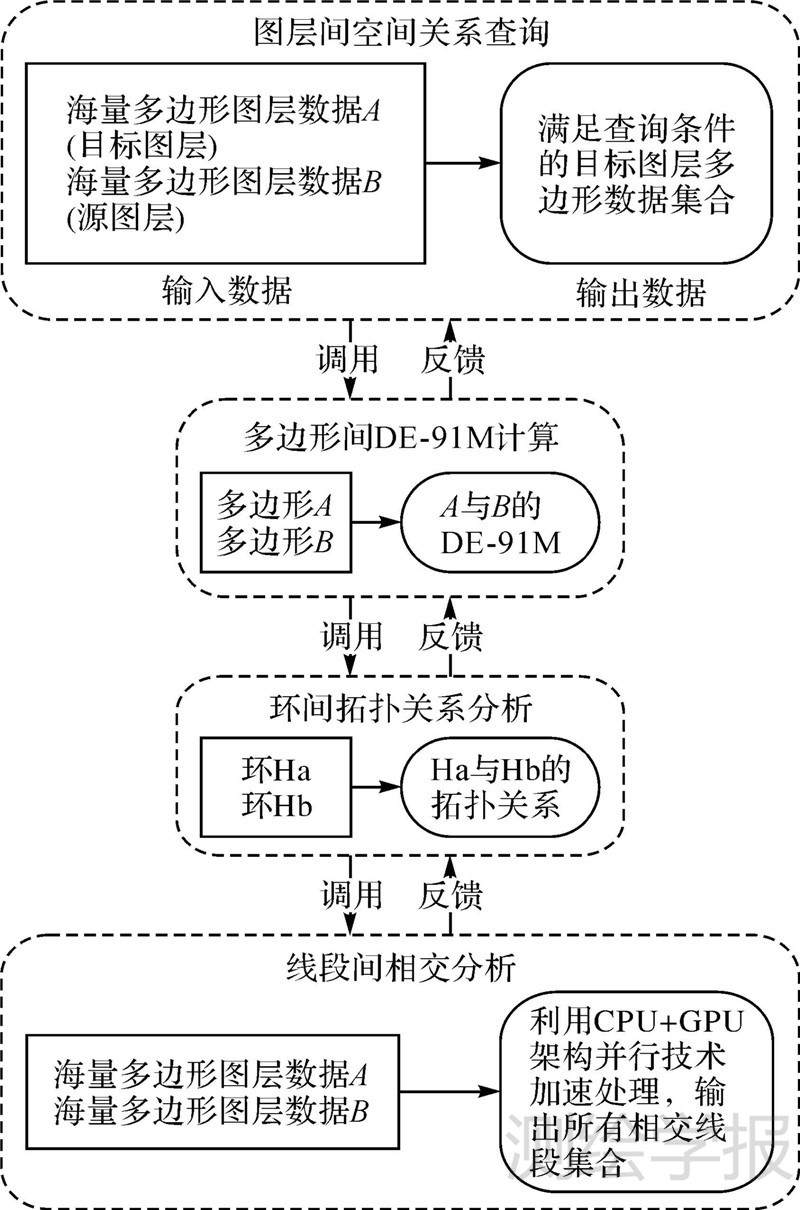
1 多边形间空间关系查询的并行算法本文的空间关系查询对象,是两个海量的多边形数据集合。两个空间数据集分别作为目标数据集合和源数据集合,其中,需要被统计的图层作为目标图层,以空间关系条件进行比对的图层作为源图层。该空间关系查询计算流程(图 1)主要由线段相交分析、环间拓扑关系分析和多边形间DE-9IM计算3个模块组成。
|
| 图 1 多边形间空间查询计算方法 Fig. 1 Spatial query calculation method between polygons |
在对线段相交判断之前,需要对两个多边形数据集进行预处理,预处理过程分为以下两个步骤。
第1步:几何要素与图形要素的转换。将空间数据中的点(Point)转化为图形节点(Node)信息,空间数据中的线段(Segment)转换为图形边(Edge)信息。边中会记录构建该边的两个端点的节点信息,节点中也会记录以该节点为某端点的所有边信息。图形要素中携带更多的标识信息,其中很多信息是空间几何要素无法表达和记录的,这些信息便于位置关系的构建和计算。
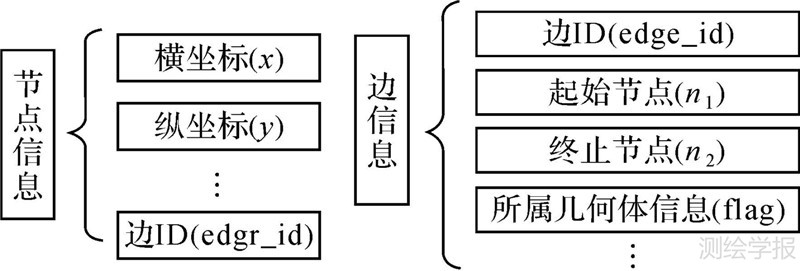
本文在进行空间关系查询时,首先遍历两个多边形数据集合的所有多边形要素,将所有的点和线段信息转换并统一整合到同一个具有拓扑特性的节点和边集合中。同时,获取的空间信息还包括原始数据的最大空间范围以及节点集中节点的个数。参数信息如图 2所示。
|
| 图 2 节点和边的数据结构信息 Fig. 2 The data structure information of the nodes and edges |
第2步:构建索引。为了减小计算量,首先需要先对两个图层的多边形进行过滤,根据多边形的最小外包矩形过滤掉一定不相交的多边形组合。本文选择STR树索引进行过滤,STR树索引是一种使用Sort-Tile-Recursive(STR)算法创建的只负责查询处理的R树。它针对二维空间数据,十分易于操作并且可以最大化地利用内存空间存储数据[15]。主要做法是:假设有两个多边形集合分别为A和B,先对A和B分别构建STR树,将多边形的最小外包矩形作为STR树节点的空间范围,多边形本身作为STR树节点中存储的空间对象,然后遍历B中多边形的最小外包矩形在A的STR树中查询,遍历A中多边形的最小外包矩形在B的STR树中查询,最终得到两个过滤后的多边形集合A和B。
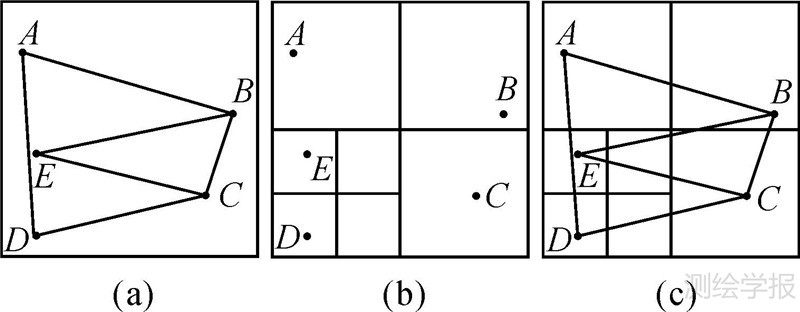
对于过滤后的多边形集合A和B,利用OpenMP并行技术[16]对它们的节点集合和边集合构建空间四叉树索引[17, 18],并置于计算机内存中,以便在树节点中快速获取边边组合,为下一步边边相交计算做准备。如图 3(a)所示,假设一个多边形为待构建四叉树索引的空间几何体,完成空间四叉树索引的步骤可分为以下两步。
|
| 图 3 空间四叉树索引建立过程 Fig. 3 The process of establishing the spatial quadtree index |
步骤a:提取该多边形的所有节点构成节点集,构建点四叉树。如图 3(b)所示,最大空间范围决定了四叉树根节点的空间范围,每个叶子节点所容纳结点的最小个数为1。由于各节点的分裂是完全独立的,故可以利用OpenMP并行技术进行新节点的分裂,直至各进程内的四叉树都分裂完全。
步骤b:完善空间索引的边信息。依照已构建的空间点四叉树索引,对于每一个叶子节点,提取其代表的空间范围信息,依次与所有边信息的最小外包矩形相比较,若两个空间范围有交集,则将此边加入候选集合(先对它们的边界进行相交判断是为了节省计算成本,进行一次粗过滤),然后再精确地判断此边与叶子节点所代表的空间范围是否相交,如果相交,则被认为属于该叶子节点,最终完成边信息的插入,构建成一个包含了点信息和边信息的空间四叉树索引。如图 3(c)所示,这样构成的四叉树索引可能会将一条边存储在多个叶子节点中,但这是为了在后续的计算中能保证每个叶子节点内所有的相交线段都能被统计到,以保证最终计算结果的准确性。
1.2 线段相交判断边边组合准备好后,需要对其相交类型进行判断,在此之前,需要对边边组合进行精度判断。虽然GPU已经支持双精度浮点运算,但与其单精度浮点运算能力相比较,其双精度浮点运算能力还是偏弱,不如CPU的处理效率高。本文提取空间四叉树索引中每一个叶子节点内所有的边边组合(每一个边边组合的两条边来源于不同的数据集),计算每一对边边组合中两条边的4个端点的相对坐标,以此方法,大幅度降低端点坐标的位数,使其有可能在计算误差允许范围内参与单精度浮点运算。根据单精度浮点计算的数值范围,判断相对坐标是否满足单精度浮点运算所需的几何计算精度要求[19, 20]。若4个端点都满足精度要求,则将该组存储于满足单精度浮点运算的边边组合候选集中,将每一边边组合放入GPU的每一个线程中进行相交判断的并行计算。若4个端点中有任一端点不满足,则将该边边组合直接置于CPU中进行相交判断和相交情况的计算。
本文使用CUDA编程模型进行线段相交的并行计算,运行在GPU上的程序称为内核函数(kernal),CPU在调用内核函数时,先通过边边组合的数量声明内核函数中的需要开启的线程数量,每一个线程都有自己的block ID和thread ID用于与其他线程相区分。然后,CPU将数据从主存转移到设备内存,GPU将每一组数据分配给一个线程,由于每个线程只负责处理一组边边组合的相交判断,所以各线程间无须通信,计算完成后直接将计算结果返回即可。
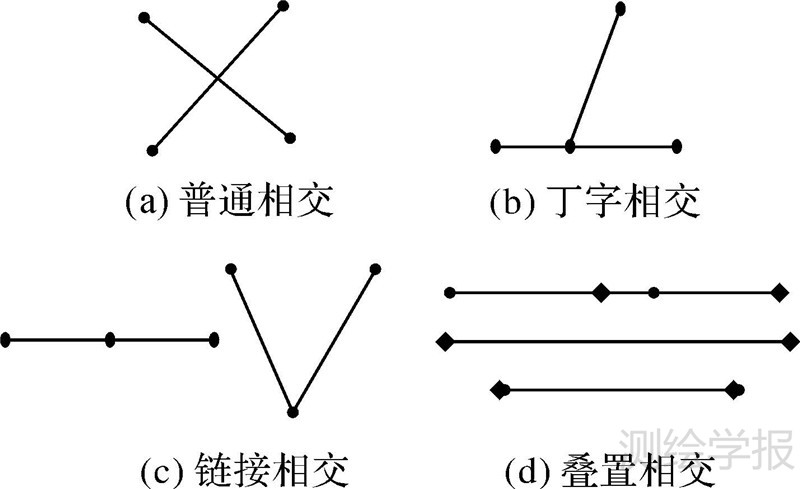
在进行边边相交类型判断时,利用向量混合积判断两条边是否相交[21],若判断得到边边相交,如图 4所示,依据交点特征可将相交情况可分为普通相交、丁字相交、连接相交和叠置相交四大类:若交点不是相关两条边的4个端点中的任何一个,则为普通相交;若交点是相关两条边的4个端点中的一个,则为丁字相交;若交点是相关两条边的4个端点中的两个,则为连接相交;若交点的相关两条边有公共重合部分,则为叠置相交。
|
| 图 4 4种线段相交的类型 Fig. 4 Four types of line segments intersect |
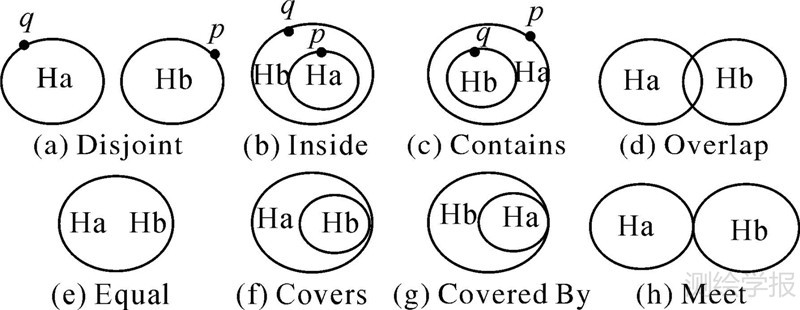
一个多边形是由多个环组成,一个环是由多条边组成。欲求两个多边形之间的空间关系,可以先从环间的拓扑关系计算入手,而环间的拓扑关系需要根据线段相交类型进行判断。环间的拓扑关系分为以下8种:Disjoint、Meet、Equal、Overlap、Covers、Covered By、Contains和Inside,如图 5所示。基于九交模型理论,环与环之间一定发生且只发生8种关系中的一种[22, 23]。
|
| 图 5 环间的8种拓扑关系 Fig. 5 Eight kinds of topological relations between the rings |
假设待计算的两个环为Ha、Hb,则根据线段相交类型判断两环关系的主要过程如下:①若两环没有相交线段出现,则关系一定为Disjoint、Inside或Contains中的一种,再通过两环上两点p、q与环间的位置关系具体确定;②若有普通相交出现,则两环拓扑关系属于Overlap;③若两环的所有边都发生了叠置相交,则两环的拓扑关系为Equal;④若除了普通相交,其他相交类型均有出现,则关系一定为Covers、Covered By或Meet中的一种,再根据两环位置关系具体判定;⑤由于九交模型只有8种情况,所以其他情况两环的拓扑关系为Overlap。
1.4 多边形间空间关系的判断方法在1.1节中由STR树索引过滤后得到两个多边形集合,需要依次对有可能相交的多边形组合判断它们之间的空间关系,为了进一步提高效率,本文使用BOOST库多线程并行判断多边形间的空间关系。并行判断涉及数据划分,由于本文计算量最大的线段相交的判断已经在最开始由CPU和GPU协作完成,则对于每一对多边形组合,只需调用计算好的线段相交类型来判断环间拓扑关系,进而判断它们的空间关系,所以在计算量上不会有很大差距。那么对多边形数据的划分,可以按照有可能相交的目标多边形按数量平均分组,以保证每个线程的负载基本相同,然后将每一组多边形组合分配给一个线程进行空间关系的判断,最后合并计算的结果。
多边形之间的空间关系由维度扩展九交模型(DE-9IM)来表达,根据维度扩展九交模型的参数值,比较空间关系的查询条件,即可输出满足条件的多边形集合。根据OGC的标准,与DE-9IM参数值对应的7类空间关系查询条件为:分离关系、重叠关系、相等关系、接触关系、包含关系、包含于关系以及相交关系(不属于分离关系的所有空间关系都为相交关系)[24]。根据环间拓扑关系分析模块,分别得到的两个多边形内、外环之间的拓扑关系,利用此拓扑关系逐步判断两个多边形间内部、边界和外部的相交值,从而确定多边形间的DE-9IM参数值,最后将计算出的DE-9IM参数值与7类空间关系对应的DE-9IM参数进行比对,以最终确定多边形间的空间关系。
2 试验设计与结果分析 2.1 试验环境 2.1.1 硬件环境CPU:Intel(R)Core(TM)i7-3770。
内存:8.00GB。
GPU:独立显卡NVIDIA GTX 660(Device2-Graphics)。
2.1.2软件环境操作系统:Win7 64位操作系统。
编程环境:Visual Studio 2012。
编程语言:C++、CUDA。
开源库:GDAL库(版本为1.1.0 )、GEOS库(版本为3.4.2)、BOOST库(版本为1.53.0)、CUDA库(版本为5.0)、OpenMP库(版本为2.0)。
2.2 验证并行算法正确性与稳健性任意两个带洞多边形(即除了一个外环还可能有任意个内环的多边形)之间一定发生且只能发生18种拓扑关系中的一种[25],这18种拓扑关系分别为:disjoint、fillingHole、holeFIlled、meet、equal、inside、holeCoveredBy、coveredBy、contains、holeCovers、covers、insideOverfill、containsOverfill、insideContains、coversCoveredBy、coversOverfill、CoveredByOverfill、overlap。
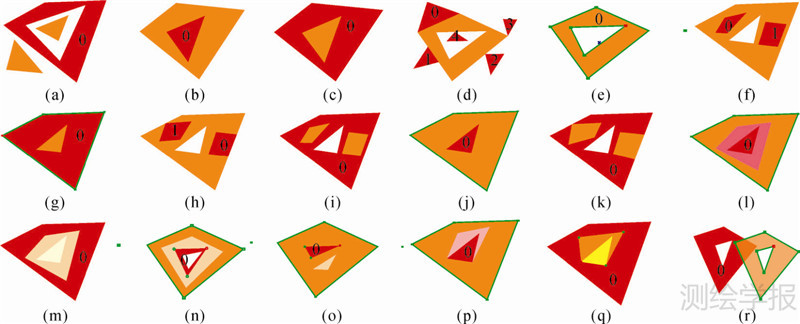
根据18种拓扑关系,利用ArcGIS软件逐一绘制相应的多边形计算数据,如图 6所示。每一种拓扑关系都可能对应于多种不同的多边形模型,多边形数据中红色多边形为目标数据,黄色多边形为源数据。这些模型中的多边形样式或形态不同,但其拓扑关系相同且唯一,保证了试验数据的稳健性。
|
| 图 6 根据带洞多边形间18种拓扑关系绘制的多边形数据 Fig. 6 Polygon data according to 18 kinds topological relations between the polygons with holes |
对于不同的试验数据,测试的空间关系查询条件也不相同,其主要目的是验证并行算法是否准确,比对并行程序输出的多边形ID与ArcGIS中“按位置选择”功能选择出的多边形ID是否相一致。
经过并行算法与ArcGIS中“按位置选择”功能对18种代表不同的拓扑关系的多边形数据与其对应的空间关系查询条件进行测试,分别得到的多边形ID如表 1所示。从表中可以看出,对于每一种多边形数据,按照对应的空间关系查询条件进行查询,并行算法查询到的多边形ID与ArcGIS查询到的多边形ID都相同。
| 序号 | 拓扑关系 | 对应查询条件 | 并行算法查询结果 | ArcGIS查询结果 |
| 1 | disjoint | 分离 | 0 | 0 |
| 2 | fillingHole | 接触 | 0 | 0 |
| 3 | holeFIlled | 接触 | 0 | 0 |
| 4 | meet | 接触 | 0 1 2 3 4 | 0 1 2 3 4 |
| 5 | equal | 相等 | 0 | 0 |
| 6 | inside | 被包含 | 0 1 | 0 1 |
| 7 | holeCoveredBy | 被包含 | 0 | 0 |
| 8 | coveredBy | 被包含 | 0 1 | 0 1 |
| 9 | contains | 包含 | 0 | 0 |
| 10 | holeCovers | 包含 | 0 | 0 |
| 11 | covers | 包含 | 0 | 0 |
| 12 | insideOverfill | 相交 | 0 | 0 |
| 13 | containsOverfill | 相交 | 0 | 0 |
| 14 | insideContains | 相交 | 0 | 0 |
| 15 | coversCoveredBy | 相交 | 0 | 0 |
| 16 | coversOverfill | 相交 | 0 | 0 |
| 17 | CoveredByOverfill | 相交 | 0 | 0 |
| 18 | overlap | 相交 | 0 | 0 |
| 注:试验结果的正确与否参考ArcGIS中“按位置选择”功能的计算结果。 | ||||
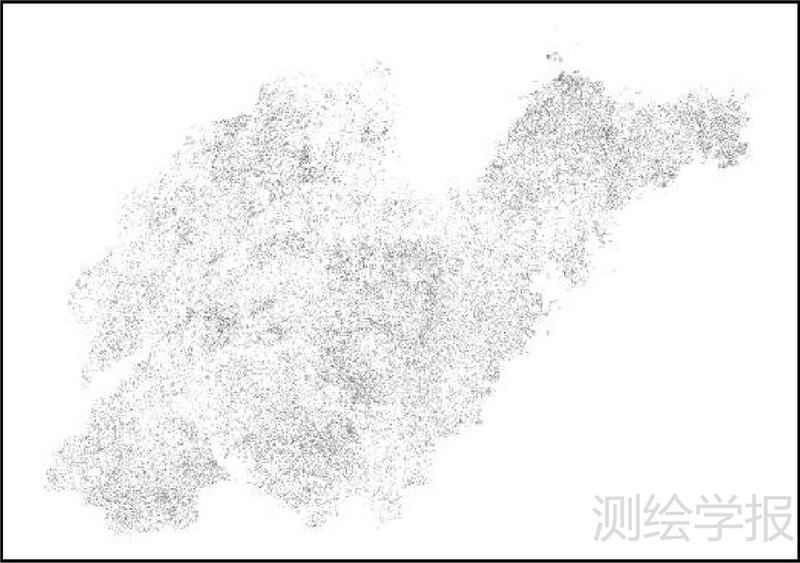
如图 7所示,本文试验数据为从1990年山东省土地利用图中提取出的50000个多边形,将所有多边形统一构建成为一个海量多边形图层,并作为目标图层数据,同时对上述海量多边形图层的副本进行整体或局部的修改,作为源图层数据。
|
| 图 7 试验数据 Fig. 7 The experiment data |
为了验证并行算法的计算效率,本文利用ArcGIS组件式开发技术,制作了一套仅具有数据输入输出、“按位置选择”和时间记录3种功能的小型测试软件。先记录各个空间关系查询条件下并行算法的测试时间,然后利用开源代码库GEOS中的空间关系计算测试时间,再利用小软件记录ArcGIS在各个空间关系查询条件下的测试时间,最后对比3个测试的计算结果和测试时间。
本文把相等关系、相交关系、接触关系、包含关系和被包含关系作为5个空间关系查询条件进行测试(由于相交即不分离,故不需要对分离关系再做测试)。对于相等关系的测试,本文保留原始数据的6000个多边形位置不变,将其他多边形进行平移作为源图层。对于其余4个关系的测试,本文将原始数据的副本做了全局性的平移,使其在位置上不同于原始数据,将新的数据作为源图层。
将并行算法计算出的多边形个数,与ArcGIS中“按位置选择”功能相对应的空间关系查询条件计算得到的多边形个数相对比,试验结果统计如表 2所示,可以发现,并行算法的计算结果都是正确的。
| 空间关系 | 对应于“按位置选择”功能中的条件描述 | ArcGIS计算结果 | 并行算法测试结果 |
| 相等 | 与源图层要素完全相同 | 6000 | 6000 |
| 相交 | 与源图层要素相交 | 6248 | 6248 |
| 接触 | 接触源图层要素的边界 | 7 | 7 |
| 包含 | 包含源图层要素 | 16 | 16 |
| 被包含 | 在源图层要素范围内 | 11 | 11 |
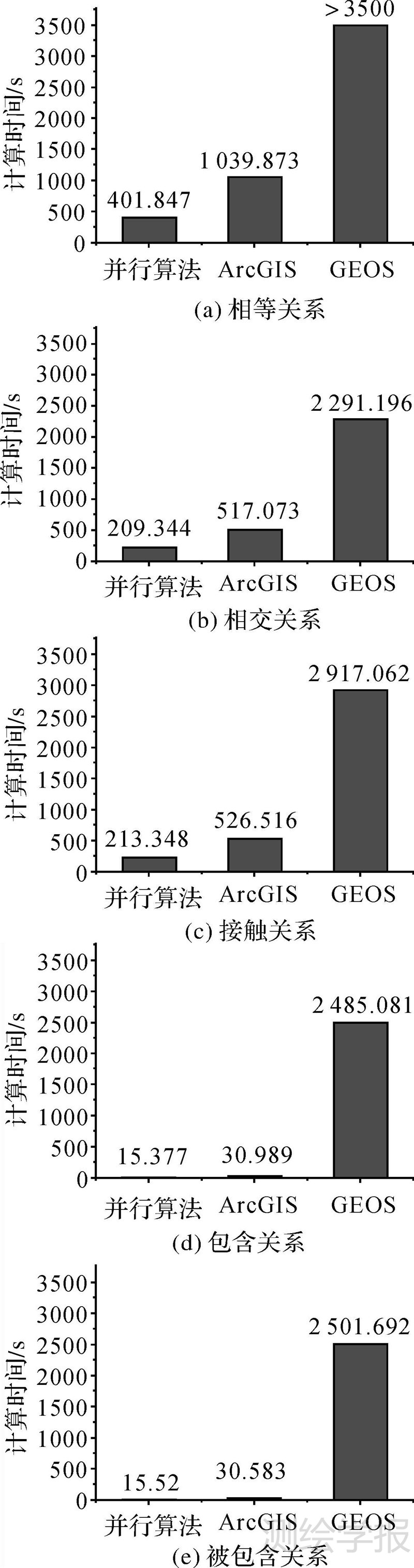
本文对5种空间关系查询的计算时间进行了统计,包括数据预处理(构建STR树索引及几何要素转化为图形要素),构建四叉树索引,线段相交判断(包括精度判断时间)以及最后计算DE-9IM(包括环间拓扑关系计算)的时间,统计结果如表 3所示。同时,本文也将并行算法的时间与ArcGIS的计算时间以及GEOS的计算时间进行了统计对比,每个算法的测试时间对比如图 8所示。经过对比可以发现,在5种关系查询的时间测试中,并行算法的测试时间比GEOS和ArcGIS的计算时间都要短,在计算效率上具有较大优势。以相等关系查询为例:GEOS计算时间大于3500s,ArcGIS计算时间为1039.873s,而并行算法总时间仅为401.847s,比ArcGIS用时节省了638.026s,计算效率是ArcGIS的2.59倍。
| 空间关系 | 计算时间 | ||||
| 数据预处理 | 构建四叉树索引 | 线段相交判断 | 计算DE-9IM | 总计算时间 | |
| 相等 | 32.646 | 204.237 | 130.532 | 34.432 | 401.847 |
| 相交 | 26.109 | 109.074 | 56.039 | 18.122 | 209.344 |
| 接触 | 27.039 | 109 | 59.127 | 18.182 | 213.348 |
| 包含 | 13.716 | 0.083 | 1.18 | 0.398 | 15.377 |
| 被包含 | 14.022 | 0.071 | 1.249 | 0.178 | 15.52 |
|
| 图 8 针对5种空间关系查询3种算法的时间对比 Fig. 8 Time comparison if three kinds of algorithm for five kinds of spatial relations query |
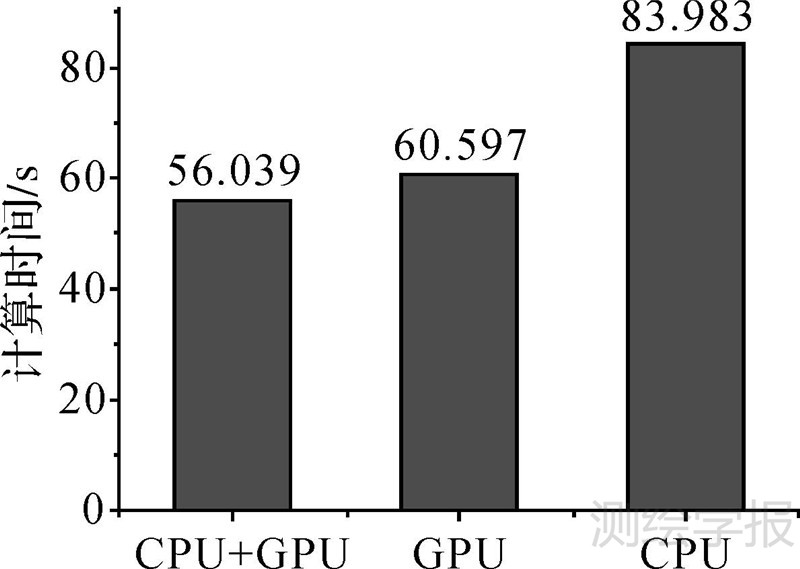
由于本文是综合利用CPU+GPU架构的算法来进行空间关系的查询,为了验证本算法对线段相交判断处理的优势,笔者以相交关系的判断为例,统计所有线段相交均由CPU处理和均由GPU处理的时间进行对比,对比结果如图 9所示。可以发现,综合利用CPU和GPU对线段相交处理的速度比单独用CPU或GPU对线段相交处理的速度都要快,说明综合利用CPU和GPU进行线段相交的判断是优于其他两种方法的。
|
| 图 9 不同硬件处理线段相交的时间对比 Fig. 9 Time comparison of different hardware processing line segment intersection |
针对以上试验结果,从正确性和高效性两方面,对本文提出的空间关系并行算法的实际应用进行评价。
(1) 正确性:在小规模的多边形数据情形下,依据18种带洞多边形的拓扑关系,构建各式多边形模型数据,保证了所有的多边形之间的空间关系可以被涵盖在测试数据中。18种多边形数据经过不同的查询条件计算,与ArcGIS的“按位置选择”功能的计算结果作比对,结果是完全正确的。当数据扩展到50000个多边形数据时,计算结果依然与ArcGIS的计算结果相同,证明本文提出的空间关系并行查询算法,在对于各种数据规模时,计算结果都是正确的。
(2) 高效性:对于规模较大的数据,进行空间关系查询是非常费时的过程。本算法综合利用CPU和GPU并行判断线段相交情况,突破了Plane Sweep算法逐一扫描判断的特性;在计算多边形间空间关系时,利用CPU多线程并行判断,因此大幅缩减了计算时间,经过试验验证,本文提出的空间关系查询并行算法的计算速度是明显快于GEOS中的空间关系算法和ArcGIS中按位置选择功能,所以本算法具有比较显著的高效性。
3 结 论本文算法充分利用CPU和GPU的并行计算能力,提高了对海量数据空间关系查询的处理效率。本文算法能够保证在查询结果准确的情况下高效地处理海量数据的空间关系查询问题,在目标数据和源数据都为50000个多边形的情况下,以相等关系为例,并行算法比ArcGIS计算时间节省了638.026s,计算效率约为ArcGIS的2.6倍,通过其他关系的查询时间对比也可以看出,并行算法能有效地提升查询效率。由于本算法是根据多核CPU和GPU的硬件架构而设计的通用算法,因此可以预测在其他拥有多核CPU和GPU的硬件环境下,本算法也可以同样提升计算效率。
| [1] | 王结臣, 王豹, 胡玮, 等. 并行空间分析算法研究进展及评述[J]. 地理与地理信息科学, 2011, 27(6): 1-5. WANG Jiechen, WANG Bao, HU wei, et al. Review on Parallel Spatial Analysis Algorithms[J]. Geography and Geo-Information Science, 2011, 27(6): 1-5. |
| [2] | 陈军, 赵仁亮. GIS空间关系的基本问题与研究进展[J]. 测绘学报, 1999, 28(2): 95-102. CHEN Jun, ZHAO Renliang. Spatial Relations in GIS: A Survey on Its Key Issues and Research Progress[J]. Acta Geodaetica et Cartographica Sinica, 1999, 28(2): 95-102. |
| [3] | SHAMOS M I, HOEY D. Geometric Intersection Problems[C]//17th Annual Symposium on Foundations of Computer Science, 1976. Houston, TX: IEEE, 1976: 208-215. |
| [4] | BENTLEY J L, OTTMANN T A. Algorithms for Reporting and Counting Geometric Intersections[J]. IEEE Transactions on Computers, 1979, C-28(9): 643-647. |
| [5] | BARTUSCHKA U, MEHLHORN K, NÄHER S. A Robust and Efficient Implementation of a Sweep Line Algorithm for the Straight Line Segment Intersection Problem[C]//Proceedings of Workshop on Algorithm Engineering. 1997. |
| [6] | CHAZELLE B, EDELSBRUNNER H. An Optimal Algorithm for Intersecting Line Segments in the Plane[J]. Journal of the ACM, 1992, 39(1): 1-54. |
| [7] | BALABAN I J. An Optimal Algorithm for Finding Segments Intersections[C]//Proceedings of the 11th Symposium on Computational Geometry. New York: ACM, 1995: 211-219. |
| [8] | 陈军, 刘万增, 李志林, 等. 线目标间拓扑关系的细化计算方法[J]. 测绘学报, 2006, 35(3): 255-260. CHEN Jun, LIU Wanzeng, LI Zhilin, et al. The Refined Calculation Method of Topological Relationships between Line Objects[J]. Acta Geodaetica et Cartographica Sinica, 2006, 35(3): 255-260. |
| [9] | 陈斐, 周晓光. 基于平面分割的线/线相接、交叉类型判断[J]. 测绘学报, 2014, 43(2): 186-192. CHEN Fei, ZHOU Xiaoguang. An Algorithm for Determining the Touching and Crossing Relations between a Pair of Lines Based on One Line Splitting Plane to Two Parts[J]. Acta Geodaetica et Cartographica Sinica, 2014, 43(2): 186-192. |
| [10] | GOODRICH M T, GHOUSE M R, BRIGHT J. Sweep Methods for Parallel Computational Geometry[J]. Algorithmica, 1996, 15(2): 126-153. |
| [11] | ATALLAH M J, GOODRICH M T. Efficient Plane Sweeping in Parallel[C]//Proceedings of the Second Annual Symposium on Computational Geometry. New York: ACM, 1986: 216-225. |
| [12] | AGGARWAL A, CHAZELLE B, GUIBAS L, et al. Parallel Computational Geometry[J]. Algorithmica, 1988, 3(1-4): 293-327. |
| [13] | OWENS J D, LUEBKE D, GOVINDARAJU N, et al. A Survey of General-Purpose Computation on Graphics Hardware[J]. Computer Graphics Forum, 2007, 26(1): 80-113. |
| [14] | 张舒, 褚艳利. GPU高性能运算之CUDA[M]. 北京: 中国水利水电出版社, 2009. ZHANG Shu, CHU Yanli. CUDA GPU High-performance Computing[M]. Beijing: China Water Power Press, 2009. |
| [15] | LEUTENEGGER S T, LOPEZ M A, EDGINGTON J. STR: A Simple and Efficient Algorithm for R-Tree Packing[C]//Proceedings of the 13th International Conference on Data Engineering. Birmingham: IEEE, 1997: 497-506. |
| [16] | 周伟明. 多核计算与程序设计[M]. 武汉: 华中科技大学出版社, 2009. ZHOU Weiming. Multi-core Computing and Programming[M]. Wuhan: Huazhong University of Science and Technology Press, 2009. |
| [17] | SAMET H, WEBBER R E. Storing a Collection of Polygons Using Quadtrees[J]. ACM Transactions on Graphics (TOG), 1985, 4(3): 182-222. |
| [18] | SAMET H, WEBBER R E. On Encoding Boundaries with Quadtrees[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 1984, 6(3): 365-369. |
| [19] | SHEWCHUK J R. Adaptive Precision Floating-point Arithmetic and Fast Robust Geometric Predicates[J]. Discrete & Computational Geometry, 1997, 18(3): 305-363. |
| [20] | MULLER J M, BRISEBARRE N, DE Dinechin F, et al. Handbook of Floating-point Arithmetic[M]. Boston: Birkhäuser, 2009. |
| [21] | 王舒鹏, 方莉. 混合积判断线段相交的方法分析[J]. 电脑开发与应用, 2006, 19(10): 34-35. WANG Shupeng,FANG Li.An Analysis of Two Segments Intersection Judgment with Mixed Product[J]. Computer Development & Applications, 2006, 19(10): 34-35. |
| [22] | EGENHOFER M J, HERRING J R. Categorizing Binary Topological Relations Between Regions, Lines and Points in Geographic Databases[R]. Orono: University of Maine 1991. |
| [23] | 虞强源, 刘大有, 谢琦. 空间区域拓扑关系分析方法综述[J]. 软件学报, 2003, 14(4): 777-782. YU Qiangyuan, LIU Dayou, XIE Qi. A Survey of Analysis Methods of Topological Relations between Spatial Regions [J]. Journal of Software, 2003, 14(4): 777-782. |
| [24] | HERRING J R. OpenGIS® Implementation Standard for Geographic Information——Simple Feature Access-Part 1: Common architecture[S]. [S.l.]: OGC Document, 2011. |
| [25] | MCKENNEY M, PAULY A, PRAING R, et al. Local Topological Relationships for Complex Regions[M]//Advances in Spatial and Temporal Databases. Heidelberg: Springer, 2007: 203-220. |


