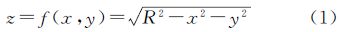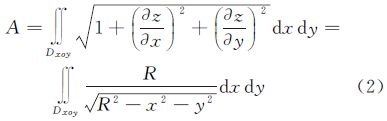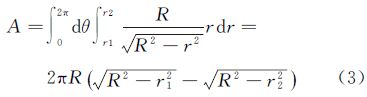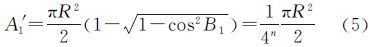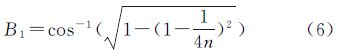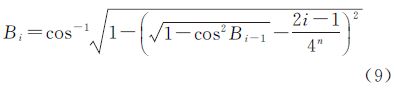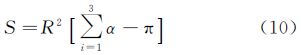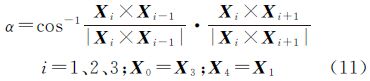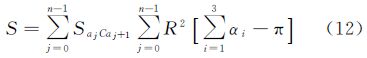随着全球一体化研究的深入,越来越多的宏观应用需要在大范围甚至全球尺度上进行,传统地图投影在有效性、精确性和连续性等方面具有一定的局限性[1, 2]。而全球离散格网(discrete global grid,DGG)模型的提出,为构建大范围、多分辨率、全球统一无缝的空间定位基础框架提供了一个新的解决思路。其中,文献[3]提出的四元三角网(quaternary triangular mesh,QTM)模型具有层次组织、全球连续和格网单元形状统一等特性,在许多领域得到了较为广泛的应用,如全球数据的组织与管理[4, 5, 6]、全球数据质量与地图综合[3]、全球地形可视化[7]、全球多分辨率水淹模拟[8, 9]、全球影像数据检索[10]、数字地形索引及压缩模型[11],等。但是该模型同层格网面积变化较大,且变化区域呈带状分布,误差较难控制,使许多地学应用的统计分析无法进行。所以,构建QTM等面积(或近似等面积)剖分单元模型问题,已成为目前制约其广泛应用的主要因素之一。而传统的球面等面积格网剖分模型,除了应用等面积投影(如Rosca&Plonka等面积投影[12]、Snyder等面积投影[13])外,大多数是采用变经纬度剖分方案[14, 15, 16, 17, 18, 19],其格网单元多为球面四边形,不但存在着嵌套困难及邻近搜索复杂等缺陷[2, 20],且很难移植到QTM模型上。为此,文献[21]提出了一种基于小圆弧的等面积剖分模型,但该方法计算复杂,坐标转换困难。而文献[22]针对传统投影方法计算复杂的缺陷,推导出一种新的等面积投影公式。该公式具有对称性,计算简便,但是仍然没有解决传统投影方法边界扭曲严重的缺陷,且球面点定位复杂,影响坐标转换的效率。文献[23]提出的基于传统QTM剖分的改进模型——“纬线法”剖分方案,主要提高了格网数据与地理坐标的转换效率,但其剖分单元面积变化问题仍然没有得到实质性的改变。
为此,本文在“纬线法”QTM剖分的基础上,引入Bj∅rke变经纬度剖分的思想,提出一个基于“纬线环法”的球面近似等面积四元三角剖分模型。该方案既保留了传统QTM剖分模型的层次嵌套性、格网统一性和全球无缝连续性等特点,又将同层格网单元的面积变化控制在了很小的范围内,完全满足了绝大部分应用的需求。
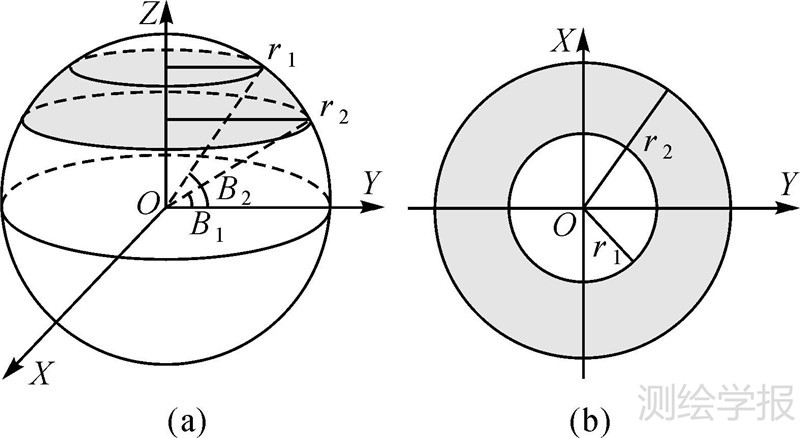
1 “纬线环法”剖分方案基本原理 1.1 “分割纬线”的纬度计算方法将球面上两条相邻纬线间的环状区域称为“纬线环”(图 1)。以八分之一球面为例,具体剖分原理如下:对于某个特定的剖分层次,首先用八分之一球面的面积去除该层次包含格网单元的个数,得到理想剖分单元的面积;接下来从极点开始(B0=90°),依次确定每条分割纬线的位置,使得相邻两条纬线间的“纬线环”面积,等于该条“纬线环”所包含的三角形的个数与理想剖分单元面积的乘积,从而确保该条“纬线环”的面积无变化。该方法可以将剖分单元面积变化控制在“纬线环”的内部,从而控制面积变化及变化积累,达到近似等面积剖分的效果。所以,该剖分方法称为“纬线环法”。分割纬线纬度的计算方法及推导过程如下。
|
| 图 1“纬线环”及其在XOY面上的投影 Fig. 1 “Parallel loop” and its projection on the XOY |
式(1)为球心位于坐标原点的球面方程。根据二重积分的原理,可以求得相邻两条纬线所夹的“纬线环”的面积(如图 1(a)中阴影部分),计算过程如下
上述积分中,A表示“纬线环”的面积;Dxoy为纬线环在XOY面上的投影区域;R为球面半径。化为极坐标形式解上述二重积分可得
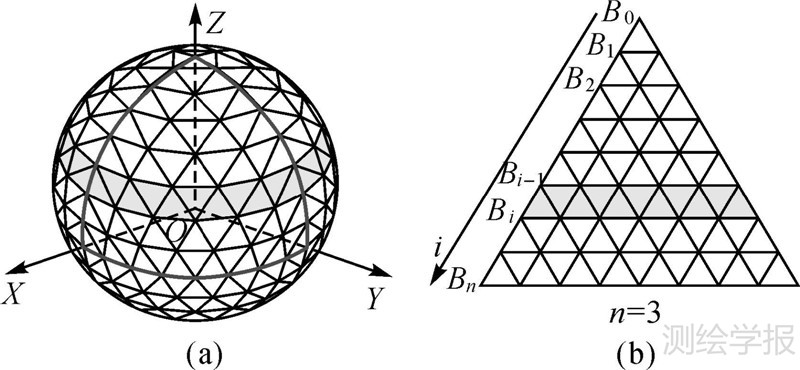
以正八面体的一个面为例,解出八面体上一条“纬线环”(如图 2(b)中阴影部分)的面积如下
|
| 图 2 分割纬线求解过程示意图 Fig. 2 Schematic diagram of solving segmentation parallel |
式(4)中,r1=RcosB1、r2=RcosB2,其中,B1、B2为待求的未知数,用每一条“纬线环”所包含的格网单元个数乘以理想剖分单元面积,得到该条“纬线环”的理想面积,并代入式(4)的右端构造方程,可解出每条分割纬线的纬度。进而按照等分经度的方法进一步分割,得到每一个QTM格网结点的经纬度坐标。分割纬线纬度求解的具体步骤如下。
(1) 首先确定第1条分割纬线的位置(i=1)。此时,B0=90°、r1=RcosB0、r2=RcosB1,n表示剖分层次。代入式(4)可得
解式(5)可得,第1条纬线的纬度B1为
(2) 根据第1条分割纬线的位置确定第2条的位置(i=2)。将r1=RcosB1、r2=RcosB2代入式(4)可得
解式(7),得到第2条纬线的纬度B2为
(3) 以此类推,递归求解各分割纬线的位置,第i条纬线的纬度Bi见式(9),其中0≤i≤2n,B0=90°
(4) 接下来按“平分经度”的方法确定模型的经度间隔,得到剖分单元节点的经纬度坐标。借鉴“纬线法”QTM剖分方案[20],用大圆弧线连接三角形格网的左右两边,而底边用两点间的纬线代替。
总之,在本文的剖分方法中,由于采用了“纬线环”的递归细分方法,下一级单元将保留其上一级单元的分割纬线,而“经度平分”则保证了上下层单元的格网节点具有简单明确的层次对应关系。这些特性将有利于全球多层次格网数据之间的查询与检索。
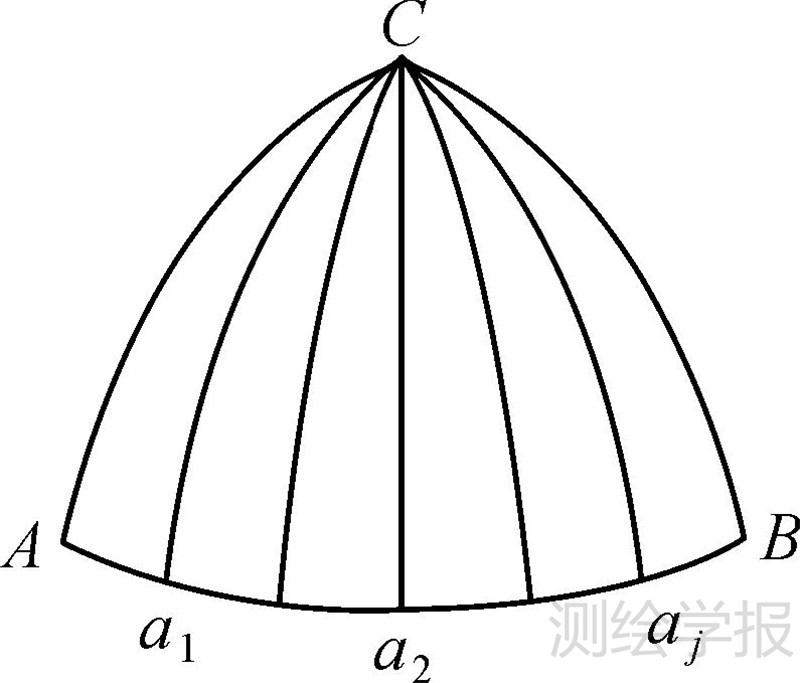
1.2 剖分单元面积计算球面三角形的3条边是大圆弧线,由于上述剖分方案中的三角形格网的底边是纬线,因此不能直接应用球面三角形面积计算公式进行计算。笔者采取文献[23]求解的方法,将三角形格网的底边纬线细分,用大圆弧线代替细分后的纬线求解子三角形的面积(如图 3所示)。细分得越密,计算精度越高。
|
| 图 3 剖分单元面积的近似计算 Fig. 3 Approximate computation of area of subdivision unit |
设A、B、C为球面上任意3点,X1、X2、X3分别为A、B、C 3点的向量(笛卡儿坐标系坐标),则球面三角形ABC的曲面面积为
如图 3所示,现将三角形格网单元ABC的纬线底边AB按经度平分成n段,纬线AB的长度用n段大圆弧线ajaj+1代替,三角形格网ABC的面积用n个小的球面三角形ajCaj+1来代替,三角形格网的曲面面积的计算公式如下
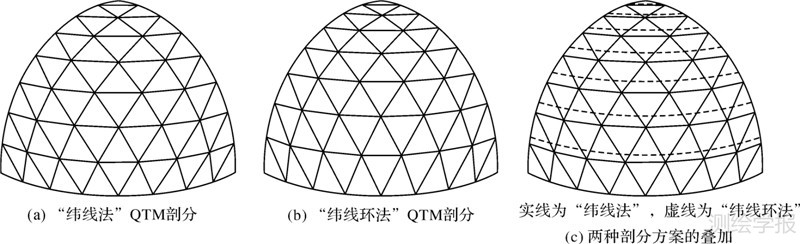
2 试验结果及分析本试验采用上述方法构建了改进的球面QTM模型,并与“纬线法”QTM模型进行了对比。以八分之一球面为例,两种QTM剖分模型及它们之间的叠加效果如图 4所示。从图中可以看出,改进后的“纬线环”法剖分,其分割纬线向极点方向移动,纬度大于相应的“纬线法”分割纬线的纬度。本节将从剖分模型的收敛性、格网单元面积的空间分布以及格网单元面积变化率的分布区段3个方面出发,对比两种剖分模型的差异。
|
| 图 4 两种剖分方案及其叠加效果 Fig. 4 Two kinds of subdivision schemes and their superposition |
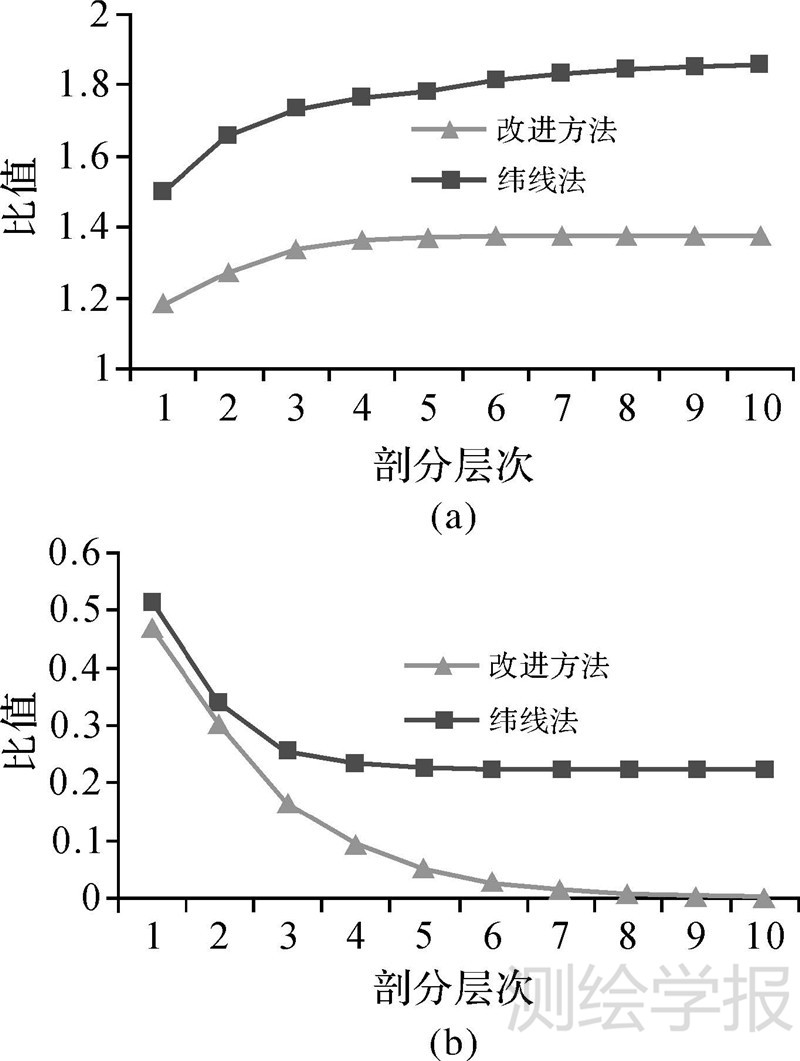
以八面体的一个面为例,计算了10个层次的格网单元面积的最大最小值比(area_max/min)、标准差(area_SD)(表 1)及其两种剖分模型随层次变化的变化趋势图(图 5)。从图中可以看出:随着剖分层次的增加,两种模型的剖分单元面积最大、最小值比越来越大,但其变化速度越来越小,最终收敛到1.38和1.73左右;剖分单元面积标准差越来越小,其变化速度也越来越小,最终趋于稳定。
| 层次 | 三角形个数 | 纬线法 | 改进方法 | ||||
| area-max/min | area_SD | area-max/min | area_SD | ||||
| 1 | 4 | 1.353 812 565 | 0.517 136 445 | 1.186 661 755 | 0.471 404 521 | ||
| 2 | 16 | 1.530 463 278 | 0.343 590 689 | 1.269 627 924 | 0.304 228 748 | ||
| 3 | 64 | 1.677 029 977 | 0.258 487 516 | 1.338 029 710 | 0.167 748 119 | ||
| 4 | 256 | 1.714 716 465 | 0.236 651 898 | 1.364 597 114 | 0.095 451 834 | ||
| 5 | 1024 | 1.724 207 897 | 0.229 680 661 | 1.371 282 896 | 0.054 390 527 | ||
| 6 | 4096 | 1.726 584 916 | 0.227 455 224 | 1.372 956 182 | 0.030 400 488 | ||
| 7 | 16 384 | 1.727 178 871 | 0.226 769 805 | 1.373 372 874 | 0.016 687 041 | ||
| 8 | 65 536 | 1.727 326 077 | 0.226 565 927 | 1.373 472 871 | 0.009 031 593 | ||
| 9 | 262 144 | 1.727 359 000 | 0.226 507 913 | 1.373 485 470 | 0.004 836 264 | ||
| 10 | 1 048 576 | 1.727 344 400 | 0.226 498 479 | 1.373 420 285 | 0.002 568 582 | ||
|
| 图 5area_max/min和area_SD随剖分层次的收敛特征 Fig. 5 Convergent characters of area_max/min and area_SD by partition levels increasing |
根据式(13)计算格网单元相对于理想剖分单元的面积变化率。其中,area为剖分单元面积;areanorm为理想剖分单元面积。
原“纬线法”QTM剖分单元面积变化率分布区段见表 2。可以看出:原有模型在前几层剖分中面积变化率的分布无明显规律,在第4层以后趋于稳定,只有22%左右的格网单元面积变化率在±5%以内,同时,模型的面积变化情况并没有随着层次的增加得到改善。
| % | |||||||
| 层次 | -∞~-20% | -20%~-10% | -10%~-5% | -5%~5% | 5%~10% | 10%~20% | 20%~+∞ |
| 1 | 0.00 | 50.00 | 0.00 | 0.00 | 25.00 | 25.00 | 0.00 |
| 2 | 12.50 | 12.50 | 0.00 | 43.75 | 12.50 | 0.00 | 18.75 |
| 3 | 12.50 | 21.88 | 0.00 | 28.13 | 14.06 | 15.63 | 7.81 |
| 4 | 6.25 | 22.66 | 10.16 | 22.27 | 12.50 | 19.53 | 6.64 |
| 5 | 3.13 | 23.05 | 14.84 | 21.00 | 10.55 | 22.27 | 5.18 |
| 6 | 4.64 | 22.85 | 12.70 | 21.95 | 10.69 | 21.80 | 5.37 |
| 7 | 3.87 | 24.28 | 11.43 | 22.36 | 10.75 | 21.20 | 6.12 |
| 8 | 3.49 | 24.46 | 11.93 | 22.17 | 10.68 | 20.68 | 6.59 |
| 9 | 3.68 | 24.31 | 11.74 | 22.33 | 10.70 | 20.57 | 6.67 |
| 10 | 3.77 | 24.29 | 11.74 | 22.25 | 10.69 | 20.57 | 6.69 |
改进后的“纬线环法”QTM剖分单元面积变化率分布区段见表 3。可以看出:该改进模型在前几层剖分中面积变化率的分布无明显规律,在第5层以后趋于稳定,50%以上的格网单元面积变化率分布在(-1%,1%)以内;将该区段进一步细分,并统计了剖分单元面积率在6—10层的分布情况,可以看出,格网单元面积变化情况继续得到改善,第8层以后剖分单元面积变化率被控制在±0.25%以内达90%以上,到第10层则达到99.3%。
| % | |||||||
| 层次 | -∞~-5% | -5%~-3% | -3%~-1% | -1%~1% | 1%~3% | 3%~5% | 5%~+∞ |
| 1 | 50.00 | 0.00 | 0.00 | 25.00 | 0.00 | 0.00 | 25.00 |
| 2 | 31.25 | 0.00 | 6.25 | 31.25 | 0.00 | 0.00 | 31.25 |
| 3 | 4.69 | 20.32 | 17.19 | 18.75 | 12.50 | 9.38 | 17.19 |
| 4 | 2.73 | 1.95 | 28.51 | 32.80 | 29.29 | 1.56 | 3.13 |
| 5 | 0.88 | 0.88 | 16.41 | 62.30 | 17.97 | 0.59 | 0.98 |
| 层次 | -∞~-0.75% | -0.75%~-0.5% | -0.5%~-0.25% | -0.25%~0.25% | 0.25%~0.5% | 0.5%~0.75% | 0.75%~+∞ |
| 6 | 6.35 | 12.55 | 15.06 | 31.90 | 15.04 | 12.60 | 6.54 |
| 7 | 1.99 | 1.46 | 15.41 | 62.10 | 15.58 | 1.47 | 2.02 |
| 8 | 0.62 | 0.64 | 2.22 | 93.02 | 2.22 | 0.64 | 0.63 |
| 9 | 0.17 | 0.20 | 0.90 | 97.50 | 0.89 | 0.20 | 0.17 |
| 10 | 0.04 | 0.05 | 0.26 | 99.30 | 0.26 | 0.05 | 0.04 |
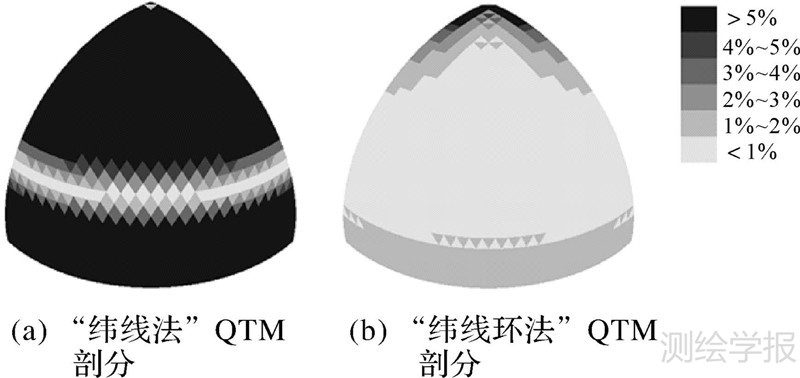
以八面体的一个面为例,将球面剖分5、6、7层,给每个面积变化率分布区段对应一个特定的灰度值,借助DirectX绘制了剖分模型面积变化率的位置分布灰度图(如图 6、7、8)。图中浅色区域的格网单元面积变化率较小,深色区域较大。
|
| 图 6 剖分单元面积变化率的位置分布(第5层) Fig. 6 Location distributions of the area variation rate of subdivision units (the 5th level) |

|
| 图 7 剖分单元面积变化率的位置分布(第6层) Fig. 7 Location distributions of the area variation rate of subdivision units (the 6th level) |

|
| 图 8 剖分单元面积变化率的位置分布(第7层) Fig. 8 Location distributions of the area variation rate of subdivision units (the 7th level) |
从图 6—图 8及其层次变化可以看出:①“纬线法”剖分得到的QTM剖分模型,只有中纬度区域有少量格网面积变化在1%以内,并呈带状分布,高纬度和赤道附近区域大部分格网单元的面积变化率均大于5%;②改进后的“纬线环法”QTM剖分模型,中低纬度区域大部分格网单元的面积变化率集中在1%以内,且分布均匀,只有高纬度近极点区域格网面积变化率较大;③随着剖分层次的增加,“纬线法”剖分模型的变化区域无明显变化,而改进后“纬线环法”剖分模型,其变化边界(变化率=1%)逐渐向极点方向移动,变化率<1%的范围越来越大。
3 结 语本文针对传统QTM模型格网面积变形较大的缺陷,在“纬线法”QTM剖分的基础上,提出一种近似等面积的剖分方案——“纬线环法”QTM剖分模型。通过与“纬线法”剖分模型进行对比试验,得出以下结论:
(1) 面积变化小。随着格网的不断细化,格网单元面积的最大最小值之比越来越大,标准差越来越小,变化速度越来越小,最终都趋于收敛。相比之下,改进后的“纬线环法”剖分模型的面积收敛性更好,这表明改进模型的格网面积分布更加均匀,各格网单元之间有更好的相似性。改进后的剖分模型,格网单元的面积变化率更小,至第10层剖分,“纬线法”QTM模型只有22%左右的格网面积变化率在5%以内,而“纬线环法”QTM模型99%以上的格网面积变化率被控制在0.25%以内。
(2) 位置分布明确。随着剖分层次的增加,改进后的“纬线环法”剖分模型,变化边界向两极移动,中低纬度区域近似等面积剖分。此外,面积变化不会随剖分层次的增加而积累,相反会逐渐减小。这一特点,非常有利于误差控制与分析。
(3) 计算简便。相比于“投影法”以及“小圆弧法”得到的等面积球面离散格网模型,该改进后的QTM剖分模型由于不需要复杂的数学变换,计算更加简便。
此外,由于改进模型的三角形格网的底边或顶边(上三角形对应底边,下三角型对应顶边)为纬线,格网与常规地理坐标间的对应关系更加明确。
| [1] | LUKATELA H. A Seamless Global Terrain Model in the Hipparchus System[EB/OL]. [2000-12-30]. http://www.geodyssey.com/global/papers. |
| [2] | 赵学胜, 侯妙乐, 白建军. 全球离散格网的空间数字建模[M]. 北京: 测绘出版社, 2007.ZHAO Xuesheng, HOU Miaole, BAI Jianjun. Spatial Digital Modeling of the Global Discrete Grids[M]. Beijing: Surveying and Mapping Press, 2007. |
| [3] | DUTTON G H.Lecture Notes in Earth Sciences:A Hierarchical Coordinate System for Geoprocessing and Cartography[M].Berlin: Springer-Verlag, 1999. |
| [4] | GOODCHILD M F,SHIREN Y.A Hierarchical Spatial Data Structure for Global Geographic Information Systems[J]. CVGIP:Graphical Models andImage Processing, 1992, 54(1): 31-44. |
| [5] | 白建军, 孙文彬, 赵学胜. 基于QTM的WGS-84椭球面层次剖分及其特点分析[J]. 测绘学报, 2011, 40(2): 243-248.BAI Jianjun, SUN Wenbin, ZHAO Xuesheng. Character Analysis and Hierarchical Partition of WGS-84 Ellipsoidal Facet Based on QTM[J]. Acta Geodaetica et Cartographica Sinica, 2011, 40(2): 243-248. |
| [6] | 关丽, 程承旗, 吕雪锋. 基于球面剖分格网的矢量数据组织模型研究[J]. 地理与地理信息科学, 2009, 25(3): 23-27.GUAN Li, CHENG Chengqi, LV Xuefeng. Study on the Organization Model for Vector Data Based on Global Subdivision Grid[J]. Geography and Geo-Information Science, 2009, 25(3): 23-27. |
| [7] | 赵学胜, 白建军, 王志鹏. 基于QTM的全球地形自适应可视化模型[J]. 测绘学报, 2007, 36(3): 316-320.ZHAO Xuesheng, BAI Jianjun, WANG Zhipeng. An Adaptive Visualized Model of the Global Terrain Based on QTM[J]. Acta Geodaetica et Cartographica Sinica, 2007, 36(3): 316-320. |
| [8] | SATOSHI I, FENG X. A Global Shallow Water Model Using High Order Multi-moment Constrained Finite Volume Method and Icosahedra Grid[J]. Journal of Computational Physics, 2010, 229(5): 1774-1796. |
| [9] | 邢华桥. 基于QTM的全球多分辨率水淹模拟[D]. 北京: 北京建筑工程大学, 2012.XING Huaqiao. Global Multi-resolution Submerging Simulation Based on QTM[D]. Beijing: Beijing University of Civil Engineering and Architecture, 2012. |
| [10] | SEONG J C. Implementation of an Equal-area Gridding Method for Global-scale Image Archiving[J]. Photogrammetric Engineering & Remote Sensing, 2005, 71(5): 623-627. |
| [11] | LUGO J A, CLARKE K C. Implementation of Triangulated Quadtree Sequencing for a Global Relief Data Structure[C]//Proceedings, AUTO CARTO 12.Charlotte, NC:[s.n.],1995. |
| [12] | ROŞCA D, PLONKA G. An Area Preserving Projection from the Regular Octahedron to the Sphere[J]. Results in Mathematics, 2012, 62(3-4): 429-444. |
| [13] | SNYDER J P. An Equal-area Map Projection for Polyhedral Globes[J]. Cartographica: The International Journal for Geographic Information and Geovisualization, 1992, 29(1): 10-21. |
| [14] | BJØRKE J T, GRYTTEN J K, HGER M, et al. A Global Grid Model Based on “Constant Area” Quadrilaterals[C]//ScanGIS.Horten: Norwegian Defence Research Establishment,2003, 3: 238-250. |
| [15] | BJØRKE J T, NILSEN S. Examination of a Constant-area Quadrilateral Grid in Representation of Global Digital Elevation Models[J]. International Journal of Geographical Information Science, 2004, 18(7): 653-664. |
| [16] | LEOPARDI P. A Partition of the Unit Sphere into Regions of Equal Area and Small Diameter[J]. Electronic Transactions on Numerical Analysis, 2006, 25(1): 309-327. |
| [17] | BECKERS B, BECKERS P. A General Rule for Disk and Hemisphere Partition into Equal-area Cells[J]. Computational Geometry, 2012, 45(7): 275-283. |
| [18] | ZHOU Mengyun, CHEN Jing, GONG Jianya. A Pole-oriented Discrete Global Grid System: Quaternary Quadrangle Mesh[J]. Computers & Geosciences, 2013, 61: 133-143. |
| [19] | TALBOT B G, TALBOT L M. Fast-earth: A Global Image Caching Architecture for Fast Access to Remote-sensing Data[C]//Proceedings of 2013 IEEE Aerospace Conference. Big Sky, MT: IEEE,2013: 1-10. |
| [20] | SAHR K, WHITE D, KIMERLING A J. Geodesic Discrete Global Grid Systems[J]. Cartography and Geographic Information Science, 2003, 30(2): 121-134. |
| [21] | SONG Lian,KIMERLINGA J,SAHR K. Developing an Equal Area Global Grid by Small Circle Subdivision[C]//GOODCHILD M, KIMERLING A J.Discrete Global Grids.Santa Barbara, CA:National Center for Geographic Information & Analysis, 2002. |
| [22] | HOLHOŞ A, ROŞCA D. An Octahedral Equal Area Partition of the Sphere and Near Optimal Configurations of Points[J].Computers & Mathematics with Applications, 2014, 67(5): 1092-1107. |
| [23] | 赵学胜, 孙文彬, 陈军. 基于QTM的全球离散格网变形分布及收敛分析[J]. 中国矿业大学学报, 2005, 34(4): 438-442.ZHAO Xuesheng, SUN Wenbin, CHEN Jun. Distortion Distribution and Convergent Analysis of the Global Discrete Grid Based on QTM[J]. Journal of China University of Mining & Technology, 2005, 34(4): 438-442. |