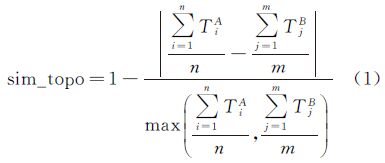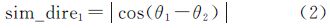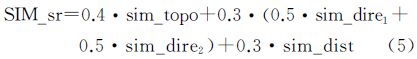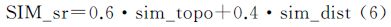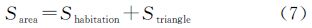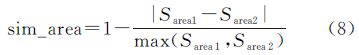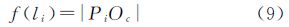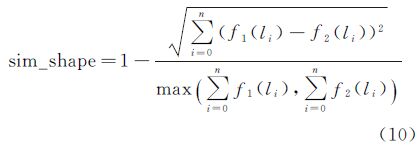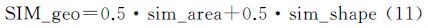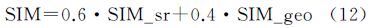城市化进程的加速使得道路变化周期越来越短,如何对道路数据进行准确、及时的更新以满足地理空间数据现势性的要求成为当前测绘工作者面临的重点和难点。与此同时,不同部门对相同区域重复采集生产了大量道路数据,如何将这些多源道路数据进行有效集成与融合以达到数据共享与优势互补的目的则是当前GIS工作者面临的另一项难题。无论是道路数据更新还是多源道路数据集成与融合均建立在同名实体匹配的基础上。同名实体是指在两个或两个以上不同数据源中反映现实世界同一地物或地物集的空间实体。受制图误差、不同应用目的以及制图综合等因素的影响,不同数据源中的同名实体通常都存在着差异。同名实体匹配就是通过分析空间实体的差异和相似性识别出不同数据来源中表达现实世界同一地物或地物集的过程[1]。同名实体间匹配关系准确、快速的识别与建立是后续道路数据更新以及集成与融合的基础,具有重要意义[2]。
国内外学者对道路网匹配进行了广泛的研究,如文献[3]利用“缓冲区增长法”确定待匹配线的候选匹配集;文献[4]提出了非对称性缓冲区增长法,在匹配过程中可动态调整缓冲区半径;文献[5]在基于概率理论匹配模型的基础上,综合运用多个匹配指标,通过计算实体匹配概率大小来确定匹配实体;文献[6]将道路目标分为3个匹配层次,利用缓冲区分析和拓扑关系开发了系列算法完成匹配;文献[7]改局部寻优为全局寻优,综合利用道路节点与弧段的特征信息,通过概率松弛法获得匹配关系;文献[8]提出一种基于结构模式的道路网节点匹配方法;文献[9]利用概率松弛法对道路网进行自动匹配;对于多尺度道路网的匹配问题,文献[10]利用距离指标对道路间是否匹配进行衡量。
上述研究极大推动了道路匹配技术的发展,为解决道路数据的集成与更新提供了有力支持。总结分析上述方法可得:多数多源同比例尺道路匹配方法通常利用道路自身的几何、拓扑、语义等特征进行匹配,而相对较少顾及道路邻域环境中其他要素对匹配过程的影响与约束,从而可能影响匹配效果的进一步提高;同时,在大多数匹配方法中,道路空间位置的邻近程度始终是确定匹配关系的重要依据,而一旦匹配数据间存在位置偏差以及更为复杂的旋转偏差时,匹配结果可能会受到更大的影响。由于不同来源的道路数据的获取方式和精度可能不相同,使得同名实体间产生了较大位置偏差,虽然在实际操作的数据预处理过程中,通过系统改正方法能够对这种偏差进行纠正,但是待匹配双方数据之间可能存在着非均匀的位置偏差,并且从目前实际作业情况看,许多数据来源渠道多样,投影不同,投影类型未知,也给统一修正偏差带来了较大难度,如果盲目修改偏差,则可能会导致数据质量下降。因此即使通过整体性的坐标系统纠正,待匹配数据双方中的要素也可能无法实现完全的精确配准,数据间仍可能存在一定的偏差[11],从而影响后续匹配过程,所以需要对这种情况单独进行讨论。
实际上,任何空间要素都不是孤立存在的,与其邻域要素之间必然存在一定的联系[12]。对道路而言,无论在现实世界还是在地图中,居民地都是与其联系最为密切的要素。例如,人们在熟悉一条陌生街道的过程中,通常会参照该街道周围建筑物的分布状况,形成“心象地图”,当需要再次寻找该街道时,将该道路周边的建筑物作为重要的定位依据。空间数据匹配中的相似性度量过程与人类的这种空间认知过程十分相似,因此本文借鉴上述人类空间认知特点,将道路邻域居民地群组的相似性作为判断匹配的衡量指标,提出一种顾及邻域居民地群组相似性的道路网匹配方法。
1 顾及邻域要素相似性的匹配思路地理要素自身具有一定的空间特征,同时也与其邻域要素之间存在着较多的空间联系。对于空间数据中互相匹配的同名实体而言,除了其自身空间几何特征应具有高度相似性外,其邻域环境也应非常相似,有时只考虑实体自身的特征进行匹配不足以得到正确的匹配结果,例如,可能出现两个或多个对象之间虽然具有较高的位置、形状相似度,但它们之间并不匹配的情况[13]。所以在匹配过程中顾及同名实体邻域环境的相似性,能够增强匹配过程中辨别同名实体的能力。这种相似性主要体现在邻域环境自身的空间关系(拓扑关系、方向关系、度量关系等)以及几何特征(形状、大小、分布等)应具有相似性,故匹配过程应主要从这两方面衡量邻域环境的相似性。由于匹配数据双方语义信息可能存在较多的缺失和较大的差异,所以本文方法均不考虑邻域环境中要素的语义相似性。
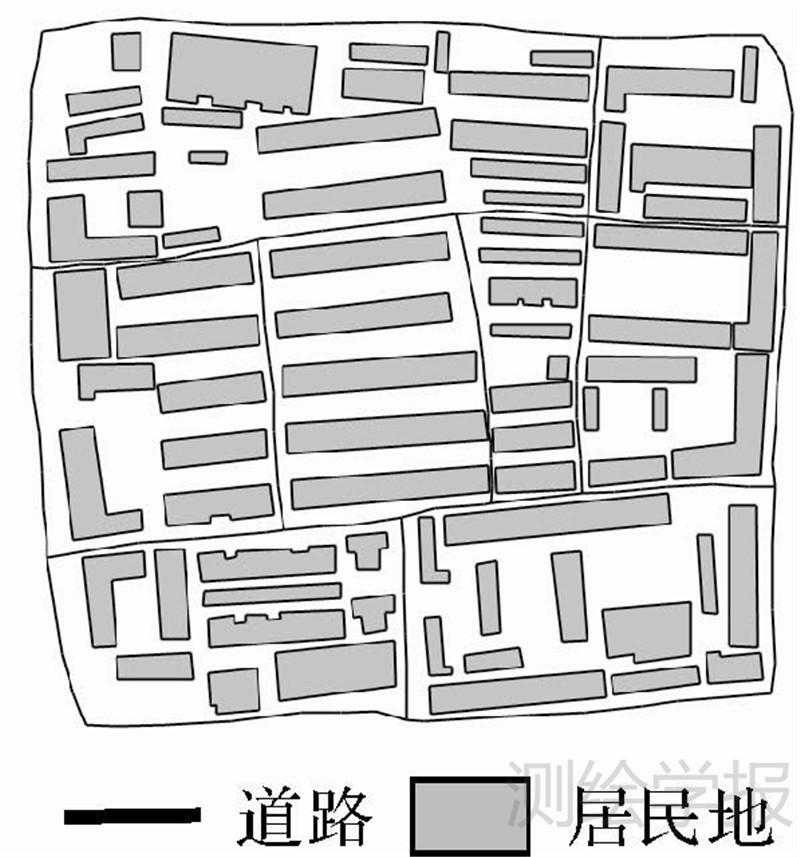
2 利用城市骨架线网确定道路邻域居民地群组在大比例尺城市地图中,相比植被、水系、地貌,道路和居民地是最为重要的两类要素,是城市地图重点表达的主体,所以本文只将居民地作为道路的邻域对象进行研究。如图 1所示,大比例尺城市地图中居民地要素一般散列地分布在道路两侧,所以道路邻域范围内的居民地呈现出面状群组的形式。确定道路邻域居民地群组最直观的方法是根据居民地距道路的距离进行判断,如果距离满足阈值则将其视为与道路相邻的居民地。由于不同来源的数据间存在一定程度的差异,因此设置合适的阈值较为困难。一旦阈值设置不当,则可能造成同名道路的邻域居民地群组之间存在差异,从而影响居民地群组相似性计算,进而影响后续的匹配过程。为此本文利用城市骨架线网确定道路邻域居民地群组,该方法能够提取一致程度较高的道路邻域居民地群组。
|
| 图 1 道路、居民地示例 Fig. 1 Example of road and habitation |
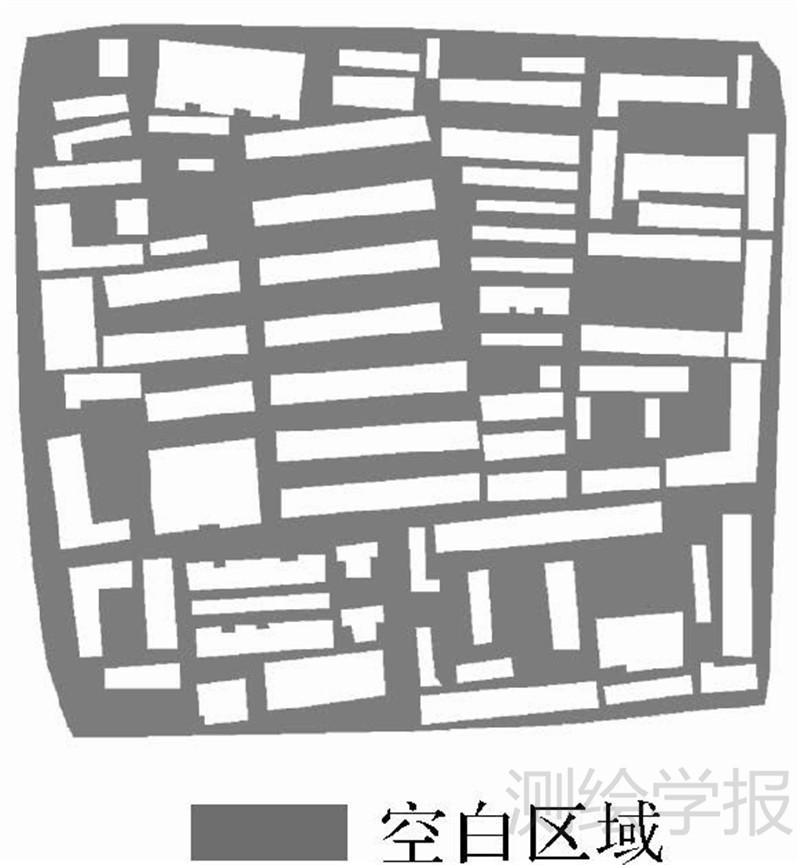
城市骨架线网由道路和空白区域骨架线两部分构成。具体来说,地图中存在道路的地方,直接将道路视为骨架线;地图中道路和居民地以外的空白区域,则提取其骨架线。图 1中道路和居民地数据的空白区域如图 2所示,空白区域指的是地图幅面中除道路和居民地外剩余所有区域的总和。
|
| 图 2 空白区域示意图 Fig. 2 Sketch map of blank region |
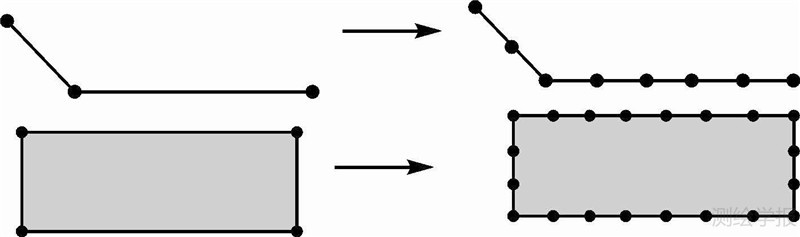
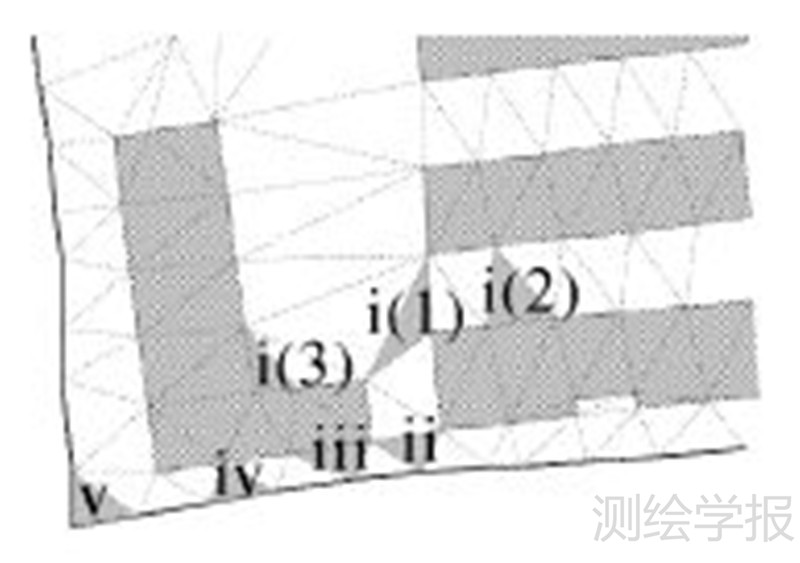
采用约束Delaunay三角网方法提取空白区域骨架线[14],具体步骤为:①数据节点加密,初始道路和居民地数据中节点总数相对较少,为了构建满足空白区域骨架线提取要求的约束Delaunay三角网,在构网前需对道路和居民地数据进行节点加密处理(如图 3);②以道路和居民地外围轮廓为约束边,构建约束Delaunay三角网(如图 4);③提取空白区域骨架线。依据三角形顶点在居民地和道路上的数量与位置将三角形分为5类(图 5):ⅰ类三角形,3个顶点均在居民地轮廓上,其中根据顶点位于几个不同居民地轮廓上又分为3小类,ⅰ(1)类三角形,3个顶点分别在3个不同的居民地轮廓上,ⅰ(2)类三角形,3个顶点在两个不同的居民地轮廓上,ⅰ(3)类三角形,3个顶点在同一居民地轮廓上;ⅱ类三角形,一个顶点在道路上,另两个顶点在两个不同居民地轮廓上;ⅲ类三角形,一个顶点在道路上,另两个顶点在同一居民地轮廓上;ⅳ类三角形,两个顶点在道路上,另一个顶点在居民地轮廓上;ⅴ类三角形,3个顶点均在道路上。
|
| 图 3 道路和居民地加密处理 Fig. 3 Densification of road and habitation |

|
| 图 4 构建约束Delaunay Fig. 4 Constructing constraint Delaunay triangulation network |
|
| 图 5 三角形分类 Fig. 5 Classification of triangle |
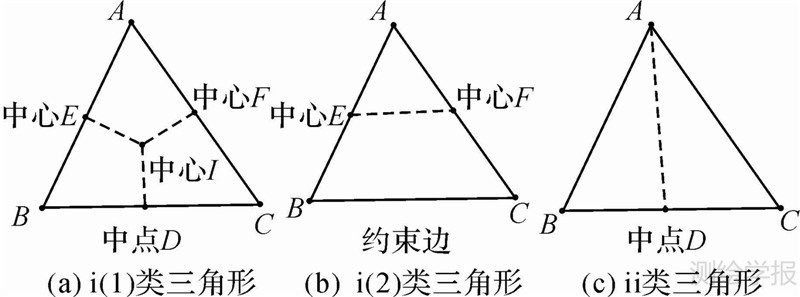
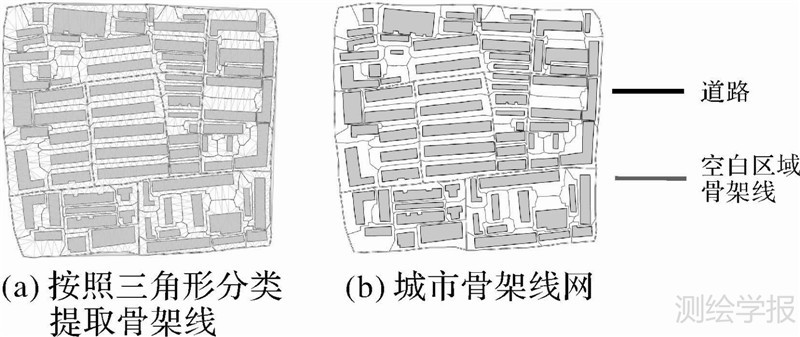
如图 6所示,ⅰ(1)类三角形,分别连接三角形中心和三边的中点形成骨架线;ⅰ(2)类三角形,首先判断其唯一的约束边,然后连接两非约束边的中点形成骨架线;ⅱ类三角形,连接在道路上的唯一顶点与其对边中点形成骨架线;ⅲ、ⅳ、ⅴ类三角形不进行任何处理。所有三角形按照上述方法连接后即可得到空白区域的骨架线(图 7(a)),空白区域骨架线和道路一起构成城市骨架线网(图 7(b))。
|
| 图 6 不同类型三角形骨架线提取方法 Fig. 6 Skeleton line extraction methods of different triangles |
|
| 图 7 城市骨架线网提取结果 Fig. 7 Urban skeleton-line network |
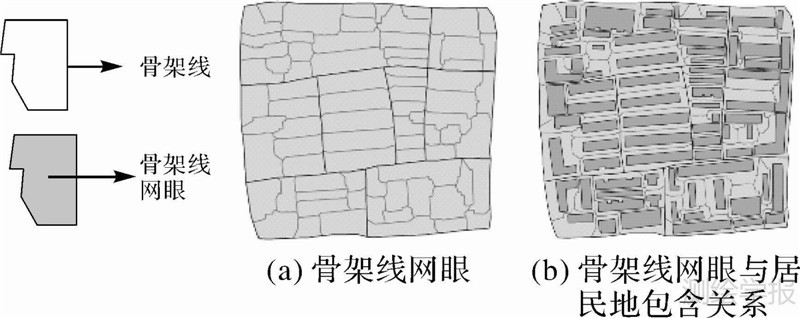
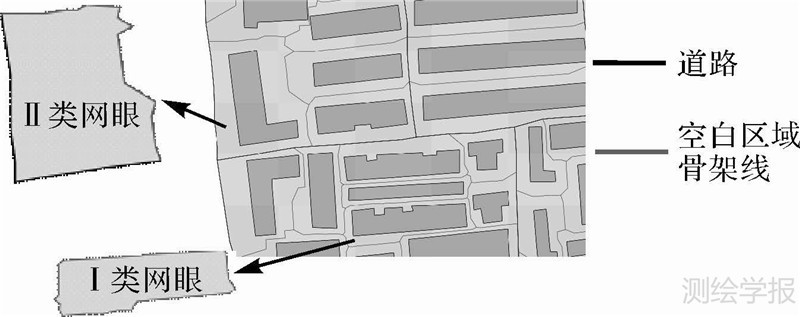
在城市骨架线网中,将骨架线围成的最小闭合区域称为“骨架线网眼”,图 8(a)中灰色区域即为骨架线网眼。骨架线网眼的特点如下:①骨架线网眼为面状要素,其轮廓由城市骨架线组成;②每个骨架线网眼中均只包含一个居民地要素(图 8(b));③骨架线网眼之间均为相接拓扑关系。根据骨架线网眼轮廓是否包含道路这一原则对骨架线网眼进行分类,如图 9所示,Ⅰ类骨架线网眼轮廓均由空白区域骨架线组成,Ⅱ类骨架线网眼轮廓由空白区域骨架线和道路共同组成。
|
| 图 8 骨架线网眼构建 Fig. 8 Skeleton-line mesh |
|
| 图 9 骨架线网眼分类 Fig. 9 Classification of skeleton-line mesh |
将一条道路参与构成的所有Ⅱ类骨架线网眼中包含的居民地视为其相邻居民地,由此可确定出道路的邻域居民地群组。图 10中,红色居民地即为与加粗显示道路的相邻居民地,所有与该道路相邻的居民地共同构成其邻域居民地群组。由于本文主要针对相同比例尺的道路数据进行匹配,数据中居民地综合程度基本相同,所以同名道路通过该方法确定的居民地群组具有较高的相似性,因此能够以此作为道路匹配与否的判断指标。通过构建城市骨架线网的方法确定道路邻域居民地群组具有较强的稳定性,使得多源数据中同名道路的邻域居民地群组具有较高的一致性。

|
| 图 10 道路邻域居民地群组 Fig. 10 Neighborhood habitation cluster of road |
利用道路邻域居民地群组相似性进行匹配的前提是对邻域居民地群组(面群要素)的空间关系以及几何特征进行描述和计算,进而通过比较其相似性来确定其对应的道路之间是否匹配[15]。
3.1 空间关系相似度计算 3.1.1 拓扑相似度通常将居民地的邻居居民地数量作为其拓扑总数,由于大比例尺城市地图中居民地之间一般为相离关系,所以直接确定居民地的邻居居民地数量较为困难。考虑到骨架线网眼之间均为相接拓扑关系,并且每个骨架线网眼中均唯一包含一个居民地,所以可通过计算骨架线网眼的邻居网眼数量代替居民地的邻居居民地数量,从而获得居民地的拓扑总数。骨架线网眼相接关系分为公共节点相接和公共边相接两种情况,本文只将具有公共边的两骨架线网眼互相视为邻居骨架线网眼。一个总数为n的居民地群组A和一个总数为m的居民地群组B,二者的拓扑相似度计算如下[16]
式中,TiA为居民地群组A中第i(i=1,2,…,n)个居民地的拓扑总数;TjB为居民地群组B中第j(j=1,2,…,m)个居民地的拓扑总数;sim_topo为居民地群组A和B之间的拓扑相似度。 3.1.2方向相似度 3.1.2 .1 居民地群组整体方向计算道路邻域居民地群组一般沿道路分布,所以其整体呈现出一定的方向性,并且这种方向大多与道路延伸方向较为接近。在计算居民地群组整体方向时,利用居民地的几何中心代替居民地,即将面群转化为点群计算[17]。采用文献[18]中的标准差椭圆法计算点群的整体方向,标准差椭圆是用来描述群组目标分布方向偏离的。对整体方向角为θ1、θ2的两个居民地群组,其方向相似度计算公式为
3.1.2 .2居民地群组中单个居民地方向计算居民地群组整体方向描述的是面群目标方向的“集中趋势”,但不能有效顾及居民地群组内单个面要素目标之间的方向一致性,很可能出现居民地群组整体方向虽然一致,但是其可能并不相似的情况,所以需要对居民地群组内单个居民地的方向进行计算。面要素按照其轮廓形状划分,可分为比较规则的面要素(如建筑物等)和不规则的面要素(如水域、植被等)。由于居民地(建筑物)外形较为规则,所以通常利用最小面积外接矩形计算其方向(图 11)。最小面积外接矩形的最长边与水平方向的夹角即为单个居民地的方向,该方向与人们的直观认知较为一致[19]。

|
| 图 11 最小面积外接矩形计算居民地方向 Fig. 11 Habitation direction calculation by minimum area bounding rectangle |
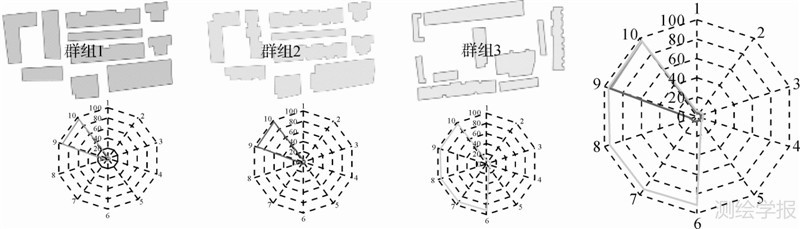
将居民地群组中每个居民地的方向利用雷达图进行表示来计算居民地群组中单个居民地方向的整体趋势相似度,因为雷达图不仅包含了居民地群组中所有单个居民地的方向信息,而且能够对其全体方向特点进行统计显示。如图 12所示,居民地群组1和居民地群组2中单个居民地的方向较为近似,所以其对应的雷达图的图形相似度较高,而与居民地群组3相比,单个居民地方向整体趋势差异较大,所以其对应的雷达图的图形相似度较低。所以通过雷达图能够较好反映居民地群组中单个居民地方向的全体统计规律,具体的相似度计算公式为
式中,Area1、Area2分别为两居民地群组雷达图的面积;OverlapArea为两群组雷达图叠加图中重叠区域的面积。
|
| 图 12 居民地群组雷达图 Fig. 12 Radar chart of habitation cluster |
空间距离能够反映面群要素之间的亲疏程度,空间距离越大,则分布越稀疏,空间距离越小则分布越密集。面状要素之间的距离可分为中心距离、极小距离和极大距离,本文选取中心距离作为空间距离的度量指标。中心距离为两个面要素几何中心之间的距离,所以对两个居民地群组,设dis1、dis2为两个居民地群组中居民地之间的平均空间距离,故其距离相似度计算公式为
3.1.4空间关系总相似度上面分别定义了道路邻域居民地群组空间关系的拓扑、方向和距离相似度,根据Egenhofer和Mark提出的“拓扑关系起主导作用,其他可度量关系起提炼作用”的原则[20],突出拓扑关系在空间关系中的关键作用,在对居民地群组之间空间关系相似度进行整体度量时,对上述3种空间关系相似度分别赋予不同的权值。采用文献[15]中对拓扑、方向以及距离关系的权值设置,分别赋予上述3种相似度0.4、0.3、0.3的权值。所以,道路邻域居民地群组空间关系总相似度的计算公式为
需要特别指出:对于存在旋转偏差的数据匹配问题,居民地群组间的方向相似度受到旋转影响差异较大,所以在计算空间关系总相似度时应不考虑方向相似度,只计算群组间的拓扑相似度和距离相似度,仍根据上述原则设置权重值,具体计算公式为
3.2 几何特征相似度计算空间群组的几何特征通常包括群组的个体数量、分布范围、分布密度、分布中心、分布轴线等。由于个体数量比较简单,对其单独进行讨论意义不大,且在空间关系中拓扑相似度的计算过程中已经隐含了对个体数量的描述,故不再考虑居民地的数量;同理,分布中心和分布轴线与计算方向时的方法比较类似,所以也不再进行计算。由于道路邻域居民地群组中居民地数量一般不会过多,故讨论其分布密度意义不大。所以主要讨论居民地群组的分布范围。
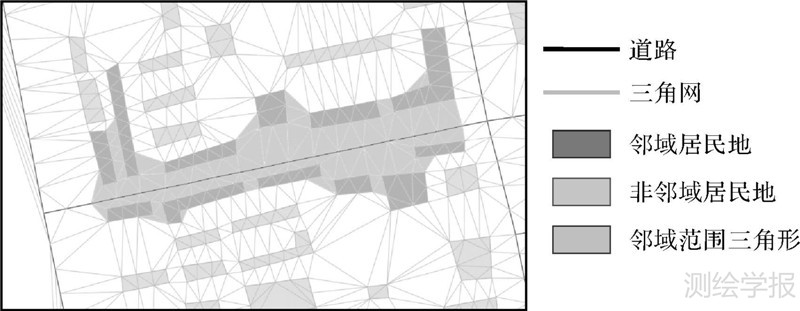
邻域居民地群组的分布范围是个不确定问题,选取合适的包容所有居民地的多边形作为分布范围,必须符合人的直观认知。传统方法中用凸壳来表达面群的分布范围是不太准确的,因为可能将大面积的没有居民地覆盖的凹部区域也视为面群的分布范围[21]。通过对三角网进行“剥皮”操作得到的居民地群组分布范围较为符合人类的视觉习惯(图 13)。将3个顶点均在邻域居民地群组轮廓上和道路上的三角形视为邻域居民地范围内的三角形,所以道路邻域居民地群组分布范围的面积可表示为
式中,Sarea代表邻域居民地群组分布范围的总面积;Shabitaion代表邻域居民地群组中居民地的总面积;Striangle代表邻域范围内三角形的总面积。对于两个邻域范围面积分别为Sarea1和Sarea2的居民地群组,其分布范围面积相似度计算公式为
|
| 图 13 邻域居民地群组范围确定 Fig. 13 Neighborhood habitation area |
只对分布范围的面积进行相似度计算还不足以描述其相似度,因为可能出现形状差异很大的群组分布范围具有相同或相近的面积,所以需对分布范围进行形状相似度计算。由于居民地群组分布范围多边形的形状不规则并且具有较多的节点,所以采用文献[22]提出的多级弦长法对其进行形状描述。设形状描述函数为
以多边形边界上各点Pi到形心点Oc的距离|PiOc|作为形状描述函数的值,以轮廓上的某节点为匹配起始点P0到轮廓上任一点Pi的弧长li作为形状描述的参数,所以两个居民地群组分布范围的形状相似度计算公式为
由于没有明显的侧重,邻域居民地群组几何特征的总相似度为分布范围面积相似度和形状相似度的平均值[15],计算公式如下
3.3 总体相似度计算空间目标相似性研究中,文献[23]提到一个重要原则,即空间目标之间的拓扑、方向和距离关系是最为关键的。所以在计算两个居民地群组总体相似度时,主要突出群组的空间关系相似度,赋予邻域居民地群组的空间关系相似度较大的权重。本文同样参考文献[15]中的经验值,将空间关系相似度权重设为0.6,则几何特征相似度权重为0.4。所以居民地群组总体相似度计算公式可表达为
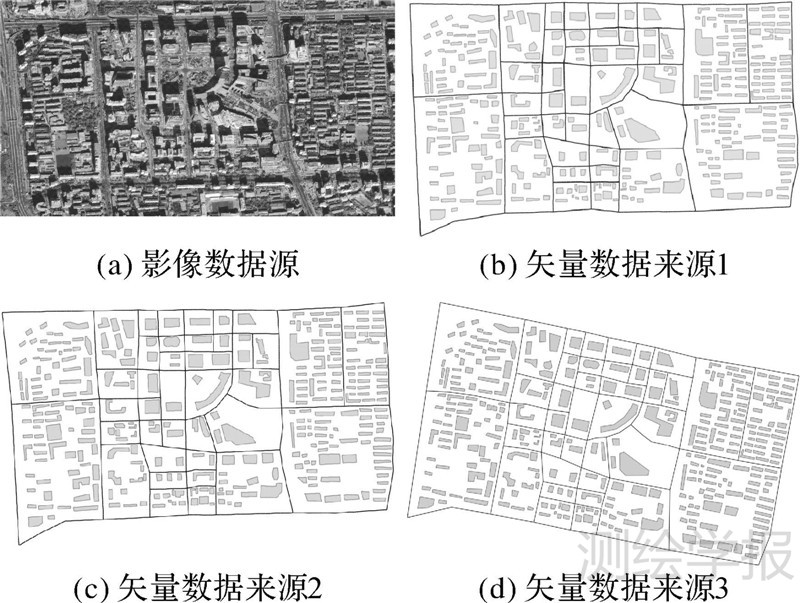
式中,SIM为居民地群组总体相似度;SIM_sr为居民地群组空间关系相似度;SIM_geo为居民地群组几何特征相似度。 4 道路网匹配实例及对比分析 4.1 数据来源说明图 14(a)为北京中关村部分区域影像,选取该区域相同比例尺不同来源的矢量数据进行匹配试验。如图 14(b)、(c)、(d)所示,数据中均包含居民地和道路要素,数据来源为大比例尺城市地图数据,道路网在交叉口处表现为断开的路段。
|
| 图 14 试验数据来源 Fig. 14 Test data of matching |
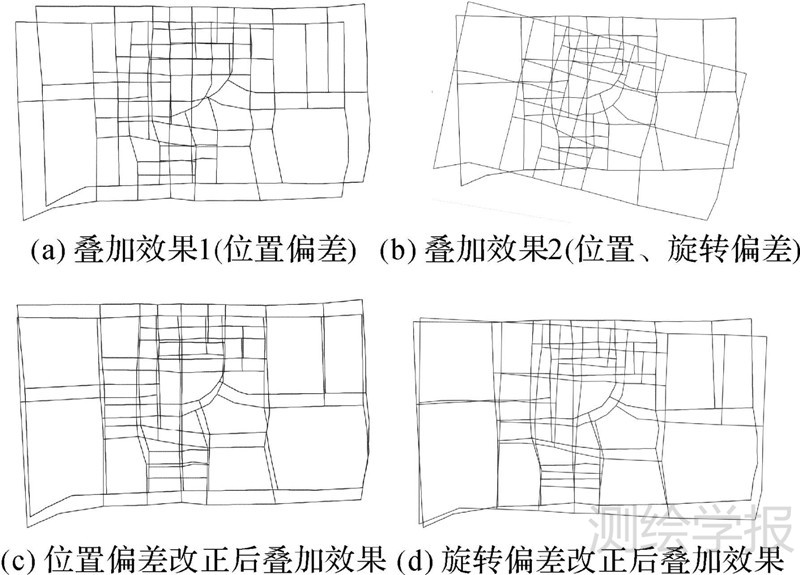
从数据源1和数据源2、3的叠加效果(图 15(a)、(b))可得数据源间分别具有较大的位置偏差和旋转偏差,所以需对数据源进行系统误差改正。由于不同来源的数据具有较强的不确定性,在经过系统误差改正后发现:数据源1和数据源2之间的位置偏差中的横坐标偏差得到了较好的修正,但纵坐标偏差修正效果不理想,仍存在一定的偏差(图 15(c));数据源1和数据源3之间的旋转偏差虽得到了一定的削弱但仍未完全消除,仍存在一定的旋转偏差(图 15(d))。所以在系统误差改正后,仍可能需要面对数据偏差对匹配过程造成的困难与影响。
|
| 图 15 数据系统误差改正 Fig. 15 Systematic error compensation |
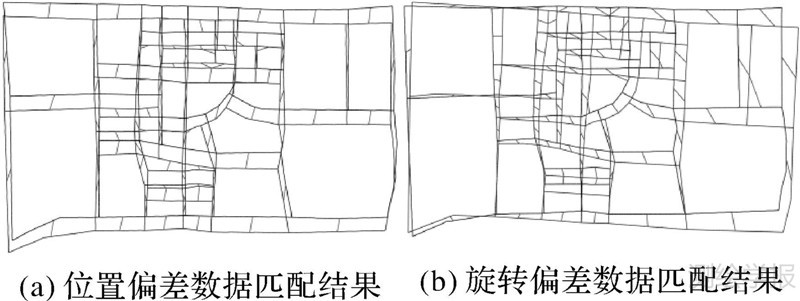
选取道路网匹配方法中较为成熟的缓冲区增长算法进行对比匹配试验,在该方法匹配过程中单纯依靠道路落入缓冲区内的长度与总长度的比值这一条件进行判断,而未顾及道路邻域居民地群组的相似性。图 16(a)、(b)分别为缓冲区增长算法对存在位置偏差与旋转偏差数据的匹配结果显示。
|
| 图 16 缓冲区增长算法匹配结果 Fig. 16 Matching results of the buffer growth method |
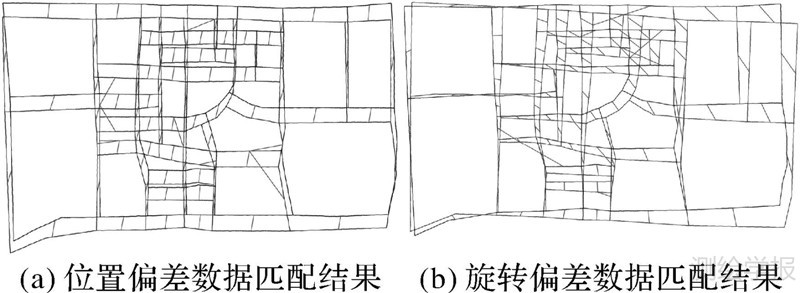
分别对上述系统误差改正处理后仍存在位置和旋转偏差的两组道路网数据利用本文提出的顾及道路邻域居民地群组相似性的方法进行匹配试验。具体的匹配流程为:①对待匹配道路建立缓冲区,在匹配数据源中确定候选匹配对象,由于匹配数据之间位置偏差较大,所以缓冲区半径应设置较大,确保候选匹配集中包含匹配对象;②对匹配双方构建城市骨架线网,并确定每条道路的邻域居民地群组;③在候选匹配集中进行遍历,计算其中每条道路与待匹配道路的邻域居民地群组相似度,将相似程度最高的道路作为匹配对象。按照上述流程进行匹配试验,图 17(a)为存在位置偏差的道路数据的匹配结果显示,图 17(b)为存在旋转偏差的道路数据的匹配结果显示,图中短线为匹配关系标识线。
|
| 图 17 本文方法匹配结果 Fig. 17 Matching results of the proposed method |
对本文匹配算法和缓冲区增长算法进行匹配质量评价(表 1),得出本文算法的匹配正确率较高,表明本方法能够较好解决系统误差改正后仍存在位置或旋转偏差的道路网数据的匹配问题。
| 匹配情况1 | 匹配方法 | 匹配正确率/(%) | 匹配情况2 | 匹配方法 | 匹配正确率/(%) |
| 位置偏差 | 本文算法 | 84.7 | 旋转偏差 | 本文算法 | 84.0 |
| 缓冲区增长算法 | 50.0 | 缓冲区增长算法 | 70.4 |
对两种匹配算法作如下分析:由于系统误差改正后仍未完全消除位置或旋转偏差,利用位置邻近原则的匹配方法会受到影响,造成缓冲区增长算法的匹配正确率相对较低。但是数据间的位置和旋转偏差不会影响道路邻域居民地群组的分布状况,即不会改变道路与居民地以及居民地群组之间的空间关系和几何特征,因而能够通过对道路邻域居民地群组的相似性度量进行匹配,这有效弥补了位置和旋转偏差对匹配的影响。本方法顾及了道路邻域环境(居民地群组)的相似性,能够得到相对较好的匹配结果。针对系统误差纠正后位置精度较高的数据,试验结果表明本方法也能得到较为满意的匹配结果,所以本方法具有一定的通用性。
对于本方法匹配结果中的错误匹配情况,其原因是多源数据具有不确定性,本方法在确定道路的邻域居民地群组时,只能期望最大程度的保证其一致性;居民地数据的不确定性导致即便同名道路的邻域居民地群组,其空间特征和几何特征相似度也可能不高,而非同名道路间的邻域居民地群组也可能具有较高的相似度,这也可能造成错误匹配。总体而言,上述两种情况出现概率不高,所以本方法能够确保大部分道路匹配结果的正确性。
5 结 论本文提出一种顾及邻域居民地群组相似性的道路网匹配方法,相比只单独利用道路自身特征进行匹配的方法,本方法的特点在于:顾及了道路周边居民地群组的相似性,将居民地群组的空间关系和几何特征作为道路匹配的重要衡量指标,使得匹配过程不再对位置条件过于依赖,能够有效解决存在位置或旋转偏差的道路数据间的匹配问题。本方法在居民地群组相似度计算过程中采用的是一般经验权重值,所以在后续工作中需对居民地群组相似性的指标权重进行更多讨论,以使其相似性的计算结果更为准确可靠,以进一步确保匹配质量。
| [1] | 郝燕玲, 唐文静, 赵玉新, 等. 基于空间相似性的面实体匹配算法研究[J]. 测绘学报, 2008, 37(4): 501-506. HAO Yanling, TANG Wenjing, ZHAO Yuxin, et al. Areal Feature Matching Algorithm Based on Spatial Similarity[J]. Acta Geodaetica et Cartographica Sinica, 2008, 37(4): 501-506. |
| [2] | QUDDUS M A, OCHIENG W Y, NOLAND R B. Map Matching Algorithms for Intelligent Transport Systems Application[C]//Proceedings of the 13th World Congress on Intelligent Transport Systems and Services. London: TRID, 2006. |
| [3] | WALTER V, FRITSH D. Matching Spatial Data sets: A Statical Approach[J]. International Journal of Geographical Information Science, 1999, 13(5): 445-473. |
| [4] | ZHANG Meng, MENG Liqiu. An Iterative Road-Matching Approach for the Integration of Postal Data[J]. Computers, Environment and Urban Systems, 2007, 31(5): 597-615. |
| [5] | 童小华, 邓愫愫, 史文中. 基于概率的地图实体匹配方法[J]. 测绘学报, 2007, 36(2): 210-217. TONG Xiaohua, DENG Susu, SHI Wenzhong. A Probabilistic Theory-based Matching Method[J]. Acta Geodaetica et Cartographica Sinica, 2007, 36(2): 210-217. |
| [6] | 胡云岗, 陈军, 赵仁亮, 等. 地图数据缩编更新中道路数据匹配方法[J]. 武汉大学学报(信息科学版), 2010, 35(4): 451-456. HU Yungang, CHEN Jun, ZHAO Renliang, et al. Matching of Roads under Different Scales for Updating Map Data[J]. Geomatics and Information Science of Wuhan University, 2010, 35(4): 451-456. |
| [7] | 赵东保, 盛业华. 全局寻优的矢量道路网自动匹配方法研究[J]. 测绘学报, 2010, 39(4): 416-421. ZHAO Dongbao, SHENG Yehua. Research on Automatic Matching of Vector Road Networks Based on Global Optimization[J]. Acta Geodaetica et Cartographica Sinica, 2010, 39(4): 416-421. |
| [8] | 栾学晨, 杨必胜, 李秋萍. 基于结构模式的道路网节点匹配方法[J]. 测绘学报, 2013, 42(4): 608-614. LUAN Xuechen, YANG Bisheng, LI Qiuping. Pattern-basede Node Matching Approach for Road Network[J]. Acta Geodaetica et Cartographica Sinica, 2013, 42(4): 608-614. |
| [9] | 张云菲, 杨必胜, 栾学晨. 利用概率松弛法的城市路网自动匹配[J]. 测绘学报, 2012, 41(6): 933-939. ZHANG Yunfei, YANG Bisheng, LUAN Xuechen. Automated Matching Urban Road Networks Using Probabilistic Relaxation[J]. Acta Geodaetica et Cartographica Sinica, 2012, 41(6): 933-939. |
| [10] | 陈玉敏, 龚健雅, 史文中. 多尺度道路网的距离匹配算法研究[J]. 测绘学报, 2007, 36(1): 84-90. CHEN Yumin, GONG Jianya, SHI Wenzhong. A Distance-based Matching Algorithm for Multi-scale Road Networks[J]. Acta Geodaetica et Cartographica Sinica, 2007, 36(1): 84-90. |
| [11] | 刘志勇. 城市地图数据库合并中的面实体匹配方法研究[D]. 南京: 河海大学, 2006. LIU Zhiyong. Research on Areal Feature Matching Algorithm in the Conflation of Urban Geographic Databases[D]. Nanjing: Hohai University, 2006. |
| [12] | 焦洋洋, 王卉, 翟仁健. 顾及邻域相似性的面要素匹配方法[J]. 辽宁工程技术大学学报(自然科学版), 2013, 32(7): 947-952. JIAO Yangyang, WANG Hui, ZHAI Renjian. Matching Method for Areal Feature Considering Context-dependent Similarity[J]. Journal of Liaoning Technical University: Natural Science, 2013, 32(7): 947-952. |
| [13] | 吴建华. 顾及环境相似的多特征组合实体匹配方法[J]. 地理与地理信息科学, 2010, 26(4): 1-6. WU Jianhua. Entity Matching Methods Based on Combining Multi-Similarity-Characteristics Considering Environment Similarity[J]. Geography and Geo-Information Science, 2010, 26(4): 1-6. |
| [14] | 钱海忠, 武芳, 朱鲲鹏, 等. 一种基于降维技术的街区综合方法[J]. 测绘学报, 2007, 36(1): 102-107. QIAN Haizhong, WU Fang, ZHU Kunpeng, et al. A Generalization Method of Street Block Based on Dimension-reducing Technique[J]. Acta Geodaetica et Cartographica Sinica, 2007, 36(1): 102-107. |
| [15] | 刘涛. 空间群(组)目标相似关系及计算模型研究[D]. 武汉: 武汉大学, 2011. LIU Tao. Similarity of Spatial Group Objects[D]. Wuhan: Wuhan University, 2011. |
| [16] | 刘涛, 闫浩文. 空间面群目标几何相似度计算模型[J]. 地球信息科学学报, 2013, 15(5): 635-642. LIU Tao, YAN Haowen. Geometry Similarity Assessment Model of Spatial Polygon Groups[J]. Journal of Geo-Information Science, 2013, 15(5): 635-642. |
| [17] | 江浩, 褚衍东, 闫浩文, 等. 多尺度地理空间点群目标相似关系的计算研究[J]. 地理与地理信息科学, 2009, 25(6): 1-4. JIANG Hao, CHU Yandong, YAN Haowen, et al. Study on Computation of Similarity Relationships of Multi-scale Point Objects[J]. Geography and Geo-Information Science, 2009, 25(6): 1-4. |
| [18] | 刘涛, 杜清运, 闫浩文. 空间点群目标相似度计算[J]. 武汉大学学报(信息科学版), 2011, 36(10): 1149-1153. LIU Tao, DU Qingyun, YAN Haowen. Spatial Similarity Assessment of Point Clusters[J]. Geomatics and Information Science of Wuhan University, 2011, 36(10): 1149-1153. |
| [19] | 刘涛, 杨树文, 李轶鲲, 等. 空间线群目标方向相似度计算模型[J]. 测绘科学, 2013, 38(1): 156-159. LIU Tao, YANG Shuwen, LI Yikun, et al. Direction Similarity Calculation Model of Spatial Line Groups[J]. Science of Surveying and Mapping, 2013, 38(1): 156-159. |
| [20] | EGENHOFER M J, MARK D M. Naive Geography[C]//FRANK A, KUHN W. Spatial Information Theory: A Theoretical Basis for GIS, International Conference COSIT' 95. Semmering, Austria: Springer-Verlag, 1995, 988: 1-15. |
| [21] | 艾廷华, 刘耀林. 保持空间分布特征的点群化简方法[J]. 测绘学报, 2002, 31(2): 175-181. AI Tinghua, LIU Yaolin. A Method of Point Cluster Simplification with Spatial Distribution Properties Preserved[J]. Acta Geodaetica et Cartographica Sinica, 2002, 31(2): 175-181. |
| [22] | 安晓亚, 孙群, 肖强, 等. 一种形状多级描述方法及在多尺度空间数据几何相似性度量中的应用[J]. 测绘学报, 2011, 40(4): 495-501. AN Xiaoya, SUN Qun, XIAO Qiang, et al. A Shape Multilevel Description Method and Application in Measuring Geometry Similarity of Multi-scale Spatial Data[J]. Acta Geodaetica et Cartographica Sinica, 2011, 40(4): 495-501. |
| [23] | BRUNS H T, EGENHOFER M J. Similarity of Spatial Scenes[C]//KRAAK J M, MOLENAAR M. Proceedings of the 7th International Symposium on Spatial Data Handling. Delft: Taylor & Francis, 1996: 173-184. |