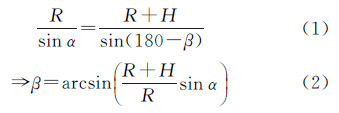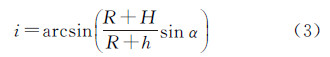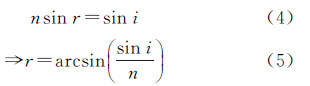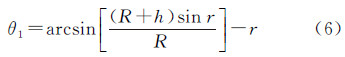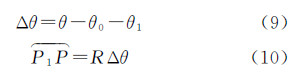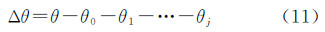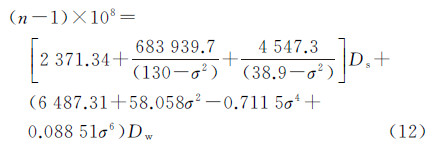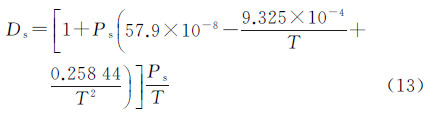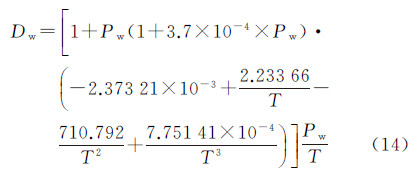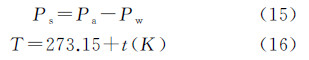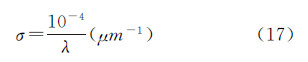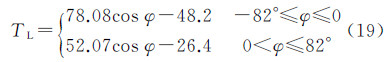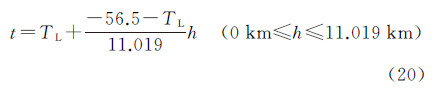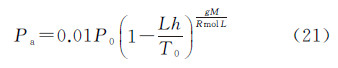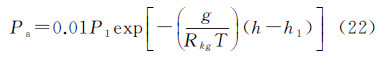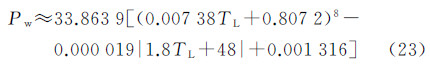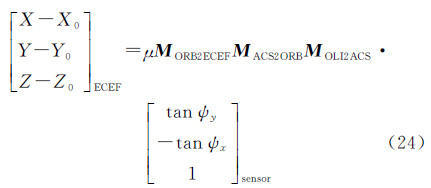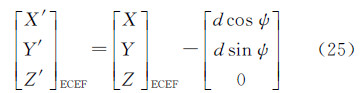2. 二十一世纪空间技术应用股份有限公司， 北京 100096
2. Twenty First Century Aerospace Technology Co., Ltd., Beijing 100096, China
1 引 言
卫星遥感图像几何定位在于确定遥感图像像点坐标与其大地坐标的对应关系。在现代光学卫星严密几何定位处理中，都是基于共线方程使用成像载荷内方位和卫星平台姿轨外方位参数建立的严密几何模型来实现遥感图像的精确几何定位[1, 2, 3, 4, 5, 6, 7, 8]。成像载荷的光学参数(如焦距、像点尺寸)、镜头光学畸变、CCD线阵扭曲和卫星平台的星历与姿态、成像时刻等参数的测量精度决定着遥感图像的严密几何定位精度。然而，在卫星对地观测过程中，遥感图像的严密几何定位精度是内方位、外方位参数、地球曲率与地形、大气折射、光线星地传输延时等误差因子综合影响的结果[1]。在这些误差因子中，大气折射会改变地物反射太阳光在星地间的直线传播方向，破坏了地物点、成像载荷透视中心、CCD探元三点共线的条件，造成严密几何定位模型的非严密，使得基于共线方程的严密几何定位结果存在一定的大气折射误差。针对这种现象，文献[9, 10]基于单层球形大气模型，使用解析法模拟分析了中分辨率±55°宽视场MODIS遥感载荷不同观测天顶角下的大气折射角度偏差及其在地球椭球面上的位置偏差。当观测天顶角为30°和55°时，大气折射产生的位置偏差分别约为2 m和11 m，并指出位置偏差随着观测天顶角的增加而迅速增大。而国内针对大气折射遥感成像几何定位影响分析，也只是集中在航空摄影测量应用上[11]。如文献[12]就模拟分析了11 km高度范围内大气折射对航空CCD成像几何精度的影响，指出有必要对倾斜航空摄影图像进行大气折射误差校正。对于我国高分辨率对地观测系统中米级甚至亚米级敏捷卫星平台和宽视场成像载荷的大量出现及其遥感图像的广泛应用，有必要针对卫星对地观测的特点，进一步提升卫星成像严密几何模型的精度。
针对高分辨率光学卫星窄视场、敏捷平台成像的特点，本文从成像载荷CCD探元视向量出发，使用ISO国际标准分层大气模型和Owens大气折射系数算法精确计算任意纬度、海拔高度不同色光的大气折射系数[13, 14]。根据大气折射系数在标准分层大气中的分布规律，把8层标准大气简化为对流层和同温层的双层大气，采用CCD探元视线跟踪几何算法，计算不同色光大气折射产生的几何定位偏差，实时修正地心地固坐标系(ECEF)中共线严密几何模型解算的CCD探元视向量与地球椭球的交点坐标，实现高分辨率遥感图像严密几何定位的大气折射校正。对比文献[9]的解析法大气折射几何定位误差计算方法，本文综合考虑大气折射系数随纬度、海拔高度在分层大气中的变化规律，跟踪不同波段CCD探元视向量在分层大气中的折射传播方向，更加符合CCD探元视线在分层大气中的传播特性。计算结果表明，在进行大视场的中高分辨率遥感图像或大侧视角的遥感图像严密几何定位处理时，对不同侧视条件下不同CCD严密几何定位结果的大气折射误差补偿，能够有效提升几何模型的严密性，提高遥感图像的无参考控制几何定位精度。
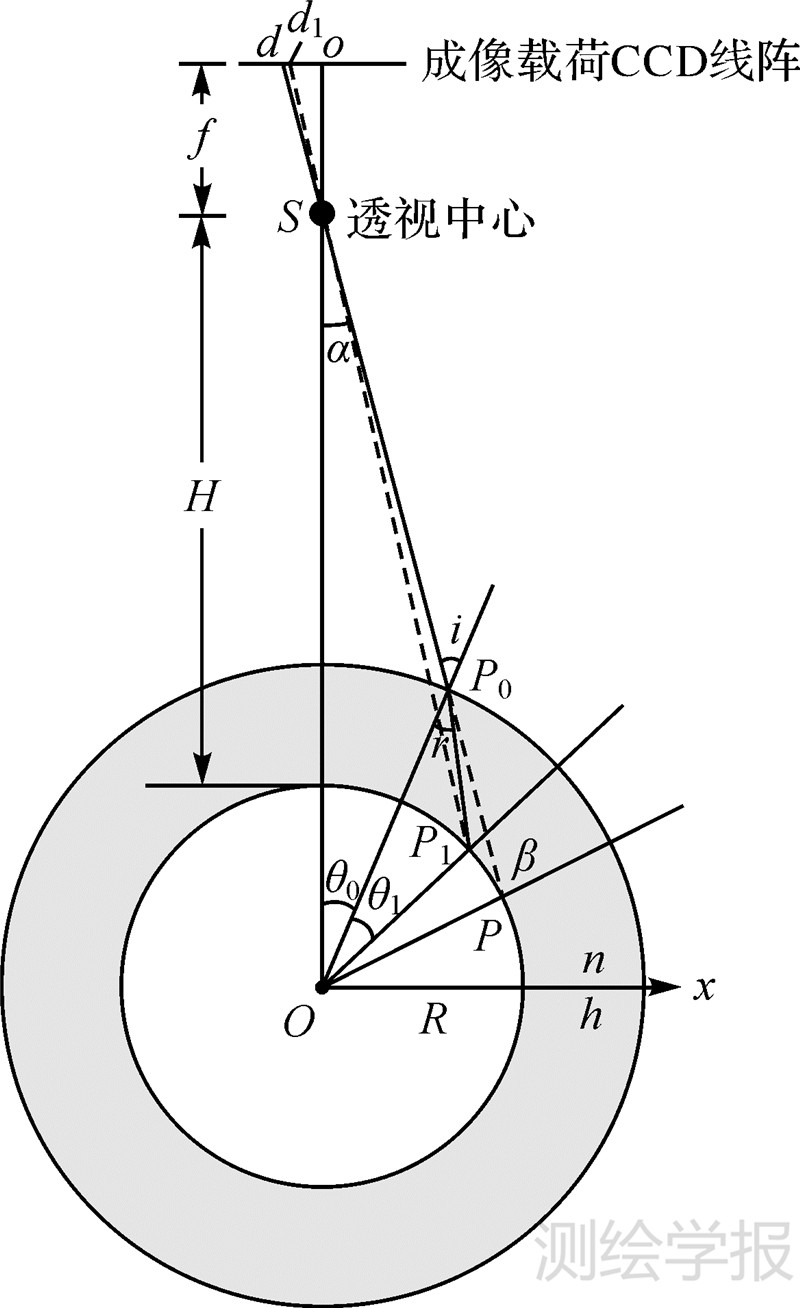
2 大气折射几何偏差计算地球大气层是由气体分子、水蒸气和气溶胶等物质组成，具有明显的分层特性[13]。当地物反射的太阳光线穿过大气层到达遥感卫星轨道高度真空环境中成像载荷CCD探元时，由于大气层大气折射的存在，地物反射光线的传播方向会发生偏离。如果从卫星成像载荷CCD探元视角出发，大气折射会造成CCD探元视线偏离原来的传播方向，导致基于共线方程的严密几何模型存在大气折射误差。如图1，设dSP为不考虑大气折射的CCD探元视线；P点为CCD探元视线与地球椭球的交点；P0为探元视线与大气层顶的交点。为了便于视向量光线跟踪几何算法的表述，假定大气层为大气分子和水蒸气组成的单层均匀球形大气，大气层厚度为h，其折射系数为n(n>1)。由于大气折射的存在，从侧视角为α的CCD探元视线出发，大气折射造成CCD探元视线经过大气层时与地球椭球相交于P1点，d1SP1则为大气折射补偿后CCD探元视线。设f为成像载荷焦距；S为投影中心；d为成像探元与CCD线阵主点的距离；H为卫星平台高度；R为地球平均半径；OP0、OP和OP1分别为CCD探元视线与大气层顶、地球椭球交点的法线；P点与P1点间的地表距离即为严密几何模型的大气折射偏差。
|
| 图 1 单层球形大气的CCD探元视线传播示意图 Fig. 1 Line of sight of CCD detector propagated in single layer spherical atmosphere |
如图1，在△SOP中，根据正弦定律
式中，α为CCD探元侧视角；β为不考虑大气折射误差的CCD探元视线在地球椭球面上的入射角；R为地球平均半径；H为卫星轨道高度。
同理，CCD探元视线在大气层顶的入射角为
式中，i为CCD探元视线在大气层顶的入射角；h为大气层厚度。
在卫星对地观测中，大气层外太空为真空，其折射系数为1。根据斯涅耳折射定律，大气层顶入射角为i的光线的折射出射角r为
设∠SOP为θ、∠SOP0为θ0、∠P0OP1为θ1、∠P1OP为Δθ。在△P0OP1中，已知OP0=R+h、OP=R和折射角r，则
在△SOP0中，已知卫星侧视角α；大气层顶入射角i和地球椭球入射角β，则
联立式(6)、式(7)、式(8)，得出CCD探元视线大气折射偏差对地心的张角Δθ及其在地球椭球面上的弧长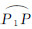
地表弧长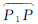 
即为单层球形大气条件下大气折射产生的几何定位偏差。
如果已知大气的分层特性和任意纬度、海拔高度的大气折射系数，使用式(5)和式(6)循环迭代计算出每层大气折射偏差对应的地心张角θj，则成像载荷CCD探元视线通过分层大气到达地球椭球面的大气折射偏差对地心的张角Δθ为
式中，i为大气分层层数。最后，把多层大气折射产生的位置偏离量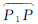
补偿到严密几何模型中，实现大气折射几何定位误差的校正。
3 不同色光大气折射系数计算
光学遥感卫星常使用0.45～0.52 μm的蓝波段、0.53～0.60 μm的绿波段、0.63～0.69 μm的红波段和0.76～0.90 μm的近红外波段获取多光谱图像，以及0.45～0.8 μm的波谱范围获取全色图像[15]。当不同波长的单色光穿过大气层时，其折射系数不同。波长越短，大气折射系数越大。文献[16]使用Owens大气折射系数算法模型分析了大气折射对不同波长色光天文观测的影响。对于45°天顶角、环境温度为15℃、大气压为760 mmHg(1 mmHg=133.322 Pa)、无水汽压的观测条件，大气折射对0.5 μm波长单色光的折光差约为57.5″。
已知大气温度t(℃)、大气压Pa和水汽压Pw，使用Owens大气折射系数计算公式计算任一波长单色光的大气折射系数[16, 17]。Owens(1967)给出的不同干燥空气大气压Ps(含0.03%二氧化碳)和水汽压Pw条件下大气折射系数计算公式为
式中 式中，Ps为水汽压修正后的干燥空气大气压(单位为mbar)；Pw为水汽压(单位为mbar)；T为绝对温度；σ为波长λ单色光的波数 3.1 计算大气温度t
使用国际化标准组织1975年定义的国际标准大气模型(ISO 2533:1975)[13]，计算随海拔高度变化的地球大气层温度。1975年国际标准大气模型定义海平面平均温度为15℃、大气压为760 mmHg，并把大气层划分为温度随海拔高度线性变化的多层大气。不同海拔高度大气层温度计算公式为
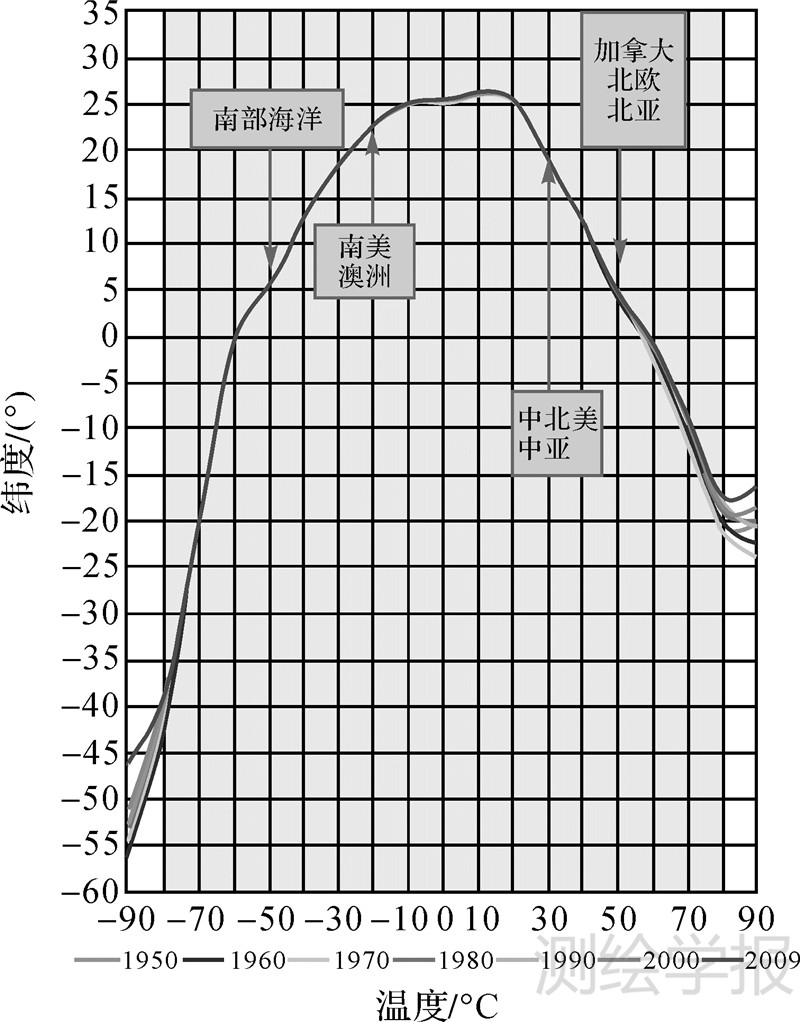
式中，h为海拔高度；t为海拔高度h处的大气层温度(℃)。然而，海平面平均温度是随着地理纬度变化而变化的。文献[18]在进行全球降水随经纬度变化的关系研究时，总结出1950年至2009年间每10年的海平面平均温度随纬度的变化关系，如图2。
|
| 图 2 年度海平面平均温度与纬度的关系 Fig. 2 Sea level mean temperature changed with latitude |
从图2可以看出，在南纬82°至北纬82°的太阳同步极轨遥感卫星观测范围内，海平面平均温度随纬度的变化趋势稳定。以纬度φ余弦值cos φ为自变量分南北半球进行线性拟合，得到不同纬度海平面平均温度计算公式
式中，φ为纬度。
由于海平面平均温度的变化仅对对流层温度的分布造成影响。不同纬度处对流层底层温度由式(20)计算得到，顶层温度为-56.5℃，层内温度线性变化，则对流层内不同海拔高度处大气温度计算公式为
式中，TL为不同纬度处海平面平均温度(℃)；h为海拔高度。
联合式(18)-式(20)，即能计算出卫星对地观测区域内不同海拔高度处的大气温度。
3.2 计算大气压Pa从地球表面到中间层的大气压按指数曲线平滑变化[19]。随着海拔高度的增加，大气压逐渐下降。已知任意海拔高度的大气温度，使用式(21)计算出该海拔高度处的大气压Pa
式中，Pa为任意海拔高度h(m)处的大气压(mbar)。1975国际标准大气的海平面大气压P0=1.013 25×105Pa、地表重力加速度g=9.806 65 m/s2、干燥空气摩尔质量M=0.028 964 4 kg/mol、气体常数Rmol=8.314 47 J/(mol·K)、海平面标准温度T0=288.15 K、L为不同大气分层的温度下降率(K/m)。
但对于对流顶层和平流顶层的温度不变层，大气压仅与距离该层底的距离相关，计算公式为
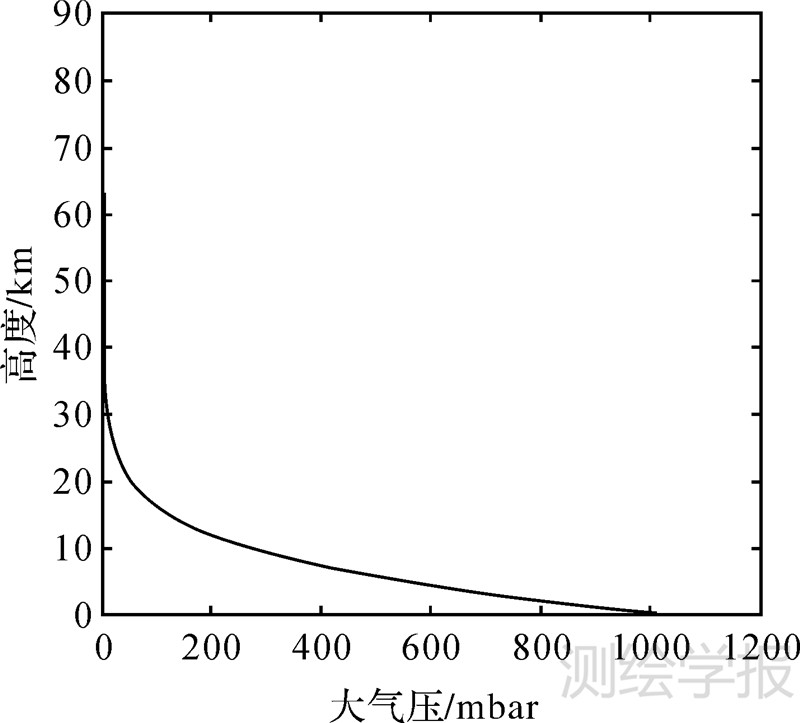
式中，g为地表重力加速度；气体常数Rkg=287.052 87(J/kg)/K；T为绝对温度；h1为底层高度(m)；h为海拔高度(m)；P1为底层高度处大气压(mbar)。
联合式(21)和式(22)，能够计算出随海拔高度变化的大气压Pa。大气压Pa随海拔高度变化的曲线如图3所示。
|
| 图 3 大气压Pa随海拔高度变化的曲线 Fig. 3 Atmosphere pressure changed with attitude |
大气的水汽压仅与空气温度相关，使用式(23)估算不同温度下的水汽压Pw[20]
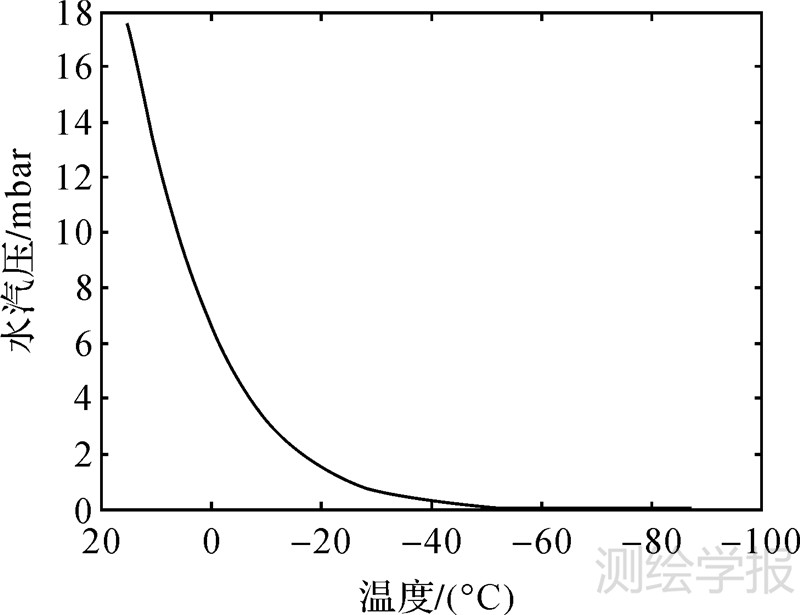
式中，Pw为水汽压(mbar)；TL为摄氏温度(℃)。
从海平面标准温度15℃到中间层顶层-86.28℃温度范围的水汽压曲线如图4。
|
| 图 4 水汽压Pw随温度变化的曲线 Fig. 4 Vapor pressure of water changed with temperature |
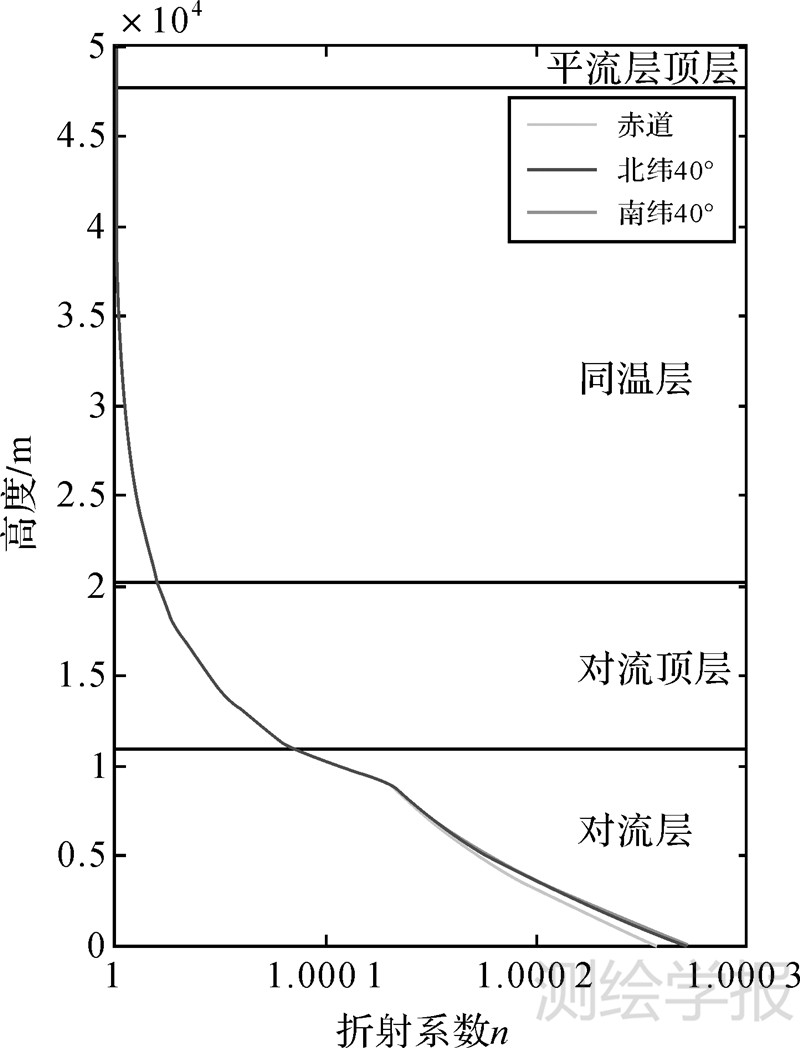
已知卫星观测区域内不同海拔高度处的大气温度t、大气压Pa、水汽压Pw和单色光中心波长λ，联合式(12)-式(17)即能计算出CCD探元视线穿过大气层不同海拔高度的大气折射系数。图5显示了赤道和南北纬40°处，中心波长0.5 μm的蓝光在不同海拔高度的大气折射系数。
|
| 图 5 大气折射系数与海拔高度的关系 Fig. 5 Index of atmosphere refraction changed with attitude |
图5反映出在轨成像载荷CCD探元视线到达同温层顶层47 350 m时，大气折射系数为1，无大气折射现象发生。当视线穿过同温层顶层到达对流顶层底端时，大气折射系数仅随海拔高度的下降而增大。当视线穿过对流层到达地表时，大气折射系数随纬度和海拔高度的变化而变化。又从式(12)-式(14)可知，在大气压Pa和水汽压Pw相同的条件下，大气折射系数与温度负相关，温度越高，大气折射系数越低。因此，对于平均温度约为25℃的赤道和12.5℃的南北纬40°，地表到对流顶层间赤道处的大气折射系数最小，南北纬40°处的基本相等。
大气折射系数在分层大气中的变化规律如表1。
| 层数 | 大气层名 | 基层高度/m | 顶层高度/m | 大气折射系数变化规律 |
| 1 | 对流层 | 0 | 11 019 | 随纬度、海拔高度变化而变化 |
| 2 | 对流顶层 | 11 019 | 20 063 | 仅随海拔高度变化而变化 |
| 3 | 同温层 | 20 063 | 32 162 | |
| 4 | 同温层 | 32 162 | 47 350 | |
| 5 | 平流顶层 | 47 350 | 51 413 | 折射系数为1 |
| 6 | 中间层 | 51 413 | 71 802 | |
| 7 | 中间层 | 71 802 | 86 000 | |
| 8 | 中间层顶 | 86 000 | - |
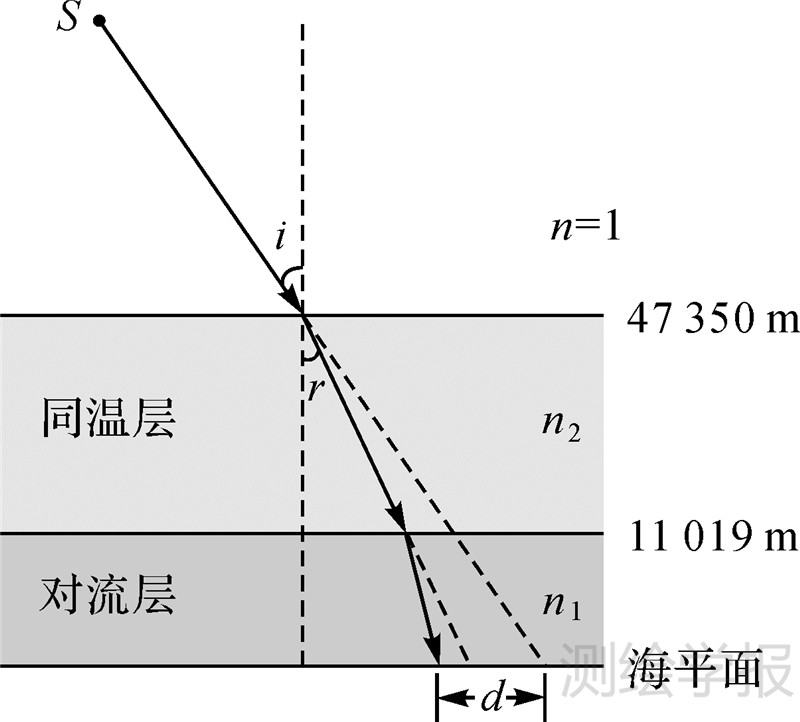
根据大气层的分层特性和大气折射系数的变化规律，使用光线跟踪几何算法计算大气折射角度偏差时，可以把8层标准大气模型简化为0～11 019 m的对流层和11 019～47 350 m的同温层双层大气模型，如图6所示。
|
| 图 6 光线在简化双层大气中的传播路径 Fig. 6 Two layers atmosphere refractive model |
设简化双层大气中对流层的大气折射系数为n1，同温层的大气折射系数为n2。如图6，从卫星平台S发出的光线在同温层顶的入射角为i，d为双层大气折射产生的CCD视线在海平面的位移量。由于大气折射系数随纬度和海拔高度的变化而变化，本文采用分层加权平均算法计算对流层和同温层的大气折射系数。在对流层中，加权平均每间隔1000 m的大气折射系数作为该层的大气折射系数；在同温层中，加权平均每间隔2000 m的大气折射系数作为该层的大气折射系数。以计算中心波长为0.5 μm蓝光的大气折射系数为例，北纬40°处对流层大气折射系数n1＝1.000 184 2，赤道处对流层大气折射系数n1=1.000 178 7，同温层大气折射系数n2＝1.000 016 7。
4 大气折射误差校正共线严密几何模型实现了相机坐标系CCD探元视向量到地心地固坐标系ECEF的旋转，通过计算CCD探元视线与地球椭球交点的ECEF坐标(X,Y,Z)，并将地心坐标变换为大地经纬度，完成遥感图像的严密几何定位[5]。严密几何模型描述为
式中，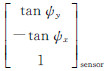
为CCD探元在相机坐标系中的视向量；MOLI2ACS为相机坐标系到姿态控制坐标系的偏置矩阵；MACS2ORB为平台姿态矩阵；MORB2ECEF为使用星历计算的轨道到ECEF的旋转矩阵；μ为比例系数； 
为星历内插的成像时刻卫星平台的位置； 
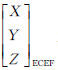为CCD探元视线与地球椭球交点的地心直角坐标。该严密几何模型基于CCD探元、投影中心和地物点三点共线原理实现了遥感图像像元坐标到大地坐标的转换。内方位、外方位和载荷装配参数的精度决定了该严密几何模型的定位精度。
然而，当CCD探元视线穿过如图6所示的大气层时，大气折射改变了探元视线的直线传播方向，产生大气折射偏差。以中心波长为0.5 μm蓝光在北纬40°和赤道处的大气折射系数为例，使用式(1)－式(10)计算45°侧视角范围内双层球形大气折射产生的几何定位偏差，并与文献[9]的解析法大气折射几何偏差进行对比(设卫星轨道高度H=650 km，地球平均半径R=6371 km)。大气折射几何偏差计算结果见表2。
从大气折射几何偏差计算结果可以得出以下4点结论。
(1) 大气折射几何偏差随卫星侧视角的增大而增大。当卫星侧视角度小于20°时，本文计算结果与文献[9]的结论一致。随着侧视角的进一步增大，本文计算的几何偏差逐步大于文献[9]的计算结果，主要原因是本文从卫星成像载荷CCD探元视线出发，分别计算对流层和同温层的大气折射系数及其对CCD探元视线的折射偏差，而文献[9]是从地面观测点出发，将对流层和同温层统一为假定的单层大气模型来计算大气折射偏差。当侧视角增大时，文献[9]低估的大气折射系数是导致与本文结果偏差越来越大的主要原因。
(2) 对于星下点成像的严密几何定位，无须考虑大气折射对几何定位偏差的影响。
(3) 对于米级或亚米级对地观测卫星，当侧视角大于30°，有必要补偿大气折射产生的几何定位偏差。
(4) 虽然对流层大气折射系数随纬度变化而变化，导致不同纬度处的大气折射几何偏差不同，但在工程应用中，可以统一使用赤道处不同海拔高度大气折射系数来计算不同侧视角下大气折射几何定位偏差。如表2计算结果所示，当卫星侧摆45°成像时，分别使用赤道和北纬40°处的大气折射系数计算的几何位置偏差仅相差0.2 m，可忽略这种偏差对卫星遥感图像几何定位的影响。又如，文献[21]在进行0.5 m分辨率Pleiades图像严密几何定位时，就使用赤道处的大气折射系数值来计算和校正大气折射造成的几何定位偏差。
设卫星观测方位角为ψ，共线严密几何模型计算的地物点ECEF坐标为[X,Y,Z]T，大气折射位置偏差为d，大气折射补偿后地物点的ECEF坐标为[X′，Y′，Z′]T，则卫星侧视条件下严密几何定位大气折射误差补偿计算公式为
式中，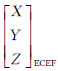
为式(24)计算的结果； 
为大气折射偏差补偿后的结果；d为使用式(1)-(10)计算的大气折射位置偏差；ψ为卫星观测方位角。联合式(24)、式(25)，即为大气折射位置偏差校正的严密几何定位模型。
因此，根据在轨卫星的侧视角和观测方位角，使用本文算法流程，直接在ECEF坐标系中补偿严密几何定位结果的大气折射位置偏差，进一步提升了严密几何模型的定位精度。
5 结 论光学遥感卫星对地观测中，大气层的大气折射改变了成像载荷CCD探元视线的直线传播方向，使得基于CCD探元、光学投影中心、地物点三点共线的严密几何模型非严密，产生大气折射几何偏差。
本文分析结果表明：在我国高分专项敏捷卫星平台和宽视场成像载荷遥感图像严密几何定位处理中，可以直接使用本文的大气折射几何偏差算法和严密几何定位大气折射偏差校正模型，在几何定位处理中实时补偿成像载荷CCD探元不同侧视条件下几何定位结果中存在的大气折射几何偏差，提高无参考控制高分辨率遥感图像的几何定位精度。本文算法模型，已应用在将于2015年发射的1 m分辨率北京二号敏捷小卫星星座的严密几何定位处理中。
需要指出的是，本文仅从大气折射视角分析了严密几何模型的非严密性。在高分辨率遥感图像严密几何建模时，还应考虑光行差、CCD探元视线星地传输延时对几何定位精度的影响，从内方位元素、外方位参数、星地间光线传输全链路综合分析严密几何建模的误差源，消除各类误差源对严密几何定位精度的影响。
| [1] | THIERRY T. Review Article: Geometric Processing of Remote Sensing Images: Models,Algorithms and Methods[J]. International Journal of Remote Sensing,2004,25(10): 1893-1924. |
| [2] | POLI D,THIERRY T. Review of Developments in Geometric Modelling for High Resolution Satellite Pushbroom Sensors[J]. The Photogrammetric Record,2011,27(137): 58-73. |
| [3] | CRESPI M,FRATARCANGELI F,GIANNONE F,et al. SISAR: A Rigorous Orientation Model for Synchronous and Asynchronous Pushbroom Sensors Imagery[C]//ISPRS Hannover Workshop: High-resolution Earth Imaging for Geospatial Information Vol. XXXVI-1/W51,2007. |
| [4] | PAN Hongbo,ZHANG Guo,TANG Xinming,et al. The Geometrical Model of Sensor Corrected Products for ZY-3 Satellite[J]. Acta Geodaetica et Cartographica Sinica,2013,42(4): 516-522. (潘红播,张过,唐新明,等. 资源三号测绘卫星传感器校正产品几何模型[J]. 测绘学报,2013,42(4): 516-522.) |
| [5] | FAN Dazhao,LIU Chubin,WANG Tao,et al. Building & Validation of Rigorous Geometric Model of ALOS PRIISM Imagery[J]. Acta Geodaetica et Cartographica Sinica,2011,40(5): 569-574,581. (范大昭,刘楚斌,王涛,等. ALOS卫星PRISM影像严格几何模型的构建与验证[J]. 测绘学报,2011,40(5): 569-574,581.) |
| [6] | TANG Xinming,ZHANG Guo,ZHU Xiaoyong,et al. Triple Linear Array Imaging Geometry Model of ZiYuan-3 Surveying Satellite and Its Validation[J]. Acta Geodaetica et Cartographica Sinica,2012,41(2): 191-198. (唐新明,张过,祝小勇,等. 资源三号测绘卫星三线阵成像几何模型构建与精度初步验证[J]. 测绘学报,2012,41(2): 191-198.) |
| [7] | JIANG Yonghua,ZHANG Guo,TANG Xinming,et al. High Accuracy Geometric Calibration of ZY-3 Three Line Image[J]. Acta Geodaetica et Cartographica Sinica,2013,42(4): 523-529. (蒋永华,张过,唐新明,等. 资源三号测绘卫星三线阵影像高精度几何检校[J]. 测绘学报,2013,42(4): 523-529.) |
| [8] | DE LUSSY F,GRESLOU D,DECHOZ C,et al. Pleiades HR in Flight Geometrical Calibration: Location and Mapping of the Focal Plane[C]//Proceedings of the International Archives of the Photogrammetry,Remote Sensing and Spatial Information Sciences,XXXIX-B1,2012: 519-523,DOI: 10.5194/isprsarchives-XXXIX-B1-519-2012. |
| [9] | NOERDLINGER P D.Atmospheric Refraction Effects in Earth Remote Sensing[J]. ISPRS Journal of Photogrammetry & Remote Sensing,1999,54(5-6): 360-373. |
| [10] | GIANNONE F. A Rigorous Model for High Resolution Satellite Imagery Orientation[D]. Rome: University of Rome,2006. |
| [11] | WANG Zhizhuo. Principle of Photogrammetry[M]. Wuhan: Wuhan University Press,2007. (王之卓. 摄影测量原理[M]. 武汉: 武汉大学出版社,2007.) |
| [12] | WEI Zheng,HU Fangchao,ZHANG Bing. The Influence of Atmospheric Refraction on Aerial Digital Remote Sensing[J]. Journal of Remote Sensing,2006,10(5): 651-655. (卫征,胡方超,张兵. 大气折射对航空CCD成像精度影响的研究[J]. 遥感学报,2006,10(5): 651-655.) |
| [13] | The International Organization for Standardization. ISO 2533: 1975-Standard Atmosphere[S].1975. |
| [14] | OWENS J C. Optical Refractive Index of Air: Dependence on Pressure,Temperature and Composition[J]. Applied Optics,1967,6(1): 51-59. |
| [15] | YAN Ming,YU Bingyang,WANG Zhiyong. Design of Width of Panchromatic Spectra of High Resolution Optical Remote Sensing Camera Based on Pansharpening[J]. Spacecraft Recovery & Remote Sensing,2013,34(3): 1-8. (严明,于冰洋,王智勇. 从融合视角优化设计星载高分光学相机全色波段展宽[J]. 航天返回与遥感,2013,34(3): 1-8.) |
| [16] | STONE R C. An Accurate Method for Computing Atmosphere Refraction[J]. Publication of the Astronomical Society of the Pacific,1996,108: 1051-1058. |
| [17] | LIPCANUM. A Direct Method for the Calculation of Astronomical Refraction[C]//Proceedings of the Romanian Academy: Series A. [S.l.]: The Publishing House of the Romanian Academy,2005,6(2): 1-7. |
| [18] | ROPER L D. Precipitation Rate Versus Latitude and Longitude[J/OL]. [2011-04-26]. http://www.roperld.com/science/PrecipLatitudeLongitude.htm. |
| [19] | Portland State Aerospace Society. A Quick Derivation Relating Altitude to Air Pressure[J/OL]. [2004-12-22]. http://psas.pdx.edu/RocketScience/PressureAltitude_Derived.pdf. |
| [20] | BOSENJ F. A Formula for Approximation of the Saturation Vapor Pressure over Water[J]. Monthly Weather Review,1960,88(8): 275-276. |
| [21] | DE FRANCHIS C,MEINHARDT-LLOPIS E,MICHELY J,et al. Automatic Sensor Orientation Refinement of Pléiades Stereo Images[C]//2014 IEEE International Geoscience and Remote Sensing Symposium (IGARSS). Quebec: IEEE,2014:1639-1642. |