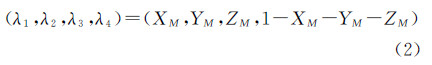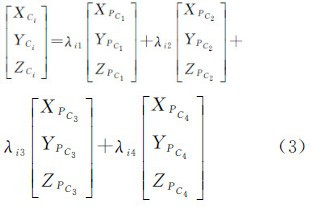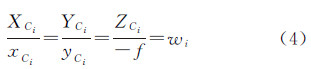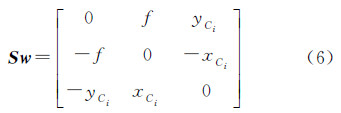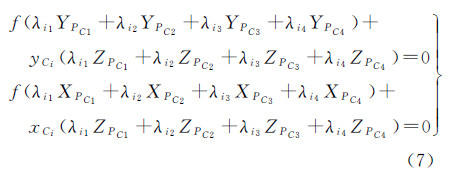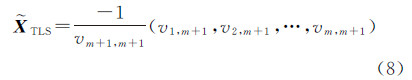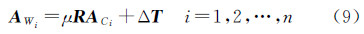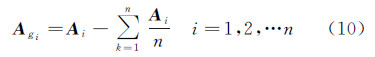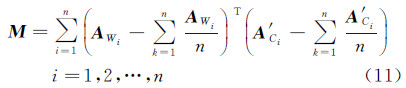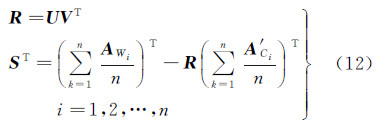1 引 言
空间后方交会是摄影测量和计算机视觉领域的一个基础性问题，在影像匹配、空三加密、三维重建等诸多领域发挥着至关重要的作用。它是指通过若干物方控制点及其在影像上对应像点坐标反算出相机的位置(外方位线元素)与姿态(外方位角元素)的过程[1]。其传统解算方法主要有欧拉角法[1, 2]、角锥体法[3]和直接线性变换法[4]。其中，欧拉角法需已知外方位元素良好初值，一般适用于竖直摄影；角锥体法较强依赖于外方位线元素初值；直接线性变换法不适合高精度的测量任务[5]。然而，随着倾斜影像的普及，传统方法往往因无良好外方位元素初值而迭代不收敛。
为了有效地解决初值强依赖问题，学者们提出了许多具有参考价值的解算方法，主要可以分为迭代解法和非迭代解法两类[6]。迭代解法具有较高的精度和鲁棒性，但是计算复杂度高且对未知数初值具有一定的依赖性：如文献[7—8]提出的利用单位四元数描述相机旋转矩阵进行迭代求解的方法，文献[9]采用对偶四元数描述坐标系之间的旋转和平移，文献[10,11]以线性解作为初始值进行高斯-牛顿全局优化。与之相反，非迭代解法解算效率高且无须初值，但是精度和鲁棒性较低，比较有代表性的有：文献[12]利用单位四元数分步求解外方位角元素和线元素的方法，文献[13]通过4个非共面虚拟点作为控制点解求摄像机的位置和姿态。这些方法都不同时具备高精度和无须初值这两个特点，并且均不能保证其对于任意影像姿态均能正确解算。
重心坐标是一种参考无关坐标，它只与所选坐标四面体相关，而与坐标四面体所在坐标系无关，现已广泛应用于在工程学和图形学领域，如有限元计算[14]、复杂曲面构造[15]、多边形面片的参数化等[16, 17]。基于此性质，本文引入重心坐标来描述控制点物方空间坐标，采用总体最小二乘[18, 19, 20, 25]求出其在像空间坐标系中的坐标，将后方交会问题转换为坐标系绝对定向问题。通过与3种迭代算法的对比，验证了本文方法具有高精度，高效率，无须初值，适应于任意影像姿态等特点。
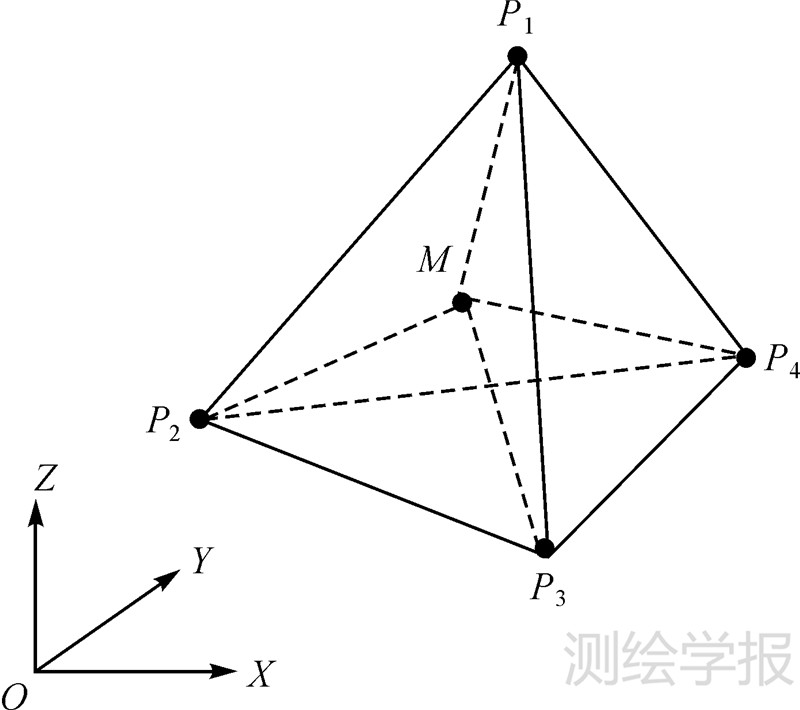
2 重心坐标概念和性质在数学中，三维重心坐标是由四面体顶点定义的坐标。如图1所示，三维欧氏空间R3中任取一个四面体P1P2P3P4作为坐标四面体，对R3任意一点M(XM,YM,ZM)T，下列4个四面体的有向(点M在四面体P1P2P3P4内部时为正)体积的比值VMP2P3P4：VP1MP3P4：VP1P2MP4：VP1P2P3M=u1：u2：u3：u4称为点M关于坐标四面体P1P2P3P4的重心坐标[21]，若令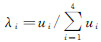 
，则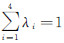 
，u2：u3：u4称(λ1,λ2,λ3,λ4)为点M的规范重心坐标[22]。
|
| 图 1 三维重心坐标 Fig. 1 Barycentric coordinates in 3D Euclidean space |
根据重心坐标的定义，点M(XM,YM,ZM)T与坐标四面体4个顶点P1、P2、P3、P4的欧氏空间坐标(XPi,YPi,ZPi)T(i=1,2,3,4)存在以下关系[21]
当选取M所在直角坐标系原点O(0,0,0)T为P4，以及X、Y、Z轴上单位长度点X(1,0,0)T、Y(0,1,0)T、Z(0,0,1)T分别为P1、P2、P3时，由式(1)可得点M的规范重心坐标为
从以上定义和性质可知，规范重心坐标只与所选坐标四面体相关，而与坐标四面体所在参考坐标系无关。因此，在空间后方交会中，控制点在物方空间坐标系与像空间坐标系中拥有相同的规范重心坐标。
3 基于重心坐标的空间后方交会本文方法分为下面3个步骤：坐标四面体顶点的像空间坐标解算；坐标系绝对定向分解外方位元素；外方位元素值优化。为了方便表述，物方空间坐标和像方空间坐标分别用下标W和C表示。
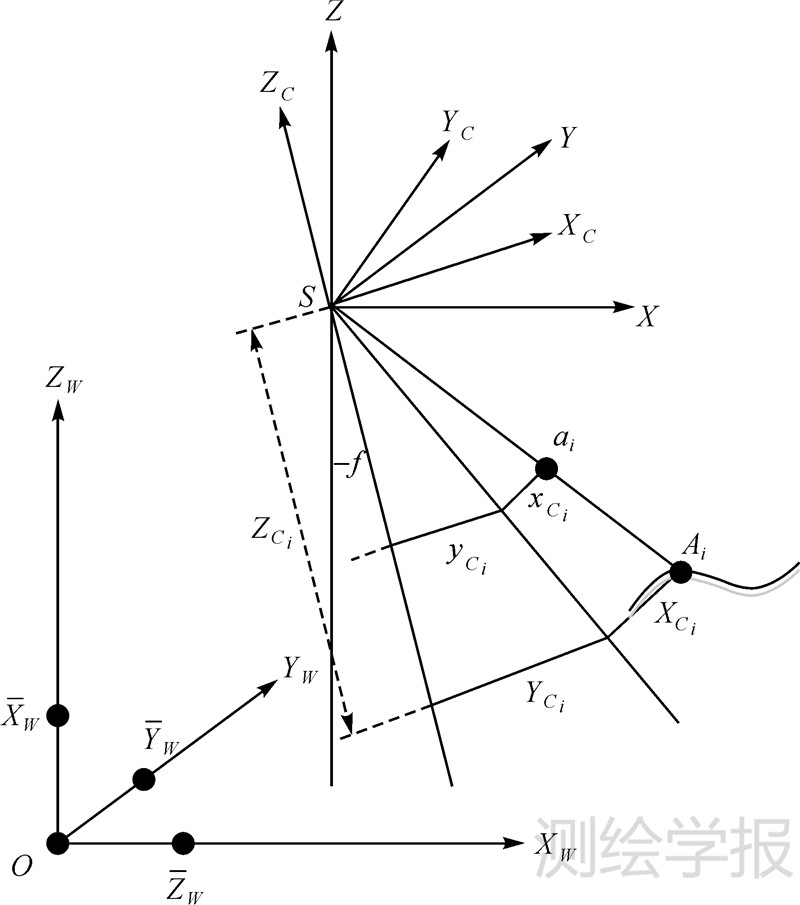
3.1 坐标四面体顶点像空间坐标解算如图2所示，传统空间后方交会将摄影中心S、像点ai及其对应控制点Ai统一纳入到像空间辅助坐标系S-XYZ，利用其与物方空间坐标系O-XWYWZW坐标轴平行，坐标原点不同这一关系，推导出共线条件方程来求解6个外方位元素，具体推导过程见文献[1]。与文献[1]不同，本文将S、ai和Ai三点共线条件应用于像空间坐标系S-XCYCZC，利用控制点的规范重心坐标，解求坐标四面体顶点的像空间坐标PCi(XPCi,YPCi,ZPCi)T(i=1,2,3,4)。
|
| 图 2 共线方程 Fig. 2 Collinear equation |
首先，选取原点O(0,0,0)T及XW、YW、ZW轴上单位长度点XW(1,0,0)T、YW(0,1,0)T、ZW(0,0,1)T分别为P4、P1、P2、P3构成坐标四面体P1P2P3P4，则由公式(2)可以求出Ai的规范重心坐标(λi1,λi2,λi3,λi4)(i=1,2,…,n)，根据其参考坐标系无关性，Ai对应的像空间坐标ACi(XCi,YCi,ZCi)T(i=1,2,…,n)可以表示为
设ai的像平面坐标为(xCi,yCi)(i=1,2,…,n)，则其像空间坐标为(xCi,yCi,-f)，i=1,2,…,n，利用图2所示像方空间三点共线关系有
写成矩阵形式并顾及式(3)，则有 式中，wi是尺度因子；f是焦距。为消除尺度因子wi，在式(5)两边同时乘以向量(xCi,yCi,-f)的反对称矩阵Sw
得到3个线性方程。然而由于矩阵Sw的秩为2(文献[23])，仅有两个方程是线性独立的[24]，故取其前两个方程构成方程组式(7)
式中，未知数PCi(XPCi,YPCi,ZPCi)T(i=1,2,3,4)个数为12，当控制点个数n≥6，可以组成齐次线性方程组AX=0，其中A是系数矩阵，X是未知数。考虑到系数矩阵可能包含有误差，采用文献[25]中所用总体最小二乘(TLS)方法进行求解，目的是从m个线性方程组中求解n个未知数的总体最小二乘估值(m≥n)，具体计算步骤描述如下。
(1) 将线性方程组写成AX=b矩阵，其中A为未知数系数，X为未知数，b为常数项。
(2) 构成增广矩阵[A,b]，进行奇异值分解[A,b]=UΣVT，其中U和V为酉矩阵，Σ为奇异值矩阵。
(3) 由V最后一列求得未知数的TLS解为
式中，vi,m+1(i=1，2，…m+1)为V的最后一列。 3.2 坐标系绝对定向分解6个外方位元素
求得PCi(i=1,2,3,4)的坐标值后，利用式(3)便可计算控制点的像空间坐标ACi(i=1,2,…,n)。至此，控制点在像空间坐标系和物方空间坐标系中的三维坐标都已知，空间后方交会问题便转化为摄影测量中的7参数绝对定向(即两空间三维坐标系的相似变换)问题，因而有
式中，μ是坐标系比例尺缩放系数；R是像空间坐标系到物方空间坐标系的3阶旋转矩阵；ΔT为坐标原点的3维平移列向量。目前，绝对定向问题已有许多比较成熟的解法，如文献[26]采用单位四元数描述旋转矩阵的线性解法，文献[27]利用正交矩阵的闭合解求法等，本文选用文献[27]的正交矩阵方法进行求解。下面简单描述其基本解算步骤。
步骤1：计算控制点的像空间和物方空间重心化距离dCi和dWi，并求解两组对应距离的比例系数μ的最小二乘解。利用μ将两坐标系统一到相同尺度，重心化公式为
式中，Ai表示空间坐标；Agi表示重心化后的空间坐标。
步骤2：对统一尺度的控制点像空间坐标A′Ci和物方空间坐标AWi通过式(11)构成矩阵M
步骤3：对矩阵M进行SVD分解，UΣVT=M，获得旋转矩阵R和摄站中心S的解为
3.3 外方位元素值优化
为提高算法精度，首先把旋转矩阵R作为已知值，利用文献[25]的算法求出摄站中心S的总体最小二乘解STLS，再把摄站中心STLS作为已知值，反求出旋转矩阵的总体最小二乘解RTLS，最后比较3组解(R,S)，(R,STLS)，(RTLS,STLS)的像点残差中误差[28]，选取中误差最小的解作为最终解。
4 试验结果与分析分别采用模拟和真实数据来评价本文算法的精度、稳定性以及速度，并与欧拉角LS法、欧拉角TLS解法、单位四元数法进行对比。
4.1 模拟数据试验首先采用6张模拟像片数据验证本文算法的正确性和可行性。其次，固定摄站中心坐标S，通过随机函数产生三维相机姿态列向量，构成旋转矩阵。然后分别对上述两组控制点由共线条件方程算出其对应像点坐标，并加入[-0.01 mm,0.01 mm](大约±2像素)范围内的随机误差，再由控制点及其像点坐标出发，分别采用上述方法解算出外方计算值，将计算值与真值进行比较来判断此次解算正确与否。重复执行上述过程1000次，通过错误解算的次数多少来说明该算法对相机不同姿态的适用性，同时统计1000次解算的总时间来比较算法的效率，并利用所有正确解算的平均中误差来评价各个算法的精度。
4.1.1 正确性及精度试验数据来自文献[7]，相机内方位元素为(x0，y0，f)=(0,0,100 mm)，外方位元素(XS、YS、ZS、φ、ω、κ)的设计值及数据信息见表1。由于影像数据无先验的位置和姿态信息，因此欧拉角LS法、欧拉角TLS法和单位四元数法在解算时所必需的姿态初始值取像片处于水平时的姿态，位置初值取0，解算结果见表2。
| 影像 | 说明 | XS/m | YS/m | ZS/m | φ | ω | κ |
| 1 | 小倾角大航高 | 16 200 | 16 200 | 20 250 | -100′ | 70′ | 20′ |
| 2 | 大倾角大航高 | 16 200 | 16 200 | 20 250 | 20° | 30° | 40° |
| 3 | 特大倾角大航高 | -16 200 | -16 200 | 20 250 | 80° | 80° | 40° |
| 4 | 小倾角小航高 | 1620 | 1620 | 2250 | -100′ | 70′ | 20′ |
| 5 | 大倾角小航高 | 1620 | 1620 | 2250 | 20° | 30° | 40° |
| 6 | 特大倾角小航高 | -1620 | -1620 | 2250 | 80° | 80° | 40° |
| 影像 | 方法 | XS/m | YS/m | ZS/m | φ | ω | κ | 迭代次数 |
| 1 | 本文方法 | 16 199.999 929 | 16 199.999 935 | 20 249.999 975 | -100′ | 70′ | 20′ | 1 |
| 欧拉角 | 16 199.999 955 | 16 199.999 900 | 20 250.000 005 | -100′ | 70′ | 20′ | 7 | |
| 欧拉角TLS | 16 199.999 981 | 16 199.999 942 | 20 249.999 997 | -100′ | 70′ | 20′ | 7 | |
| 单位四元数 | 16 199.999 955 | 16 199.999 900 | 20 250.000 005 | -100′ | 70′ | 20′ | 4 | |
| 2 | 本文方法 | 16 199.999 986 | 16 200.000 027 | 20 249.999 952 | 20° | 30° | 40° | 1 |
| 欧拉角 | 迭代不收敛 | — | — | — | — | — | — | |
| 欧拉角TLS | 迭代不收敛 | — | — | — | — | — | — | |
| 单位四元数 | 16 199.999 987 | 16 200.000 027 | 20 249.999 950 | 20° | 30° | 40° | 7 | |
| 3 | 本文方法 | -16 199.999 963 | -16 200.000 015 | 20 250.000 042 | 80° | 80° | 40° | 1 |
| 欧拉角 | 迭代不收敛 | — | — | — | — | — | — | |
| 欧拉角TLS | 迭代不收敛 | — | — | — | — | — | — | |
| 单位四元数 | -16 199.999 958 | -16 200.000 022 | 20 250.000 042 | 80° | 80° | 40° | 25 | |
| 4 | 本文方法 | 1 619.999 999 | 1 620.000 002 | 2 250.000 000 | -100′ | 70′ | 20′ | 1 |
| 欧拉角 | 1 620.000 009 | 1 619.999 993 | 2 250.000 000 | -100′ | 70′ | 20′ | 8 | |
| 欧拉角TLS | 1 619.999 999 | 1 620.000 000 | 2 250.000 000 | -100′ | 70′ | 20′ | 8 | |
| 单位四元数 | 1 620.000 009 | 1 619.999 993 | 2 250.000 000 | -100′ | 70′ | 20′ | 4 | |
| 5 | 本文方法 | 1 620.000 010 | 1 620.000 004 | 2 250.000 001 | 20° | 30° | 40° | 1 |
| 欧拉角 | 迭代不收敛 | — | — | — | — | — | — | |
| 欧拉角TLS | 迭代不收敛 | — | — | — | — | — | — | |
| 单位四元数 | 1 619.999 983 | 1 620.000 012 | 2 249.999 997 | 20° | 30° | 40° | 6 | |
| 6 | 本文方法 | -1 620.000 014 | -1 619.999 983 | 2 249.999 954 | 80° | 80° | 40° | 1 |
| 欧拉角 | 迭代不收敛 | — | — | — | — | — | — | |
| 欧拉角TLS | 迭代不收敛 | — | — | — | — | — | — | |
| 单位四元数 | -1 620.000 038 | -1 620.000 027 | 2 249.999 957 | 80° | 80° | 40° | 29 | |
| 注：因为本文算法为非迭代解法，故迭代次数由1来表示。 | ||||||||
对于该模拟试验，衡量精度的标准采用真误差[28]，即计算值减去设计值的绝对值。其中，除欧拉角法(包含LS和TLS解法)因有4张像片迭代不收敛只有2组数据参与统计外，其他方法均求出6张像片外方位元素的真误差，并以其平均值作为该算法的最终误差，具体数值在表3中给出。
| 方法 | ΔXS/m | ΔYS/m | ΔZS/m | Δφ/(°) | Δω/(°) | Δκ/(°) | 参与统计张数 |
| 本文方法 | 0.000 025 | 0.000 024 | 0.000 027 | 0 | 0 | 0 | 6 |
| 欧拉角 | 0.000 027 | 0.000 054 | 0.000 003 | 0 | 0 | 0 | 2 |
| 欧拉角TLS | 0.000 010 | 0.000 027 | 0.000 002 | 0 | 0 | 0 | 2 |
| 单位四元数 | 0.000 027 | 0.000 033 | 0.000 027 | 0 | 0 | 0 | 6 |
| 注：ΔXS、ΔYS、ΔZS、Δφ、Δω、Δκ分别表示6个外方位元素的真误差平均值。 | |||||||
分析表2可以发现，对于近似竖直摄影(小倾角)影像，4种方法均能正确解算外方位元素，但当倾角大于某个值后，在没有任何先验信息的情况下，欧拉角法(LS和TLS解法)迭代计算无法收敛，解算失败，而其他方法则能得到正确结果。同时，欧拉角法(LS和TLS解法)迭代次数最多，单位四元数法相对较少，而本文方法则无须迭代计算。再看表3，欧拉角TLS解法由于考虑了观测值误差，因而整体精度最高，而本文方法在精度上也基本达到甚至优于其他两种基于迭代的算法。
4.1.2 适用性和效率选取文献[7]中的2组控制点数据(每组9个)，对上述3种方法分别进行了1000次试验。其中，第1组数据的摄站点坐标设计值固定为S1(16 200,16 200,20 250)，第2组数据的摄站点坐标设计值为S2(1620，1620，2250)，相机姿态由函数随机产生，试验结果见表4。
| 方法 | 第1组 | 第2组 | ||||
| Terror | m0/mm | 时间/s | Terror | m0/mm | 时间/s | |
| 本文算法 | 0 | 0.008 35 | 0.580 | 3 | 0.009 21 | 0.567 |
| 欧拉角 | 745 | 0.008 21 | 16.265 | 666 | 0.009 26 | 16.073 |
| 欧拉角TLS | 733 | 0.007 57 | 15.653 | 689 | 0.008 86 | 15.605 |
| 单位四元数 | 231 | 0.008 27 | 15.989 | 226 | 0.009 59 | 15.204 |
| 注：Terror为1000次试验中错误解算次数；m0为像点残差中误差。 | ||||||
试验中采用摄站点坐标的相对误差ε来评判某方法该次解算正确与否，ε由式(13)给出
式中，S为相机摄站中心坐标真值；S′表示某方法的摄站中心坐标解算值；||·||表示二维范数，即欧氏距离。对于该试验的两组数据，当相对误差ε≤5×10-5时(对应于这两组数据的摄站中心位置绝对误差分别为1.5289 m和0.1606 m)，外方位元素解算正确，否则错误。此外，试验中所有算法程序及其运行时间都是在同一台计算机的MatLab平台上编写和统计的，并且认为所有试验均没有任何关于6个外方位元素的先验信息。
分析表4两组数据可以发现，欧拉角法(LS和TLS解法)对影像的姿态非常敏感，单位四元数法能够处理绝大多数影像姿态场景，而本文算法则几乎对任意影像姿态均能正确解算。同时可以看出，欧拉角(LS和TLS解法)和单位四元数这些迭代解法的精度很高，但是运行效率较低。而本文算法则兼顾精度与效率，不仅在精度上基本达到基于迭代的解算方法，而且在速度上比基于迭代的方法快接近30倍，这主要得益于本文方法无须迭代的特点，大大减少了计算的时间复杂度。
4.2 真实数据试验为了验证本文算法对真实数据的处理能力，采用3张影像进行试验。第1张影像是采用Canon EOS 450D数码相机对三维室内精准控制场进行摄影获得，焦距f=23.64 mm，摄影比例尺为1∶200，控制点个数为10。后两组数据选用SWDC数字航空摄影仪在平顶山市拍摄的航空影像，该相机由5个子相机组成，一个中心相机和4个倾斜相机。其中，第2张影像是由中心相机拍摄所得，焦距f=82.215 mm，像元大小0.006 8 mm，摄影比例尺为1∶8000，相对航高700 m，12个控制点。第3张影像是由倾斜相机拍摄，焦距f=99.86 mm，像元大小0.006 8 mm，摄影比例尺为1∶8000，相对航高700 m，15个控制点。在平差计算过程中，认为没有任何关于影像外方位元素的先验信息，解算结果见表5。
| 影像 | 方法 | ΔXS/m | ΔYS/m | ΔZS/m | Δφ /(°) | Δω/(°) | Δκ/(°) | m0/像素 | 迭代次数 |
| 1 | 本文 | 3.373 | -0.141 | 0.930 | -0.684 | 5.728 | -2.350 | 0.180 | 1 |
| 欧拉角 | 3.373 | -0.141 | 0.930 | -0.684 | 5.728 | -2.350 | 0.180 | 5 | |
| 欧拉角TLS | 3.373 | -0.141 | 0.930 | -0.684 | 5.728 | -2.350 | 0.179 | 5 | |
| 单位四元数 | 3.373 | -0.141 | 0.930 | -0.684 | 5.728 | -2.350 | 0.180 | 5 | |
| 2 | PATB | 424 012.476 | 3 739 009.098 | 788.896 | -3.210 | -0.545 | 19.802 | ||
| 本文 | 424 012.124 | 3 739 008.779 | 788.943 | -3.183 | -0.520 | 19.753 | 0.803 | 1 | |
| 欧拉角 | 错误收敛 | 26 | |||||||
| 欧拉角TLS | 错误收敛 | 26 | |||||||
| 单位四元数 | 424 012.600 | 3 739 009.100 | 788.888 | -3.223 | -0.531 | 19.752 | 0.708 | 7 | |
| 3 | PATB | 424 575.333 | 3 739 022.993 | 788.700 | -46.113 | -12.674 | 104.718 | ||
| 本文 | 424 575.552 | 3 739 023.205 | 789.270 | -46.139 | -12.687 | 104.708 | 0.889 | 1 | |
| 欧拉角 | 错误收敛 | 16 | |||||||
| 欧拉角TLS | 错误收敛 | 16 | |||||||
| 单位四元数 | 错误收敛 | 16 | |||||||
| 注：PATB表示商业软件PATB的区域网平差结果。 | |||||||||
分析表5可得，当影像的3个姿态角都为小角时(如影像1)，3种方法均能正确解算，本文方法与欧拉角(LS和TLS解法)及单位四元数法结果一致，精度基本相同；当影像姿态角较大时(如影像2)，在没有任何先验信息的情况下，欧拉角法(LS和TLS解法)出现错误收敛，解算失败，而本文方法与单位四元数法的解算结果则与商业软件PATB的区域网平差结果基本一致，且像点残差中误差均在1个像素以内；当影像姿态角非常大时(如影像3)，以PATB结果作为标准，只有本文算法能够正确解算，像点残差中误差为0.889像素，小于1个像素。
可见，本文算法具有很好的实用性，为无人机影像、倾斜相机影像等数据提供了一种可靠稳定的几何定位处理技术。
5 结 论本文提出了一种以重心坐标为基准的非迭代空间后方交会方法。该方法借助规范重心坐标的坐标系参考无关性，将空间后方交会问题转换为绝对定向问题。并对算法的正确性、解算效率、解算精度、适用性进行验证，得到以下几点结论：
与欧拉角(LS和TLS解法)和单位四元数等迭代解法相比，本文算法无须外方位元素初始值以及迭代求解，故具有较高的解算效率，并且避免了迭代过程中法方程病态的情形。同时，本文算法顾及了系数矩阵误差，采用总体最小二乘求解，并对结果进行了有效优化，取得了与迭代解法相当的精度。此外，本文算法几乎对任意影像姿态均能正确解算，拥有很好的实用性。
随着倾斜摄影测量的快速发展，获取的影像姿态变化范围不断扩大，此时，传统方法将不再适用，而本文算法可为此提供一种稳定可靠的处理技术。需要指出的是，本文算法的抗粗差能力较弱，粗差的自动剔除将是下一步的研究重点。
| [1] | ZHANG Jianqing, PAN Li, WANG Shugen. Photogrammetry[M]. Wuhan: Wuhan University Press, 2009. (张剑清, 潘励, 王树根. 摄影测量学[M]. 武汉: 武汉大学出版社, 2009.) |
| [2] | WANG Zhizhuo. Principles of Photogrammetry[M]. Beijing: Surveying and Mapping Press, 1979. (王之卓. 摄影测量原理[M]. 北京: 测绘出版社, 1979.) |
| [3] | HARALICK B M, LEE C N, OTTENBERG K, et al. Review and Analysis of Solutions of the Three Point Perspective Pose Estimation Problem[J]. International Journal of Computer Vision, 1994, 13(3): 331-356. |
| [4] | FENG Wenhao. Close Range Photogrammetry[M]. Wuhan: Wuhan University Press, 2002. (冯文灏. 近景摄影测量[M]. 武汉: 武汉大学出版社, 2002.) |
| [5] | FU Zhongliang, ZHOU Fan, YU Zhiqiang. A Space Resection Synthesized the Multiple Features[J]. Acta Geodaetica et Cartographica Sinica, 2014, 43(8): 827-834. (付仲良, 周凡, 俞志强. 综合多种特征的后方交会法[J]. 测绘学报, 2014, 43(8): 827-834.) |
| [6] | JI Qiang, COSTA M S, HARALICK R M, et al. A Robust Linear Least-squares Estimation of Camera Exterior Orientation Using Multiple Geometric Features[J]. ISPRS Journal of Photogrammetry & Remote Sensing, 2000, 55(2): 75-93. |
| [7] | JIANG Gangwu,JIANG Ting, WANG Yong, et al. Space Resection Independent of Initial Value Based on Unit Quaternions[J]. Acta Geodaetica et Cartographica Sinica, 2007, 36(2): 169-175. (江刚武, 姜挺, 王勇, 等. 基于单位四元数的无初值依赖空间后方交会[J]. 测绘学报, 2007, 36(2): 169-175.) |
| [8] | GONG Hui, JIANG Ting, JIANG Gangwu, et al. A Globally Convergent Algorithm of Space Resection Based on Quaternion[J]. Acta Geodaetica et Cartographica Sinica, 2011, 40(5): 539-645. (龚辉, 姜挺, 江刚武, 等. 一种基于四元数的空间后方交会全局收敛算法[J]. 测绘学报, 2011, 40(5): 639-645.) |
| [9] | JI Ting, SHENG Qinghong, WANG Huinan, et al. Dual Quaternion of Space Resection with Single-image[J]. Journal of Image and Graphics, 2012, 17(4): 494-503. (姬亭, 盛庆红, 王惠南, 等. 对偶四元数单片空间后方交会算法[J]. 中国图象图形学报, 2012, 17(4): 494-503.) |
| [10] | PENATE-SANCHEZ A,ANDRADE-CETTO J,MORENO- NOGUER F. Exhaustive Linearization for Robust Camera Pose and Focal Length Estimation[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence,2013, 35(10): 2386-2400. |
| [11] | LEPETIT V, MORENO-NOGUER F, FUA P. EPnP: An Accurate O(n) Solution to the PnP Problem[J]. International Journal of Computer Vision,2008, 81(2): 155-166. |
| [12] | GUAN Yunlan, CHENG Xiaojun, ZHOU Shijian, et al. A Solution to Space Resection Based on Unit Quaternion[J]. Acta Geodaetica et Cartographica Sinica, 2008, 37(1): 30-35. (官云兰, 程效军, 周世健, 等. 基于单位四元数的空间后方交会解算[J]. 测绘学报, 2008, 37(1): 30-35.) |
| [13] | MORENO-NOGUER F, LEPETIT V, FUA P. Accurate Noniterative O(n) Solution to the PnP Problem[C]//Proceedings of the IEEE 11th International Conference on Computer Vision.Rio de Janeiro: IEEE, 2007: 1-8. |
| [14] | WACHSPRESSE L. A Rational Finite Element Basis[M]. New York: Academic Press, 1975. |
| [15] | LOOP C T, DEROSE T D. A Multisided Generalization of Bézier Surfaces[J]. ACM Transactions on Graphics, 1989, 8(3): 204-234. |
| [16] | ECKM, DEROSE T, DUCHAMP T, et al. Multiresolution Analysis of Arbitrary Meshes[C]//Proceedings of the 22nd Annual Conference on Computer Graphics and Interactive Techniques. New York: ACM, 1995: 173-182. |
| [17] | FLOATER M S. Parametrization and Smooth Approximation of Surface Triangulations[J]. Computer Aided Geometric Design, 1997, 14(3): 231-250. |
| [18] | CHEN Yi, LU Jue. Performing 3D Similarity Transformation by Robust Total Least Squares[J]. Acta Geodaetica et Cartographica Sinica, 2012, 41(5): 715-722. (陈义, 陆珏. 以三维坐标转换为例解算稳健总体最小二乘方法[J]. 测绘学报, 2012, 41(5): 715-722.) |
| [19] | GE Xuming, WU Jicang. Generalized Regularization to Ill-posed Total Least Squares Problem[J]. Acta Geodaetica et Cartographica Sinica, 2012, 41(3): 372-377. (葛旭明, 伍吉仓. 病态总体最小二乘问题的广义正则化[J]. 测绘学报, 2012, 41(3): 372-377.) |
| [20] | YUAN Qing, LOU Lizhi, CHEN Weixian. The Application of the Weighted Total Least-squares to Three Dimensional- Datum Transformation[J]. Acta Geodaetica et Cartographica Sinica, 2011, 40(S): 115-119. (袁庆, 楼立志, 陈玮娴. 加权总体最小二乘在三维基准转换中的应用[J]. 测绘学报, 2011, 40(增刊): 115-119.) |
| [21] | UNGAR A A. Barycentric Calculus in Euclidean and Hyperbolic Geometry: A Comparative Introduction[M]. London: World Scientific, 2010. |
| [22] | XIE Wei. The Properties and Applications of Barycentric Coordinates in 3D Euclidean Space[J]. Mathematics Learning and Research: Teaching and Research Version, 2009, (1): 90, 92. (谢伟. 重心坐标在三维欧氏空间中的性质及其应用[J]. 数学学习与研究: 教研版, 2009, (1): 90, 92.) |
| [23] | JOSEPHSON K, BYROD M. Pose Estimation with Radial Distortion and Unknown Focal Length[C]//IEEE Conference on Computer Vision and Pattern Recognition. Miami, FL: IEEE, 2009: 2419-2426. |
| [24] | HARTLEY R I, ZISSERMAN A. Multiple View Geometry in Computer Vision[M]. Cambridge: Cambridge University Press, 2004. |
| [25] | CHEN Yi, LU Jue, ZHENG Bo. Application of Total Least Squares to Space Resection]J]. Geomatics and Information Science of Wuhan University, 2008, 33(12): 1271-1274. (陈义, 陆珏, 郑波. 总体最小二乘方法在空间后方交会中的应用[J]. 武汉大学学报: 信息科学版, 2008, 33(12): 1271-1274.) |
| [26] | SCHUT G H. On Exact Linear Equations for the Computation of the Rotational Elements of Absolute Orientation[J]. Photogrammetria, 1960-1961, 17: 34-37. |
| [27] | HORN B K P, HILDEN H M, NEGAHDARIPOUR S. Closed-form Solution of Absolute Orientation Using Orthonormal Matrices[J]. Journal of the Optical Society of America A, 1988, 5(7): 1127-1135. |
| [28] | LI Deren, YUAN Xiuxiao. Error Processing and Reliability Theory[M]. Wuhan: Wuhan University Press, 2002. (李德仁, 袁修孝. 误差处理与可靠性理论]M]. 武汉: 武汉大学出版社, 2002.) |