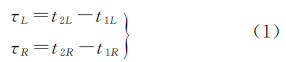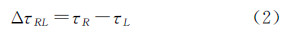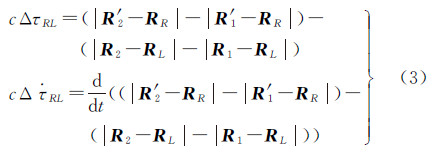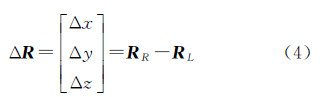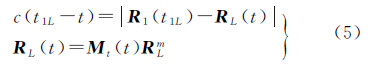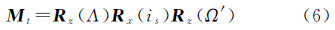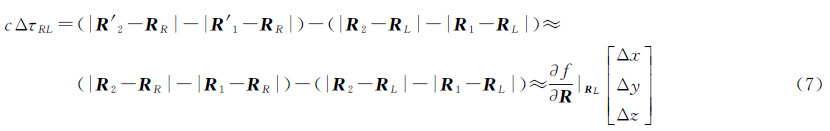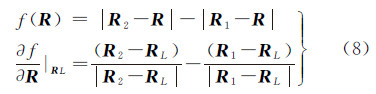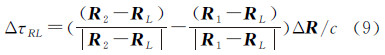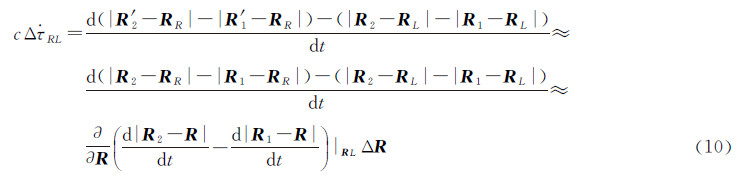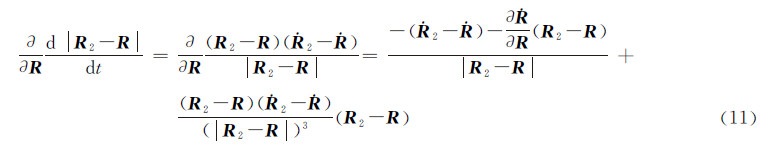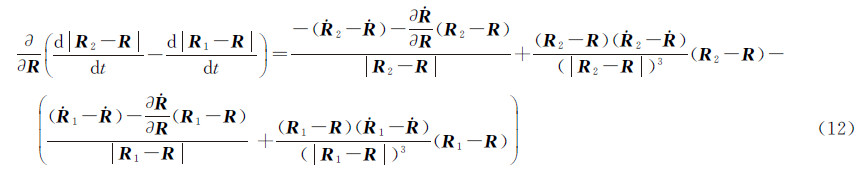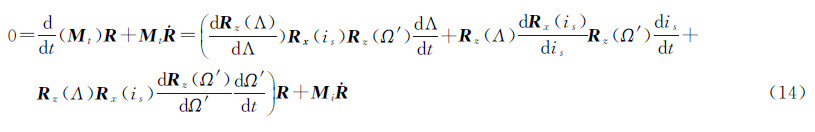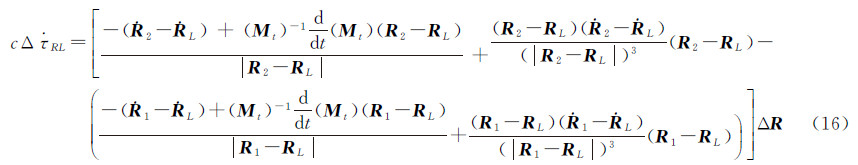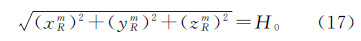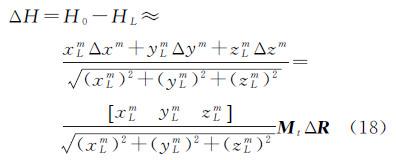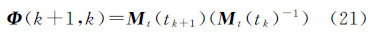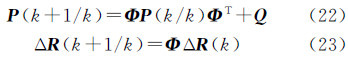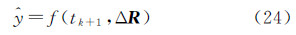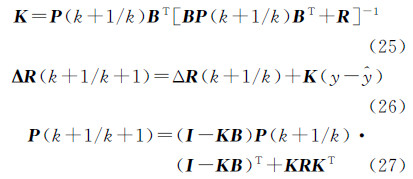2. 中国西安卫星测控中心， 陕西 西安 710034
2. Xi'an Satellite Control Center, Xi'an 710034, China
1 引 言
我国探月工程已顺利实现“落月”的阶段性目标。利用月球车等载荷工具在月面开展进一步的科学观测和试验，其重要基础是着陆器、巡视器等多个目标的相对位置确定，对其协同工作，撞击预警等具有重要作用。在未来探测器返回任务中，目标分离、对接等过程同样需要精确的相对位置关系。相对定位方法主要有两类，一类是基于目标之间的相互观测，如雷达探测、视觉定位等，适用于探测器的自主导航与控制，另一类基于地面观测，在地面干预和事后评估方面有一定的优势。
同波束干涉测量(same beam interferometry,SBI)技术属于后一类，它以甚长基线干涉测量(VLBI)技术为基础，利用两个地面站同时接收两个相近空间目标下行信号进行差分处理，以此抵消大气、等离子体等引入的传输时延误差和接收设备的时延等误差项，可实时解算得到两个航天器的高精度相对位置数据[1]。SBI的应用已较为广泛，中国科学院上海天文台在数据的预处理和解算方面做了大量工作，可提供精度最高达到皮秒(ps)级的测量数据[2, 3, 4]。文献[5—6]详细介绍了其原理和理论模型，文献[7]利用同波束测量进行了月球轨道精密确定及重力场解算的理论研究。文献[8]详细论述了同波束在精密测轨定位中的应用。文献[9]对定位精度进行了详细的仿真和理论分析，并使用地球轨道航天器验证了其结论。针对月面相对定位，文献[10]推导了基于USB测距和SBI观测数据的定位算法，精度较高，但不适用于缺少测距信息的情形，在不具备USB观测条件时无法应用。
对于在月球表面活动的目标,其位置应满足月球数字地形模型的约束。月球数字地形模型含有通过地形测绘得到的月面高程随经纬度的变化信息[11]，例如美国的ULCN2005模型[12]，日本的SELENE数据模型[13]，我国通过嫦娥系列探测器携带的CCD相机、激光测高仪等测量设备也获得了较精确的数字地形模型[14, 15, 16]。上述模型的高程精度都在百米以内，最高达到10 m，可以用于相对定位计算。文献[17]进行了相关研究，并分析了测量误差。
本文根据SBI测量原理，提出基于着陆器先验位置和差分时延、差分时延率观测数据的巡视器月面相对定位卡尔曼滤波算法，引入高程约束和月球数字高程模型，并评估算法的应用效果。
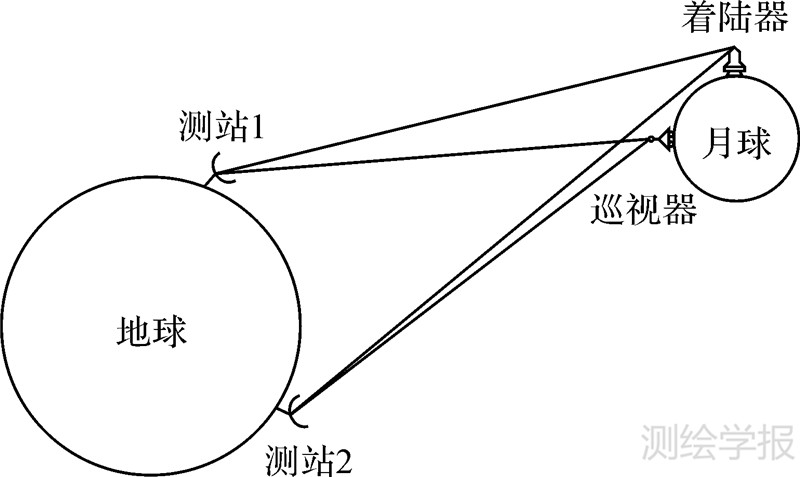
2 观测原理SBI 技术是VLBI测量技术的一种衍生技术。它是指: 当两个航天器在角度上非常接近时,可在一个地面天线的同一主波束内被观测,使用两面深空天线对两个航天器的同时观测量,即可生成差分干涉观测量[18]。SBI观测模型如图1所示。
|
| 图 1 同波束干涉测量示意图 Fig. 1 Schematic diagram of the same beam interferometry |
本文不涉及观测信号的预处理。假设已得到数据相关处理结果，一般为在同一时刻得到的多条基线相位时延值，对应不同测站的波前没有对齐。而本文考虑物理意义更加直观的同一波前传输原理，即相位时延为同一波前到达基线两个站的时间差。因此需要将探测器与巡视器的时延及差分数据插值修正至同一波前[2]。设某一时刻t着陆器和巡视器同时发出信号，测站1接收到着陆器、巡视器信号的时刻分别为t1L、t1R，测站2接收到着陆器、巡视器信号的时刻分别为t2L、t2R。则VLBI时延观测量(以测站1为主站，测站2为从站)即
相应的，SBI差分时延观测量为
设信号传播速度为常量c，差分时延和时延率可由下式表示
式中，R2、R1分别为t1L时刻对应测站1、t2L时刻对应测站2的惯性系矢量；R′2、R′1分别为t1R时刻对应测站1、t2R时刻对应测站2的惯性系矢量。由于向量在坐标转换后模不变，上述关系在月球固连坐标系下同样适用。 3 月面相对定位的观测方程
式(3)即使用SBI数据进行相对定位的基础。设待估量为巡视器惯性系的位置与着陆器位置的差
可以直接测量得到的为式(1)和式(2)中的ΔτRL、τR、τL和t1L、t1R、t2L、t2R等。则式(3)中对应每个时刻的测站位置可由测站地理坐标根据地球自转等关系计算(可视为以时间为变量的函数)，此处不再赘述。
在式(3)的未知量中，首先需要计算RR、RL对应的时刻t(即着陆器和巡视器发出信号的时刻)，由测站1到着陆器光行时的计算关系可知
式中，着陆器惯性系位置矢量为RL(t)，上标为m表示月球固连坐标系下的坐标(后同)，可由给定的月球固连坐标系位置RLm和月球固连坐标系到J2000惯性系的转换矩阵Mt(t)计算；Mt(t)根据JPL星历(或IAU公式，原理同之)计算
式中，Rz为绕Z轴旋转的坐标转换矩阵；Rx为绕X轴旋转的坐标转换矩阵；Λ、is、Ω′可由JPL星历查得。
由式(5)，先设t的初值为t1L，计算RL(t)，代入等式c(t1L-t)=R1(t1L)-RL(t)的右侧更新左侧时间t。如此多次迭代最终得到精确的信号发出时刻t及对应的RL。
式(3)中差分时延可转化为
式中
式(7)用到了两个简化。第1个是在计算测站位置R2、R′2、R1、R′1时认为t1L≈t1R、t2L≈t2R 。假设着陆器和巡视器足够近，满足RL-RR≤10 km，则着陆器和巡视器的信号先后到达同一测站的时间差小于3×10-5s，对应地球自转引起测站的位置变化与纬度相关，约为毫米级。根据测站观测几何，该变化矢量与R′2-RR、R′1-RR有一定夹角，且存在差分关系，因此引起的影响进一步缩小，将|R′2-RR|-|R′1-RR|简化为|R2-RR|-|R1-RR|满足精度要求。第2个简化是将f(R)在RL处展开且只取一阶项。
综上，可得单个基线的差分时延观测方程为
根据差分时延率的定义，类似的，可得
由于
可得
根据式(5)，当着陆器、巡视器在月固系下位置不变时有
即 则式(12)中的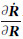
可由下式计算
式中，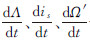
也可由JPL星历查得，进而计算出Mt和
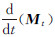，则式(10)可进一步改写为
式(16)即单个基线差分时延率合理简化后的观测方程。
4 约束方程及相对定位滤波算法由于差分时延、时延率对距离和速度作了差分，造成绝对位置信息的丢失，需要补充约束方程，否则会引起方程组的奇异。文献[6]中引入了USB测距、测速的约束，但依赖有效的观测弧段。本文针对月面目标特点，引入了数字月球模型和强制高程约束。
强制高程约束为指定巡视器在月球固连坐标系下经纬高中的高程，即
将巡视器高程减去着陆器高程，经过一阶近似，可得
对于月面目标，如果其所在当地月面地势足够平坦，则可以认为ΔH为0。也可由月球地形模型得到H0和HL并计算ΔH。月球地形模型通过一系列测绘数据积累和处理得到了月球表面经纬度(λ,φ)与高程的二元函数关系
以美国的ULCN2005模型为例，其数据文件按照一定间隔离散化经纬度并给出了对应的高程，可直接查表插值计算。实际使用中可由式(19)插值计算高程并代入式(18)得到约束方程。
综合约束与观测方程，即可求解ΔR。可使用最小二乘法对每个采样时间点的一组观测数据进行解算，此处不再赘述。本文同时提出以下带约束的卡尔曼滤波算法。
以惯性系的两器相对位置ΔR为状态量，由于ΔR转到月固坐标系后随时间变化保持不变，所以其状态转移矩阵可表示为
观测量为ΔτRL和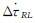
，观测方程见式(9)和式(16)。同时将约束式(11)也作为观测方程(ΔH为观测量)[19, 20]，即可应用如下的卡尔曼滤波算法流程。
(1) 计算状态转移矩阵
(2) 计算协方差矩阵及状态量的预测值
式中，使用数字月球模型时，需要首先由ΔR(k+1/k)计算对应的巡视器经纬度，代入式(19)得到ΔH。
(4)根据实际观测量更新状态量及协方差矩阵
式中，Q可以根据JPL星历的精度得到；R中关于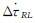
和ΔτRL的部分由观测噪声得出。约束量ΔH的方差在指定高程时设为接近零，使用数字月球模型时则按照模型实际精度设置。
需要说明的是，根据差分时延和差分时延率的特点，差分时延率对测量精度要求更高，但在实际应用中难以满足，因而对状态改进的贡献较小。但是当差分时延存在常值系统差时，侧重使用差分时延率数据可以有效消除系统差引起的不利影响(系统差的导数为零)。
5 仿真实例首先利用仿真数据验证算法的有效性。设着陆器经度、纬度、高程分别为(-20.3°，44.1°，-2632 m)，巡视器相对着陆器经纬高分别为(0.007°，0.006°，0 m)，其高程完全符合ULCN2005模型。由式(3)生成4个深空测量站(上海、北京、乌鲁木齐、昆明)共6条基线2013年12月15日0时至0时30分的仿真差分时延、差分时延率数据，采样间隔为5 s，并分别加入100 ps和10 ps/s的随机误差。
相对定位计算时取着陆器先验经度、纬度、高程分别为(-20.3°，44.1°，-2632 m)，巡视器初始的相对经纬度取为(0°，0°)。
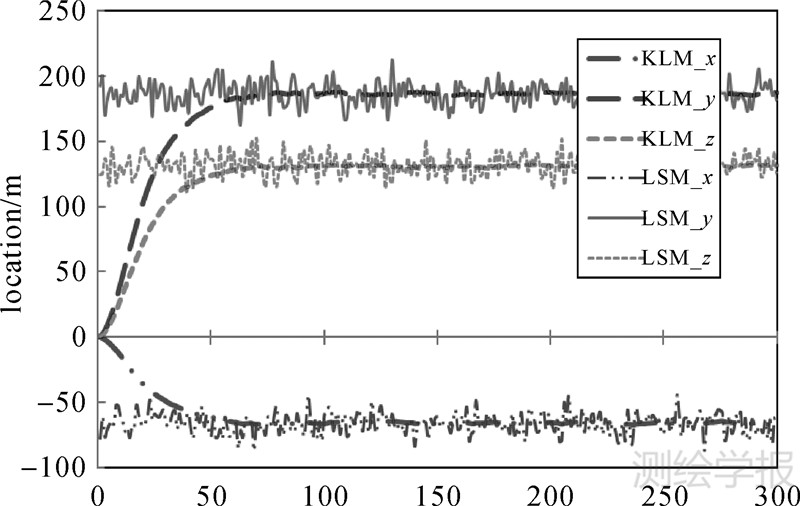
5.1 算法精度验证使用ULCN2005模型时，卡尔曼滤波(KLM)与最小二乘(LSM)单点解算的结果比对见图2，其横轴为观测量序列，纵坐标为月固系下的三维相对位置，理论值为(-65.82 m，186.68 m，130.51 m)。
|
| 图 2 仿真数据计算结果 Fig. 2 Calculation result of simulation data |
可见使用带约束的卡尔曼滤波算法后能够有效消除随机噪声，如果高程模型完全匹配，最终收敛结果与理论值的偏差在0.02 m以内(相对误差1e-4)，对应经纬度偏差在1e-6°以内。
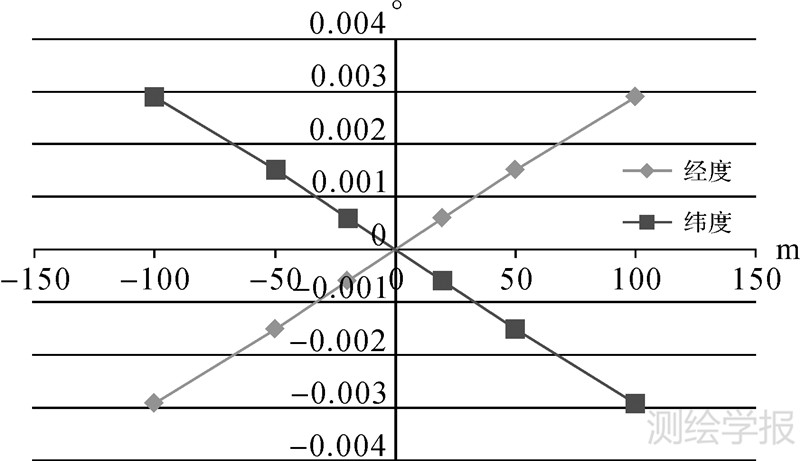
5.2 高程模型系统差的影响设约束量ΔH存在一定的系统偏差(±100 m以内)，则其不同取值对定位结果的影响见图3。可以看到高程模型偏差被平均至经纬度偏差中，由于月面经纬度1°对应距离约30 km，将单位由度数转换为米后对应的总偏差与约束量ΔH的偏差相当，结论与约束式(18)相符。
|
| 图 3 高程模型误差对应的定位偏差 Fig. 3 Deviation of position determination corresponding to height model error |
设着陆器先验位置存在一定的误差(经纬度±1°，高程±3 km以内)，则不同的误差取值对应计算结果见表1和表2。可见计算结果对着陆点位置误差较不敏感：经纬度1°对应3 m左右，而高程3 km对应0.4 m左右的偏差。
| 着陆器经纬度偏差/(°) | 定位计算结果 | 总偏差/m | |
| 经度/(°) | 纬度/(°) | ||
| -1 | 0.006 932 | 0.005 912 | 3.00 |
| -0.5 | 0.006 964 | 0.005 955 | 1.55 |
| -0.2 | 0.006 985 | 0.005 982 | 0.63 |
| 0.2 | 0.007 014 | 0.006 017 | 0.59 |
| 0.5 | 0.007 037 | 0.006 045 | 1.56 |
| 1 | 0.007 079 | 0.006 091 | 3.19 |
| 着陆器高程偏差/m | 定位计算结果 | 总偏差/m | |
| 经度/(°) | 纬度/(°) | ||
| 3000 | 0.006 987 | 0.005 989 | 0.42 |
| 1000 | 0.006 995 | 0.005 996 | 0.16 |
| 200 | 0.006 999 | 0.005 999 | 0.04 |
| -200 | 0.007 001 | 0.006 000 | 0.02 |
| -1000 | 0.007 004 | 0.006 003 | 0.12 |
| -3000 | 0.007 012 | 0.006 010 | 0.39 |
本文根据同波束干涉测量技术的原理，推导了具有一定程度简化的差分时延、差分时延率观测方程，并结合高程约束提出了一种月面目标的相对定位卡尔曼算法，同时引入高程约束方程作为观测方程的补充。通过仿真实例表明该算法在高程模型无系统差时能够达到1e-4以内的相对精度，特别适用于平坦月面近距离(此时两器相对高程信息较准确)的相对定位；在高程模型存在偏差时定位精度与高程模型精度相当。算法对着陆器先验位置的误差较不敏感，且不需要测距测速等附加观测信息，适应性强，能够满足探月任务月面相对定位的精度需求(1～10 m)。由于该算法对给定的先验高程约束较敏感，因此如果定位精度要求高于数字高程模型精度，就需要寻求其他约束联合使用，这部分工作将是后续研究的重点。
| [1] | KAHN R D, FOLKNERW M, EDWARDS C D. Position Determination of a Lander and Rover at Mars with Earth Based Differential Tracking[R]. [S.l.]: TDA Progress Report 42-108, 1992: 279-293. |
| [2] | CHEN Ming, LIU Qinghui. Calculation and Analysis of Same Beam VLBI Diferential Phase Delay Closure of Lunar Satellite[J]. Progress in Astronomy, 2010, 28(4): 415-423. (陈明, 刘庆会. 探月卫星同波束VLBI差分相位时延闭合计算与分析[J]. 天文学进展, 2010, 28(4): 415-423.) |
| [3] | ZHENG Xin, CHEN Guanlei, WU Yajun, et al. Research on the Same Bean Interferometry VLBI Techniques for Relative Positioning of Lunar Rover[C]// Proceedings of the 9th Academic Conference of China Astronavigation Academic Committee of Deep Space Exploration Technology. Hangzhou: [s.n.], 2012: 125-137. (郑鑫, 陈冠磊, 吴亚军, 等. 月球车相对定位同波束VLBI技术研究[C]// 中国宇航学会深空探测技术专业委员会第九届学术年会论文集. 杭州: [s.n.], 2012: 125-137.) |
| [4] | HE Qingbao, LIU Qinghui, ZHENG Xin, et al. Study of Differential Delay Rate by Processing Same Beam VLBI Data[J/OL]. [2013-12-27]. http://www.cnki.net/kcms/detail/53.1189.P.20131227.1633.005.html. (贺庆宝, 刘庆会, 郑鑫, 等. 同波束VLBI差分时延率研究[J/OL]. [2013-12-27]. http://www.cnki.net/kcms/detail/53.1189.P.20131227.1633.005.html.) |
| [5] | GUO Li. Reduction of the Instantaneous State Vectors of Spacecraft Based on VLBI Tracking Data[D]. Shanghai: Shanghai Astronomical Observatory, CAS, 2007. (郭丽. 基于VLBI跟踪观测的空间飞行器瞬时状态参量归算[D]. 上海: 中国科学院上海天文台, 2007.) |
| [6] | YI Hui, WEI Erhu, YAN Wei, et al. On the Theoretical Location Model of Lunar Detector with VLBI and Space VLBI Observations[J]. Bulletin of Surveying and Mapping, 2009(2): 4-6. (易慧, 魏二虎, 严韦, 等. VLBI, SVLBI技术用于月球探测器定位的理论模型[J]. 测绘通报, 2009(2): 4-6.) |
| [7] | YAN Jianguo, LI Fei, LIU Qinghui, et al. Application of Same Beam VLBI Technique in Precise Orbit Determination of Lunar Bi-spacecraft and Gravity Field Determination[J]. Journal of Astronautics, 2011, 31(11): 2536-2541. (鄢建国, 李斐, 刘庆会, 等. 同波束VLBI技术用于月球双探测器精密定轨及重力场解算[J]. 宇航学报, 2011, 31(11): 2536-2541.) |
| [8] | LIU Qinghui, CHEN Ming, GOOSSENS S, et al. Applications of Same-beam VLBI in the Orbit Determination of Multi-spacecrafts in A Lunar Sample-return Mission[J]. Scientia Sinica Physics, Mechanics & Astronomy, 2010, 40(6): 809-818. (刘庆会, 陈明, GOOSSENS S, 等. 同波束VLBI在采样返回式多目标探测器精密测轨测位中的应用[J]. 中国科学: 物理学 力学 天文学, 2010, 40(6): 809-818.) |
| [9] | XI Wenjun, REN Zhong, ZHANG Xu. Research on Measurement Accuracy Simulation of Same Beam Interferometry (SBI) Technology[J]. Telecommunication Engineering, 2010, 50(1): 1-7. (席文君, 任重, 张旭. 同波束干涉测量技术测量精度仿真研究[J]. 电讯技术, 2010, 50(1): 1-7.) |
| [10] | DONG Guangliang, HAO Wanhong, LI Haitao, et al. Relative Position Determination on the Lunar Surface Using Same-beam Interferometry[J]. Journal of Tsinghua University: Science & Technology, 2010, 50(7): 1-7. (董光亮, 郝万宏, 李海涛, 等. 同波束干涉测量对月面目标相对定位[J]. 清华大学学报: 自然科学版, 2010, 50(7): 1-7.) |
| [11] | CHEN Junyong, ZHANG Chuanyin, DANG Yamin. Lunar Spatial Exploration, Surveying and Mapping[J]. Acta Geodaetica et Cartographica Sinica, 2005, 34(3): 189-195. (陈俊勇, 章传银, 党亚民. 月球航天探测和月球测绘[J]. 测绘学报, 2005, 34(3): 189-195.) |
| [12] | ARCHINAL B A, ROSIEK M R, KIRK R L, et al. The Unified Lunar Control Network 2005: Version 1.0[R]. Washington, D C: Geological Survey Open-file Report 2006-1367, 2006. |
| [13] | ARAKI H, TAZAWA S, NODA H, et al. Lunar Global Shape and Polar Topography Derived from Kaguya-LALT Laser Altimetry[J]. Science, 2012, 323(5916): 897-900. |
| [14] | LI Chunlai, REN Xin, LIU Jianjun, et al. Laser Altimetry Data of Chang'E-1 and the Global Lunar DEM Model[J]. Science China: Earth Sciences, 2010, 40(3): 281-293. (李春来, 任鑫, 刘建军, 等. 嫦娥一号激光测距数据及全月球DEM模型[J]. 中国科学: 地球科学, 2010, 40(3): 281-293.) |
| [15] | LI Chunlai. Photogrammetric Processing and Lunar Global Topographic Map from the Chang'E 1 3-line Array CCD Data[J]. Acta Geodaetica et Cartographica Sinica, 2013, 42(6): 853-860. (李春来. 嫦娥一号三线阵CCD数据摄影测量处理及全月球数字地形图[J]. 测绘学报, 2013, 42(6): 853-860.) |
| [16] | PING Jinsong, HUANG Qian, YAN Jianguo, et al. Lunar Topographic Model CLTM-s01 from Chang'E-1 Laser Altimeter[J]. Science China Series G: Physics, Mechanics and Astronomy, 2008, 38(11): 1601-1612. (平劲松, 黄倩, 鄢建国, 等. 基于嫦娥一号卫星激光测高观测的月球地形模型CLTM-s01[J]. 中国科学G辑: 物理学 力学 天文学, 2008, 38(11): 1601-1612.) |
| [17] | LIU Qinghui, CHEN Ming, XIONG Weiming, et al. Relative Position Determination of a Lunar Rover Using High-accuracy Multi-frequency Same-beam VLBI[J]. Science China Physics, Mechanics and Astronomy, 2010, 53(3): 571-578. (刘庆会, 陈明, 熊蔚明, 等. 基于超高精度多频点同波束VLBI技术的月球车精密相对定位[J]. 中国科学G 辑: 物理学 力学 天文学, 2010, 40(2): 253-260.) |
| [18] | THORNTON C L, BORDER J S. Radiometric Tracking Techniques for Deep Space Navigation[M]. Pasadena, California, USA: Jet Propulsion Laboratory, California Institute of Technology, 2000. |
| [19] | SIMON D, CHIA T L. Kalman Filtering with State Equality Constraints[J]. IEEE Transactions on Aerospace and Electronic Systems, 2002, 38(1): 128-136. |
| [20] | HU Congwei, LIU Dajie, YAO Lianbi. Adaptive Filtering with Constraint for GPS Positioning[J]. Acta Geodaetica et Cartographica Sinica, 2002, 31(sup.): 39-44. (胡丛玮, 刘大杰, 姚连璧. 带约束条件的自适应滤波及其在GPS定位中的应用[J]. 测绘学报, 2002, 31(增刊): 39-44.) |