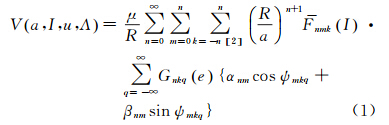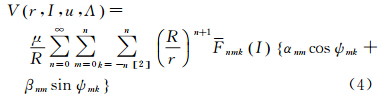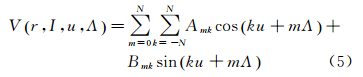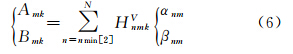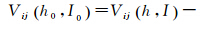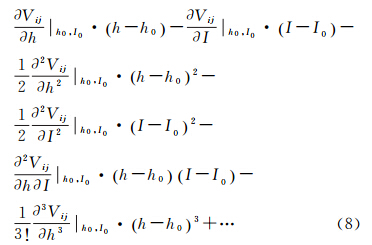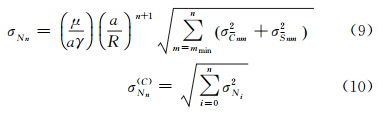2. 中国测绘科学研究院地理空间信息工程国家测绘地理信息局重点实验室,北京 100830;
3. 国家测绘地理信息局卫星测绘应用中心,北京 101300
2. Key Laboratory of Geo-informatics of SBSM, Chinese Academy of Surveying and Mapping, Beijing 100830, China;
3. Satellite Surveying and Mapping Application Center, National Administration of Surveying, Mapping and Geoinformation, Beijing 101300, China
1 引 言
2009年3月17日,欧空局成功发射了GOCE (Gravity field and steady-state Ocean Circulation Explorer)卫星,旨在探测高精度高分辨率的地球重力场和稳态海洋环流,具体目标为:利用卫星引力梯度数据和卫星跟踪卫星(satellite-satellite tracking,SST)数据分别以1 mGal和1~2 cm的精度恢复地球重力异常和大地水准面,同时要求空间分辨率达到100 km,即重力场模型至少为200阶次[1, 2]。2013年10月,GOCE卫星结束使命,共测得约42个月的卫星引力梯度数据。利用该类数据反演地球重力场模型的方法大致可分为3类:直接法、空域法和时域法[3, 4, 5]。直接法利用卫星位置处观测值与球谐系数的严密数学关系式进行解算。空域法将观测值看作是卫星位置的函数,可直接利用最小二乘法求解球谐系数,也可将观测值归算并内插成平均轨道球面上的均匀格网值,进而利用解析法等方法进行解算。时域法将观测值看作是沿轨时间序列,按解算方法的不同,又可分为时间域时域法和频率域时域法,前者直接通过沿轨观测值与球谐系数的线性关系利用最小二乘法进行解算,而后者又称半解析法,即SA(semi-analytical)方法[6],根据观测值与集总系数的关系式,通过1D-FFT或2D-FFT技术得到频域内的集总系数,再根据集总系数与球谐系数的线性关系用块对角最小二乘法解算球谐系数,2D-FFT对应的SA方法称为Torus方法[6, 7]。
国内外学者对如何利用SA方法解算地球重力场模型进行了大量研究,快速傅里叶技术和块对角最小二乘法的使用极大地提高了计算效率。对于利用1D-FFT的SA方法解算地球重力场模型已有大量相关研究,所用数据为GOCE引力梯度数据和SST数据[8, 9, 10, 11]。而对于利用Torus方法解算模型的研究中,所用数据为模拟的GOCE轨道数据、卫星引力梯度数据和SST数据,利用模拟引力梯度数据恢复模型的最高阶次为120,受格网化误差的影响,利用模拟GOCE卫星引力梯度分量Vzz解算模型的精度优于Vxx、Vyy分量的解算结果。Torus方法的解算精度与直接法相当,但Torus方法所需时间仅为直接法的1%[12]。
本文介绍了利用卫星引力梯度数据反演地球重力场模型的Torus法的理论和算法,利用GOCE实测轨道数据模拟无噪声和含白噪声情况下的卫星引力梯度数据,分析Torus方法解算地球重力场模型的精度,极空白、归算误差、格网化误差以及白噪声等对结果的影响。
2 求解地球重力场模型的Torus方法
根据卫星轨道摄动理论,局部轨道坐标系(local orbit reference frame,LORF)下引力位与卫星6个轨道根数之间的关系可表示为[13]
式中,a为卫星轨道长半轴;I为轨道倾角;u为升交角距,u=ω+M,ω和M分别为近地点角距和平近点角;Λ为升交点经度,Λ=Ω-θG,其中Ω为升交点赤经,θG为格林尼治恒星时角;μ为地心引力常数,即万有引力常数与地球质量的乘积;R为地球平均半径;n、m为球谐函数的阶和次,第3个加和下标中的[2]表示k的变化步长为2。nmkI和Gnkq(e)分别为正规化的倾角函数和偏心率函数,e为偏心率,ψmkq为u、Λ和M的函数,Ψmkq=ku+mΛ+qM。球谐系数αnm和βnm随n-m的奇偶性取不同的值,具体关系如下 式中,Cnm、Snm为完全规格化球谐系数。对于e≈0的近圆轨道,式(1)可以简化为[4, 13, 14, 15]
式中,r为地心向径;ψmk=ku+mΛ,此时,u=ω+f,f为真近点角。式(4)中级数求和的n应取至无穷大,但实际计算中常截止到某最高阶N。经过符号代换,式(4)可写为[6]
式中,Amk、Bmk为集总系数,是转换系数HnmkV和球谐系数(αnm和βnm)的线性组合式中,加和下标n=nmin[2],nmin=maxk,m+δ,若k与maxk,m奇偶性相同,则δ=0,否则δ=1。
转换系数建立了球谐系数与集总系数的线性关系。6个引力梯度分量对应的转换系数如下[6]
式中,F′nmkI为倾角函数FnmkI关于轨道倾角I的一阶导数。式(5)是SA方法的基本表达式,是傅里叶级数的形式,集总系数Amk和Bmk为傅里叶系数。SA方法要求使用名义轨道上的观测值,名义轨道具有3个特点:轨道为圆形、轨道倾角为常量、轨道受J2项影响而长周期进动[6, 7],同时,为便于FFT快速计算,要求等间隔采样的观测值。式(5)中变量u和Λ分别为定义在两个不同方向的圆周,其变化范围均为[0,2π),这两个圆周可形成一个封闭的圆环,若观测值均匀分布在该圆环面上,则可以利用2D-FFT方法解算集总系数,因此D-FFT对应的SA方法称为Torus方法。
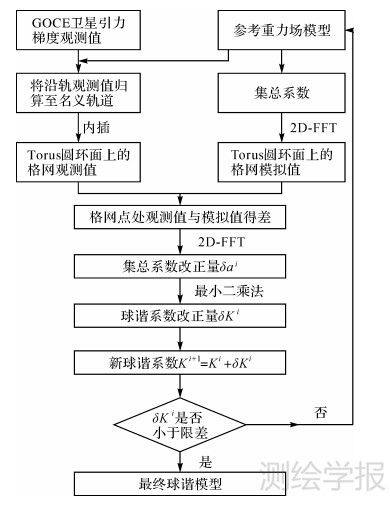
采用Torus方法由GOCE沿轨卫星引力梯度观测值确定地球重力场模型的流程如图 1所示,其中ai表示第i次迭代的集总系数,Ki+1为第i次迭代后的球谐系数。
|
| 图 1 利用Torus方法解算GOCE卫星重力场模型的流程 Fig. 1 Flow chart for GOCE satellite gravity field determination using Torus approach |
选择2009年11月01日至2009年12月31日,共61 d(GOCE卫星轨道重复周期)的SST_PRD_2数据产品,该产品提供了地固系(earth-fixed reference frame,EFRF)下采样间隔为10 s的简化动力学轨道,计算6个轨道根数[13,16-17],确定名义轨道的高度r0=6 637.655 km和倾角I0=96.628°。由于在地球重力场模型解算中,引力梯度分量Vzz的影响较大,所以仅以该分量为例。
3.1 名义轨道格网引力梯度模拟数据
为验证无误差情况下Torus方法反演地球重力场模型的精度,分别利用EGM2008模型[18]的前60、80、90、110、150和200阶次系数,采用2D-FFT方法由式(5)计算名义轨道格网点的引力梯度分量Vzz。
利用2D-FFT方法和按次排列的块对角最小二乘法求解地球重力场模型系数,并计算模型的阶误差[19],如图 2所示,其中60、110、200阶模型的球谐系数误差谱如图 3所示。仅从阶误差曲线来看,60阶模型的阶误差小于10-21,而200阶模型的阶误差达10-16,且随着模型最高阶次的增大,阶误差有增大的趋势,且阶误差呈现奇偶性的差异。图 3中横轴中心对应的次为0,左右两边分别表示Cnm和Snm的误差谱。图左右两边基本对称,说明同阶次的Cnm和Snm的误差基本一致。另外,较大的误差集中在低次项系数,这主要是受GOCE任务极空白的影响[20],且极空白的影响随着最高阶次的增大而增大,这是导致模型阶误差随着最高阶增加而增大的主要原因。从200阶重力场模型的误差谱可以看出,尽管受到极空白的影响,球谐系数误差均小于10-16,说明当观测值满足Torus方法的理论要求时可以完全恢复重力场模型。

|
| 图 2 不同阶次模型的阶误差比较 Fig. 2 Comparisons of degree error among different models |

|
| 图 3 最高阶为60、110和200的模型误差谱 Fig. 3 Error spectrum of models with maximum degree 60,110 and 200 |
Torus方法要求使用圆环面均匀格网点的观测值,而GOCE卫星的轨道并非圆形,且倾角也不是常数,为了分析在GOCE卫星实测轨道情况下Torus方法解算地球重力场的能力,利用EGM2008模型前200阶次的系数模拟了局部轨道坐标系下的沿轨卫星引力梯度分量Vzz,将其作为实际观测值,以验证方法的正确性和严密性。
为满足Torus方法的要求,GOCE卫星的沿轨引力梯度观测值应归算并内插至名义轨道的格网点。设点P为GOCE卫星轨道上的任意一点,其轨道高度和倾角分别为h和I,Pt为名义轨道上的点,其轨道高度和倾角分别为常数h0、I0。利用泰勒级数展开可以得到Pt点处的引力梯度分量Vij(h0,I0)为[12]
式中,Vij(h,I)为P点的引力梯度分量,下标ij表示局部轨道坐标系下引力梯度张量的6个分量(xx,xy,xz,yy,yz,zz),式(8)中引力梯度分量在轨道高度和倾角方向的改正量可以利用式(5)求偏导得到。表 1给出仅考虑引力梯度分量Vzz的情况下61 d轨道对应的式(8)中6项偏导分量的STD以及它们与Vzz分量的比值。其中,关于h的偏导分量较大,一阶偏导分量达9.746 E,占Vzz分量的3.580×10-3,二阶偏导分量达26.84 mE,与Vzz分量的比值为9.681×10-6,三阶偏导分量小于1 mE;关于I的偏导分量较小,其中一阶偏导分量最大,为1.352 mE,仅占Vzz分量的4.969×10-7,二阶偏导分量和交叉偏导分量更小。相对于GOCE卫星引力梯度分量Vzz中的噪声而言,轨道高度方向三阶以上的偏导分量,以及轨道倾角三阶及三阶以上的分量均可忽略。
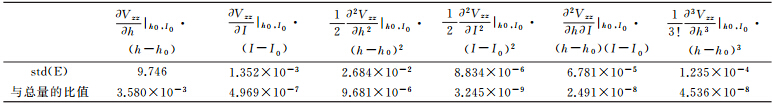 |
利用Kriging方法将归算后的离散Vzz分量内插至格网点,其中,半变异函数模型选用球状模型,搜索半径为1°。利用模型EGM2008前200阶次的系数采用2D-FFT方法模拟格网点的引力梯度值,并计算格网点引力梯度的差值,统计结果见表 2,格网点引力梯度差值反映了归算误差和格网化误差的影响,由表 2可知Vzz的误差约为0.110 mE,与GOCE卫星重力梯度仪精度指标(5 mE)相比,归算和格网化的精度满足要求。
| min | max | mean | std |
| -8.688×10-4 | 3.831×10-4 | -1.176×10-5 | 1.102×10-4 |
为了消除归算误差并减小格网化误差,本文选择EGM96为参考模型,并利用其前200阶次的球谐系数模拟了局部轨道坐标系下的沿轨引力梯度参考值(仅指Vzz分量),将残差格网化,并利用2D-FFT和按次排列的块对角最小二乘法求解球谐系数改正量,对参考模型进行改正,并将改正后的重力场模型作为新的参考模型进行迭代。
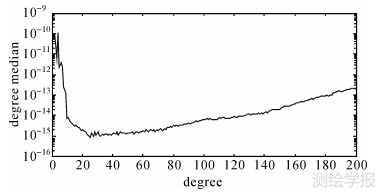
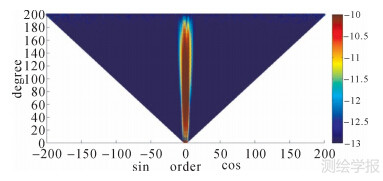
3次迭代后,除小于10次的球谐系数受极空白的影响改正量较大外,其他系数的改正量小于10-12。图 4和图 5分别显示了模型的误差阶中值和误差谱,受低次系数误差较大的影响,低阶部分的误差阶中值也较大。
|
| 图 4 无噪声情况下模型阶中值 Fig. 4 Degree median of models from simulated noise-free data |
|
| 图 5 无噪声情况下模型误差谱 Fig. 5 Error spectrum of models from simulated noise-free data |
为了分析Torus方法解算模型在不同阶的大地水准面精度,利用式(9)和(10)计算模型的大地水准面阶误差和累积误差
图 6给出了EGM2008模型的大地水准面信号、无噪声时Torus方法解算的重力场模型相对于EGM2008的大地水准面阶误差和累积误差。由于次小于10的系数受极空白影响较大,所以在计算大地水准面阶误差和累积误差时未考虑低次部分。在格网化误差的影响下,随着阶的增大,大地水准面阶误差有增大的趋势,200阶时阶误差达到最大值,为0.022 mm,累积误差为0.099 mm,远小于EGM2008模型的大地水准面信号。另外,相对于GOCE任务对大地水准面的精度要求(1~2 cm),格网化误差基本可以忽略。

|
| 图 6 无噪声情况下模型的大地水准面阶误差和累积误差 Fig. 6 Degree and cumulative geoid error of models from simulated noise-free data |
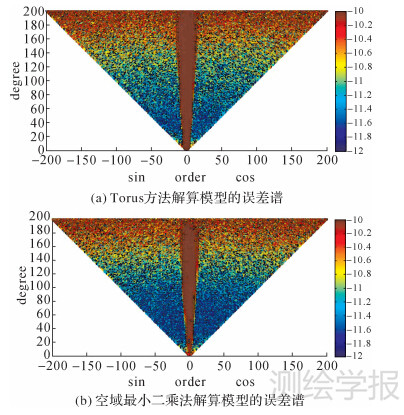
为探究含白噪声时Torus方法解算地球重力场模型的精度,按照GOCE卫星任务的设计要求[1],在模拟数据中加入了功率谱密度为5 mE/Hz1/2的白噪声,然后解算位系数,需要注意的是,利用无误差的模拟观测值解算地球重力场模型时,迭代可以减小格网化的影响,但当观测值中含5 mE/Hz1/2白噪声时,噪声远大于格网化误差,所以不需要迭代。为了与Torus方法的解算结果作比较,利用相同观测数据,采用空域最小二乘法解算地球重力场模型[21],图 7显示了两种方法解算模型的误差谱,相比空域最小二乘法,Torus方法受极空白影响相对更大,模型解算的精度略低,特别是140阶以内,空域最小二乘法的精度明显更高。与无噪声的结果相比,含白噪声时误差大了3~4个数量级,同时,极空白影响的范围变大,主要是次小于13的系数误差较大,误差随着阶的增大而变大。
|
| 图 7 观测值中含白噪声时模型误差谱 Fig. 7 Error spectrum of models from observations with white noise |
为了进一步比较两种方法的解算精度,分别利用式(9)和式(10)计算大地水准面阶误差和累积误差,其中mmin=13,计算结果见图 8,随着阶的增大,两种方法解算模型的阶误差和累积误差不断增大,Torus方法和空域最小二乘法解算模型的累积误差曲线分别在约193阶和196阶处与EGM2008模型曲线相交。受格网化误差和极空白的影响,Torus方法的大地水准面阶误差和累积误差略大于空域最小二乘法,140阶以内尤为明显,这与图 7有良好的一致性。Torus模型的阶误差和累积误差的最大值分别为1.58 cm和6.37 cm,而空域最小二乘法对应的最大值分别为1.45 cm和5.55 cm。但就计算效率而言,利用空域最小二乘法解算200阶重力场模型,使用106个CPU同时计算,所需时间约为9.4 h,而由于采用了2D-FFT技术和按次排列的块对角最小二乘法,使用1个CPU的情况下,Torus方法仅需要51 min,计算效率大大提高。
目前发布的GOCE卫星重力场模型中,go_cons_gcf_2_dir_r1(直接法)和go_cons_gcf_2_tim_r1(时域法)均联合采用71 d(2009-11-01—2010-01-11)的实测GOCE卫星引力梯度数据和卫星跟踪卫星数据[5],不考虑次小于13的系数,计算两个第1代模型的大地水准面阶误差和累积误差,结果见图 8,200阶时,直接解和时域解的大地水准面阶误差分别为1.06 cm、2.63 cm,累积误差分别为7.00 cm、12.27 cm。

|
| 图 8 观测值中含白噪声时模型的大地水准面阶误差和累积误差 Fig. 8 Degree and cumulative geoid error of models from observations with white noise |
本文在介绍Torus方法解算地球重力场模型的基本原理和方法步骤的基础上,利用GOCE卫星实测轨道和EGM2008模型,分别模拟了名义轨道上的格网引力梯度值、实测轨道上无误差和含5 mE/Hz1/2白噪声的GOCE卫星引力梯度观测值,利用这3类数据分别解算了200阶次地球重力场模型,分析了无误差、受格网化误差影响以及观测值中含白噪声3种情况下模型的精度,结果表明在无误差的情况下,Torus方法解算模型的精度较高,受极空白的影响,低次项系数误差较大,且随着模型最高阶次的增大,阶误差有增大的趋势。200阶模型低阶项的阶误差优于10-16,随着阶的增大,阶误差减小,200阶时,阶误差仅10-21;观测值中不含白噪声的情况下,迭代3次后,受极空白和格网化误差的影响,次小于10的系数误差较大,阶中值达10-10。在不考虑低次系数的情况下,大地水准面阶误差随着阶的增大而增大,200阶时,阶误差为0.022 mm,累积误差为0.099 mm。观测值中含有5 mE/Hz1/2白噪声时,解算模型比无噪声模型的精度差了3~4个数量级。模型的大地水准面阶误差和累积误差(未考虑次小于13的系数)随着阶的增大而增大,200阶时,两种误差分别为1.58 cm和6.37 cm,而空域最小二乘解的误差分别为1.45 cm和5.55 cm,受格网化误差和极空白的影响,Torus方法的误差略大于空域最小二乘法的误差,但由于在Torus方法的解算过程中采用了2D-FFT技术和按次排列的块对角最小二乘法,在计算效率方面,Torus方法明显占优。
模拟表明利用Torus方法可以高精度地恢复地球重力场,为利用GOCE引力梯度观测值反演地球重力场模型提供了一种独立有效的方法,由于采用了二维快速傅里叶技术和块对角最小二乘法,极大地提高了解算效率。但受极空白的影响,重力场模型低次项的精度较差,可采用Kaula正则化等方法[22, 23, 24]解决。另外,GOCE卫星实测引力梯度数据中存在有色噪声,可采用移动恢复法或维纳滤波方法[5, 25]进行处理。为满足Torus方法的要求,需将梯度仪坐标系下的卫星引力梯度观测值转换至局部轨道坐标系,转换过程中低精度分量会影响高精度分量的精度,可利用先验模型或迭代解计算的观测值代替低精度分量,以减小坐标转换产生的影响。
| [1] | ESA. Gravity Field and Steady-state Ocean Circulation Mission. Reports for Mission Selection of the Four Candidate Earth Explorer Core Missions[R]. ESA Publications Division, ES SP-1233(1), 1999. |
| [2] | DRINKWATER M R, HAAGMANS R, MUZI D, et al. The GOCE Gravity Mission: ESA's First Core Earth Explorer[R]. Proceedings of the 3rd International GOCE User Workshop, Frascati, Italy, ESA Special Publication, SP-627, ISBN 92-9092-938-3, 2006: 1-8. |
| [3] | RUMMEL R, VAN GELDEREN M, KOOP R, et al. Spherical Harmonic Analysis of Satellite Gradiometry[M]. Netherlands Geodetic Commission: Publications on Geodesy, New Series 39, 1993. |
| [4] | KOOP R. Global Gravity Field Modeling Using Satellite Gravity Gradiometry[M]. Netherlands Geodetic Commission: Publications on Geodesy, New Series 38, 1993. |
| [5] | PAIL R, BRUINSMA S, MIGLIACCIO F, et al. First GOCE Gravity Field Models Derived by Three Different Approaches[J]. Journal of Geodesy, 2011, 85(11): 819-843. |
| [6] | SNEEUW N J. A Semi-analytical Approach to Gravity Field Analysis from Satellite Observations[D]. Munich, Germany: Institut für Astronomische und Physikalische Geodsie, Technische Universitt München, 2000. |
| [7] | SNEEUW N J. Space-wise, Time-wise, Torus and Rosborough Representations in Gravity Field Modeling[J]. Space Science Reviews, 2003, 108(1-2): 37-46. |
| [8] | KLEES R, DITMAR P. The Performance of the Time-wise Semi-analytical Inversion of Satellite Gravity Gradients[M]//DM J, SCHWARZ K P. Vistas for Geodesy in the New Millennium, International Association of Geodesy Symposia. Berlin Heidelberg: Springer, 2001, 125: 253-258. |
| [9] | SCHUH W D, PAIL R, PLANK G. Assessment of Different Numerical Solution Strategies for Gravity Field Recovery[C]// Proceedings of the 1st International GOCE User Workshop, ESA WPP-188, 87-95, ESA/ESTEC, 2001. |
| [10] | PAIL R, WERMUTH M. GOCE SGG and SST Quick-look Gravity Field Analysis[J]. Advances in Geosciences, 2003, 1: 5-9. |
| [11] | PAIL R, PLANK G. GOCE Gravity Field Processing Strategy[J]. Studia Geophysica et Geodaetica, 2004, 48(2): 289-309. |
| [12] | XU Chen. The Torus-based Semi-analytical Approach in Spaceborne Gravimetry[D]. Calgary: Department of Geomatics Engineering, University of Calgary, 2008. |
| [13] | KAULA W M. Theory of Satellite Geodesy: Applications of Satellites to Geodesy[M]. Waltham Massachusetts: Blaisdell Publishing Company, 1966. |
| [14] | SCHRAMA E J O. The Role of Orbit Errors in Processing of Satellite Altimeter Data[M]. Netherlands Geodetic Commission: Publications on Geodesy, New Series 33, 1989. |
| [15] | PAIL R, PLANK G. Assessment of Three Numerical Solution Strategies for Gravity Field Recovery from GOCE Satellite Gravity Gradiometry Implemented on a Parallel Platform[J]. Journal of Geodesy, 2002, 76(8): 462-474. |
| [16] | ESA. GOCE HPF: GOCE Level 2 Product Data Handbook[R]. Technical Note, GO-MA-HPF-GS-0110, 2010. |
| [17] | CAPITAINE N, WALLACE P T, MCCARTHY D D. Expressions to Implement the IAU 2000 Definition of UT1[J]. Astronomy & Astrophysics, 2003, 406(3): 1135-1149. |
| [18] | PAVLIS N K, HOLMES S A, KENYON S C, et al. An Earth Gravitational Model to Degree 2160: EGM2008[J]. EGU General Assembly, 2008, 10: 13-18. |
| [19] | ESA. GOCE L1b Products User Handbook[R]. Technical Note, GOCE-GSEG-EOPGTN-06-0137, 2006. |
| [20] | SNEEUW N J, VAN GELDEREN M. The Polar Gap[M]//SANSÓ F, RUMMEL R. Geodetic Boundary Value Problems in View of the One Centimeter Geoid. Lecture Notes in Earth Sciences. Berlin Heidelberg: Springer, 1997, 65: 559-568. |
| [21] | XU Xinyu, LI Jiancheng, JIANG Weiping, et al. Simulation Study for Recovering GOCE Satellite Gravity Model Based on Space-wise LS Method[J]. Acta Geodaetica et Cartographica Sinica, 2011, 40(6): 697-702. (徐新禹, 李建成, 姜卫平, 等. 基于空域最小二乘法求解 GOCE 卫星重力场的模拟研究[J]. 测绘学报, 2011, 40(6): 697-702.) |
| [22] | RUDOLPH S, KUSCHE J, IIK K H. Investigations on the Polar Gap Problem in ESA's Gravity Field and Steady-state Ocean Circulation Explorer Mission (GOCE)[J]. Journal of Geodynamics, 2002, 33(1-2): 65-74. |
| [23] | XU Xinyu, LI Jiancheng, WANG Zhengtao, et al. The Simulation Research on the Tikhonov Regularization Applied in Gravity Field Determination of GOCE Satellite Mission[J]. Acta Geodaetica et Cartographica Sinica, 2010, 39(5): 465-470. (徐新禹, 李建成, 王正涛, 等. Tikhonov正则化方法在GOCE重力场求解中的模拟研究[J]. 测绘学报, 2010, 39(5): 465-470.) |
| [24] | ZHU Guangbin, LI Jiancheng, WEN Hanjiang, et al. Slepian Localized Spectral Analysis of the Determination of the Earth's Gravity Field Using Satellite Gravity Gradiometry Data[J]. Acta Geodaetica et Cartographica Sinica, 2012, 41(1): 1-7. (朱广彬, 李建成, 文汉江, 等. 卫星重力梯度数据确定地球重力场的Slepian局部谱分析方法[J]. .测绘学报, 2012, 41(1): 1-7) |
| [25] | BAUR O, SNEEUW N, GRAFAREND E W. Methodology and Use of Tensor Invariants for Satellite Gravity Gradiometry[J]. Journal of Geodesy, 2008, 82(4-5): 279-293. |