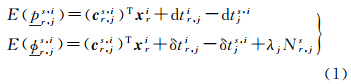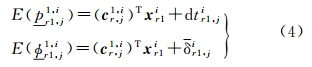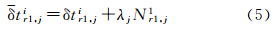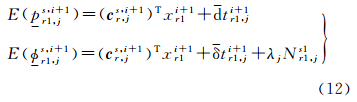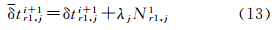2. 北京空间信息中继传输技术研究中心，北京 100094
2. Beijing Space Information Relay and Transmission Technology Research Centre, Beijing 100094, China
1 引 言
两台GNSS接收机可形成一条基线，对其同步观测的伪距和相位观测值实施双差，可建立一组包含相对位置和双差模糊度等参数的观测方程，以用于实施相对定位等应用[1, 2, 3]。其中，实时数据处理和整周模糊度固定能分别确保各类参数估值的时效性和可靠性[4, 5]。为此，通常采用卡尔曼滤波估计参数，并需要在相邻历元之间传递双差模糊度的滤波值。然而，当前后历元的双差模糊度所对应的参考星不同时，还需要构造一个转换矩阵，用于将双差模糊度“映射”至当前历元的参考星，以确保传递的准确性和滤波的连续性。实际中，造成参考星发生改变的典型因素包括：①原参考星不可视；②原参考星的相位观测值被探测出粗差或周跳；③原参考星的高度角变低(若始终将高度角最大的卫星用作参考星)等。
本文提出了一种基于站间单差观测方程的GNSS单基线滤波算法。在消除了由于接收机相位钟差和站间单差模糊度所引起的列秩亏后，可估的模糊度参数将仍具备双差形式和整数特性。另外，该算法还能更为直接地估计若干类“偏差”参数：①接收机钟差，可服务精密授时、时间传递等应用[6, 7, 8, 9, 10]；②接收机差分伪距偏差，用于获取“无偏的”电离层延迟等信息[11, 12, 13, 14, 15, 16]；③接收机相位钟差，常用作频率传递的基本输入[9, 10]。
理论上，当在随机模型中考虑由双差(或单差)运算所引起的数学相关，并假定经双差(或单差)过程所消去的各类参数均为时变参数(即历元间无关联)时，滤波分别采用双差和单差观测方程实施参数估计将具备等价性[17, 18]。本文侧重于强调滤波基于两种观测方程的实施差异。针对双差滤波模型，概括了处理参考星变换的具体方案，构造了对应于不同参考星的两组双差模糊度间的转换矩阵，同时论述了定义不同参考星对双差模糊度和接收机相位钟差可估性的影响。在此基础上，明确了单差滤波模型的两种实际便利性：①无须变换参考星，避免了传递双差模糊度滤波值时的“映射”等运算；②接收机相位钟差滤波值中不再存在“整周跳跃”现象，因此能更真实地反映接收机钟的频率稳定性。
2 单基线GNSS数据处理
经由线性化，GNSS非差伪距和相位观测方程可联合地表示为[19, 20]
式中，E(·)是数学期望运算符；
和
分别表示伪距和相位观测值，其上标s和i代表卫星和历元，下标r和j则为接收机和频率；xri是4×1的几何参数向量，分别包含了三维位置增量和天顶对流层延迟(ZTD)；系数cr,js,i由r-s单位方向向量和ZTD投影函数构成；dtr,ji和δtr,ji对应于接收机伪距和相位钟差，各自分别吸收了接收机伪距和相位偏差；dtjs,i和δtjs,i为卫星伪距和相位钟差；Nr,js为非差模糊度，单位为周；系数λj表示波长。本文假定，除Nr,js外，其余参数均为时变参数。在确保结论适用性的前提下，为简化随后的推导和论述，此处假定电离层延迟可被站间单差(针对短基线)或形成消电离层组合(针对中长基线)等手段消除，式(1)中因此未包含电离层延迟参数。
2.1 双差滤波模型的参考星变换方案与影响
假定构成基线的两台接收机(r=1，2)在当前历元i共观测了m颗卫星(s=1,2，…，m)在f个频率(j=1,2，…，f)上的伪距和相位观测值，此时全部非差观测值的个数为4fm。为构造对应的双差观测值，可分别将第1颗卫星和第1个接收机用作参考星和参考站，以定义双差算子Drs[16]
式中，Dr=[-11]和Ds=[-em-IIm-1]分别为站间和星间单差算子；I为单位矩阵，下标表示其维数；em-1是各元素均为1的m-1维列向量。
将Drs依次左乘全部的非差伪距和相位观测值，可得2f(m-1)个相应的双差观测值，其观测方程即为
式中，s≠1和r≠1；(·)r1s1、(·)s1和(·)r1分别代表双差、星间单差和站间单差变量。
由于双差运算完全消除了各类钟差参数，式(3)无法直接地满足时频传递应用，为此，还需引入2f个对应于参考星(s=1)的站间单差观测方程
式中 式中，dtr1,ji和δtr1,ji分别为可估的接收机伪距和相位钟差，各自包含了绝对和相对的时间信息，可分别用于实施时间比对和频率传递[9, 10]。
在利用卡尔曼滤波处理多历元(i≥2)观测值时，须合理地考虑双差模糊度不随时间变化的特性，以递归地增强各类参数的滤波解精度。因此，需要对上一历元的双差模糊度滤波值实施一步时间预报，并将该预报值用作当前历元双差模糊度参数的“伪观测值”。在此之前，若相邻历元构造双差观测值时所定义的参考星不同，还需要借助线性变换运算，用于“对齐”两个历元的双差模糊度。
以两相邻历元i和i+1为例，设各自对应的双差模糊度向量为
即，它们均对应m颗相同的卫星(s=1,2,…，p，q，…,m)，但分别以第p和q颗卫星作为参考星(卫星排序为q=p+1≥2)。此时，可定义如下的转换矩阵Ti，以实现TiMi=Mi+1 式中，将单位阵Im-1的第q-1列用-em-1代替，即可得矩阵Iq-1m-1，以用于将对应于参考星p的双差模糊度“映射”至参考星q。
若当卫星排序为1≤q+1=p时，Ti则可定义为
式中，矩阵Iqm-1的定义与式(7)中的Iq-1m-1类似，此处不再详述。
在滤波过程中，须涉及上述双差模糊度“映射”运算的情况包括：
(1) 原参考星p消失。此时，通过选定新的参考星q(此处仅考虑q=p+1)，构造形如式(7)的Ti矩阵，可分别将Mi和其协方差QMi转换为Mi和QMi
式中，(·)T表示矩阵转秩运算。之后，剔除Mi中的第p个元素(即p相对于q的双差模糊度)，并删除QMi所包含的第p个行、列向量后，即可联合地被预报至历元i+1。
(2) 原参考星p的相位观测值存在周跳。由于前后历元卫星个数不变，在完成式(9)所涉及的运算后，即可将Mi和QMi传递至历元i+1，以用作“伪观测值”向量。此时，可认为Mi中第p个元素包含“粗差”，为消除其影响，可对其引入一个额外的未知参数。
值得注意，对于上述情况，需确保新参考星q在相邻历元i和i+1均可视。
另外，之前已指出，估计接收机钟差直接依赖参考星的站间单差观测方程，参考星变换还会对接收机钟差的可估性造成影响。若两历元i和i+1对应的参考星分别是p和q，由式(5)可知，两历元的接收机相位钟差tr1,ji和tr1,ji+1之差，包含了由λjNr1,jqp(即q和p之间的双差模糊度)所引起的“整周跳跃”。
2.2 无须变换参考星的单差滤波模型
类似的，若将If
DrIm左乘全部4fm个非差观测值，可得2fm个站间单差观测值，其相应的观测方程为
易知，式(10)对应的设计矩阵列秩亏，可导致参数解不唯一[21]。为此，可将第1颗卫星(s=1)的模糊度Nr1,j-1定义为“基准”，用于消除接收机相位钟差(δtr1,ji)与所有模糊度(Nr1,js)之间的线性相关。此后，式(10)即具备如下的满秩形式
式中，tr1,ji的定义与式(5)中的对应参数相同。另外，可估的模糊度Nr1,js1为双差形式，且与式(3)中的相关参数一致。
与双差模型类似，当滤波采用式(11)所表示的单差观测方程时，也需要传递相邻历元间的双差模糊度滤波值。针对历元i+1，若对应于“基准”模糊度参数(即Nr1,j1)的卫星(即s=1，其作用类似双差模型所定义的参考星)消失，其处理方式尽管仍可采用双差模型中变换参考星的策略，但这并非必要。
需要明确，针对每一颗卫星，在其可被连续跟踪的时段内，其单差模糊度是时不变参数，个数为j。这也意味着，对于多历元数据处理而言，由单差模糊度和接收机相位钟差所引起的秩亏数也始终为j，而与历元数无关。因此，当在某个历元(如i)选取了某颗卫星(如s=1)的j个单差模糊度(即Nr1,j1)作为“基准”时，其余卫星的单差模糊度(Nr1,js,s=2,3,…,m)将吸收Nr1,j1，从而具备了双差形式(即Nr1,js1)。当被预报至随后历元(如i+1)时，即使对应的卫星s=1消失，Nr1,js1中的Nr1,j1分量可继续充当“基准”模糊度。
综合上述考虑，历元i+1的单差观测方程可被表示为
式中，s=2,3,…,m。对比历元i的单差观测方程(见式(11))可知：
(1) 可估的双差模糊度Nr1,js1仍相对于卫星s=1。这也表明，两历元(i和i+1)的双差模糊度均对应相同的“基准”单差模糊度，因此不需要实施“映射”运算。
(2) 可估的接收机相位钟差的含义为
与历元i的ir1,j估值相比(含义见式(5))，除真正钟差的变化外，两者均包含了相同的“基准”单差模糊度(对应卫星s=1)，即不再受“整周跳跃”的影响。
针对联合两个历元i和i+1的数据处理，双差模型选后定义了第s=1和s=q共两个参考星，而在单差模型中，其双差模糊度则始终对应于卫星s=1。但两种模型所包含的双差模糊度个数相等，且可被一致地“映射”至参考星s=q(该卫星在两历元内均可视)，由此可简单地证明其等价性。
3 试验分析
本节分别利用双差和单差滤波模型处理了两条基线的双频GPS观测数据，用于分析参考星变换对双差模糊度和接收机相位钟差可估性的影响。
3.1 数据处理
表 1描述了两条基线的若干基本要素。其中，CUAA-CUT3的基线长度仅为8.4m，站间单差运算可充分消除观测值中的大气延迟。此时，双差模糊度固定的效率和成功率较高，相关的数据处理结果将用于分析参考星变换对双差模糊度可估性的影响。STAR-LALB的基线长度约为105km，相应的单差/双差观测方程中需引入电离层延迟和ZTD参数，其数据处理结果将用于考察参考星变换对接收机相位钟差可估性的影响。另外，该基线的观测时长仅为21h。
| 基线名称 | 基线长度 | 观测时段 | 观测类型 | 采样间隔 | 近似位置 |
| CUAA- CUT3 | 8.4m | DOY 275, 2013 | C1-P2- L1-L2 | 30s | 115.9°E, 32.0°S |
| STAR- LALB | 105km | DOY 190, 2014 | 143.4°E, 35.7°S |
数据处理采用了广播星历，用于计算各GPS卫星在信号发射时刻的位置：对于本节所分析的基线长度而言，站间单差运算将能充分地消除星历误差。天顶方向卫星的非差伪距和相位标准差分别选取为30cm和0.3cm。采用高度角加权并考虑数学相关性，以最终确定单差和双差观测值的标准差。卫星截止高度角为20°，以尽量剔除低精度、强多路径的观测值。
式(3)和式(4)对应于双差滤波模型的观测方程。为形成双差观测值，确定参考星的准则是：在首个观测历元(i=1)，选取PRN最小的卫星作为参考星。之后，在该参考星消失(或被探测出周跳)的当前历元，选取另一个PRN最小的卫星作为新参考星(该卫星还需在当前和上一个历元均可视)。需要强调，该参考星选取准则是为了人为地增加参考星变换的频率，以便于验证本文推导和相关论述的正确性。
类似的，式(11)对应单差滤波模型的观测方程。需要指出，为克服模糊度与接收机相位钟差之间的秩亏，在首个观测历元将对应于PRN最小卫星的单差模糊度约束为“基准”。显然，该卫星与双差模型中第一次使用的参考星一致。
最后，各类滤波参数的初始值采用最小二乘平差首个历元的全部观测数据得到。之后，滤波一步时间预报仅传递时不变的双差模糊度。
3.2 结果分析 3.2.1 CUAA-CUT3基线
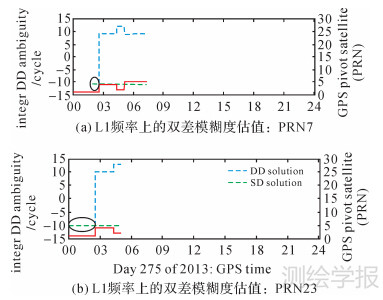
图 1中列出了两颗卫星(PRN 7和PRN 23)相对于某(些)参考星的L1频率双差模糊度滤波值。以图 1(a)中PRN 7结果为例，分析可得以下两点结论。
|
| 图 1 L1频率上两个卫星(PRN 7和23)的双差模糊度估值 Fig. 1 L1 DD integer ambiguities of two representative satellites (PRNs 7 and 23) |
(1) 在该卫星出现的约5h时段内，双差滤波模型先后定义了4个不同的参考星(见红色线)，导致了其双差模糊度滤波值(蓝色虚线)中存在3次“跳跃”。尽管对应于不同的参考星，所有双差模糊度的滤波值均非常接近(不同的)整数，证明了采用本文式(9)“映射”双差模糊度的正确性。
(2) 对于单差滤波模型，其双差模糊度滤波值(绿色虚线)均包含了第一颗参考星(PRN 1)的“基准”模糊度，其估值在整个观测时段内保持连续，且接近同一个整数。同样，在最初的一段时间内，由于对应相同的参考星，两种滤波模型所估计的双差模糊度相等。
另外，对于图 1(b)所绘PRN 23的两类双差模糊度的滤波值，其特性类似。
前文已述，针对双差滤波模型，若参考星由上一历元的p变为当前历元的q时，以某非参考星s为例，其相对于新、旧参考星p和q的双差模糊度分别为Nr1,jsp和Nr1,jsq，其差值应等于-Nr1,jqp。为验证该结论的可靠性，图 2列出了16次参考星变换时刻Nr1,1qp和Nr1,2qp的估值(固定解，分别对应L1和L2频率)。对比可知，图 1(a)中(或 (b)中)，蓝色线所表示的双差模糊度滤波值在参考星变换后所发生3次(或2次)“跳跃”的量级确实与图 2中圆圈所表示的前3(或前2)组结果大小相等、符号相反。
|
| 图 2 参考星变换时刻，由新、旧参考星所形成的双差模糊度整数估值(L1和L2) Fig. 2 At the instants of changing pivot satellite,the estimates of integer DD ambiguities associated with two (old and new) pivots satellites |
图 3(a)和图 3(b)中分别绘出了接收机伪距钟差(对应C1)与双频接收机相位钟差(分别对应L1和L2)之差，并除以相应的波长，以将单位转换为周。需要指出，该差值实际上是双频接收机相位偏差[22]。以图 3(a)结果为例，分析可知：
|
| 图 3 接收机伪距钟差(C1)与双频接收机相位钟差(L1和L2)与之差 Fig. 3 The offsets between receiver phase clock (L1 and L2)and receiver code clock (C1) |
(1) 在滤波开始的前3个多小时内(对应图中黑色椭圆)，双差滤波模型所采用的参考星为PRN 1(用红色线表示)，而单差滤波模型同样将该卫星的模糊度定义为“基准”。在此期间，由于其可估性一致，两种滤波模型所估计的接收机相位偏差(分别用蓝线和绿线表示)互相重合。
(2) 当PRN 1消失时，双差滤波模型重新定义了PRN 4作为新的参考星。此时，相应的接收机相位钟差的可估性发生改变，导致了图 3(a)中的接收机相位偏差出现了“跳跃”现象。其原因是，在参考星变换前后的两个历元时刻，接收机相位钟差内分别包含了对应于PRN 1和PRN 4的模糊度，上述“跳跃”的量级即为PRN 4和PRN 1之间的双差模糊度，并具备整数特性。相反，由于在滤波过程中实现了“基准”模糊度在历元间的传递，单差滤波模型估计的接收机相位偏差中始终包含一致的“基准”模糊度，即使在PRN 1消失后，也仍能保持连续。
(3) 值得注意的是，在双差滤波模型估计的接收机相位偏差发生“跳跃”后，与相对应的单差滤波模型结果相比，两者存在一个整数常偏，但变化行为一致。即，在有效地补偿该“跳跃”后，两类滤波模型所估计的接收机相位钟差(偏差)将完全相等。
图 3(b)中所表示的L2频率接收机相位偏差估值具备类似的行为，此处不再详细讨论。
对于双差滤波模型，当参考星由p变为q后，接收机相位偏差的滤波值将出现量级为λjNr1,jqp的“整周跳跃”。与图 2类似，图 4列出了全部变换参考星时刻(共10次)的Nr1,1qp和Nr1,2qp估值(固定解，分别对应L1和L2频率)。分析可知，图 3中双频接收机相位偏差滤波值(蓝色线)所经历的10次“跳跃”的量级与图 4中10组Nr1,jqp估值的大小完全相等。
|
| 图 4 参考星变换时刻，由新、旧参考星所形成的双差模糊度整数估值(L1和L2) Fig. 4 At the instants of changing pivot satellite,the estimates of integer DD ambiguities associated with two (old and new) pivots satellites |
针对单基线GNSS数据处理，通常采用双差观测值，以消除接收机/卫星的钟差、伪距和相位偏差等参数，同时还能削弱大气延迟和轨道误差。在采用卡尔曼滤波估计参数时，通常预报并传递相邻历元的双差模糊度，以增强各类参数的滤波解精度。在此过程中，当前后历元定义的参考星发生变化时，需要对相应的双差模糊度实施“映射”，以确保滤波连续。此后，两类参数如双差模糊度和接收机相位钟差的估值中将出现量级相等、符号相反的“整周跳跃”。
若上述数据处理采用站间单差观测值，则需要事先克服接收机相位钟差与单差模糊度线性相关所引起的列秩亏。本文通过定义某卫星的单差模糊度为一类“基准”参数，消除了相应的秩亏，此后剩余的可估模糊度即具备了双差形式和整周特性。在实施滤波的过程中，一步时间预报相邻历元的双差模糊度，可自动传递该“基准”模糊度参数，使得不同历元的双差模糊度参数均对应于统一的“基准”，由此避免了“映射”双差模糊度的过程，进而消除了存在于部分参数中的“整周跳跃”现象。由此表明，与双差滤波模型相比，单差滤波模型的运算效率更高，估计的接收机相位钟差可直接用作频率传递的输入。
最后，需要指出，为形成双差，本文采用剩余卫星与某一颗参考星作差的方式。实际上，构造双差的方式并不唯一。例如，通过对所有卫星序贯作差也可以形成双差。但这类双差滤波模型的实施过程更为复杂：除首尾卫星外，任何卫星的消失均需要“映射”双差模糊度，因此接收机相位钟差估值中也会存在更为频繁的“整周跳跃”。比较而言，单差滤波模型的优势也更加明显。
| [1] | WANG Qianxin, XU Tianhe, XU Guochang. Adaptively Changing Reference Station Algorithm and Its Application in GPS Long Range Airborne Kinematic Relative Positioning [J]. Acta Geodaetica et Cartographica Sinica, 2011, 40(4): 429-434. (王潜心, 徐天河, 许国昌. 自适应换站算法及其在长距离机载 GPS 动态相对定位中的应用[J]. 测绘学报, 2011, 40(4): 429-434.) |
| [2] | WEI Ziqing, GE Maorong. Mathematical Models for GPS Relative Positioning [M]. Beijing: Surveying and Mapping Press, 1998. (魏子卿, 葛茂荣. GPS 相对定位的数学模型[M]. 北京: 测绘出版社, 1998.) |
| [3] | HU Congwei. The Basic Models for Short GPS Baseline and Data Process Methods for GPS Kinematic Positioning [J]. Acta Geodaetica et Cartographica Sinica, 2000, 29(3): 282-285. (胡丛玮. GPS短基线模型与动态定位[J]. 测绘学报, 2000, 29(3): 282-285.) |
| [4] | GAO Xingwei, LIU Jingnan, GE Maorong. An Ambiguity Searching Method for Network RTK Baselines between Base Stations at Single Epoch [J]. Acta Geodaetica et Cartographica Sinica, 2002, 31(4): 305-309. (高星伟, 刘经南, 葛茂荣. 网络 RTK 基准站间基线单历元模糊度搜索方法[J]. 测绘学报, 2002, 31(4): 305-309.) |
| [5] | RIZOS C. Network RTK Research and Implementation—A Geodetic Perspective [J]. Journal of Global Positioning Systems, 2002, 1(2): 144-150. |
| [6] | ZHANG Xiaohong, CAI Shixiang, LI Xingxing, et al. Accuracy Analysis of Time and Frequency Transfer Based on Precise Point Positioning [J]. Geomatics and Information Science of Wuhan University, 2010, 35(3): 274-278. (张小红, 蔡诗响, 李星星, 等. 利用GPS精密单点定位进行时间传递精度分析[J]. 武汉大学学报: 信息科学版, 2010, 35(3): 274-278.) |
| [7] | HUANG Guanwen, YANG Yuanxi, ZHANG Qin, et al. A New Continuous Time and Frequency Transfer Algorithm Based on GPS Single Different Carrier Phase Observations [J]. Geomatics and Information Science of Wuhan University, 2013, 38(9): 1018-1022. (黄观文, 杨元喜, 张勤, 等. 一种单差观测值的连续实时载波相位时频传递方法[J]. 武汉大学学报: 信息科学版, 2013, 38(9): 1018-1022.) |
| [8] | GUO Hairong, YANG Sheng, YANG Yuanxi, et al. Numerical Prediction Methods for Clock Difference Based on Two-way Satellite Time and Frequency Transfer Data[J]. Geomatics and Information Science of Wuhan University, 2007, 32(1): 43-46. (郭海荣, 杨生, 杨元喜, 等. 基于卫星双向时间频率传递进行钟差预报的方法研究[J]. 武汉大学学报: 信息科学版, 2007, 32(1): 43-46.) |
| [9] | DEFRAIGNE P, BAIRE Q. Combining GPS and GLONASS for Time and Frequency Transfer [J]. Advances in Space Research, 2011, 47(2): 265-275. |
| [10] | BRUYNINX C, DEFRAIGNE P, SLEEWAEGEN J M. Time and Frequency Transfer Using GPS Codes and Carrier Phases: Onsite Experiments [J]. GPS Solutions, 1999, 3(2): 1-10. |
| [11] | LI Wei, CHENG Pengfei, BEI Jinzhong, et al. Calibration of Regional Ionospheric Delay with Uncombined Precise Point Positioning and Accuracy Assessment [J]. Journal of Earth System Science, 2012, 121(4): 989-999. |
| [12] | ZHANG Baocheng, OU Jikun, YUAN Yunbin, et al. Calibration of Slant Total Electron Content and Satellite-receiver's Differential Code Biases with Uncombined Precise Point Positioning Technique [J]. Acta Geodaetica et Cartographica Sinica, 2011, 40(4): 447-453. (张宝成, 欧吉坤, 袁运斌, 等. 利用非组合精密单点定位技术确定斜向电离层总电子含量和站星差分码偏差[J]. 测绘学报, 2011, 40(4): 447-453.) |
| [13] | JIANG Weiping, ZOU Xuan, TANG Weiming. A New Kind of Real-time PPP Method for GPS Single-frequency Receiver Using CORS Network [J]. Chinese Journal of Geophysical Research, 2012, 55(5): 1549-1556. (姜卫平, 邹璇, 唐卫明. 基于CORS网络的单频GPS实时精密单点定位新方法[J]. 地球物理学报, 2012, 55(5): 1549-1556.) |
| [14] | YANG Yuanxi, JING Yifan, ZENG Anmin. Adaptive Parameter Estimation and Inner and External Precision [J]. Acta Geodaetica et Cartographica Sinica, 2013, 43(5): 441-445. (杨元喜, 景一帆, 曾安敏. 自适应参数估计与内外部精度的关系[J]. 测绘学报, 2014, 43(5): 441-445.) |
| [15] | YANG Yuanxi, LI Jinlong, XU Junyi, et al. Contribution of the Compass Satellite Navigation System to Global PNT Users [J]. Chinese Science Bulletin, 2011, 56(26): 2813-2819. (杨元喜, 李金龙, 徐君毅, 等. 中国北斗卫星导航系统对全球PNT用户的贡献[J]. 科学通报, 2011, 56(21): 1734-1740.) |
| [16] | ZOU Xuan, GE Maorong, TANG Weiming, et al. URTK: Undifferenced Network RTK Positioning [J]. GPS Solutions, 2013, 17(3): 283-293. |
| [17] | XU Guochang. GPS—Theory, Algorithms and Applications [M]. Heidelberg: Springer, 2003. |
| [18] | DE JONGE P J. A Processing Strategy for the Application of the GPS in Networks [D]. Delft: Delft University of Technology, 1998. |
| [19] | LI Zhenghang, HUANG Jinsong. GPS Surveying and Data Processing [M]. Wuhan: Wuhan University Press, 2005. (李征航, 黄劲松. GPS 测量与数据处理[M]. 武汉: 武汉大学出版社, 2005.) |
| [20] | LIU Jingnan YE Shirong. GPS Precise Point Positioning Using Undifferenced Phase Observation [J]. Geomatics and Information Science of Wuhan University, 2002, 27(3): 234-240. (刘经南, 叶世榕. GPS 非差相位精密单点定位技术探讨 [J]. 武汉大学学报: 信息科学版, 2002, 27(3): 234-240.) |
| [21] | TEUNISSEN P.Zero Order Design:Generalized Inverses,Adjustment, the Datum roblem and S-transformations [C]//GRAFAREND E W, SANSÒ F. Optimization and Design of Geodetic Networks.Berlin: Springer, 1985: 11-55. |
| [22] | ZHANG Xiaohong, LI Pan, LI Xingxing, et al. An Analysis of Time-varying Property of Widelane Carrier Phase Ambiguity Fractional Bias [J]. Acta Geodaetica et Cartographica Sinica, 2013, 42(6): 798-803. (张小红, 李盼, 李星星, 等. 宽巷载波相位模糊度小数偏差估计及其时变特性分析. 测绘学报, 2013, 42(6): 798-803.)" |