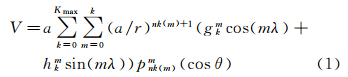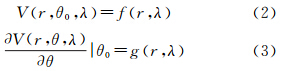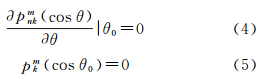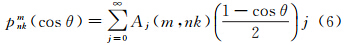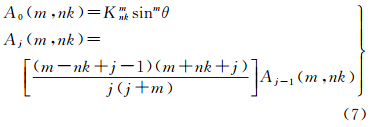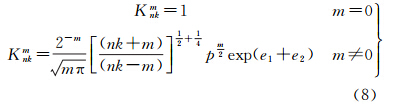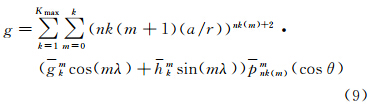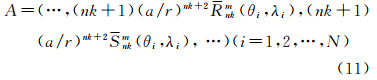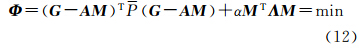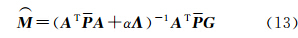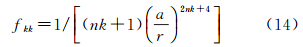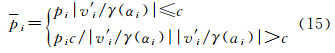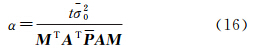1 引 言
随着观测技术和手段的不断创新，以及相关科学理论的发展，目前已形成了海陆空全方位的地球重力场测量观测体系。重力数据在某些地域呈现出多源化状态，即在同一区域内，存在着多种不同手段获取的重力数据。由于测量的手段不同，以及测量技术上的差异等，造成同一区域内的重力场在不同测量方法下获取的重力数据呈现不一致性，甚至有相互矛盾的数据存在。必须将这些具有不同误差特性的重力数据有效地融合在一起，并消除不同数据体之间的差别，解出统一、准确、可靠的局部重力基础数据。
数据融合算法中，最小二乘配置算法具有天然的优势[1]，因为它能够方便地将多种不同源的数据联合起来求解，是多源数据融合过程中常用到的方法。但是使用最小二乘配置方法融合数据，需要计算多源数据之间的协方差函数矩阵[2]，在局部重力场中，当观测数据较多时，数据运算量大。也有学者采用球谐模型进行多源数据的融合研究，通过迭代算法融合重力异常数据[3]。球谐函数虽然是球坐标系下满足位理论边界条件的谱函数，但其特征函数与局部区域不对应，不能满足有限区域边值问题的定解条件，因此求解得到的球谐系数不稳定[4]。而且若要拟合分辨率为5′×5′的重力数据，根据奈奎斯特采样定律，球谐函数需展开到2159阶，总共需要计算4672082个球谐系数，计算量巨大。
文献[5]成功运用球冠谐理论研究保守力场，指出运用球冠谐展开逼近局部力场的可能性；文献[6]将球冠谐理论引入海面地形的研究；文献[7]提出并推导了球冠谐分析法逼近区域地壳垂直形变场的模型；文献[8]利用球冠谐分析建立了2005—2010年中国地区地磁场长期变化模型；文献[9]利用球冠谐理论建立了我国的局部重力场模型。这些研究工作都取得了比较满意的结果。由于在球冠谐模型中使用非整阶勒让德函数，余纬的定义域从[0，π]变换到[0，θ]，因此只需要少量的系数就可以拟合局部重力场，能够集中反映局部重力场的高频特征，并充分发挥局部地区重力资料采样密集的优势。由此本文提出一种基于球冠谐模型，使用抗差岭估计算法融合多源重力数据的方法，以期建立高精度的局域重力场模型。
2 球冠谐模型分析
文献[9]从Sturm-Liouvide方程(简称S-L方程)出发，给出了局部重力场的球冠谐和函数表达式。在无源区，重力位V在球冠坐标下的拉普拉斯方程的解为
式中，a是地球平均半径；r是计算点的地心半径；θ与Λ是球冠坐标下的余纬和经度[10]；k是球冠谐和分析中根的阶序号；Kmax是球冠谐和分析最大截断阶数；psub>nk(m)m<(cosθ)是非整阶勒让德函数(m是整级次，nk(m)是非整阶次);gnm与hnm为高斯系数(也称为球冠谐系数)。
相对球谐分析，球冠谐分析是在地球的某一球冠部分内进行的球谐分析,因此必须满足一定的边界条件[11]。在球冠极点处(经度和余纬θ=0)与球谐分析一致，但在θ=θ0处，重力位V要满足以下两个条件
式中，f与g是球冠边界上的函数，与θ无关。通常情况下，球冠极与地理极是不重合的，因此在进行球冠谐分析前，需要进行坐标变换。首先将各观测点的大地经纬度(B，L)坐标转换为地心经度和余纬，然后通过球面三角公式转换为球冠极点对应的球冠坐标下的经度和余纬[12]。
文献[5]证明可以通过选取适当的基函数Vnm，使得当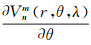
|θ0=0和Vnm(r,θ0,Λ)=0成立时，式(2)和式(3)成立。由式(1)可以看到，重力位V与θ有关的函数只包含在函数pnk(m)m(cosθ)中，因此在给定m和θ0后，只需根据下列两式，通过确定根nk，来完成基函数的选取
满足式(4)和式(5)的根nk是非整阶的，根据给定的m和θ0计算可以得到两组根序列，将这两组根序列按大小排序，从m起始编号，得到根的阶序号k。当k-m=偶数时，取式(4)的根，k-m=奇数时，取式(5)的根。根据S-L理论，这两组根构成的基函数Vnm在组内是正交的，但组间并不正交。式(1)中非整阶勒让德函数pnkm(cosθ)在给定nk和m值，可以通过如下递推公式计算[12]
式中 式中，knm的近似式用Stirling公式[5]导出
式中，
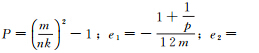
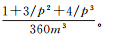
3 抗差岭估计算法融合多源重力数据
因为重力是重力位沿球冠半径的梯度[13]，即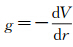
，所以重力异常的展开式是[14]
注意到在球冠边界重力位一般不等于零，因此只需要满足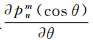
|θ0=0条件的一组根，即k-m=偶数的根。Psub>nk(m)m<(cosθ)是完全规格化非整阶勒让德函数[15, 16]，gkm和hkm是完全规格化的球冠谐系数。
设有一系列重力异常观测值G=(g1，g2，…,gn)T，球冠谐系数M=(…,gkm,hkm,…)T，(k=0,1,2,…,Kmax；m=0，1,2,…，k；k-m=偶数)，则将式(9)写成矩阵的形式
令Rnkm(θ,Λ)=pnkm(cosθ)cos(mΛ)，Snkm(θ,Λ)=pnkm(cosθ)sin(mΛ)，则由基函数组成求解系数矩阵为
根据式(10)使用LS估计计算球冠谐系数时，由于系数矩阵A中包含复共线性关系，因此LS估计的法方程矩阵是病态的，存在接近零值的特征根。结果导致LS估计在线性无偏估计中虽然方差最小，但其均方误差很大，降低了其参数估值的准确度和稳定性。针对这个问题，已经有大量文献讨论使用正则化方法计算方程(10)的解。另一方面，LS估计算法本身不具备抗差性，观测值的粗差会对估计的结果造成很大干扰，估计的稳定性受到质疑[17]。为了克服法方程的病态性对估计的影响，又能具备抵抗数据粗差的影响，本文根据Tikhonov正则化方法构造最小化目标函数
解得球冠谐系数M的抗差估计表达式为
式中，等价权矩阵P是对角阵；α是岭参数；Λ是正定阻尼矩阵。
在应用式(9)计算重力异常时，由于只需要k-m=偶数的一组根，其基函数Vnm是正交的，可以与球谐分析类似[18]，在式(12)、式(13)中，正定阻尼矩阵Λ设计为一个对角矩阵，其对角元素由下列公式给出
使用抗差算法通过式(13)计算球冠谐系数M时，需要迭代计算。方法如下：若已经解得第l步的系数M的估计值，根据观测残差v=AM-G，计算等价权阵P和岭参数α，然后根据式(13)计算第l+1步的参数估计，最后计算相邻两次参数估计值的差，当差值小于指定值时，结束迭代计算，解得球冠谐系数M的估计。
等价权矩阵P的计算采用GM估计方法[19]，由观测值的残差vi=AM-G，根据式(15)计算得到
式中，v′i=vi/σ^；σ^=med(|vi|)/0.6745；c=0.354；γ(αi)=
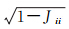；Jii是J=A(ATPA)-1ATP的第i个主对角线元素。岭参数α的选取是正则化方法的核心问题，α的取值不同，参数的估计值可能不同。确定岭参数的方法很多[20]，常用的有岭迹法、L曲线法、GCV法等。其中岭迹法优点是比较直观，但是具有主观随意性；GCV法能够解析地求得一个最优岭参数,但是该方法变化过于平缓，难以收敛；L曲线法是比较成熟的一种方法，但是其确定的岭参数不是最优的，而且在抗差迭代过程中，等价权阵P是变化的，需要在每次迭代过程中都使用L曲线法确定岭参数。本文利用Hoerl和Kennard从广义岭估计出发确定普通岭估计中岭参数的思想，使用法方程直接计算岭参数[21]
式中，0=med(|vi-med(vi)|)/0.6745；med(vi)是残差的中位数。
4 数值计算
为了验证上述方法的正确性，选取36.95°N—38.05°N，76.95°E—78.05°E范围作为数据融合区域，球冠半角α约为0.71°。这里位于中国的青藏高原[22, 23]，地势复杂，海拔落差大。北部地壳厚度47～58km，中部地壳厚度67～73km。壳幔密度的差异大，低频重力场变化显著。通过http://bgi.omp.obs-mip.fr网站获取该地区分辨率为2.5′×2.5′卫星重力异常网格数据，共676个数据点。地面重力异常观测值分辨率为3′×3′网格数据，共有395个点。将地面重力异常数据分为两个点集合，其中点集S1包含354个点，用于模型融合试验。点集S2包含41个点，用于融合模型的外符合精度检测。精度检验标准采用地面重力异常观测值与模型计算的重力异常值差值的均方根衡量。卫星重力数据和地面实测重力数据的分布如图 1所示。将卫星重力异常插值到地面观测点位置并统计其差值，见表 1。
|
| 图 1 重力测量数据点位分布 Fig. 1 Distribution of the data points of gravity surveying |
| 10-5m/s | ||||
| 差值均值 | 差值均方根 | 最大差值 | 最小差值 | 比较点数 |
| 7.69 | 36.89 | 215.13 | -86.48 | 395 |
根据球冠谐阶数nk和球冠半角α的关系式nk=90°(Kmax+0.5)/α-0.5[4]，以及与网格分辨率的关系Δθ=180°/nk，可取截断阶数Kmax=22，这时球冠谐模型能够拟合的网格分辨率大约为4′×4′。设σA和σT分别是卫星重力数据和地面重力数据的观测噪声，若观测噪声不相关，则噪声协方差矩阵为ΣΔ=diag{…σA…,…σT…}，式(13)中先验矩阵取观测数据噪声协方差矩阵的逆，即P=Σ-1Δ。在观测噪声σA=8×10-5m/s2和σT=3×10-5m/s2情况下，设卫星重力数据和地面重力数据都存在粗差，应用式(13)迭代计算得到融合后的球冠谐模型的系数估计值。最后通过式(10)计算球冠谐模型的重力异常，并使用地面重力数据进行检核，其内外符合精度见表 2。比较表 1和表 2中的数据，可以看到融合后的球冠谐模型要比卫星重力异常更接近地面重力异常。
| 10-5m/s2 | |||||
| 差值均值 | 差值均方根 | 最大差值 | 最小差值 | 比较点数 | |
| 内符合精度 | -0.16 | 5.29 | 30.94 | -23.34 | 354 |
| 外符合精度 | 0.83 | 7.64 | 14.37 | -17.83 | 41 |
通过不同的测量手段获取的重力观测值，其数据精度是不同的。通常地面静态重力测量和船载海洋重力测量的数据精度最高，但作业效率低；通过卫星遥测方式可以获得全球的重力观测值，但由于受电离层和潮汐效应等因素的影响，数据的观测噪声较高，而且存在粗差。为了进一步研究数据粗差和观测值噪声对融合效果的影响，首先将卫星数据和地面数据的观测噪声分别设置为①σA=8×10-5m/s2和σT=8×10-5m/s2；②σA=8×10-5m/s2和σT=5×10-5m/s2；③σA=8×10-5m/s2和σT=3×10-5m/s2共3种情况。其次将粗差的影响分为①卫星数据和地面数据都存在粗差；②仅卫星数据存在粗差，而地面数据无粗差，这时只需在式(15)中计算卫星数据对应的等价权阵，而地面数据对应的权阵不变。最后根据数据噪声和粗差的不同，设计6种计算方案。按上述方案计算的融合球冠谐模型内外符合精度见表 3和表 4。
| 10-5m/s2 | ||||
| σA=8× 10-5m/s2 σT=8× 10-5m/s2 | σA=8× 10-5m/s2 σT=5× 10-5m/s2 | σA=8× 10-5m/s2 σT=3× 10-5m/s2 | ||
| 卫星 数据 和地 面数 据都 存在 粗差 | 差值均值 | -5.79 | -2.43 | -0.16 |
| 差值均方根 | 24.44 | 14.07 | 5.29 | |
| 最大差值 | 51.08 | 37.64 | 30.94 | |
| 最小差值 | -107.64 | -62.73 | -23.34 | |
仅卫 星数 据有 粗差 | 差值均值 | -0.03 | -0.007 | 0.003 |
| 差值均方根 | 3.44 | 2.26 | 1.43 | |
| 最大差值 | 9.14 | 5.99 | 3.78 | |
| 最小差值 | -8.8 | -5.94 | -3.79 | |
| 10-5m/s2 | ||||
| σA=8× 10-5m/s2 σT=8× 10-5m/s2 | σA=8× 10-5m/s2 σT=5× 10-5m/s2 | σA=8× 10-5m/s2 σT=3× 10-5m/s2 | ||
| 卫星 数据 和地 面数 据都 存在 粗差 | 差值均值 | 0.74 | 0.43 | 0.83 |
| 差值均方根 | 17.60 | 15.24 | 7.64 | |
| 最大差值 | 33.28 | 29.22 | 14.37 | |
| 最小差值 | -44.77 | -37.08 | -17.83 | |
仅卫 星数 据有 粗差 | 差值均值 | 0.79 | 0.54 | 0.29 |
| 差值均方根 | 6.44 | 4.73 | 3.41 | |
| 最大差值 | 11.72 | 8.77 | 7.28 | |
| 最小差值 | -15.10 | -10.28 | -6.38 | |
从表 3和表 4的统计结果来看，随着地面重力数据观测噪声的逐步下降，融合后的球冠谐模型的精度逐步提高。当卫星重力数据和地面重力数据都存在粗差时，融合后的球冠谐模型受观测数据噪声的影响较大，当两者的观测噪声一样时，内符合精度为24.44×10-5m/s2，模型的精度最低。实际上这时融合后球冠谐模型更接近卫星重力数据，模型与卫星重力数据的差值均方根为9.4×10-5m/s2。表 4中外符合精度反而比表 3中的内符合精度高，原因可能是地面数据的检测点多分布于融合区域中部，而模型与地面观测数据误差大的点多分布在球冠边界位置，造成模型的内符合精度低于外符合精度，说明这时球冠谐模型存在一定的边界效应。
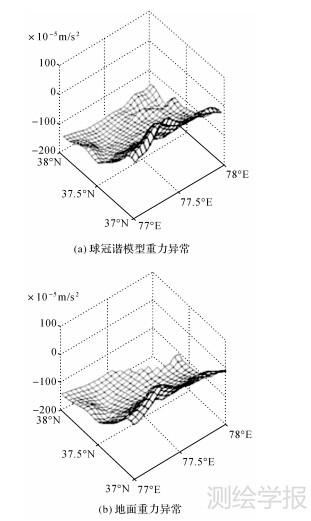
当地面重力数据无粗差时，观测数据噪声对融合后的球冠谐模型的内符合精度影响不大，当两者的观测误差一致时，内符合精度可以达到3.44×10-5m/s2，外符合精度也有6.44×10-5m/s2。当地面观测数据噪声最小时，模型精度最高，外符合精度可达到3.41×10-5m/s2。此时球冠谐模型重力异常(分辨率2.5′×2.5′)和地面重力异常(分辨率3′×3′)如图 2所示。
|
| 图 2 模型与地面重力异常 Fig. 2 The model and the ground gravity anomaly |
通过上面的数据分析，发现数据存在粗差以及数据的观测噪声大小，都对融合后的球冠谐模型精度有一定的影响，从中可以得出以下几点结论。
(1) 当卫星和地面重力数据都存在粗差时，模型的精度随着地面数据的观测噪声降低而显著提高。当地面数据的观测噪声相对较小时，模型的精度受数据粗差的影响较小。
(2) 当地面重力数据不存在粗差时，模型的精度虽然也随着地面数据的观测噪声降低而提高，但受其影响较小。在两者观测噪声一致时，模型外符合精度也有6.44 ×10-5m/s2。而当地面数据的观测噪声进一步减小到3×10-5m/s2时，模型的外符合精度可以达到3.41×10-5m/s2，如图 2所示能够很好地拟合地面重力数据。
综上所述，在局部重力场中，使用多种数据源，通过抗差岭估计迭代算法构建球的冠谐模型，既能克服法矩阵病态性的影响，又具有抵抗粗差的能力。该模型能够利用较低分辨率的高质量局部区域重力数据和较高分辨率的含有粗差的卫星重力数据，构建高精度的局部重力场，在理论和实践上都有重要意义。
| [1] | ZHAI Zhenhe, SUN Zhongmiao. The Adaptive Fusion of Multi-source Gravity Data in Bohai Gulf[J]. Acta Geodaetica et Cartographica Sinica, 2010, 39(5): 444-449. (翟振和, 孙中苗. 渤海湾多源重力数据的自适应融合处理[J]. 测绘学报, 2010, 39(5): 444-449.) |
| [2] | ZHAI Zhenhe, SUN Zhongmiao. Combining Airborne Gravity Data and Terrestrial Gravity Data Based on Least Squares Collocation[J]. Geomatic Science and Engineering,2008, 28(1): 10-14. (翟振和, 孙中苗. 基于最小二乘配置的航空和地面重力数据融合处理[J]. 测绘科学与工程, 2008, 28(1): 10-14.) |
| [3] | HAO Yanling, CHENG Yi, LIU Fanming, et al. Simulation of Combination Algorithm for Heterogeneous Marine Gravity Data[J]. Journal of System Simulation, 2007, 19(21): 4897-4900. (郝燕玲, 成怡, 刘繁明, 等. 融合多类型海洋重力数据算法仿真研究[J]. 系统仿真学报, 2007, 19(21): 4897-4900.) |
| [4] | WANG Xichen, WANG Guangjie, LI Tonglin, et al. Extracting Different Wavelength Gravity Anomaly by the Spherical Cap Harmonic Analysis Method[J]. Global Geology, 1996, 15(3): 80-83. (王喜臣, 王光杰, 李桐林, 等. 利用球冠谐分析方法提取不同波长重力场异常[J]. 世界地质, 1996, 15(3): 80-83.) |
| [5] | HAINES G V. Spherical Cap Harmonic Analysis[J]. Journal of Geophysical Research, 1985, 90(B3): 2583-2591. |
| [6] | HWANG C, CHEN S K. Fully Normalized Spherical Cap Harmonics: Application to the Analysis of Sea-level Data from TOPEX/POSEIDON and ERS-1[J]. Geophysical Journal International, 1997, 129(2): 450-460. |
| [7] | ZHANG Qin, ZHAO Chaoying. The Spherical Cap Harmonic Analysis Method for Crust Vertical Deformation Field Fitting[J], Acta Geodaetica et Cartographica Sinica, 2004, 33(1): 39-42. (张勤, 赵超英. 地壳垂直形变场逼近的球冠谐分析法[J]. 测绘学报, 2004, 33(1): 39-42.) |
| [8] | CHEN Bin, GU Zuowen, GAO Jintian, et al. Analyses of Geomagnetic Field and Its Secular Variation over China for 2005. 0 Epoch Using Spherical Cap Harmonic Method[J]. Chinese Journal of Geophysics, 2011, 54(3): 771-779. (陈斌, 顾左文, 高金田, 等. 2005. 0年代中国地区地磁场及其长期变化球冠谐和分析[J]. 地球物理学报, 2011, 54(3): 771-779.) |
| [9] | LI Jiancheng. Spherical Cap Harmonic Expansion for Local Gravity Field Representation[J]. Manuscripta Geodaetica, 1995(20): 265-277. |
| [10] | YOUNIS G K A, JGER R, BECKER M. Transformation of Global Spherical Harmonic Models of the Gravity Field to a Local Adjusted Spherical Cap Harmonic Model[J]. Arabian Journal of Geosciences, 2013, 6(2): 375-381. |
| [11] | WU Zhaocai, LIU Tianyou, GAO Jinyao. Derivative Calculation and Applicationin Spherical Cap Harmonic Analysis of Local Gravity Field[J]. Oceanologia et Limnologia Sinica, 2006, 37(6): 488-492. (吴招才, 刘天佑, 高金耀. 局部重力场球冠谐分析中的导数计算及应用[J]. 海洋与湖沼, 2006, 37(6): 488-492.) |
| [12] | ZHAO Jianhu, WANG Shengping, LIU Hui, et al. Study on Establishing Local Geomagnetic Model Using Spherical Cap Harmonic Analysis[J]. Science of Surveying and Mapping, 2010, 35(1): 51-53. (赵建虎, 王胜平, 刘辉, 等. 海洋局域地磁场球冠谐分析建模方法研究[J]. 测绘科学, 2010, 35(1): 51-53.) |
| [13] | WANG Sanjun. The Spherical Cap Harmonic Analysis of GPS Leveling Height[J]. Science of Surveying and Mapping, 2008, 33(2): 13-14. (王三军. 利用球冠谐模型研究GPS水准问题[J]. 测绘科学, 2008, 33(2): 13-14.) |
| [14] | CAO Yueling, WANG Jiexian. Application of Spherical Cap Harmonic Analysis to Fit GPS Level Height[J]. Geomatics and Information Science of Wuhan University, 2008, 33(7): 740-743. (曹月玲, 王解先. 利用球冠谐分析拟合GPS水准高程[J]. 武汉大学学报: 信息科学版, 2008, 33(7): 740-743.) |
| [15] | DESANTIS A. Translated Origin Spherical Cap Harmonic Analysis[J]. Geophysical Journal International, 1991, 123(6): 253-263. |
| [16] | PENG Fuqing, YU Jinhai.The Characters and Computation of Legendre Function with Non-integral Degree in SCHA[J]. Acta Geodaetica et Cartographica Sinica, 2000, 29(3): 204-208. (彭富清, 于锦海. 球冠谐分析中非整阶Legendre函数的性质及其计算[J]. 测绘学报, 2000, 29(3): 204-208.) |
| [17] | WEI Bocheng, LU Guobin, SHI Jianging. Introduction to Statistical Diagnostics[M]. Nanjing: Publishing House of Dongnan University, 1991. (韦博成, 鲁国斌, 史建清. 统计诊断引论[M]. 南京: 东南大学出版社, 1991.) |
| [18] | KORTE M, HOLME R. Regularization of Spherical Cap Harmonics[J]. Geophysical Journal International, 2003, 153(1): 253-262. |
| [19] | YANG Yuanxi, SONG Lijie, XU Tianhe. Robust Parameter Estimation for Geodetic Correlated Observations[J]. Acta Geodaetica et Cartographica Sinica, 2002, 31(2): 95-99. (杨元喜, 宋力杰, 徐天河. 大地测量相关观测抗差估计理论[J]. .测绘学报, 2002, 31(2): 95-99) |
| [20] | YANG Yuanxi. Robust Estimation and Its Applications[M]. Beijing: Bayi Publishing House, 1993. (杨元喜. 抗差估计理论及其应用[M]. 北京: 八一出版社,1993.) |
| [21] | WANG Guisong. Theory and Application of Liner Model[M]. Hefei: Press of Anhui Education, 1987. (王松桂. 线性模型理论及其应用[M]. 合肥: 安徽教育出版社, 1987.) |
| [22] | GAO Rui, XIONG Xiaosong, LI Qiusheng, et al. The Moho Depth of Qinghai-Tibet Plateau Revealed by Seismic Detection[J]. Acta Geoscientica Sinica, 2009, 30(6): 761-773. (高锐, 熊小松, 李秋生, 等. 由地震探测揭示的青藏高原莫霍面深度[J]. 地球学报, 2009, 30(6): 761-773.) |
| [23] | TIAN Qianning, GENG Tao, YANG Huiqun, et al. Gravity Anomalies Forward Fitting and Geological Explanation in the Western Qinghai-Tibet Plateau[J]. Geological Bulletin of China, 2008, 27(12): 2108-2116. (田黔宁, 耿涛, 杨汇群, 等. 青藏高原西部重力异常剖面拟合及其地质解释[J]. 地质通报, 2008, 27(12): 2108-2116.) |