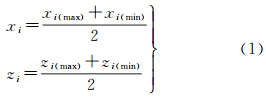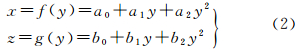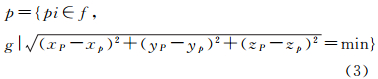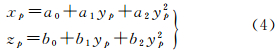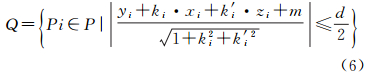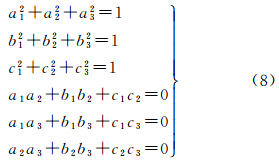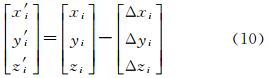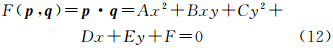2. 河南省遥感测绘院,河南 郑州 450003;
3. 国家测绘产品质量检验测试中心,北京 100830
2. Henan Remote Sensing and Mapping Institute, Zhengzhou 450003, China;
3. National Quality and Texting Center for Surveying and Mapping Products, Beijing 100830, China
1 引 言
地铁隧道收敛变形是指在地铁建设及运营过程中,由土体扰动、地面周边建筑物负载、隧道工程施工以及列车运行振动等综合因素引起的隧道变形。现有的收敛计监测方法虽然精度较高,但整个监测过程都需人工操作和记录,工作效率和自动化水平较低,且形变监测点过于稀疏,无法获取整个隧道断面全方位的形变信息[1, 2]。近年来,随着我国城市地铁工程建设规模的扩大,利用三维激光扫描仪进行地铁隧道变形监测已成为当前研究的热点。文献[3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13]将三维激光扫描仪应用于地铁隧道变形监测领域,并取得了一些成果,但截至目前尚未建立完善的监测方法体系。
本文提出以隧道中轴线为基础的连续截取任意间隔隧道横断面方法,通过对比不同时期点云在同一断面上相同方位处的坐标值,将不同形变量的点以不同颜色表示,如果断面内形变点数量超过设定的阈值,就将其视为重点变形区域进行下一步更加详细的断面轮廓线拟合及形变分析,从而得到该时期内隧道整体的变化情况。
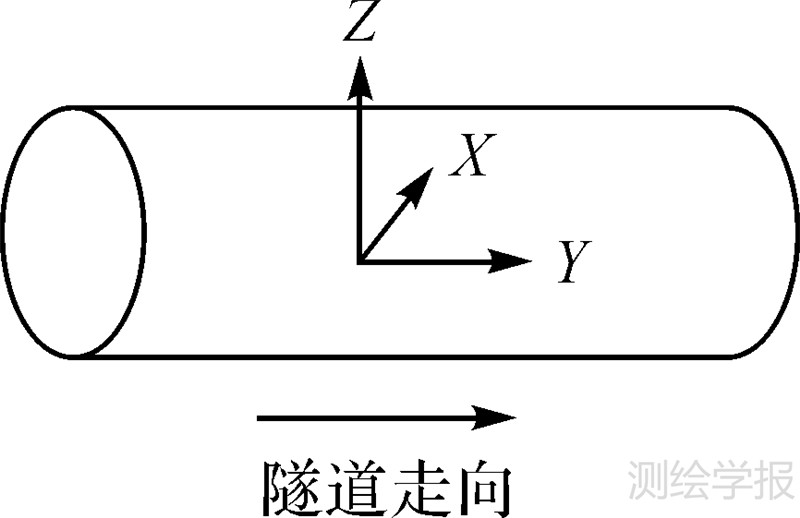
2 基于点云的隧道断面提取方法 2.1 坐标系定义三维激光扫描系统采集到的点云空间位置信息是以仪器坐标系统作为坐标基准,不同仪器采用的坐标基准也不尽相同。本文定义的直角坐标系的原点位于激光束发射处,Z轴位于仪器竖向扫描面内,向上为正;X、Y轴均位于仪器的横向扫描面内,其中Y轴正方向指向隧道走向,如图 1所示。
|
| 图 1 仪器坐标系定义 Fig.1 Coordinate system definition |
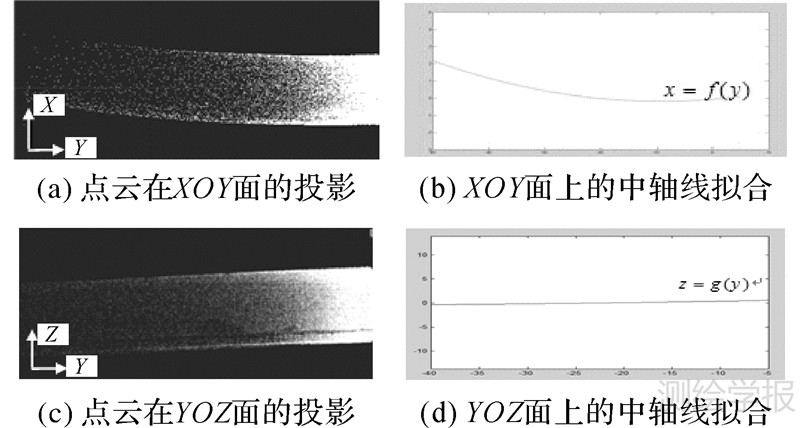
中轴线反映了隧道整体的走向和姿态。本文提出的中轴线提取方法是任意选取隧道一段区间的点云数据,将其分别投影至XOY面和YOZ面,并沿Y方向设置适当步长Δy,求出该步长范围内投影后的点云在X、Z方向上的最大值和最小值及其平均值;采用二次多项式对选定区间的中值进行曲线拟合,得到在XOY和YOZ面上的中轴线方程,如图 2所示,具体步骤如下。
|
| 图 2 隧道中轴线提取 Fig.2 Extracting of tunnel axis |
(1) 将点云数据分别投影至XOY和YOZ面,并从Y方向的最小值开始,以Δy=0.1 m步长,沿Y方向对X、Z搜索最大值和最小值。
(2) 计算任一点yi(i=1,2,…,n)分别对应X方向和Z方向上的平均值
式中,xi(max)、xi(min)分别表示yi处X值的最大值、最小值;zi(max)、zi(min)同理。
(3) 将yi分别与xi、zi,进行二次曲线拟合,得到的隧道中轴线可表示为
2.3 隧道断面的离散点集提取及构建隧道中轴线上某点p及其邻域点满足曲线方程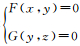 ,则过p点的切向量为
,则过p点的切向量为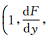
 ;以该切向量作为所要截取断面的法向量即可构建过p点的隧道断面。建立隧道壁上任意一点处的断面必须首先在中轴线上找到其对应点,且两者之间应满足距离最小条件。考虑到点云落在特定平面上的数量较少,因此本文提出将隧道内壁一定间隔(本文称之为“断面厚度”)内的点视为处于同一平面上,并据此构建隧道横断面。具体算法如下。
;以该切向量作为所要截取断面的法向量即可构建过p点的隧道断面。建立隧道壁上任意一点处的断面必须首先在中轴线上找到其对应点,且两者之间应满足距离最小条件。考虑到点云落在特定平面上的数量较少,因此本文提出将隧道内壁一定间隔(本文称之为“断面厚度”)内的点视为处于同一平面上,并据此构建隧道横断面。具体算法如下。
对于隧道壁上任一点P(xp,yp,zp),首先在中轴线上搜索与其对应的点p(xp,yp,zp),使其之间的距离为最小,即满足
式中,i=1,2,…,n。点p(xp,yp,zp)满足下列方程
则垂直于p点切线的平面方程可表示为
式中,(1,kp,k′p)是p点处的瞬时切向量,可根据式(2)计算,即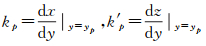 。
。
设断面厚度为d,则属于该范围内的点集Q定义为
3 隧道断面形变自动检测方法 3.1 点云配准利用标靶可将各站扫描获得的激光点云数据转换至同一坐标系。由于激光点云坐标为仪器自定义的空间直角坐标系,因此需要转换至统一的工程坐标系。为解算坐标转换的7个参数,必须在各扫描站内均匀布设至少3个标靶,然后分别使用扫描仪及全站仪获取各标靶在独立坐标系及工程坐标系中的三维坐标。根据地铁测量的实际环境,本文采用文献[19]提出的适用于大旋转角情况的三维坐标转换模型
模型中的旋转矩阵仅含有3个独立的旋转角参数,顾及旋转矩阵的正交性,可列出6个限制性条件
解算时,将式(8)作线性化处理[20],然后按附有限制性条件的间接平差求解可得到3个平移参数、3个旋转参数和1个尺度参数。分别解算各站的转换七参数,最后将各站的点云数据统一到工程坐标系。
3.2 非点滤除原始点云数据中包含有不属于隧道断面上的点(本文简称非点),如盾构环片上的连接螺栓孔、螺帽、注浆孔、电缆、照明设备等附着物。为保证搜索得到的点尽可能位于隧道内壁上,在构建断面之前,必须从点云数据中滤除非点。本文采用基于椭圆柱面拟合的滤波方法,即根据隧道形状特点将其横截面视为椭圆,通过对分割后的各区域点云进行椭圆柱面拟合及平差模型的解算,实现隧道点云的滤波。滤波效果如图 3所示。

|
| 图 3 隧道点云滤波前、后效果图 Fig.3 The filtering of tunnel points |
沿隧道中轴线方向等间隔设置n个点,以任意点pi为中心截取厚度为d的断面离散点集Qi。在pi点前、后以d/2为间隔各设1个点,共3个点;以每个点为中心,在与该点切线正交的平面内按照等角度α进行点云搜索,并保存这些点的坐标信息;若某一方向上未搜到对应点,则对该方向上一定邻域内的离散点进行局部曲线拟合,内插得出该方向所对应的断面点坐标。对比两期点云相同位置的坐标值,将超过规定变形阈值的点以不同的颜色表示出来;如果Q内的变形点所占百分比超过设定的阈值,就将其视为重点变形区域,然后进行更加详细的断面轮廓线拟合及变形分析。
3.4 断面变形分析对不同监测时期提取的断面进行自动变化检测,筛选出变形量较大的离散点集进行投影及断面轮廓线拟合,并采用极坐标法进行断面变形分析,具体过程如下。
3.4.1 断面投影如图 4所示,设以pi为中心的断面所在平面为L,根据隧道点云的特点将未落在平面L上且到平面距离小于h/2的断面离散点均视为L上的点,并投影至L,得到pi处的断面离散点集。投影计算公式为

|
| 图 4 断面点投影 Fig.4 Projection of section point |
式中,Pi(xi,yi,zi)为投影前的非平面点,投影后表示为P′i(x′i,y′i,z′i);Δxi、Δyi和Δzi分别表示点Pi投影前、后在坐标轴3个方向上的位移变化量。投影后点的坐标为
3.4.2 断面轮廓线拟合实际扫描作业中,由于障碍物遮挡或受隧道空间扫描角度的限制,会出现部分点云空洞,难以保证断面上处处都有激光斑点,因此需要对投影后的断面离散点集进行曲线拟合。本文提出采用最二乘椭圆拟合法[21],即认为隧道断面轮廓线是椭球与断面所在平面的相交线,且椭球中心与断面中心重合,均落在隧道中轴线上;此外,理论上盾构隧道断面设计为圆形,但在外力作用下实际上是一个离心率很小的椭圆,可用一个二次多项式方程来表示。因此,隧道断面的轮廓线应同时满足两个曲线方程,联立求解出椭球参数可得到断面的轮廓线方程,具体计算步骤如下。
(1) 断面点投影后的椭圆方程可表示为
式中,a、b、c为椭球的中心。
(2) 平面二次曲线方程一般形式为
式中,p=[A B C D E F];q=[q1q2…qn];qi=[xi2 xi yi yi2 xi yi 1]T。根据最小二乘准则,曲线上所有的点均应符合式(12),对不在曲线上的点需进行最小二乘拟合,组成法方程进行迭代至收敛,即可求出方程系数矩阵p。
(3) 公式(11)和公式(12)表示的是同一条曲线,联合求解可得到各个参数之间的函数关系为
式中,k、k′、m可由公式(5)算得;p=[A B C D E F]由公式(12)按最小二乘得到;(a,b,c)和λ1、λ2、λ3是待求的椭圆未知参数。通过式(11)可依次求出椭圆的中心、长半轴和短半轴。
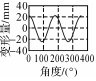
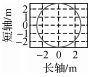
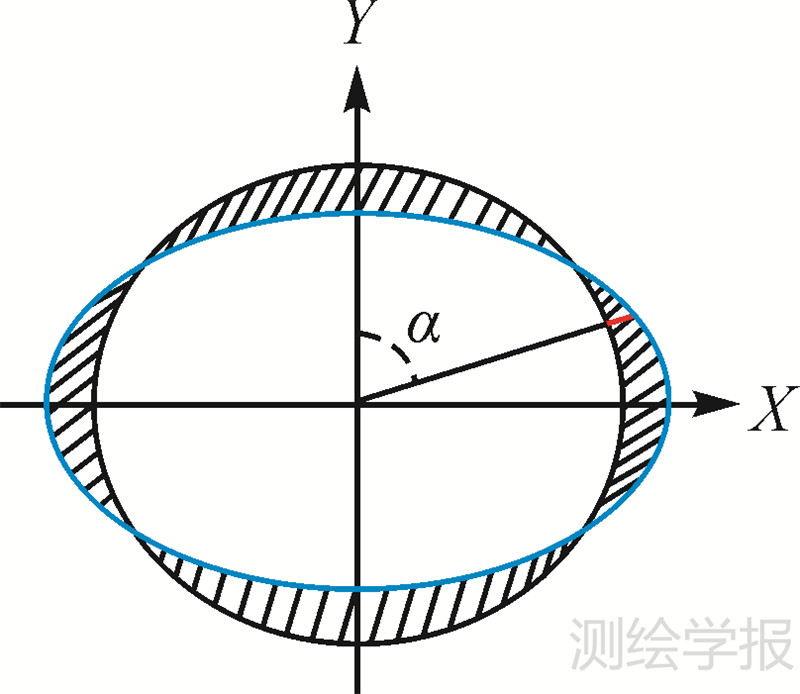
3.4.3 极坐标法分析断面变形本文提出通过构建不同监测时期同一位置的隧道断面,叠加后采用极坐标法进行变形分析的方法,即可得到该期间隧道在各个方向上的位移变化量,如图 5所示。
|
| 图 5 隧道断面不同时期的形变量 Fig.5 Deformation of tunnel section at different times |
图 5中,黑色和蓝色线表示同一位置提取的两期断面轮廓线,阴影部分为该期间隧道整体的变形区域;红色线段表示隧道在角度α上的位移变化。将每个断面在某时段的各个方位的变化量绘制出来,可更直观地用于隧道变形趋势分析。
4 实例验证 4.1 试验方案设计及数据采集本文选择郑州市地铁1号线民航路站区间某段隧道(长度约130 m)作为试验研究区,该区域位于市中心繁忙的主干道上,地面上高层建筑物林立,地下管网稠密,容易发生隧道变形。试验数据包括全站仪实测地面标靶的坐标数据、隧道环片标贴的中心提取数据以及地铁隧道两期扫描数据。第1期数据采集于2013年3月,分6站进行扫描;第2期数据采集于2013年7月,分4站扫描。每站平均有450万点云,测站之间拼接误差均在±2 mm内。试验使用Riegl VZ400三维激光扫描仪,扫描距离500 m,100 m处的单点扫描精度为±2 mm,激光发射频率为30万点/s;每隔10 m布设一个断面,共布设了13个监测断面。为证明本方法的有效性,本文将激光扫描得到的断面上的监测标贴坐标值,经转换后与全站仪观测结果进行对比分析,并计算观测值的均方差是否符合地铁工程形变监测规范要求。
4.2 隧道断面多期监测数据处理与形变分析 4.2.1 点云配准利用标靶将两期扫面数据统一到工程坐标系中,标靶在扫描仪坐标系中的坐标由Rigel自带软件自动得到,在工程坐标系中的坐标利用隧道内定期复测的高精度控制点通过精密全站仪测得,第1期数据含有5个标靶,第2期数据含有4个标靶,图 6为配准后同一坐标系下分别用红、蓝两种颜色表示的两期点云。

|
| 图 6 同一坐标系下的两期点云 Fig.6 Point clouds in the same coordinate system |
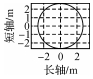
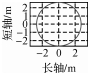
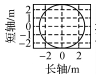
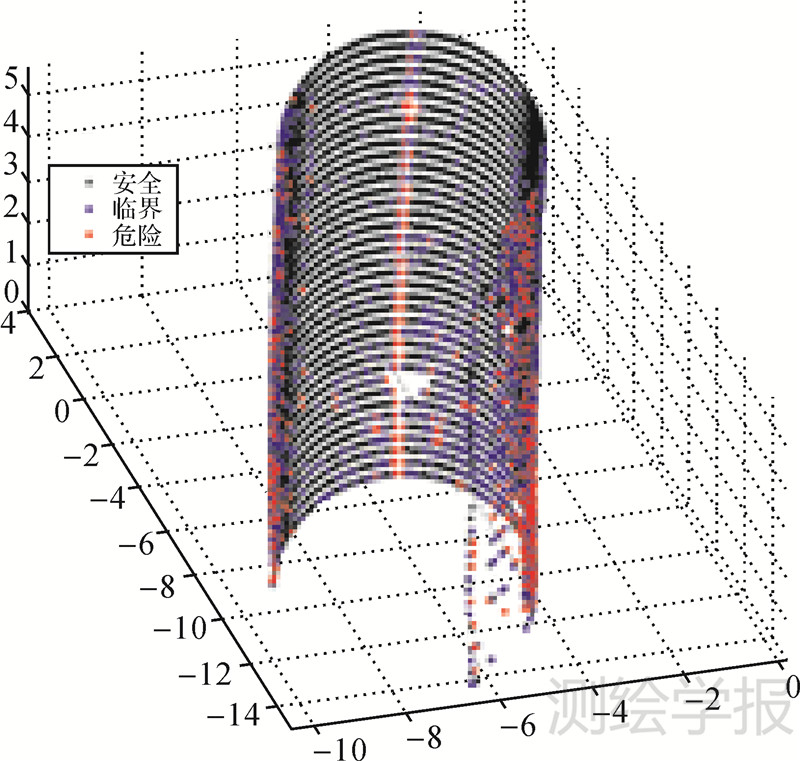
试验选择构建隧道断面的区间长度约为45 m,根据上述断面变化自动检测方法,利用第1期点云数据提取出隧道中轴线,并从起始点开始截取若干个连续断面,保存截取位置和对应方位的断面离散点坐标;对第2期点云数据处理时,为保证两期扫描数据在处理时截取位置的一致性,仍选用第1期的隧道中轴线表达式。本文利用Matlab语言和Point Cloud数据处理平台,根据上述断面提取方法,首先进行断面变化自动检测,对两期隧道离散点的坐标变化进行对比分析,并将《城市轨道交通工程测量规范》中Ⅲ级变形监测所要求的点位中误差±6 mm作为阈值,分3种情况分析位移变化量δ的监测结果(如图 7所示):①δ≤6 mm,用黑色显示;②6 mm<δ≤12 mm,用蓝色显示;③δ≥12 mm,用红色显示。
|
| 图 7 隧道断面位移变化情况 Fig.7 Deformation of tunnel section |
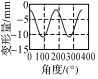
由图 7可以看出,隧道断面的顶部和两侧变形较大。设断面厚度为50 mm,选择变形点所占比例较大的3个断面离散点集进行断面轮廓线拟合,将点集中心点前、后25 mm范围内的离散点全部投影至该点所在的断面,拟合成二次曲线进行变形分析。角度α的选取区间为[-135°,135°],形变结果见表 1和表 2。
| 角度α | -135° | -108° | -90° | -81° | -54° | -27° | 0° | 27° | 54° | 81° | 90° | 108° | 135° |
| 断面1 | -6.4 | -10.1 | -10.9 | -10.7 | -7.8 | -3.7 | -1.8 | -3.7 | -7.8 | -10.7 | -10.9 | -10.1 | -6.4 |
| 断面2 | -15.7 | -11.3 | -10.3 | -10.5 | -14.0 | -18.9 | -21.2 | -18.9 | -14.0 | -10.5 | -10.3 | -11.3 | -15.7 |
| 断面3 | -1.1 | -19.9 | -24.3 | -23.2 | -8.2 | 12.6 | 22.2 | 12.6 | -8.2 | -23.2 | -24.3 | -19.9 | -1.1 |
由表 1和表 2可以看出,3个断面变形量的最大值分别为10.9 mm、21.2 mm和24.3 mm,且均位于水平方向或竖直方向(0°),这是由于地面建筑物对隧道顶部的压力要远远大于两侧的压力,使得隧道竖直方向上的变形速度大于水平方向,这与断面拟合时采用椭圆二次曲线拟合时的设想相一致,表明了本文所提出的方法可以更直观、更全面地分析隧道整体变形。
5 结 语本文提出了基于激光点云的隧道断面构建和断面叠加形变分析方法,建立了提取隧道任意位置断面的算法模型以及全方位整体形变分析方法。通过对试验研究区采集的两期扫描数据进行标贴中心提取、点云滤波处理、测站拼接等工作,构建了同一位置不同时期的隧道断面,采用叠加分析法得到了隧道的整体形变情况,并与常规监测方法进行了对比分析,验证了本方法的有效性。
| [1] | BIAN Dayong, LU Xiaoping, LI Yongqiang, et al. On Survey Technique in Subway Sectional Shield Construction[J]. Bulletin of Surveying and Mapping, 2011(4): 51-55. (边大勇, 卢小平, 李永强, 等. 地铁盾构区间施工测量技术研究[J]. 测绘通报, 2011(4): 51-55.) |
| [2] | HUANG Teng, SUN Jingling, TAO Jianyue, et al. Subsidence Monitoring and Analyzing in Subway Tunnel Construction[J]. Journal of Southeast University: Natural Science Edition, 2006, 36(2): 262-266. (黄腾, 孙景领, 陶建岳, 等. 地铁隧道结构沉降监测及分析[J]. 东南大学学报: 自然科学版, 2006, 36(2): 262-266.) |
| [3] | JIAN Xiao, TONG Peng. Tunnel Deformation Monitoring by Surface Laser Radar Technology[J]. Railway Investigation and Surveying, 2011, 37(6): 19-22. (简骁, 童鹏. 基于地面激光雷达技术的隧道变形监测方法研究[J]. 铁道勘察, 2011, 37(6): 19-22.) |
| [4] | LI Jian, WAN Youchuan, JIANG Menghua, et al. Tunnel Deformation Monitoring Based on the Terrestrial Laser Scanning Technology[J]. Geospatial Information, 2012, 10(1): 14-17. (李健, 万幼川, 江梦华, 等. 基于地面激光技术的隧道变形监测技术[J]. 地理空间信息, 2012, 10(1): 14-17.) |
| [5] | QIU Dongwei, LIANG Qinghuai, YANG Songlin. Integral Monitoring of Beijing Subway Tunnel Deformation[J]. Science of Surveying and Mapping, 2008, 33(S): 16-17. (邱冬炜, 梁青槐, 杨松林. 北京地铁隧道结构整体变形监测的研究[J]. 测绘科学, 2008, 33(S): 16-17.) |
| [6] | XIA Guofang, WANG Yanmin. Application Research of Three-Dimensional Laser Technology in the Transect and Vertical Section Surveying of Tunnels[J]. Journal of Beijing Institute of Civil Engineering and Architecture, 2010, 26(3): 21-24. (夏国芳, 王晏民. 三维激光扫描技术在隧道横纵断面测量中的应用研究[J]. 北京建筑工程学院学报, 2010, 26(3): 21-24.) |
| [7] | LIU Yanping, CHENG Xiaojun, JIA Dongfeng. Tunnel Convergence Analysis Based on 3D Laser Scanning[J]. Journal of Geotechnical Investigation & Surveying, 2013, 41(3): 74-77. (刘燕萍, 程效军, 贾东峰. 基于三维激光扫描的隧道收敛分析[J]. 工程勘察, 2013, 41(3): 74-77.) |
| [8] | WANG Lingwen, CHENG Xiaojun, WAN Chenghui. Study on the 3D Laser Scanning Technology for Tunnel Inspection[J]. Journal of Geotechnical Investigation & Surveying, 2013, 41(7): 53-57. (王令文, 程效军, 万程辉. 基于三维激光扫描技术的隧道检测技术研究[J]. 工程勘察, 2013, 41(7): 53-57.) |
| [9] | SHA Congshu, LIU Shaotang. Tunnel Deformation Monitoring Based on Laser Scanning[J]. Urban Rapid Rail Transit, 2013, 26(6): 88-91. (沙从术, 刘绍堂. 基于激光扫描技术的隧道变形分析方法[J]. 都市快轨交通, 2013, 26(6): 88-91.) |
| [10] | SUI Lichun, ZHANG Yibin, LIU Yan,et al. Filtering of Airborn LiDAR Point Cloud Data Based on the Adaptive Mathematical Morphology[J]. Acta Geodaetica et Cartographica Sinica, 2010, 39(4): 390-396. (隋立春, 张熠斌, 柳艳, 等. 基于改进的数学形态学算法的LiDAR点云数据滤波[J]. 测绘学报, 2010, 39(4): 390-396.) |
| [11] | KANG Xiaochen, LIU Jiping, LIN Xiangguo. Parallel Filter of Progressive TIN Densification for Airborne LiDAR Point Cloud Using Mult-core CPU[J]. Acta Geodaetica et Cartographica Sinica, 2013, 42(3): 331-336. (亢晓琛, 刘纪平, 林祥国. 多核处理器的机载激光雷达点云并行三角网渐进加密滤波方法[J]. 测绘学报, 2013, 42(3): 331-336.) |
| [12] | ZHENG Dehua, YUE Dongjie, YUE Jianping. Geometric Feature Constraint Based Algorithm for Building Scanning Point Cloud Registration[J]. Acta Geodaetica et Cartographica Sinica, 2008, 37(4): 464-468. (郑德华, 岳东杰, 岳建平. 基于几何特征约束的建筑物点云配准算法[J]. 测绘学报, 2008, 37(4): 464-468.) |
| [13] | ZHOU Langming, ZHENG Shunyi, HUANG Rongyong, A Registration Algorithm for Point Clouds Obtained by Scanning Objects on Turntablet[J]. Acta Geodaetica et Cartographica Sinica, 2013, 42(1): 73-79. (周朗明, 郑顺义, 黄荣永. 旋转平台点云数据的配准方法[J]. 测绘学报, 2013, 42(1): 73-79.) |
| [14] | GORDON S J, LICHTI D D. Modeling Terrestrial Laser Scanner Data for Precise Structural Deformation Measurement[J]. Journal of Surveying Engineering, 2007, 133(2): 72-80. |
| [15] | MONSERRAT O, CROSETTO M. Deformation Measurement Using Terrestrial Laser Scanning Data and Least Squares 3D Surface Matching[J]. ISPRS Journal of Photogrammetry & Remote Sensing, 2008, 63(1): 142-154. |
| [16] | FISCHLER M A, BOLLES R C. Random Sample Consensus: A Paradigm for Model Fitting with Applications to Image Analysis and Automated Cartography[J]. Communications of the ACM, 1981, 24(6): 381-395. |
| [17] | ZHANG Yi, YAN Li. 3D Diffusion Filtering Method of Intensity Noise for Terrestrial Laser Scanning Point Cloud[J]. Acta Geodaetica et Cartographica Sinica, 2013, 42(4): 568-573(张毅, 闫利. 地面激光点云强度噪声的三维扩散滤波方法[J]. 测绘学报, 2013, 42(4): 568-573.) |
| [18] | GE Xiaotian, LU Xiaoping, WANG Yupeng, et al. Registration Method of Laser Point Cloud Data in Multi-stations[J]. Bulletin of Surveying and Mapping, 2010(11): 15-17. (葛晓天, 卢小平, 王玉鹏, 等. 多测站激光点云数据的配准方法[J]. 测绘通报, 2010(11): 15-17.) |
| [19] | CHEN Yi, SHEN Yunzhong, LIU Dajie.A Simplified Model of Three Dimensional Datum Transformation Adapted to Big Rotation Angle[J]. Geomatics and Information Science of Wuhan University, 2004, 29(12): 1101-1105. (陈义, 沈云中, 刘大杰. 适用于大旋转角的三维基准转换的一种简便模型[J]. 武汉大学学报: 信息科学版, 2004, 29(12): 1101-1105.) |
| [20] | ZHU Ningning. Two Simplified Models to Calculate Seven-Parameter Initial Value Conversion of the Three-Dimensional Baseline[J]. Gemomatics & Spatial Information Technology, 2014, 37(4): 78-82. (朱宁宁. 三维基准转换七参数初始值解算的两种简便模型[J]. 测绘与空间地理信息, 2014, 37(4): 78-82.) |
| [21] | XU Zhengwen, YAO Lianbi. Direct Least Square Robust Estimation Method for Ellipse Fitting[J]. Journal of Geodesy and Geodynamics, 2008, 28(1): 77-80. (许正文, 姚连璧. 基于稳健估计的直接最小二乘椭圆拟合[J]. 大地测量与地球动力学, 2008, 28(1): 77-80.) |