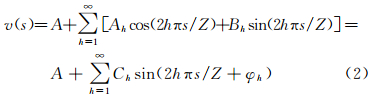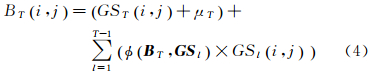2. 中国矿业大学(北京)地球科学与测绘工程学院,北京 100083
2. College of Geoscience and Surveying Engineering, China University of Mining & Technology(Beijing), Beijing 100083, China
现有的高光谱影像融合算法在提高影像空间分辨率的同时,都会或多或少地造成地物光谱曲线失真,影响影像后续的解译与应用[1, 2]。为此,本文提出一种基于谐波分析的高光谱影像融合(harmonic analysis fusion,HAF)算法[3],该算法是在分析并确定了光谱曲线谐波余相分量对光谱曲线波形形态无影响的基础上,通过采用空间信息更为丰富的高空间分辨率影像替换谐波余相,然后对替换后的高空间分辨率影像与谐波振幅与相位进行谐波逆变换的一种高光谱融合算法,HAF算法在提高影像空间分辨率的同时完全保持光谱曲线的波形形态,但是由于直接采用高空间分辨率影像替换光谱曲线的谐波余项分量,导致原有的地物光谱曲线反射率受到了破坏。
文献[4, 5, 6, 7]为了对电力系统谐波污染进行有效地监测与控制,提出了谐波分析算法;文献[8, 9]在其研究成果中首次将谐波分析理论应用到AVHRR和MODIS等遥感影像植被的NDVI时间序列分析当中;文献[10]在其后续的谐波研究中将该算法应用到了农作物物种识别当中;国内也有学者利用谐波分析理论对山东省典型植被季节变化特征进行了分析[11];文献[12]则在谐波分析理论的辅助下对小目标地物进行了目标探测试验;文献[2, 3]通过分析光谱曲线谐波各个特征分量的物理意义,将谐波分析理论应用到了影像融合当中,并取得了一定的研究成果,但由于初次尝试,很多问题考虑不足,最终造成融合后地物光谱反射率整体出现过多偏移,地物光谱曲线物理解析特性遭到破坏,所以该算法还需进行改进与完善。
Gram-Schmidt(GS)变换融合算法可以较好地改善原始影像的空间细节特征,提高原始影像的空间分辨率,且能最大限度地保持原始影像的光谱物理特性[13, 14]。鉴于此,本文将GS变换引入HAF算法当中,提出了结合Gram-Schmidt变换的高光谱影像谐波分析融合(Gram-Schmidt transform combined with harmonic analysis fusion,GSHAF)改进算法。
1 理论与方法 1.1 高光谱影像的谐波分析法文献[15, 16]认为,谐波分析是将目标的时间序列曲线f(t)表示为正(余)弦波相叠加的形式。谐波变换说明了任何连续的周期曲线f(t)都可以表示成为傅里叶级数形式[6]。高光谱遥感影像中,像元在各个波段的灰度值所组成的光谱曲线v(s)是一条连续的曲线,那么也可进行谐波分解,可将像元光谱曲线v(s)分解为谐波余项、谐波振幅与谐波相位相叠加的形式,其变换公式为
式中,s代表波段号数;A0/2表示谐波余项;Z代表波段总数;h表示谐波分析次数;Chsin(2hπ/L+φh)表示第h次谐波分量;φh表示第h次谐波的初相位;Ch表示第h次谐波的振幅,Ch2表示功率谱。
1.2 高光谱影像的谐波分析融合算法根据式(1)可知,谐波余项(A0/2)分量计算结果为一个常数,该分量在曲线叠加过程中并不影响光谱曲线波形的形状,只是地物对电磁波反射的综合反应,其包含着影像丰富的空间信息。鉴于此,利用空间信息更为丰富的高空间分辨率影像直接替换谐波余项分量,如式(2)所示
式中,A代表高空间分辨率遥感影像,其他符号意义同式(1)。
随后对替换后的谐波特征分量进行谐波逆变换,完成高光谱影像与高空间分辨率影像的融合,这便是HAF算法的基本原理。至此,在保证高光谱影像光谱曲线波形不变的基础上,将高光谱影像的融合问题转换成了各像元光谱曲线的谐波余相特征分量组成的二维影像与高空间分辨率影像之间的融合。
1.3 Gram-Schmidt变换融合算法Gram-Schmidt(GS)[13, 14, 17]变换是统计学中经常用到的一种多维线性正交变换,采用GS变换对高光谱影像多维数据进行正交化处理,可以消除冗余信息。Gram-Schmidt变换融合的基本流程如下。
(1) 首先利用原始低空间分辨率影像模拟出一幅全色影像。
(2) 随后利用该全色影像作为GS变换的第一个分量来对低空间分辨率影像进行GS变换,具体变换公式为
式中,GST表示经GS变换后的第T个正交分量;BT表示原始低空间分辨率遥感影像第T波段;μT为原始低空间分辨率遥感影像第T波段像元灰度值的均值;φ(BK,GSl)为原始低空间分辨率影像第K波段与GSl之间的协方差;i和j分别表示原始低空间分辨率影像的行数和列数;M和N表示整幅影像的行数和列数。
(3) 用高空间分辨率影像替换GS变换后的第一分量,即GS1分量。
(4) 最后再通过式(4)对上述替换后的数据集进行GS逆变换,完成低空间分辨率影像与高空间分辨率影像融合
式中,所有符号含义同式(3)。
1.4 结合Gram-Schmidt变换的谐波分析融合算法HAF算法在保持融合影像光谱曲线波形形态方面极具优势,但是高光谱影像与高空间分辨率影像光谱范围不同,所表示的光谱响应均值也不同,直接进行替换会对地物光谱曲线的反射率造成影响。针对该问题,本文提出结合Gram-Schmidt变换的谐波分析融合算法。GSHAF算法具体流程是在原始高光谱影像被谐波分析算法分解为谐波余项、谐波振幅和谐波相位相叠加的形式后,根据式(3)和式(4),首先对该光谱曲线的谐波余项分量与高空间分辨率影像进行GS变换融合,这样可以利用GS变换融合算法的优点既提高谐波余项的空间分辨率,同时也有效地修正了高空间分辨率影像与谐波相位像元灰度值之间巨大的差异,使GS变换融合后影像像元灰度值更接近谐波余项分量。随后对经GS变换融合后的影像与谐波振幅与谐波相位相两个特征分量根据式(5)进行谐波逆变换,完成高光谱分辨率与高空间分辨率的影像融合,这样便使融合后像元光谱曲线反射率更接近真实地物的光谱反射率,拓宽了融合影像后续应用范围,增强了GSHAF算法的适用性。公式(5)计算方法为
式中,G代表原始高光谱影像像元光谱曲线的谐波余项与高空间分辨率遥感影像经过GS变换融合后的影像,其他符号意义同式(1)。
2 试验与分析 2.1 试验数据试验数据为美国EO-1卫星在2005年7月底获取的Hyperion高光谱遥感影像与ALI高空间分辨率遥感影像全色波段影像,如图 1、图 2所示,其中图 1为该地区经过假彩色合成后的Hyperion高光谱影像立体(RGB合成波段号为33、63、93),图 2中显示的是其对应的ALI高空间分辨率全色波段影像。本次试验采用ALI获取的全色波段充当影像融合所需的高空间分辨率影像。

|
| 图 1 Hyperion高光谱影像 Fig.1 Hyperion hyperspec-tral image |

|
| 图 2 ALI全色波段影像 Fig.2 ALI panchromatic band image |
试验数据经过了一系列预处理操作,详细流程见文献[18, 19, 20]。待原始影像完成预处理之后,首先对原始Hyperion高光谱影像按照式(1)进行最佳分解次数的谐波分解[3],将其分解为谐波余项、谐波振幅与谐波相位相叠加的表示形式,随后根据式(3)、式(4)首先采用GS变换融合算法对原始高光谱影像的谐波余项分量与ALI高空间分辨率影像进行融合,最后再按照式(5)对融合影像与原始高光谱影像的谐波振幅与谐波相位进行谐波逆变换,完成高光谱影像与高空间分辨率影像的融合。融合结果如图 3所示的高光谱假彩色立体(RGB合成波段号为33、63、93),为了直观地说明改进后的GSHAF算法比HAF算法具有更强的优越性,本次试验同样对试验数据进行HAF算法的融合处理,融合结果如图 4所示(RGB合成波段号为33、63、93),随后对HAF算法与GSHAF算法试验结果进行对比分析。

|
| 图 3 GSHAF算法融合后Hyperion影像 Fig.3 The fused Hyperion image based on the GSHAF |

|
| 图 4 HAF算法融合后Hyperion影像 Fig.4 The fused Hyperion image based on the HAF |
通过目视评价融合后影像可知,GSHAF算法与HAF算法融合后的影像在空间分辨率方面均具有很大的改善,但是在影像色调方面GSHAF保持的更加贴近原始影像。为了更加客观地分析经过GSHAF算法与HAF算法融合后影像的光谱信息保持性情况,随机地在两种融合算法融合后影像上选择植被和建筑物两种地物的对应像元,并绘制每种地物像元的光谱曲线,如图 5、图 6所示,图中虚线为HAF算法融合之后影像对应像元的光谱曲线,粗实线为GSHAF算法融合之后影像对应像元的光谱曲线,细实线为原始高光谱影像对应像元的光谱曲线。其中图 5为植被融合前后的光谱曲线,图 6表示的是建筑物融合前后的光谱曲线。从这两个图中可以看出,GSHAF算法与HAF算法在光谱波形形态方面都完全保留了原始影像的光谱曲线形态,但是GSHAF算法融合后的影像地物像元的光谱反射率与其原始的地物像元反射率更为接近,尤其在建筑物方面,几乎完全与原始光谱曲线重合。以上分析客观地证明了GSHAF算法在光谱信息保持方面更为优秀,更符合一个优秀融合算法的要求,其融合后的影像具有更为广泛的应用前景。

|
| 图 5 融合前后植被光谱曲线 Fig.5 The vegetation spectra of original image and fused image |

|
| 图 6 融合前后建筑物光谱曲线 Fig.6 The building spectra of original image and fused image |
好的融合算法不仅需要具有优良的可行性,同时也需要具有良好的普适性,为了验证GSHAF算法是否对其他数据源也具有良好的可行性,本节仅采用国产HJ-1A卫星数据为例,利用该影像数据对本文提出的GSHAF算法进行普适性验证。本次普适性验证试验数据采用2013年4月25日获取的陕西某城市郊区及其附近山区的影像,如图 7所示为经过假彩色合成后的该区域高光谱影像立体(RGB合成波段号为60、90、110),本次试验采用多光谱遥感影像的第3波段充当高空间分辨率影像,如图 8所示。

|
| 图 7 HJ-1A高光谱影像 Fig.7 HJ-1A hyperspectral image |

|
| 图 8 HJ-1A卫星CCD第3波段影像 Fig.8 The third band image of HJ-1A CCD |
同样对HJ-1A卫星的数据进行预处理工作,具体流程参阅文献[21, 22],随后分别进行GSHAF与HAF两种融合算法的融合,其结果如图 9、10所示的高光谱假彩色立体(RGB合成波段号为60、90、110)。通过目视评价可知,经过GSHAF算法与HAF算法融合后的影像空间分辨率都获得了很大的提高,在其色调方面两幅融合后影像整体差异不大,但是仔细观察融合前后影像中的河流,还是可以发现GSHAF算法融合后的影像色调更接近原始影像。

|
| 图 9 GSHAF算法融合HJ-1A影像 Fig.9 The fused HJ-1A image based on the GSHAF |

|
| 图 10 HAF算法融合HJ-1A影像 Fig.10 The fused HJ-1A image based on the HAF |
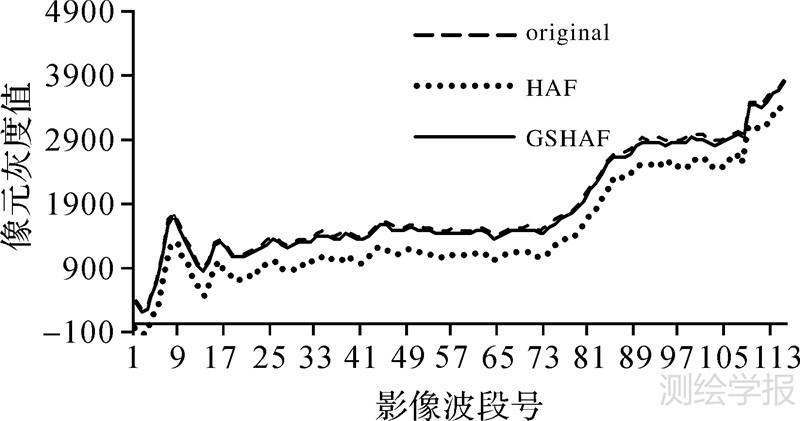
为了客观了解GSHAF算法在光谱信息保持性方面的情况,同样绘制出融合前后影像中对应位置随机像元A、B的光谱曲线,如图 11、图 12所示,图中3条曲线所代表的影像像元意义与图 5、6相同。可以明显看出,该算法所表示出来的结果与可行性分析试验完全相同,光谱曲线波形形态两种方法都完全地保留下来,反射率方面GSHAF算法融合影像更为接近原始影像,图 12所示GSHAF算法融合后的光谱曲线也几乎与原始影像光谱曲线重合,以上分析客观真实地证明了GSHAF算法不仅具有优良的可行性,对其他数据还具有良好的普适性。

|
| 图 11 融合前后随机像元A光谱曲线 Fig.11 The A random pixel spectra of original image and fused image |
|
| 图 12 融合前后随机像元B光谱曲线 Fig.12 The B random pixel spectra of original image and fused image |
本文在分析基于谐波分析理论的高光谱遥感影像融合算法缺陷的基础上,提出了结合Gram-Schmidt变换的谐波分析融合改进算法,该算法可以在完全保留融合前后影像光谱曲线波形形态的基础上,有效地减少HAF算法融合后像元光谱曲线与原始光谱曲线反射率差异较大、地物像元光谱物理特性失真这一缺陷,使融合后影像获得更广泛的用途,并通过试验来证明这一假设。通过试验与分析可得:①HAF算法和GSHAF算法在影像融合过程中都可以完全地保留原始影像的光谱曲线波形形态;②GSHAF算法在光谱物理特性保持方面比HAF算法更具优势,融合后地物的光谱反射率值更接近原始影像地物光谱反射率值;③GSHAF算法不仅具有优良的可行性,还具有良好的普适性;④虽然GS变换对HAF算法具有一定的改进作用,但是还是无法完全地保留地物光谱全部的物理特性,然而,本文已经在保证融合前后光谱曲线波形不变的情况下,将高光谱遥感影像融合简化,只要找到合适的算法,后续的研究中将会进一步将地物光谱信息保留下来。
| [1] | DONG Guangjun, ZHANG Yongsheng, FAN Yonghong. Image Fusion for Hyperspectral Data of PHI and High Resolution Aerial Image[J]. Journal of Infrared and Millimeter Waves, 2006, 25(2): 123-126. (董广军, 张永生, 范永弘. PHI高光谱数据和高空间分辨率遥感图像融合技术研究[J]. 红外与毫米波学报, 2006, 25(2): 123-126.) |
| [2] | YANG Keming, ZHANG Tao, WANG Libo, et al. Harmonic Analysis Fusion of Hyperspectral Image and Its Spectral Information Fidelity Evaluation[J]. Spectroscopy and Spectral Analysis, 2013, 38, 33(9): 2498-2501. (杨可明, 张涛, 王立博, 等. 谐波分析法高光谱影像融合及其光谱信息保真度评价[J]. 光谱学与光谱分析, 2013, 33(9): 2498-2501.) |
| [3] | YANG Keming, ZHANG Tao, WANG Libo, et al. A New Algorithm on Hyperspectral Image Fusion Based on the Harmonic Analysis[J]. Journal of China University of Mining & Technology, 2014, 43(3): 547-553. (杨可明, 张涛, 王立博, 等. 高光谱影像的谐波分析融合算法研究[J]. 中国矿业大学学报, 2014, 43(3): 547-553.) |
| [4] | JAKUBAUSKAS M E, LEGATES D R, KASTENS J H. Harmonic Analysis of Time-series AVHRR NDVI Data[J]. Photogrammetric Engineering & Remote Sensing, 2001, 67(4): 461-470. |
| [5] | REN Zihui, QIU Runhe, ZHANG Yan. Formation of Power System Harmonic Model of Mine and Design of Harmonic Filter for Mine Hoister[J]. Journal of China University of Mining & Technology, 2004, 33(1): 45-49. (任子晖, 仇润鹤, 张艳. 煤矿电网谐波分析模型的建立与滤波器设计[J]. 中国矿业大学学报, 2004, 33(1): 45-49.) |
| [6] | GEORGE J W. Power Systems Harmonics Fundamentals, Analysis and Filter Design[M]. Translated by XU Zheng. Beijing: China Machine Press, 2003: 4-13. (GEORGE J W. 电力系统谐波——基本原理、分析方法和滤波器设计[M]. 徐政, 译. 北京: 机械工业出版社, 2003: 4-13.) |
| [7] | CHAI Xuzheng, WEN Xishan, GUAN Genzhi, et al. An Algorithm with High Accuracy for Analysis of Power System Harmonics[J]. Proceedings of the CSEE, 2003, 23(9): 68-71. (柴旭峥, 文习山, 关根志, 等. 一种高精度的电力系统谐波分析算法[J]. 中国电机工程学报, 2003, 23(9): 68-71.) |
| [8] | SAKAMOTO T, YOKOZAWA M, TORITANI H, et al. A Crop Phenology Detection Method Using Time-series MODIS Data[J]. Remote Sensing of Environment, 2005, 96(3-4): 366-374. |
| [9] | BRADLEY B A, JACOB R W, HERMANCE J F, et al. A Curve Fitting Procedure to Derive Inter-annual Phenologies from Time Series of Noisy Satellite NDVI Data[J]. Remote Sensing of Environment, 2007, 106(2): 137-145. |
| [10] | JAKUBAUSKAS M E, LEGATES D R, KASTENS J H. Crop Identification Using Harmonic Analysis of Time-series AVHRR NDVI Data[J]. Computers and Electronics in Agriculture, 2002, 37(1-3): 127-139. |
| [11] | LIANG Shouzhen, XING Qianguo, SHI Ping, et al. Harmonic Analysis on NDVI Time Series of Typical Land Covers in Shandong Province[J]. Chinese Journal of Ecology, 2011, 30(1): 59-65. (梁守真, 邢前国, 施平, 等. 山东省典型地表覆被NDVI时间序列谐波分析[J]. 生态学杂志, 2011, 30(1): 59-65.) |
| [12] | YANG Keming, XUE Zhaohui, JIA Taotao, et al. A Harmonic Analysis Model of Small Target Detection of Hyperspectral Imagery[J]. Acta Geodaetica et Cartographica Sinica, 2013, 42(1): 34-43. (杨可明, 薛朝辉, 贾涛涛, 等. 高光谱影像小目标谐波分析探测模型[J]. 测绘学报, 2013, 42(1): 34-43.) |
| [13] | LI Cunjun, LIU Liangyun, WANG Jihua, et al. Comparison of Two Methods of Fusing Remote Sensing Images with Fidelity of Spectral Information[J]. Journal of Image and Graphics, 2004, 9(11): 1376-1385. (李存军, 刘良云, 王纪华, 等. 两种高保真遥感影像融合方法比较[J]. 中国图象图形学报, 2004, 9(11): 1376-1385.) |
| [14] | YU Haiyang, YAN Bokun, GAN Fuping, et al. Hyperspectral Image Fusion by an Enhanced Gram Schmidt Spectral Transformation[J]. Geography and Geo-information Science, 2007, 23(5): 30-42. (于海洋, 闫柏琨, 甘甫平, 等. 基于Gram Schmidt变换的高光谱遥感图像改进融合方法[J]. 地理与地理信息科学, 2007, 23(5): 30-42.) |
| [15] | RAYNER J N. An Introduction to Spectral Analysis[M]. London: Pion Ltd, 1971: 15-21. |
| [16] | DAVIS J C. Statistics and Data Analysis in Geology[M]. 2nd ed. New York: John Wiley & Sons, 1986: 23-34. |
| [17] | HUANG Dengshan. Research of Pixel-level Remote sensing Image Fusion Method[D]. Changsha: Central South University, 2011: 18. (黄登山. 像素级遥感影像融合方法研究[D]. 长沙: 中南大学, 2011: 18.) |
| [18] | TAN Bingxiang, LI Zengyuan, CHEN Erxue, et al. Preprocessing of EO-1Hyperion Hyperspectral Data[J]. Remote Sensing Information, 2005(6): 36-41. (谭炳香, 李增元, 陈尔学, 等. EO-1 Hyperion高光谱数据的预处理[J]. 遥感信息, 2005(6): 36-41.) |
| [19] | CHEN Jianzhen, HE Chao, YUE Cairong. Atmospheric Correction of an Advance Land Imager (ALI) Image Based on the FLAASH Module[J]. Journal of Zhejiang A & F University, 2011, 28(4): 590-596. (陈建珍, 何超, 岳彩荣. 基于FLAASH模块的高级陆地成像仪图像的大气校正[J]. 浙江农林大学学报, 2011, 28(4): 590-596.) |
| [20] | CHANDER G, MARKHAM B L, HELDER D L. Summary of Current Radiometric Calibration Coefficients for Landsat MSS, TM, ETM+, and EO-1 ALI Sensors[J]. Remote Sensing of Environment, 2009, 113(5): 893-903. |
| [21] | MA Lingling, WANG Xinhong, TANG Lingli. A Highly Efficient Atmospheric Correction Method for HJ-1A/HSI and the Exploration on Its Application Capability[J]. Remote Sensing Technology and Application, 2010, 25(4): 525-531. (马灵玲, 王新鸿, 唐伶俐. HJ-1A高光谱数据高效大气校正及应用潜力初探[J]. 遥感技术与应用, 2010, 25(4): 525-531.) |
| [22] | ZHENG Sheng, ZHAO Xiang, ZHANG Hao, et al. Atmospheric Correction on CCD Data of HJ-1 Satellite and Analysis of Its Effect[J]. Journal of Remote Sensing, 2011, 15(4): 709-721. (郑盛, 赵祥, 张颢, 等. HJ-1卫星CCD数据的大气校正及其效果分析[J]. 遥感学报, 2011, 15(4): 709-721.) |