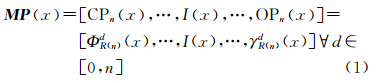2. 江苏省地理信息资源开发与利用协同创新中心,江苏 南京 210023;
3. 江苏省卫生统计信息中心,江苏 南京 210008
2. Jiangsu Center for Collaborative Innovation in Geographical Information Resource Development and Application, Nanjing 210023, China;
3. Center of Health Statistics and Information of Jiangsu Province, Nanjing 210008, China
1 引 言
高光谱遥感影像具有超高的光谱分辨率,对地物和物质类型的刻画更加精细,类别区分度更高。其数据的高维特性决定了传统的全色和多光谱分类难以直接运用于高光谱影像,势必要针对其数据特点研究适合高光谱影像的分类方法。目前高光谱影像分类主要有两种:一种是进行特征提取[1, 2]或选取[3]后再分类,将大部分信息集中在少数几个特征向量上,其本质和多光谱影像分类类似。此方法会损失许多重要的细节信息,特别是高光谱影像对地物精细表达这一优势没有很好体现。另一种是对原始高光谱影像直接分类[4],此方法主要存在以下问题:①容易引起Hughes现象;②分类过程中仅依赖标记样本数据,训练出的分类器容易过拟合;③需要大量标记样本,样本数通常是光谱维数的数倍甚至数十倍,而获取标记样本代价通常较高,相反未标记样本数量充足并易于获取,且蕴含了大量有用信息却没有得到充分运用,造成了数据资源的极大的浪费;④忽略了像元间的空间位置关系。
针对上述问题,本文结合自训练半监督学习技术[5, 6, 7, 8],根据高光谱遥感影像的特点,提出一种增量分类算法INC_SPEC_MPext。根据少量初始标记样本,发掘高光谱数据丰富而廉价的未标记样本所蕴含的信息,不断从中学习新的知识来改善分类器性能。将光谱和空间信息相结合,以支持向量机(SVM)[9, 10, 11, 12]作为基础分类器。
2 空间信息提取将高光谱影像光谱与空间信息联合[13, 14, 15, 16]参与分类可以消除光谱分类结果中的噪点(椒盐噪声)现象。文献[17, 18]分别用马尔可夫随机场(MRF)和Monte Carlo模型提取空间纹理信息,联合光谱信息优化分类。其缺点在于纹理信息提取算法的时间代价通常较高。与之相比,扩展形态学剖面信息提取具有较低时间和空间计算复杂度[19],更适合处理数据量和复杂程度较高的高光谱影像。具体的扩展形态学剖面信息提取过程如下:①利用主成分分析(PCA)提取影像若干主成分;②以每个主分量影像为基影像,用数学形态学方法提取开剖面和闭剖面,与基影像一起构成形态学剖面;③将所有主分量影像的形态学剖面进行矢量叠加,构成扩展的形态学剖面,即高光谱影像的空间信息。
式中,CP0(x)=OP0(x)=I(x);ФRd是用大小为d的结构元素e进行n次重构闭操作;γRd是用大小为d的结构元素e进行n次重构开操作。特征维度与变换次数n对应,每个像元经过一系列形态学变换,由一维扩展为2n+1维向量,包含了丰富的形态学信息。利用主成分分析(PCA)提取影像的q个主成分,对每个主分量影像PCq分别进行形态学剖面提取,组成扩展的形态学剖面[19],共q×(2n+1)维,即以半径为1,增量为3的圆形结构元为例,对两个主分量影像分别进行两次开剖面、闭剖面提取,最后组成扩展的形态学剖面如图 1所示。

|
| 图 1 高光谱影像两个主分量图像的扩展形态学剖面MPext (圆形结构元半径为1,增量为3,进行两次开闭操作) Fig. 1 Extended morphological profiles for two principle components images of hyperspectral image with twice opening and twice closing, and circular structuring element was used with radius increment 3(r=1,4 pixels) |
通过扩展形态学处理,获取了丰富的空间信息,可以对结构性的物质或物体进行区分,如桥梁和建筑物[19]。使用光谱信息可以对城区的非结构性物质加以区分,如植被和裸地。将空间与光谱信息结合可以优势互补,大大增加分类的有效信息。
3 基于光谱-空间信息的增量分类算法INC_SPEC_MPext算法分别从光谱和空间两个不同视角审视图像。利用少量初始标记样本,构建光谱分类模型Met和空间分类模型Mat,对未标记样本进行分类预测。由于光谱域、空间域蕴含的图像信息不同,两个分类模型对未标记样本的预测标记会有差异。通常情况下,两个分类模型预测结果一致的样本被正确分类的可能性更高。将二者预测结果一致的样本作为置信样本分别加入各自训练集中,这是融合光谱、空间信息的第一步。再用扩大的训练集重新训练两个分类模型,分别对剩余的未标记样本分类预测,如此迭代地执行此过程。不断增加训练集样本数量,并用扩大的训练集重复训练分类模型来对剩余未标记样本分类,直至两个分类模型再没有预测一致样本,迭代过程结束。再将光谱和空间信息进行矢量叠加融合,这是融合光谱、空间信息的第二步。将光谱、空间信息综合考虑,利用初始标记样本集和每次迭代过程中的新增置信样本一起作为训练集训练分类器,对空-谱融合后的高光谱影像进行分类。整个分类过程是增量迭代地进行,直至所有样本都获得类别标记,增量分类算法结束。算法具体描述如下。
(1)利用少量标记样本初始化标记训练集Dlt,利用Dlt训练初始光谱分类器Met和空间分类器Mat的参数,初始t=0。
(2)用分类器Met和Mat分别对未标记样本集Dut={xk|k=1,2,…,un;t=1,2,…,r}中的每一个样本进行分类预测,un为第t次迭代时的未标记样本个数。
(3)挑选Met和Mat预测一致的样本,组成集合Duct={xk′|ylet(xk′)=ylat(xk′);k′=1,2,…,un;t=1,2,…,r}。其中,ylet(xk′)和ylat(xk′)分别表示分类器Met和Mat对样本xk′预测的类别标记;将第t次迭代时两分类器预测一致样本集合Duct并入当前训练集Tt,得到Tt+1=Tt∪Duct,同时更新标记样本集和未标记样本集Dlt+1=Dlt∪Duct,Dut+1=Dut-Duct。
(4)使用训练集Tt+1重新训练分类器Met+1和Mat+1,若迭代次数达到最大次数r或集合Duct+1为空,则迭代过程结束,否则转到步骤(2)。
(5)将光谱和空间信息融合,将增量训练过程中两个分类器预测一致的样本集Duct+1及对应的类别标记Ylt+1,连同初始样本集Dl0一起作为训练样本,重新训练一个新的分类器,对融合后的特征集进行SVM分类。
算法中各符号含义如下:Dlt={xl1,xl2,…,xlm}表示第t次迭代时的标记样本集;Ylt={yl1,yl2,…,ylm}表示与标记样本集Dlt对应的标记集合;Dut={xu1,xu2,…,xun}表示第t次迭代时的未标记样本集;当前训练集Tt=Dlt-1∪{未标记样本集Dut-1中确定类别标记的样本};Duct表示第t次迭代时两个分类器预测一致的样本构成的集合。
算法共进行两次信息融合,一次是选择置信样本时,将光谱、空间信息分类结果一致的样本加入训练集;另一次是增量迭代过程结束后,对影像光谱、空间信息矢量叠加融合进行分类。算法借鉴了自训练分类的思想,并对其置信样本选取规则进行改进,摒弃按概率选取的策略,将分类模型Met和Mat预测一致的样本加入训练集,可以在一定程度上减少误标记样本的数量。另外,选取预测标记一致样本所增加的信息量要高于按概率选取所增加的信息量。
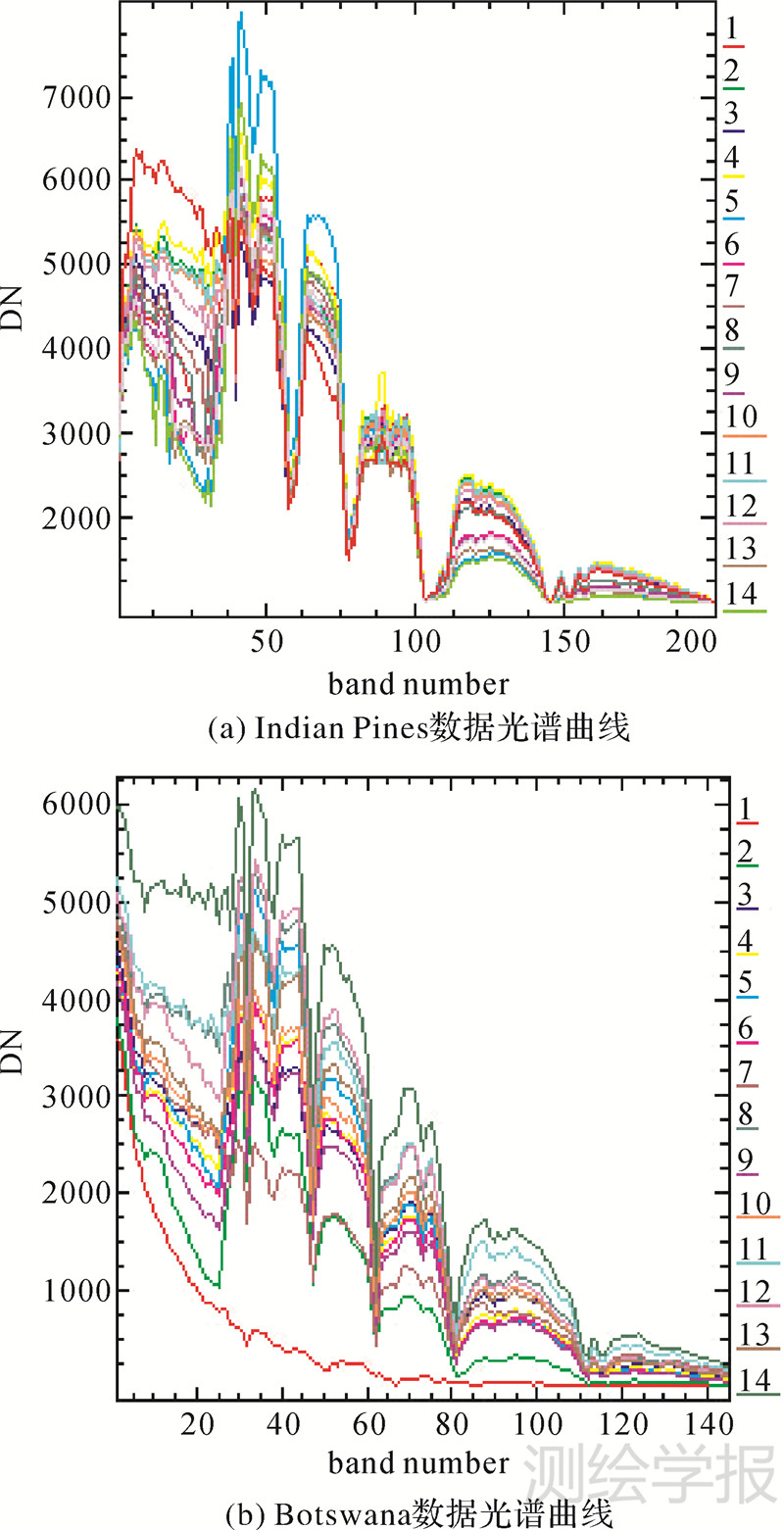
4 试验验证及精度评价试验选取不同传感器、不同地区地表覆盖类型的高光谱数据源AVIRIS Indian Pines和Hyperion EO-1 Botswana作为测试数据。两幅高光谱影像具有很好的代表性。Indian Pines数据具有较高的类间相似度,且裸地对处于生长早期的植被干扰严重,使Indian Pines数据分类较为复杂。Botswana数据一些类别光谱特征具有很好的可分性,如水体、河马草和裸沙,而有些类别则混合了不同类型的植被,如刺槐林地、刺槐灌木地、刺槐草原,类别间具有一定的重叠,如短豆木、混合豆木,导致了部分类别的类间相似度较高,相似的光谱特征和混合类的存在增大了Botswana数据的分类难度。两组数据集各类别平均光谱曲线如图 2所示。
|
| 图 2 Indian Pines和Botswana数据集各类别平均光谱曲线(类别编号分别与表2和表6相对应) Fig. 2 Average spectral signature for each class, for the two datasets(The class index corresponds to classes described in Tab. 2 and Tab. 6) |
由于支持向量机(SVM)[22]适合于处理高维数据,对大规模数据分类速度较快,故将SVM作为本次试验的基础分类器。采用高斯核函数,即kσ(xi,xj)=exp (-‖xi-xj‖2/2σ2),i=1,2,…,n,xi和xj是光谱向量。将INC_SPEC_MPext算法分别与基于光谱、空间信息以及光谱和空间信息直接融合的SVM分类作比对,验证增量分类算法的有效性。
4.1 Indian Pines数据试验验证及精度评价使用机载可见光/红外成像光谱仪(AVIRIS)1992年6月获取的美国印第安纳州西北部地区Indian Pines作为试验区域,地表覆盖类型混合了林地、农田、道路、房屋建筑等。标记样本分布不均衡,部分类别样本较少。各种农作物基本都处于生长初期,对地表的林冠覆盖程度只有5%,裸地和作物残渣对植被像元分类影响明显。以上原因导致数据集类间相似度非常高,分类难度大大增加。Indian Pines图像大小145像素×145像素,波长范围0.4~2.5 μm,220个波段,空间分辨率20 m,去除坏波段和水体吸收的波段,试验中使用200个波段。图 3(a)所示为Indian Pines数据灰度图像。图 3(b)是其对应的地面参考图,共有16种地物类别,10 249个样本。表 1是其主成分所占百分比,数据显示前3个主分量之和蕴含超过93%的方差信息。本试验针对前3个主分量提取扩展形态学剖面,使用圆形结构元素,初始半径是1,增量为3,对每个主分量进行3次开、闭操作,获得的扩展形态学剖面维数是3×(2×3+1)=21维。随机选择1000个数据作为初始训练样本,约占总样本数量的10%,各类别初始训练样本数和对应的测试样本数如表 2所示。

|
| 图 3 Indian Pines数据及地面真值 Fig. 3 Indian Pines data and the ground truth |
| 主分量所占总方差 百分比/(%) |
主分量累积所占总方差 百分比/(%) |
|
| λ 1 | 68.49 | 68.49 |
| λ 2 | 23.53 | 92.03 |
| λ 3 | 1.50 | 93.52 |
| 序号 | 类别 | 样本 | SPEC/(%) 200维 |
MP
ext/(%) 21维 |
SPEC+MP
ext/(%) 221维 |
INC_SPEC_MP
ext/(%) 221维 |
|
| 训练样本 | 测试样本 | ||||||
| 1 | 苜蓿 | 5 | 41 | 10.87 | 82.61 | 10.87 | 19.57 |
| 2 | 玉米未耕地 | 140 | 1288 | 82.42 | 72.97 | 83.33 | 83.82 |
| 3 | 玉米略耕地 | 81 | 749 | 68.07 | 87.11 | 79.16 | 86.39 |
| 4 | 玉米 | 24 | 213 | 62.45 | 72.15 | 64.98 | 75.53 |
| 5 | 草地-牧场 | 48 | 435 | 90.06 | 89.03 | 92.13 | 91.30 |
| 6 | 草地-林地 | 72 | 658 | 98.22 | 97.12 | 99.18 | 99.32 |
| 7 | 收割后草地-牧场 | 3 | 25 | 50.00 | 67.86 | 50.00 | 57.14 |
| 8 | 干草堆 | 47 | 431 | 99.58 | 98.54 | 99.79 | 100.00 |
| 9 | 燕麦 | 2 | 18 | 10.00 | 10.00 | 10.00 | 15.00 |
| 10 | 大豆未耕地 | 95 | 877 | 75.72 | 85.49 | 77.78 | 84.98 |
| 11 | 大豆略耕地 | 232 | 2223 | 84.15 | 91.20 | 86.64 | 92.42 |
| 12 | 收割后的大豆 | 58 | 535 | 71.84 | 56.32 | 76.90 | 74.87 |
| 13 | 小麦 | 21 | 184 | 99.51 | 93.17 | 99.02 | 99.51 |
| 14 | 林地 | 124 | 1141 | 96.05 | 95.57 | 97.39 | 98.10 |
| 15 | 建筑物-草地-乔木-汽车 | 38 | 348 | 62.95 | 80.57 | 68.13 | 72.28 |
| 16 | 石头-钢制品-塔 | 10 | 83 | 89.25 | 74.19 | 93.55 | 97.85 |
| OA/(%) | 样本总数 | 83.05 | 85.75 | 85.78 | 88.97 | ||
| κ/(%) | 1000 | 9249 | 80.57 | 83.66 | 83.73 | 87.37 | |
为了测试本算法的分类结果,分4组试验对Indian Pines数据分类结果进行比对,分别是:①使用原始光谱信息进行SVM分类;②使用提取的扩展形态学剖面(空间信息)进行SVM分类;③将光谱和空间信息矢量叠加融合进行SVM分类;④将光谱和空间信息融合后进行增量分类。其中,①和②分别使用光谱、空间信息作为SVM的输入,③和④用光谱空间融合信息作为SVM的输入,参数C和σ均由十折交叉验证获取。4组试验所用的训练样本完全相同,且通过随机选取策略获得,剩余样本全部作为测试样本。试验采用混淆矩阵进行分类结果精度评价,INC_SPEC_MPext算法对应的混淆矩阵如表 3所示。
| 序号 | 类别 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 |
| 1 | 苜蓿 | 9 | 0 | 0 | 0 | 1 | 0 | 0 | 35 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 |
| 2 | 玉米未耕地 | 0 | 1197 | 10 | 6 | 1 | 5 | 0 | 0 | 0 | 37 | 157 | 15 | 0 | 0 | 0 | 0 |
| 3 | 玉米略耕地 | 0 | 18 | 717 | 15 | 0 | 0 | 0 | 0 | 0 | 3 | 65 | 12 | 0 | 0 | 0 | 0 |
| 4 | 玉米 | 0 | 14 | 25 | 179 | 0 | 1 | 0 | 0 | 0 | 2 | 8 | 8 | 0 | 0 | 0 | 0 |
| 5 | 草地-牧场 | 0 | 0 | 0 | 3 | 441 | 1 | 0 | 3 | 0 | 3 | 19 | 4 | 0 | 9 | 0 | 0 |
| 6 | 草地-林地 | 0 | 0 | 0 | 0 | 0 | 725 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 3 | 2 | 0 |
| 7 | 收割后的草地-牧场 | 0 | 0 | 0 | 0 | 2 | 0 | 16 | 5 | 0 | 0 | 5 | 0 | 0 | 0 | 0 | 0 |
| 8 | 干草堆 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 478 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 9 | 燕麦 | 0 | 0 | 0 | 0 | 0 | 7 | 0 | 0 | 3 | 0 | 0 | 0 | 3 | 0 | 7 | 0 |
| 10 | 大豆未耕地 | 0 | 21 | 6 | 0 | 0 | 4 | 0 | 0 | 0 | 826 | 99 | 16 | 0 | 0 | 0 | 0 |
| 11 | 大豆略耕地 | 0 | 67 | 25 | 6 | 2 | 14 | 0 | 0 | 0 | 61 | 2269 | 11 | 0 | 0 | 0 | 0 |
| 12 | 收割后的大豆 | 0 | 55 | 18 | 14 | 1 | 1 | 0 | 0 | 0 | 4 | 54 | 444 | 0 | 0 | 1 | 1 |
| 13 | 小麦 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 204 | 0 | 0 | 0 |
| 14 | 林地 | 0 | 0 | 0 | 0 | 0 | 2 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 1241 | 21 | 0 |
| 15 | 建筑物-草坪-乔木-汽车 | 0 | 0 | 0 | 0 | 7 | 24 | 0 | 0 | 0 | 2 | 7 | 0 | 7 | 60 | 279 | 0 |
| 16 | 石头-钢制品-塔 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 91 |
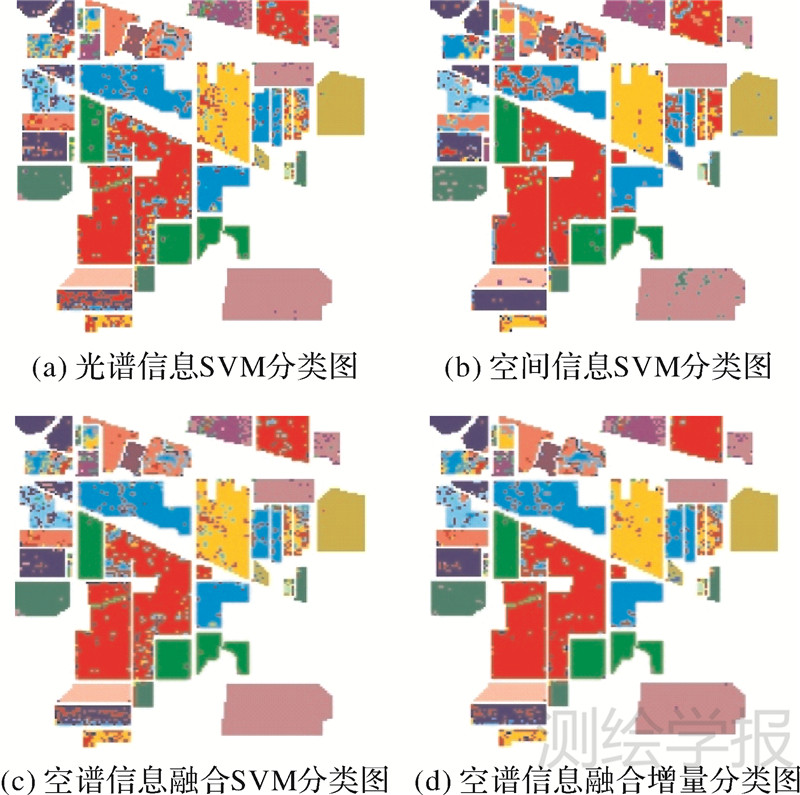
表 2给出Indian Pines数据不同分类算法对应的总体分类精度、各类别平均分类精度(OA)及Kappa系数(κ)。Indian pines试验数据具有一定的空间分布特征,提取的扩展形态学剖面能够较好地反映样本空间信息。因此,基于MPext的Indian Pines数据分类精度要优于光谱分类。将光谱和空间信息直接融合分类比光谱分类精度提高了2.73%,与MPext相比只提高了0.03%,说明对于Indian Pines数据,直接融合空-谱信息的分类效果优于光谱、空间单独分类,但对空间信息分类精度提高有限。本文算法INC_SPEC_MPext融合了光谱和空间信息,与光谱、空间分类结果相比,总体精度(OA)分别提高了5.92%、3.22%,Kappa系数(κ)分别提高了6.82%、3.73%。同时,INC_SPEC_MPext对自训练的置信样本选取规则进行改进,不断优选Met和Mat预测标记一致的样本参与分类器训练,增加了更多有用信息。与光谱和空间信息直接融合分类相比,INC_SPEC_MPext算法总体分类精度(OA)和Kappa系数(κ)分别提高了3.19%和3.66%。算法只需3次迭代即可选出所有Met和Mat分类预测标记一致的样本。当结构元半径取值为1,步长取值为3时,每次迭代Met和Mat预测一致样本个数及对应的光谱、空间分类精度如表 4所示。前两次迭代过程中,Met和Mat分别有6979、818个预测标记一致的样本,迭代至第3次时Met和Mat已没有预测一致的样本,此时将光谱和空间信息进行矢量叠加融合分类。从表 4可以看出,INC_SPEC_MPext算法的分类精度随着训练集中样本数量的增加而不断提高,进一步验证了增量分类算法的有效性。各算法对应的分类图如图 4所示。
| 迭代次数t | Indian Pines | Botswana | ||||
| 一致样本个数(合并) | SPEC/(%) | MPext/(%) | 一致样本个数(合并) | SPEC/(%) | MPext/(%) | |
| 1 | 6979 | 83.05 | 85.75 | 2430 | 92.15 | 88.27 |
| 2 | 818 | 86.62 | 87.87 | 156 | 94.64 | 90.58 |
| 3 | # | 87.55 | 88.23 | # | 95.10 | 91.01 |
|
| 图 4 Indian Pines 数据不同算法对应的分类结果图 Fig. 4 Classification maps for different algorithms of Indian Pines data |
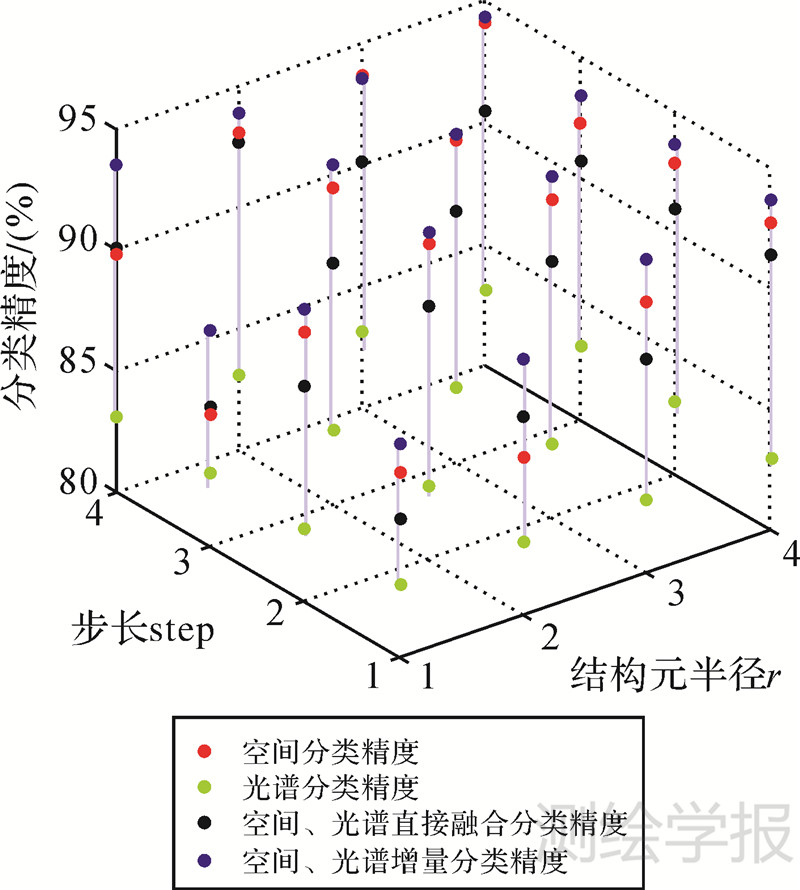
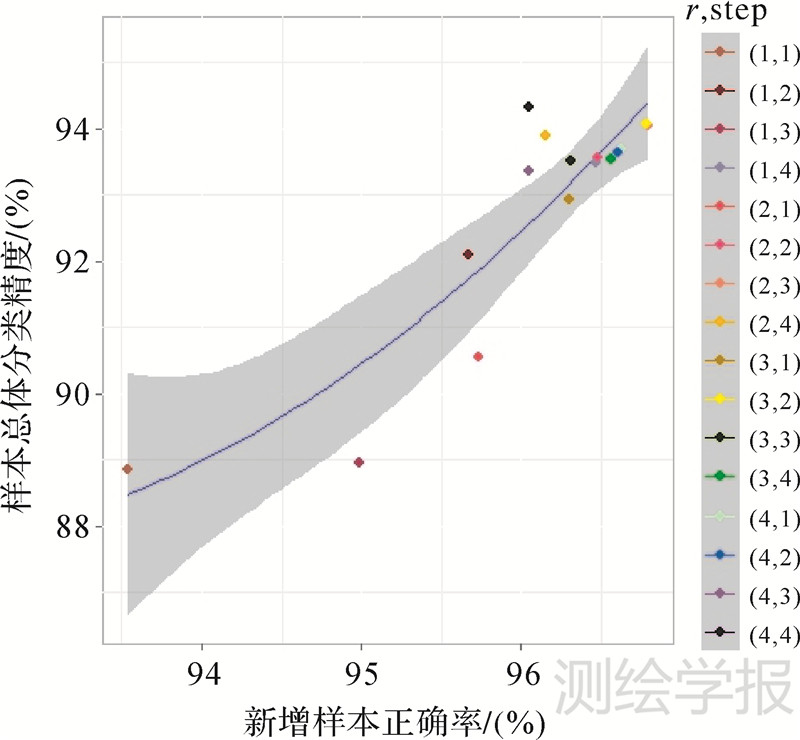
另外,为了说明提取扩展形态学剖面数据时,结构元素参数对本文算法精度的影响,采用不同结构元素半径和增量大小对Indian Pines数据集进行测试。结构元素半径取值范围{1,2,3,4},增量大小取值范围{1,2,3,4},共计16组不同参数组合进行测试。图 5为不同算法对应的总体分类精度随两个参数变化的三维散点图。从图 5可以看出无论哪种参数组合方式,本文提出的INC_SPEC_MPext算法都优于光谱、空间以及光谱和空间直接融合分类,能够获得更好的分类效果。图 6为不同参数组合情况下新增样本的正确率及其与INC_SPEC_MPext算法总体分类精度的关系图。虽然步长和结构元半径取值不同会对分类精度具有一定的影响,但从图中可以看出,INC_SPEC_MPext算法总体分类精度与新增样本正确率呈正相关,即新增标记样本正确率越高,则分类效果越好。同时,总体分类精度受新增训练样本的数量和知识增益的影响,会随着新增标记样本正确率不同呈现差异性。
|
| 图 5 Indian Pines数据集不同分类算法对应的总体分类精度随结构元素参数变化散点图 Fig. 5 The scatter plot for global classification accuracy under different SE parameters and different algorithms of Indian Pines data set |
|
| 图 6 Indian Pines数据集不同步长和结构元半径组合时新增样本的正确率及其与INC_SPEC_MPext 算法总体分类精度关系图 Fig. 6 The plot for overall classification accuracy of INC_SPEC_MPext algorithm corresponds to the correctness of incremental samples under different SE parameters of Indian Pines data set |
第2个试验数据是2001年5月由Hyperion EO-1传感器获取的Okavango三角洲地区高光谱影像。试验所用样本呈现了三角洲影像边缘地区季节性沼泽、偶发性沼泽、枯林地的地表覆盖类型,主要反映洪水对研究区植被的影响。其中类别3、4都是季节性淹没的泛滥平原草地,而在其他的水文周期则呈现不同的地表覆盖类型。类别9、10、11表示刺槐林地、灌丛带和草原的不同类型混合,分别以面积占优的地物命名地类。影像大小610像素×340像素,空间分辨率30 m,光谱范围0.4~2.5 μm,光谱分辨率0.01 μm,242个波段。去除坏波段和低信噪比波段后,共145个光谱波段可用。图 7(a)所示为Botswana数据灰度图像。图 7(b)是其对应的地面参考图,共有14种地物类别,3248个样本。表 5是其主成分所占百分比,数据显示前两个主分量之和蕴含超过99%的方差信息。本试验针对前两个主分量提取扩展形态学剖面。试验中采用圆形结构元素,初始半径是1,增量为3,对每个主分量进行3次开、闭操作,扩展形态学剖面维数是2×(2×3+1)=14维。随机选择300个数据作为初始训练样本,约占总样本数量的9%,各类别初始训练样本数和对应的测试样本数如表 6所示。

|
| 图 7 Botswana数据及地面真值 Fig. 7 Botswana data and the ground truth |
| 主分量所占总方差 | 主分量累积所占总方差 | |
| λ 1 | 98.70 | 98.70 |
| λ 2 | 0.82 | 99.51 |
| 序号 | 类别 | 样本 | SPEC/(%) 145维 |
SPEC/(%) 14维 |
SPEC+MP
ext/(%) 159维 |
INC_SPEC_MP
ext/(%) 159维 |
|
| 训练样本 | 测试样本 | ||||||
| 1 | 水体 | 25 | 245 | 100.00 | 100.00 | 100.00 | 100.00 |
| 2 | 河马草 | 9 | 92 | 93.07 | 69.31 | 92.08 | 93.07 |
| 3 | 泛滥草原1 | 23 | 228 | 97.61 | 92.03 | 99.60 | 99.60 |
| 4 | 泛滥草原2 | 20 | 195 | 80.93 | 81.40 | 89.77 | 93.02 |
| 5 | 芦苇1 | 25 | 244 | 92.19 | 93.31 | 99.26 | 97.40 |
| 6 | 河岸 | 25 | 244 | 76.58 | 73.61 | 75.84 | 88.48 |
| 7 | 火迹2 | 24 | 235 | 98.07 | 98.84 | 98.07 | 98.84 |
| 8 | 内岛 | 19 | 184 | 95.57 | 64.53 | 82.76 | 72.91 |
| 9 | 刺槐林地 | 29 | 285 | 89.49 | 79.94 | 86.94 | 96.82 |
| 10 | 刺槐灌木地 | 23 | 225 | 91.94 | 95.56 | 97.58 | 100.00 |
| 11 | 刺槐草原 | 28 | 277 | 95.74 | 97.70 | 95.41 | 98.36 |
| 12 | 短豆木 | 16 | 165 | 95.58 | 96.69 | 98.34 | 98.34 |
| 13 | 混合豆木 | 25 | 243 | 89.93 | 85.45 | 94.03 | 92.16 |
| 14 | 裸沙 | 9 | 86 | 97.89 | 100.00 | 98.96 | 100.00 |
| OA/(%) | 样本总数 | 92.15 | 88.27 | 93.26 | 95.14 | ||
| κ/(%) | 300 | 2948 | 94.96 | 90.89 | 92.70 | 94.73 | |
同样分4组试验对Botswana数据分类结果进行比对,分别是:①使用原始光谱信息进行SVM分类;②使用提取的扩展形态学剖面(空间信息)进行SVM分类;③将光谱和空间信息矢量叠加融合进行SVM分类;④将光谱和空间信息融合进行增量分类。其中,①和②分别使用光谱、空间信息作为SVM的输入,③和④使用光谱空间融合信息作为SVM的输入,参数C和σ均由十折交叉验证获取。4组试验所用的训练样本完全相同,且通过随机选取策略获得,剩余样本全部作为测试样本。试验采用混淆矩阵进行分类结果精度评价,INC_SPEC_MPext算法对应混淆矩阵如表 7所示。
| 序号 | 类别 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 |
| 1 | 水体 | 270 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 2 | 河马草 | 0 | 94 | 0 | 0 | 7 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 3 | 泛滥草原1 | 0 | 0 | 250 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 4 | 泛滥草原2 | 0 | 0 | 0 | 200 | 8 | 7 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 5 | 芦苇1 | 0 | 1 | 0 | 3 | 262 | 2 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 |
| 6 | 河岸 | 0 | 0 | 0 | 0 | 7 | 238 | 0 | 0 | 20 | 0 | 0 | 1 | 3 | 0 |
| 7 | 火迹2 | 0 | 0 | 0 | 1 | 0 | 2 | 256 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 8 | 内岛 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 148 | 0 | 0 | 2 | 52 | 0 | 0 |
| 9 | 刺槐林地 | 0 | 0 | 0 | 0 | 0 | 10 | 0 | 0 | 304 | 0 | 0 | 0 | 0 | 0 |
| 10 | 刺槐灌木地 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 248 | 0 | 0 | 0 | 0 |
| 11 | 刺槐草原 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 5 | 300 | 0 | 0 | 0 |
| 12 | 短豆木 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 178 | 3 | 0 |
| 13 | 混合豆木 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 16 | 0 | 4 | 247 | 0 |
| 14 | 裸沙 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 95 |
表 6给出Botswana数据不同分类算法对应的总体分类精度、各类别平均分类精度及Kappa系数(κ)。由于试验采集样本空间不连续,因此提取的空间信息有限,导致空间分类精度不如光谱分类,这是由试验数据分布情况决定的。光谱和空间信息直接融合分类比光谱分类精度提高了1.11%,比MPext提高了4.99%。因此,光谱和空间信息直接融合的分类效果优于光谱、空间单独分类。本文算法INC_SPEC_MPext通过融合光谱和空间信息,比光谱、空间单独分类的总体精度分别提高了2.99%和6.87%。同时,INC_SPEC_MPext算法对自训练的置信样本选取规则进行改进,不断优选Met和Mat预测标记一致的样本参与分类器训练,增加了更多有用信息。与光谱和空间信息直接融合分类相比,INC_SPEC_MPext算法总体分类精度(OA)和Kappa系数(κ)分别提高了1.88%和2.03%。算法只需3次迭代即可选出所有Met和Mat分类预测标记一致的样本。当结构元半径取值为1,步长取值为3时,每次迭代Met和Mat预测一致样本个数及对应的光谱、空间分类精度如表 4所示。前两次迭代过程中,Met和Mat分别共有2430、156个预测标记一致的样本。迭代至第3次时Met和Mat已没有预测一致的样本,此时将光谱和空间信息进行矢量叠加融合分类。从表 4可以看出,INC_SPEC_MPext算法总体分类精度随着训练集中样本数量的增加而不断提高,进一步验证了增量分类算法的有效性。
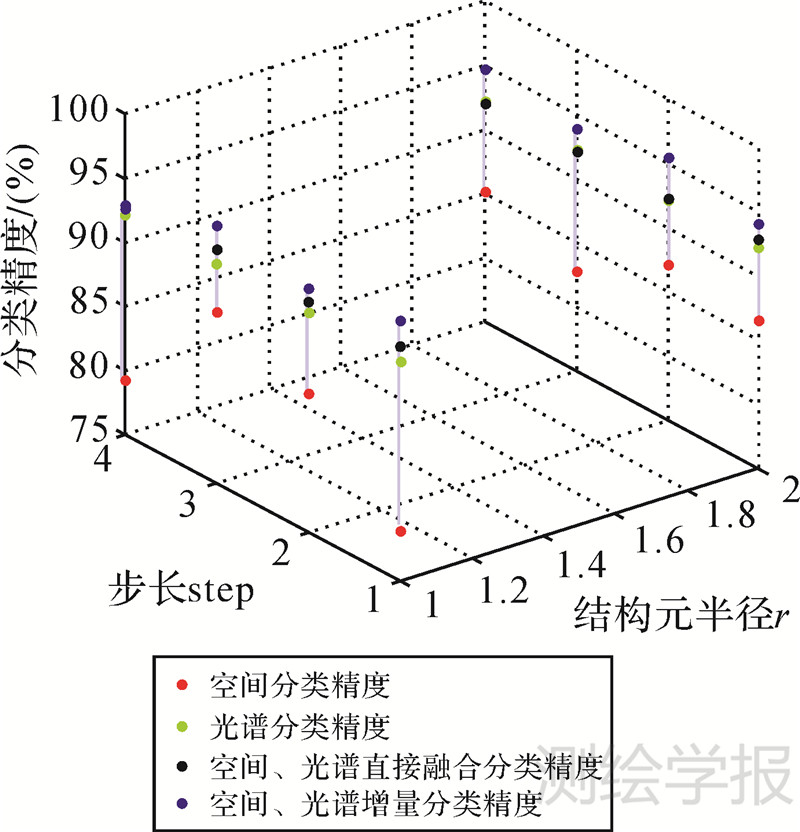
另外,为了说明提取扩展形态学剖面数据时,结构元素参数对本文算法精度的影响,试验采用不同结构元素半径和增量大小对Botswana数据集进行测试。结构元素半径取值范围{1,2},增量大小取值范围{1,2,3,4},共计8组不同参数组合。图 8为不同算法对应的总体分类精度随两个参数变化的三维散点图。从图 8可以看出无论哪种参数组合方式,本文提出的INC_SPEC_MPext算法都优于光谱、空间以及光谱和空间直接融合分类,能够获得更好的分类效果。
|
| 图 8 Botswana数据集不同分类算法总体分类精度随结构元素参数变化散点图 Fig. 8 The scatter plot for global classification accuracy under different SE parameters and different algorithms of Botswana data set |
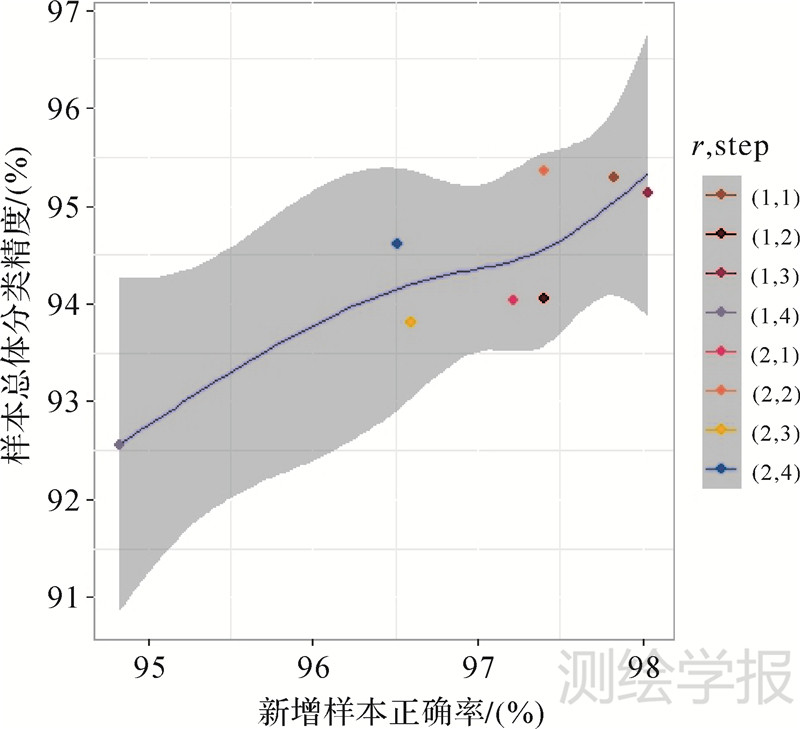
图 9为不同参数组合情况下新增样本的正确率及其与INC_SPEC_MPext算法总体分类精度的关系图。虽然步长和结构元半径取值不同会对分类精度具有一定的影响,但从图中可以看出,INC_SPEC_MPext算法总体分类精度与新增样本正确率呈正相关,即新增标记样本正确率越高,则分类效果越好。同时,总体分类精度受新增训练样本的数量和知识增益的影响,会随着新增标记样本正确率不同呈现差异性。
|
| 图 9 Botswana数据集不同步长和结构元半径组合时新增样本的正确率及其与INC_SPEC_MPext算法总体分类精度关系图 Fig. 9 The plot for overall classification accuracy of INC_SPEC_MPext algorithm corresponds to the correctness of incremental samples under different SE parameters of Botswana data set |
本文分两次试验分别针对不同地表覆盖类型的高光谱影像进行了算法测试。Indian Pines数据空间分布特征明显,提取的MPext信息分类精度优于光谱分类。而Botswana影像由于试验样本采样不连续,导致空间分布特征没有很好地保留,故提取的MPext空间信息分类精度不如光谱分类。针对这两种具有代表性的数据试验结果可以看出,与基于光谱、空间信息以及光谱和空间信息直接融合的分类方法相比,INC_SPEC_MPext算法在标记样本数量有限条件下,通过最大限度利用未标记样本蕴含的知识,不断优化分类器学习能力,可以获得更好的分类效果。
5 结 论针对高光谱遥感影像标记样本获取成本高的问题,本文提出了高光谱遥感影像增量分类算法INC_SPEC_MPext,旨在充分利用大量未标记样本所蕴含的知识的同时,以获得更好的分类性能。与基于光谱分类相比,融合高光谱遥感影像的光谱和空间结构信息,使待分类高光谱数据的信息更加丰富,可以在一定程度上减轻同物异谱和异物同谱对分类的影响。同时,改进了传统的自训练算法,重新定义增量迭代过程中的置信样本选取规则,将两个分类模型预测一致的样本加入训练集,不断优化分类器。修改后的规则可以使分类器获取更多的知识,选取的样本置信度更高。试验结果表明,对于不同地表覆盖类型的高光谱影像,当标记样本数量不充足时,INC_SPEC_MPext算法将大量高置信度、高信息量的样本加入训练集,只需几次迭代即可收敛。算法在降低分类成本的同时,总体分类精度(OA)和Kappa系数(κ)都有不同程度提高。同时,对源于自训练算法本身的未标记样本误分现象,本算法虽然降低了误标记样本的数量,但并没有将其完全消除。后续的研究需要对此作进一步合理的分析、研究和试验,将误标记样本的数量控制在最小范围。
| [1] | KUO B C, LANDGREBE D A. A Robust Classification Procedure Based on Mixture Classifiers and Nonparametric Weighted Feature Extraction[J]. IEEE Transactions on Geoscience and Remote Sensing, 2002, 40(11): 2486-2494. |
| [2] | LEE C, LANDGREBE D A. Feature Extraction Based on Decision Boundaries[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 1993, 15(4): 388-400. |
| [3] | LIU Chunhong, ZHAO Chunhui, ZHANG Lingyan. A New Method of Hyperspectral Remote Sensing Image Dimensional Reduction[J]. Journal of Image and Graphics, 2005, 10(2): 218-222. (刘春红, 赵春晖, 张凌雁. 一种新的高光谱遥感图像降维方法[J]. 中国图象图形学报, 2005, 10(2): 218-222.) |
| [4] | LUO Jiancheng, ZHOU Chenghu, LIANG Yi, et al. Support Vector Machine for Spatial Feature Extraction and Classification of Remotely Sensed Imagery[J]. Journal of Remote Sensing, 2002, 6(1): 50-55. (骆剑承, 周成虎, 梁怡, 等. 支撑向量机及其遥感影像空间特征提取和分类的应用研究[J].遥感学报, 2002, 6(1): 50-55.) |
| [5] | WANG Junshu, JIANG Nan, ZHANG Guoming, et al. Semi-supervised Classification Algorithm for Hyperspectral Remote Sensing Image Based on DE-self-training[J]. Transactions of the Chinese Society for Agricultural Machinery, 2015, 46(5): 239-244. (王俊淑, 江南, 张国明, 等. 高光谱遥感图像DE-self-training半监督分类算法[J]. 农业机械学报, 2015, 46(5): 239-244.) |
| [6] | ZHOU Zhihua, ZHAN Dechuan, YANG Qiang. Semi-supervised Learning with Very Few Labeled Training Examples[C]//Proceedings of the National Conference on Artificial Intelligence. Cambridge, MA London: [s.n.], 2007, 22(1): 675-680. |
| [7] | CHAWLA N V, KARAKOULAS G. Learning from Labeled and Unlabeled Data: An Empirical Study across Techniques and Domains[J]. Journal of Artificial Intelligence Research, 2005, 23(1): 331-366. |
| [8] | LI Yuanqing, GUAN Cuntai, LI Huiqi, et al. A Self-training Semi-supervised SVM Algorithm and Its Application in an EEG-based Brain Computer Interface Speller System[J]. Pattern Recognition Letters, 2008, 29(9): 1285-1294. |
| [9] | TAN Kun, DU Peijun. Wavelet Support Vector Machines Based on Reproducing Kernel Hilbert Space for Hyperspectral Remote Sensing Image Classification[J]. Acta Geodaetica et Cartographica Sinica, 2011, 40(2): 142-147. (谭琨, 杜培军. 基于再生核Hilbert空间的小波核函数支持向量机的高光谱遥感影像分类[J]. 测绘学报, 2011, 40(2): 142-147.) |
| [10] | MELGANI F, BRUZZONE L. Classifcation of Hyperspectral Remote Sensing Images with Support Vector Machines[J]. IEEE Transactions on Geoscience and Remote Sensing, 2004, 42(8): 1778-1790. |
| [11] | MANTHIRA MOORTHI S, MISRA I, KAUR R, et al. Kernel Based Learning Approach for Satellite Image Classification Using Support Vector Machine[C]//IEEE Recent Advances in Intelligent Computational Systems (RAICS). Trivandrum: IEEE, 2011: 107-110. |
| [12] | DELL’ACQUA F, GAMBA P, FERRARI A, et al. Exploiting Spectral and Spatial Information in Hyperspectral Urban Data with High Resolution[J]. IEEE Geoscience and Remote Sensing Letters, 2004, 1(4): 322-326. |
| [13] | LIANG Liang, YANG Minhua, LI Yingfang. Hyperspectral Remote Sensing Image Classification Based on ICA and SVM Algorithm[J]. Spectroscopy and Spectral Analysis, 2010, 30(10): 2724-2728. (梁亮, 杨敏华, 李英芳. 基于ICA与SVM算法的高光谱遥感影像分类[J]. 光谱学与光谱分析, 2010, 30(10): 2724-2728.) |
| [14] | WU Jian. PENG Daoli. Vegetation Classification Technology of Hyperspectral Remote Sensing Based on Spatial Information[J]. Transactions of the Chinese Society of Agricultural Engineering, 2012, 28(5): 150-153. (吴见, 彭道黎. 基于空间信息的高光谱遥感植被分类技术[J]. 农业工程学报, 2012, 28(5): 150-153.) |
| [15] | GAO Hengzhen, WAN Jianwei, WANG Libao, et al. Research on Classification Technique for Hyperspectral Imagery Based on Spectral-spatial Composite Kernels[J]. Signal Processing, 2011, 27(5): 648-652. (高恒振, 万建伟, 王力宝, 等. 基于谱域-空域组合核函数的高光谱图像分类技术研究[J].信号处理, 2011, 27(5): 648-652.) |
| [16] | CHEN Shanjing, HU Yihua, SHI Liang, et al. Classification of Hyperspectral Imagery Based on Ant Colony Compositely Optimizing SVM in Spatial and Spectral Features[J]. Spectroscopy and Spectral Analysis, 2013, 33(8): 2192-2197. (陈善静, 胡以华, 石亮, 等. 空-谱二维蚁群组合优化SVM 的高光谱图像分类[J]. 光谱学与光谱分析, 2013, 33(8): 2192-2197.) |
| [17] | POGGI G, SCARPA G, ZERUBIA J B. Supervised Segmentation of Remote Sensing Images Based on a Tree-structure MRF Model[J]. IEEE Transactions on Geoscience and Remote Sensing, 2005, 43(8): 1901-1911. |
| [18] | JACKSON Q, LANDGREBE D A. Adaptive Bayesian Contextual Classification Based on Markov Random Fields[J]. IEEE Transactions on Geoscience and Remote Sensing, 2002, 40(11): 2454-2463. |
| [19] | FAUVEL M, BENEDIKTSSON J A, CHANUSSOT J, et al. Spectral and Spatial Classification of Hyperspectral Data Using SVMs and Morphological Profiles[J]. IEEE Transactions on Geoscience and Remote Sensing, 2008, 46(11): 3804-3814. |
| [20] | CRESPO J, SERRA J, SCHAFER R W. Theoretical Aspects of Morphological Filters by Reconstruction[J], Signal Processing, 1995, 47(2): 201-225. |
| [21] | FAUVEL M, TARABALKA Y, BENEDIKTSSON J A, et al. Advances in Spectral-spatial Classification of Hyperspectral Images[J]. Proceedings of the IEEE, 2013, 101(3): 652-675. |
| [22] | CHANG C C, LIN C J. LIBSVM: A Library for Support Vector Machines[J]. ACM Transactions on Intelligent Systems and Technology (TIST), 2011, 2(3): 27. |