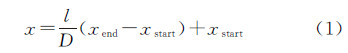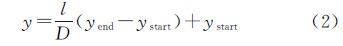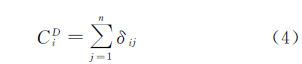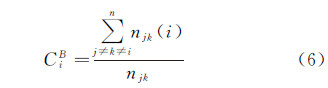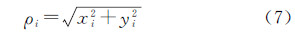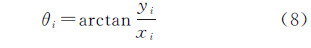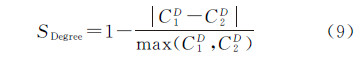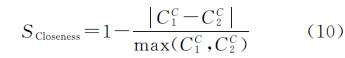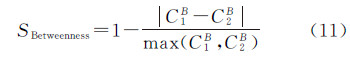1 引 言
空间数据作为地球空间信息的基础越来越受到各行各业的重视和关注。不同单位对同一地区采集生产了大量数据,并各自建立了相应的数据库,如何将这些多源数据进行有效集成与融合,以达到数据共享、优势互补的目的,成为当前GIS需要解决的问题之一[1]。与此同时,随着基础空间数据库建库工作的逐渐完成,数据库维护工作的重点已经转向空间数据更新[2, 3],如何准确、及时、快速地更新数据,以满足空间数据现势性的要求,则是GIS面临的又一突出问题。无论是空间数据集成与融合还是空间数据更新,都需要解决同名实体匹配这项关键技术。同名实体是指在两个或两个以上不同数据源中反映现实世界同一地物或地物集的空间实体。受制图误差、不同应用目的以及制图综合等因素的影响,不同数据源中的同名实体通常都存在着差异[4]。同名实体匹配就是通过分析空间实体的差异和相似性识别出不同数据来源中表达现实世界同一地物或地物集的过程[5]。同名实体间匹配关系准确、快速地建立是后续数据集成与融合以及数据更新的基础。
随着近年来我国经济建设的快速发展,城市居民地要素变化周期越来越短,其轮廓和结构也发生着巨大的变化[6]。在大比例尺城市地图中,面状居民地要素往往占有较大的比例,建立多源面状居民地之间正确的匹配关系是其集成与融合的前提和基础。当前面状居民地匹配方法主要有以下4种:①利用面积重叠率或面要素缓冲区面积重叠率进行匹配,该方法以面要素或面要素缓冲区之间的面积重叠程度作为匹配依据,重叠度越高,则匹配的可能性就越大,该方法简单易行,是面要素匹配的常用方法[7, 8, 9];②利用面要素轮廓形状相似性进行匹配,该方法主要利用形状描述函数来比较面要素轮廓形状的相似性进行匹配,其中常用的形状描述函数有傅里叶描述子、正切形调函数及矩描述子等[10, 11, 12];③利用降维技术进行匹配,该方法首先提取面要素的骨架线,从而将二维面要素匹配问题转换为一维线要素匹配问题,其优点是能够降低面要素匹配过程中的复杂性和不确定性[13, 14];④利用面要素之间空间方向相似性进行匹配,该方法通常用东、南、西、北等定性方位关系描述空间方向进而通过比较方向相似性来匹配,其优点是能够一定程度削弱位置差异造成的影响[15, 16]。上述面要素匹配方法极大地推动了空间数据匹配及更新技术的发展。与此同时,在匹配研究过程中发现:方法①—③对存在较大几何位置偏差或整体位移的面要素数据进行匹配时,可能会产生较多无匹配或误匹配结果;方法④通过空间方向相似性进行匹配在一定程度上能够削弱几何位置偏差造成的影响,但无论是4方位模型还是8方位模型在描述方向关系时都略显粗略,对一些几何位置偏差较大并且方向关系复杂的数据可能仍不能得到较好的匹配效果。通过对上述面要素匹配方法的分析可得:当多源居民地数据间存在较大几何位置偏差时,会增加匹配难度并可能在一定程度上影响匹配正确率。本文提出一种利用空白区域骨架线网眼进行面状居民地匹配的方法,将居民地匹配转换为骨架线网眼匹配,通过构建骨架线网眼对偶图以及对骨架线网眼进行极化变换,增加匹配过程中的定量拓扑约束以及相对位置约束,从而较好地解决了几何位置偏差较大的居民地数据间的匹配问题。
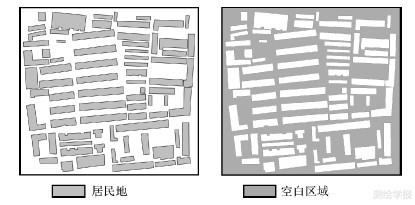
2 空白区域骨架线网眼构建 2.1 空白区域概述本文研究对象为大比例尺城市面状居民地(排除其他要素),空白区域是指除面状居民地外地图幅面内所有区域,如图 1所示。空白区域是一类特殊的面状要素,其具有范围大、孔洞多的特点,并且与面状居民地互补构成完整的地图幅面。
|
| 图 1 空白区域示意图 Fig. 1 Sketch map of blank region |
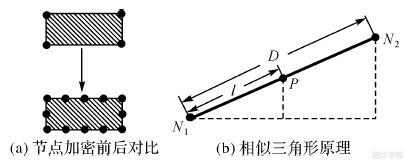
为了提取满足匹配要求的空白区域骨架线,利用约束Delaunay三角网法进行空白区域骨架线的提取[17],具体步骤为:①确定居民地数据边界,如图 2所示;②加密居民地节点,面状居民地一般只在其重要形态特征处具有节点,居民地数据中节点较少,为了构建满足后续骨架线提取要求的约束Delaunay三角网,在构网前需加密居民地节点(图 3(a))。在两个原有节点之间利用相似三角形原理计算加密节点坐标,设图 3(b)中加密弧段首节点N1坐标为(xstart,ystart),末节点N2坐标为(xend,yend),加密节点P坐标为(x,y),则根据相似三角形原理,可得
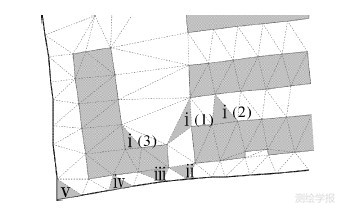
式中,l为加密步长(步长设定以能正确构建Delaunay三角网为准则,即构建的三角形之间连续而不相交),D为弧段N1N2的长度;③构建约束Delaunay三角网,以居民地轮廓和边界为约束边,构建约束Delaunay三角网,如图 4所示;④提取空白区域骨架线,依据三角形3个顶点在居民地和边界上的数量与位置进行分类,具体分类结果如图 5所示。ⅰ类三角形:3个顶点均在居民地轮廓上,其中根据顶点在居民地轮廓的不同又分为3小类,ⅰ(1)类三角形,3个顶点分别在3个不同的居民地轮廓上;ⅰ(2)类三角形,3个顶点在两个不同的居民地轮廓上;ⅰ(3)类三角形,3个顶点在同一居民地轮廓上。ⅱ类三角形:一个顶点在边界上,另两个顶点在两个不同的居民地轮廓上。ⅲ类三角形:一个顶点在边界上,另两个顶点在同一居民地轮廓上。ⅳ类三角形:两个顶点在边界上,另一个顶点在居民地轮廓上。ⅴ类三角形:3个顶点均在边界上。

|
| 图 2 居民地数据边界 Fig. 2 Boundary of habitation data |
|
| 图 3 居民地数据节点加密 Fig. 3 Nodes densification of habitation |

|
| 图 4 构建约束Delaunay三角网 Fig. 4 Constructing constraint Delaunay triangulation network |
|
| 图 5 三角形分类 Fig. 5 Classification of triangle |
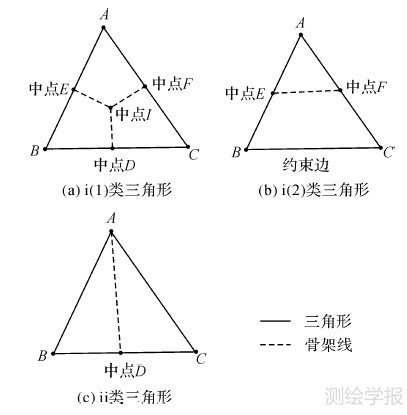
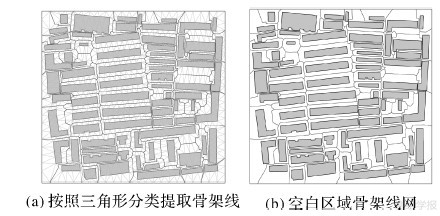
三角形分类后,按照图 6所示的方法提取骨架线。对ⅰ(1)类三角形,分别连接三角形中心和3边的中点形成骨架线(图 6(a));对ⅰ(2)类三角形,首先判断出唯一的约束边,然后连接两非约束边的中点形成骨架线(图 6(b));对ⅱ类三角形,边界上的唯一顶点直接连接其对边的中点形成骨架线(图 6(c));对ⅲ、ⅳ、ⅴ类三角形不进行任何处理。所有三角形按照上述方法连接后即可得到空白区域的骨架线,如图 7(a)所示,空白区域骨架线和地图边界一起构成骨架线网,如图 7(b)所示。
|
| 图 6 不同类型三角形骨架线提取方法 Fig. 6 Skeleton line extraction methods of different triangles |
|
| 图 7 空白区域骨架线网提取结果 Fig. 7 Skeleton line network of blank region |
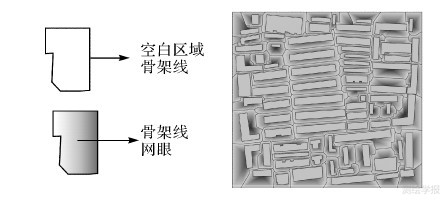
在空白区域骨架线网中,将骨架线所围成的最小闭合区域称为“空白区域骨架线网眼”(为表达简洁,后文均称为“骨架线网眼”),图 8中渐变填充区域即为骨架线网眼。骨架线网眼有如下特点:骨架线网眼为面状要素,其轮廓由对应的空白区域骨架线组成;每个骨架线网眼中只包含一个居民地;相邻骨架线网眼之间的拓扑关系均为相接关系。
|
| 图 8 空白区域骨架线网眼构建 Fig. 8 Skeleton line mesh of blank region |
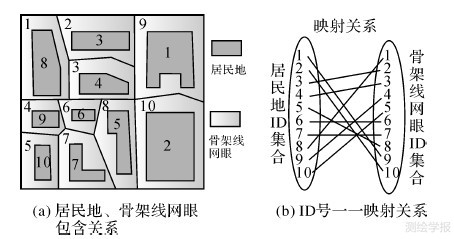
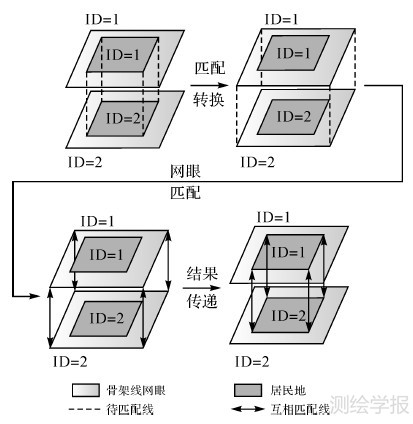
图 9(a)为骨架线网眼和居民地包含关系示意图,由于每个骨架线网眼中只包含一个居民地,故可建立居民地与骨架线网眼之间的一一映射关系,通过关联居民地ID号和骨架线网眼ID号实现(图 9(b)),从而根据这种一一映射关系将居民地匹配转换为骨架线网眼匹配。如图 10所示,匹配时不直接对居民地匹配,而是对其映射的骨架线网眼进行匹配,一一映射关系决定了两个互相匹配的骨架线网眼中所包含的两个居民地也一定互相匹配,从而可将骨架线网眼匹配结果按照映射关系进行传递,最终得到居民地匹配结果。
|
| 图 9 居民地和骨架线网眼映射关系建立 Fig. 9 Mapping relationship between habitation and skeleton line mesh |
|
| 图 10 匹配转换及匹配结果传递过程 Fig. 10 Transformation of matching and transmission of matching results |
简单的面要素拓扑关系包括相离、相接、相交、覆盖、被覆盖、包含、被包含、相等共8种[18]。在大比例尺城市地图中,面状居民地之间的拓扑关系普遍为相离关系,因此较难利用拓扑关系约束匹配过程。相比之下,相邻骨架线网眼之间均为相接拓扑关系,因此可参考线要素对偶图的构建方法[19]对骨架线网眼(面要素)构建对偶图,并计算其中心性指标对拓扑关系进行定量描述,为匹配过程增加拓扑约束条件,这是直接对居民地匹配不具备的优势。
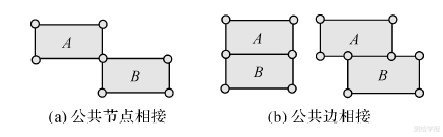
需特别说明的是:构建骨架线网眼对偶图时,由于面要素相接关系分为公共节点相接和公共边相接两种情况(图 11),本文在构建面要素对偶图时规定只将两个面要素之间存在公共边的情况视为相接,其对应的对偶图节点之间具有连通关系线。据此将骨架线网眼对偶图的构建方法定义为
|
| 图 11 面要素相接关系分类 Fig. 11 Classification of connection relationship in areal feature |
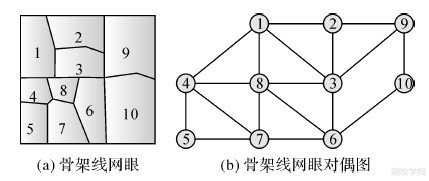
式中,N为对偶图Gmesh中所有节点组成的集合;E为N中所有节点之间存在的连接边的集合,其中将每个骨架线网眼视为对偶图中的节点,具有公共边的两骨架线网眼在对偶图中对应节点之间具有连接边,因此节点集N表示全部骨架线网眼的集合,E表示骨架线网眼之间存在的公共边的集合。因此图 12(a)所示的骨架线网眼可构建如图 12(b)所示的对偶图。
|
| 图 12 骨架线网眼对偶图构建 Fig. 12 Dual graph of skeleton line mesh |
在对偶图中,主要利用度中心性、邻近中心性、中介中心性这3个指标判断节点在整个对偶图网络中的连接情况[20]。其中,度中心性是指与某一节点直接相连的其他节点数量,计算公式为
式中,δij表示节点j是否与节点i具有连接关系,如果具有连接关系,则δij=1,否则为0。接近中心性是指某一节点到其他所有节点的最短路径之和的倒数。这里的最短路径主要表达的是在拓扑意义上的距离,而不是实际距离,可以理解为从一个节点到另一个节点所需要的转换次数,因此规定两个相邻的节点之间距离为1,计算公式为
式中,nij是节点j到节点i所经过最短路径的距离数值。中介中心性表示一个节点作为媒介的能力,计算公式为
式中,njk表示节点j与k之间最短路径的数量;njk(i)表示经过节点i的数量。
上述3个对偶图节点中心性指标中,度中心性为局部指标,能够反映出骨架线网眼与周围网眼的连接情况,度中心性越大则说明与该骨架线网眼相接的其他骨架线网眼数量越多;接近中心性和中介中心性为全局指标,能够反映某个骨架线网眼在全部骨架线网眼中的相对位置。
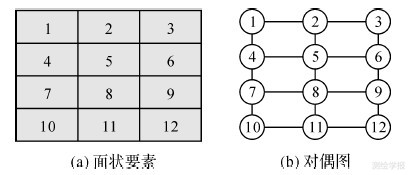
4 骨架线网眼匹配 4.1 利用极化变换确定候选匹配集在骨架线网眼对偶图中,每个节点均对应一组中心性指标值,如果按照“中心性指标越相近,匹配的可能性就越大”这一原则进行匹配,则可能会造成错误匹配。因为在空间上相距较远的节点也可能具有相同或相近的中心性指标,如图 13所示,节点1、3、10、12相距较远但是具有完全相同的中心性指标值。本文通过对骨架线网眼进行极化变换,从而根据极坐标值确定候选匹配集来解决上述问题。极化变换是指将点要素的坐标从平面直角坐标系转换为极坐标系,极坐标能够反映节点在整体中的相对位置,而相对位置较为接近的节点之间中心性指标差异明显。
|
| 图 13 位置不同、指标相同的情况 Fig. 13 The condition of same indexes in different position |
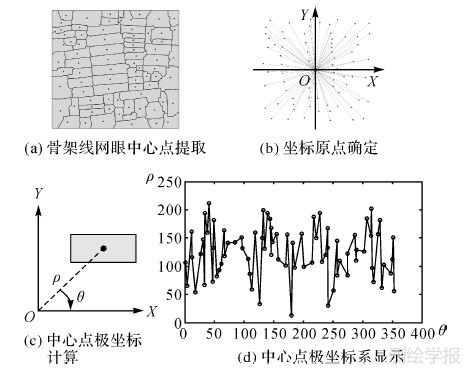
利用极化变换方法确定骨架线网眼候选匹配集的步骤为:①提取骨架线网眼中心点,将骨架线网眼的几何中心视为其中心点(图 14(a));②确定平面直角坐标系原点,将幅面中心作为坐标原点(图 14(b));③计算骨架线网眼中心点极坐标(图 14(c)),计算每个骨架线网眼中心点到坐标原点的距离ρ,以及中心点和坐标原点连线与X轴正方向所形成的顺时针夹角θ,其中θ的范围为[0°,360°],设骨架线网眼i的中心点坐标为(xi,yi),则计算公式为
|
| 图 14 骨架线网眼极化变换 Fig. 14 Polarization transformation of skeleton line mesh |
图 14(d)为极化变换后的坐标在极坐标系下的显示情况;④匹配时将极坐标差异在阈值范围内的对象加入候选匹配集。本文设定角度差异在±10°、长度差异在±10个单位长度范围内的实体为候选匹配对象。
虽然匹配数据源之间绝对位置偏差较大,但是绝对位置偏差不会影响某个居民地在整个数据中的相对位置,而极坐标能够定量度量实体的相对位置,因此对骨架线网眼进行极化变换确定候选匹配集的过程实际上是对匹配过程增加了相对位置的约束条件,从而弥补了匹配过程中由于绝对位置差异造成的位置约束条件的缺失。
4.2 利用层次分析法确定中心性相似度综合指标不同数据源中骨架线网眼之间匹配关系建立的依据是:两个互相匹配的骨架线网眼应具有相同或相近的各项中心性指标值,如果两个网眼的中心性指标越接近,则互相匹配的概率越大;反之,若两个网眼的中心性指标差异较大,则一般可认为其不是同名实体,不具有匹配关系。主要通过中心性指标相似性进行判断,这里定义度中心性相似度、接近中心性相似度、中介中心性相似度3个判断指标,其中度中心性相似度计算公式为
接近中心性相似度计算公式为 中介中心性相似度计算公式为 为了综合上述3个指标相似度的信息,定义中心性相似度综合指标为 式中,ω1、ω2、ω3分别为3个相似度指标的权重,本文采用层次分析法计算各权重值。
层次分析法中各指标间的重要程度评价分为{同等重要、稍微重要、明显重要、强烈重要、极端重要}5个等级,分别用数值1、3、5、7、9量化。由于度中心性反映的是对偶图节点与相邻节点的连接情况,所以其计算较为简单并且受骨架线网眼构建质量的影响较小,利用其作为匹配评价指标更为可靠;接近中心性和中介中心性指标计算较为复杂,其受骨架线网眼构建质量的影响较大,因此相对度中心性,其可靠程度较低。因此在描述骨架线网眼拓扑关系时,度中心性比接近中心性稍微重要,而比中介中心性明显重要;接近中心性比中介中心性稍微重要,由此可得判断矩阵为
利用和积法求解得到特征向量ω=[0.9161 0.37150.1506],最大特征值λmax=3.0385,一致性指标为0.033 < 0.1,判断矩阵满足一致性要求,对特征向量进行归一化处理得到各项中心性相似性指标的权重分别为:ω1=0.637、ω2=0.258、ω3=0.105,因此中心性相似度综合指标的公式为
4.3 骨架线网眼匹配及结果传递
骨架线网眼匹配的具体过程为:①计算待匹配网眼的各项中心性指标值;②确定候选匹配集,并在其中判断出与待匹配网眼中心性相似度综合指标最大的网眼;③判断是否满足阈值,若该最大指标在设定的阈值范围内,则该网眼即为待匹配网眼的同名实体,建立二者的匹配关系,若不在阈值范围内,则说明待匹配网眼不具有匹配关系,为新增网眼。据此完成骨架线网眼的匹配,并根据骨架线网眼和居民地之间的一一映射关系将匹配结果进行传递得到居民地匹配结果。
5 试验及对比分析 5.1 试验数据及匹配方法选取同一地区不同来源的大比例尺居民地数据进行匹配试验,数据叠加显示(图 15)反映出匹配数据源之间存在较大几何位置偏差,因此利用常用的面积重叠率法进行匹配时,会出现大量的无匹配或错误匹配的情况,故在对本文方法进行试验验证的同时,选取缓冲区面积重叠率匹配方法作为对比。

|
| 图 15 不同来源居民地数据叠加显示 Fig. 15 Habitation data overlap from different source |
首先对本文方法进行验证,图 16(a)、(b)为两不同数据源居民地的空白区域骨架线网提取效果;图 16(c)为骨架线网眼构建结果,建立骨架线网眼和居民地之间的映射关系并将居民地匹配转换为骨架线网眼匹配;对骨架线网眼利用4.2节的方法进行匹配得到图 16(d)所示的结果;最后根据映射关系得到居民地匹配结果(图 16(e)),其中黑色短线为匹配关系线。

|
| 图 16 本文方法匹配试验及结果 Fig. 16 Matching experiment and results of the proposed method |
对同一数据利用缓冲区面积重叠率匹配方法进行对比试验,分别选取6组不同缓冲区半径(radius)进行试验,其匹配结果如图 17所示。选取6组缓冲区半径匹配结果中匹配正确率最高的一组(radius=7.5)与本文方法的匹配结果进行对比(表 1),得出缓冲区面积重叠率法的匹配正确率只略大于60%,而本文方法的匹配正确率超过了90%。

|
| 图 17 不同半径的缓冲区面积重叠率法匹配试验结果 Fig. 17 Matching results of buffer area covering rate method with different radiuses |
| 匹配方法 | 正确匹
配数 |
错误匹
配数 |
假匹
配数 |
正确未
匹配数 |
假未匹
配数 |
匹配正
确率/(%) |
| 本文方法 | 44 | 2 | 2 | 1 | 2 | 91.7 |
| 缓冲区面积
重叠率法 (radius=7.5) |
31 | 17 | 2 | 1 | 0 | 62.0 |
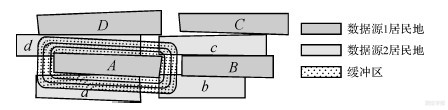
当多源居民地数据间存在较大位置偏差时,缓冲区面积重叠率法通过增大缓冲区半径能够增加与同名实体之间的重叠,但同时也会增加与周边邻近非同名实体的重叠,对匹配造成干扰。如图 18所示,居民地A与居民地a为同名居民地,随着缓冲区半径的增大,居民地A与非同名实体b、c、d的面积重叠率也在增大,特别是非同名实体d会对匹配造成较强的干扰,从而影响匹配效果。
|
| 图 18 缓冲区面积重叠率法处理较大几何位置偏差数据的问题 Fig. 18 Problems of buffer area covering rate matching method in solving the data which has large location differences |
相比之下,本文方法将居民地匹配转换为骨架线网眼匹配,并通过构建骨架线网眼对偶图定量获得匹配过程中的拓扑约束,对骨架线网眼进行极化变换确定候选匹配集则增加了相对位置约束;拓扑约束与相对位置约束是对数据之间几何位置绝对偏差的有效补充,使得匹配结果不会因位置条件的缺失而产生大量错误。应用本方法的关键在于对城市地图中的空白区域提取正确的骨架线网,从而构建正确的骨架线网眼,因此本方法的匹配效果主要取决于不同数据源空白区域骨架线网的提取效果。
6 结 论在处理几何位置偏差较大的居民地数据间的匹配问题时,与已有的居民地匹配方法相比,本方法有以下特点:通过构建空白区域骨架线网眼,将居民地匹配转换为骨架线网眼匹配,能够充分利用骨架线网眼的特点进行匹配;构建骨架线网眼对偶图并计算中心性指标,对匹配过程进行了定量拓扑约束;利用极化变换方法确定候选匹配网眼,为匹配过程增加了相对位置约束条件,弥补了位置约束条件的缺失对匹配造成的影响。目前本方法只是针对同比例尺数据进行了研究试验,如何使其适用于不同比例尺下居民地数据的匹配将是下一步的研究方向。
| [1] | LI Deren, GONG Jianya, ZHANG Qiaoping. Conflation of Geographic Database Technology[J]. Science of Surveying and Mapping, 2004, 29(1): 1-4. (李德仁, 龚健雅, 张桥平. 论地图数据库合并技术[J]. 测绘科学, 2004, 29(1): 1-4.) |
| [2] | CHEN Jun, WANG Donghua, SHANG Yaoling, et al. Master Design and Technical Development for National 1:50 000 Topographic Database Updating Engineering in China[J]. Acta Geodaetica et Cartographica Sinica, 2010, 39(1): 7-10. (陈军, 王东华, 商瑶玲, 等. 国家1:50 000数据库更新工程总体设计研究与技术创新[J]. 测绘学报, 2010, 39(1): 7-10.) |
| [3] | XU Junkui, WU Fang, QIAN Haizhong. The Establishment and Usage of the Neighborhood Scale Settlement Features' Links in Spatial Data Updating Process[J]. Acta Geodaetica et Cartographica Sinica, 2013, 42(6): 898-905. (许俊奎, 武芳, 钱海忠. 多比例尺地图中居民地要素之间的关联关系及其在空间数据更新中的应用[J]. 测绘学报, 2013, 42(6): 898-905.) |
| [4] | WALTER V, FRITSH D. Matching Spatial Data Sets: A Statistical Approach[J]. International Journal of Geographical Information Science, 1999, 13(5): 445-473. |
| [5] | HAO Yanling, TANG Wenjing, ZHAO Yuxin, et al. Areal Feature Matching Algorithm Based on Spatial Similarity[J]. Acta Geodaetica et Cartographica Sinica, 2008, 37(4): 501-506. (郝燕玲, 唐文静, 赵玉新, 等. 基于空间相似性的面实体匹配算法研究[J]. 测绘学报, 2008, 37(4): 501-506.) |
| [6] | XU Junkui, WU Fang, WEI Huifeng. Areal Settlements Matching Algorithm Based on Artificial Neural Network Technique[J]. Journal of Geomatics Science and Technology, 2013, 30(3): 293-298. (许俊奎, 武芳, 魏慧峰. 人工神经网络在居民地面状匹配中的应用[J]. 测绘科学技术学报, 2013, 30(3): 293-298.) |
| [7] | ZHANG Qianping, LI Deren, GONG Jianya. Areal Feature Matching among Urban Geographic Databases[J]. Journal of Remote Sensing, 2004, 8(2): 107-112. (张桥平, 李德仁, 龚健雅. 城市地图数据库面实体匹配技术[J]. 遥感学报, 2004, 8(2): 107-112.) |
| [8] | VONGOESSELN G, SESTER M. Change Detection and Integration of Topographic Updates from ATKIS to Geoscientific Data Sets[C]//International Conference on Next Generation Geospatial Information.Boston:[s.n.],2003: 19-21. |
| [9] | GUO Li, ZHENG Haiying, WANG Hao. Study for Area Feature Matching Technique Based on Area Similarity[J]. Hydrographic Surveying and Charting, 2009, 29(3): 12-15. (郭黎, 郑海鹰, 王豪. 面状矢量空间数据匹配技术研究[J]. 海洋测绘, 2009, 29(3): 12-15.) |
| [10] | FU Zhongliang, LU Yuefeng. Establishment of the Comprehensive Model for Similarity of Polygon Entity by Using the Bending Radius Complex Function[J]. Acta Geodaetica et Cartographica Sinica, 2013, 42(1): 145-151. (付仲良, 逯跃锋. 利用弯曲度半径复函数构建综合面实体相似度模型[J]. 测绘学报, 2013, 42(1): 145-151.) |
| [11] | FU Zhongliang, SHAO Shiwei. Methods of Complex Polygon Element Fast Shape Matching[J]. Bulletin of Surveying and Mapping, 2011(3): 26-28. (付仲良, 邵世维. 复杂面状矢量要素快速形状匹配方法[J]. 测绘通报, 2011(3): 26-28.) |
| [12] | ZHANG D, LU G. A Comparative Study on Shape Retrieval Using Fourier Descriptors with Different Shape Signatures[J]. Journal of Visual Communication and Image Representation, 2003, 14(1): 41-60. |
| [13] | HUANG Zhishen, QIAN Haizhong, GUO Min, et al. Matching Algorithm of Polygon Habitations Based on Their Skeleton-lines Using Fourier Transform[J]. Acta Geodaetica et Cartographica Sinica, 2013, 42(6): 913-921. (黄智深, 钱海忠, 郭敏, 等. 面状居民地匹配骨架线傅里叶变化方法[J]. 测绘学报, 2013, 42(6): 913-921.) |
| [14] | HUANG Zhishen, QIAN Haizhong, WANG Xiao, et al. Dimension Decrease-oriented Habitation Matching Method[J]. Journal of Geomatics Science and Technology, 2012, 29(1): 75-78. (黄智深, 钱海忠, 王骁, 等. 基于降维技术的面状居民地匹配方法[J]. 测绘科学技术学报, 2012, 29(1): 75-78.) |
| [15] | XU Junkui, WU Fang,QIAN Haizhong,et al.Settlement Matching Algorithm Using Spatial Similarity Relations as Constraints[J]. Geomatics and Information Science of Wuhan University, 2013, 38(4): 484-488. (许俊奎, 武芳, 钱海忠, 等. 一种空间关系相似性约束的居民地匹配算法[J]. 武汉大学学报: 信息科学版, 2013, 38(4): 484-488.) |
| [16] | GUO Li, CUI Tiejun, ZHENG Haiying, et al. Arithmetic for Area Vector Spatial Data Matching on Spatial Direction Similarity[J]. Journal of Geomatics Science and Technology, 2008, 25(5): 380-382. (郭黎, 崔铁军, 郑海鹰, 等. 基于空间方向相似性的面状矢量空间数据匹配算法[J]. 测绘科学技术学报, 2008, 25(5): 380-382.) |
| [17] | QIAN Haizhong, WU Fang, ZHU Kunpeng, et al. A Generalization Method of Street Block Based on Dimension-reducing Technique[J]. Acta Geodaetica et Cartographica Sinica, 2007, 36(1): 102-107. (钱海忠, 武芳, 朱鲲鹏, 等. 一种基于降维技术的街区综合方法[J]. 测绘学报, 2007, 36(1): 102-107.) |
| [18] | DENG Min, LIU Wenbao, FENG Xuezhi. A Generic Model Describing Topological Relations among Area Objects in GIS[J]. Acta Geodaetica et Cartographica Sinica, 2005, 34(1): 85-90. (邓敏, 刘文宝, 冯学智. GIS面目标间拓扑关系的形式化模型[J]. 测绘学报, 2005, 34(1): 85-90.) |
| [19] | DUAN Yingying, LU Feng. The Impact of Different Granularity Representations on Robustness Evaluation of City Road Network[J]. Journal of Image and Graphics, 2013, 18(9): 1197-1205. (段滢滢, 陆锋. 不同表达粒度对城市路网结构健壮性评价的影响[J]. 中国图象图形学报, 2013, 18(9): 1197-1205.) |
| [20] | LUAN Xuechen, YANG Bisheng, ZHANG Yunfei. Structural Hierarchy Analysis of Streets Based on Complex Network Theory[J]. Geomatics and Information Science of Wuhan University, 2012, 37(6): 728-732. (栾学晨, 杨必胜, 张云菲. 城市道路复杂网络结构化等级分析[J]. 武汉大学学报: 信息科学版, 2012, 37(6): 728-732.) |