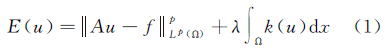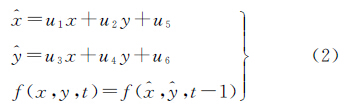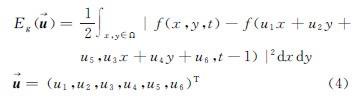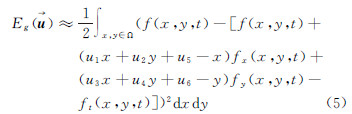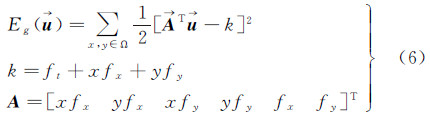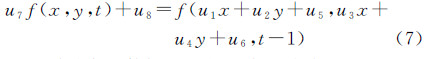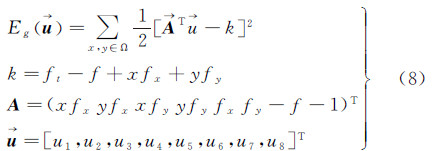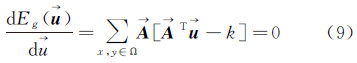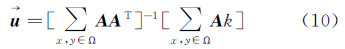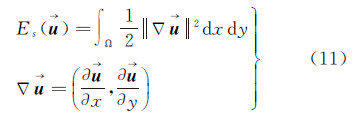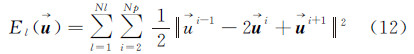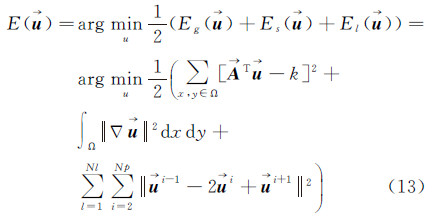2. 武汉大学测绘遥感信息工程国家重点实验室, 湖北 武汉 430079;
3. 军械工程学院电子与光学工程系, 河北 石家庄 050003;
4. 北京市遥感信息研究所, 北京 100192
2. State Key Laboratory of Information Engineering in Surveying, Mapping and Remote Sensing, Wuhan University, Wuhan 430079, China;
3. Electronic & Optical Engineering Department, Mechanical Engineering College, Shijiazhuang 050003, China;
4. Institute of Information in Remote Sensing in Beijing, Beijing 100192, China
1 引 言
影像配准是指根据某种相似性度量准则获得影像间的坐标变换关系，使得从不同时间、不同视角或不同传感器获取的同一地区的两幅或者多幅影像能够在几何上对齐。影像配准是遥感影像处理领域一个具有挑战性的问题。经过多年的发展，基于遥感影像的配准技术已经取得了丰硕的研究成果，目前根据所用信息的不同可以分为基于特征和基于灰度两种[1]主要方法。基于特征的配准方法主要以控制点(ground control points,GCP)为基础，即点特征、线特征、面特征和虚拟特征[2]。点特征主要有Frstner算子[3]、Haar特征[4]、SUSAN[5]和SIFT(scale invariant feature transform )特征[6]以及它们的变体[7]。基于特征点的配准在灰度差异较大时，检测率大大下降，直接影响配准效果。线特征主要有LSD(line segment detector)[8]、Edison[9]等。面特征主要是分割的方法，有主动轮廓[10]和马尔可夫随机场模型(Markov random fields,MRF)[11]。虚拟特征常有虚拟点、虚拟三角形和虚拟圆等。经典的基于灰度的配准方法包括相关法[12]、最大互相关法[13]和互信息方法[14]以及它们的变体。相关法对同源遥感影像配准具有有效性和准确性，然而对影像间的灰度差异比较敏感，特别是非线性的灰度差异[15]；互信息是一种统计相关性测量方法，能够较好地抵抗影像之间的灰度差异，对噪声有更好的鲁棒性，但是由于计算量较大，限制了其在遥感影像配准领域的广泛应用[16]。
基于特征的配准方法依赖特征的提取精度，并且利用特征去建立整体的变换模型，往往会导致局部变形不能顾及。传统基于灰度的配准方法利用搜索窗口和模板之间的相似性决定匹配位置，对噪声点、灰度差异敏感，分析其原因主要是模型欠佳，求解过程过于简单，缺少对配准实质的理解。为了解决这些问题，本文提出一种视觉驱动的变分配准方法，该方法采用一种充分考虑局部变形、整体约束和迭代反馈机制的配准模型。
2 视觉驱动变分配准模型的建立变分法是一种寻求泛函极值(极大值或极小值)的优化方法，已广泛应用于图像处理领域[17, 18]。图像处理中变分模型的一般形式由两部分构成：数据项和先验项，一维形式可以表示为
式中，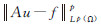
为数据项，也叫残差或忠诚项，用于保证待求图像u保留观察图像f的主要特征；
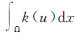为先验项，即先验约束项，也叫正则项，用于保证在该约束项下能量泛函极小化问题是良态的；λ>0是尺度参数，起到平衡忠诚项和正则项的作用。求解上面的能量泛函也就是求解minE(u)所对应的u值。
本文采用的配准测度是基于灰度的均方根误差(mean square error，MSE ),避免了基于特征的特征选择问题。变分模型建立中，基于局部变换、整体平滑和视觉约束的思想，同时为了应对灰度的局部变化，在模型中考虑了亮度和对比度的变化。
2.1 变分模型中数据项的建立 基于灰度的MSE配准测度，就是使对应同名点的灰度差异最小，变分模型中的数据项就是保证这个测度的。设待配准影像为f(x,y,t)，参考影像为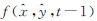
，采用局部和整体的仿射变换来建立变换关系，假设配准影像对之间不存在灰度差异，则两者之间有如下的关系存在，如式(2)所示
式中，u1、u4为仿射变换中X和Y方向的尺度参数；u2、u3为旋转参数；u5、u6为平移参数。
为了估计这些参数，建立如式(3)所示数据项模型
即式(4)
式中，Ω是一个空间邻域，式(4)是一个非线性的，在一个闭合区间内不可微，求解分析比较困难，因此采用一阶泰勒级数进行展开，如式(5) 式中，fx(x,y,t)、fy(x,y,t)和ft(x,y,t)是f(x,y,t)对空间和时间上的偏导数。式(5)可以表示成矢量形式
为了应对配准影像之间的亮度差异，模型中加入对比度u7和亮度u8，即
则对应的数据项的矢量表达式为
如果不考虑先验项的话，最小化能量函数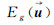
，则求解式(8)为
则
从上述分析可以看出参数的估计依赖于Ω空间邻域的大小，该邻域越大，则式(10)越可逆，但是局部的仿射变换和亮度/对比度的变换就不是一个常数，则计算出来的参数不精确。为了得到一种权衡，笔者采用模型先验项的约束来进行建模。
2.2 视觉驱动的模型先验项建立变分模型中的先验项是指应用一些先验知识进行约束，在配准中要保证求解参数在空间上是平滑的，同时也要保证遥感影像中的空间属性满足视觉的要求，不能出现扭曲变形，如：房屋的直边缘、道路的边缘等，也就是需要建立一种视觉驱动的模型。
2.2.1 基于H1半范数的先验模型为了保障求解参数在空间的平滑性，笔者利用H1半范数的先验，先验模型如下
2.2.2 基于直线约束的先验模型
人的眼睛对一些形状物体非常敏感，而很多形状都可以以直线的形式进行表达，物体一旦出现变形人眼会立即辨别出来，这其实是视觉的一种驱动。为了保证配准前后物体的形状特征保持不变，在模型中加入直线的约束。
关于直线的提取本文采用近两年出现的理论较完善、效果较好，并且对参数不敏感的LSD线段检测算法[8]。它能够对任何图像进行检测而不用调整参数，并且能够控制错误检测。
直线约束的先验约束就是对LSD检测出来的直线上的点进行约束，即直线上的点的变换参数要保持匀速性变化，从而达到一种智能化的平滑作用，模型如式(12)
式中，Nl是直线的条数；l是指第l条直线；Np是直线l上的点数；i是直线l第i个点；
和
是直线l上第i-1、i和i+1个点的变换参数。
3 模型的最优化求解
综上模型的建立，整个变分模型概括为式(13)
对式(13)求偏导，其对应的欧拉-拉格朗日方程为
式中，Δu为拉普拉斯算子；
是指同一条直线上以该点为中心的左右两个相邻点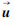
的平均值。
在求解过程中为了防止病态问题出现，对式(14)进行正则化处理，添加正则项L，式(14)变为
式中，L是一个8×8、对角元素为λi、非对角元素为0的对角阵，本文中λi均为1.0×1010。
要解决每个点的变换参数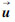
是一个相当庞大的任务，这里不直接采用传统的变分求解方法而是将上式表达为一种离散形式，可得式(15)的离散表达式
是计算拉普拉斯算子中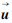
的相邻点的均值，因此可以采用直接迭代的方式进行求解，即
式中，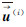
和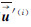
是利用当前的第i次迭代
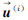值来进行估计，初始的估计
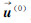用式(10)在一个较小的邻域内估计。在实际实现中，先利用整个影像作为Ω来整体估计一个变换，然后再采用小的邻域范围(如本文中采用5×5)进行局部的估计。因为规整项
中采用了泰勒级数的一阶展开式代替了非线性的变换模型，这样会带来一些误差，为了减少这些影响，采用多水平差分策略求解。多水平差分策略是一种从粗到精的处理过程，即对上一个低分辨率水平级的变换结果进行重采样作为下一级精处理的初始值，这样可以兼顾局部变形和整体约束，从而得到一个满足视觉要求的高精度配准影像。
4 试验结果与分析
为了验证该配准方法的有效性，本文选取了两组ZY-3卫星数据。数据1和数据2都是局部变形较大的多光谱和全色影像对，待配准多光谱影像空间分辨率为5.8m，波段数为4，分别为蓝色、绿色、红色和近红外波段，参考的全色影像空间分辨率为2.1m，影像大小均为1024像素×1024像素。如图1所示，(a)、(b)和(e)为数据1的参考全色影像、待配准多光谱影像和红框内局部放大的配准前影像之间错位情况；(c)、(d)和(f)为数据2的参考全色影像、待配准多光谱影像和红框内局部放大的配准前影像之间错位情况，其中多光谱影像采用3、2、1组合显示模式。
|
| 图 1 待配准影像对 Fig. 1 Unregistered image pairs |
为了客观评价，采用经典的SIFT特征[6, 19]的多项式模型进行比较，因为该算法对同源影像配准具有很好的稳定性，可以匹配密集的特征点，被广泛地应用。多光谱与全色影像对，一般用于影像融合，因此本文对配准结果采用影像融合的效果以及传统的选择检查点两种方式进行综合评价,其中融合方法采用SSCSVR(spectral and spatial correlation based synthetic variable ratio)[20]，因为该方法可以得到高空间分辨率且光谱信息保持度高的融合影像。利用融合后影像与参考影像(全色影像)之间的高通相关(high pass correlation coefficient，HCC)[21]来评价配准效果。HCC值越大表明多光谱影像与全色影像细节越相近，也就说明配准效果越好。
从图1(e)和(f)可以看出配准前两幅影像之间存在明显的错位。图2是基于SIFT方法和本文方法的配准结果，其中图2(a)和(e)为基于SIFT方法配准影像局部放大图，可以看出较配准前错位明显减小，但依然存在较大的配准误差，究其原因主要是它采用整体的多项式配准模型，不能很好地顾及局部变形。因为配准误差的存在导致配准后影像之间的融合结果在配准误差处存在明显的伪痕，如图2(b)和(f)中红色矩形框中的位置。
|
| 图 2 配准结果目视比较 Fig. 2 Visual comparison of registered results |
为了克服这些局部变形，本文提出了视觉驱动的局部变换和整体约束相结合的变分配准方法，配准结果的局部放大图如图2(c)和(g)所示，可以看出配准结果套合很好，局部变形得到解决，图2(d)和(h)为配准后影像融合结果的局部放大图，可以看出由配准误差引起的伪痕已经消除。
为了定量评价配准结果，采用融合效果的HCC来评价，见表1。从表1可以看出利用本文配准方法融合后影像HCC系数较传统方法有了较大提高，说明本文方法的整体配准精度比传统方法要高。
| 配准方法 | 数据1 | 数据2 | ||
| SIFT | 本文方法 | SIFT | 本文方法 | |
| HCC | 0.989 | 0.995 | 0.987 | 0.992 |
评价配准精度传统的方法往往是人工选择一些检查点，然后利用检查点的精度来评价方法的有效性，本文也遵照这样的原则，选择了均匀分布的25个检查点来进行评价。检查点的误差情况详见表2：dx、dy表示检查点在参考影像中的坐标与配准后影像中的坐标之差，dxy表示dx和dy的平方和开方，即(x,y)方向的欧氏距离误差。从表2中可以看出数据1中SIFT配准的影像在x方向的最大偏差为-2.60个像素，y方向的最大偏差为-4.90个像素，(x,y)方向的最大欧氏距离偏差为4.93个像素；而相对应的本文方法配准的影像在x方向的最大偏差为0.87个像素，y方向的最大偏差为-1.07个像素，(x,y)方向的最大欧氏距离偏差为1.12个像素。可以看出对于单个检查点来说，本文方法可以有效地提高精度。为了整体评价检查点的震荡情况，本文还计算了总体的平均误差，SIFT配准的影像在x方向的总平均误差为0.33个像素，y方向为-0.15个像素，(x,y)方向的欧氏距离总平均偏差为1.69个像素；相对应的本文方法配准的影像在x方向的总平均误差为-0.02个像素，y方向为0.08个像素，(x,y)方向的欧氏距离总平均偏差为0.48个像素。数据2中SIFT配准的影像在x方向的最大偏差为2.60个像素，y方向的最大偏差为-7.70个像素，(x,y)方向的最大欧氏距离偏差为8.13个像素；对应的本文方法x方向最大偏差为-0.50个像素，y方向的最大偏差为-0.90个像素，(x,y)方向的最大欧氏距离偏差为0.9个像素。SIFT配准影像在x方向的总平均误差为-0.16个像素，y方向为-0.74个像素，(x,y)方向的欧氏距离总平均偏差为1.36个像素；而对应本文方法在x方向的总平均误差为0.02个像素，y方向为-0.02个像素，(x,y)方向的欧氏距离总平均偏差为0.23个像素。可以看出无论是从单个检查点的角度还是整体检查点的震荡情况，本文方法都明显优于传统的SIFT算法。
| 试验数据1 | 试验数据2 | |||||||||||
| Sift方法 | 本文方法 | Sift方法 | 本文方法 | |||||||||
| d x | d y | d xy | d x | d y | d xy | d x | d y | d xy | d x | d y | d xy | |
| 总平均误差 | 0.33 | -0.15 | 1.69 | -0.02 | 0.08 | 0.48 | -0.16 | -0.74 | 1.36 | 0.02 | -0.02 | 0.23 |
| 最大残差 | 2.60 | -4.90 | 4.93 | 0.87 | -1.07 | 1.12 | 2.60 | -7.70 | 8.13 | -0.5 | -0.9 | 0.9 |
从两组数据的目视和定量评价结果可以看出，本文方法配准精度较传统整体SIFT配准算法，精度有了很大提高，可以同时顾及影像的局部及整体的变形。
5 结 论针对传统整体配准模型不能充分顾及局部变形问题，本文提出了一种视觉驱动的变分配准方法。通过对两组ZY-3卫星数据进行试验，从主观目视效果上，较传统的整体SIFT配准方法相比，本文方法的配准结果和参考影像能够更好地套合在一起；在定量评价指标上，本文方法较基于SIFT方法的配准影像的融合结果的HCC值以及检查点精度都有了较大的提高。综上可知，本文方法能够较多地顾及影像的局部以及整体的变形，配准精度较传统整体配准算法有了较大提高。
| [1] | DAWN S, SAXENA V, SHARMA B. Remote Sensing Image Registration Techniques: A Survey[C]//ELMOATAZ A, LEZORAY O, NOUBOUD F, et al. Image and Signal Processing. Lecture Notes in Computer Science Volume 6134. Berlin, Heidelberg: Springer, 2010: 103-112. |
| [2] | YU Xianchuan, LV Zhonghua, HU Dan. Review of Remote Sensing Image Registration Techniques [J]. Optics and Precision Engineering, 2013, 21(11): 2960-2972. (余先川, 吕中华, 胡丹. 遥感图像配准技术综述[J]. 光学精密工程, 2013, 21(11): 2960-2972.) |
| [3] | FRSTNER W, GVLCH E. A Fast Operator for Detection and Precise Location of Distinct Points, Corners and Centres of Circular Features[C]//ISPRS Intercommission Workshop. Interlaken: [s.n.], 1987. |
| [4] | HARRIS C, STEPHENS M. A Combined Corner and Edge Detection[C]//Proceedings of the Fourth Alvey Vision Conference. Manchester: [s.n.], 1988: 147-151. |
| [5] | ZHANG Qian, LIU Zhengkai, PANG Yanwei, et al. Automatic Registration of Aerophotos Based on SUSAN Operator[J]. Acta Geodaetica et Cartographica Sinica, 2003, 32(3): 245-250. (张迁, 刘政凯, 庞彦伟, 等. 基于SUSAN算法的航空影像的自动配准[J]. 测绘学报, 2003, 32(3): 245-250.) |
| [6] | LOWE D G. Distinctive Image Features from Scale-invariant Keypoints[J]. International Journal of Computer Vision, 2004, 60(2): 91-110. |
| [7] | LUO Nan, SUN Quansen, GENG Leilei, et al. An Extended SURF Descriptor and Its Application in Remote Sensing Images Registration[J]. Acta Geodaetica et Cartographica Sinica, 2013, 42(3): 383-388. (罗楠, 孙权森, 耿蕾蕾, 等. 一种扩展SURF描述符及其在遥感图像配准中的应用[J]. 测绘学报, 2013, 42(3): 383-388.) |
| [8] | VON GIOI R G, JAKUBOWICZ J, MOREL J M, et al. LSD: a Line Segment Detector[J/OL]. Image Processing on Line, 2012, http://www.ipol.im/pub/art/2012/gjmr-lsd/. |
| [9] | MEER P, GEORGESCU B. Edge Detection with Embedded Confidence[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2001, 23(12): 1351-1365. |
| [10] | ZHANG Kaihua, ZHOU Wengang, ZHANG Zhen,et al. Improved C-V Active Contour Model[J]. Opto-Electronic Engineering, 2008, 35(12): 112-116. (张开华, 周文罡, 张振, 等. 一种改进的C-V主动轮廓模型[J]. 光电工程, 2008, 35(12): 112-116.) |
| [11] | BOUMAN C A, SHAPIRO M. A Multiscale Random Field Model for Bayesian Image Segmentation[J]. IEEE Transactions on Image Processing, 1994, 3(2): 162-177. |
| [12] | MARTINEZ A, GARCIA-CONSUEGRA J, ABAD F.A Correlation-Symbolic Approach to Automatic Remotely Sensed Image Rectification[C]//IEEE 1999 International Geoscience and Remote Sensing Symposium. Hamburg: IEEE, 1999: 336-338. |
| [13] | EMERY W J, BALDWIN D, MATTHEWS D. Maximum Cross Correlation Automatic Satellite Image Navigation and Attitude Corrections for Open-Ocean Image Navigation[J]. IEEE Transactions on Geoscience and Remote Sensing, 2003, 41(1): 33-42. |
| [14] | CHEN H M, VARSHNEY P K, ARORA M K. Performance of Mutual Information Similarity Measure for Registration of Multitemporal Remote Sensing Images[J]. IEEE Transactions on Geoscience and Remote Sensing, 2003, 41(11): 2445-2454. |
| [15] | HEL-OR Y, HEL-OR H, DAVID E. Fast Template Matching in Non-Linear Tone-Mapped Images[C]//2011 IEEE International Conference on Computer Vision. Barcelona: IEEE, 2011: 1355-1362. |
| [16] | YE Yuanxin. Multi-Source Remote Sensing Image Registration Based on Phase Congruency[D]. Wuhan: Wuhan University, 2013. (叶沅鑫. 基于相位一致性的异源遥感影像配准[D]. 武汉: 武汉大学, 2013.) |
| [17] | RUDIN L I, OSHER S, FATEMI E. Nonlinear Total Variation Based Noise Removal Algorithms[J]. Physica D: Nonlinear Phenomena, 1992, 60(1-4): 259-268. |
| [18] | CHUMCHOB N, CHEN K. Improved Variational Image Registration Model and a Fast Algorithm for Its Numerical Approximation[J]. Numerical Methods for Partial Differential Equations, 2012, 28(6): 1966-1995. |
| [19] | WU C C. SiftGPU: A GPU Implementation of Scale Invariant Feature Transform (SIFT)[J/OL]. http://cs.unc.edu/-ccwu/siftgpu/, 2007. |
| [20] | WANG H X, JIANG W S, LEI C Q, et al. A Robust Image Fusion Method Based on Local Spectral and Spatial Correlation[J]. IEEE Geoscience and Remote Sensing Letters, 2014, 11(2): 454-458. |
| [21] | ZHOU J, CIVCO D L, SILANDER J A. A Wavelet Transform Method to Merge Landsat TM and SPOT Panchromatic Data[J]. International Journal of Remote Sensing, 1998, 19(4): 743-757. |