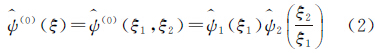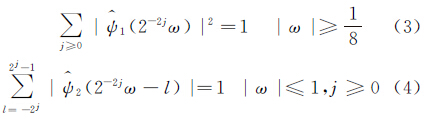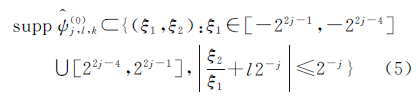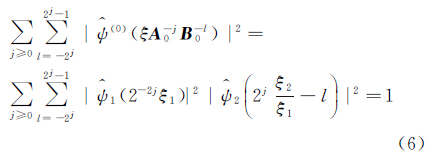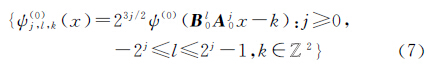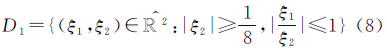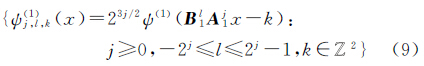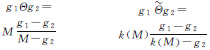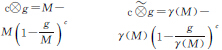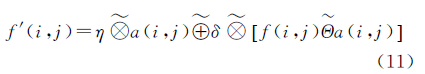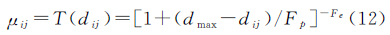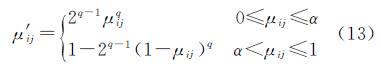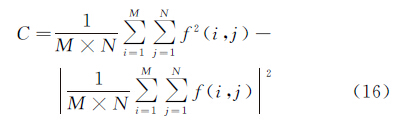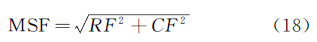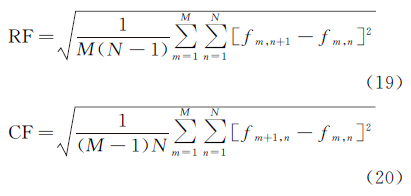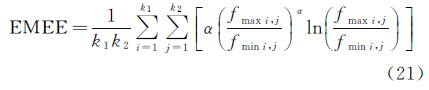2. 国土资源部地质信息技术重点实验室, 北京 100037;
3. 兰州大学甘肃省西部矿产资源重点实验室, 甘肃 兰州 730000;
4. 江西省数字国土重点实验室, 江西 南昌 330013;
5. 中国地质科学院矿产资源研究所国土资源部成矿作用与资源评价重点实验室, 北京 100037
2. Key Laboratory of Geological Information Technology, Ministry of Land and Resources, Beijing 100037, China;
3. Key Laboratory of Western China's Mineral Resources of Gansu Province, Lanzhou University, Lanzhou 730000, China;
4. Jiangxi Province Key Laboratory for Digital Land, East China Institute of Technology, Nanchang 330013, China;
5. MLR Key Laboratory of Metallogeny and Mineral Assessment, Institute of Mineral Resources, Chinese Academy of Geological Sciences, Beijing 100037, China
1 引 言
随着遥感技术的不断普及，在土地利用调查、地形测绘、地质找矿、地表资源普查、灾情监测、目标监视、农作物长势调查等诸多领域有着广泛的应用。但遥感图像获取过程中，受传感器自身机理、大气辐射等诸多因素影响，部分遥感图像会出现对比度较低、图像模糊等问题，视觉效果较差[1, 2]。为了便于对遥感图像进行直观解释[3]，在对遥感图像进行后续分析之前，必须先进行增强预处理。
现有的遥感图像增强方法可大致分为基于空间域的方法和基于变换域的方法两大类。基于空间域的增强方法直接对图像灰度值进行处理[4]，常见的方法包括灰度变换[5]、直方图均衡、反锐化掩模、对数图像处理(logarithmic image processing,LIP)模型[6]等。文献[5]将传统的分段线性增强算子改进为带参数的算子，利用遗传优化算法自适应地选取参数，该类方法能提升图像的对比度，然而有时会忽略图像的细节信息，同时放大噪声，反而有可能降低图像的质量。LIP模型与人类视觉系统处理过程类似[7]，但往往会放大图像中的噪声。文献[8—9]提出参数化对数图像处理(parameterized logarithmic image processing,PLIP)模型，该模型可以对图像中感兴趣的部分进行自适应调整，但也会产生噪声，影响图像细节表现。然而，基于变换域的增强方法可以对低频分量和高频分量做不同方式的增强处理。低频分量包含了原始图像的大量基本信息，且基本滤除了噪声，对低频分量采用PLIP模型进行处理，有望在增强图像对比度的同时能有效地抑制图像的高频噪声；而高频分量主要包含图像在各个方向的边缘细节信息，可用其他方式对图像的边缘细节进行增强。故本文采用基于变换域的增强方法。目前常用的变换域增强方法主要基于多尺度变换，包括基于小波[10, 11, 12, 13]、Contourlet[14, 15]、非下采样Contourlet[16]、Shearlet[17]等变换。由于小波变换[11]只能描述点奇异性，捕获的方向信息有限，缺乏平移不变性，使其不能有效地表示图像中的边缘、轮廓及纹理细节特征，因此基于小波变换的增强方法往往使图像的边缘变得粗糙，降低了图像的清晰度。Shearlet变换[18]是一种新的高维信号稀疏表示工具，与Contourlet变换相比，具有相似的分解过程，能实现图像的最优逼近和多分辨率分析，但其数学结构较为简单，运算复杂度有所降低，用于图像去噪[19]、图像融合[20]领域。文献[17]提出了基于Shearlet变换的遥感图像增强方法，图像熵和均值有了大幅度提升，但对比度不高。文献[19]利用全变差和Shearlet变换对图像进行了去噪，以达到增强图像的目的。然而，Shearlet变换不具备平移不变性，易产生伪吉布斯失真，目标边缘附近会出现伪影。而非下采样Contourlet变换(non-subsampled contourlet transform,NSCT)是Contourlet变换的扩展，具有平移不变性，但其运算量也较大。非下采样Shearlet变换(non-subsampled shearlettansform,NSST)是Shearlet变换的扩展，弥补了上述NSCT的缺陷，且同时具备多尺度、多方向等优点[20]，将其应用于遥感图像增强，有望改善遥感图像视觉效果。
基于上述分析，本文提出了一种基于非下采样Shearlet变换和参数化对数图像处理模型的遥感图像增强方法。文中给出了所提增强方法的具体实现步骤，利用本文方法对大量遥感图像进行了试验分析，并依据主观视觉效果及对比度增益、清晰度增益、信息熵等4项客观定量评价指标，与双向直方图均衡增强、以及近年来提出的基于平稳小波变换[10]、基于Contourlet变换[14]、基于NSCT[16]、基于Shearlet变换[17]等5种增强方法进行了比较，验证了本文方法的优越性。
2 非下采样Shearlet变换Shearlet变换通过具有合成膨胀的仿射系统构造。它构造简单，通过对函数进行伸缩、平移、旋转操作生成基函数，且具有各向异性、最优稀疏表征图像等优点。当维数为2时，其仿射系统表示为
式中，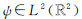
；A和B均为2×2的可逆矩阵。若
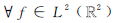，满足
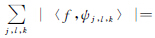
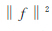，则MAB(ψ)的元素称为合成小波。Shearlet是合成小波的一种特殊情况，此时矩阵A为具有各向异性的膨胀矩阵，
；矩阵B为剪切矩阵，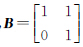
。
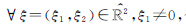令
，supp
。
如果假设
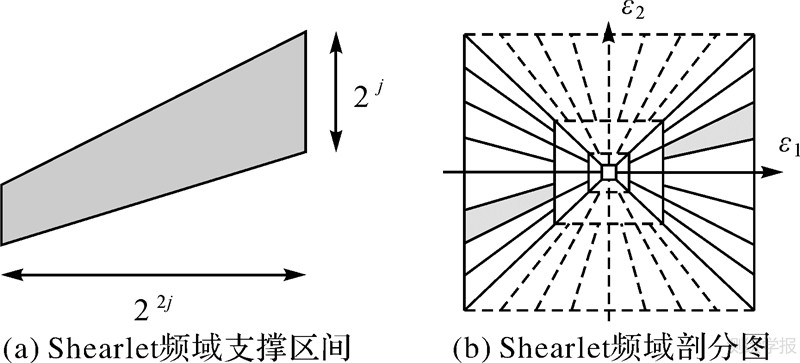
则小波函数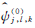
的频域支撑如图1(a)所示，支撑区域为一对大小约为22j×2j、斜率为l2-j的梯形，其支撑区间公式为
|
| 图 1 Shearlet频域支撑区间和频域剖分图 Fig. 1 Shearlet frequency domain support interval and frequency subdivision |
综合式(3)、式(4)可得
式中，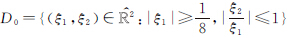
，
则函数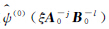
构成了D0的一部分，如图1(b)所示。且由此可得函数集L2(D02)的紧支撑为
下面令
；
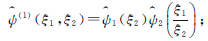NSST的离散化过程主要分为多尺度分解和方向局部化两个步骤。NSST的多尺度分解采用非下采样金字塔(non-subsampled pyramid,NSP)实现；方向局部化则由改进的剪切滤波器(Shearlet filter,SF)完成，它将Shearlet中的标准SF从伪极化网络系统映射到笛卡尔坐标系统，整个过程直接通过二维卷积完成，从而避免下采样操作，使其具有平移不变性。具体实现过程如下：①用非下采样金字塔分解将图像分解为低通图像和细节图像；②对细节图像构建Meyer窗，进行多尺度分解，获得不同的方向子带系数；③对每一个方向子带系数进行傅里叶逆变换，从而得到非下采样剪切波系数。
3 基于NSST的遥感图像增强方法 3.1 基于参数化对数图像处理模型的低频分量增强方法 3.1.1 参数化对数图像处理模型PLIP模型通过对传统的对数图像处理模型进行扩展得到。LIP模型[21]是一种基于抽象线性数学的数学框架，它采用非线性运算代替线性算术运算，如加、减和数乘运算，可以更加准确地表示图像计算中的非线性特性。在LIP模型中，一幅图像可以近似理解为，近光通过一个光滤波器形成了图像，其吸收函数称之为灰度色调函数。图像的灰度级则表示为通过光滤波器的光的总量，每一个像素点的灰度色调函数称为该点的灰色调g(i,j)，并且它与像素点灰度值f(i,j)的关系为g(i,j)=M-f(i,j)，其中，M为光源强度。LIP模型利用对数法则和人类视觉系统处理光线时的对数特性，更加符合物理特性，例如：LIP模型中的加法运算与透光率图像形成模型和人眼的饱和度特性一致。表1中列出了相应的LIP运算。
PLIP模型是改进后的LIP模型，它使用参数化的灰度色调函数对算法进行操作，表1给出了PLIP运算[6]。这些运算使用了参数化后的灰度色调函数g(i,j)。用来计算灰度色调函数的μ(M)可以依据实际图像进行调整，可取图像中灰度的最大值，或者取更大的值，如μ(M)=1046。图像的加和数乘运算均使用了参数γ(M)，可将数乘理解为由相加进行多次得到的。
表1中，f(i,j)表示原始灰度图像；g(i,j)、g1、g2表示灰度色调函数；c为常量；参数μ(M)、γ(M)、k(M)是关于M的函数，可依据不同的图像对参数进行调整。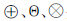
分别为LIP的加、减和数乘运算，
则为PLIP的加、减和数乘运算。
LIP运算利用对光吸收滤波器进行建模，PLIP进行了LIP扩展，引入部分参数，并通过调整这些参数，可设计各种类型的光滤波器，具有很强的稳健性。
3.1.2 PLIP LA算法(Lee algorithm,LA)文献[6]提出了一种常用的图像增强算法，可具体表示为
式中，F(i,j)和F′(i,j)分别表示原始图像和处理后图像的像素值；A(i,j)表示中心位于(i,j)处n×n大小的窗口内像素灰度值的平均值；θ、ζ表示权重系数。
LA方法先将图像分成平滑图像和差值图像两部分，然后将这两部分与权重系数相乘后并相加。使用LIP算子对LA进行扩展，可将其用于图像增强。亦可采用PLIP算子对LA进一步扩展，形成PLIP LA，公式为
式中，f′(i,j)表示输出灰度色调函数；f(i,j)表示输入灰度色调函数；a(i,j)为给定像素邻域内的像素的PLIP平均值；η、δ是权重系数。
采用PLIP LA方法增强图像的同时，会放大图像中的噪声。而对于图像的低频分量，由于它是对源图像的近似，大体反映图像概貌，基本不含边缘、区域轮廓等高频细节信息，在采用PLIPLA对低频分量增强时，提高图像对比度的同时可以抑制噪声的放大。故本文仅针对NSST分解后的低频分量进行PLIP增强，抑制高频噪声，提高图像的对比度，突出目标特征，改善图像的视觉效果。
3.2 基于改进模糊增强的高频分量调整经NSST分解后的低频分量包含原始图像的大量基本信息，且基本滤除了噪声。而图像经NSST分解后的高频分量主要包含图像在各个方向的边缘细节信息。本文采用改进的模糊增强方法对高频分量进行增强，改善边缘纹理等细节。
在模糊算法中，构造的隶属度函数为[22] 式中，Fp和Fe分别为倒数模糊参数和指数模糊参数，其影响模糊平面的不确定性；T()表示隶属度变换，将图像的灰度值映射到模糊域；dij为当前像素的灰度值；dmax是最大灰度值；Fp∈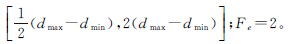
接着采用广义对比度增强算子对μij进行增强，即
式中，乘幂q取2。式(13)中的阈值α通常设置为0.5，但往往并不合理。本文采用OTSU[23]算法自适应地选取最佳阈值α。OTSU方法即将图像中的像素按灰度值以阈值T分成两类，即类C1和类C2。第1类C1由灰度值在[0,T]之间的像素组成，第2类C2由灰度值在[T+1,255]之间的像素组成。第1类与第2类之间的类间方差为
式中，W1(t)和W2(t)分别为C1和C2中包含的像素数占图像总像素数的比例；U1(t)和U2(t)分别为C1和C2中像素平均灰度值；T在[0, 255]内依次取值，使得类间方差最大的T值即为OTSU最佳阈值α。
最后对调整后的隶属度μ′ij进行T-1逆变换，得到增强后(i,j)位置上的高频系数Dij，即
3.3 本文方法的具体步骤
(1) 对遥感图像进行非下采样Shearlet变换，得到低频分量和高频分量；
(2) 依据3.1节对低频分量采用PLIP LA算法进行调整，增强图像的对比度，抑制高频噪声；
(3) 根据式(13)对高频分量进行调整，增强边缘细节和纹理细节特征；
(4) 对调整后的高频分量和低频分量进行非下采样Shearlet逆变换，得到增强后的图像。
基于NSST和PLIP的遥感图像增强方法的具体流程如图2所示。
|
| 图 2 本文方法流程图 Fig. 2 Flowchart of proposed method |
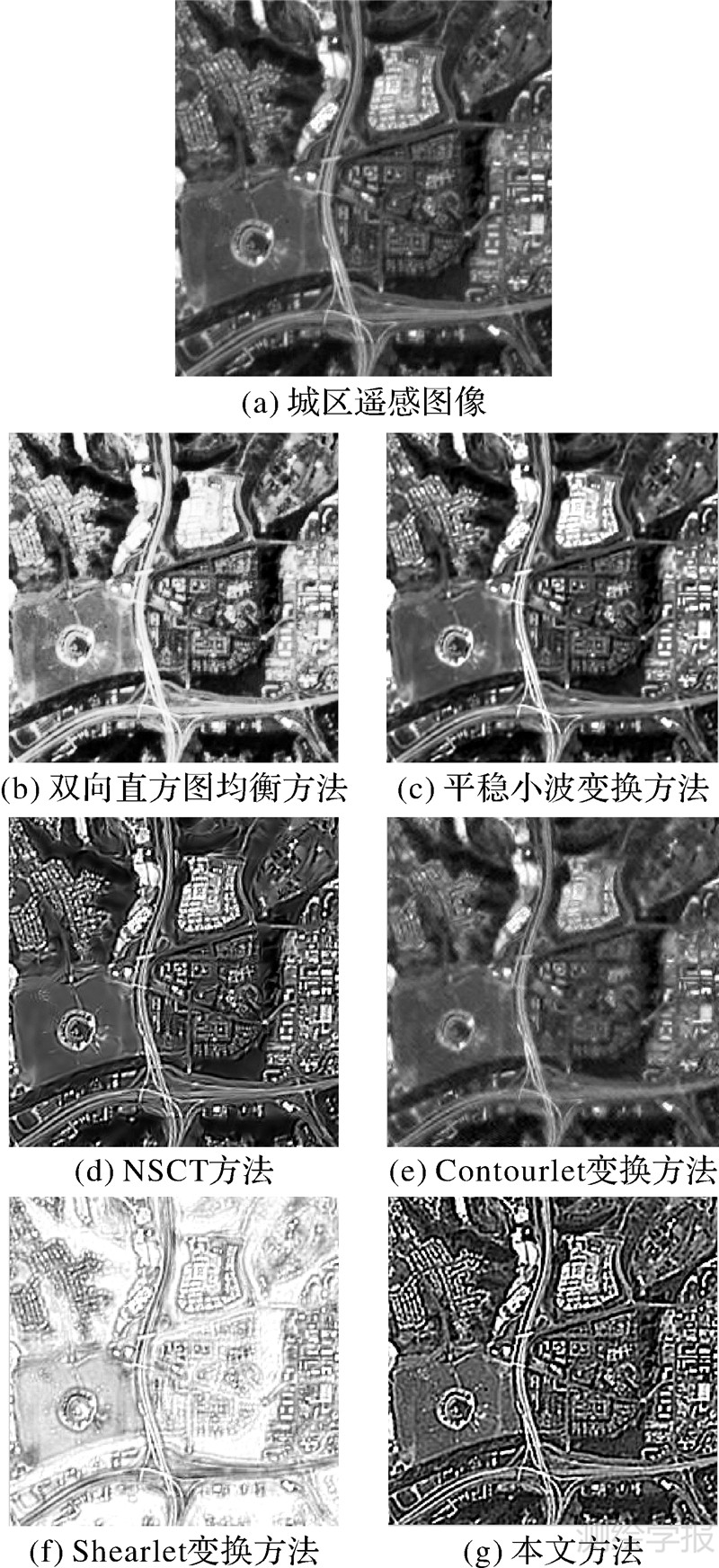
为了验证本文方法对遥感图像增强的有效性，利用本文提出的基于非下采样Shearlet变换和参数化对数图像处理模型的图像增强方法对大量遥感图像进行了增强处理试验，作了大量测试，并与传统的双向直方图均衡、以及近年来提出的基于平稳小波变换[10]、基于Contourlet变换[14]、基于NSCT[16]、基于Shearlet变换[17]等5种图像增强方法的增强结果进行了比较。由于篇幅限制，现以3组遥感图像为例加以说明。图3给出了某地区的土地遥感图像及其6种方法的增强结果。其中，图3(a)为土地遥感图像，有点模糊不清，图像大小为512像素×512像素。图4为某地区的沉积岩遥感图像及其6种方法的增强结果，其中，图4(a)为沉积岩遥感图像，图像大小为512像素×512像素。图5为某地区的城区遥感图像及其6种方法的增强结果，其中，图5(a)为城区遥感图像，图像大小为256像素×256像素，为SPOT影像的全色波段图像。
|
| 图 3 土地遥感图像及6种方法的增强结果 Fig. 3 Land remote sensing image and results of six enhancement methods |
|
| 图 4 沉积岩遥感图像及6种方法的增强结果 Fig. 4 Sedimentary rocks remote sensing image and results of six enhancement methods |
|
| 图 5 城区遥感图像及6种方法的增强结果 Fig. 5 Urban remote sensing image and results of six enhancement methods |
试验参数设置如下：非下采样Shearlet变换中，采用“maxflat”滤波器进行尺度分解，方向分解级数取2，各层带通方向子带数目为[6, 6]；PLIP模型算法参数μ(M)=1206，k(M)=γ(M)=500，η=0.9，δ=15。Contourlet变换、NSCT、Shearlet的方向分解级数均取[2, 3]，两层带通方向子带数目即为4和8。图像增强试验环境：CPU为Intel core i2，2.0GHz，内存为2GB的PC机，32位Win7操作系统，Matlab版本为Matlab7.8.0 (R2009a)。
由于受天气环境等因素的影响，图3(a)的遥感图像有些模糊不清，图3(b)为采用双向直方图均衡增强后的结果，图像的对比度很高，但图像的亮度却发生了很大的变化，使图像的整体视觉效果变差，并且图像中较暗区域的细节信息较难以辨认；图3(c)为基于平稳小波变换方法的增强结果，增强效果较好。图3(d)是基于NSCT方法的增强结果，图像中的道路区域对比度不够明显。图3(e)为基于Contourlet变换方法的增强结果，该方法的增强效果较差，与原始图像相差不大。图3(f)为基于Shearlet变换方法增强的结果，增强后失真度较大，图像过亮，细节不清楚。图3(g)为本文方法的增强结果，可见图像中房屋、道路等细节对比度明显，边缘轮廓细节最清晰，视觉效果最佳。图4(a)是原始沉积岩遥感图像，图4(b)为采用双向直方图均衡的增强结果，图中的细节信息不够清晰，对比度偏低。图4(c)为基于平稳小波变换方法的增强结果，该方法在亮度大的地方，细节表现不够清楚。图4(d)为基于NSCT方法的增强结果，图中的纹理较为清晰。图4(e)是基于Contourlet变换方法的增强结果，该方法的增强结果不够清楚，有些模糊，效果较差。图4(f)为基于Shearlet变换方法的增强结果，增强后图像失真度较大，图像过亮，细节模糊。图4(g)为利用本文方法的增强结果，可见图像边缘轮廓细节最为清晰，纹理较为丰富，视觉效果最佳。图5(a)的城区遥感图像细节不清楚，对比度偏低；图5(b)为采用双向直方图均衡增强后的结果，但图像的亮度却发生了很大的变化，使图像的整体视觉效果变差，图像过亮，细节很不清楚；图5(c)为基于平稳小波变换方法的增强结果，部分区域过亮；图5(d)是基于NSCT方法的增强结果，增强效果较好，细节仍有待加强；图5(e)为基于Contourlet变换方法的增强结果，该方法的增强效果较差，细节模糊；图5(f)为基于Shearlet变换方法增强的结果，增强后的失真度较大，图像过亮，细节极不清楚；图5(g)为本文方法的增强结果，边缘轮廓细节最清晰，增强效果最佳。从3组图像的主观视觉效果来看，本文方法的增强效果最佳。
为了客观定量评价上述6种方法的增强结果，表2给出了采用上述6种方法增强后图像的对比度增益、清晰度增益、信息熵、熵增强EMEE等4种客观定量指标[24]。
| 增强方法 | 图3 | 图4 | 图5 | ||||||||||||
| 对比度增益 | 清晰度增益 | 信息熵 | EMEE | 综合指标 | 对比度增益 | 清晰度增益 | 信息熵 | EMEE | 综合指标 | 对比度增益 | 清晰度增益 | 信息熵 | EMEE | 综合指标 | |
| 平稳小波变换方法 | 2.342 | 1.635 | 5.170 | 2.629 | 2.753 | 1.774 | 1.420 | 4.825 | 10.724 | 4.068 | 1.925 | 1.501 | 5.284 | 8.173 | 3.719 |
| Contourlet方法 | 1.056 | 1.164 | 4.802 | 0.563 | 1.739 | 0.958 | 0.836 | 5.368 | 9.856 | 3.583 | 0.960 | 0.910 | 5.123 | 2.446 | 2.074 |
| NSCT方法 | 1.322 | 1.882 | 4.899 | 1.901 | 2.321 | 1.417 | 2.301 | 4.966 | 9.639 | 4.036 | 1.861 | 2.480 | 5.186 | 18.830 | 6.105 |
| Shearlet方法 | 1.192 | 1.656 | 4.809 | 0.774 | 1.971 | 0.263 | 0.831 | 4.422 | 0.736 | 1.359 | 0.722 | 1.318 | 4.408 | 1.018 | 1.697 |
| 双向直方图均衡方法 | 3.844 | 1.951 | 4.642 | 4.351 | 3.537 | 1.110 | 1.052 | 5.247 | 10.284 | 3.754 | 2.561 | 1.052 | 5.247 | 8.161 | 3.765 |
| 本文方法 | 2.472 | 2.543 | 5.115 | 3.403 | 3.208 | 1.483 | 1.558 | 5.320 | 10.979 | 4.172 | 1.971 | 2.209 | 5.244 | 19.264 | 6.155 |
图像的对比度C的计算公式为
式中，M、N分别代表图像f(i,j)的大小；对比度越大，增强后的图像视觉效果越好。
信息熵，即平均信息量，其定义为
式中，P(xi)是灰度值为xi的像素数L(xi)与总像素数L之比，即P(xi)=L(xi)/L。图像信息熵反映了图像包含信息量的大小，熵越大，说明图像的信息量越大，效果也越好。
清晰度定义为图像的空间频率，它反映图像的总体活跃程度，空间频率越大，图像越活跃。对M×N的矩阵，其空间频率MSF为
式中，RF为行频率，CF为列频率，RF、CF计算公式为
熵增强EMEE的计算公式为
计算EMEE时，首先将图像f(i,j)划分为k1×k2个相同子块，fmax i,j和fmin i,j分别表示子块(i,j)中的最大值和最小值，其中一般取α=1，子块的大小取为4×4。
为综合这几个评价标准，选取一个综合指标来评价最终遥感图像的增强效果。图像的清晰度和对比度是反映图像质量的重要参数，取权重系数各为0.3，信息熵和EMEE各取0.2。故定义指标E=对比度增益×0.3+清晰度增益×0.3+信息熵×0.2+EMEE×0.2，将其作为综合评价指标，评价遥感图像的增强效果，具体结果如表2所示。
从表2可以看到，基于Contourlet变换方法的增强结果对比度增益最低，清晰度也较低，增强效果较差。其次是基于Shearlet变换的增强方法，在各类指标上均不占优势，图像视觉效果也较差，图像过亮。基于NSCT方法的增强结果，效果有一定的改善，但不是最佳。对土地遥感图像而言，利用双向直方图均衡增强后的对比度增益最高，但图像存在着过增强，视觉效果反而不佳。而对图4(a)沉积岩遥感图像而言，基于平稳小波变换方法增强后的图像对比度较高，但清晰度偏低，在亮度大的区域，细节表现不好。本文方法综合来看，视觉效果最佳，在清晰度增益、信息熵、EMEE指标上优势明显。从综合评价指标看，采用双向直方图均衡方法的第一幅图像，其综合指标值最高，但该图像存在过增强现象，视觉效果并不好，细节模糊。而其他两幅图像，本文方法所得结果的综合指标值最高，从视觉效果中也得到了验证。
5 结 论本文提出了一种基于非下采样Shearlet变换和参数化对数图像处理模型的遥感图像增强方法。首先对遥感图像进行非下采样Shearlet分解后，得到低频分量和高频分量。利用PLIP LA算法对低频分量进行调整，增强低频图像的对比度，抑制高频噪声；利用改进模糊增强方法对高频方向分量进行调整，最后经过非下采样Shearlet逆变换得到增强后的遥感图像。针对所提出的方法进行了大量的遥感图像增强试验，并与传统的双向直方图均衡、基于平稳小波变换、Contourlet变换、NSCT等5种增强方法进行了比较。结果表明：在主观视觉效果和对比度增益、清晰度等客观定量评价指标两个方面，本文提出的方法均有优势，能得到更好的视觉效果，更有效地提高了遥感图像的对比度，突出了边缘细节，可为后续遥感图像解译提供有效的支持。
| [1] | LEE E, KIM S, KANG W, et al. Contrast Enhancement Using Dominant Brightness Level Analysis and Adaptive Intensity Transformation for Remote Sensing Images[J]. IEEE Geoscience and Remote Sensing Letters, 2013, 10(1): 62-66. |
| [2] | JANG J H, KIM S D, RA J B. Enhancement of Optical Remote Sensing Images by Subband-Decomposed Multiscale Retinex with Hybrid Intensity Transfer Function[J]. IEEE Geoscience and Remote Sensing Letters, 2011, 8(5): 983-987. |
| [3] | WU Zhaocong, HU Zhongwen, ZHANG Qian, et al. On Combining Spectral, Textural and Shape Features for Remote Sensing Image Segmentatiton[J]. Acta Geodaetica et Cartographica Sinica, 2013, 42(1): 44-50. (巫兆聪, 胡忠文, 张谦, 等. 结合光谱, 纹理与形状结构信息的遥感影像分割方法[J]. 测绘学报, 2013, 42(1): 44-50.) |
| [4] | KNAG Mu, WANG Baoshu. An Image Filtering Algorithm with Image Enhancement[J]. Geomatics and Information Science of Wuhan University, 2009, 34(7): 822-825. (康牧, 王宝树. 一种基于图像增强的图像滤波方法[J]. 武汉大学学报: 信息科学版, 2009, 34(7): 822-825.) |
| [5] | XIONG Xinghua, QIAN Zengbo, CHEN Ying, et al. Remote Sensing Image Enhancement Based on Genetic Optimization[J]. Acta Geodaetica et Cartographica Sinica, 2004, 33(4): 341-346. (熊兴华, 钱曾波, 陈鹰, 等. 基于遗传优化的分段线性影像增强[J]. 测绘学报, 2004, 33(4): 341-346.) |
| [6] | JOURLIN M, PINOLI J C. A Model for Logarithmic Image Processing[J]. Journal of Microscopy, 1988, 149(1): 21-35. |
| [7] | PANETTA K A, WHARTON E J, AGAIAN S S. Human Visual System-based Image Enhancement and Logarithmic Contrast Measure[J]. IEEE Transactions on Systems, Man, and Cybernetics, Part B: Cybernetics, 2008, 38(1): 174-188. |
| [8] | PANETTA K, AGAIAN S, ZHOU Y, et al. Parameterized Logarithmic Framework for Image Enhancement[J]. IEEE Transactions on Systems, Man, and Cybernetics, Part B: Cybernetics, 2011, 41(2): 460-473. |
| [9] | WHARTON E J, PANETTA K, AGAIAN S S. Logarithmic Edge Detection with Applications[C]//IEEE International Conference on Systems, Man and Cybernetics.Montreal, Que.: IEEE, 2007: 3346-3351. |
| [10] | GONG Changlai, LUO Cong, YANG Dongtao, et al. Infrared Image Enhancement Method Based on Stationary Wavelet Domain[J]. Laser & Infrared, 2013, 43(6): 703-707. (龚昌来, 罗聪, 杨冬涛, 等. 一种基于平稳小波域的红外图像增强方法[J]. 激光与红外, 2013, 43(6): 703-707.) |
| [11] | DEMIREL H, ANBARJAFARI G. Image Resolution Enhancement by Using Discrete and Stationary Wavelet Decomposition [J]. IEEE Transactions on Image Processing, 2011, 20(5): 1458-1460. |
| [12] | DEMIREL H, OZCINAR C, ANBARJAFARI G. Satellite Image Contrast Enhancement Using Discrete Wavelet Transform and Singular Value Decomposition [J]. IEEE Transactions on Geoscience and Remote Sensing Letters, 2010, 7(2): 333-337. |
| [13] | WANG X H, ISTEPANIAN R S H, SONG Y H. Microarray Image Enhancement by Denoising Using Stationary Wavelet Transform [J]. IEEE Transactions on Nano Bioscience, 2003, 2(4): 184-189. |
| [14] | PENG Zhou, ZHAO Baojun. Novel Scheme for Infrared Image Enhancement Based on Contourlet Transform and Fuzzy Theory[J]. Laser & Infrared, 2011, 41(6): 635-640. (彭州, 赵保军. 基于Contourlet变换和模糊理论的红外图像增强算法[J]. 激光与红外, 2011, 41(6): 635-640.) |
| [15] | CHEN Zhigang, YIN Fuchang. Enhancement of Remote Sensing Image Based on Contourlet Transform [J]. Optics and Precision Engineering, 2008, 16(10): 2030-2037. (陈志刚, 尹福昌. 基于Contourlet变换的遥感图像增强算法[J]. 光学精密工程, 2008, 16(10): 2030-2037.) |
| [16] | LIANG Dong, YIN Bing, YU Mei, et al. Image Enhancement Based on the Nonsubsampled Contourlet Transform and Adaptive Threshold[J]. Acta Electronica Sinica, 2008, 36(3): 527-530. (梁栋, 殷兵, 于梅, 等. 基于非抽样Contourlet变换的自适应阈值图像增强算法[J]. 电子学报, 2008, 36(3): 527-530.) |
| [17] | YANG Bo, JIA Zhenhong, QIN Xizhong, et al. Remote Sensing Image Enhancement Based on Shearlet Transform[J]. Journal of Optoelectronics·Laser, 2013, 24(11): 2249-2253. (杨波, 贾振红, 覃锡忠, 等. 基于Shearlet变换的遥感图像增强[J]. 光电子·激光, 2013, 24(11): 2249-2253.) |
| [18] | LIM W Q. Nonseparable Shearlet Transform[J]. IEEE Transactions on Image Processing, 2013, 22(5): 2056-2065. |
| [19] | FENG Wensen, LEI Hong. Single-image Super-resolution with Total Generalised Variation and Shearlet Regularisations[J]. IEEE Transactions on Image Processing, 2014, 8(12): 833-845. |
| [20] | GAO Guorong, XU Luping, FENG Dongzhu. Multi-focus Image Fusion Based on Non-Subsampled Shearlet Transform[J]. IEEE Transactions on Image Processing, 2013, 7(6): 633-639. |
| [21] | DENG G, CAHILL L W, TOBIN G R. The Study of Logarithmic Image Processing Model and Its Application to Image Enhancement [J]. IEEE Transactions on Image Processing: A Publication of the IEEE Signal Processing Society, 1994, 4(4): 506-512. |
| [22] | LI Guo, GONG Zhihui, YOU Hui, et al. Application of Improved Adaptive Genetic Algorithms in Image Fuzzy Enhancement [J]. Science of Surveying and Mapping, 2012, 37(2): 77-79. (李国, 龚志辉, 尤辉, 等. 改进的自适应遗传算法在图像模糊增强中的应用[J]. 测绘科学, 2012, 37(2): 77-79.) |
| [23] | LI Min, LUO Hongyan, ZHENG Xiaolin, et al. Image Segmentation Based on Improved Otsu Algorithm[J]. Journal of Nanjing University of Science and Technology, 2012, 36(2): 332-337. (李敏, 罗洪艳, 郑小林, 等. 一种改进的最大类间方差图像分割法[J]. 南京理工大学学报, 2012, 36(2): 332-337.) |
| [24] | PANETTA K, ZHOU Yicong, AGAIAN S, et al. Nonlinear Unsharp Masking for Mammogram Enhancement [J]. IEEE Transactions on Information Technology in Biomedicine, 2011, 15(6): 918-928. |