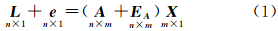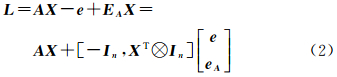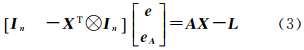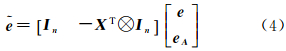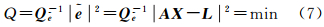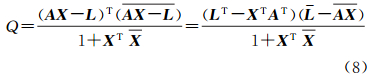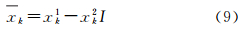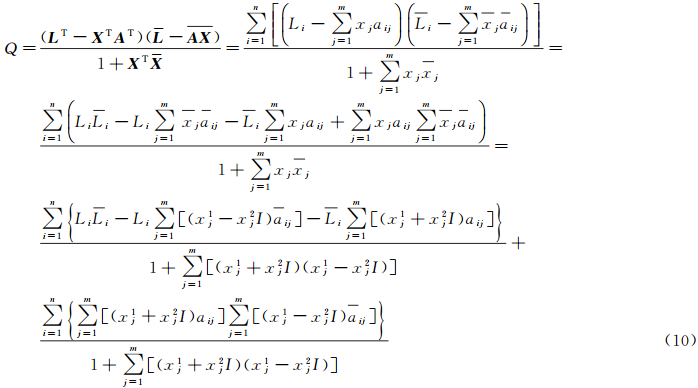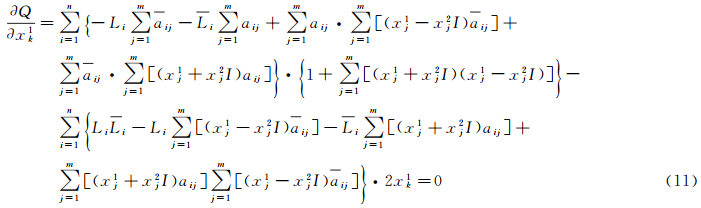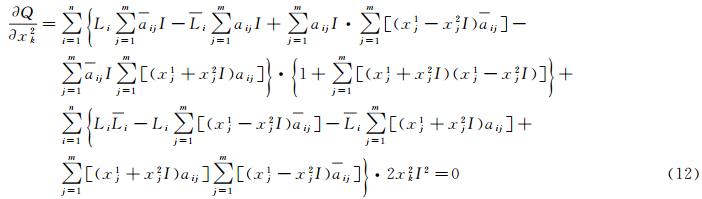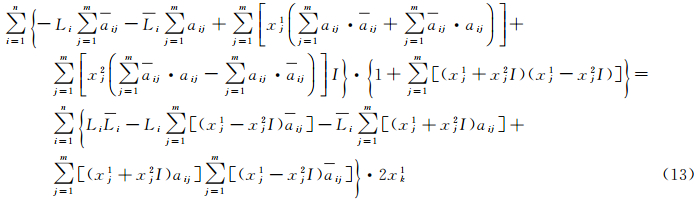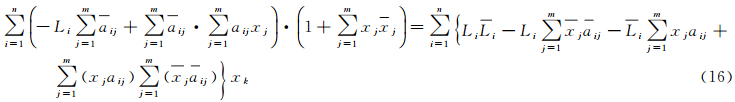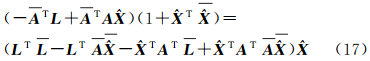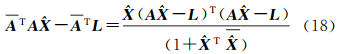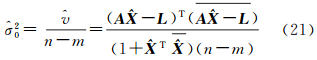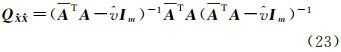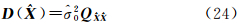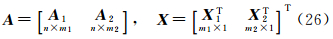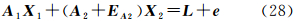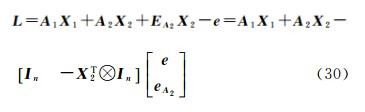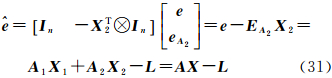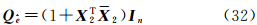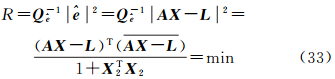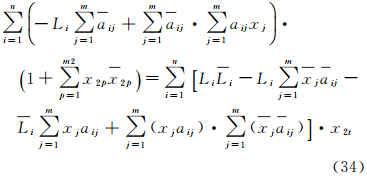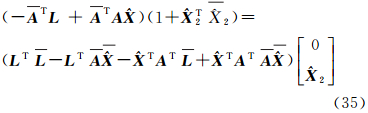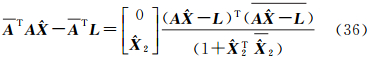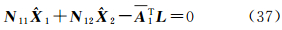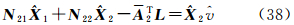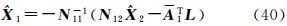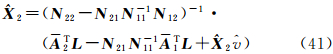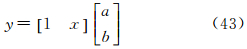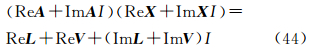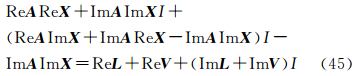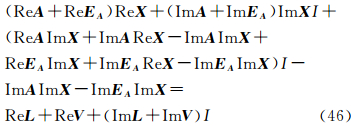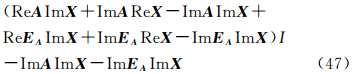2. 江西省数字国土重点实验室, 江西 南昌 330013;
3. 流域生态与地理环境监测国家测绘地理信息局重点实验室, 江西 南昌 330013
2. Jiangxi Province Key Laboratory for Digital Land, Nanchang 330013, China;
3. Key Laboratory of Watershed Ecology and Geographical Environment Monitoring, NASG, Nanchang 330013, China
1 引 言
在测量数据处理中经典最小二乘法的应用最为广泛，各种新方法、新公式的推导都是在经典最小二乘的基础上进行的，然而，这些研究都是在实数域内进行的。在复数域内，最小二乘同样发挥着重要的作用，但其研究比较少，在当前的复数最小二乘算法研究中，文献[1]最早提出了复数线性最小二乘算法，探讨了最小二乘估计、线性最优无偏估计及马尔科夫估计之间的关系，得出在一定条件下，最小二乘估计和马尔科夫估计两者等价；文献[2]在平差准则1下将目标函数矢量具体化后推导了复数最小二乘方法的估计公式；文献[3]和文献[4]研究了基于U-D分解的复数最小二乘估计方法，推导了既加权又使用遗忘因子的复参数最小二乘估计方法；文献[5]给出了复数最小二乘估计公式的证明，验证了该算法的有效性；文献[6]探讨了以相对误差为平差准则的复数最小二乘估计法，改进了一般复数最小二乘算法，并通过算例说明了该改进算法的优势。在应用方面，目前复数域最小二乘主要被应用在汛期预报[2]、解决如何确定复自忆系数问题[7]、月平均气温的预报[8]、地震传感器的相对和绝对定向[9]、逆变器故障实时监测[10]、PolInSAR 植被高反演[11]中。实数域内，由于最小二乘平差准则只考虑了观测向量含有误差的情况，而假定系数矩阵不受噪声的扰动影响，而在有些情况下，如在坐标转换中，此时的系数矩阵元素并不是精确值，而是通过测量得到的坐标数据组成，这时系数矩阵就必然含有误差，如果仅考虑观测量的误差显然是不合理的；因此，近年来针对实数域内系数矩阵含有误差的总体最小二乘方法进行了大量的研究[12, 13, 14, 15, 16, 17, 18, 19, 20, 21, 22, 23, 24, 25, 26]。在复数域中，系数矩阵含有误差的情况是同样存在的，虽然复数域最小二乘的相关研究已经取得一定的成果，但在复数总体最小二乘方面，国内外未见相关研究报道。本文基于复数域内最小二乘的基础上，提出复数域内总体最小二乘平差方法，并推导了复数总体最小二乘和复数混合总体最小二乘的估计公式，通过两个算例比较分析了复数观测值的残差的模的平方和最小(平差准则1)下[2, 11]的复数最小二乘、复数观测值的残差的实部和虚部的平方和分别最小(平差准则2)下[11]的复数最小二乘、复数观测值和系数矩阵的残差的模的平方和最小(平差准则3)下的复数总体最小二乘以及复数观测值和系数矩阵的残差的实部和虚部的平方和分别最小(平差准则4)下的复数总体最小二乘方法计算得到的结果，得出在复数观测向量和系数矩阵都含有误差且独立等精度的情况下，平差准则3下的复数总体最小二乘要优于平差准则1下的复数最小二乘；平差准则3下复数总体最小二乘和平差准则1下复数最小二乘要分别比在平差准则4和平差准则2下得到的结果稳定和合理。在下文中，对相应的平差准则分别简称为平差准则1和平差准则2等。
2 复数域内总体最小二乘平差模型为
式中，L为观测值向量；e为观测值的噪声；A为n×m的系数矩阵；EA为系数矩阵的噪声；X为m个未知参数且A、L、e、EA、X都为复数。将式(1)改写为
式中，eA=vec(EA)为EA的按列拉直变换；
为Kronecker直积；
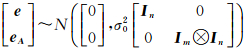因此，式(2)可以表示为
令
于是式(3)可以改写为
定义：设复随机向量Y=AX+B，其中，Y、X、B是m×1向量，A是m×m复数矩阵，X~CN(0,Im)，则Y服从的分布为[27]
式中，CN为复数标准正态分布。
根据式(4)及上述定义，由协因数传播定律容易得到e协因数阵为
式中，( )表示共轭。则满足平差准则3的目标函数为
在实数域内，式(7)对X求偏导并令等式为零即可求得参数的最佳估值；但在复数域内，不能像实数那样直接求导[2]，又因为在数学中，模的平方等于实部的平方加上虚部的平方，所以将式(7)写成矢量形式，即
令xk=xk1+xk2I (k=1,2,3,…,m)
则
式中，xk1为实部；xk2为虚部；xk1、xk2均为实变量；I为复数单元；xk表示X的每个分量。
这样对参数X中每个分量的求导便可以转化为分别对实部xk1及虚部xk2求偏导并分别令其偏导等于零，且在对虚部求偏导过程中存在的I2不求出其具体值即-1，而是保持其为I2的形式。为此，把Q的每一项具体写出
式中，xj为参数X的第j个具体参数；aij为系数矩阵A中第i行第j列对应的具体元素；Li表示L中第i个观测量。
Q对实部xk1求偏导并令其等于零，即
同理，Q对虚部xk2求偏导并令其等于零，得
将式(11)移项并整理得
将式(12)移项并整理得
式(13)减式(14)得
将式(15)简化为
将式(16)表示成
式中，
为X的估计量。将式(17)进一步简化为
令
则式(18)可表示为
式(20)可以通过迭代解算得到参数估值，计算步骤如下：
时，计算结束(ε是个微小量)。
由文献[1]中单位权方差的极大似然估计可知，复数域内的单位权方差估计原理同实数域内是一致的，因此本文中单位权方差的估计可以通过式(21)得到
由式(20)可得
由协因数传播律可得
因此，参数的协方差阵为
3 复数域内混合总体最小二乘
设函数模型为
假设矩阵A1没有误差影响，m=m1+m2，并且A1、A2均为列满秩，将其系数矩阵进行分块处理如下
则式(25)可以表示为
顾及系数矩阵和观测向量的误差，混合总体最小二乘函数模型为
且假定误差向量
将式(28)改写成
式中，eA2=vec(EA2)，令
与式(6)同理，根据式(31)可以得出e的协因数阵为
于是平差准则可以表示为
令x2t=x2t1+x2t2I (t=1,2,3,…,m2)，则x2t=x2t1-x<2tsup>2I，式中，x2t1为实部；x2t2为虚部；x2t1、x2t2均为实变量；I为复数单元；x2t表示X2的每个分量。将R的每一项具体写出，对参数的每个分量的实部和虚部求偏导并令其等于零后整理可得
式中，x2p表示参数X2中的第p个具体参数。令、2分别为参数X、X2的估值，由式(34)可得
式(35)可简化为
将A=[A1 A2],X=[X1T X2T]T代入式(36)得
式中
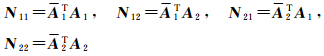
因为A1为列满秩矩阵，所以N11也为满秩矩阵，且存在唯一逆矩阵，则由式(37)可以得到
将式(40)代入式(38)并整理得
2可以通过迭代解算得到，步骤如下：
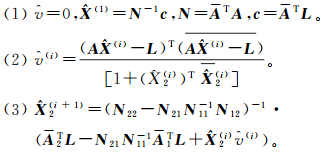
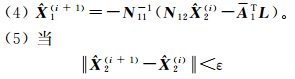
时计算结束(ε为微小量)。
本文中，在平差准则4下总体最小二乘是将系数矩阵和观测向量残差的实部和虚部分开分别利用实数域内总体最小二乘迭代算法分别得到参数估值的实部和虚部值，将两者结合得到复数参数的最终估值。
4 算例与分析 4.1 算例1模拟系数矩阵和参数真值，并对系数矩阵A和观测向量L分别加入服从正态分布的误差。模拟数据如下，系数矩阵A的真值为
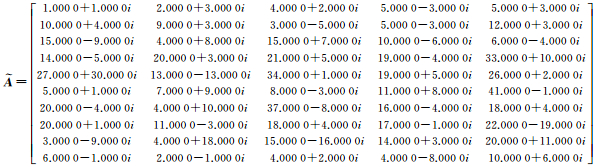
参数X的真值为
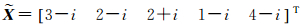
观测向量L的真值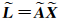
。对系数矩阵
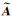和观测向量
分别加入服从同一正态分布的误差即e~N(0,σ02 I10),EA~N(0,σ02 I50 )，本文中σ02取值为0.01，由Matlab随机给出。具体解算方案见表 1，表 1中4种方案模拟100次结果的平均值见表 2。
| 方案 | 方 法 |
| 1 | 复数观测值的残差的模的平方和最小(平差准则1)下的复数最小二乘方法 |
| 2 | 复数观测值的残差的实部和虚部的平方和分别最小(平差准则2)下的复数最小二乘方法 |
| 3 | 复数观测值和系数矩阵的残差的模的平方和最小(平差准则3)下的复数总体最小二乘方法 |
| 4 | 复数观测值和系数矩阵的残差的实部和虚部的平方和分别最小(平差准则4)下的复数总体最小二乘方法 |
| 方案1 | 方案2 | 方案3 | 方案4 | 真值 | |
| 3.003 340 83-1.000 687 64i | 1.004 037 30-1.728 913 29i | 3.003 945 46-1.000 672 18i | 0.084 396 28-5.288 390 62i | 3-i | |
| 2.000 710 70-1.002 189 43i | 2.163 272 39-4.740 143 88i | 2.001 339 66-1.002 497 03i | 5.298 365 82-10.218 177 00i | 2-i | |
| 1.998 290 09+0.999 535 14i | 4.026 257 04-1.293 460 00i | 1.998 290 20+0.999 679 04i | 7.055 812 25-4.111 981 57i | 2+i |
| 0.997 514 01-0.994 099 19i | -0.850 242 39+2.503 706 61i | 0.996 646 74-0.994 561 71i | -7.767 501 99+4.696 560 29i | 1-i | |
| 3.998 853 55-1.004 069 73i | 4.913 143 71+4.653 193 54i | 3.998 791 41-1.003 960 90i | 5.896 062 77+6.050 186 36i | 4-i | |
| 0.038 621 73 | 0.080 778 11 | 0.038 645 48 | 0.195 657 75 | ||
| 标准差 | 0.045 730 50 | 0.120 452 85 | 0.045 758 26 | 0.368 880 93 | |
| 0.027 360 04 | 0.119 846 50 | 0.027 366 43 | 0.446 910 54 | ||
| 0.060 595 36 | 0.179 466 61 | 0.060 641 39 | 0.648 054 57 | ||
| ‖ΔX‖ | 0.025 287 67 | 0.055 409 73 | 0.025 296 60 | 0.160 127 38 | |
| 0.089 296 30 | 8.743 591 78 | 0.089 280 72 | 18.376 667 09 |
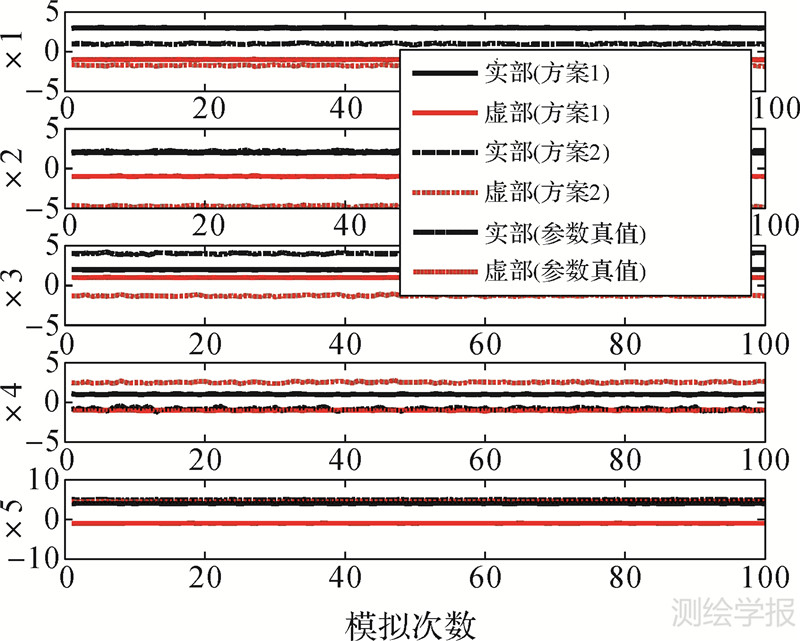
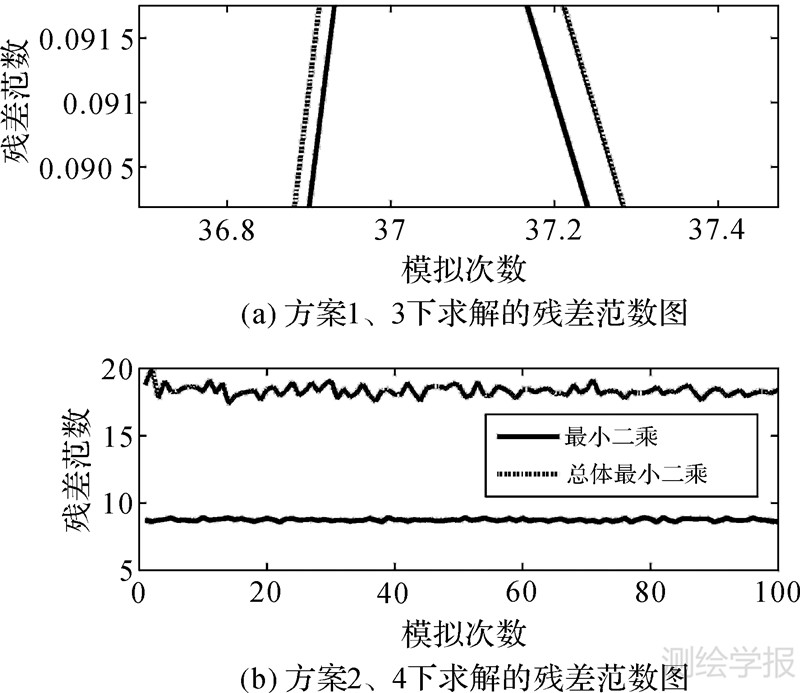
参数的变化图和残差(估值与真值之差)范数‖ΔX‖的变化图如图 1-3所示，图 3的局部放大图如图 4所示。本文将参数估值的实部和虚部进行分开单个显示在图形上，图中黑色线条为实部，红色线条为虚部。
|
| 图 1 不同方案下复数最小二乘参数估值变化 Fig. 1 The map of parameters of CLSAM under different adjustment criterions |
|
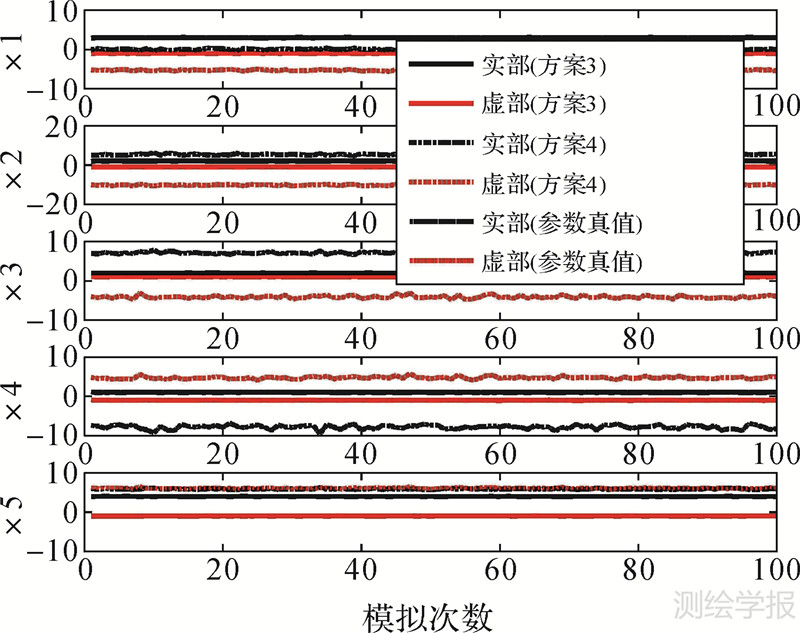
| 图 2 不同方案下复数总体最小二乘参数估值变化 Fig. 2 The map of parameters of CTLSAM under different adjustment criterions |
|
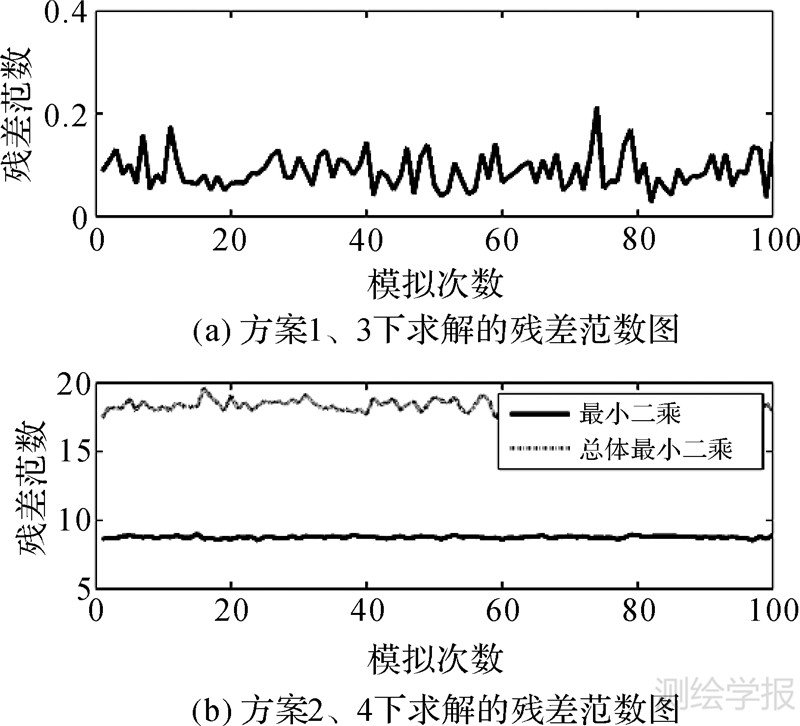
| 图 3 不同方案下参数估值与真值残差范数图 Fig. 3 The map of the norm of the parameters residual under different methods |
|
| 图 4 对图3结果的放大图 Fig. 4 The map of amplification to Fig.3 |
将文献[11]中简单例子加以修改，利用复数域线性模型y=a+bx构造算例，其中待求参数a、b的真值为[3-i 1+2i]T，x及y的真值为[11]
将式(42)模型变为
在Matlab中对y和x分别加入服从同一正态分布的复数模拟误差，模拟方差σ2取值为1；由于系数矩阵中有一列为常数项，应用复数域内混合总体最小二乘来进行参数的求解。结果同样为模拟100次的平均值，利用表 1中4种方案计算得到的结果见表 3，参数估值和残差(估值与真值之差)范数变化如图 5-图 7所示。
|
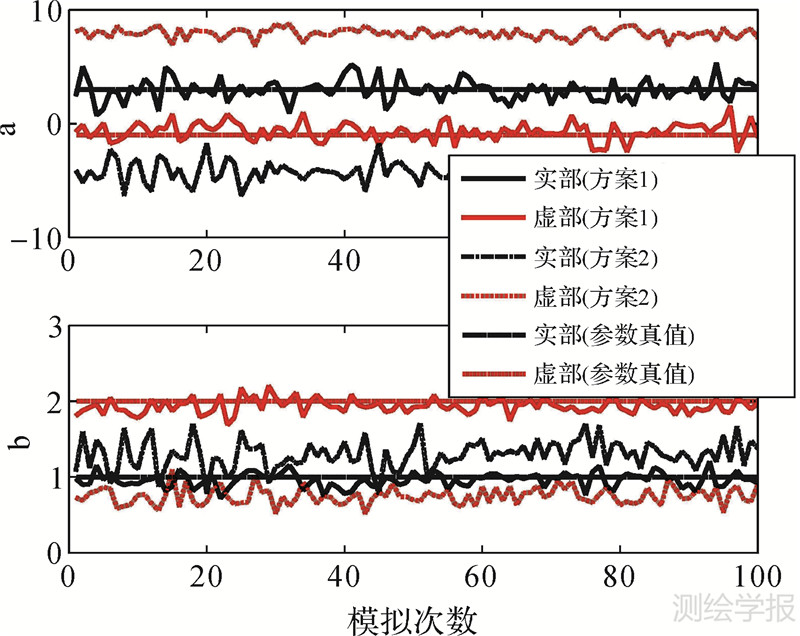
| 图 5 不同方案下复数最小二乘参数估值变化图 Fig. 5 The map of parameters of CLSAM under different adjustment criterions |
|
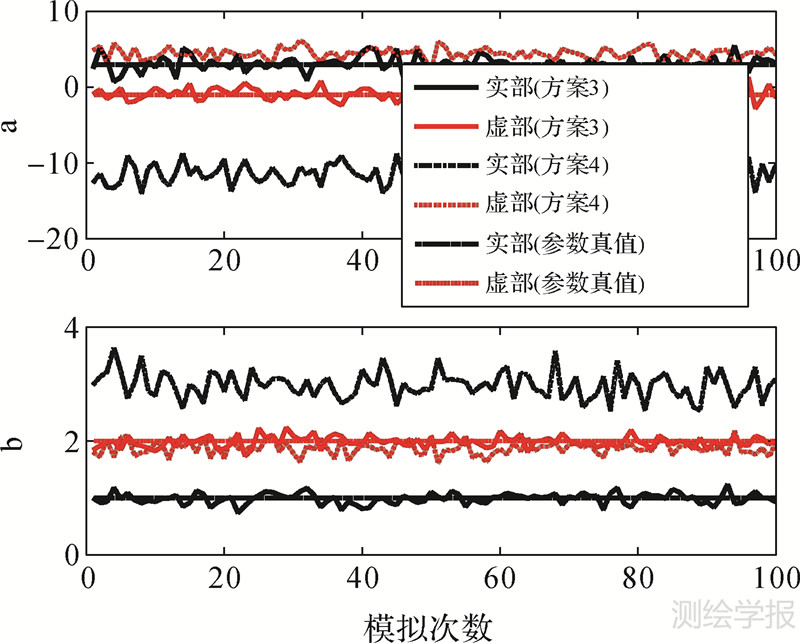
| 图 6 不同方案下复数总体最小二乘参数估值变化图 Fig. 6 The map of parameters of CTLSAM under different adjustment criterions |
|
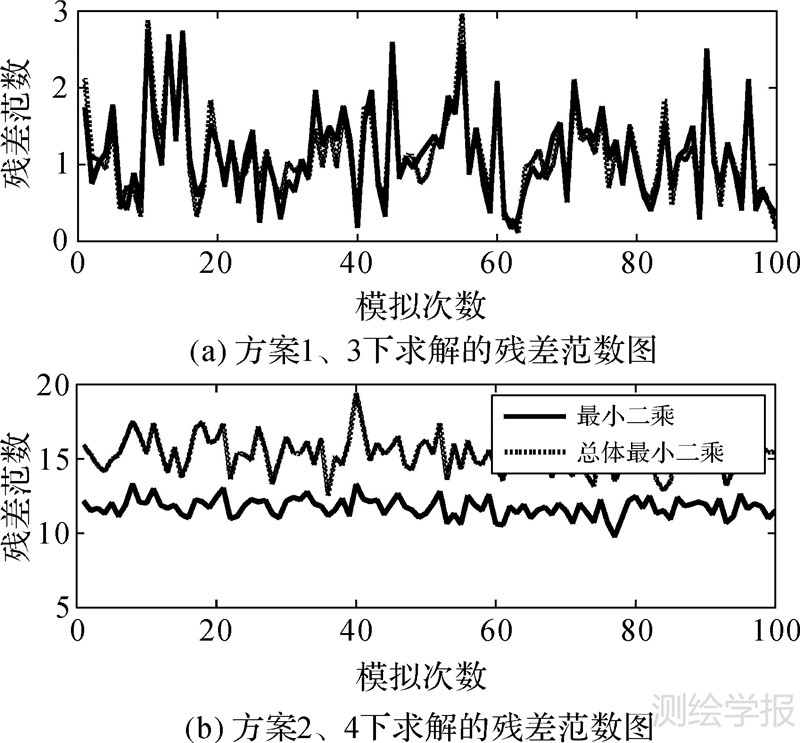
| 图 7 不同方案下参数估值与真值残差范数图 Fig. 7 The map of the norm of the parameters residual under different methods |
(1) 从算例1和算例2可以得出，平差准则3下复数总体最小二乘(方案3)和平差准则1下复数最小二乘(方案1)得到的差值范数‖ΔX‖分别比在平差准则4下复数总体最小二乘(方案4)和平差准则2下复数最小二乘(方案2)得到的结果小；表 2中方案3和方案4得到的差值范数分别为0.08928072和18.37666709、方案1和方案2为0.08929630和8.74359178；表 3中方案3和方案4得到的结果分别为1.12672065和15.70155110、方案1和方案2为1.16616775和11.87688595。综合表 2、表 3和图 1、图 2、图 5、图 6可以得出，对于复数域平差问题，平差准则1下的最小二乘和平差准则3下的总体最小二乘得到的参数估值分别比在平差准则2下的最小二乘和平差准则4下的总体最小二乘得到的参数估值要更为准确和合理。
(2) 表 2中方案3和方案1得到的差值范数‖ΔX‖相差不大，分别为0.08928072和0.08929630，方案3要稍优于方案1；表 3中方案3明显优于方案1，两种方案得到的‖ΔX‖分别为1.12672065和1.16616776。综合两个算例可以看出，在复数观测值和系数矩阵都存在误差的情况下，平差准则3下的复数总体最小二乘得到的结果在整体上要优于平差准则1下的复数最小二乘结果。
| 方案1 | 方案2 | 方案3 | 方案4 | 真值 | |
| â | 3.010 710 80-0.627 511 26i | -4.563 208 73+8.020 677 27i | 3.066 988 23-0.921 036 99i | -11.495 309 9+4.627 551 08i | 3-i |
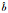 | 0.979 465 30+1.957 702 07i | 1.331 805 04+0.743 217 17i | 1.005 655 55+2.009 954 86i | 3.020 393 66+1.852 550 37i | 1+2i |
| 标准差 | 1.236 839 34 | 1.169 280 43 | 1.270 766 32 | 1.577 819 28 | |
| 0.135 954 14 | 0.251 905 93 | 0.139 264 44 | 0.264 535 20 | ||
| ‖ΔX‖ | 1.166 167 75 | 11.876 885 95 | 1.126 720 65 | 15.701 551 10 |
(3) 从试验结果看，表 1中方案1和方案3得到的差值范数差异很小，而表 2中两种方案之间的差异相对大些。造成上述结果的原因可以从以下两方面来解释：①在算例1中，系数矩阵的模拟误差很小(σ02=0.01)，而算例2中系数矩阵的模拟误差较大(σ2=1)，所以导致算例1中平差准则3下的复数总体最小二乘和平差准则1下的复数最小二乘的结果相差甚小，算例2中差异明显；②当系数矩阵存在误差时，此时用最小二乘方法求解造成的偏差与系数矩阵的信噪比即SN=‖A‖/σa的二次方成反比[28]，其中‖A‖为系数矩阵的量级，σa为系数矩阵的标准差。算例1中，系数矩阵的信噪比的数量级约为102，可得最小二乘估计的偏差大约为10-4，此时得到的总体最小二乘解和最小二乘解差异甚微；同理可得在算例2中，系数矩阵的信噪比的数量级约为10，最小二乘估计偏差大约为10-2，此时总体最小二乘方法得到的结果和最小二乘得到的结果有明显的差异。
(4) 从两个算例的解算结果看，方案3得到的结果要优于方案1，而方案2却优于方案4。因为将残差的实部和虚部的平方和分别最小的平差准则(平差准则2或平差准则4)将原矩阵分裂为实部和虚部，然后用实数域的方法求解，破坏了原矩阵的完整性，丢失了其中的一些蕴含信息，使数据失真[7]。如果把实部和虚部分开采用实数最小二乘来分别求解得到的结果是不能使平差准则取得最小的，并不是真正意义上的最小二乘[2, 8]，总体最小二乘也一样。在这种情况下，总体最小二乘尽管考虑了系数矩阵的误差，但同时也损失了更多的信息。下面通过推导进行简单说明。假设ReA、ImA、ReEA、ImEA分别为系数矩阵A和其误差EA对应的实部和虚部，ReL、ImL、ReV、ImV分别为观测值L和观测值误差V对应的实部和虚部，ReX、ImX分别为参数X对应的实部和虚部，则复数情况下最小二乘下的观测方程可表示为
将式(44)展开为
式中，I为复数单元。则在方案2下求得的解等价于最小二乘准则下分别对实部观测方程ReAReX=ReL+ReV和虚部观测方程ImAImX=ImL+ImV进行求解后得到的解的结合，损失的信息为
(ReAImX+ImAReX-ImAImX)I-ImAImX
同上，复数总体最小二乘情况下的观测方程可同样的表示成
则利用方案4求解时损失的信息为
因此，相比方案2，利用方案4求解时虽然顾及了系数矩阵的误差，但同时也损失了系数矩阵误差项的部分信息，数据的失真要更为严重，得到的结果更加不合理。
5 结 论本文在复数域最小二乘的基础上，提出了复数域总体最小二乘平差方法，并推导出了相关的一般复数总体最小二乘公式和复数混合总体最小二乘公式，通过算例结果得出：平差准则1下复数最小二乘较平差准则2下得到的结果更加合理，平差准则3下复数总体最小二乘较平差准则4下得到的结果更为准确；当顾及复数系数矩阵误差时，平差准则3下复数总体最小二乘方法要优于平差准则1下复数最小二乘方法。本文通过模拟算例探讨了在系数矩阵和观测向量独立等精度情况下的复数总体最小二乘方法，关于其应用方面和当观测值及系数矩阵不等精度时的复数加权总体最小二乘方法还需要作进一步研究。
| [1] | MILLER K S. Complex Linear Least Squares[J]. SIAM Review, 1973, 15(4): 706-726. |
| [2] | GU Xiangqian, KANG Hongwen, CAO Hongxing. The Least-square Method in Complex Number Domain[J]. Progress in Natural Science, 2006, 16(1): 49-54. (谷湘潜, 康红文, 曹洪兴. 复数域内的最小二乘法[J]. 自然科学进展, 2006, 16(1): 49-54.) |
| [3] | CUI Bowen, CHEN Jian, CHEN Xinzhao, et al. U-D Factorization Based Least Squares Methods for Complex Estimation[C]//CHENG Daizhan, WANG Xingyu. Proceedings of the 23rd Chinese Control Conference. Shanghai: East China University of Science and Technology Press, 2004: 264-267. (崔博文, 陈剑, 陈心昭, 等. 基于U-D分解的复参数最小二乘估计方法[C]//程代展, 王行愚. 第二十三届中国控制会议论文集. 上海: 华东理工大学出版社, 2004: 264-267.) |
| [4] | CUI Bowen, CHEN Jian, CHEN Xinzhao, et al. Least Square Method for Complex Estimation[J]. Journal of Anhui University:Natural Science Edition, 2005, 29(3): 5-10. (崔博文, 陈剑, 陈心昭, 等. 复参数最小二乘估计方法[J]. 安徽大学学报:自然科学版, 2005, 29(3): 5-10.) |
| [5] | DONG Yong, LI Mengxia. The Prove to the Formula of Complex Least Squares[J]. Journal of Yangtze University (Natural Science Edition) 2007, 4(2): 129-130. (董勇, 李梦霞. 复数域内最小二乘法估计公式的证明[J]. 长江大学学报:自然科学版, 2007, 4(2): 129-130.) |
| [6] | LI Mengxia, CHEN Zhong. The Modification of Least Square Method (LSM) in the Complex Field[J]. Journal of Yangtze University:Natural Science Edition, 2008, 5(3): 7-8. (李梦霞, 陈忠. 复数域内最小二乘法的一种改进[J]. 长江大学学报:自然科学版, 2008, 5(3): 7-8.) |
| [7] | GU Xiangqian. A Spectrum Model Basing on the Principle of Atmospheric Self-memorial[J]. Chinese Science Bulletin, 1998, 43(9): 909-917. (谷湘潜. 一个基于大气自忆原理的谱模式[J]. 科学通报, 1998, 43(9): 909-917.) |
| [8] | GU Xiangqian, KANG Hongwen, JIANG Jianmin. Monthly Temperature Forecasts by Using a Complex Autoregressive Model[J]. Journal of Applied Meteorological Science, 2007, 18(4): 435-440. (谷湘潜, 康红文, 江剑民. 用复数自回归模式预报月平均气温[J]. 应用气象学报, 2007, 18(4): 435-440.) |
| [9] | GRIGOLI F, CESCA S, DAHM T, et al. A Complex Linear Least-squares Method to Derive Relative and Absolute Orientations of Seismic Sensors[J]. Geophysical Journal International, 2012, 188(3): 1243-1254. |
| [10] | CUI Bowen. Real-time Fault Detection Technique for Inverter Based on Complex Parameter Estimation[J]. Chinese Journal of Scientific Instrument, 2006, 27(6): 393-395. (崔博文. 基于复参数估计的逆变器故障实时检测[J]. 仪器仪表学报, 2006, 27(6): 393-395.) |
| [11] | ZHU Jianjun, XIE Qinghua, ZUO Tingying, et al. Criterion of Complex Least Squares Adjustment and Its Application in Tree Height Inversion with PolInSAR Data[J]. Acta Geodaetica et Cartographica Sinica, 2014, 43(1): 45-51. (朱建军, 解清华, 左廷英, 等. 复数域最小二乘平差及其在 PolInSAR 植被高反演中的应用[J]. 测绘学报, 2014, 43(1): 45-51.) |
| [12] | GOLUB G H, VAN LOAN C F. An Analysis of the Total Least Squares Problem[J]. SIMA Journal on Numerical Analysis, 1980, 17(6): 883-893. |
| [13] | SCHAFFRIN B, WIESER A. On Weighted Total Least Squares Adjustment for Linear Regression[J]. Journal of Geodesy, 2008, 82(7): 415-421. |
| [14] | SHEN Yunzhong, LI Bofeng, CHEN Yi. An Iterative Solution of Weighted Total Least-squares Adjustment[J]. Journal of Geodesy, 2010, 85(4): 229-238. |
| [15] | WANG Leyang, XU Caijun. Total Least Squares Adjustment with Weighting Scaling Factor[J]. Geomatics and Information Science of Wuhan University, 2011, 36(8): 887-890. (王乐洋, 许才军. 附有相对权比的总体最小二乘平差[J]. 武汉大学学报:信息科学版, 2011, 36(8): 887-890.) |
| [16] | WANG Leyang. Research on Theory and Application of Total Least Squares in Geodetic Inversion[D]. Wuhan: Wuhan University, 2011. (王乐洋. 基于总体最小二乘的大地测量反演理论及应用研究[D]. 武汉: 武汉大学, 2011.) |
| [17] | TONG Xiaohua, JIN Yanmin, LI Lingyun. An Improved Weighted Total Least Squares Method with Applications in Linear Fitting and Coordinate Transformation[J]. Journal of Surveying Engineering, 2011, 137(4): 120-128. |
| [18] | XU Caijun, WANG Leyang, WEN Yangmao, et al. Strain Rates in the Sichuan-Yunnan Region Based upon the Total Least Squares Heterogeneous Strain Model from GPS Data[J]. Terrestrial, Atmospheric and Oceanic Sciences, 2011, 22(2): 133-147. |
| [19] | GE Xuming, WU Jicang. Generalized Regularization to Ill-posed Total Least Squares Problem[J]. Acta Geodaetica et Cartographica Sinica, 2012, 41(3): 372-377. (葛旭明, 伍吉仓. 病态总体最小二乘问题的广义正则化[J]. 测绘学报, 2012, 41(3): 372-377.) |
| [20] | ZHOU Yongjun, ZHU Jianjun, DENG Caihua. The Consistency between Row-wised Weighted Total Least Squares and Condition Adjustment with Parameters[J]. Acta Geodaetica et Cartographica Sinica, 2012, 41(1): 48-53. (周拥军, 朱建军, 邓才华. 附参数的条件平差与按行独立的加权总体最小二乘法估计的一致性研究[J]. 测绘学报, 2012, 41(1): 48-53.) |
| [21] | WANG Leyang, XU Caijun. Progress in Total Least Squares[J]. Geomatics and Information Science of Wuhan University, 2013, 38(7): 850-856. (王乐洋, 许才军. 总体最小二乘研究进展[J]. 武汉大学学报:信息科学版, 2013, 38(7): 850-856.) |
| [22] | WANG Leyang, XU Caijun, WEN Yangmao. Fault Parameters of 2008 Qinghai Dacaidan Mw 6.3 Earthquake from STLN Inversion and InSAR Data[J]. Acta Geodaetica et Cartographica Sinica, 2013, 42(2): 168-176. (王乐洋, 许才军, 温扬茂. 利用STLN和InSAR数据反演2008年青海大柴旦Mw 6.3级地震断层参数[J]. 测绘学报, 2013, 42(2): 168-176.) |
| [23] | WANG Leyang, YU Dongdong. Virtual Observation Method to Ill-posed Total Least Squares Problem[J]. Acta Geodaetica et Cartographica Sinica, 2014, 43(6): 575-581. (王乐洋, 于冬冬. 病态总体最小二乘问题的虚拟观测解法[J]. 测绘学报, 2014, 43(6): 575-581.) |
| [24] | HU Chuan, CHEN Yi. An Iterative Algorithm for Nonlinear Total Least Squares Adjustment[J]. Acta Geodaetica et Cartographica Sinica, 2014, 43(7): 668-674. (胡川, 陈义. 非线性整体最小平差迭代算法[J]. 测绘学报, 2014, 43(7): 668-674.) |
| [25] | YAO Yibin, KONG Jian. A New Combined LS Method Considering Random Errors of Design Matrix[J]. Geomatics and Information Science of Wuhan University, 2014, 39(9): 1028-1032. (姚宜斌, 孔建. 顾及设计矩阵随机误差的最小二乘组合新解法[J]. 武汉大学学报:信息科学版, 2014, 39(9): 1028-1032.) |
| [26] | XU Peiliang, LIU Jingnan, ZENG Wenxian, et al. Effects of Errors-in-variables on Weighted Least Squares Estimation[J]. Journal of Geodesy, 2014, 88(7): 705-716. |
| [27] | The Complex Random Matrix Submit to Normal Distribution[DB/OL]. (2012-05-20)[2013-06-17]. http://www.docin.com/p-668298205.html. |
| [28] | ZENG Wenxian. Effect of the Random Design Matrix on Adjustment of an EIV Model and Its Reliability Theory[D]. Wuhan: Wuhan University, 2013: 27-55. (曾文宪. 系数矩阵误差对EIV模型平差结果的影响研究[D]. 武汉: 武汉大学, 2013: 27-55.) |