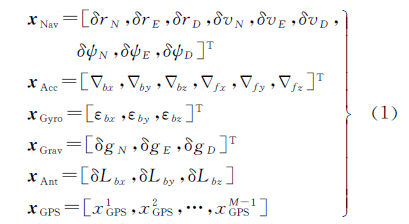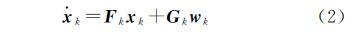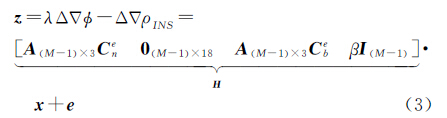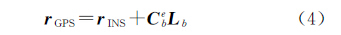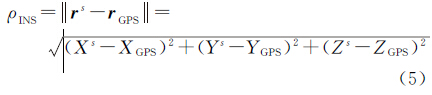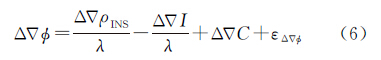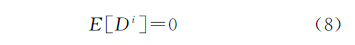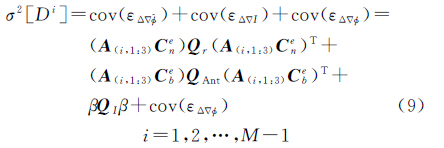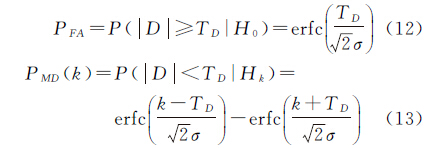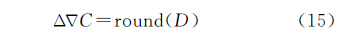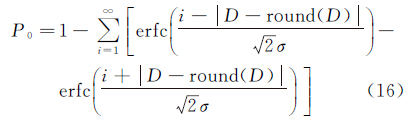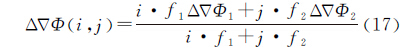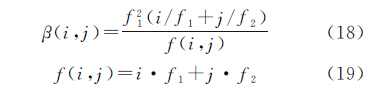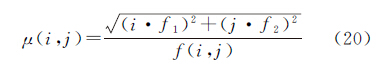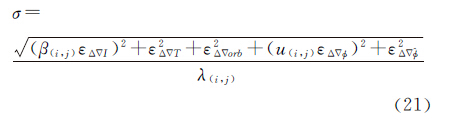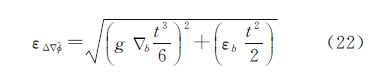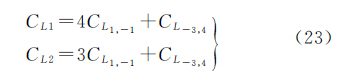2. 中国矿业大学环境与测绘学院， 江苏 徐州 221116
2. School of Environment Science and Spatial Informatics, China University of Mining and Technology, Xuzhou 221116, China
1 引 言
全球定位系统(GPS)/惯性导航系统(INS)组合导航系统已广泛应用于车辆导航、移动测图系统(MMS)、航空摄影测量等高精度定位定姿应用中，紧组合系统由于具有精度高、可视卫星数量不足时仍能导航解算等优势，已获得更多关注。在GPS动态定位应用中，受到观测环境的限制，信号干扰噪声大、多路径效应严重，而在城市环境中，信号受遮挡中断频繁，周跳的频繁发生影响了导航的效率，周跳的准确修复是进行高精度定位的前提。
目前，周跳探测的方法主要有高次差法[1]、电离层残差法[2]、伪距相位组合法[3, 4]、Kalman滤波法[5]、小波分析法[6]等，而这些方法都受到伪距观测值精度以及多路径误差的影响，且对于小周跳的探测修复能力不足。文献[2]对经典伪距/相位组合法进行了改进，文献[7]研究了三差解检测与修复周跳方法，文献[8]针对GPS动态测量提出了一种连续周跳检验方法。文献[9]提出了基于历元间电离层总电子含量变化率(TECR)和双频码相组合(MW-WL)结合的方法探测周跳，克服了电离层折射误差的影响，但仍依赖伪距精度，且需要长时间数据的对TECR进行准确估计。目前，随着我国北斗卫星导航系统的应用，已有学者提出了基于三频的全球导航卫星系统(GNSS)周跳探测方法[10]，文献[11]利用两个无几何相位组合和一个三频伪距/载波组合联和修复北斗三频周跳，克服了方程解不稳定的问题；文献[12]采用伪距相位组合实时探测与修复三频观测值周跳，已有方法能有效解决GNSS周跳探测问题，但目前GPS仍以双频观测值为主。此外，这些周跳探测方法是基于GPS观测值的，对于载体的动态不敏感，高动态条件下信噪比下降，已有方法的精度和可靠性难以保证。在GPS/INS组合系统 中，惯性信息可用于辅助GPS周跳探测，有效解决GPS周跳问题。文献[13]对INS辅助GPS周跳探测进行了细致分析，文献[14]进一步研究了精密单点定位(PPP)/INS组合系统周跳探测问题。
2 紧组合定位模型惯性导航系统(INS)能够输出更为平滑、连续的高速率导航解，且其导航性能不受观测环境的影响，但INS定位误差随着时间累积，通常需要利用GPS观测值进行周期修正。在差分GPS/INS紧组合导航Kalman滤波中，系统动态模型的建立依赖于选定的误差状态，为了更好地描述各种误差对系统状态的影响，选定的误差状态为9个导航解误差xNav(位置误差、速度误差及平台误差角)、加速度计仪器误差xAcc(3个偏心误差及3个尺度因子误差)、陀螺仪器误差xGyro(3个偏心误差)、3个重力异常误差xGrav、3个天线偏心误差xAnt，在长距离精密定位中建立GPS电离层延迟误差xGPS
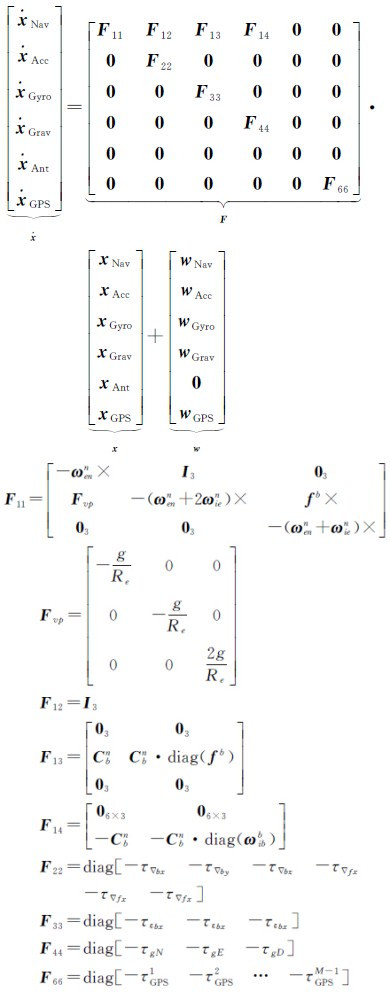
式中，下标N、E、D表示导航系；下标bx、by、bz表示载体系；M为可视卫星数。
系统误差方程为[15]
其具体表达式为
在城市等复杂环境中，GPS失锁情况较多，集中式Kalman滤波器效率受限，而采用惯性信息可以辅助GPS模糊度解算与周跳探测，一旦GPS双差整周模糊度固定，载波相位观测量即可转换为高精度的距离观测量，进行GPS双差载波/INS紧组合导航解算，滤波结果实时反馈修正惯性传感器误差，而INS高精度导航输出又可以辅助GPS周跳探测与模糊度解算，实现高精度的实时导航定位[16]。系统观测方程为
式中，z为双差观测量；λ为载波波长；Δ▽为双差算子；Δ▽Φ为双差载波相位；Δ▽ρINS为INS预测双差卫地距；A 为双差观测值设计矩阵；Cne为导航系到地球系的旋转矩阵；Cbe为载体系到地球系的旋转矩阵；β为电离层延迟因子；e 为观测噪声。
由于GPS天线相位中心与INS器件参考中心的偏心经常难以准确测量，在计算卫地距时需要考虑天线偏心的影响，在地球坐标系下，GPS天线相位中心位置可表示为
卫地距为
式中，rs(Xs,Ys,Zs)为卫星坐标；rGPS(XGPS,YGPS,ZGPS)为GPS天线相位中心位置。 3 惯性辅助周跳探测 3.1 周跳探测模型
在GPS信号完好时，INS/GPS组合系统可用来校正惯性测量单元(IMU)仪器误差，并估计大气延迟，维持INS独立高精度定位。利用高精度INS的预测双差卫地距可实现周跳的有效探测，周跳探测模型为
式中，Δ▽I为电离层误差；D为周跳探测统计量；Δ▽C为周跳；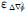
为INS预测位置误差引起的几何距离误差；εΔ▽I为电离层残余误差；εΔ▽Φ为双差相位观测误差及未建模误差。针对短基线或参考站与流动站高程差异不大的情形，由于双差残余对流层误差及星历误差为厘米级，对周跳影响较小，式中未列出。
惯性信息辅助的周跳探测可以克服载体动态的影响，并且INS预测双差卫地距有效避免了伪距多路径及伪距噪声的影响。INS位置误差由Kalman滤波估计进行修正，由Kalman滤波性质可知，在周跳未发生时，决策量具有稳定的均值与方差
式中，Qr为位置误差方差；QAnt为天线偏心误差方差QI为电离层误差方差；其中方差矩阵由Kalman率波先验预测P阵得到，顾及统计特性，取3倍P阵对应分量为式中的误差方差(置信水平为99.74%)。
经过系统建模，各种系统误差及相关性得到削弱，决策量满足高斯分布，构造检验统计量，取无周跳为零假设，模型在t时刻发生周跳为备选假设[13]
式中，k为周跳值。
周跳完备性探测取决于两个统计量：在模型有效的前提下，统计量超过周跳检测阈值，导致误报，发生第1类错误；系统模型失效，出现第2类错误，即发生周跳，但算法未报警，称为漏检
式中，TD为周跳检测阈值；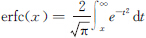
。式(13)中k=1时得到最大漏检率。
由于周跳探测统计量受到GPS观测值残余误差及INS误差影响，INS定位误差对每一组预测双差卫地距的影响是一致的，而GPS误差受卫星高度角影响，因此检测阈值的选取应考虑卫星差异，在确定周跳误探率的前提下可选择检测阈值
式中，εα为置信水平α下的临界值，选取周跳误探率为5%，即ε95%=1.96；标准差σ由周跳未发生时的探测统计量时间序列的均方根误差进行实时估计。对于最小的1周周跳探测，即检测阈值小于0.5，要实现1%的周跳漏检率，由式(13)可得，标准差σ应小于0.195周。
当模型检测到周跳发生，利用惯性信息的辅助进行周跳修复
式中，round表示求取最接近D的整数值。
给定置信水平α，若P0大于α，则认为周跳修复成功。
3.2 组合量构造及误差分析周跳探测与修复的成功率受到周跳统计量方差的影响，因此构造合适的载波相位组合量将有利于提高周跳探测的可靠性。对于双频GPS观测量，其组合相位双差观测值可表示为[19, 20]
式中，i、j为载波组合系数。
组合电离层延迟因子为
组合噪声因子为
制约周跳探测的因素包括INS定位精度、组合观测值的噪声、大气延迟残余误差和轨道误差，按照式(21)计算周跳探测统计量的精度为
对于不同精度的惯导，INS独立导航定位误差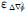有显着不同，随着GPS失锁时间的延长，INS定位精度显著降低，因此优选组合量对于周跳探测十分重要，表 1给出了所选的组合观测值。
| No. | (i,j) | λ/m | β(i,j) | μ(i,j) |
| 1 | (1，-1) | 0.861 9 | 5.742 2 | -1.283 3 |
| 2 | (-3，4) | 1.628 1 | 37.012 0 | 18.251 9 |
| 3 | (4，-5) | 1.831 6 | 53.744 8 | -23.260 4 |
| 4 | (-7，9) | 14.652 6 | 762.968 5 | 350.350 0 |
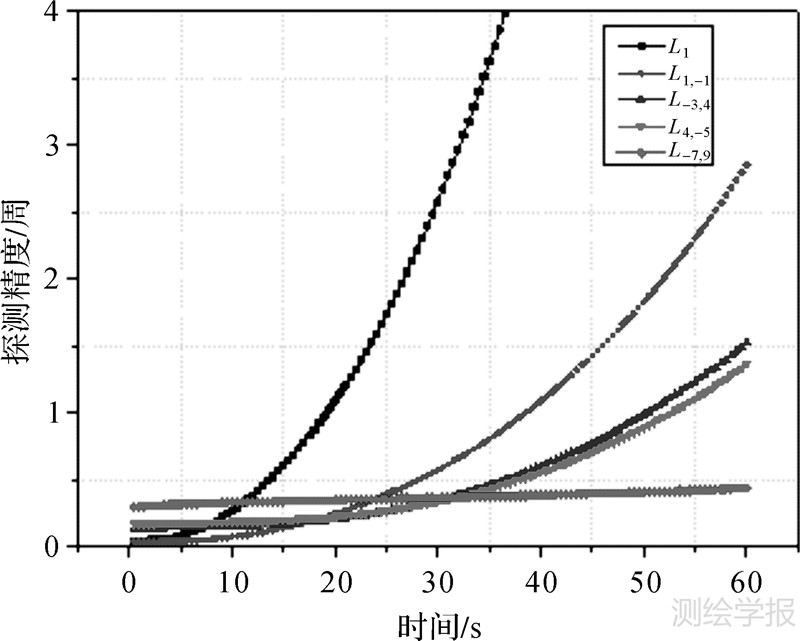
图 1给出了不同INS独立定位时间内，周跳探测统计量的精度。
|
| 图 1 INS定位误差对周跳探测的影响 Fig. 1 The impact of INS positioning error on cycle slip detection |
相位观测误差设为5 mm，电离层残余误差为5 mm，电离层误差功率谱密度为10-6 m2/s，不考虑对流层残余误差和星历误差，模拟的INS仪器误差为加速度计零偏▽b=100μg，陀螺漂移εb=1°/h，INS定位误差按经验公式计算[21]，即
分析图 1得出：①在INS定位精度较高时，L1,-1组合探测精度较高，GPS失锁时间小于20 s时该组合的精度优于0.24周，随着INS定位误差增大精度迅速降低；②L-3,4与L4,-5周跳探测的精度接近，在INS独立定位时间小于35 s时探测精度仍优于0.5周；③不同精度的INS定位误差对L-7,9组合的影响最大值为0.43周，对于GPS失锁时间较长(大于40 s)的情况可以作为周跳检测量，其受电离层误差影响较大；④所有组合的周跳探测效率较原始观测值均更具优越性。
在进行周跳探测与修复时，根据式(9)确定两个误差最小的组合，进行统计量检验，实现周跳修复，如周跳探测量组合选择为L1,-1和L-3,4，则原始观测值的周跳值为
图 2给出了周跳探测与修复的流程。由于周跳探测是针对单颗卫星，故可实现单历元多周跳的实时检测与修复。
|
| 图 2 INS辅助GPS/INS紧组合周跳探测 Fig. 2 Inertial aided cycle slip detection and correction for GPS/INS tightly coupled system |
为验证本文周跳检测算法的效果，采用新南威尔士大学校园内采集的试验数据进行分析，所采用的惯性仪器C-MIGITS II为战术级IMU(5°/h，500 μg)，采样率为100 Hz，移动站和基准站均采用Leica SR530双频接收机，采样间隔为1 s，截止高度角设为15°，试验过程中载体为低速运动，天空可视条件良好，试验过程中观测到5~6颗卫星，PDOP值略小于3[22]。
采用15 min数据(446 723—447 622 s，1331周) 进行分析，构建DGPS/INS紧组合导航模型计算导航解，紧组合滤波器经过约60历元达到收敛，收敛后加速度零偏和陀螺漂移总体比较稳定，估计误差值与仪器标称精度在同一水平，各轴仪器误差有一定差别，滤波稳定后，加速度计各轴零偏RMS为3 μg，陀螺各轴漂移RMS为0.03°/h。利用滤波器准确估计出的仪器误差修正IMU原始数据将有效抑制INS误差累积，可延长INS独立可靠定位时间。
为验证算法对于多周跳的探测能力，人为地在原始观测数据中加入周跳，所加周跳以及各卫星的高度角见表 2。同时，由于INS定位误差随时间累积，随着INS定位误差的增大，动态周跳检测与修复将更加困难，此次车载导航过程中的电离层误差变化较小，对系统周跳探测不产生太大影响。
| 星号 | 高度角/(°) | L1周跳 | L2周跳 |
| 30(参考星) | 65—67 | — | — |
| 2 | 38—33 | 1 | 1 |
| 5 | 59—51 | -5 | 6 |
| 6 | 40—46 | 4 | 3 |
| 10 | 55—55 | 9 | 7 |
| 21 | 20—25 | 1 | 0 |
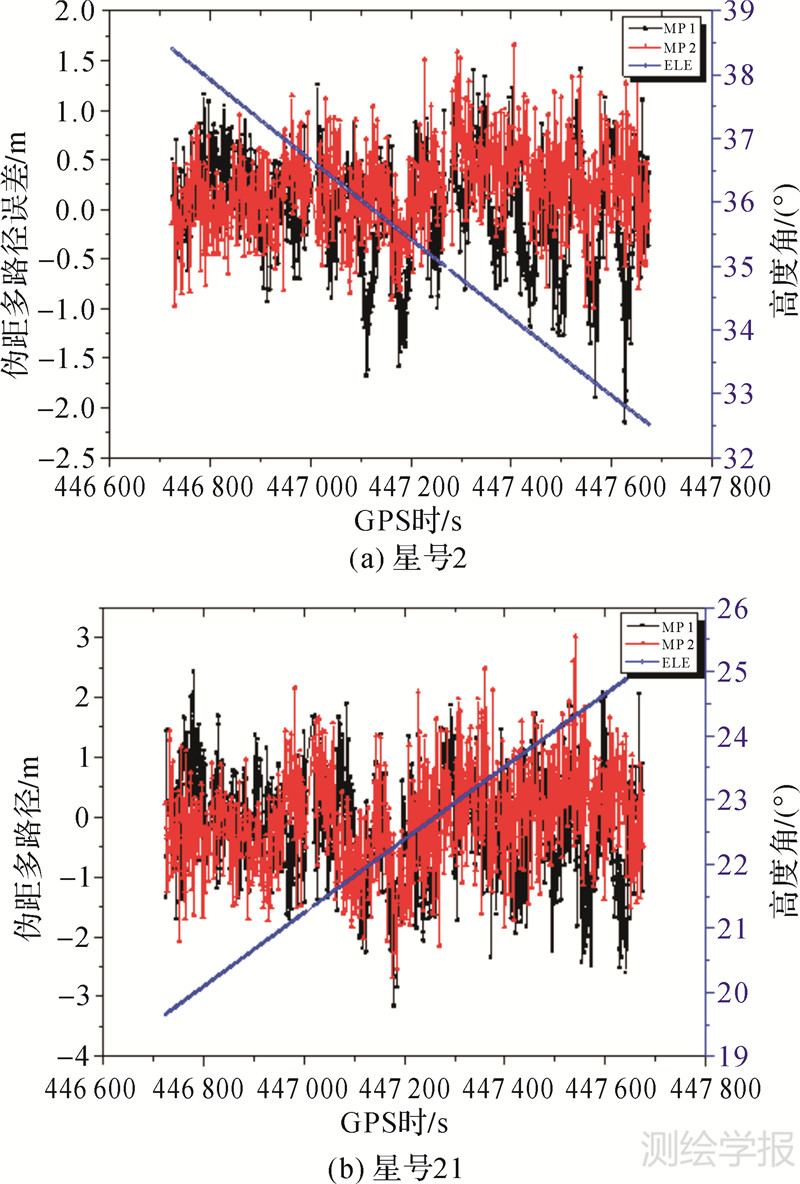
为了检验GPS信号中断时的周跳检测效果，模拟不同的GPS信号中断时间(5～30 s)，中断结束的时刻在原始观测序列中加入表 2中给出的周跳(如表 4所示)。在城市环境中的导航定位应用中，受到观测条件的限制，经常出现卫星少于4颗的观测时段，而紧组合滤波器在卫星数不足时仍能有效滤波，提高了系统的可用性。为此，模拟部分卫星失锁，保留高度角较高的3颗卫星(PRN30、PRN5和PRN10)，同样，在信号恢复的时刻加入模拟的周跳，表 5给出了不同的信号失锁时段。为了说明传统伪距/相位组合法在动态周跳探测中的不足，图 3给出了卫星PRN2和PRN21动态双差多路径误差(包含伪距噪声)，从图 3中可以看出，由于移动站接收机L1载波上为C/A码，噪声较大，动态环境中出现较大的波动，L1和L2上的伪距多路径误差均达到了米级，将不利于周跳探测，而高度角较低的卫星(PRN21)误差则更大。
|
| 图 3 GPS伪距多路径误差 Fig. 3 GPS pseudo-range multipath error |
| GPS时/s | 星号 | 组合 | PFA/(%) | PMD/(%) | P0/(%) |
| 446 923 | 10 | L1,-1，L-3,4 | (0，0) | (0，0) | (100，100) |
| 446 993(5 s) | 5 | L1,-1，L-3,4 | (0，0) | (0，0) | (100，100) |
| 447 033(10 s) | 21 | L1,-1，L-3,4 | (0，0) | (0，0) | (100，100) |
| 447 088(15 s) | 6 | L1,-1，L-3,4 | (0，0) | (0，0) | (100，100) |
| 447 143(20 s) | 2 | L-3,4，L4,-5 | (0. 75，1.32) | (0，0.02) | (100，100) |
| 21 | L-3,4，L4,-5 | (0.77，1.83) | (0，0.04) | (100，99.78) | |
| 447 248(25 s) | 10 | L-3,4，L4,-5 | (1.83，1.99) | (0.04，0.05) | (100，100) |
| 2 | L-3,4，L4,-5 | (4.17，4.36) | (0.23，0.25) | (99.41，99.91) | |
| 10 | L4,-5，L-7,9 | (6.50，7.40) | (0.56，0.74) | (99.03，99.94) | |
| 447 353(30 s) | 5 | L-3,4，L4,-5 | (2.55，2.65) | (0.08，0.09) | (100，100) |
| 2 | L4,-5，L-7,9 | (11.54，11.29) | (1.82，1.74) | (99.50，99.84) |
| GPS时/s | 星号 | 组合 | PFA/(%) | PMD/(%) | P0/(%) |
| 447 353(30 s) | 10 | L1,-1，L-3,4 | (0，0) | (0，0) | (100，100) |
| 21 | L1,-1，L-3,4 | (0，0) | (0，0) | (100，100) | |
| 447 523(60 s) | 10 | L1,-1，L-3,4 | (0，0) | (0，0) | (100，100) |
| 21 | L-3,4，L4,-5 | (1.91，3.38) | (0.04，0．15) | (100，99.96) | |
| 447 623(90 s) | 5 | L1,-1，L-3,4 | (0，0) | (0，0) | (100，100) |
| 2 | L-3,4，L4,-5 | (5.83，6.74) | (0.45，0.61) | (100，99.93) |
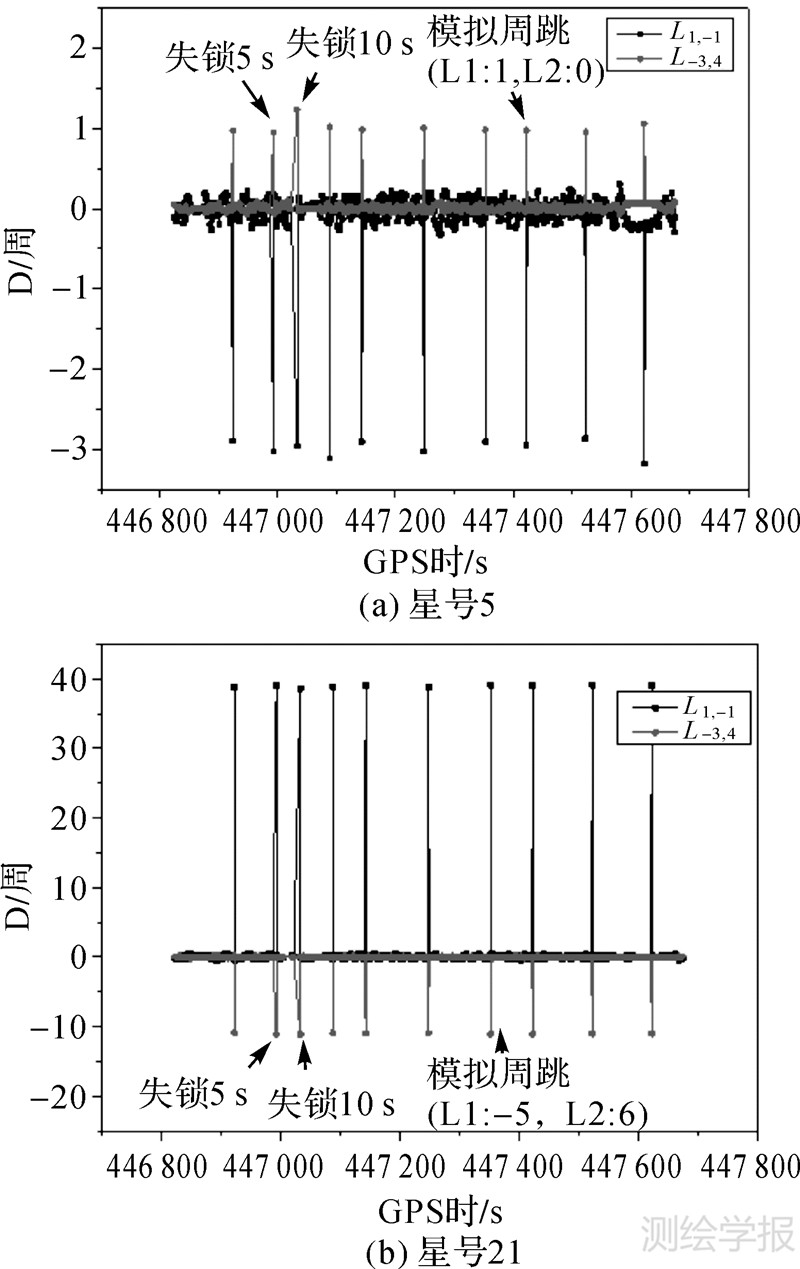
图 4给出了系统导航时段内卫星PRN5和PRN21的周跳探测决策量变化，从图 4中可以看出在周跳未发生时，周跳探测决策量变化平稳，没有超过探测阈值。加入模拟周跳后，系统能够准确确定周跳组合值，周跳探测与修复的成功率与实际所加的周跳大小无关，卫星信号短时失锁后，利用惯性系统预测伪距观测值仍能准确探测周跳。表 3给出了组合量L1,-1和L-3,4对应的周跳探测决策量均方根误差值(RMS)和标准差(STD)(不包含模拟周跳时的探测量)，从中可以看出，RMS值与STD值相当，这是由于IMU仪器误差经过组合滤波校正后使INS定位误差得到周期修正，INS定位误差并未出现明显的漂移。周跳探测决策量的稳定性与组合量以及卫星高度角有关，其中周跳探测组合量L1,-1的RMS较小，而低高度角卫星(PRN21)的RMS较大，由于卫星PRN21在部分观测条件较差的时段不可见，其对应的周跳探测决策量均值相对较小。根据表 3中列出的周跳探测统计RMS结果，给定周跳误探率为5%，由式(12)针对不同卫星自适应确定周跳检测阈值TD。
|
| 图 4 周跳探测决策量 Fig. 4 Estimated cycle slip decision statistics for PRN5 and PRN21 |
| 星号 | L1,-1 | L-3,4 | ||
| RMS/周 | STD/周 | RMS/周 | STD/周 | |
| 2 | 0.034 | 0.033 | 0.103 | 0.102 |
| 5 | 0.035 | 0.034 | 0.122 | 0.120 |
| 6 | 0.044 | 0.043 | 0.154 | 0.152 |
| 10 | 0.032 | 0.032 | 0.107 | 0.106 |
| 21 | 0.059 | 0.059 | 0.174 | 0.174 |
| 平均 | 0.041 | 0.040 | 0.132 | 0.131 |
根据模拟的周跳及信号中断时段，将周跳探测的部分结果列入表 4和表 5，周跳探测组合量周跳修复成功率置信水平取为99.7%，其中未列于表中的卫星均已成功进行周跳探测与修复，若周跳探测误报率和漏检率小于0.01%则取为0，若周跳修复成功率大于99.99%则取为1。从两表中可以看出，在同一历元加入多个周跳，本文提出的算法均能有效探测。在不同GPS信号失锁时段内，根据滤波方差，确定不同的观测量组合进行周跳探测。GPS完全失锁20 s内，对于给定的置信水平，算法能够准确修复所有模拟的周跳，修复的成功率与具体的周跳值无关。随着信号中断时间进一步延长，周跳探测误报率和漏检率进一步增大，周跳修复变得更加困难，在信号失锁25 s和30 s时，出现了PRN2、PRN2和PRN10周跳修复失败的情况见表 4。在GPS部分信号失锁时，由于部分可视卫星的观测信息能够辅助导航解算，抑制了INS定位误差发散，对于模拟的部分信号失锁时段(30 s、60 s、90 s)，算法成功修复了所有周跳，提高了系统可靠性与可用性。
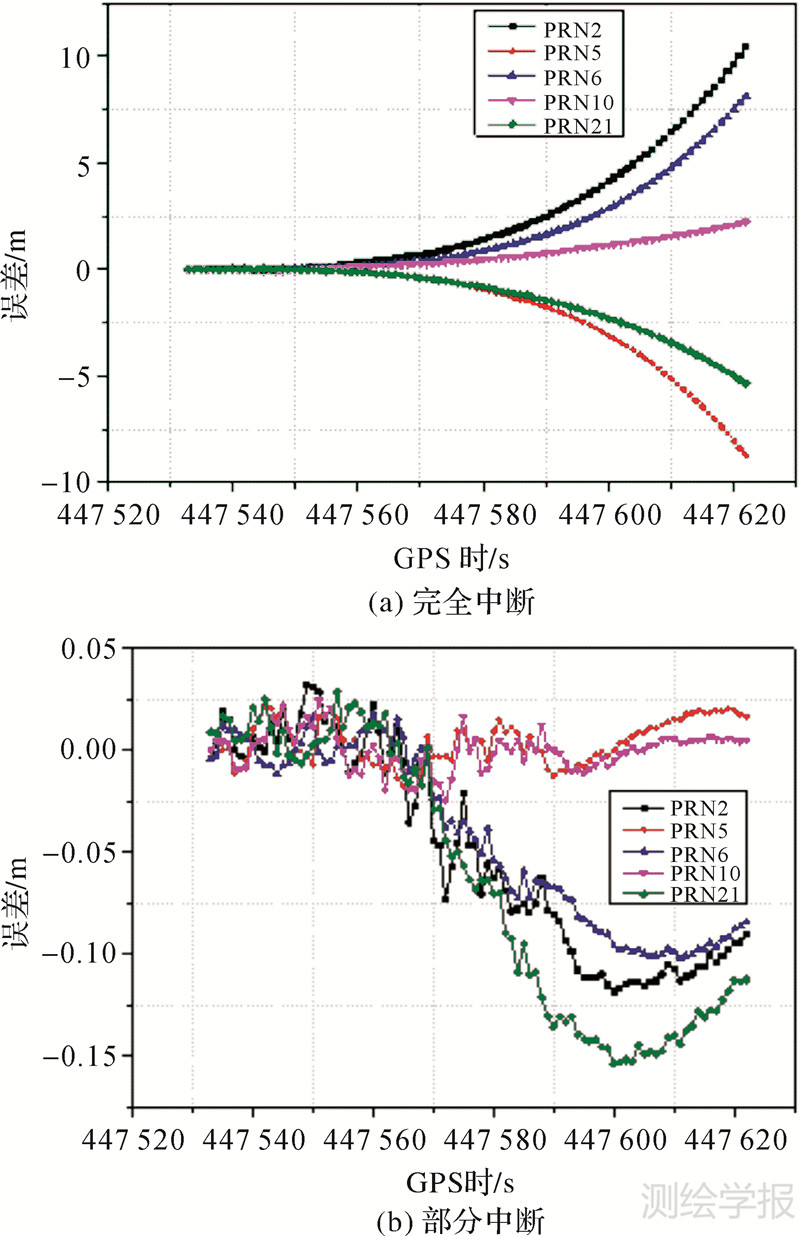
图 5为模拟GPS信号中断时INS预测卫地距与GPS卫地距差值，GPS卫地距由GPS信号完好时的固定解推求得到。从图 5可以看出，GPS信号完全失锁30 s内，除PRN2以外，其他卫星INS预测卫地距误差均在0.20 m以内，PRN2的误差为0.37 m，误差随时间累积，在90 s时最大误差达到了10 m。当GPS信号仅部分失锁时，系统定位误差得到较大抑制，90 s内定位误差仍未超过0.2 m，提高了系统周跳修复的成功率。
|
| 图 5 GPS信号中断时INS预测卫地距与GPS卫地距互差 Fig. 5 Difference between INS-predicted L1 DD range and GPS DD range during GPS outage |
为测试算法的稳健性，在原始观测值中模拟密集周跳。在滤波收敛后，对于每组双差观测值均加入5 s间隔的周跳，总模拟周跳历元数为170，采用周跳探测成功率(PTD)和周跳正确修复率(PTF)来描述算法的效果，表 6为周跳探测统计结果。从表 6中可以看出，所有模拟周跳均能准确探测，探测成功率不受周跳密集程度的影响。周跳修复成功率受到卫星观测值残余误差的影响，低高度角卫星PRN21周跳修复受观测值误差影响较大，出现4个历元未能正确修复周跳，而周跳的大小并不影响周跳探测与修复的成功率。
| 星号 | PTD/(%) | PTF/(%) |
| 2 | 100 | 100 |
| 5 | 100 | 99.41 |
| 6 | 100 | 100 |
| 10 | 100 | 100 |
| 21 | 100 | 97.65 |
| 平均 | 100 | 99.41 |
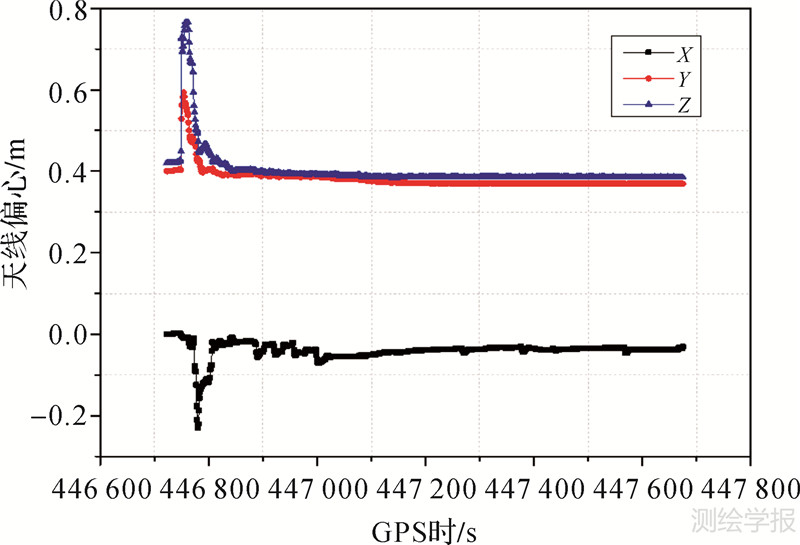
在对模拟周跳进行成功修复后，滤波估计得到的GPS天线相位中心与INS器件中心的偏心分量见图 6，载体运动后，滤波快速收敛，得到稳定后的前、右、下的偏心分量为0.369 m、0.385 m、-0.034 m。系统双差载波残差如图 7所示，L1载波PRN5和PRN21的RMS值分别为6.5 mm和8.0 mm，L2载波RMS值分别为7.0 mm和9.9 mm，其中低高度角卫星L2频点载波残差略大，系统整体导航结果达到厘米级精度。
|
| 图 6 天线偏心分量估计结果 Fig. 6 The lever arm estimation |
|
| 图 7 紧组合载波滤波残差 Fig. 7 DD carrier phase residuals of L1 and L2 |
本文通过构造GPS/INS紧组合导航模型，利用INS信息有效辅助GPS周跳探测与修复，得出以下结论：
(1)基于惯性辅助的周跳探测方法精度高，不受伪距观测值噪声及多路径误差的影响，并且该方法不受载体动态的影响，可靠性较高。
(2)惯性辅助的周跳探测可针对GPS观测值多星多周跳进行实时单历元检测与定位，方法简单易行，周跳探测和修复与周跳值无关，可以探测观测值中仅为1周的小周跳。
(3)周跳探测与修复的成功率受到周跳统计量方差的影响，构造不同相位观测量，基于周跳探测统计量的精度优选观测量组合，可以减小周跳探测漏检(弃真)和误报(纳伪)的概率，提高周跳修复的成功率。
(4)INS信息辅助可以有效解决GPS信号失锁而出现的周跳探测问题，在GPS信号完全失锁20 s内，该方法能准确检测和修复所有周跳，中断时间的延长降低了周跳修复的成功率；GPS信号部分失锁时，在模拟的90 s中断时段内仍能修复所有周跳；通过模拟的170历元的5 s间隔密集周跳，结果表明，周跳探测成功率为100%，正确修复率为99.41%。
由于本文的算法对电离层折射误差进行了有效建模，对于长距离基线同样有效，针对多星多频与低成本IMU的融合周跳探测与修复需作进一步研究。
| [1] | XU Guochang. GPS: Theory, Algorithms and Applications [M]. 2nd ed. Berlin: Springer, 2007. |
| [2] | BLEWITT G. An Automatic Editing Algorithm for GPS Data[J]. Geophysical Research Letters, 1990, 17(3):199-202. |
| [3] | HAN S. Carrier Phase-based Long-range GPS Kinematic Positioning[D]. New South Wales: University of New South Wales, 1997. |
| [4] | ZHANG Chengjun, XU Qifeng, LI Zuohu. Impoving Method of Cycle Slip Detection and Correction Based on Combination of GPS Pseudo Range and Carrier Phase Observations[J]. Acta Geodaetica et Cartographica Sinica, 2009, 38(5): 402-407. (张成军, 许其凤, 李作虎. 对伪距/相位组合量探测与修复周跳算法的改进[J]. 测绘学报, 2009, 38(5): 402-407.) |
| [5] | YANG Yuanxi. Adaptive Navigation and Kinematic Positioning [M]. Beijing: Surveying and Mapping Press, 2006. (杨元喜. 自适应动态导航定位[M]. 北京: 测绘出版社, 2006.) [6] HUANG Dingfa, ZHUO Jiancheng. Wavelet Analysis for Cycle Slip Detection and Reconstruction of GPS Carrier Phase Measurements [J]. Acta Geodaetica et Cartographica Sinica, 1997, 26(4): 352-357. (黄丁发, 卓健成. GPS相位观测值周跳检测的小波分析法[J]. 测绘学报, 1997, 26(4): 352-357.) |
| [7] | YUAN Hong, WAN Weixing, NING Baiqi, et al. A New Cycle Slip Detection and Correction Method Using Triple Differences Solution [J]. Acta Geodaetica et Cartographica Sinica, 1998, 27(3): 189-194. (袁洪, 万卫星, 宁百齐, 等. 基于三差解检测与修复GPS载波相位周跳新方法[J]. 测绘学报, 1998, 27(3): 189-194.) |
| [8] | HE Haibo, YANG Yuanxi. Detection of Successive Cycle Slips for GPS Kinematic Positioning [J]. Acta Geodaetica et Cartographica Sinica, 1999, 28(3): 199-203. (何海波, 杨元喜. GPS动态测量连续周跳检验[J]. 测绘学报, 1999, 28(3): 199-203.) |
| [9] | LIU Zhizhao. A New Automated Cycle Slip Detection and Repair Method for a Single Dual-frequency GPS Receiver[J]. Journal of Geodesy, 2011, 85(3):171-183. |
| [10] | DELACY M C, REGUZZONI M, SANSò F. Real-time Cycle Slip Detection in Triple-frequency GNSS[J]. GPS Solutions, 2012, 16(3):353-362. |
| [11] | HUANG Lingyong, SONG Lijie, WANG Yan, et al. BeiDou Triple-frequency Geometry-free Phase Combination for Cycle-slip Detection and Correction [J]. Acta Geodaetica et Cartographica Sinica, 2012, 41(5): 763-768. (黄令勇, 宋力杰, 王琰, 等. 北斗三频无几何相位组合周跳探测与修复[J]. 测绘学报, 2012, 41(5): 763-768.) |
| [12] | LI Jinlong, YANG Yuanxi, XU Junyi, et al. Real-time Cycle-slip Detection and Repair Based on Code-phase Combinations for GNSS Triple-frequency Un-differenced Observations[J]. Acta Geodaetica et Cartographica Sinica, 2011, 40(6): 717-722, 729. (李金龙, 杨元喜, 徐君毅, 等. 基于伪距相位组合实时探测与修复GNSS三频非差观测数据周跳[J]. 测绘学报, 2011, 40(6): 717-722, 729.) |
| [13] | ALTMAYER C. Enhancing the Integrity of Integrated GPS/INS Systems by Cycle Slip Detection and Correction [C]//RILLINGS J. Proceedings of the IEEE Intelligent Vehicles Symposium, 2000. Dearborn: IEEE, 2000:174-179. [14] DU Shuang, GAO Yang. Inertial Aided Cycle Slip Detection and Identification for Integrated PPP GPS and INS[J]. Sensors, 2012, 12(11):14344-14362. [15] GREJNER-BRZEZINSKA D A, DA R, TOTH C. GPS Error Modeling and OTF Ambiguity Resolution for High-accuracy GPS/INS Integrated System[J]. Journal of Geodesy, 1998, 72(11): 626-638. |
| [16] | SUN Hongxing. DGPS/INS Integrated Position and Attitude Determination and Its Application in MMS [D]. Wuhan: Wuhan University, 2004. (孙红星. 差分GPS/INS组合定位定姿及其在MMS中的应用[D]. 武汉: 武汉大学, 2004.) [17] GE M, GENDT G, ROTHACHER M, et al. Resolution of GPS Carrier-phase Ambiguities in Precise Point Positioning (PPP) with Daily Observations[J]. Journal of Geodesy, 2008, 82(7):389-399. |
| [18] | DONG D N, BOCK Y. Global Positioning System Network Analysis with Phase Ambiguity Resolution Applied to Crustal Deformation Studies in California[J]. Journal of Geophysical Research: Solid Earth (1978-2012), 1989, 94(B4):3949-3966. |
| [19] | FENG Yanming. GNSS Three Carrier Ambiguity Resolution Using Ionosphere-reduced Virtual Signals[J]. Journal of Geodesy, 2008, 82(12):847-862. |
| [20] | LI Bofeng, SHEN Yunzhong, ZHOU Zebo. A New Method for Medium and Long Range Three Frequency GNSS Rapid Ambiguity Resolution[J]. Acta Geodaetica et Cartographica Sinica, 2009, 38(4): 296-301. (李博峰, 沈云中, 周泽波. 中长基线三频GNSS模糊度的快速算法[J]. 测绘学报, 2009, 38(4): 296-301.) |
| [21] | CHIANG K W, DUONG T T, LIAO J K. The Performance Analysis of a Real-time Integrated INS/GPS Vehicle Navigation System with Abnormal GPS Measurement Elimination[J]. Sensors, 2013, 13(8): 10599-10622. |
| [22] | DING Weidong, WANG Jinling, RIZOS C, et al. Improving Adaptive Kalman Estimation in GPS/INS Integration[J]. Journal of Navigation, 2007, 60(3): 517-529. |