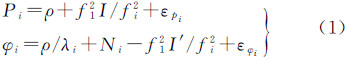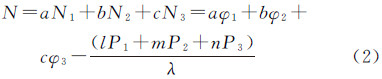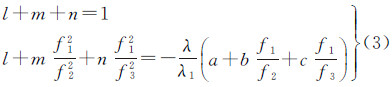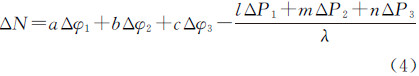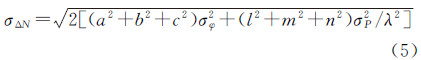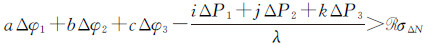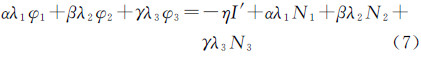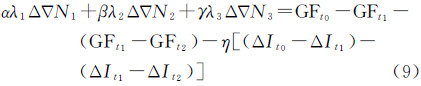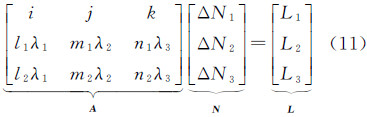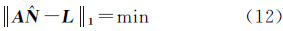Download PDF  
文章快速检索  
  高级检索
引用本文
黄令勇，翟国君，欧阳永忠，等。削弱电离层影响的三频TurboEdit周跳处理方法[J]. 测绘学报，2015,44(8)：840-847，883. DOI:10.11947/j.AGCS.2015.20140380
HUANG Lingyong, ZHAI Guojun, OUYANG Yongzhong, et al. Triple-frequency TurboEdit Cycle-slip Processing Method of Weakening Ionospheric Activity[J]. Acta Geodaetica et Cartographica Sinica, 2015, 44(8): 840-847, 883. DOI:10.11947/j.AGCS.2015.20140380
削弱电离层影响的三频TurboEdit周跳处理方法
黄令勇1,2,3, 翟国君3, 欧阳永忠3, 陆秀平3, 吴太旗3, 邓凯亮3    
1. 中国天绘卫星中心，北京 102102;
2. 信息工程大学地理空间信息学院，河南 郑州 450001;
3. 海洋测绘研究所，天津 300061
收稿日期：2014-07-21；修回日期：2014-11-24
基金项目：国家自然科学基金(41274015;41274045;41374042;U1431115)；国家863计划(2013AA122501).
第一作者简介：黄令勇(1987—)，男，博士，研究方向为测量数据处理。E-mail:hlylj87@126.com
摘要：针对电离层活跃期或磁暴发生时，现有三频周跳探测方法难以正确探测与修复周跳的问题，借鉴双频TurboEdit思想，提出了能够削弱电离层延迟影响的三频TurboEdit方法。该算法中的三频无几何无电离层码相组合和两次历元差分后的相位无几何组合，均能有效削弱电离层延迟对周跳探测的影响。随后利用三频实测数据对本文算法进行了验证，试验结果表明该方法能够消除电离层延迟影响，实现电离层活跃观测条件下动态非差周跳的实时探测与修复。
关键词： 三频GNSS     周跳探测与修复     无几何无电离层码相组合     相位无几何组合     两次历元差分    
Triple-frequency TurboEdit Cycle-slip Processing Method of Weakening Ionospheric Activity
HUANG Lingyong1,2,3, ZHAI Guojun3, OUYANG Yongzhong3, LU Xiuping3, WU Taiqi3, DENG Kailiang3     
1. Tianhui Satellite Center of China, Beijing 102102, China;
2. Institute of Surveying and Mapping, Information Engineering University, Zhengzhou 450052, China;
3. Navy Hydrographic Surveying and Charting, Tianjin 300061, China
Foundation support: The National Natural Science Foundation of China(Nos.41274015;41274045;41374042); The National High-tech Research and Development Program of China(No.2013AA122501).
First author: HUANG Lingyong(1987—), male, PhD, majors in surveying data processing. E-mail: hlylj87@126.com
Abstract: The existing triple-frequency cycle-slip detection method usually can not detect and repair the cycle-slip correctly in the ionospheric activity phase or when the magnetic storm happening. To solve the problem, the triple-frequency TurboEdit method for weakening the ionospheric error is advanced based on the dual-frequency TurboEdit method. Both the triple-frequency geometry-free and ionospheric-free combination and second-order time-difference phase geometry-free combination in this algorithm can whittle the influence of ionospheric error effectively. And then, the triple-frequency data is used to validate this algorithm, the experiment results show that this method can weaken the ionospheric error and realize the no-difference dynamicreal-time cycle-slip detection and correction under ionospheric activity phase.
Key words: triple-frequency GNSS     cycle-slip detection and correction     geometry-free and ionospheric-free combination     phase geometry-free combination     second-order time-difference    

 1 引 言

周跳发生的原因主要有：①接收机高速运动造成信号失锁；②接收机硬件或算法引起错误；③卫星信号遮挡或受环境影响导致信噪比较低[1, 2]。非高动态测量环境下，正确的测站选址和卫星高度的设置可有效降低信号遮挡引发周跳的概率，而此时周跳的发生多由电离层活跃造成相位剧烈波动而引发[3, 4]，尤其磁暴发生时，TEC显著变化更易引起周跳发生[5]。文献[6]研究表明，周跳与电离层活动季节性变化成正相关，为此有必要考虑电离层活跃期的周跳探测问题。为正确处理电离层活跃期的周跳问题，文献[7, 8]分别提出了MW组合+电离层延迟变化率验证法和MW组合+两次历元差分电离层残差组合法进行双频周跳探测。而随着三频信号的发播，基于三频优势的精密定位算法逐渐成为一个研究热点[9, 10, 11, 12]，目前有关三频周跳处理的方法主要包括伪距/载波组合法[13, 14]，相位无几何组合法[15]以及混合组合法[16]，但以上3种方法均未考虑历元间电离层延迟变化对周跳的影响。为充分展现三频GNSS技术优势尤其是我国BDS三频技术[17]，有必要进一步研究顾及电离层延迟变化的三频周跳实时处理方法，以适应未来三频导航定位的需要。

本文借鉴TurboEdit算法中MW组合特性，构造了三频无几何无电离层码相组合和两次历元差分后的三频相位无几何组合，分析了高电离层延迟条件下周跳探测的可行性,并对两种组合进行了优化选取。基于两种组合，提出了顾及电离层延迟影响的三频TurboEdit方法，并利用三频数据进行了验证分析，最后给出了相应结论。

2 三频无几何无电离层码相组合

MW宽巷组合能够消除几何误差项、电离层延迟一阶项影响，为此可借鉴这一特性构造三频相位无几何无电离层码相组合。首先给出伪距和载波相位原始观测方程

式中，P和φ分别表示伪距和载波观测值；ρ表示包含对流层延迟、钟差的站星距离；I和I′分别为第一频点以米和以周为单位的电离层延迟；λ、f和N分别为波长、频率和整周模糊度；εp和εφ分别表示伪距和载波观测噪声；下标i(i=1,2,3)表示各观测频点。

由式(1)组合得到三频相位无几何无电离层码相组合

式中，a、b、c∈Z为载波组合系数和l、m、n∈R为伪距组合系数。

式(2)组合系数应满足式(3)的条件

由于伪距噪声远大于载波噪声，为此在构造三频无几何无电离层码相组合时，应尽可能降低伪距组合系数，并尽可能构造波长较长的(超)宽巷组合。假定下一历元发生周跳，式(2)历元差分得到周跳探测方程

式中，Δ表示历元差分。

由文献[18]可知，电离层延迟二阶项远小于电离层延迟一阶项，为此只要组合后的电离层延迟放大因子相对较小，即可忽略电离层延迟影响，仅考虑噪声因素。假定各频点伪距和载波观测误差大小相同，由误差传播定律可计算式(4)标准差

式中，σφ和σP分别为载波和伪距观测标准差。

以为探测阈值，只要满足式(6)即认为周跳发生

设GPS、BDS伪距噪声为0.3 m，载波噪声为0.01周，根据三频组合观测原理[19]，对三频无几何无电离层组合进行优化选取，具体如表 1所示。

表 1 三频无几何无电离层码相组合 Tab. 1 Triple-frequency geometry-free and ionosphere-free code-phase combination
(a,b,c)lmnλ3σΔN4σΔN
GPS(0,1,-1)0.012 109 0.444 991 0.542 900 5.86 0.160.22
(1,-3,2)0.842 594 0.156 314 0.001 092 1.22 0.911.21
(1,-4,3)1.061 142 0.080 347 -0.141 489 1.54 0.911.22
(1,-2,1)0.699 407 0.206 086 0.094 507 1.01 0.931.26
(1,-5,4)1.435 797 -0.049 883 -0.385 914 2.09 0.951.33
BDS(0,-1,1)0.019 945 0.552 577 0.427 478 4.88 0.190.26
(1,1,-2)0.750 616 0.041 406 0.207 978 1.29 0.771.03
(1,3,-4)1.577 791 -0.537 279 -0.040 512 2.76 0.801.06
(1,0,-1)0.597 328 0.148 645 0.254 027 1.02 0.831.11
(1,4,-5)3.609 763 -1.958 831 -0.650 933 6.37 0.881.31
表选项

由表 1可知，三频无几何无电离层码相组合并不是波长越长，周跳探测阈值越小，其阈值大小主要取决于伪距组合系数大小。以3σΔN(置信水平为99.7%)作为周跳探测阈值，表中组合理论上均能满足对1周小周跳的探测，尤其GPS组合(0,1,-1)和BDS组合(0,-1,1)，即使选择4σΔN(置信水平为99.99%)作为周跳探测阈值，仍能好很地满足对1周小周跳的探测。与MW组合性质一样，以上三频无几何无电离层码相组合均无法探测ΔN1=ΔN2=ΔN3这些特殊周跳组合，且以上任意3个组合均线性相关。为此若实现对所有周跳的完全探测，则需选择一个i+j+k≠0的探测量。而根据TurboEdit思想，可引入三频相位无几何组合进行周跳探测，但由于相位无几何组合受电离层延迟影响严重，需对其进一步处理。

3 两次历元差分的三频相位无几何组合

根据式(1)构造三频相位无几何组合

式中，电离层延迟放大系数η=αλ1+βλ2f1/f2+γλ3f1/f3；组合系数满足α+β+γ=0。

周跳发生时，式(7)历元差分，得到

由式(8)可知，相位无几何组合未能完全消除电离层延迟一阶项，若历元间电离层变化较大，三频相位无几何组合受电离层延迟误差影响，波动剧烈无法进行周跳探测[7]。为此相位无几何组合要进行高电离层延迟变化条件下的周跳探测必须减弱电离层残差影响。一种方法可选择η趋于0的三频相位无几何组合，以减弱电离层延迟影响，另一种方法可对三频相位无几何组合进行两次历元差分，进一步消除电离层延迟一阶项，由文献[8]的试验可知，即使强磁暴条件下，两次历元差分仍能有效消除电离层延迟一阶项影响。两次历元差分的相位无几何周跳探测方程可表示为

式中，GF=αλ1Δφ1+βλ2Δφ2+γλ3Δφ3；Δ∇表示两次历元差分；t0、t1和t2表示先后依次3个历元。

由误差传播定律，可解式(9)的标准差为

由于相位无几何组合仅受载波噪声影响，其阈值相对较小，为尽可能保证周跳探测准确性，三频无几何组合采取4σ作为周跳探测阈值，由组合理论得到的较优三频相位无几何组合如表 2所示。

表 2 三频相位无几何组合 Tab. 2 Triple-frequency phase geometry-free combination
(α,β,γ)η4σ探测变化N
GPS(2,-11,9)0.004 3850.28-0.012 324
(3,-16,13)-0.007 340.41-0.023 719
(1,-5,4)-0.011 730.13-0.011 412
(1,-6,5)0.016 1150.16-8.e-4195
(0,1,-1)-0.055 80.03-0.010 63
(1,-1,0)-0.283 30.02-0.053 90
(1,0,-1)-0.339 10.03-0.064 50
BDS(4,13,-17)-0.000 90.41-0.021 015
(3,10,-13)0.006 880.32-0.012 719
(1,3,-4)-0.007 80.09-0.044 32
(2,7,-9)0.014 70.23-0.004 539
(0,-1,1)-0.062 60.03-0.012 03
(1,-1,0)-0.293 20.03-0.056 30
(1,0,-1)-0.230 60.02-0.044 30
表选项

如表 2中倾斜表示的η趋于0的三频相位无几何组合，其电离层延迟均较小，不超过第一频点电离层延迟的6%，但其探测阈值均大于0.1周，而且是特殊周跳N1=N2=N3=1引起的探测变化值(如表中第4和9列“探测变化”所示)的数倍，以至无法探测某些较小的N1=N2=N3的这类特殊周跳。进一步由第5和10列所示可探到的N1=N2=N3最小周跳值可知，每个η趋于0的三频无几何组合均存在数目不等无法探测的N1=N2=N3特殊周跳。为此，若采用该组合与三频无几何无电离层码相组合共同探测周跳仍会存在不敏感周跳。而表中加粗表示的两次历元差分的无几何组合可实现对N1=N2=N3=1特殊周跳的探测，为此挑选表中加粗表示的两次历元差分后的无几何组合作为周跳探测检验量是比较合理的。

4 顾及电离层延迟变化的三频TurboEdit方法

由2、3节可知，三频无几何无电离层码相组合，两次历元差分的三频相位无几何组合，均能有效消除电离层残差影响，有利于电离层活跃期的周跳探测。借鉴双频TurboEdit方法，联合以上两种组合构造3个线性无关的周跳探测检验量进行周跳探测与修复，并称该方法为顾及电离层延迟变化的三频TurboEdit方法。根据两种组合参与周跳探测的数目不同，可分为以下两种情况：①由一个三频相位无几何无电离层码相组合和两个三频相位无几何组合联立构造3个线性无关的探测检验量；②选择两个三频无几何无电离层码相组合和一个三频相位无几何组合，联立构造3个线性无关的周跳探测量。理论上，方法②具备两个三频无几何无电离层码相组合，消除电离层延迟一阶项更彻底，但三频相位无几何周跳探测检验量的探测阈值更小，更有利于探测小周跳。当以4σΔN为探测阈值时，GPS和BDS系统三频相位无几何无电离层组合仅有一个组合可满足对1周小周跳的探测。而情况②即使在选择4σΔN为探测阈值时，仍能较好地满足条件。为此，更推荐使用情况②具体周跳探测与修复公式，即

式中，i、j、k为三频无几何无电离层码相组合中载波组合系数；li、mi、ni(i=1,2)为三频相位无几何组合系数；ΔNi和Li(i=1,2,3)分别为周跳和周跳探测检验量，其中L1可直接取整固定；A为系数矩阵；N和L为周跳向量和观测向量。

式(11)可直接解算周跳修复值，但无几何组合中仍含有电离层延迟一阶残差项，故式(11)解算值可能受其影响，解算不正确。此时，本文借鉴文献[11]的空间搜索和1范数最小原则进行周跳修复值的搜索确认，其确认公式为

式中，为周跳估值向量。

5 试验分析

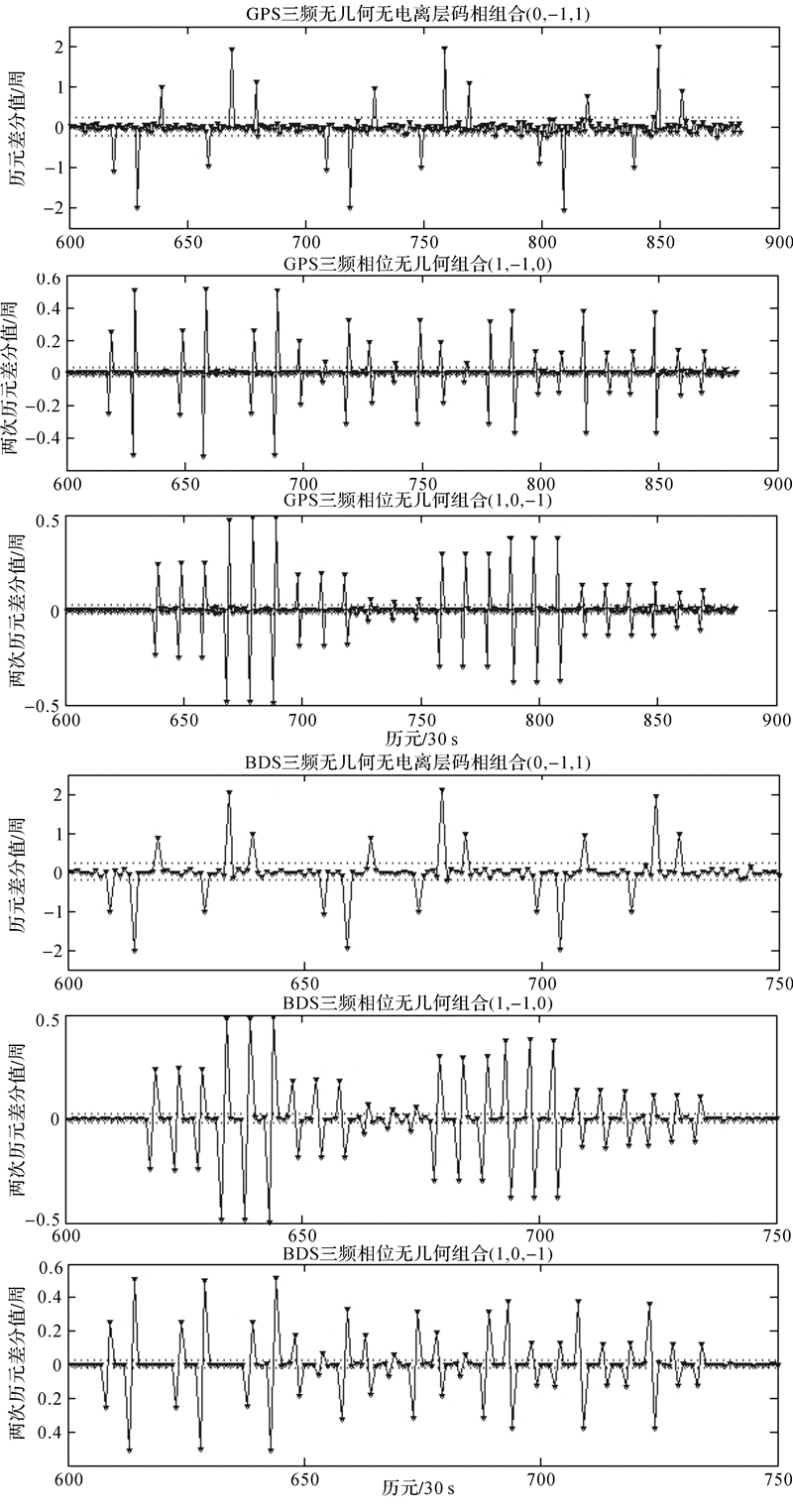
由文献[20]研究可知，2013年3月17日发生了大磁暴，赤道、中纬度地区以及极光区上空TEC变化显著。选择电离层延迟变化较显著的cut0站点(32.00°S，115.50°E)由Trimble NetR9接收机观测到的GPS G25和BDS C10三频数据进行分析，数据采样间隔为30 s，卫星高度角＞10°。选择GPS三频无几何无电离层组合(0，1，-1)和相位无几何组合(1，-1，0)(1，0，-1)，BDS三频无几何无电离层组合(0，-1，1)和相位无几何组合(1，-1，0)(1，0，-1)进行周跳探测与修复。

如图 1所示，由于受电离层活跃剧烈影响，GPS三频相位无几何组合(1，-1，0)(1，0，-1)(左图所示)和BDS三频相位无几何组合(1，-1，0)(1，0，-1) (右图所示)历元差分值分别在第650和第500历元以后超出了4σ探测阈值(图中虚线所示)，导致其无法进行正确的周跳探测，而两次历元差分后，相应的三频相位无几何组合历元差分值大幅度减小，可满足周跳探测要求。由图中GPS三频无几何无电离层码相组合(0，1，-1)(1，-3，2)以及BDS三频无几何电离层码相组合(0，-1，1)(1，1，-2)可知，受伪距噪声影响，历元差分值明显大于两次历元差分后的相位无几何组合差分值，尤其GPS(1，-3，2)和BDS(1，1，-2)组合受观测噪声影响，探测阈值较大，不易实现对小周跳的探测。而GPS(0，1，-1)和BDS(0，-1，1)组合受观测噪声影响相对较小，由此证明了式(11)选择两个两次历元差分后的三频相位无几何组合一个三频无几何无电离层码相组合进行联合探测与修复周跳的方法更合理。

图 1 周跳探测量差分值 Fig. 1 The difference value of detection combination
图选项

为验证算法效果，借鉴文献[15]方法同样在以上观测历元中依次加入(0，0，1)至(2，2，2)共计26个小周跳(具体如表 3所示)，具体如图 2所示。

图 2 小周跳探测情况 Fig. 2 The case of small cycle-slip detection
图选项

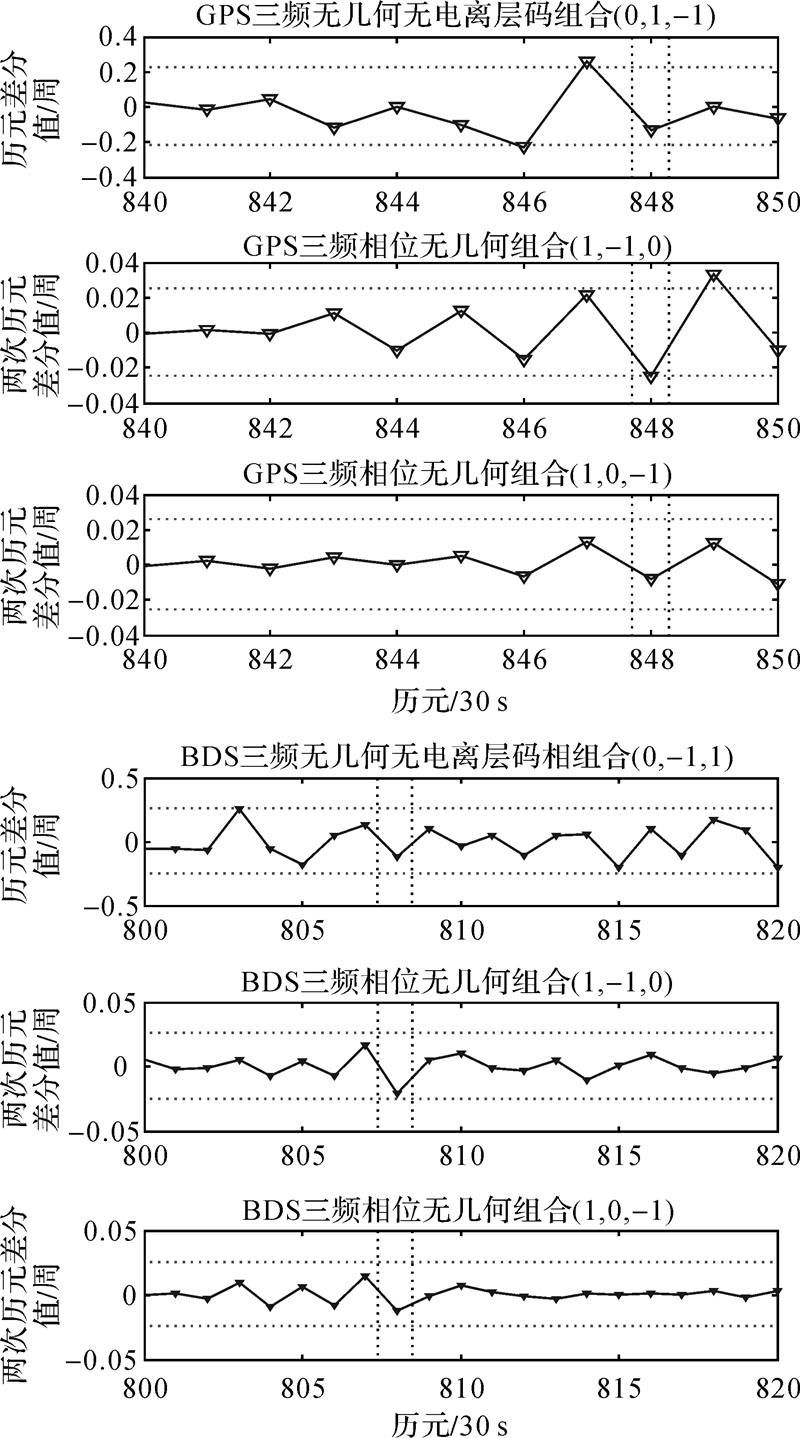
由图 2可知算法可实现对所有小周跳的探测。而直接利用式(11)解算得到的部分周跳修复值不正确(见表 3中加粗所示)，造成该修复失败主要由于相位无几何组合受电离层延迟残差和观测噪声的影响。而采用文献[21]的空间搜索法和最小1范数准则对以上解算不正确的结果进行周跳修复、确认，解算结果如表 4所示。由表 4可知，GPS和BDS系统中，均存在一个1范数最优解不正确，而次优解却为正确周跳值的现象。将图 2无周跳时800—860历元的周跳探测检验量差分值放大得到图 3，由图 3可知，1范数最小原则确认失败历元时刻(图中虚线所表示范围)，三频无几何组合(1,-1,0)受观测噪声影响，周跳探测检验量几乎接近于探测阈值，由此对周跳修复产生误判。为此，完成周跳修复后，有必要对周跳修复值进一步确认，而最简单有效的办法就是周跳修复后再次进行周跳探测。而表 4中不正确的周跳值很容易被探测发现。由于小周跳正确探测与修复的实现难度高于大周跳的探测与修复，为此本文不再进行大周跳的探测与修复试验。

表 3 周跳修复值 Tab. 3 The cycle-slip correction results
周跳GPS探测值修复值BDS探测值修复值
(0,0,1)-1.103,0.001,-0.253 (0,0,1)0.990,-0.002,-0.237(0,0,1)
(0,0,2)-2.001,0.002,-0.507(0,0,2)1.869,0.002,-0.473(0,0,2)
(0,1,0)0.996,-0.240,0.004(0,1,0)-0.980,-0.248,0.003(0,1,0)
(0,1,1)0.012,-0.252,-0.263(0,1,1)-0.026,-0.248,-0.235(0,1,1)
(0,1,2)-0.955,-0.249,-0.518(0,1,2)0.874,-0.250,-0.470 (0,1,2)
(0,2,0)1.950,-0.485,-0.003 (1,3,1)-2.017,-0.494,-0.001(0,2,0)
(0,2,1)1.133,-0.486,-0.254(0,2,1)-1.005,-0.501,-0.241(0,2,1)
(0,2,2)-0.151,-0.488,-0.506(0,2,2)-0.103,-0.500,-0.472(0,2,2)
(1,0,0)-0.000,0.191,0.192(1,0,0)0.100,0.186,0.190 (1,0,0)
(1,0,1)-1.056,0.196,-0.063(1,0,1)0.947,0.197,-0.047 (0,-1,0)
(1,0,2)-2.000,0.187,-0.320(1,0,2)1.880,0.196,-0.279 (1,0,2)
(1,1,0)0.981,-0.057,0.188(1,1,0)-1.061,-0.064,0.194(2,2,1)
(1,1,1)-0.097,-0.050,-0.064(1,1,1)-0.128,-0.055,-0.042(1,1,1)
(1,1,2)-1.000,-0.053,-0.320(1,1,2)1.182,-0.061,-0.283 (1,1,2)
(1,2,0)1.972,-0.295,0.189(1,2,0)-1.921,-0.309,0.180 (0,1,-1)
(1,2,1)1.087,-0.299,-0.061(1,2,1)-0.964,-0.309,-0.051(1,2,1)
(1,2,2)0.101,-0.296,-0.317(1,2,2)-0.046,-0.305,-0.288(0,1,1)
(2,0,0)-0.101,0.381,0.382(2,0,0)-0.207,0.378,0.377(2,0,0)
(2,0,1)-0.899,0.383,0.129(2,0,1)0.943,0.389,0.154(2,0,1)
(2,0,2)-2.055,0.379,-0.125(1,-1,1)2.103,0.364,-0.101(3,1,3)
(2,1,0)0.764,0.135,0.377(2,1,0)-0.914,0.131,0.387(3,2,1)
(2,1,1)-0.121,0.135,0.127(2,1,1)-0.247,0.138,0.141(1,0,0)
(2,1,2)-1.014,0.131,-0.129(2,1,2)1.105,0.138,-0.090(2,1,2)
(2,2,0)2.002,-0.133,0.373(-1,0,-2)-2.240,-0.100,0.393(2,2,0)
(2,2,1)0.898,-0.096,0.139(2,2,1)-0.967,-0.111,0.134(1,1,0)
(2,2,2)0.007,-0.103,-0.127(2,2,2)0.029,-0.120,-0.093(2,2,2)
表选项

表 4 空间搜索法修复的周跳值 Tab. 4 The cycle-slip correction results of the space search method
周跳值修复值最小一范数值
GPS(0,2,0)(0,2,0)0.000 832 33
GPS(2,0,2)(2,0,2)0.001 521 925
GPS(2,2,0)(-2,-1,-3)0.007 507 354
(2,2,0)0.032 741 95
BDS(1,0,1)(1,0,1)0.001 779 447
BDS(1,1,0)(1,1,0)0.005 560 025
BDS(1,2,0)(1,2,0)0.016 378 379
BDS(1,2,2)(1,2,2)0.007 433 265
BDS(2,0,2)(7,4,6)0.014 241 154
(2,0,2)0.032 573 627
BDS (2,1,0)(2,1,0)0.001 766 615
BDS (2,1,1)(2,1,1)0.004 040 216
BDS (2,2,1)(2,2,1)0.012 506 533
表选项

图 3 无周跳时探测量历元差分值 Fig. 3 The difference value of detection combination with no cycle-slip
图选项

6 结 论

顾及电离层延迟变化的三频TurboEdit方法能有效消除电离层延迟影响，且周跳探测阈值较小，可实现电离层活跃观测条件下2周内所有小周跳的探测。周跳修复解算中，空间搜索法的周跳修复正确率明显高于直接解算法。但确认周跳值的1范数最小原则，易受观测噪声影响，当观测噪声过大时，1范数最优解可能不是正确的周跳修复值，此时需进一步通过周跳探测来确认周跳修复的准确性。总之，本文周跳探测方法适用于电离层延迟活跃期的周跳探测与修复，且无须差分解算，可适用于精密单点定位的数据预处理。另外由于目前掌握的极端电离层活跃强度下的三频数据有限，电离层更活跃条件下的三频周跳探测与修复有待于进一步验证分析。

致谢：特别感谢信息工程大学地理空间信息学院吕志平教授在本人读博期间给予的支持。

参考文献
[1] XU Guochang. GPS: Theory, Algorithms and Application[M]. 2nd ed. Berlin: Springer, 2007.
[2] LI Zhenghang, ZHANG Xiaohong. New Techniques and Precise Data Processing Methods of Satellite Navigation and Positioning[M]. Wuhan: Wuhan University Press, 2009. (李征航, 张小红. 卫星导航定位新技术及高精度数据处理方法[M]. 武汉: 武汉大学出版社, 2009.)
[3] SKONE S, DE JONG M. The Impact of Geomagnetic Substorms on GPS Receiver Performance[J]. Earth, Planets and Space, 2000, 52(11): 1067-1071.
[4] CONKER R S, EI-ARINI M B, HEGARTY C J, et al. Modeling the Effects of Ionospheric Scintillation on GPS/Satellite-based Augmentation System Availability[J]. Radio Science, 2001, 38(1): 1001-1009.
[5] LIU Zhizhao, CHEN Wu. Study of the Ionospheric TECRate in Hong Kong Region and Its GPS/GNSS Application[C]//Proceedings of the International Technical Meeting on GNSS Global Navigation Satellite System-Innovation and Application.Beijing: IGNSS, 2009: 129-137.
[6] ZHANG Donghe, FENG Man, XIAO Zuo, et al. The Seasonal Dependence of Cycle Slip Occurrence of GPS Data over China Low Latitude Region[J].Science in China Series E: Technological Sciences, 2007, 50(4): 422-429.
[7] LIU Zhizao. A New Automated Cycle Slip Detection and Repair Method for a Single Dual-frequency GPS Receiver[J]. Journal of Geodesy, 2011, 85(3): 171-183.
[8] CAI Changsheng, LIU Zhizhao, XIA Pengfei, et al. Cycle Slip Detection and Repair for Undifferenced GPS Observations under High Ionospheric Activity[J]. GPS Solutions, 2013, 17(2): 247-260.
[9] GENG Jianghui, BOCK Y. Triple-frequency GPS Precise Point Positioning with Rapid Ambiguity Resolution[J]. Journal of Geodesy, 2013, 87(5): 449-460.
[10] LI Bofeng, FENG Yanming, SHEN Yunzhong. Three Carrier Ambiguity Resolution: Distance-independent Performance Demonstrated Using Semi-generated Triple Frequency GPS Signals[J]. GPS Solutions, 2010, 14(2): 177-184.
[11] FENG Yanming. GNSS Three Carrier Ambiguity Resolution Using Ionosphere-reduced Virtual Signals[J]. Journal of Geodesy, 2008, 82(12): 847-862.
[12] YU Xingwang. Multi-frequency GNSS Precise Positioning Theory and Method Research[D]. Wuhan: Wuhan University, 2011. (于兴旺. 多频GNSS精密定位理论与方法研究[D]. 武汉: 武汉大学, 2011.)
[13] LI Jinlong, YANG Yuanxi, XU Junyi, et al. Real-time Cycle-slip Detection and Repair Based on Code-phase Combinations for GNSS Triple-frequency Undifferenced Observations[J]. Acta Geodaetica et Cartographica Sinica, 2011, 40(6): 717-722. (李金龙, 杨元喜, 徐君毅, 等. 基于伪距相位组合实时探测与修复三频GNSS非差观测数据周跳[J]. 测绘学报, 2011, 40(6): 717-722.)
[14] SUN Baoqi,OU Jikun,SHENG Chuanzhen, et al. Optimal Multi-frequency Data Combination for Compass Cycle Slip Detection and Reparation[J]. Geomatics and Information Science of Wuhan University, 2010, 35(10): 1157-1160. (孙保琪, 欧吉坤, 盛传贞, 等. 一种适于Compass周跳探测的三频数据优化组合[J]. 武汉大学学报: 信息科学版, 2010, 35(10): 1157-1160.)
[15] DAI Zhen, KNEDLIK S, LOFFELD O. Instantaneous Triple-frequency GPS Cycle-slip Detection and Repair[J]. International Journal of Navigation and Observation, 2009, 23(1): 28-43.DOI: 10.1155/2009/407231.
[16] HUANG Lingyong, SONG Lijie, WANG Yan, et al. BeiDou Triple-frequency Geometry-free Phase Combination for Cycle-slip Detection and Correction[J]. Acta Geodaetica et Cartographica Sinica, 2012, 41(5): 763-768. (黄令勇, 宋力杰, 王琰, 等. 北斗三频无几何相位组合周跳探测与修复[J]. 测绘学报, 2012, 41(5): 763-768.)
[17] YANG Yuanxi. Progress, Contribution and Challenges of Compass/BeiDou Satellite Navigation System[J]. Acta Geodaetica et Cartographica Sinica, 2010, 39(1): 1-6. (杨元喜. 北斗卫星导航系统的进展、贡献与挑战[J]. 测绘学报, 2010, 39(1): 1-6.)
[18] WU Yue. The Theory and Application of Multi-frequency Data Processing of GNSS2[D]. Wuhan: Wuhan University, 2005. (伍岳. 第二代导航卫星系统多频数据处理理论及应用[D]. 武汉: 武汉大学, 2005.)
[19] LI Tao, WANG Jinling, LAURICHESSE D. Modeling and Quality Control for Reliable Precise Point Positioning Integer Ambiguity Resolution with GNSS Modernization[J]. GPS Solutions, 2014, 18(3): 429-442.
[20] JIN Rui, JIN Shuanggen, TAO Xuelin. Ionospheric Anomalies during the March 2013 Geomagnetic Storm from BeiDou Navigation Satellite System(BDS)Observations[C]//Proceedings of China Satellite Navigation Conference (CSNC).Nanjing:CSNC, 2014: 97-105.
http://dx.doi.org/10.11947/j.AGCS.2015.20140380
中国科学技术协会主管、中国测绘地理信息学会主办。
0

文章信息

黄令勇，翟国君，欧阳永忠，陆秀平，吴太旗，邓凯亮
HUANG Lingyong, ZHAI Guojun, OUYANG Yongzhong, LU Xiuping, WU Taiqi, DENG Kailiang
削弱电离层影响的三频TurboEdit周跳处理方法
Triple-frequency TurboEdit Cycle-slip Processing Method of Weakening Ionospheric Activity
测绘学报，2015，44(8)：840-847，883.
Acta Geodaetica et Cartographica Sinica, 2015, 44(8): 840-847, 883.
http://dx.doi.org/10.11947/j.AGCS.2015.20140380

文章历史

收稿日期：2014-07-21
修回日期：2014-11-24

相关文章

工作空间