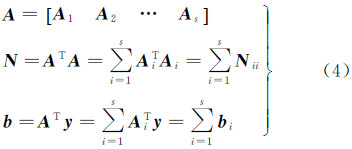2. 地球空间环境与大地测量教育部重点实验室,湖北 武汉 430079
2. Key Lab of Geospace Environment and Geodesy, Ministry of Education, Wuhan University, Wuhan 430079, China
1 引 言
CHAMP、GRACE和GOCE等新一代卫星重力计划的成功实施,为解决全球高覆盖率、高空间分辨率和高时间重复率的重力测量开辟了新途径。同时,这些卫星任务的高采样率、全球观测特点使得海量数据的处理问题成为了获取高阶次卫星地球重力场模型亟待解决的关键问题[1, 2, 3, 4]。为了利用海量卫星重力观测值快速求解高精度的地球重力场模型,许多学者一方面提出了一些快速解算方法,用于改进现有的重力场恢复方法,如快速球面配置法(FSC)[5]、时域最小二乘迭代解法[6]、SA块对角结构快速迭代解法[7]、块对角最小二乘方法[8];另一方面基于并行计算机编写并行算法,以提高计算速度[9, 10, 11, 12, 13]。国外,文献[9]在机群上比较了预条件共轭梯度多重平差法、半解析法以及分布式无近似平差方法(DNA)等方法恢复地球重力场的运行效率及求解精度,结果显示DNA方法可获得较高解算精度,但其运行速度较慢。为了满足我国重力卫星发展需求,国内学者对卫星重力场反演的并行算法进行了跟踪研究:文献[12]针对新一代卫星海量重力数据处理问题,采用基于OpenMP的并行算法,提高了卫星重力场反演的数据处理效率;文献[13]在OpenMP并行化技术支撑下,探讨了多种矩阵乘法、矩阵求逆的并行算法在恢复卫星重力场模型的计算效率和稳定性。上述几种方法解算地球重力场模型时,或截断阶次较小,或依然比较耗时,或单个计算节点内存耗用过高,不可广泛应用于各种并行计算平台。为进一步优化计算效率,拓展算法适用性,本文将优化上述并行算法的数据读取、存储与计算方式,引入MPI(message passing interface)并行技术,实现卫星重力场快速解算方法,使其适用于大规模集群系统计算,为我国发展新一代重力卫星提供软件支撑。
2 基于最小二乘直接法的卫星重力场模型反演利用卫星重力观测数据恢复重力场的常用方法包括空域法和时域法。虽然两种方法的建模方式不同,但最终均可归结为基于最小二乘的位系数求解问题。以扰动重力梯度径向分量求解重力场位系数为例[14, 15]
式中,Tzz表示地球外部任意一点(r,φ,λ)处的二阶径向扰动重力梯度;GM为地心引力常数;R为地球平均半径;nmax为模型展开的最大阶次;Cnm、Snm为待求的n阶m次规格化位系数;Pnm(sin φ)为规格化的缔合勒让德函数。常用于求解重力场的并行算法有两类:一类是迭代解法,它是从一个给定的初值出发,通过多次迭代逐步逼近真解,其优点是避开了法方程矩阵的直接求逆,缺点是无法完成求解结果的精度评定,且需要用外部数据进行检核;另一类是直接解法,指在没有舍入误差的情况下经过有限次运算求得线性方程的精确解[11, 15],这种方法需要一定的硬件条件,且计算较为耗时,但它不仅可以给出精确解,同时也给出了用于精度评定的参数协因数阵,具有重要的研究价值。MPI作为基于消息传递实现并行编程的主要代表,可实现大粒度进程级的并行[16]。因此,本文将基于最小二乘直接解法,研究快速恢复地球重力场的MPI并行算法。
重力场模型的最小二乘直接求解主要包括构建设计矩阵、形成法方程和解算法方程等计算流程,其算法的时间复杂度与空间复杂度与观测值个数nobs和模型最大阶次nmax密切相关。通过模拟计算分析可知:构建设计矩阵A、形成法方程系数阵N以及解算法方程3个部分为计算的“热点”,应该引入并行算法进行优化。设解算地球重力场的最大阶次为nmax,对应N阵的维数为u=nmax2+2nmax+1,A阵的大小为nobs×u。表 1给出了利用30 d、5 s采样的卫星重力观测数据(共518 400 个观测值)恢复不同阶次位系数所需的内存空间。显然,利用普通计算机编写的串行程序不能够完成高阶次的重力场模型反演;特别的,高于120阶次的地球重力场模型反演所需内存超过了计算机集群单个节点的内存峰值,为拓展并行算法的适用范围,应该对各个矩阵的存储进行特殊处理。
| nmax | u | A阵/GB | N阵 |
| 30 | 961 | 3.71 | 7.05 MB |
| 60 | 3 721 | 14.37 | 105.64 MB |
| 120 | 14 641 | 56.55 | 1.60 GB |
| 240 | 58 081 | 224.33 | 25.13 GB |
| 360 | 130 321 | 503.35 | 126.54 GB |
高性能服务器单个节点内存通常在16~128 GB之间,为了保证并行算法能够解决大规模的计算问题,不仅要顾及计算效率,还要考虑解算程序在单个节点上的内存耗用量。因此,下文将在顾及并行计算机性能的前提下,分别实现反演地球重力场过程中各个密集型任务的MPI并行算法。为表述方便,设观测值个数为nobs,参与计算的处理器个数为p,当前进程标识为myrank,待求解球谐系数个数为u,参数m=nobs/p。
3.1 构建设计矩阵的并行以扰动重力梯度的径向分量Tzz为例,观测方程的设计矩阵A为[14]
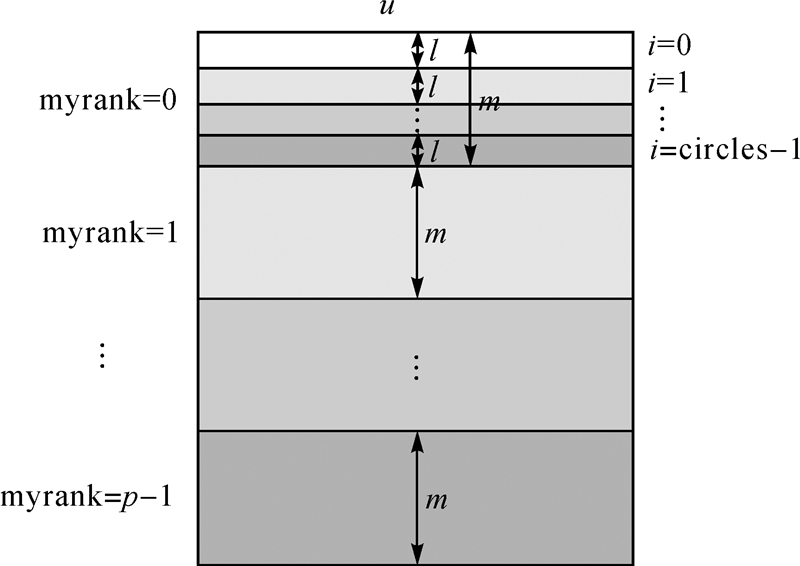
式中,i为设计矩阵A的行编号。对于第i个观测值,可依照式(2)和式(3)计算设计矩阵A的第i行。由于设计矩阵A的行与行之间无相关性,且每行的构建具有相似性,因此能够实现高效的并行计算。设计子函数按行构建A,然后在每个处理器中调用该函数,生成m行的矩阵Ablock(m,u),并使用并行接口MPI_FILE_WRITE_AT[17, 18]将数据写入文件中,为后续矩阵乘法的并行提供数据支持。考虑到单个节点的内存是有限的,当使用多个月的卫星重力数据参与计算时,单个Ablock(m,u)仍然会超出单个节点的内存极限。为此,引入circles参数对A阵完成进一步划分(图 1),即每个计算节点生成的子块减小至Ablock(l,u),其中l=m/circles;为减小节点内存负荷,每生成一个Ablock,就将数据存入二进制文件中的对应位置。若数据类型为双精度浮点数,则每个分块Ablock在文件中的存储位置相对于文件起始位置的偏移为fhAlocal=(myrank×m+circles×l)×u×8。采用这种分块方式,每个节点使用的内存由p×m×u×8减少至p×l×u×8,拓展了并行算法的可移植性。
|
| 图 1 A阵分块示意图 Fig. 1 The diagram of A partitioned matrix |
将A阵划分成s(s=circles×p)个子块,然后按照式(4)构建法方程,可以把法方程系数阵的形成转化为s个子矩阵的乘法运算
由表 1可知,当计算阶次达到120及以上时,存储每个N阵需要的内存将大于1.6 GB。若每个节点有24个进程参与计算,则单个节点的内存耗用量将大于38.4 GB。为了保证并行算法的普适性,需要对N阵进一步划分,实现矩阵乘法的并行分块算法。
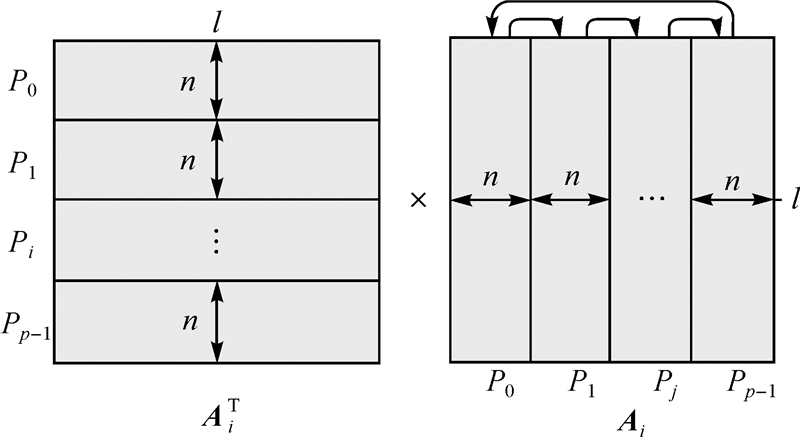
计算过程中,每次都从存储A阵的文件中读取一个子矩阵Ai(l,u),并分别对AT(u,l)和Ai(l,u)进行行列划分(图 2),即每个处理器按顺序读取子块a(n,l)和b(l,n)(其中,n=u/p)。为便于计算结果存储以及后续矩阵并行求逆,将结果矩阵N也进行行、列划分,即通过分块乘法得到p×p个大小为n×n的子矩阵Nb。记矩阵N第i行第j列的子矩阵为Nbij,显然有Nbij=ai×bj。计算过程中,每做完一次分块矩阵乘法,就使用MPI_SEND将b发送给下一个邻近的处理器,直到b被每个处理器均发送一次。发送b过程中,为了避免通信死锁[19],奇数号和偶数号处理器的收发顺序应该错开,即奇数号处理器先发送后接收,而偶数号处理器首先将b存于缓冲区中,然后使用MPI_RECV接收前一个处理器发送的b,最后将缓冲区中的数据发送给后一个处理器。经过p轮计算,每个处理器将得到N阵的一个子块Nb(n,u),将这p个子块按顺序并行写入文件中,即为法方程系数阵。
|
| 图 2 分块乘法示意图 Fig. 2 The diagram of block multiplication |
最小二乘原理反演地球重力场模型对应的法方程系数阵为对称正定阵,无论采用行主序还是列主序的Gauss-Jordan(G-J)算法,计算结果均相同。本文所有代码均采用Fortran编写,而Fortran为列优先的数组存储模式,因此下面将实现基于列交换的G-J并行算法。具体步骤为:首先,对矩阵N进行列交叉划分,即编号为i(i=0,1,…,p-1)的处理器存有N的第i,i+p,…,i+(m-1)p列,形成矩阵分块Nb。为了减少单个节点内存占用率和通信时间,可以采用函数MPI_FILE_READ_AT并行读取每个分块。其次,依次将第v列(v=0,1,…,u-1)作为主列,按照式(5)和式(6)对主行主列、主列元素进行操作,并将其存入向量f中,使用函数MPI_BCAST广播给所有处理器。再次,在处理器myrank中依次利用主列j对N的其余各列k(k≠j)作初等列变换。发送主列数据的处理器按照式(7)和式(8),利用主列对Nb主列之外的m-1列向量作列变换;其余处理器按照式(7)和式(8),利用主列对Nb的m列向量作列变换。最后,各进程中均使用函数MPI_FILE_WRITE_AT实现并行打印输出。公式(5)—(8)为
4 算例与分析本文采用的计算工作平台为武汉大学高性能计算系统的曙光集群,该集群包括93个计算节点,每个节点有2个CPU(每个CPU 12核,主频2.2 GHz),节点内存32 GB,节点之间由40 Gbps的IB交换机互联。编译环境为Intel Visual Fortran 10.1,程序采用MPI最新版本MPICH 3.1.1 编写。由于该集群为同构系统,MPI程序只需要在登录节点编译一次。常用于衡量并行算法计算效率的标准有加速比、相对效率等。加速比Sp=Tser/Tpar,其中Tser是串行执行时间,Tpar为使用p个处理器并行执行时间。相对效率E=Sp/p,若相对效率达到100%,称该算法能够达到“线性加速比”[20]。加速比越大,相对效率越接近于100%,并行算法计算效率越高[21]。
4.1 设计矩阵计算与分析基于GOCE卫星模拟轨道,采用不同阶次的EIGEN-GL04C模型模拟30 d、5 s采样间隔的轨道观测数据(共518 400个观测值)。采用MPI分块并行算法,使用96个内核(8个计算节点,每个节点12个核)构建了设计矩阵,分别设定参数circles为4、10,每个计算节点的内存耗用量峰值如表 2所示。计算结果表明:在现有的并行计算机(节点内存32 GB)上,使用一般方法(Aser)只能够反演60阶次的地球重力场模型;而使用分块的方法(Apar4、Apar10)可以大幅度减小单个节点内存耗用量,其峰值可由circles参数控制,适用于多种计算集群。
| Nmax | U | Aser/GB | Apar4 | Apar10 |
| 60 | 3721 | 14.37 | 459.90 MB | 183.96 MB |
| 120 | 14 641 | 56.55 | 1.77 GB | 723.83 MB |
| 240 | 58 081 | 224.33 | 7.01 GB | 2.80 GB |
| 360 | 130 321 | 503.35 | 15.73 GB | 6.29 GB |
为验证分块方法的并行效率,分别使用不同的进程数、circles值构建了240阶次的设计矩阵(表 3)。随着进程数的增多,加速比逐渐增大,计算时间逐步减小。由于A阵各列之间无相关性,计算效率峰值可以达到约95%,基本能够达到线性加速比。需要特别注意的是,当进程数为16和32时,circles值为10的效率大于circles值为4的情况;当进程数为64时,结果正好相反。这主要是因为基于MPI的相对效率与通信时间和集群CPU的高速缓存大小密切相关:分块小于高速缓存大小时,计算效率高;而分块过小,又会增加通信时间。因此,在进行分块大小选择时,在集群内存大小允许的前提下,要平衡高速缓存大小与通信时间的关系。
| 指标 | 进程数 | |||||
| 16 | 32 | 64 | ||||
| circles | 4 | 10 | 4 | 10 | 4 | 10 |
| 计算 时间/s | 462.47 | 278.45 | 329.03 | 143.43 | 181.45 | 166.96 |
| 加速比 | 14.32 | 15.18 | 20.13 | 29.47 | 36.508 | 25.31 |
| 效率 /(%) | 89.52 | 94.88 | 62.91 | 92.10 | 57.044 | 39.56 |
为验证并行算法的稳定性,输出了分块矩阵乘法BlockMul算法生成的N阵,计算结果显示互为对称的元素严格相等。由于N阵严格对称,计算中只考虑了其上三角部分,可进一步减少计算时间和内存占用率。由于该算法占用内存较少,理论上能够实现任意时长观测序列反演地球重力场模型。为了检验BlockMul的并行效率,使用518 400个沿轨扰动位观测值恢复了60阶次地球重力场模型(表 4)。circles值相同的情况下,加速比与相对效率随着进程数的增加而增大;在相同计算任务量的前提下,circles值越大,加速比与相对效率也越大,且相对效率峰值可达到68.0%。
| circles | 并行效率 | 进程数 | |||
| 16 | 32 | 48 | 64 | ||
| 4 | 计算时间/s | 5 300.2 | 1 642.7 | 938.0 | 753.8 |
| 加速比 | 3.0 | 9.8 | 17.1 | 21.3 | |
| 效率/(%) | 18.9 | 30.5 | 35.7 | 33.3 | |
| 10 | 计算时间/s | 4 347.7 | 1 241.4 | 831.8 | 368.9 |
| 加速比 | 3.7 | 12.9 | 19.3 | 43.5 | |
| 效率(%) | 23.1 | 40.4 | 40.2 | 68.0 | |
使用不同的进程数测试了G-J并行求逆算法,地球重力场模型的截断阶次分别为60、120,计算结果如表 5所示:在相同任务量前提下,随着参与计算的进程数增加,计算所需时间依次减小,加速比、相对效率逐步增大,效率约为45%~60%;计算任务量越大(即u越大),并行效率越高。
| U | 指标 | 进程数 | |||
| 1 | 16 | 24 | 32 | ||
| 3721 | 计算时间/s | 207.5 | 26.1 | 19.2 | 12.9 |
| 加速比 | 1.0 | 8.0 | 10.8 | 16.1 | |
| 效率/(%) | 49.8 | 45.2 | 50.4 | ||
| 14 641 | 计算时间/s | 12 931.4 | 1 291.70 | 995.9 | 735.9 |
| 加速比 | 1.0 | 10.0 | 13.0 | 17.6 | |
| 效率/(%) | 62.6 | 54.1 | 54.9 | ||
直接法能够输出待求值的方差-协方差阵,即N阵的逆阵N-1。使用两种方法衡量G-J并行求逆算法的精度:①由N-1阵的对角线元素得到各球谐系数的均方差,记为CS_Error,计算中设单位权方差为1.0;②用N乘以求得的逆阵N-1,并与单位阵E相减,得到求逆误差,记为N_Ninv-E。分别统计上述两种方法的计算结果,计入表 6中。结果表明,球谐系数误差量级约为10-19~10-20;求逆误差量级为10-13~10-14,由误差传播定律可知:N-1阵中各个元素的解算误差均方根约为10-21量级,可认为该部分误差是由于数据发送接收误差、计算机截断误差和解算误差等引起的,对求逆精度的影响极小。
| 方法 | 样本大小 | 最大值 | 最小值 | 平均值 | 均方根 |
| CS_Error | 3721 | 3.4D-19 | 7.1D-22 | 2.4D-20 | 2.9D-20 |
| 14 641 | 1.9D-18 | 8.5D-22 | 1.1D-19 | 8.9D-19 | |
| N_Ninv-E | 3721 | 7.2D-13 | 0.0D0 | 9.5D-16 | 4.4D-14 |
| 14 641 | 1.1D-11 | 0.0D0 | 9.3D-15 | 2.8D-13 |
为了分析MPI并行算法反演卫星重力场的计算效率,本文设计了两个模拟算例:基于GOCE卫星模拟轨道,分别采用120、240阶次的EIGEN-GL04C模型计算了沿轨30 d、5 s采样间隔的扰动位数据(SST)和径向扰动重力梯度数据(SGG-Vzz)[21],然后基于最小二乘直接法求解了相应截断阶次的地球重力场模型。计算时间和单个节点(CPUs=16)的内存耗用量峰值如表 7所示。采用传统的串行算法难以实现高阶次的卫星重力场模型反演,且利用小型计算平台计算高阶次重力场模型极为耗时,而采用本文的并行算法恢复包含一个月卫星重力观测信息的120阶、240阶重力场模型,仅需要40 min、7 h,内存耗用峰值仅为289 MB、1.57 GB,既保证了计算效率又提高了算法的可移植性。
| 观测值 | 计算过程 | A | N | N-1 | 总计 |
| T120(p=128) | 计算时间/s | 97 | 1837 | 229 | 2174 |
| circles=25 | 耗用内存/MB | 289 | 205 | 205 | 289 |
| T240(p=256) | 计算时间/s | 318 | 16 709 | 7 395 | 24 483 |
| circles=15 | 耗用内存/GB | 0.93 | 1.57 | 1.57 | 1.57 |
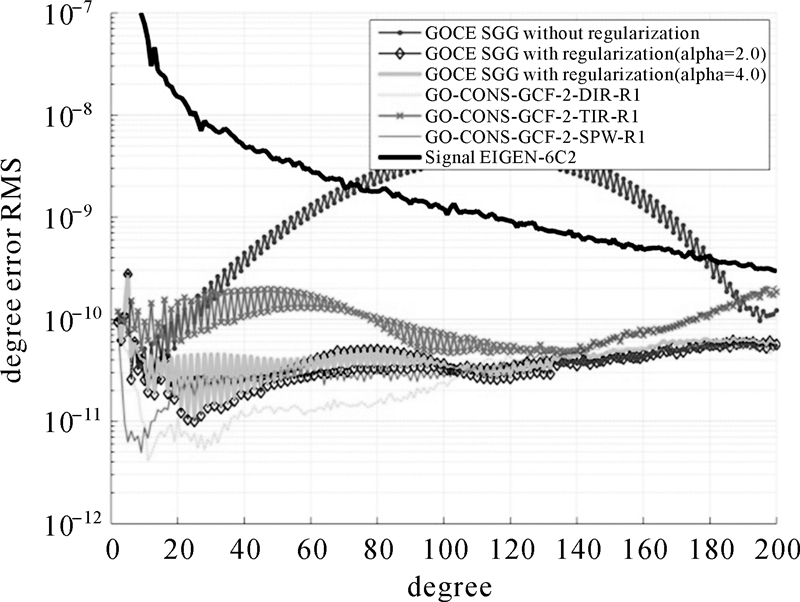
在模拟数据中加入与GOCE卫星载荷同等水平的观测噪声,基于空域最小二乘法获取了SGG模式下的重力场模型,并基于Kaula正则化进行了约束求解,计算结果如图 3所示。GOCE轨道特性导致法方程病态,引入正则化方法能够达到稳定求解的目的,且不同的正则化因子对解算结果影响较大,本文根据L曲线法最终选取最优正则化因子为2.0。通过与ESA发布模型的比较,本文的重力梯度解算模型在高阶次部分精度高,在120阶次之后优于GOCE直接解(GO-CONS- GCF-2-DIR-R1),与GOCE空域解精度相当(GO-CONS- GCF-2-SPW-R1);而在低阶次部分,由于未引入高低跟踪数据,计算精度不及GOCE直接解和空域解;整体解算精度高于GOCE时域解。
|
| 图 3 正则化前后的阶误差RMS及其与ESA模型的比较 Fig. 3 Degree error RMS solved before and after regularization and their comparation with ESA models |
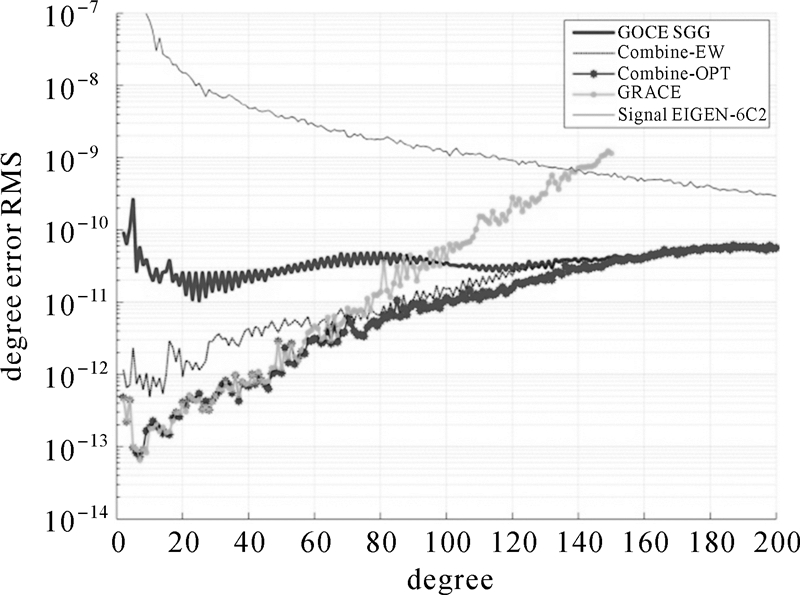
GRACE卫星对扇谐系数不敏感,而GOCE卫星的极空白特性导致带谐系数解算精度差,且星间距离变率和重力梯度的重力场响应频段各不相同,联合二者可提高重力场解算精度。本文分别基于动力积分法和空域最小二乘法获得了GRACE和GOCE SGG独立解,并基于联合平差给出了二者的联合解,计算结果如图 4所示。
|
| 图 4 GOCE SGG和GRACE及其联合解的阶误差RMS Fig. 4 Degree error RMS solved from GRACE,GOCE SGG and their combination |
GRACE解算模型在低阶次部分精度较高,重力梯度解算模型在高阶次部分精度高,联合解算模型在150阶次之前相比SGG精度均有提升,且理论最优解算模型(Combine-OPT)在全波段均优于等权解算模式(Combine-EW)。特别的,由于充分考虑了两种卫星任务的频谱特性,联合解算模型在80至150阶次部分的精度优于GRACE和GOCE的独立解算模型。上述计算结果验证了本文算法的可靠性和准确性。
5 结束语本文针对卫星重力场模型反演中的海量计算问题,实现了基于MPI的直接法求解卫星重力场模型并行算法。数值计算结果表明:分构建设计矩阵、法方程的构建与解算是密集型计算任务;采用分块方法构建设计矩阵和法方程系数阵,并行计算相对效率峰值可分别达到95%、68%,单个计算节点的内存占用率大幅度减小,算法的可移植性强;采用基于列交换的G-J法直接求逆,解算误差约为10-21量级,相对效率峰值约为63%;采用上述并行计算方法恢复120阶、240阶重力场模型仅需要40 min、7 h,内存耗用峰值仅为289.53 MB、1.57 GB,且基于GOCE卫星同等噪声水平的观测数据获取的重力场模型精度与GOCE已发布模型的精度相当,基于GOCE和GRACE卫星任务的联合解算可实现二者的频谱互补,本文的算法特别适用于基于大规模计算平台实现恢复高阶次地球重力场模型,可为长时间序列观测值反演高阶地球重力场模型提供软件支撑。
基于列交换的G-J求逆并行算法未能充分利用法方程系数阵为对称正定阵的特性,将在后续工作中利用该特性实现更为高效的并行求逆算法。此外,Intel MKL、ScaLAPACK等并行函数库提供了大量矩阵运算接口,OpenMP提供了共享存储模式下的并行标准,如何联合MPI和上述高性能并行函数库也将是进一步需要研究的问题。
| [1] | NING Jinsheng. The Satellite Gravity Surveying Technology and Research of Earth’s Gravity Field[J]. Journal of Geodesy and Geodynamics, 2002, 22(1): 1-5. (宁津生. 卫星重力探测技术与地球重力场研究[J]. 大地测量与地球动力学, 2002, 22(1): 1-5.) |
| [2] | NING Jinsheng, LUO Zhicai. The Progress and Application Prospects of Satellite-to-Satellite Tracking Technology[J]. Science of Surveying and Mapping, 2000, 25(4): 1-4. (宁津生, 罗志才. 卫星跟踪卫星技术的进展及应用前景[J]. 测绘科学, 2000, 25(4): 1-4.) |
| [3] | XU Houze. Satellite Gravity Missions-New Hotpoint in Geodesy[J]. Science of Surveying and Mapping, 2001, 26(3): 1-3. (许厚泽. 卫星重力研究: 21世纪大地测量研究的新热点[J]. 测绘科学, 2001, 26(3): 1-3.) |
| [4] | SUN Wenke. Satellitein Low Orbit(CHAMP, GRACE, GOCE) and High Precision Earth Gravity Field: The Latest Progress of Satellite Gravity Geodesy and Its Great Influence on Geoscience[J]. Journal of Geodesy and Geodynamics, 2002, 22(1): 92-100. (孙文科. 低轨道人造卫星(CHAMP、GRACE、GOCE)与高精度地球重力场: 卫星重力大地测量的最新发展及其对地球科学的重大影响[J]. 大地测量与地球动力学, 2002, 22(1): 92-100.) |
| [5] | SANS F, TSCHERNING C C. Fast Spherical Collocation: Theory and Examples[J]. Journal of Geodesy, 2003, 77(1-2): 101-112. |
| [6] | KLEES R, KOOP R, VISSER P, et al. Efficient Gravity Field Recovery from GOCE Gravity Gradient Observations[J]. Journal of Geodesy, 2000, 74(7-8): 561-571. |
| [7] | SNEEUW N. A Semi-analytical Approach to Gravity Field Analysis from Satellite Observations[D].München:University of München, 2000. |
| [8] | LI Xinxing, WU Xiaoping, LI Shanshan, et al. The Application of Block Diagonal Least Squares Methods in Geopotential Model Determination[J]. Acta Geodaetica et Cartographica Sinica, 2014, 43(8): 778-785. (李新星, 吴晓平, 李姗姗, 等. 块对角最小二乘方法在确定全球重力场模型中的应用[J]. 测绘学报, 2014, 43(8): 778-785.) |
| [9] | PAIL R, PLANK G. Assessment of Three Numerical Solution Strategies for Gravity Field Recovery from GOCE Satellite Gravity Gradiometry Implemented on a Parallel Platform[J]. Journal of Geodesy, 2002, 76(8): 462-474. |
| [10] | KLEES R, KOOP R,VAN GEEMERT R, et al. GOCE Gravity Field Recovery Using Massive Parallel Computing [C]//SIDERIS M G. Gravity, Geoid and Geodynamics 2000.Berlin Heidelberg: Springer, 2002: 109-116. |
| [11] | WANG Zhengtao. Theory and Methodology of Earth Gravity Field Recovery by Satellite-to-Satellite Tracking Data[D]. Wuhan: Wuhan University, 2005. (王正涛. 卫星跟踪卫星测量确定地球重力场的理论与方法[D]. 武汉: 武汉大学, 2005.) |
| [12] | ZOU Xiancai, LI Jiancheng, WANG Haihong, et al. Application of Parallel Computing with Open MP in Data Processing for Satellite Gravity[J]. Acta Geodaetica et Cartographica Sinica, 2010, 39(6): 636-641. (邹贤才, 李建成, 汪海洪, 等. Open MP并行计算在卫星重力数据处理中的应用[J]. 测绘学报, 2010, 39(6): 636-641.) |
| [13] | ZHOU Hao, ZHONG Bo, LUO Zhicai, et al. Application of Parallel Algorithms Based on Open MP to Satellite Gravity Field Recovery [J]. Journal of Geodesy and Geodynamics, 2011, 31(5): 123-127. (周浩, 钟波, 罗志才, 等. Open MP并行算法在卫星重力场模型反演中的应用[J]. 大地测量与地球动力学, 2011, 31(5): 123-127.) |
| [14] | LUO Zhicai. The Theory and Methodology for Determining the Earth’s Gravity Field Using Satellite Gravity Gradiometry Data[D]. Wuhan: Wuhan Technical University of Surveying and Mapping, 1996. (罗志才. 利用卫星重力梯度数据确定地球重力场的理论和方法[D]. 武汉: 武汉测绘科技大学, 1996.) |
| [15] | ZHONG Bo. Study on the Determination of the Earth’s Gravity Field from Satellite Gravimetry Mission GOCE[D]. Wuhan: Wuhan University, 2010. (钟波. 基于GOCE卫星重力测量技术确定地球重力场的研究[D]. 武汉: 武汉大学, 2010.) |
| [16] | University of Tennessee. Message Passing Interface Forum[EB/OL]. [2012-09-21]. http://www.mpi-forum.org/. |
| [17] | ZHANG Linbo,CHI Xuebin, MO Zeyao, et al. Introduction to Parallel Computing[M]. Beijing: Tsinghua University Press, 2006. (张林波,迟学斌, 莫则尧, 等. 并行计算导论[M]. 北京: 清华大学出版社,2006.) |
| [18] | CHEN Guoliang, AN Hong, CHEN Ling, et al. The Practical Study of Parallel Algorithm[M]. Beijing: Higher Education Press,2004. (陈国良, 安虹, 陈崚, 等. 并行算法实践[M]. 北京: 高等教育出版社,2004.) |
| [19] | MO Zeyao, YUAN Guoxing. Message Passing Parallel Programming Environment MPI[M]. Beijing: Science Press, 2001. (莫则尧, 袁国兴. 消息传递并行编程环境MPI[M]. 北京: 科学出版社,2001.) |
| [20] | DU Zhihui, LI Sanli. High Performance Parallel Programming with MPI[M]. Beijing: Tsinghua University Press, 2001. (都志辉, 李三立. 高性能计算之并行编程技术—MPI并行程序设计[M]. 北京: 清华大学出版社,2001.) |
| [21] | ZHOU Hao,LUO Zhicai, ZHONG Bo. Design and Analysis of MPI Parallel Algorithm for Large-scale Matrix Inversion[J]. Journal of Geodesy and Geodynamics,2014, 34(5): 120-124.(周浩, 罗志才, 钟波.大规模矩阵的MPI并行求逆算法设计与分析[J].大地测量与地球动力学, 2014, 34(5): 120-124.) |