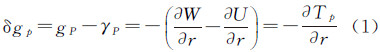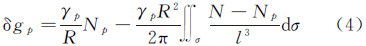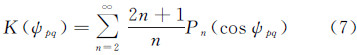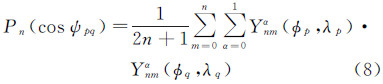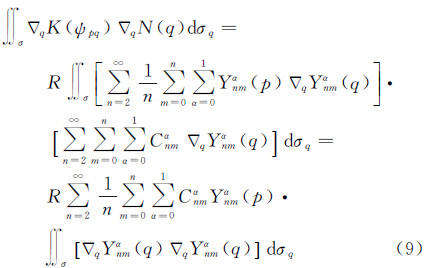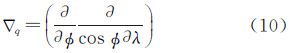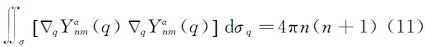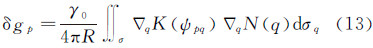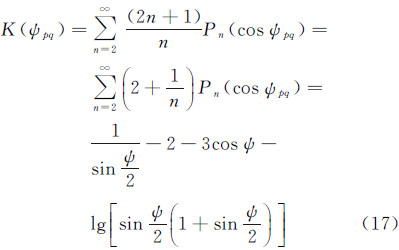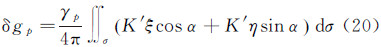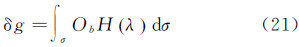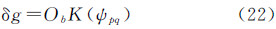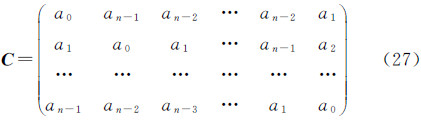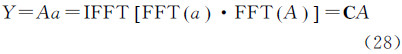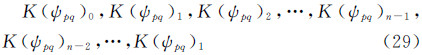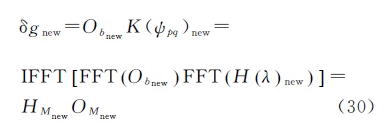2. 西安测绘研究所,陕西 西安 710054
2. Xi’an Institute of Surveying and Mapping, Xi’an 710054, China
1 引 言
传统的海洋重力场一般是指由各种观测手段获得的重力异常,随着空间大地测量学及物理大地测量学的发展,扰动重力较重力异常表现出更多优势。首先,海洋区域由于海面高的高度由卫星测高技术直接测得,扰动重力的确定可以避免重力异常计算过程中的归算问题,因此扰动重力的确定要比重力异常精确[1]。其次,从物理大地测量边值问题理论出发,以扰动重力为观测数据的Hotine公式要优于以重力异常为观测数据的Stokes公式[2, 3, 4, 5]。基于上述原因,越来越多的学者研究将扰动重力作为地球重力场的基础数据。文献[6]在频域中推导获得了由垂线偏差计算重力异常的公式;文献[7]推导获得了由垂线偏差计算重力异常的解析公式。然而到目前为止,还没有文献给出由卫星测高数据(包括垂线偏差和大地水准面)反演扰动重力的解析计算公式及实现方法。另一方面,随着卫星测高技术发展,观测数据的数量大幅提升,计算方法的精确性和快速性成为制约重力场应用的主要问题,这也是国内外学者一直关注的重点。为了解决计算慢的问题,文献[8, 9, 10, 11]较早研究分析了快速傅里叶变换(FFT)算法的应用。国内学者也对此开展了深入细致的研究,特别是在二维FFT算法应用上开展了详细的研究和分析[12, 13, 14, 15]。FFT算法可提高计算速度,但是直接用于重力场反演时将产生混叠、边缘效应等问题,这些问题使得重力场反演的精度有所下降。有学者提出在实际计算中采用补零方式解决混叠、边缘效应等问题,文献[16]指出任意长度的函数序列补零前后的傅里叶变换结果是不相同的,补零必须使得补零后的函数序列为补零前函数序列的整数倍且为2的整数次幂。针对上述问题,本文将首先推导获得由海面高及垂线偏差反演扰动重力的计算公式,进而提出一种精确快速的实现方法。
2 大地水准面高反演扰动重力卫星测高获得的直接观测量是海面高,在扣除海面地形影响后就得到大地水准面高,大地水准面上一点P的扰动重力与扰动位在球近似情况下的关系可表示为
考虑到 Tp=γpNp
大地水准面的径向导数为(球近似)
代入式(2)得大地水准面反演扰动重力的公式
3 垂线偏差反演扰动重力大地水准面高在球近似下表示为
扰动重力在球近似下可以表示如下
引入核函数K(ψpq)
考虑到
将式(8)代入式(7),则
式中,∇q表示梯度算子考虑到
则式(9)转化为对比式(6)和式(12)得到
考虑到
则核函数K(ψpq)的闭合形式如下
核函数K(ψpq)的导数推导如下
由于
综合以上各式可将式(13)转化为式(20) 式中,ξ、η分别表示垂线偏差的子午分量和卯酉分量。 4 全球及局部海洋扰动重力的精确快速计算方法将反演扰动重力方法抽象化,则扰动重力δg可看作观测量Ob与核函数K(ψpq)在计算区域的积分。具体表示如下
同时由卷积定义可知,δg可看作观测量Ob与核函数K(ψpq)关于经度λ的卷积,具体表示如下
利用一维FFT及卷积定理进而得到
式中,IFFT表示逆FFT变换。对于一维球面FFT算法而言,在每一纬度圈进行FFT计算,而在经度方向上进行求和运算。此时,Ob与核函数K(ψpq)可看作两个离散的实数序列,序列长度是同一纬度圈被计算点的格网数n。如果此时直接进行FFT计算,则如前所述,结果是不准确的,为了解决这一问题,首先对核函数K(ψpq)进行分析。对于同一纬度圈而言,在解析公式计算中,核函数K(ψpq)实际组成了一个n维的对称阵或反对称阵HM,而此时Ob序列组成一个观测矩阵OM
而对于一个卷积计算,如式(26) 式中,A、a表示两个序列,其中a=ak,(k=0,1,2,3,…,n-1)如果由序列a组成了一个循环矩阵C
则由循环矩阵的特点可知式(28)表明,如果核函数K(ψpq)组成的矩阵是一个循环矩阵,则可以直接利用一维球面FFT算法获得与原解析表达式同样精度的结果。对于全球海洋扰动重力反演而言,将观测得到的海面高数据或垂线偏差数据补充至全球区域,则可满足上述条件进而利用式(28)进行计算。
对于局部区域而言,由于观测数据覆盖地理区域有限,核函数K(ψpq)不能构成循环矩阵,则需要将核函数序列K(ψpq)进行改造,增加n-2个数,然后K(ψpq)变成新的序列K(ψpq)new
同时Ob也增加n-2个零值,形成新的序列Ob new,则
式中,HMnew、OMnew分别是K(ψpq)new、Obnew组成的矩阵,而重要的是HMnew的前n×n个元素正好构成矩阵HM,因此δgnew的前n个序列即是所要求的δg。 5 全球及局部海洋扰动重力反演试验首先进行全球海洋区域扰动重力反演,使用数据是由EGM2008地球重力场模型[17]生成2.5′分辨率的大地水准面高数据,经度范围是0°—360°,纬度范围是90°S—90°N。使用的常参数见表 1。
| 地心引力常数GM | 3 986 004.418×108 m3s-2 |
| 长半轴a | 6 378 137.0 m |
| 地球平均半径R | 6 371 000.0 m |
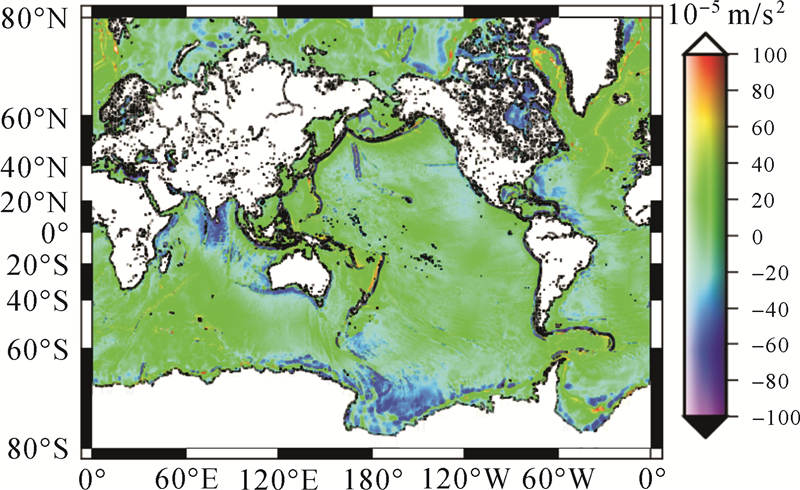
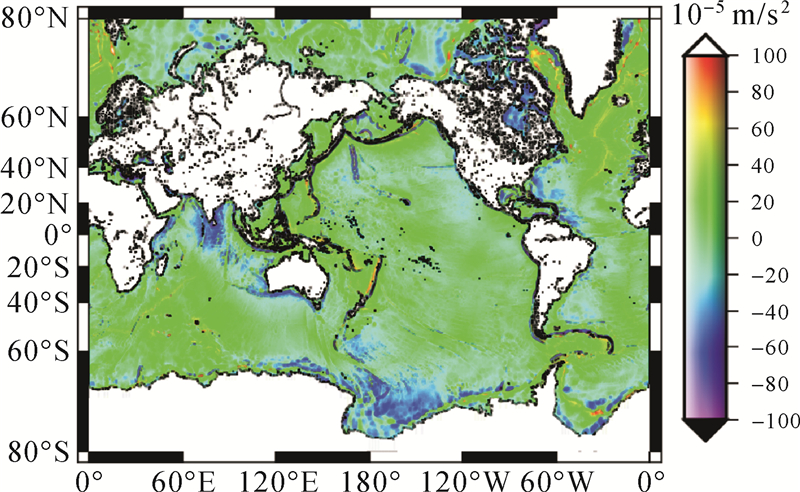
计算中,采用文献[18]给出的正常重力公式。利用大地水准面数据按照式(4)、式(28)反演获得全球海洋区域扰动重力,见图 1。在2.5′分辨率大地水准面高数据基础上,生成全球2.5′分辨率的垂线偏差,而后按照式(7)、式(28)反演获得全球海洋区域扰动重力,见图 2。
|
| 图 1 由大地水准面高反演的全球海洋区域扰动重力 Fig. 1 Global ocean disturbing gravity derived from geoid height |
|
| 图 2 由垂线偏差反演的全球海洋区域扰动重力 Fig. 2 Global ocean disturbing gravity derived from vertical deflection |
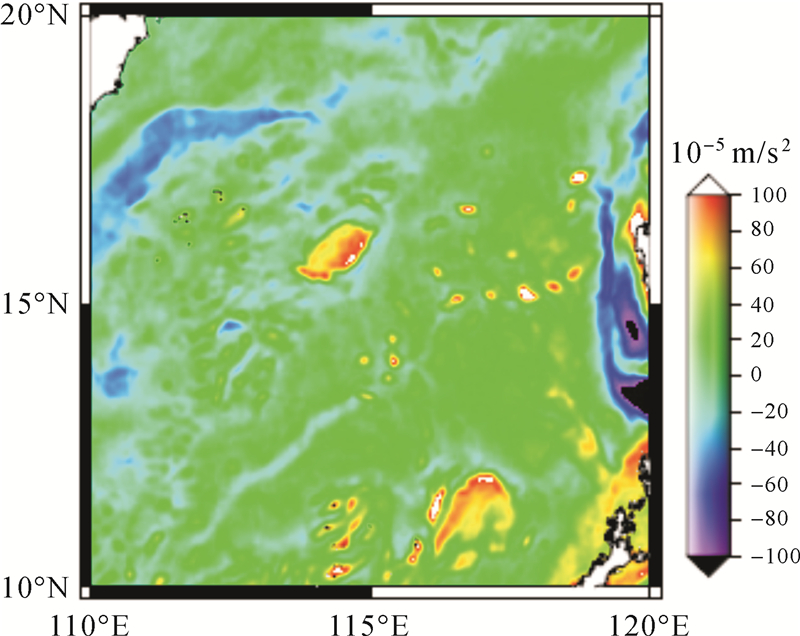
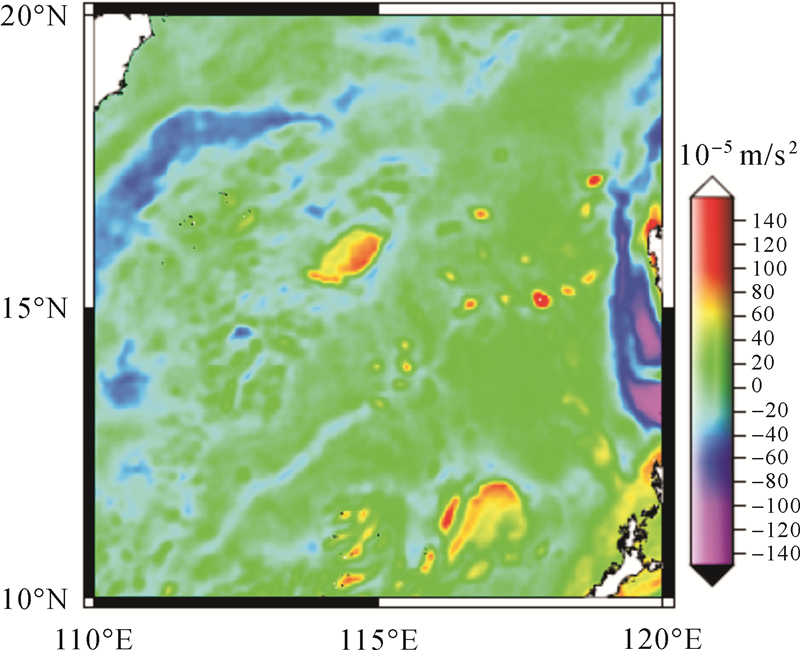
其次进行局部区域扰动重力计算,使用的数据是EGM2008地球重力场模型生成的2.5′分辨率大地水准面及垂线偏差数据,数据范围是110°E—120°E,纬度范围是10°N—20°N。采用的方法同上,在实际计算时采用了式(30)的改化方法,最终得到的局部区域海洋扰动重力见图 3、图 4。
|
| 图 3 由大地水准面高反演的局部海洋区域扰动重力 Fig. 3 Local ocean disturbing gravity derived from geoid height |
|
| 图 4 由垂线偏差反演获得的局部海洋区域扰动重力 Fig. 4 Local ocean disturbing gravity derived from vertical deflection |
首先将基于精确快速算法的计算结果与传统解析离散求和方法进行比较。结果表明,采用本文提出的精确快速算法可以得到与传统解析算法同样的结果,差异在10-5量级,且计算速度提高20倍左右。其次,将局部区域(110°E—120°E、10°N—20°N)的计算结果与全球积分获得的局部区域结果进行比较,发现在区域的边界处有约10×10-5 m/s2~30×10-5 m/s2的差异,这也说明在局部区域的计算中,边缘区域会出现结果失真的现象。因此无论使用什么方法,使用数据的范围应大于被计算的区域范围,从本文来看,数据的范围应扩大1°之上。
在目前的海洋重力场反演中,一般采用基于垂线偏差的逆Vening Meinesz方法,而很少使用大地水准面进行计算。为了进一步对两种反演方法进行对比,以局部区域反演为例对由大地水准面和垂线偏差分别计算的扰动重力进行比较,结果见表 2。
| ×10-5 m/s2 | ||||
| 比较范围 | 最大差值 | 最小差值 | 差值均值 | 标准差 |
| 10°×10° | 14.66 | -17.41 | -0.43 | 0.79 |
从图 1—图 4以及表 2可以看出,由大地水准面和垂线偏差分别反演获得的扰动重力其差异在0.8×10-5 m/s2左右,这说明两种反演方法是基本一致的,这也符合理论上的等价要求。上述计算中,大地水准面和垂线偏差数据中是假设没有误差的,但在卫星测高相邻观测点中若包含有系统误差,则在垂线偏差的求解过程中,这些系统误差会很大程度上被消除,而从公式(4)可以看出,这些系统误差却不能完全消除。因此,在实际处理中由垂线偏差反演扰动重力还是具有一定优势的。
6 结 语本文对海洋扰动重力反演理论及实现方法进行了深入研究,得到了以下结论。
(1) 从经典边值问题理论及球谐函数理论出发推导获得了由大地水准面高以及垂线偏差计算扰动重力的解析计算公式,解决了利用卫星测高数据反演海洋扰动重力的理论问题,也为扰动重力数据的来源及第二大地边值问题的应用提供了解决途径。
(2) 在前人已有工作的基础上,提出了改进的海洋扰动重力的精确快速算法。对于全球海洋扰动重力计算,通过将观测数据补充至全球区域可在每一纬度圈进行FFT计算,而后在经度方向上进行求和运算,这种处理方式保证了FFT计算后的结果与原解析算法是一致的。对于局部海洋扰动重力计算,通过对核函数和观测数据补充一定量数据从而使得核函数构成了循环矩阵,进而利用FFT计算后保证了结果与原解析算法是一致的。利用本方法,海洋扰动重力的计算速度与解析方法相比提高约20倍,且避免了海洋重力场反演中存在的混叠、边缘效应问题,计算精度等同于原解析算法,更加重要的是对观测数据的序列长度没有硬性要求,使得该方法的应用更加灵活。
(3) 利用本文提出的反演理论和方法计算获得了全球及局部海洋区域的扰动重力数据,并对两种方法进行了比较分析。本文提出的精确快速算法也可以应用于物理大地测量中大部分积分问题的求解,如求解大地水准面、垂线偏差、地形改正等。
为了进一步验证本文提出的改进方法,未来需要利用卫星测高实测数据进行计算,并利用船测重力数据深入比较由大地水准面、垂线偏差反演扰动重力的实际差别。
| [1] | GUAN Zelin,GUAN Zheng,HUANG Motao,et al. Local Gravity Field Approximation Theory and Method[M]. Beijing: Surveying and Mapping Press,1997. (管泽霖,管铮,黄谟涛,等. 局部重力场逼近理论和方法[M]. 北京: 测绘出版社,1997.) |
| [2] | VANCEK P,ZHANG Changyou,SJBERG L E. A Comparison of Stokes and Hotine’s Approaches to Geoid Computation[J]. Manuscripta Geodaetica,1992,17: 29-35. |
| [3] | CLAESSENS S. Solutions to the Ellipsoidal Boundary Value Problems for Gravity Field Modelling[D]. Curtin: Curtin University of Technology,2006. |
| [4] | WU Xiaoping,LI Shanshan,ZHANG Chuanding. Problem of the Boundary Value of Disturbing Gravity and Practical Data Processing[J]. Geomatics and Information Science of Wuhan University,2003,28(S): 73-76. (吴晓平,李姗姗,张传定. 扰动重力边值问题与实际数据处理的研究[J]. 武汉大学学报: 信息科学版,2003,28(特刊): 73-76.) |
| [5] | LI Fei,CHEN Wu,YUE Jianli. Physical Geodesy with GPS[J]. Acta Geodaetica et Cartographica Sinica,2003,32(3): 198-203. (李斐,陈武,岳建利. GPS在物理大地测量中的应用及GPS 边值问题[J]. 测绘学报,2003,32(3): 198-203.) |
| [6] | SANDWELL D T,SMITH W H F. Marine Gravity Anomaly from Geosat and Ers 1 Satellite Altimetry[J]. Journal of Geophysical Research,1997,102(B5): 10039-10054. |
| [7] | HWANG C. Inverse Vening Meinesz Formula and Deflection-geoid Formula: Applications to the Predictions of Gravity and Geoid over the South China Sea[J]. Journal of Geodesy,1998,72(5): 304-312. |
| [8] | COLOMBO O L. Numerical Methods for Harmonic Analysis on the Sphere[R]. Ohio: The Ohio State University, 1981. |
| [9] | FORSBERG R,SIDERIS M G. Geoid Computations by the Multi-banding Spherical FFT Approach[J]. Manuscripta Geodaetica,1993,18(2): 82-90. |
| [10] | HAAGMANS R,DE MIN E,GELDEREN M V. Fast Evaluation of Convolution Integrals on the Sphere Using 1D FFT,and a Comparison with Existing Methods for Stokes’ Integral[J]. Manuscripta Geodaetica,1993,18(5): 227-241. |
| [11] | SCHWARZ K P,SIDERIS M G,FORSBERG R. The Use of FFT Techniques in Physical Geodesy[J]. Geophysical Journal International,1990,100(3): 485-514. |
| [12] | LI Jiancheng,CHEN Junyong,Ning Jinsheng,et al. The Earth’s Gravitational Field Approximation Theory and the Determination of China 2000 Quasi-geoid[M]. Wuhan: Wuhan University Press,2003. (李建成,陈俊勇,宁津生,等. 地球重力场逼近理论与中国2000似大地水准面的确定[M]. 武汉: 武汉大学出版社,2003.) |
| [13] | HUANG Motao,ZHAI Guojun,GUAN Zheng,et al. On the Recovery of Gravity Anomalies from Altimeter Data[J]. Acta Geodaetica et Cartographica Sinica,2001,30(2): 179-183. (黄谟涛,翟国君,管铮,等. 利用卫星测高数据反演海洋重力异常研究[J]. 测绘学报,2001,30(2): 179-183.) |
| [14] | LI Jiancheng,NING Jinsheng,CHAO Dingbo,et al. The Applications and Progress of Satellite Altimetry in Geodesy[J]. Science of Surveying and Mapping,2006,31(6): 19-21. (李建成,宁津生,晁定波,等. 卫星测高在大地测量学中的应用及进展[J]. 测绘科学,2006,31(6): 19-21.) |
| [15] | HUANG Motao,ZHAI Guojun,GUAN Zheng,et al. Marine Gravity Field Measurement and Its Applications[M]. Beijing: Surveying and Mapping Press,2005. (黄谟涛,翟国军,管铮,等. 海洋重力场测定及其应用[M]. 北京: 测绘出版社,2005.) |
| [16] | WANG Bing,SHEN Weichang,TIAN Laike,et al. A Study on the Problem of Add Zero in the Algorithm of Cooley-Tukey Fast Fourier Transform[J]. Journal of Northwest University: Natural Science Edition,2004,34(1): 31-33. (王冰,申卫昌,田来科,等. 快速傅里叶变换Cooley-Tukey算法补零问题[J]. 西北大学学报: 自然科学版,2004,34(1): 31-33.) |
| [17] | PAVLIS N K,HOLMES S A,KENYON S C,et al. An Earth Gravitational Model to Degree 2160: EGM2008[C]. Vienna,Austria: EGU General Assembly 2008,2008. |
| [18] | HOFMANN-WELLENHOF B,MORITZ H. Physical Geodesy[M]. New York: Springer Wien,2006. |