2. 地理信息工程国家重点实验室,陕西 西安 710054
2. State Key Laboratory of Geography Information Engineering, Xi'an 710054, China
1 引 言
在地图制图综合中常将大比例尺地图转换为小比例尺地图,尽管尺度发生变化,但其所表达的信息应该保持一定的相似性,空间相似性可用来评判综合结果是否合理。广义上,空间相似性指根据特定内容和比例尺对空间的匹配和排序。文献[1]将空间相似性定义为:在某一特定比例尺和内容上被认为是两个相似的区域。已有的空间相似性方法包括空间拓扑、方向、距离、语义等关系相似性。文献[2]将多尺度地图空间相似关系分为图形相似和属性相似两大类。方向关系相似性亦属图形相似,可作为制图综合结果评判的指标之一。
相似关系的强弱模糊性难以衡量,方向关系模型中有只用于表示方向关系的定性模型,亦有用于相似度评估的定量模型[3, 4, 5, 6, 7, 8, 9],以及既为定性模型亦为定量模型的方向矩阵模型[10, 11];通过对方向矩阵模型进行改进得到一系列可应用于栅格数据或解决分区线与对象重合等问题的模型[12, 13, 14, 15, 16]。此外,根据不同的应用情况产生了各种侧重点不同的方向关系模型[17, 18, 19, 20, 21, 22, 23]。定性模型缺乏进行方向关系相似度计算的量化信息;大部分定量模型为降低计算的复杂度仅对对象的外包矩形或质心等替代物建模,且表示出的方向关系可比性较差,无法对方向关系相似度进行定量比较。
与忽略空间对象自身形状细节对方向关系的影响模型不同,方向关系矩阵模型基于空间对象自身形状建模,满足了空间方向模型应具备可形式化、可推导、形状敏感、尺度中立、可比性这5个特性。 根据方向关系矩阵模型的定量描述特点,可利用方向关系矩阵间的距离来计算方向关系间的相似度。现阶段利用方向关系矩阵进行定量计算研究较少,文献[10, 11]基于邻域图利用详细关系矩阵对空间对象的相似度的定量计算进行了尝试。
本文以方向关系矩阵模型为基础,简单直观地表达出任意空间对象间的方向关系,引入Northwest-Corner方法[24]计算方向矩阵间的距离,从而获得任意尺度空间对象的方向相似度。
2 方向相似度计算方法本文利用方向关系矩阵对空间对象间的方向关系进行描述。
2.1 格网下的方向关系矩阵表示方向关系矩阵的计算首先通过参考对象A最小外包矩形边所在直线将空间划分成9个分区{N,S,E,W,NE,SE,SW,NW,same},分别对应3×3矩阵的9个元素,元素值记录的信息决定矩阵的详细程度。本文将地图上所涉及的区域划分为固定大小的网格阵列,量化信息通过目标对象B所占的网格数目计算,即通过B在各分区的网格数目与对象所占的总网格数目之比表示,如式(1)所示
该方法可简化关系矩阵的计算。本文中点对象所占的网格数记为1,当参考对象为点时以该点所在网格的延长线进行分区。
通过动态调整格网大小,本方法使对象落在某些格网中而非在格网线上。由于参考对象的分区线与格网线重合,目标对象亦不会落在分区线上和分区线交点处。因此,采用该简化的方向矩阵即可表示任意对象之间的关系。
2.2 空间参考对象的划分本文的方向度量模型可表示任意对象对间的方向关系,实际应用时仍有特殊情况需处理:目标对象全部落在same区,表示参考对象与目标对象重合。但在实际空间场景中,选定的两个对象为相离或相邻关系,不可能出现重叠的情况,需对参考对象进行划分处理。
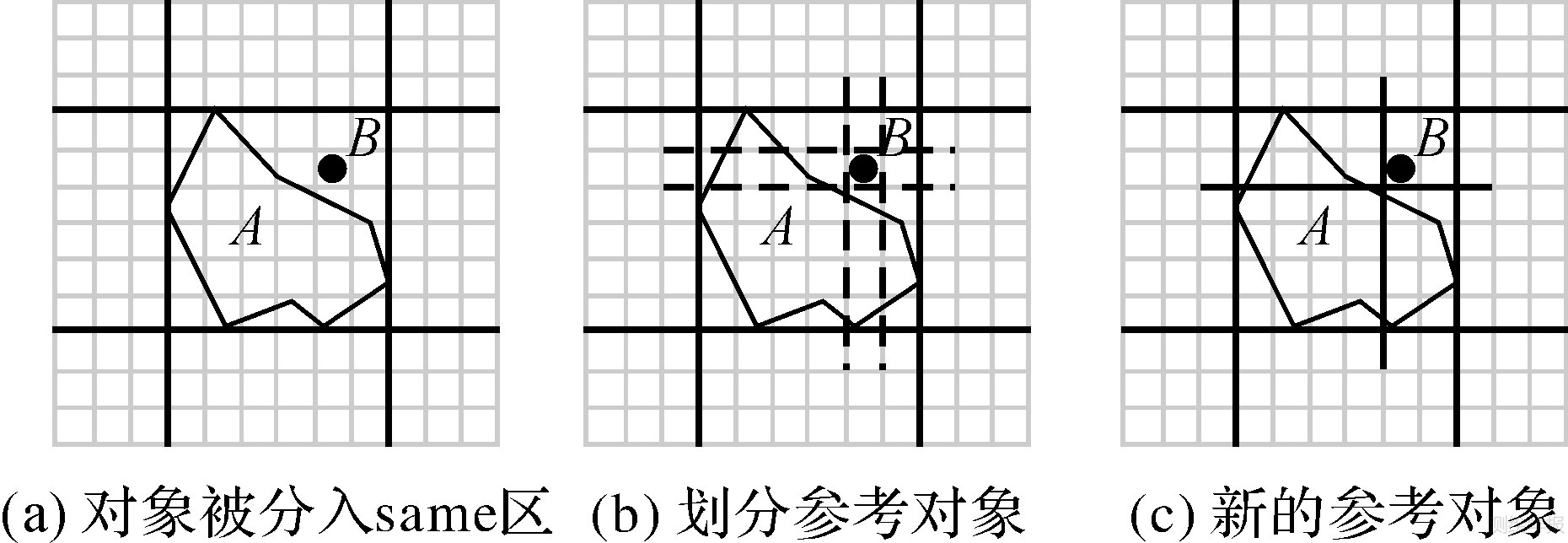
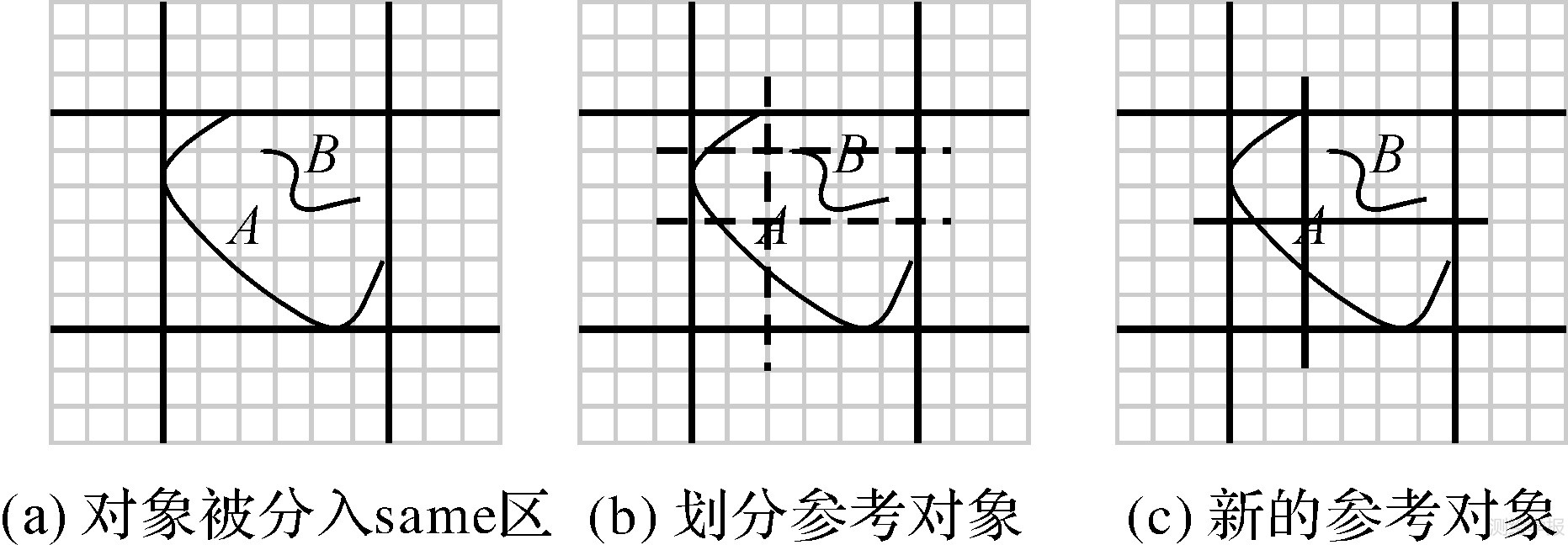
当两个对象距离很近时,可能出现方向关系判断不准确的情况。如图 1 (a)、图 2 (a)所示,两幅图中目标对象相对于参考对象的方向是明确的,但都被划分到same区,此时需对参考对象进行划分,即以目标对象所占网格的延长线对参考对象截取的最小范围作为新的参考对象,判断目标对象与参考对象间的方向关系。图 1 (b)、图 1 (c)和图 2 (b)、图 2 (c)为用B所在的栅格线的延长线对A进行划分,选取所截范围最小的两条延长线,将这两条延长线与分区线截取出的部分作为新的参考对象重新进行分区。
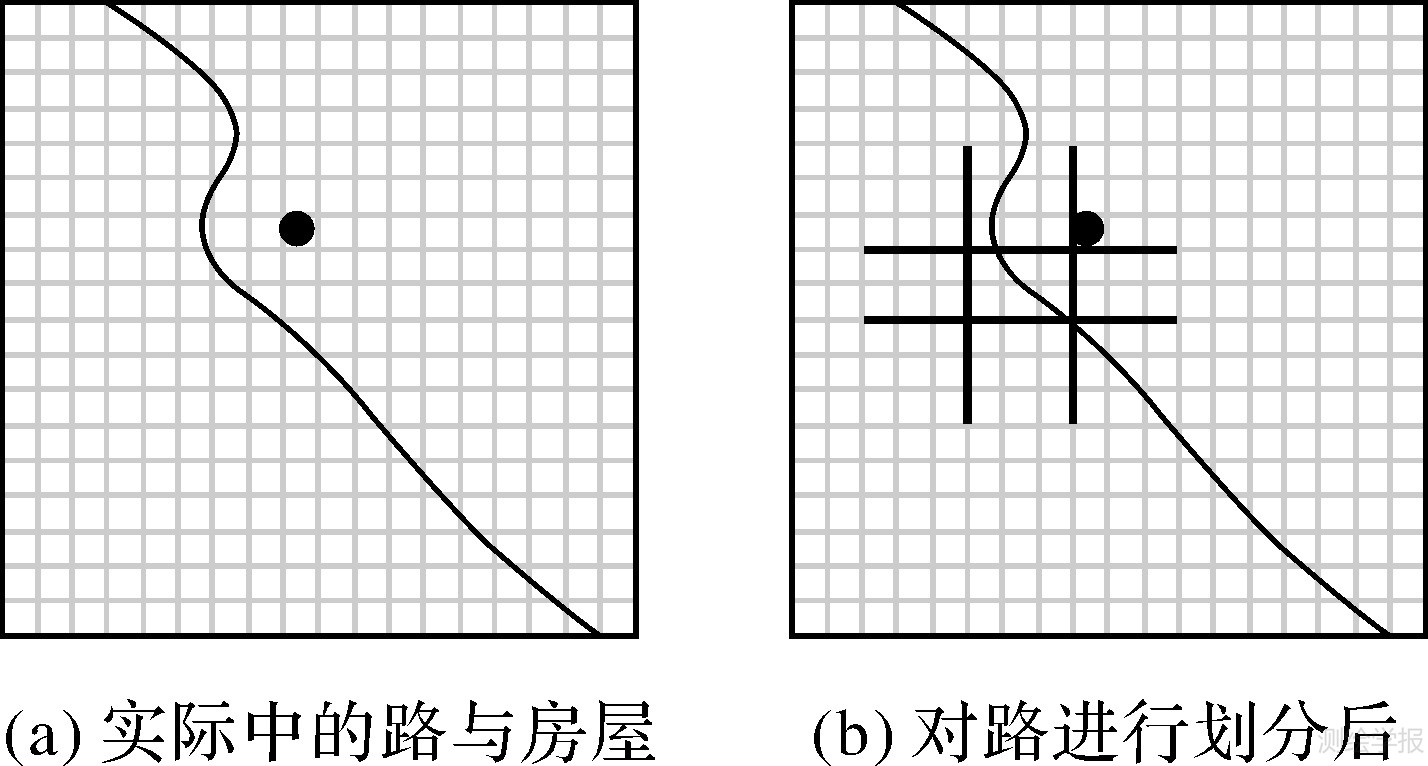
在实际应用中数据远比示例中数据大且复杂,参考对象的划分也更有必要,如线对象并不是只有上述示例中的一段,很可能是很长的一条路(图 3 (a)),当对路旁边的一个房屋的方位判断时,若使用整条线判断,得到房屋就在公路上,不符合实际。需对参考对象进行划分后再进行判断才符合实际,如图 3 (b)。
|
| 图 1 用点对象对面对象进行划分 Fig. 1 Coarse split on region reference to point |
|
| 图 2 用线对象对线对象进行划分 Fig. 2 Coarse split on line reference to line |
|
| 图 3 实际应用中的划分 Fig. 3 Coarse split applied in practice |
方向关系可通过方向关系矩阵表达,两个方向关系之间的相似度即可通过其对应的方向关系矩阵之间的相似度来反映。如图 4所示,计算方向关系之间的相似度s首先需计算方向关系矩阵之间的距离d,然后将d转换为相异度δ
最后通过δ求相似度s 式(2)与式(3)中,D为方向关系矩阵;dmax为邻域图的最大距离。相似度取值范围为[0,1],取值越大表示两个方向关系越相似,如1就表示两个方向关系完全相同。本文将任意两个方向关系矩阵之间的距离定义为从源方向矩阵D0转换成目的方向矩阵D1的最小代价,该转换通过将D0中的非零元素从原来的位置沿着邻域图的路径移动到D1中非零元素的位置来实现。距离d的计算分两种情况讨论:单元素矩阵间的距离与多元素矩阵间的距离。单元素方向矩阵只有一个非零元素,多元素方向关系矩阵中存在多个非零元素,单元素矩阵可看作一种特殊的多元素矩阵。 2.3.1 单元素方向关系矩阵间的距离单元素方向矩阵对应9种不同单元素方向关系。单元素矩阵间的最小距离与邻域图有关。在9方向分区上建立合适的邻域图有利于提高距离的计算精确度。邻域图分为4邻域图和8邻域图,4邻域图和8邻域图中各顶点之间的最小距离不同(图 5)。若采用4邻域图,式2中dmax取值为4,若采用8邻域图则其取值为2。

|
| 图 4 求解相似度的具体过程 Fig. 4 Process for assessing similarity |
这种情况亦包含两种情况。
(1) 从多元素矩阵转换为单元素矩阵,即将多元素的非零元素移入目的矩阵中唯一的非零元素中,需计算多元素矩阵中每个非零元素按其权重与单元素矩阵中非零元素的距离之和,即
式中,D0i表示源矩阵D0中的元素值;D1des表示目的矩阵D1中的非零元素,d(D0i,D1des)表示两个元素之间的距离,即两个对应位置非零的单元素矩阵之间的距离。由于距离是对称的,单元素源矩阵与多元素目的矩阵的距离可通过计算目的矩阵到源矩阵的距离获得。

|
| 图 5 4邻域图(左侧值)和8邻域图(右侧值)的单元素方向关系矩阵间距离 Fig. 5 4-neighbor distances (left) and 8-neighbor distances (right) between cardinal direction |
(2) 从多元素矩阵转换为多元素矩阵,由于这种情况下不能明确源多元素矩阵各非零元素转入目的多元素矩阵各非零元素的比例,本文利用方向矩阵间转换的最小代价计算距离。首先,了解几个与矩阵相关的概念。
定义1:矩阵D0 和D1 的共性矩阵C01
C01的每个元素的值取D0和D1相应位置上两个元素的较小值。同理,D1和D0的共性矩阵C10元素的值亦取两个矩阵中元素的较小值,因而C01=C10。定义2:矩阵D0与D1的非对称相异矩阵R01为矩阵D0与共性矩阵之差,即
同理,矩阵D1与D0的非对称相异矩阵R10为矩阵D1与共性矩阵之差,即
定义3:矩阵D0与D1的方向相异矩阵Δ01定义为两个非对称相异矩阵的差值,即
用式(6)和式(7)中的值替换到式(8)中可得
式中,Δ01元素的值范围为[-1,1]。由于方向关系矩阵间的转换与平衡传输问题有一定的共性,借用平衡传输问题的解决方法可求解矩阵间转换的最小代价。首先了解普通的平衡传输问题及其求解思想。
平衡传输表(balance transportation tableau,BTT)如图 6所示,已知仓库Wi能供给的货物量为si,市场Mj的需求量为dj,cij为从Wi到Mj运送单位货物的成本,已知仓库的总供给量等于市场的总需求量。如何分配货物才能使得运输成本最低,即平衡运输问题。

|
| 图 6 平衡传输表 Fig. 6 The balance transportation tableau |
假设最终解决方案中从Wi运送到Mj的货物为xij。问题演变成确定特定的x,使得代价z最小,即
式中,x需满足仓库供给量和市场需求量的约束为一种求解xij的方法为Northwest-Corner方法:从平衡传输表的左上方开始,先清空一个仓库或填满一个市场,将实际运输量记下,并从相应的行列中减去运输量,然后删除已空的仓库(行)或已满的市场(列),如果两者同时满足且该行不是剩下的唯一行,则优先去掉行,直到所有的行列都删除,否则继续回到新表的左上方重新开始,每次记下的运输量即为最终xij的解。
方向关系矩阵间的转换与从仓库(源矩阵非零元素对应的分区)运输货物(非零元素)到市场(目的矩阵非零元素对应的分区)类似,两矩阵若在同一位置都有非零元素,那么部分非零元素(两者中值较小的元素值)是不需运送的,即两者的共性矩阵中的非零元素无须运送,因此非零元素的运送实质是在两个非对称相异矩阵中进行。
3 空间方向相似度计算实例分析本文选取制图综合中4种可能的情况,作为示例进行分析。
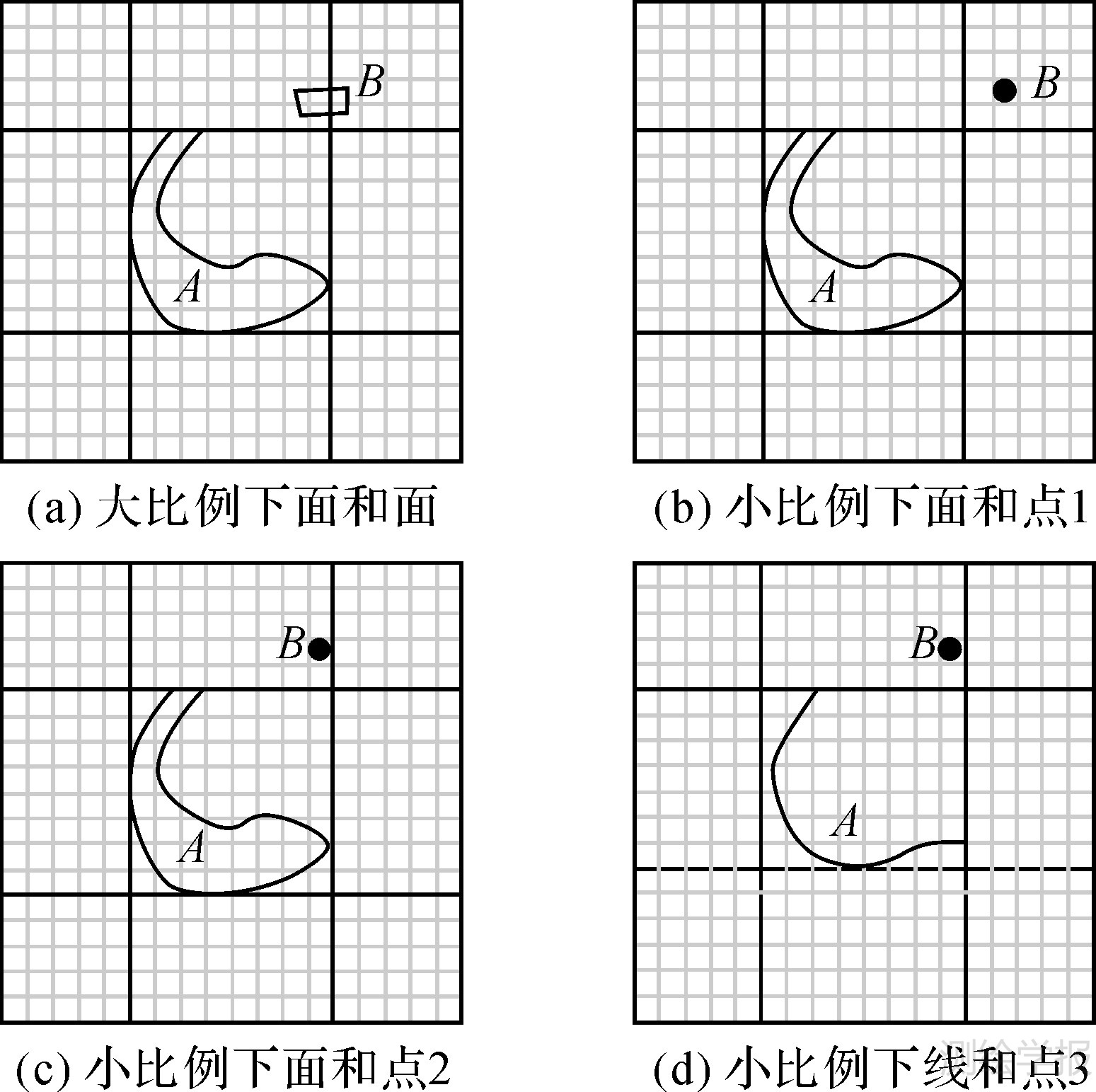
3.1 面面到面点如图 7 (a)为大比例尺下的两个面对象,图 7 (b)—7(d)为综合后的小比例尺地图,图 7 (b)和图 7 (c)中目标对象B综合为点对象,图 7 (d)中参考对象A综合为线对象。
|
| 图 7 大比例下面和面转为小比例尺的情况 Fig. 7 Collapsing a pair of regions at large scale to objects at small scale |
图 7 (a)—7(b)的关系矩阵如式(12)—式(13)所示
图 7 (c)—7(d)的方向关系矩阵如式(14)所示
计算得到:图 7(a)、(b)之间相似度S0=1-0.67×1/4 = 0.8325,图 7(a)、7(c)之间相似度S1=1-0.33×1/4=0.9175,图 7(a) 、7(d)之间相似度S2=1-0.33×1/4=0.9175。图 7(b)和图 7(c)相比较,图 7(b)、7(a)的相似度低于图 7 (c)、7(a),图 7(c)更符合制图综合的要求,图 7(d)同样也较好地保持了方向间的相似性。
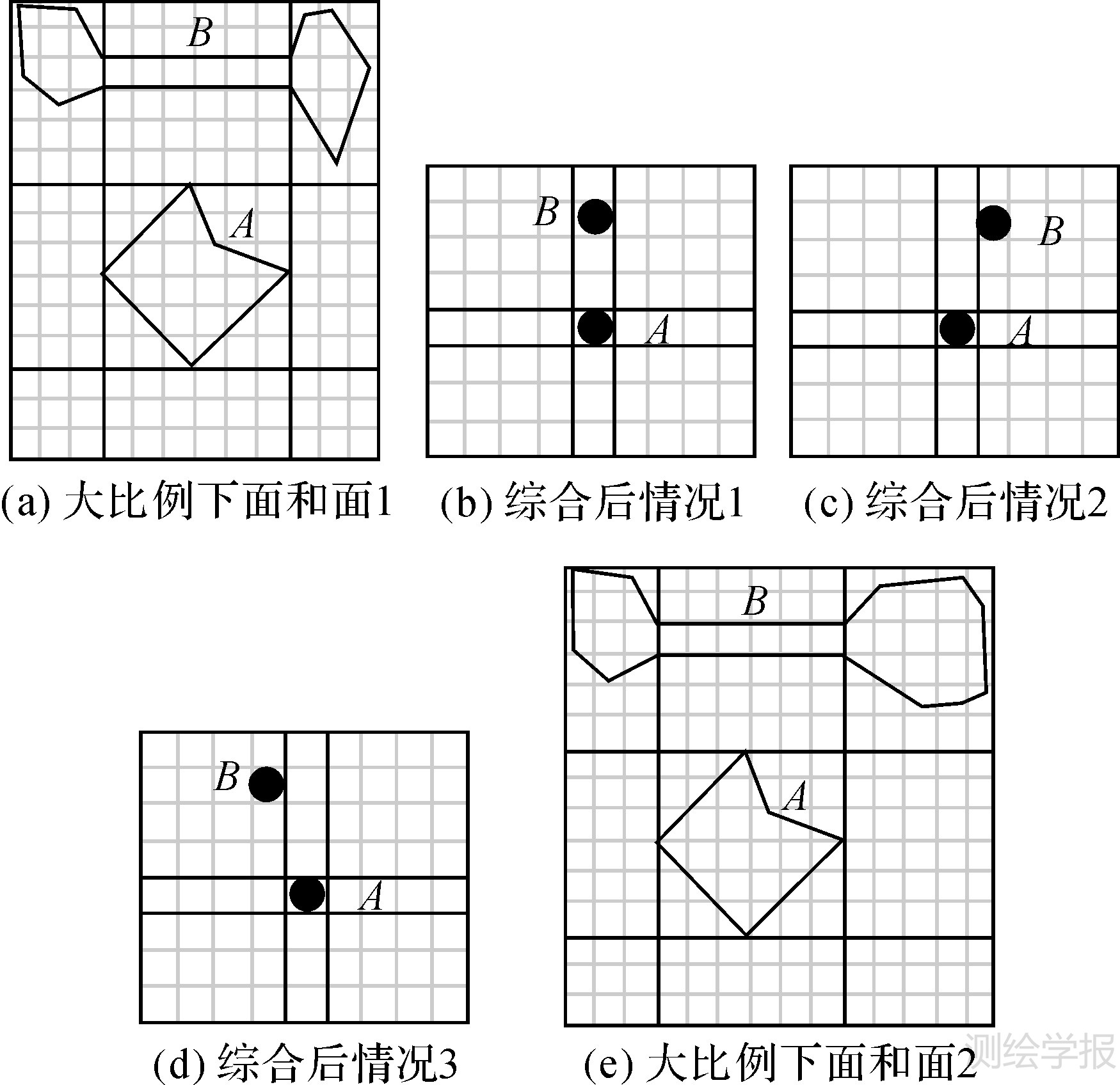
3.2 面面到点点如图 8 (a)为大比例尺下的两个面对象,图 8 (b)—8(d)为综合后的小比例尺地图,面对象均综合为点对象,不同之处在于B相对于A的位置,图 8(a) 中目标对象分别落在在参考对象的N、NE和NW这3个分区。
|
| 图 8 大比例下面和面转为小比例尺的情况 Fig. 8 Collapsing a pair of regions at large scale to objects at small scale |
图 8 (a)—8(d)的关系矩阵依次为式(15)—式(18)
计算结果:图 8(a) 、图 8(b)之间相似度S0=1-(11×1+6×0+14×1)/31/4=0.798387,图 8 (a)、8(c)之间相似度S1=1-(11×2+6×1+14×0)/31/4=0.774194,图 8 (a)、8(d)之间相似度S2=1-(11×0+6×1+14×2)/31/4=0.725806。图 8(b) —8(d)与图 8 (a)的相似度逐渐递减,即图 8 (b)更符合制图综合的要求。
若对象B的形状稍作改变,则图 8 (b)不一定仍为最佳结果。如图 8 (e)所示,得到其方向关系矩阵为
重新计算方向关系相似度结果为:图 8 (b)、(e)之间相似度S0=1-(12×1+6×0+22×1)/40/4=0.7875,图 8 (c)、(e)之间相似度S1=1-(12×2+6×1+22×0)/40/4=0.8125,图 8 (d)、(e)之间相似度S2=1-(11×0+6×1+22×2)/40/4=0.6875。此时图 8 (c)的相似度更高。当目标对象关于参考对象近似对称分布即左右部分面积相差不大时,综合后的方向接近目标对象中心点所在的位置方向,若左右部分面积相差较大则会偏向面积大的方向。
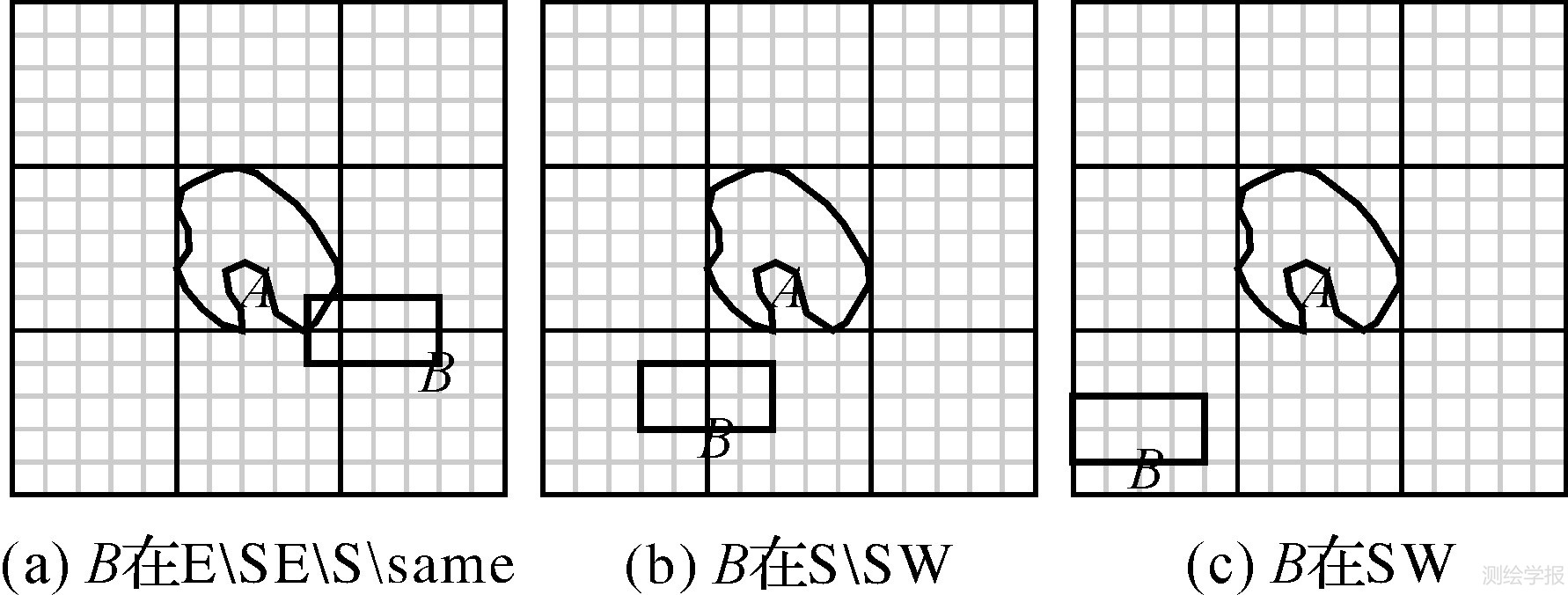
3.3 面面到面面如图 9所示,将目标对象B向西移动,比较图 9 (b)、9(c)与图 9 (a)的相似度。通过视觉可直观判断图 9 (b)与图 9 (a)的相似度更高,计算结果将对此进行验证。
图 9 (a)—9(c)的方向关系矩阵如式(20)—式(22)所示
|
| 图 9 将目标对象B向西移动 Fig. 9 Moving the target object B to west |
图 9 (a)、9(b)间的相似度需用多元素方向关系矩阵间的距离进行计算,得到两者之间的方向相异矩阵为
通过仓库即SE、E、same的供给量(正元素)和市场即S、SW的需求量(负元素)得到平衡传输表如图 10所示。

|
| 图 10 矩阵D0和D1的平衡传输表 Fig. 10 BTT between D0 and D1 |
由解集xij(i∈{1,2,3},j∈{1,2})得到的总代价z
解集应该满足式(25)的约束条件
然后用Northwest-Corner法求解xij。
(1) 从图 11 (a)左上角开始,首先满足一个仓库(E)的供给或者市场(SW)的需求,先满足两者中较小的0.375,取x11=0.375,在仓库的供给量和市场的需求量中减掉x11,此时第一行的仓库清空,删掉行,继续对新表进行操作。
(2) 现在图 11 (b)左上方为SE和SW,取x21为两者中的较小值0.125,同时两者减掉x21,此时只有该列为0,因此去掉该列。
(3) 现在图 11 (c)左上方为SE和S,SE的值较小因此取x22=0.25,将两者的值减掉x22,此时SE的值为0,而S的值为0.125,因此去掉该行。
(4) 现在图 11 (d)左上方为same和S,两者都等于0.125,因此直接取x32=0.125,并同时将两者的值减掉x32,发现两者都为0,优先删除该行,表格清空循环停止。

|
| 图 11 使用的Northwest-Corner时的平衡传输表 Fig. 11 BTT in Northwest-Corner method |
循环得到最终解集如下:x11=0.375,x21=0.125,x22=0.25,x32=0.125,x12 =x31=0。总代价为:z=3x11+2x12+2x21+x22+2x31+x32 =3×0.375+2×0+2×0.125+0.25+2×0+0.125=1.75。因此方向关系矩阵D0和D1间的距离d(D0,D1)=z =1.75,求得图 9 (a)、(b)相异度δ(D0,D1)=z/4=0.4375,相似度S0=s(D0,D1)=0.5625。
根据D0、D2求得图 9 (a)、(c)之间相似度S1=1-(0.125×(2+1)+0.375×(2+3))/4=0.4375。由计算结果可知,图 9 (a)、(b)的相似度高于图 9 (a)、9(c),符合人类的实际认知。
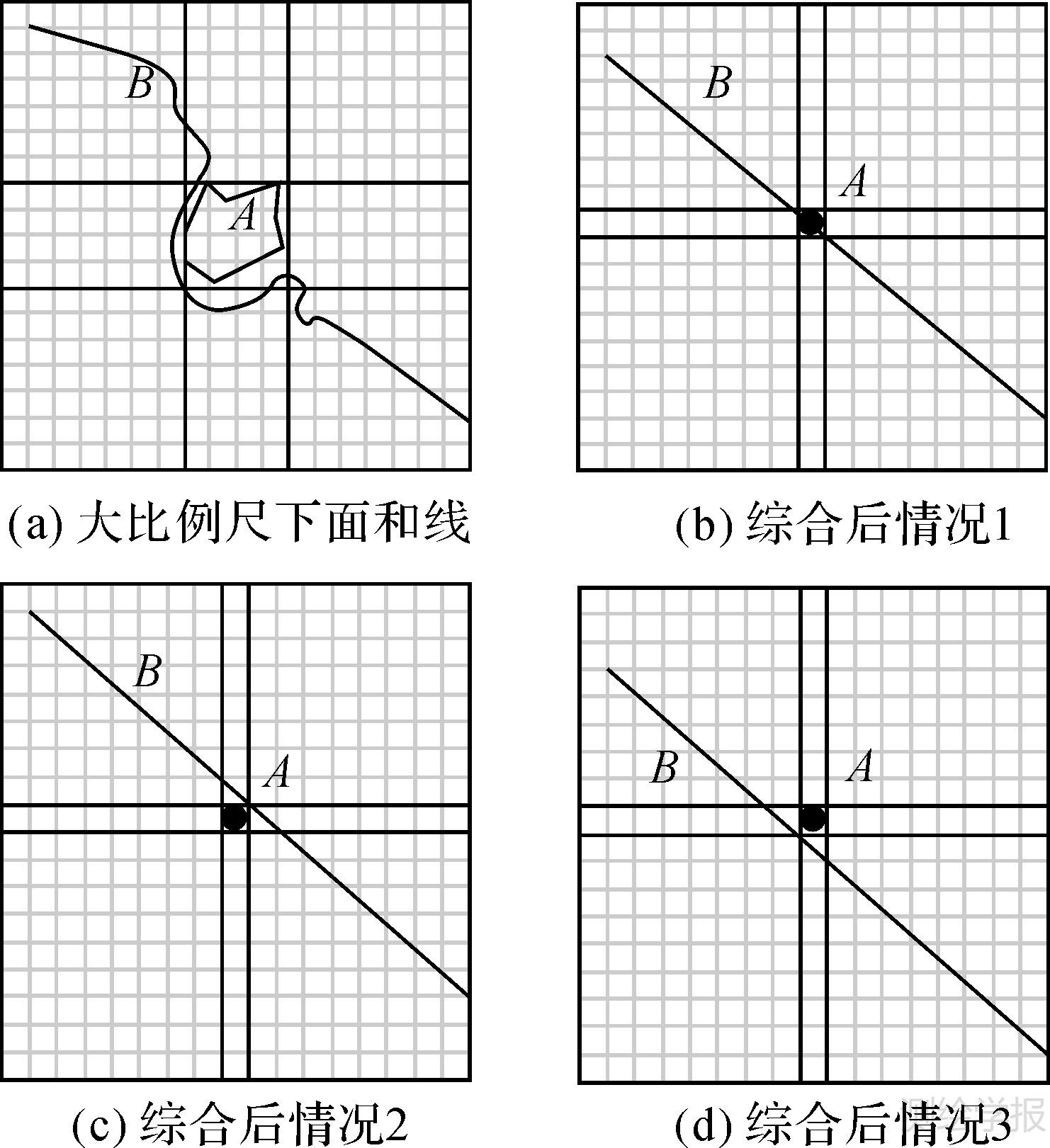
3.4 面线到点线如图 12 (a)为大比例尺下的公路与池塘,公路为线对象,池塘为面对象,图 12 (b)—12(d)为综合后的小比例尺地图,3幅图中池塘由面对象综合为点对象,而公路依然是线对象,但其形态由曲线变为直线,三者不同之处在于公路相对于池塘的位置。图 12 (b)中公路从池塘中穿过,显然不符合实际情况,为避免这种情况,应将池塘的位置稍作偏移,使其位于公路边。图 12 (c)、12(d)是偏移后的两种情况。
|
| 图 12 大比例下面和线转为小比例尺的情况 Fig. 12 Collapsing a region and a line at large scale to a point and a line at small scale |
求得图 12 (a)、图 12 (c)、图 12 (d)的方向关系矩阵如式(26)—式(28)所示
计算得到图 12(a)、12(c)之间方向相异矩阵
得到平衡传输表如图 13 (a)。解集为所示:x11=52,x21=23,x22=16,x32=26,x42=4,x43=19,x12=x13=x23=x31=x33=x41= 0,则z=329。图 12 (a)、12(c)之间相似度S0=1-(3×x11+1×x21+3×x22+2×x32+3×x42+2×x43)×1/4×1/416= 0.802284。
再计算图 12 (a)、12(d)之间方向相异矩阵如式(30)
得到平衡传输表如图 13(b),解集为:x11=39,x21=36,x31=19,x32=7,x42=13,x52=7,x12=x22=x41=x51=0,则z= 251。图 12 (a)、12(d)之间相似度S1=1-(3×x11+1×x21+2×x31+2×x32+3×x42+1×x52)×1/4×1/416=0.849159。
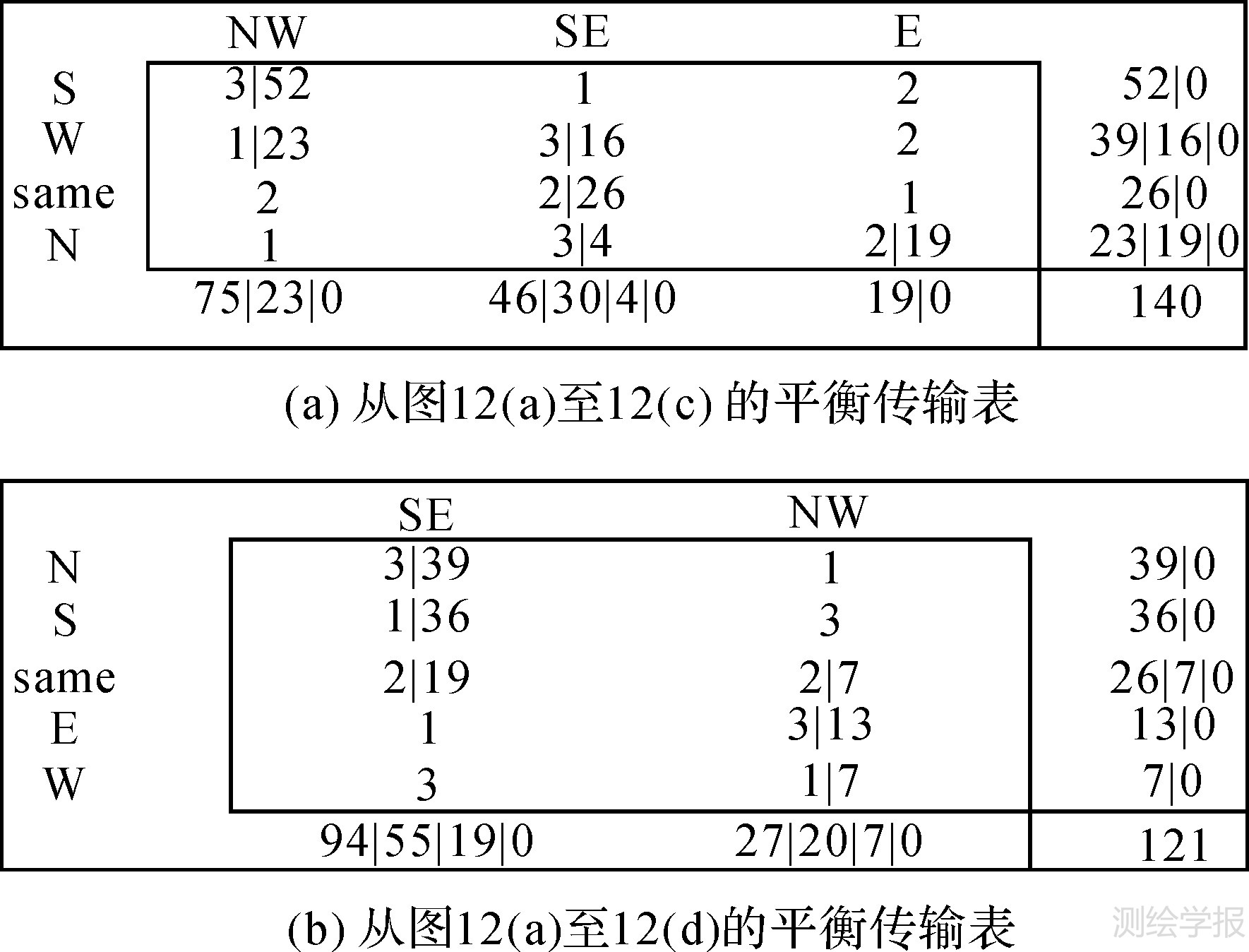
|
| 图 13 实例中的平衡传输表 Fig. 13 BTT in the example |
结果表明图 12 (a)、12 (d)之间的方向相似度略高于图 12 (a)、12(c)之间的方向相似度。图 12 (c)、12 (d)中B大部分在SE和NW分区,不同之处在于中间部分相对A的位置,图 12 (a)中A在B右上侧,但图 12 (c)中却将A移至B的左下侧,而图 12 (d)保持了图 12 (a)中A相对B的位置,计算出的相似度的差异在中间部分体现出来。
4 总 结本文通过方向关系矩阵间的相似度来评判制图综合后的结果的合理性。利用方向关系矩阵量化模型的特点,计算场景中方向对间的相似度,从而进行比较和评判。与基于对象的外包矩形或质心的建模不同,基于对象本身建模的方向关系矩阵能更精确地对多尺度空间场景中的方向关系对进行评估。本文采用4邻域图和Northwest-Corner算法计算方向关系矩阵间的距离,下一步工作将优化网格计数方法,并利用8邻域图或自定义距离的邻域图以及改良的平衡传输算法对多元素矩阵进行距离求解以提高计算精度。
| [1] | HOLT A, BENWELL G L. Using Spatial Similarity for Exploratory Spatial Data Analysis: Some Directions[C]//Proceedings of the 2nd International Conference on GeoComputation. Otago, New Zealand: SIRC, 1997. |
| [2] | YAN Haowen, CHU Yandong. On the Fundamental Issues of Spatial Similarity Relations in Multi-scale Maps[J]. Geography and Geo-Information Science, 2009, 25(4): 42-48. (闫浩文, 褚衍东. 多尺度地图空间相似关系基本问题研究[J]. 地理与地理信息科学, 2009, 25(4): 42-48.) |
| [3] | HAAR R. Computational Models of Spatial Relations[R]. Technical Report: TR-478, MSC-72-03610, Computer Science. College Park,MD: University of Maryland,1976. |
| [4] | ALLEN J F. Maintaining Knowledge about Temporal Intervals[J]. Communications of the ACM, 1983, 26(11): 832-843. |
| [5] | GUESGEN H W. Spatial Reasoning Based on Allen’s Temporal Logic[R]. Technical Report: TR-89-049. Berkley, CA:International Computer Science Institute, 1989. |
| [6] | BALBIANI P, CONDOTTA J F, DEL CERRO L F. A New Tractable Subclass of the Rectangle Algebra[C]// Proceedings of the 16th International Joint Conference on Artifical Intelligence. San Francisco: Morgan Kaufmann Publishers Inc., 1999: 442-447. |
| [7] | BALBIANI P, CONDOTTA J F, DEL CERRO L F. A Model for Reasoning about Bidimensional Temporal Relations[C]// Proceedings of Principles of Knowledge Representation and Reasoning (KR). Trento: [s.n.], 1998: 124-130. |
| [8] | CHANG S K, SHI Q Y, YAN C W. Iconic Indexing by 2-D Strings[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 1987, 9(3): 413-428. |
| [9] | PAPADIAS D, SELLIS T, THEODORIDIS Y, et al. Topological Relations in the World of Minimum Bounding Rectangles: A Study with R-trees[C]//Proceedings of the 1995 ACM SIGMOD International Conference on Management of Data. New York: ACM, 1995: 92-103. |
| [10] | GOYAL R K. Similarity Assessment for Cardinal Directions between Extended Spatial Objects[D]. Maine: The University of Maine, 2000. |
| [11] | GOYAL R K, EGENHOFER M J. Similarity of Cardinal Directions[M]// JENSEN C S, SCHNEIDER M, SEEGER B, et al. Advances in Spatial and Temporal Databases, Lecture Notes in Computer Science Volume 2121. Berlin, Heidelberg: Springer, 2001: 36-55. |
| [12] | SKIADOPOULOS S, KOUBARAKIS M. Composing Cardinal Direction Relations[J]. Artificial Intelligence, 2004, 152(2): 143-171. |
| [13] | DING Hong. A Study on Spatial Similarity Theory and Calculation Model[D]. Wuhan: Wuhan University, 2004. (丁虹. 空间相似性理论与计算模型的研究[D]. 武汉: 武汉大学, 2004.) |
| [14] | GUO Qingsheng, DING Hong. Similarity for Spatial Directions between Areal Objects in Raster Data[J]. Geomatics and Information Science of Wuhan University, 2004, 29(5): 447-450. (郭庆胜, 丁虹. 基于栅格数据的面状目标空间方向相似性研究[J]. 武汉大学学报:信息科学版, 2004, 29(5): 447-450.) |
| [15] | AN Xiaoya. Research on Theory, Methods and Applications of Geometry Similarity Measurement for Spatial Data[D]. Zhengzhou: Information Engineering University, 2011. (安晓亚. 空间数据几何相似性度量理论方法与应用研究[D]. 郑州: 信息工程大学, 2011.) |
| [16] | GUO Li, CUI Tiejun, ZHENG Haiying, et al. Arithmetic for Area Vector Spatial Data Matching on Spatial Direction Similarity[J]. Journal of Geomatics Science and Technology, 2008, 25(5): 380-382. (郭黎, 崔铁军, 郑海鹰, 等. 基于空间方向相似性的面状矢量空间数据匹配算法[J]. 测绘科学技术学报, 2008, 25(5): 380-382.) |
| [17] | YAN Haowen, GUO Renzhong. Research on Formal Description Model of Directional Relationships[J]. Acta Geodaetica et Cartographica Sinica, 2003, 32(1): 42-46. (闫浩文, 郭仁忠. 空间方向关系形式化描述模型研究[J]. 测绘学报, 2003, 32(1): 42-46.) |
| [18] | DU Shihong, WANG Qiao, YANG Yipeng. A Qualitative Description Model of Detailed Direction Relations[J]. Journal of Image and Graphics, 2004, 9(12): 1496-1503. (杜世宏, 王桥, 杨一鹏. 一种定性细节方向关系的表达模型[J]. 中国图象图形学报, 2004, 9(12): 1496-1503.) |
| [19] | DU Shihong, WANG Qiao, YANG Yipeng, et al. Fuzzy Description of Spatial Direction Relations[J]. Journal of Computer-aided Design & Computer Graphics, 2005, 17(8): 1744-1751. (杜世宏, 王桥, 杨一鹏, 等. 空间方向关系模糊描述[J]. 计算机辅助设计与图形学报, 2005, 17(8): 1744-1751.) |
| [20] | DU Shihong, WANG Qiao, WEI Bin, et al. Spatial Orientational Relations Rough Reasoning[J]. Acta Geodaetica et Cartographica Sinica, 2003, 32(4): 334-338. (杜世宏, 王桥, 魏斌, 等. 空间方向关系粗糙推理[J]. 测绘学报, 2003, 32(4): 334-338.) |
| [21] | CAO Han, CHEN Jun, DU Daosheng. Qualitative Extention Description for Cardinal Directions of Spatial Objects[J]. Acta Geodaetica et Cartographica Sinica, 2001, 30(2): 162-167. (曹菡, 陈军, 杜道生. 空间目标方向关系的定性扩展描述[J]. 测绘学报, 2001, 30(2): 162-167.) |
| [22] | HE Jianhua, LIU Yaolin. An Integrated Model for Topology & Direction Relation Reasoning[J]. Acta Geodaetica et Cartographica Sinica, 2004, 33(2): 156-162. (何建华, 刘耀林. GIS中拓扑和方向关系推理模型[J]. 测绘学报, 2004, 33(2): 156-162.) |
| [23] | WU Jing, CHENG Penggen, CHEN Fei, et al. Qualitative Reasoning for Direction Relation of Spatial Objects[J]. Acta Geodaetica et Cartographica Sinica, 2006, 35(2): 160-165. (吴静, 程朋根, 陈斐, 等. 空间目标的方向关系定性推理[J]. 测绘学报, 2006, 35(2): 160-165.) |
| [24] | STRAYER J K. Linear Programming and Its Applications[M]. New York: Springer-Verlag. |