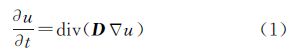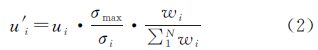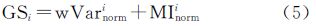1 引 言
自面向对象遥感影像分析软件eCognition[1]问世以来,面向对象的影像分析方法逐渐成为遥感影像分析领域的研究热点之一。图像分割是面向对象遥感信息提取的前提,精确的图像分割是后续的面向对象影像分析的基础。文献[2—3]对典型软件和算法进行了定量评价,结果表明eCognition软件的分形网络演化算法(fractal network evolution approach,FNEA)优于其他方法。然而,eCognition软件相对昂贵的价格限制了该方法的广泛应用。为探索高效的遥感影像分割算法,文献[4]提出了基于分水岭和最小异质性合并准则的多尺度分割算法,分割精度达到FNEA方法的分割精度。但在该算法中,同样的尺度参数得到的分割基元数量跟FNEA方法相比差异很大。文献[5]提出了一种综合利用影像的结构和光谱特征、采用区域生长和合并的分割方法,与FNEA方法的比较验证了该方法的有效性,但该方法在合并过程中仅考虑了光谱相似性。文献[6]提出了一种综合利用光谱、纹理与形状信息的分割方法。与FNEA方法相比,该方法对纹理信息较为丰富的区域能有效改善分割质量。基于图论的图像分割算法[7]是图像分割领域的研究热点[8, 9, 10, 11, 12, 13, 14]。文献[15]提出了基于最小生成树的多尺度多层次分割方法,并成功用于高分辨率遥感影像的分割,但该方法在区域合并过程中未利用区域形状特性。
本文基于eCognition软件的多尺度分割思想,提出了基于最小生成树分割和最小异质性合并准则(combining minimum spanning tree and minimum heterogeneity criteria,CMHC)的分割方法。通过与eCognition软件中FNEA方法的对比试验表明,CMHC方法是一种有效的遥感影像多尺度分割方法。
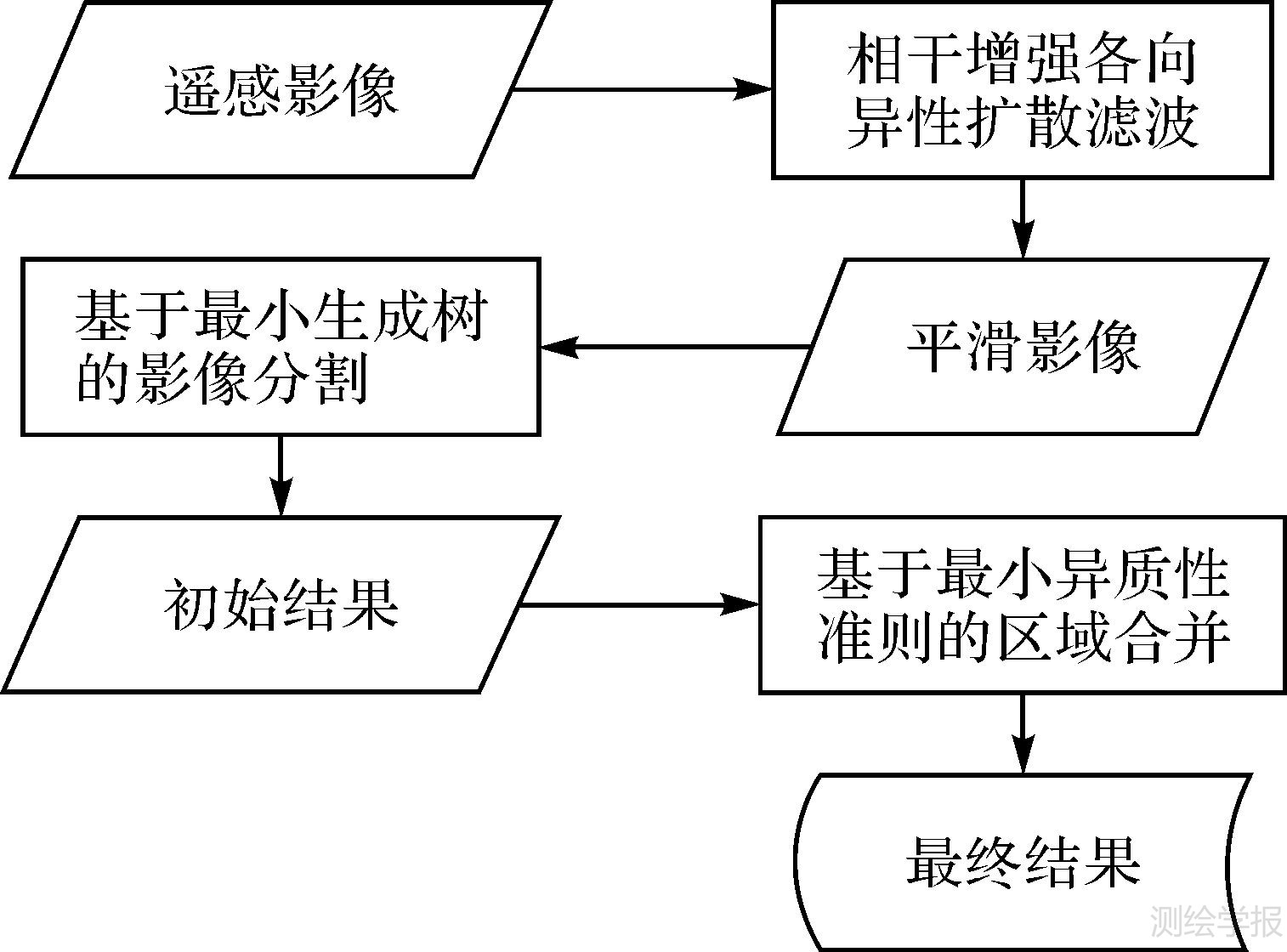
2 方 法为了高效地分割遥感影像,CMHC方法采用的技术流程见图 1:首先使用相干增强各向异性扩散滤波进行影像平滑处理,然后对平滑图像进行基于最小生成树的影像分割,接着结合光谱特性和形状特性参数采用最小异质性准则进行区域合并,最后得到分割结果。
|
| 图 1 CMHC方法流程图 Fig. 1 The procedure of the CMHC method |
为削弱噪声影响和提高效率,本文算法首先采用相干增强各向异性扩散模型[16, 17]对待分割影像进行图像平滑处理。对于图像u,该模型的基本形式为
式中,t为物理热扩散时间;▽为梯度算子;D为扩散张量矩阵;div为散度算子。扩散张量矩阵D可用特征向量(w1,w2)和特征值(λ1,λ2)表示。D的特征向量(w1,w2)由高斯噪声尺度σ(σ≥0)和高斯纹理尺度ρ(ρ≥0)确定,通常ρ>σ;D的特征值(λ1,λ2)与参数α(0<α<1)和β相关(β>0)[16]。此外,滤波处理前先对试验数据的各个波段ui进行拉伸处理
式中,ui和u′i分别为原始和拉伸后的波段i;wi为波段权重;σmax为各波段方差的最大值;N为波段数量。 2.2 基于最小生成树的分割算法本文采用基于Krusal算法实现的最小生成树算法[11]。该算法在步长为r的邻域内建立最近邻图G,其合并准则为区域间的差异必须小于两区域内部的最小差异。该算法设置了一个观察尺度参数k,以避免噪声影响或形成过小区域和抑制较大连通区域的产生,并将像元数量小于指定阈值nT的基元与其邻居基元合并。该算法涉及的主要参数有邻域步长r、观察尺度参数k和最小像元数量nT。
2.3 基于最小异质性的区域合并CMHC方法在区域合并中采用FNEA算法所使用的最小异质性合并准则[1]。基元的异质性值f由式(3)计算
式中,Wcolor和Wshape分别是光谱和形状信息权重,取值位于区间[0,1],Wcolor+Wshape=1;hcolor和hshape分别为光谱异质性和形状异质性指标,其定义及公式见文献[1]。当异质性值f小于阈值T时,则合并基元。阈值T与尺度参数s相关。经分析,阈值T还与影像最大灰度值umax、波段数量N和最大方差值σmax相关,本文采用公式为 2.4 评价准则图像分割算法评价分为监督方法和非监督方法[18],本文采用基于评价准则的非监督评价方法,评价准则采用基元内部方差最小和基元之间空间相关性最小准则[19]。全局内部方差wVar定义为所有基元的加权方差[18];基元间空间相关性准则采用Moran’s I指标(MI)[18, 20, 21]。对不同参数或不同算法的分割结果计算其在各个波段的wVar和MI统计值,并分别对其进行归一化拉伸处理[18],得到wVarnorm和MInorm。
对于每个影像波段的统计结果,按式(5)得到波段i的全局得分GSi(global score,GS),再对所有波段的GS求平均值,得到每个分割影像的全局得分GSavg
式中,N为波段数量。wVar值越小,表明基元内部同质性越高;MI值越小,表明基元间的空间相关性越小。因此GSavg值越小,表明分割结果既不过分割也不欠分割,分割效果越好。随着尺度参数增大,分割基元数量减少,各波段wVar值增大,各波段MI值减少。因此,对于同一分割方法在不同尺度参数下的分割结果,GSavg最小值对应的尺度,即为最优分割尺度。对于不同算法的分割结果,GSavg越小表明分割结果在过分割和欠分割间的平衡越好。
3 试验与分析 3.1 试验数据本文分别选用了1幅ASTER和1幅IKONOS影像子区进行试验(图 2)。ASTER影像获取时间为2000年夏天,包含绿、红及近红外3个波段,空间分辨率为15m。该子区位于加拿大安大略省中部的森林地区(46°33′51.33″N—46°34′30.22″N,83°23′50.32″W—83°26′49.27″W),大小为131行×205列。IKONOS影像获取时间为2000年5月,包含蓝、绿、红及近红外4个波段,空间分辨率为4米。该子区位于北京城区(39°57′21.58″N—39°58′27.68″N,116°23′21.74″E—116°24′49.02″E),大小为512行×512列。两个子区包含水体、树木、草地、道路、建筑物等多种地物类型,由于空间分辨率差异,前者地物边界不清晰,后者比较清晰。

|
| 图 2 试验影像 Fig. 2 The experimental images |
本文算法的参数设置情况如下:①在相干增强扩散滤波中,高斯参数σ和ρ分别设为0.8和1,α和β分别设为0.001和1.0e-10;②在最小生成树分割中,为避免过分割,邻域步长r、观察尺度k和像元数量阈值nT分别设为1、1和2;③在区域合并中,参考eCognition软件的默认参数,波段权重wi、Wshape和Wcmpct分别设为1、0.1和0.5。
作为对比,两个图像子区也用eCognition Developer 8.7[22]进行了分割。其中,波段权重wi、参数Wshape和Wcmpct的取值均同本文算法。
3.2 CMHC方法和FNEA方法比较由于尺度参数和分割基元数量均对wVar和MI有较大影响,为客观评价CMHC方法和FNEA方法,应选择最优分割尺度或接近最优分割尺度,且基元数量接近的分割结果进行比较。因此,本文首先利用GSavg值确定两种方法分别对两个影像子区的最优分割尺度参数,进而结合基元数量Nobj选择比较对象。
对于ASTER和IKONOS子区,分别采用[5, 20]区间(步长为1)和[10, 40]区间(步长为2)的尺度参数进行分割试验,GSavg和基元数量Nobj分布见图 3。对于ASTER子区,FNEA和CMHC方法分别在尺度为9(AST-FNEA-9)和8(AST-CMHC-8)时GSavg值最小,对应的基元数量接近(分别为202和235),因此选择这两个分割结果进行比较。由于两个分割结果对应的分割基元数量差异超过10%,为公平起见,将FNEA方法在尺度为8的分割结果(AST-FNEA-8)也加入比较;对于IKONOS子区,FNEA和CMHC方法分别在尺度为22(IK-FNEA-22)和24(IK-CMHC-24)时GSavg值最小,对应的基元数量差异较小(分别为3610和3628),因此选择这两个分割结果进行比较。这5个分割结果的统计见表 1。

|
| 图 3 试验图像在不同尺度S分割结果的GSavg和基元数量Nobj分布图 Fig. 3 GSavgand Nobj values of resulting maps with different scale parameter values for test images |
| 试验影像 | 方法 | 尺度S | wVar | MI | Nobj | |||||||
| B1 | B2 | B3 | B4 | B1 | B2 | B3 | B4 | |||||
| IKONOS | FNEA | 22 | 159.1 | 429.7 | 716.1 | 2075.7 | 0.25 | 0.22 | 0.21 | 0.14 | 3610 | |
| CMHC | 24 | 145.67 | 403.75 | 680.70 | 2301.87 | 0.28 | 0.25 | 0.23 | 0.17 | 3628 | ||
| ASTER | FNEA | 8 | 5.27 | 7.20 | 11.25 | 0.45 | 0.55 | 0.49 | 260 | |||
| 9 | 5.73 | 7.81 | 12.30 | 0.39 | 0.52 | 0.44 | 202 | |||||
| CMHC | 8 | 4.66 | 6.55 | 12.33 | 0.38 | 0.49 | 0.49 | 235 | ||||
对于ASTER子区,AST-CMHC-8的B1和B2的wVar和MI值均低于AST-FNEA-9和AST-FNEA-8的相应统计值,B3的wVar和MI值则略高于或等于AST-FNEA-9和AST-FNEA-8的相应统计值。因此,定量评价表明,对于ASTER影像,CMHC方法的过分割和欠分割的平衡方面优于FNEA方法。图 4显示了两种方法对ASTER子区分割结果的局部图。由图中灰色框区域可见,CMHC方法对光谱特性细微差异更为敏感,而FNEA方法的分割结果则在形状上更规则。因此,目视比较表明,对于ASTER影像,与FNEA方法相比,CMHC方法对光谱细微差异区域分割更细致。

|
| 图 4 ASTER影像分割结果 Fig. 4 Results of ASTER imagery segmentation. |
对于IKONOS子区,IK-CMHC-24的B1、B2和B3的wVar和MI值低于IK-FNEA-22的相应统计值,B4的wVar值及4个波段的MI值均略低于IK-FNEA-22的相应统计值。因此,定量评价表明,对于IKONOS影像,CMHC方法在基元内部同质性指标上优于FNEA方法,在全局空间相关性指标上略逊于后者。图 5显示了两种方法对IKONOS子区分割结果的局部图。目视比较可见,CMHC对光谱细微差异区域分割更细致(灰色框),对光谱特性差异更为敏感,而FNEA方法的分割结果则在形状上更规则。

|
| 图 5 IKONOS影像分割结果局部图 Fig. 5 Subsets of IKONOS imagery segmentation results |
此外,对于两个试验图像,CMHC与FNEA方法的最优分割尺度很接近。
综上所述,从目视比较和定量指标评价均表明,与FNEA方法相比较,CMHC能更好地分割光谱细微差异区域,而FNEA分割结果更为规则。
4 结 论为探索基于图论最优化理论的遥感影像多尺度分割方法,本文提出了基于最小生成树和最小异质性合并准则的多尺度分割方法(CMHC),并选用两幅不同空间分辨率影像的子区,对CMHC和eCognition软件的FNEA方法进行了定量指标评价和目视比较。其中,定量评价采用全局基元同质性指标与全局基元空间相关性指标。试验过程中,首先根据这两个指标确定最优分割尺度;然后选择最优分割尺度或接近最优分割尺度,并且基元数量接近的分割结果进行目视比较和定量评价。试验表明,CMHC方法在光谱细微差异区域细分方面优于FNEA方法,在基元形状规整性方面则略逊于FNEA方法,且该方法的最优分割尺度与FNEA方法很接近。由于CMHC方法在Matlab开发环境中实现,在执行效率方面有待提升,下一步将在C/C++开发环境下进行算法优化和效率提升。
| [1] | BAATZ M, SCHPE A. Multiresolution Segmentation: An Optimization Approach for High Quality Multi-scale Image Segmentation[J]. Journal of Photogrammetry and Remote Sensing, 2000, 58(3-4): 12-23. |
| [2] | NEUBERT M, HEROLD H, MEINEL G. Assessing Image Segmentation Quality——Concepts, Methods and Application[M]//BLASCHKE T, LANG S, HAY G J. Object-based Image Analysis. Berlin: Springer, 2008: 769-784. |
| [3] | MARPU P R, NEUBERT M, HEROLD H, et al. Enhanced Evaluation of Image Segmentation Results[J]. Journal of Spatial Science, 2010, 55(1): 55-68. |
| [4] | WANG M. A Multiresolution Remotely Sensed Image Segmentation Method Combining Rainfalling Watershed Algorithm and Fast Region Merging [C] //Proceedings of the International Archives of the Photogrammetry, Remote Sensing and Spatial Information Sciences. Beijing: [s.n.], 2008: 1213-1218. |
| [5] | LIU Jing, LI Peijun. A High Resolution Image Segmentation Method by Combined Structural and Spectral Characteristics[J]. Acta Geodaetica et Cartographica Sinica, 2014, 43(5): 466-473. (刘婧, 李培军. 结合结构和光谱特征的高分辨率影像分割方法[J]. 测绘学报, 2014, 43(5): 466-473.) |
| [6] | WU Zhaocong, HU Zhongwen, ZHANG Qian, et al. On Combining Spectral, Textural and Shape Features for Remote Sensing Image Segmentation[J]. Acta Geodaetica et Cartographica Sinica, 2014, 42(1): 44-50. (巫兆聪, 胡忠文, 张谦, 等. 结合光谱纹理与形状结构信息的遥感影像分割方法[J]. 测绘学报, 2014, 42(1): 44-50.) |
| [7] | MORTENSEN E N, BARRETT W A. Intelligent Scissors for Image Composition [C]//Proceedings of the 22nd Annual Conference on Computer Graphics and Interactive Techniques.New York: [s.n.], 1995: 191-198. |
| [8] | ZAHN C T. Graph-theoretical Methods for Detecting and Describing Gestalt Clusters[J]. IEEE Transactions on Computers, 1971, C-20(1): 68-86. |
| [9] | XU Y, UBERBAEHER E C. 2D Image Segmentation Using Minimum Spanning Trees[J]. Image and Vision Computing, 1997, 15(1): 47-57. |
| [10] | LERSCH J R, IVERSON A E, WEBB B N, et al. Segmentation of Multiband Imagery Using Minimum Spanning Trees [C] //Aerospace/Defense Sensing and Controls, International Society for Optics and Photonics.Orlando, FL: SPIE, 1996: 10-18. |
| [11] | FELZENSZWALB P F, HUTTENLOEHER D P. Efficient Graph-based Image Segmentation[J]. International Journal of Computer Vision, 2004, 59(2): 167-181. |
| [12] | WU Z, LEAHY R. An Optimal Graph Theoretic Approach to Data Clustering: Theory and Its Application to Image Segmentation[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 1993, 15(11): 1101-1113. |
| [13] | BOYKOV Y Y, JOLLY M P. Interactive Graph Cuts for Optimal Boundary & Region Segmentation of Objects in ND Images [C] //Proceedings of the 8th IEEE International Conference on Computer Vision.Vancouver, B C: IEEE, 2001: 105-112. |
| [14] | PENG B, ZHANG L, ZHANG D. A Survey of Graph Theoretical Approaches to Image Segmentation[J]. Pattern Recognition, 2013, 46(3): 1020-1038. |
| [15] | CUI W H, ZHANG Y. An Effective Graph-based Hierarchy Image Segmentation [J].Intelligent Automation & Soft Computing, 2011, 17(7): 969-981. |
| [16] | WEICKERT J. Anisotropic Diffusion in Image Processing [M].Stuttgart: Teubner, 1998. |
| [17] | WEICKERT J, SCHARR H. A Scheme for Coherence-enhancing Diffusion Filtering with Optimized Rotation Invariance[J]. Journal of Visual Communication and Image Representation, 2002, 13(1-2): 103-118. |
| [18] | ZHANG H, FRITTS E J, GOLDMAN S A. Image Segmentation Evaluation: A Survey of Unsupervised Methods[J]. Computer Vision and Image Understanding, 2008, 110(2): 260-280. |
| [19] | HARALICK R M, SHAPIRO L G. Image Segmentation Techniques[J]. Computer Vision, Graphics, and Image Processing, 1985, 29(1): 100-132. |
| [20] | ESPINDOLA G M, CAMARA G, REIS I A, et al. Parameter Selection for Region-growing Image Segmentation Algorithms Using Spatial Autocorrelation[J]. International Journal of Remote Sensing, 2006, 27(14): 3035-3040. |
| [21] | KIM M, MADDEN M, WARNER T. Estimation of Optimal Image Object Size for the Segmentation of Forest Stands with Multispectral IKONOS Imagery[M]//BLASCHKE T, LANG S, HAY G J. Object-based Image Analysis. Berlin: Springer, 2008: 291-307. |
| [22] | TRIMBLE GERMANY GMBH. eCognition Developer 8.7, 2009[EB/OL].[2011-09-26]. http://www.ecognition.com. |