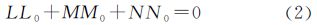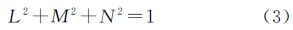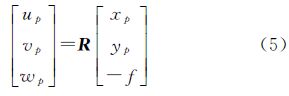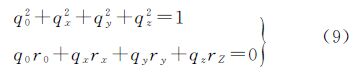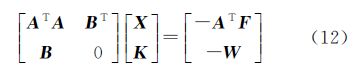1 引 言
机载激光雷达(light detection and ranging,LiDAR)系统中的激光点云与航空影像集成是地物分类与识别等摄影测量与遥感领域的研究热点[1, 2, 3],其首要任务是通过寻找同名特征确定点云与影像两者之间的相对位姿信息。常用的特征主要有点特征和线特征。由于点云具有离散性,二者的配准一般先将点云内插成图像,这会引入内插误差[4],也可先对影像进行密集匹配获取点云,但需要较好的初值[5]。而通过直接在点云与影像之间匹配建筑物上的同名直线,不需要对点云进行内插或者对影像进行密集匹配,避免了此阶段产生的误差。由于线特征比点特征更容易提取,且具有更强的几何拓扑性和几何约束性[6],因此直线特征广泛应用于空间前方交会和空间后方交会[7]、相对定向和绝对定向[8]、三维重建[9]、影像几何纠正[10]以及配准[11]等。根据LiDAR点云与影像中的同名直线以及摄影中心共面的原理,可实现基于线特征的二者配准[12],在此基础上,以广义点距离[13]作为相似性测度,配准精度可达3.6个像素。采用共线条件方程作为配准模型,利用线特征代替点特征,平面精度小于0.5m[14]。在LiDAR点云中提取建筑物边缘上的角特征,将角点当作控制点,利用光束法区域网平差解求影像的外方位元素,其平面中误差从配准前的0.96m提高到0.25m[15]。利用LiDAR点云与影像的直线特征作为配准基元,将LiDAR直线作为控制纳入三角测量,平面中误差达到0.05m[16]。在立体像对和LiDAR数据上提取相交直线及交点,用基于光束法平差的空三测量法修正影像的外方位元素,其中误差从0.5~2m减小到0.05m以下[17]。综上所述,利用线特征进行LiDAR点云与影像配准,其结果是可靠的。上述方法大多采用共面条件或共线条件方程作为配准的数学模型,分别采用正交旋转矩阵和平移矩阵进行坐标变换,影像的线方位元素和角方位元素是分开求解的,而外方位定向元素之间存在相关性,如Xs与φ、Ys与ω等,从而导致误差方程系数矩阵的列向量之间存在近似的线性关系,即回归分析中所谓的复共线性,在复共线性存在的情况下,最小二乘估计的均方差较大,不再是最优估计。
实际上,影像的位置和姿态随着时间一起发生变化,其分而治之的处理方式必然引入转动和平移的耦合误差,因此转动和平移的统一考虑不仅可简化配准模型,更能够提高影像位姿的配准精度。对偶四元数是表达刚体空间线变换的最简洁最有效的方式[18],其本质是将刚体的运动变换用转动和平动的组合,即螺旋式运动进行表示。在此基础上建立的Plücker直线几何代数,其转换组合等计算在数字上更稳定,在空间线变换应用中用螺旋的Plücker坐标更加有效,已在结构学领域得到验证。在计算机视觉领域,利用Plücker坐标进行绝对二次曲线的描述,消除了由于镜头伸缩引起的投影误差,实现了不同类型相机的自动检校[19]。在机器人运动学领域,利用Plücker直线坐标描述串行连杆机构,能同时克服奇异问题和避免机构烦琐的D-H法描述[20]。在航天器探测制导与控制领域,利用Plücker直线方程将目标航天器和追踪航天器坐标系统一表示,通过对偶四元数进行相对位置和姿态的统一求解,避免了传统算法中位置和姿态分开求解的复杂过程,程序简洁,计算速度大大提高,节省了可贵的机上资源[21]。但到目前为止,Plücker直线在摄影测量领域中的应用还未有报道。本文根据Plücker直线方程确定点云和影像中的同名直线间的相对位姿关系,利用Plücker直线建立共面条件方程,用对偶四元数同时考虑旋转变换和平移变换,实现机载LiDAR点云与航空影像的高精度配准。
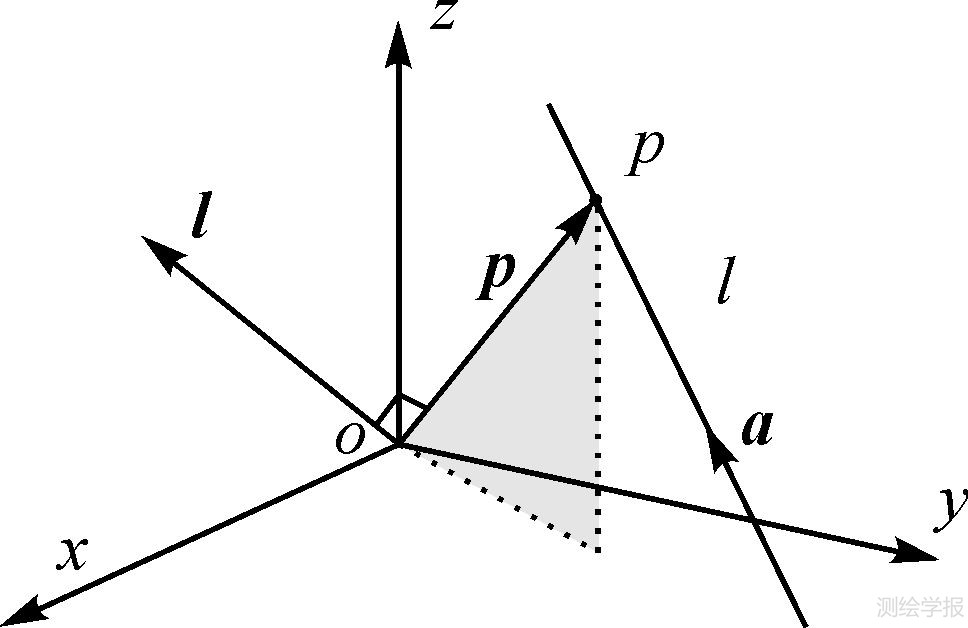
2 基于Plücker直线的LiDAR点云与航空影像配准模型 2.1 Plücker直线如图 1所示,a=(L,M,N)是三维空间内任意一条直线l的方向矢量,p是l上任意一点p的位置矢量,l=(L0,M0,N0)是l相对于原点O的矩矢量,由6个有序数(L,M,N,L0,M0,N0)可确定一条有向直线,称为直线的Plücker坐标,用Plücker坐标表示的直线称为Plücker直线。
|
| 图 1 三维线空间中的Plücker坐标 Fig. 1 Plücker coordinate of an arbitrary line in space |
由于方向矢量和矩矢量之间满足以下关系[22]
因此Plücker坐标满足条件[22]
而对于任意不为0的μ,(μa,μl)表示的是同一条直线,因此Plücker坐标还满足条件[22]
因此三维线空间中的Plücker直线有4个自由度。虽然三维线空间比三维点空间多了一个维度,但是三维线空间更易于描述直线的平行、相交和异面等空间位置关系[22]。
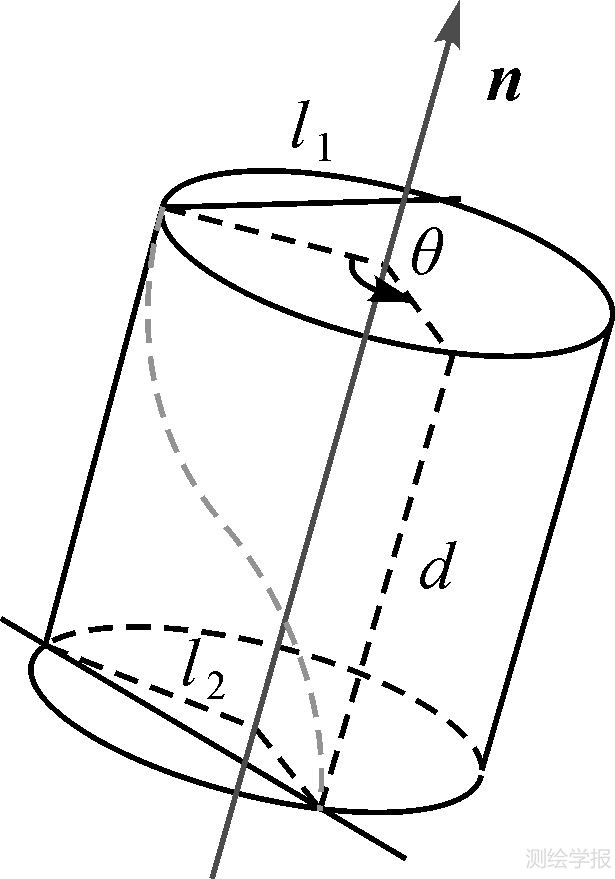
2.2 Plücker直线表示的空间螺旋运动为了描述直线在三维线空间中的坐标变换,一般用单位对偶矢量${\hat l}$将Plücker直线表示为[22, 23]:${\hat l}$=a+ε${\vec l}$,其中ε为对偶单位,满足:ε2=0,ε≠0。如图 2所示,l1围绕螺旋轴${\hat n}$转动对偶角${\hat \theta}$后得到l2,则Plücker直线螺旋运动方程为[22]
式中,${\hat q}$为单位对偶四元数;${\hat q}$-1为${\hat q}$的共轭;${\hat n}$为单位对偶矢量;${\hat \theta}$表示旋转的角度和平移的距离,${\hat \theta}$=θ+εd;${\hat l}$1=a1+εl1为初始位置的Plücker直线;${\hat l}$2=a2+εl2为新位置的Plücker直线。可见只需要一个单位对偶四元数${\hat q}$即可描述l1到l2的空间螺旋运动,即确定这两条Plücker直线的相对位姿关系。Plücker直线方程采用对偶四元数作用于线矢量来表达螺旋位移,其优点是模型简洁,降低处理问题的复杂度,同时几何意义更为直观,因此Plücker直线方程是表示空间线运动最有效的方法。
|
| 图 2 Plücker直线表示的空间螺旋运动 Fig. 2 Plücker linear spiral movement of space |
如图 3所示,l1为一条航空影像直线,l2为l1对应的LiDAR点云上的空间直线,l1过点p和g,l2过点P和G,则l1、l2和摄影中心S共面。由于只需要任意两个像点确定像方直线,任意两个空间点确定同名空间直线,因此p与P、g与G并不要求是同名点,这是直线摄影测量的最大优点。

|
| 图 3 Plücker直线共面条件配准模型 Fig. 3 The registration model of Plücker linear coplanar condition equation |
p、P、G和S 4点间的共面条件方程为[24]
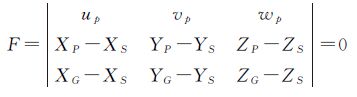
式中,(XP,YP,ZP)、(XG,YG,ZG)分别为P、G 在WGS-84坐标系下的坐标;(XS,YS,ZS)是S在WGS-84坐标系下的坐标,即影像的线元素;R为影像的角元素组成的旋转矩阵;(up,vp,wp)为p在WGS-84坐标系下的坐标;(xp,yp)是p的像平面坐标;f是相机焦距。
由于式(4)的${\hat n}$有4个自由度,${\hat \theta}$有2个自由度,符合影像作一般运动时6个自由度的要求,因此可用式(4)表示Plücker直线l1和l2之间的旋转和平移关系,即在几何意义上建立了像平面坐标系和WGS-84坐标系间的坐标变换关系,那么LiDAR点云与航空影像的配准的关键是求解${\hat q}$。设${\hat q}$的矩阵形式为:${\hat q}$=[q0qxqyqz]T+ε[r0rxryrz]T,则l1到l2的空间螺旋运动可表示为[25]
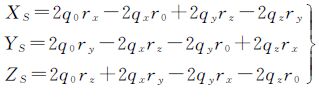
式(4)在几何意义上建立了Plücker直线和${\hat q}$的关系,式(6)可建立${\hat q}$和外方位元素的关系,再利用式(5)解算${\hat q}$。式(5)和式(6)为Plücker直线共面条件配准方程,将Plücker直线共面条件配准方程线性化,对${\hat q}$按照泰勒公式展开至一次项,严密解算公式如下
式中
A1=l1(q20+q2x-q2y-q2z)+2l2(qyqx+q0qz)+2l3(qzqx-q0qy)
A2=l2(q20-q2x+q2y-q2z)+2l1(qxqy-q0qz)+2l3(qzqy+q0qx)
A3=2[C(xq0-yqz-fqy)+D(xqz+yq0+fqx)+E(-xqy+yqx-fq0)+mrx+nry+hrz]
A4=2[C(xqx+yqy-fqz)+D(xqy-yqx+fq0)+E(xqz+yq0+fqx)-mr0-nrz+hry]
A5=2[C(-xqy+yqx-fq0)+D(xqx+yqy-fqz)+E(-xq0+yqz+fqy)+mrz-nr0-hrx]
A6=2[C(-xqz-yq0-fqx)+(Dxq0-yqz-fqy)+E(xqx+yqy-fqz)-mry+nrx-hr0]
A7=2(-mqx-nqy-hqz);A8=2(mq0+nqz-hqy)
A9=2(-mqz+nq0+hqx);A10=2(mqy-nqx+hq0);F=Cup+Dvp+Ewp
l1=(wPY′Q-vPZ′Q);l2=(uPZ′<Q-wPX′Q);l3=(vPX′Q-uPY′Q);l4=(vPZ′P-wPY′P)
l5=(wPX′P-uPZ′P);l6=(uPY′P-vPX′P);m=-(l1+l4);n=-(l2+l5);h=-(l3+l6)
C=Y′PZ′G-Y′GZ′P;D=Z′PX′G-Z′GX′P;E=X′PY′G-X′GY′P
(X′P,Y′P,Z′P)=(XP-XS,YP-YS,ZP-ZS);X′G,Y′G,Z′G=(XG-XS,YG-YS,ZG-ZS)
从式(4)中可以看出,配准时的螺旋运动模型简洁,通过对偶四元数作用于Plücker直线,能同时解算旋转与平移,避免姿态和位置间的耦合误差,同时误差方程式(7)采用了严密解算,避免了三角函数计算带来的奇异[26]和溢出[27]问题,从而降低了问题处理的复杂度,提高了影像的配准精度。
2.4 平差解算将误差方程式V写成矩阵形式为
式中
A=[A1A2A3A4A5A6A7A8A9A10]
X=[dxpdypdq0dqxdqydqzdr0drxdrydrz]T
由于${\hat q}$是单位对偶四元数,因此V还存在两个约束条件[25]
对式(9)线性化,可得约束条件方程的矩阵形式为
式中
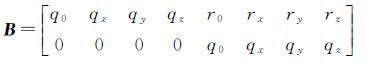
如果有n对同名直线,对每对直线按照式(8)可列一个误差方程,则Plücker直线共面条件配准方程的整体平差公式为
利用带条件的间接平差法建立法方程式为
式中,K为过渡性数值。
2.5 精度评价由于式(7)的常数项F以立方米为单位,不易判断像点p是否位于SPG平面上,难以进行精度评价。为此,可利用点p到SPG平面的距离k作为误差方程式的常数项,则单位变为米,再进一步转换为像素。由S、P和G构成的平面方程为:CX+DY+EZ=0,式中C、D、E的定义见式(7)。若像点p与“SPG平面”共面,则[24]
式中,k的几何意义为:当影像和点云完成配准时,k=0;若没有完成配准,则k≠0,其数值大小反映出同名直线的匹配程度。对式(13)微分,即可得到基于距离的Plücker直线共面条件误差方程式。由式(13)可知,其分子即为共面条件的行列式的值。因此,Plücker直线共面条件方程的各项均除以$\sqrt {{C^2} + {D^2} + {E^2}}$ ,即可得到基于距离的Plücker直线共面条件误差方程式。
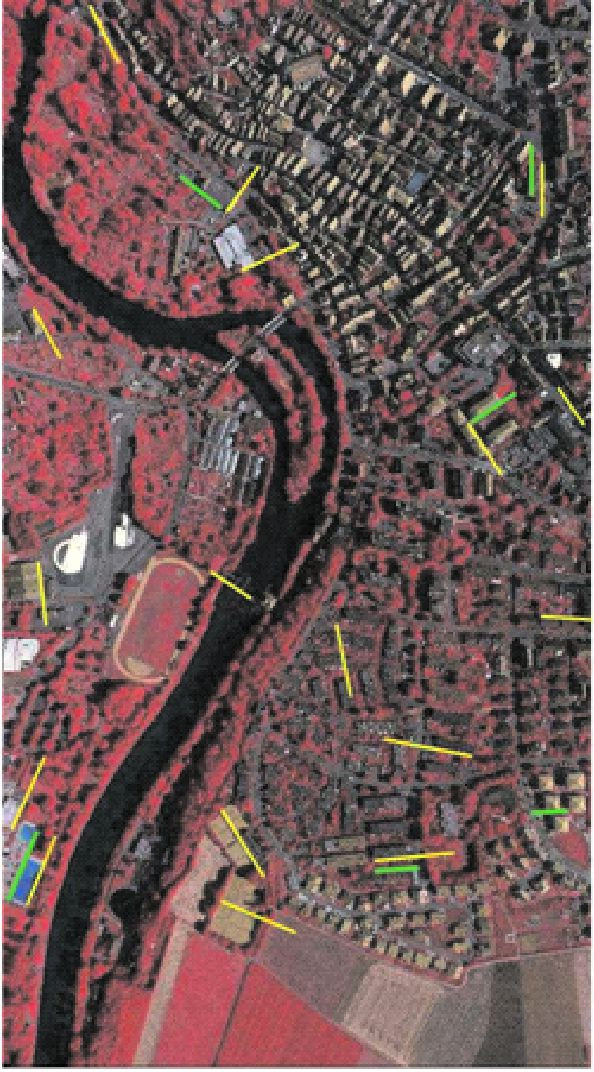
3 试验结果与分析为验证本文提出的Plücker直线法实现LiDAR点云与航空影像配准的可行性,利用德国Vaihingen区域的一幅航空影像与机载LiDAR数据进行配准试验,测区建筑物较密集。航空影像由美国Z/I Imaging公司的数字航测相机(digital mapping camera,DMC)获取。DMC相机焦距为120mm,CCD像元大小为0.012mm,航高约为900m,影像地面分辨率为8cm,辐射分辨率为11位,像幅大小为7680像元×13824像元。由Leica ALS50系统采集LiDAR数据,视场角为45°,平均飞行高度为500m,平均航带重叠为30%,中值点密度为6.7点/m2,航带内平均点密度为4点/m2。测区内有多条航带,本试验中选择与航空影像相对应的两条航带LiDAR数据,同名直线分布如图 4所示,其中黄色线段表示的Plücker直线用于配准,共17条;绿色线段表示的Plücker直线为检查直线,共6条。
|
| 图 4 同名直线分布图 Fig. 4 Distribution of conjugate lines |
摄影测量中,欲进行空间两个直角坐标系的转换,一般以外方位角元素φ、ω、κ系统,即欧拉角法来确定旋转矩阵,是解算影像外方位元素的最常用方法[28]。试验中分别应用欧拉角法和Plücker直线法求解影像的外方位元素,结果相同,都为XS=653775.55m、YS=4149669.03m、ZS=4784768.31m、φ= -7.78°、ω= -40.05°和κ= -11.63°,验证了Plücker直线共面条件配准模型的正确性。两种方法的理论配准精度对比见表 1。从表 1的结果可知,在精度评价方面,Plücker直线法相比欧拉角法线元素的中误差略有提高,欧拉角法解算的角元素中误差分别为0.162016°、0.084349°和0.100372°,Plücker直线法解算的角元素中误差分别为0.086295°、0.059783°和0.052246°,相比欧拉角法分别提高了46.7%、29.1%和47.9%,平均提高了41. 2%。由于Plücker直线法用对偶四元数代替欧拉角,避免了转动和平移的耦合误差及繁琐的三角函数运算,因此角元素精度的提高较为显著。在计算效率方面,Plücker直线法与欧拉角法的计算时间相同。
| 配准方法 | dXS/m | dYS/m | dZS/m | dφ/(°) | dω/(°) | dκ/(°) | 中误差m 0/m | 计算时间/s |
| 欧拉角法 | 2.039794 | 0.911637 | 0.984613 | 0.162016 | 0.084349 | 0.100372 | 0.000022 | 0.001000 |
| Plücker直线法 | 1.888481 | 0.844012 | 0.911575 | 0.086295 | 0.059783 | 0.052246 | 0.000020 | 0.001000 |
在点云上人工量取用于检查的Plücker直线以及对应影像上的直线,通过点云上Plücker直线在三维线空间中的螺旋运动,实现LiDAR点到其对应像点的坐标变换。图 5显示了配准前和配准后局部区域的配准效果。在LiDAR点云中截取建筑物屋顶点云,根据影像外方位元素将屋顶点云投影到影像上,图中白色的点表示投影的屋顶点。图 5中共有5组图片,每一组图片的左边为配准前的投影结果,由于原始影像的外方位元数并不准确,可以看到屋顶投影点与屋顶的实际位置存在较大的错位。右边为配准后用修正的外方位元素重新投影的结果,可以看出配准之后屋顶投影点与屋顶的实际位置基本套合。

|
| 图 5 配准前后对比 Fig. 5 Comparison before and after registration |
对图 5中5组图像共5条检查直线进行定量分析,将点云直线利用投影到影像上,分别计算它们与像方直线的距离,配准精度见表 2。分析表 2可以发现,各条直线的误差分别为-0.059、0.106、0.101、0.162、和0.520个像素,平均误差为0.19个像素。
| 序号 | 检查点到直线的距离/像素 | 误差/像素 | ||
| 1 | -1.427 | 1.167 | 0.083 | -0.059 |
| 2 | 0.993 | -1.154 | 0.480 | 0.106 |
| 3 | 0.035 | -0.229 | 0.498 | 0.101 |
| 4 | -0.063 | 0.384 | 0.165 | 0.162 |
| 5 | 0.768 | 0.731 | 0.061 | 0.520 |
针对机载LiDAR点云与航空影像的数据融合问题,本文提出了一种Plücker直线共面条件配准模型。根据点云直线与影像直线满足共面条件的原理,利用Plücker坐标构建共面条件方程,推导了Plücker直线共面条件方程各项的偏导数,建立了一般形式和基于距离的误差方程式,最终确定了点云和影像中的同名直线间的相对位姿关系,获得了影像的外方位元素。结果表明,Plücker直线共面条件配准模型数学表达式直观、明了,并且由于在坐标系变换过程中统一考虑了旋转和平移,避免了二者的耦合误差,影像的角元素的理论精度平均提高了41.2%。将点云中的检查直线投影到影像,实际误差为0.2个像素,达到了高精度三维测图的要求。根据Plücker直线方程在进行连续旋转时的优势,下一步的研究计划是研究序列航空影像与LiDAR点云的配准。
| [1] | LI Yijing, HU Xiangyun, ZHANG Jianqing, et al. Automatic Road Extraction in Complex Scenes Based on Information Fusion from LiDAR Data and Remote Sensing Imagery[J]. Acta Geodaetica et Cartographica Sinica, 2012, 41(6): 870-876. (李怡静, 胡翔云, 张剑清, 等. 影像与LiDAR数据信息融合复杂场景下的道路自动提取[J]. 测绘学报, 2012, 41(6): 870-876.) |
| [2] | ZHONG Cheng. High Quality True Orthoimage Generation with LiDAR and RS Image[J]. Acta Geodaetica et Cartographica Sinica, 2011, 40(1): 132. (钟成. 集成LiDAR和遥感影像生成高质量真正射影像研究[J]. 测绘学报, 2011, 40(1): 132.) |
| [3] | WANG Yanmin, HU Chnumei. A Robust Registration Method for Terrestrial LiDAR Point Clouds and Texture Image[J]. Acta Geodaetica et Cartographica Sinica, 2012, 41(2): 266-272. (王晏民, 胡春梅. 一种地面激光雷达点云与纹理影像稳健配准方法[J]. 测绘学报, 2012, 41(2): 266-272.) |
| [4] | DENG Fei, ZHANG Zuxun, ZHANG Jianqing. 3D Reconstruction of Old Architecture by Laser Scanner and Digital Camera[J]. Science of Surveying and Mapping, 2007, 32(2): 29-30. (邓非, 张祖勋, 张剑清. 利用激光扫描和数码相机进行古建筑三维重建研究[J]. 测绘科学, 2007, 32(2): 29-30.) |
| [5] | POTHOU A, KARAMITSOS S, GEORGOPOULOS A, et al. Assessment and Comparison of Registration Algorithms between Aerial Images and Laser Point Clouds[J]. Revue Franaise de Photogrammétrie et de Télédétection, 2006(182): 28-33. |
| [6] | ZHANG Yongjun, HU Binghua, ZHANG Jianqing. Relative Orientation Based on Multiple Conjugate Features[J]. Acta Geodaetica et Cartographica Sinica, 2011, 40(2): 194-199. (张永军, 胡丙华, 张剑清. 基于多种同名特征的相对定向方法研究[J]. 测绘学报, 2011, 40(2): 194-199.) |
| [7] | KONG Wei, ZHANG Xueming, HE Jianmei. Spatial Resection and Forward Intersection with Generalized Point Photogrammetry[J]. Science of Surveying and Mapping, 2011, 36(5): 45-48. (孔胃, 张学明, 何建美. 基于广义点摄影测量的后方交会与前方交会方法研究[J]. 测绘科学, 2011, 36(5): 45-48.) |
| [8] | ZHANG Zuxun, ZHANG Hongwei, ZHANG Jianqing. Automatic Absolute Orientation of Remote Sense Image by Line Photogrammetry[J]. Journal of Image and Graphics, 2005, 10(2): 213-217. (张祖勋, 张宏伟, 张剑清. 基于直线特征的遥感影像自动绝对定向[J]. 中国图象图形学报, 2005, 10(2): 213-217.) |
| [9] | DENG Baosong, YANG Bing, WEI Yingmei, et al. 3D Reconstruction of Line Features from Multiple Views[J]. Journal of Computer-aided Design&Computer Graphics, 2007, 19(6): 713-718. (邓宝松, 杨冰, 魏迎梅, 等. 多视点图像中线特征的三维重建[J]. 计算机辅助设计与图形学学报, 2007, 19(6): 713-718.) |
| [10] | SHAO Yongshe, LING Jing, ZHANG Shaoming, et al. Rectification Methods Based on Line Features for SPOT Imagery[J]. Journal of Tongji University(Natural Science), 2010, 38(8): 1249-1254. (邵永社, 李晶, 张绍明, 等. 基于线特征的SPOT影像几何纠正方法[J]. 同济大学学报:自然科学版, 2010, 38(8): 1249-1254.) |
| [11] | LI Fangfang, JIA Yonghong, XIAO Benlin, et al. A Multi-sensor Image Registration Algorithm Based on Line Features and SIFT Points[J]. Geomatics and Information Science of Wuhan University, 2010, 35(2): 233-236. (李芳芳, 贾永红, 肖本林, 等. 利用线特征和SIFT点特征进行多源遥感影像配准[J]. 武汉大学学报: 信息科学版, 2010, 35(2): 233-236.) |
| [12] | HABIB A, GHANMA M, MORGAN M, et al. Photogrammetric and LiDAR Data Registration Using Linear Features[J]. Photogrammetric Engineering and Remote Sensing, 2005, 71(6): 699-707. |
| [13] | DENG Fei. Research on LiDAR and Digital Images Registration and Objects Extraction[D]. Wuhan: Wuhan University, 2006. (邓非. LiDAR数据与数字影像的配准和地物提取研究[D]. 武汉: 武汉大学, 2006.) |
| [14] | MA Hongchao, YAO Chunjing, WU Jianwei. Registration of LiDAR Point Clouds and High Resolution Images Based on Linear Features[J]. Geomatics and Information Science of Wuhan University, 2012, 37(2): 136-140, 159. (马洪超, 姚春静, 邬建伟. 利用线特征进行高分辨率影像与LiDAR点云的配准[J]. 武汉大学学报: 信息科学版, 2012, 37(2): 136-140, 159.) |
| [15] | ZHANG Yongjun, XIONG Xiaodong, SHEN Xiang. Automatic Registration of Urban Aerial Imagery with Airborne LiDAR Data[J]. Journal of Remote Sensing, 2012, 16(3): 579-595. (张永军, 熊小东, 沈翔. 城区机载LiDAR数据与航空影像的自动配准[J]. 遥感学报, 2012, 16(3): 579-595.) |
| [16] | HABIB A F, GHANMA M S, MITISHITA E A, et al. Image Georeferencing Using LiDAR Data[C]//Proceedings of 25th IEEE International Geoscience and Remote Sensing Symposium. Seoul: [s.n.], 2005: 1158-1161. |
| [17] | CHOI K, HONG J, LEE I. Precise Geometric Registration of Aerial Imagery and LiDAR Data[J]. ETRI Journal, 2011, 33(4): 506-516. |
| [18] | FUNDA J, TAYLOR R H, PAUL R P. On Homogeneous Transforms, Quaternions, and Computational Efficiency[J]. IEEE Transactions on Robotics and Automation, 1990, 6(3): 382-388. |
| [19] | RONDA J I, GALLEGO G, VALDES A. Camera Autocalibration Using Plücker Coordinates[C]//Proceedings of IEEE International Conference on Image Processing 2005. Genoa: [s.n.], 2005: 3125-3128. |
| [20] | SARIYILDIZ E, TEMELTAS H. Solution of Inverse Kinematic Problem for Serial Robot Using Dual Quaternions and Plücker Coordinates[C]//Proceedings of IEEE/ASME International Conference on Advanced Intelligent Mechatronics. Singapore: [s.n.], 2009: 338-343. |
| [21] | LI Jing, WANG Huinan, LIU Haiying. Plucker Linear Based Relative Position and Attitude Determination Algorithm for RVD[J]. Chinese Space Science and Technology, 2013, 33(1): 69-74. (李静, 王惠南, 刘海颖. 基于普吕克直线的交会对接相对位姿确定算法[J]. 中国空间科学技术, 2013, 33(1): 69-74.) |
| [22] | ROONY J. A Comparison of Representation of General Spatial Screw Displacement[J]. Environment and Planning, 1978, 5(1): 45-88. |
| [23] | PENNESTRI E,STEFANELLI R. Linear Algebra and Numerical Algorithms Using Dual Numbers[J]. Multibody System Dynamics, 2007, 18(3): 323-344. |
| [24] | ZHANG Yongjun, ZHANG Zuxun, ZHANG Jianqing. Dimensional Inspection of Industrial Parts with Image Sequence[J]. Journal of Shanghai Jiaotong University, 2003, 37(9): 1447-1451. (张永军, 张祖勋, 张剑清. 基于序列图像的工业零件尺寸检测技术[J]. 上海交通大学学报, 2003, 37(9): 1447-1451.) |
| [25] | LIU Weiwei. Positioning of Mars Probes Based on Imaging Geometric Models[D]. Nanjing: Nanjing University of Aeronautics and Astronautics, 2012. (刘微微. 基于成像几何模型的火星探测器定位研究[D]. 南京: 南京航空航天大学, 2012.) |
| [26] | QIAN Ping. A Research Based on Dual Quaternion for Relative Position and Attitude Determination of RVD Spacecrafts[D]. Nanjing: Nanjing University of Aeronautics and Astronautics, 2011. (钱萍. 基于对偶四元数的航天器交会对接位姿关键技术研究[D]. 南京:南京航空航天大学, 2011.) |
| [27] | QIAN Ping, WANG Huinan. A Binocular Vision Algorithm Based on Dual Quaternion for Relative Position and Attitude Determination of RVD Spacecrafts[J]. Journal of Astronautics, 2013, 34(1): 32-38. (钱萍, 王惠南. 基于对偶四元数的航天器交会对接位姿双目视觉测量算法[J]. 宇航学报, 2013, 34(1): 32-38.) |
| [28] | ZHANG Jianqing, PAN Li, WANG Shugen. Geo-spatial Information Science[M]. Wuhan: Wuhan University Press, 2009: 28. (张剑清, 潘励, 王树根. 摄影测量学[M]. 武汉: 武汉大学出版社, 2009: 28.) |