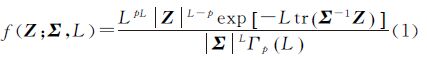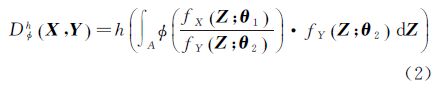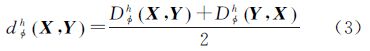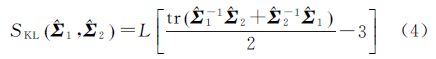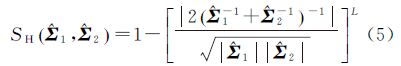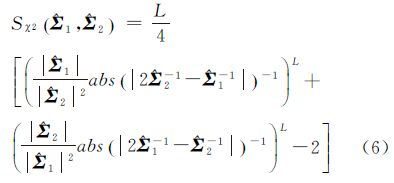1 引 言
经典的边缘检测算子如Sobel、Prewitt、Canny和LoG算子[1, 2, 3]等均为基于加性噪声构建的差分算子,不适用于具有乘性斑点噪声的SAR图像。SAR图像边缘检测主要基于均值比率(ratio of averages,RoA)算子[4]和改进算子如LoG-RoA[5]、MSP-RoA[6]、指数加权均值比算子[7]、广义似然比算子[8]以及基于RoA和最佳熵结合算法[9]。然而,这些算子仅利用了单极化SAR图像的强度信息,未考虑极化信息对边缘提取的影响。
全极化SAR图像具有比单极化更丰富的目标散射信息,可显著地增强目标识别和信息提取能力[2, 10, 11, 12]。充分利用极化信息将大大增加SAR图像边缘检测精度和可靠性[10]。经典算法是基于复Wishart分布的似然比方法[13, 14, 15]。另外,借助极化特征信息提高边缘检测精度是另一个研究方向,如最优极化对比度增强技术方法[10, 11]、基于SPAN和PWF滤波方法[16]以及改进的Duda算子[17]。随着极化SAR数据的增多,研究其边缘检测算法具有重要的应用价值。
本文从统计学中的随机距离出发,提出了基于复Wishart分布和随机距离的边缘检测算法。该算法基于八方向边缘模板,利用边缘两侧类别的随机距离与边缘方向和位置密切相关的特点进行构建。
2 概率分布的随机距离 2.1 复Wishart分布的随机距离全极化SAR对地观测得到地表的后向散射矩阵数据,经多视后得协方差矩阵Z,其概率分布为复Wishart分布
式中,L为等效视数;tr(·)是矩阵的迹;Γp(L)=π½p(p-1)Πi=0p-1Γ(L-i),L≥p,Γ(·)为Gamma函数,p=3;$Z = \frac{1}{L}\sum\limits_{k = 1}^L {u\left( k \right)} u{\left( k \right)^{ * T}}$ ,u(k) 为极化SAR单视复数据向量,k=3。
随机距离的数学定义是:假设X和Y是随机矩阵,服从概率分布函数分别为fX(Z;θ1)和fY(Z;θ2),其中θ1和θ2是分布参数向量,则两个概率分布在空间(h,φ)上的分离度(随机距离)定义为[18, 19]
由于Dφh(X,Y)是非对称的,需进一步改进为
式中,dφh(X,Y)满足3个属性:①非负性;②对称性;③当X=Y时,dφh(X,Y)=0。
随机距离可根据应用需求采用相应的概率分布函数。对于单极化SAR图像边缘检测,可选概率密度函数为Gamma分布[7, 8, 9];对于全极化SAR图像,可选复Wishart分布[11, 12, 14, 15, 16];对于具有纹理特征的SAR数据,可选非高斯统计模型如K、G0、KummerU等分布[20]。由此可见,随机距离的构建具有很强的灵活性,本文以复Wishart分布为例。
2.2 典型的随机距离函数设协方差矩阵Z服从复Wishart分布,且两个地物类别X和Y对应的理论概率密度函数分别为fX(Z;θ1)=f(Z;Σ1,L)和fY(Z;θ2)=f(Z;Σ2,L)。其中,Σ1和Σ2是X和Y协方差矩阵的数学期望。对于同一幅图像内边缘检测,可假设各类别的视数L相同,Σ1和Σ2利用局部区域的估计值$\hat \Sigma$1和$\hat \Sigma$2来代替。常用随机距离有Kullback-Leibler、Hellinger和Chi-square距离[17, 18],在复Wishart分布下的解析表达式如下。
(1) Kullback-Leibler(KL)距离
式中,SKL取值范围为[0,+∞)。
(2) Hellinger距离
式中,SH取值范围为[0,1)。
(3) χ2(Chi-square)距离
式中,Sχ2取值范围为[0,+∞)。
纵观式(6),当图像中两类别$\hat \Sigma$1=$\hat \Sigma$2即两类之间没有边缘时,其随机距离均等于零;当$\hat \Sigma$1≠$\hat \Sigma$2,即两类之间有边缘时,其随机距离均大于零。$\hat \Sigma$1和$\hat \Sigma$2之间的随机距离越大,说明极化SAR图像上$\hat \Sigma$1和$\hat \Sigma$2代表的两个类差异越显著,边缘也越明显。因此,边缘信息可以利用随机距离值来表征。此外,还有Renyi、Bhattacharyya、Jensen-Shannon、arithmetic-geometric和harmonic-mean等距离[21]。
3 PolSAR图像边缘检测理论方法 3.1 预处理预处理主要包括数据转换、多视和滤波。一般选用可保存边缘信息的滤波器,如精制Lee滤波[22]。
3.2 边缘检测算法边缘检测包含边缘的定向和定位。定向需要通过局部区域的检测窗口来确定,常用的检测窗口有四方向(图 1(a)-图 1(d))和八方向(图 1(a)-图 1(h))。图 1是8个方向的检测窗口,以5×5为例,黑色部分代表边缘,两侧白色部分代表两类样本,窗口大小根据图像分辨率和应用背景选择。若窗口过小,边缘检测易受斑点噪声影响,不利于准确地估计边缘两侧的协方差矩阵期望值;若窗口过大,则边缘定位不准确。
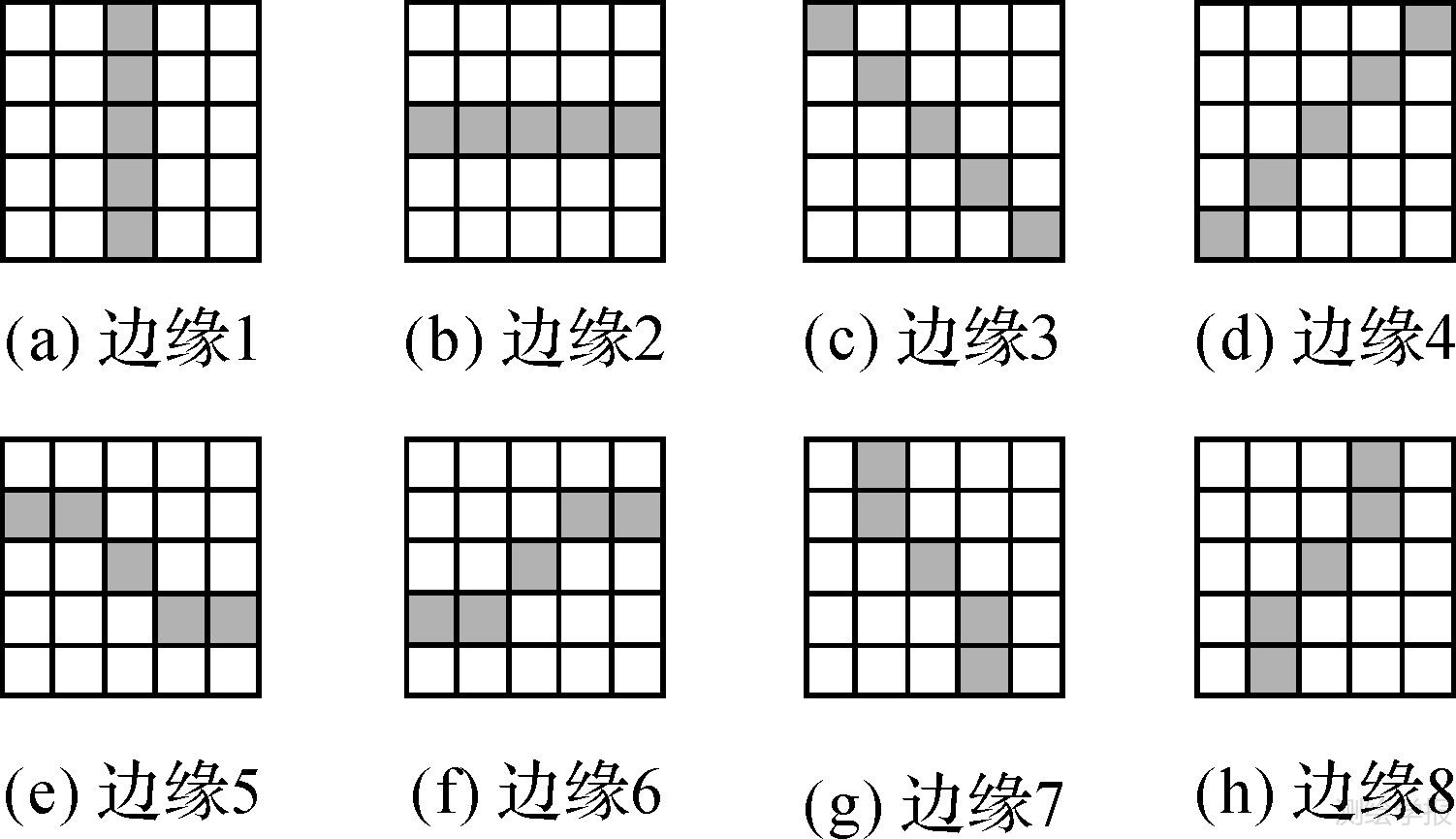
|
| 图 1 8个方向的边缘检测窗口 Fig. 1 Edge detection windows in eight directions |
边缘两侧两类样本间的随机距离取决于两个因素:①边缘走向,若实际边缘为边缘1(上下走向),那么由图 1(a)计算的随机距离最大,而用图 1(b)计算的最小;②类别间的差异,即两类样本协方差期望值的差异,局部区域没有边缘时,8个窗口计算的随机距离均应为0或非常接近0。上述因子也是边缘检测的两个关键,即边缘定向和定位。
据此,边缘检测算法包括:①选择(N×N)大小的检测窗口,计算模板边缘的随机距离VSD ={SD1,SD2,…,SD8};②取max(VSD)赋给检测窗口中心像素,并记录其边缘方向,由max(VSD)构成的图像即为随机距离的强度图像;③确定边缘检测的阈值进行边缘提取。
需要指出,上述算法不适用于如下两类特殊线或边缘,一是仅占一个像素宽度的特殊线;另一类是多边缘,这时需要减小边缘检测窗口的尺寸,使得检测窗口内近似为一个边缘。
3.3 边缘重定位与后处理
模板窗口在跨两个类别区域时,其随机距离会有一个连续性的跳跃。初始提取的边缘往往由多个像素宽度组成,而非真实单像素宽度边缘,需要边缘重定位和细化处理。
本文的边缘重定位方法是基于MSP-RoA算法[6]改进而来。根据每个边缘点的边缘走向,选择其垂直方向的相邻两个像素,共同组成N(N=3,5,7,…)个像素向量。由于初步提取的边缘线宽度由边缘检测窗口的大小和检测阈值决定,所以N的取值与窗口维度有关。例如,检测窗口为5×5时,N=3。统计该向量中的随机距离最大值。如果该向量中心点的值等于这个最大值,就保留该点为边缘候选点。否则,该点为边缘附近的点,予以剔除。
边缘重定位和细化后还会存在一些由于斑点产生的孤立点或者短线段,这些不属于边缘,因此需要对候选点进行后处理。传统方法是基于边缘方向跟踪[2, 4]筛选,本文则设计一个窗口(如9×9)对候选边缘进行滤波。滤波原则是长线段具有连通和穿通的几何拓扑特征,即若窗口模板边缘四周对应的像素没有候选边缘点,则说明这个窗口内没有长线段,可以将其内的孤立点或短线段进行滤除。
4 试验结果与分析 4.1 随机距离边缘检测的灵敏度分析试验选择一景相对定标后的机载PolSAR图像如图 2(见文末)。在试验之前,选择部分样本数据,利用Matlab中复Wishart随机数生成器模拟PolSAR图像开展边缘检测仿真研究,以KL距离为例,分析随机距离检测边缘的性能,主要包括定向和定位的性能。
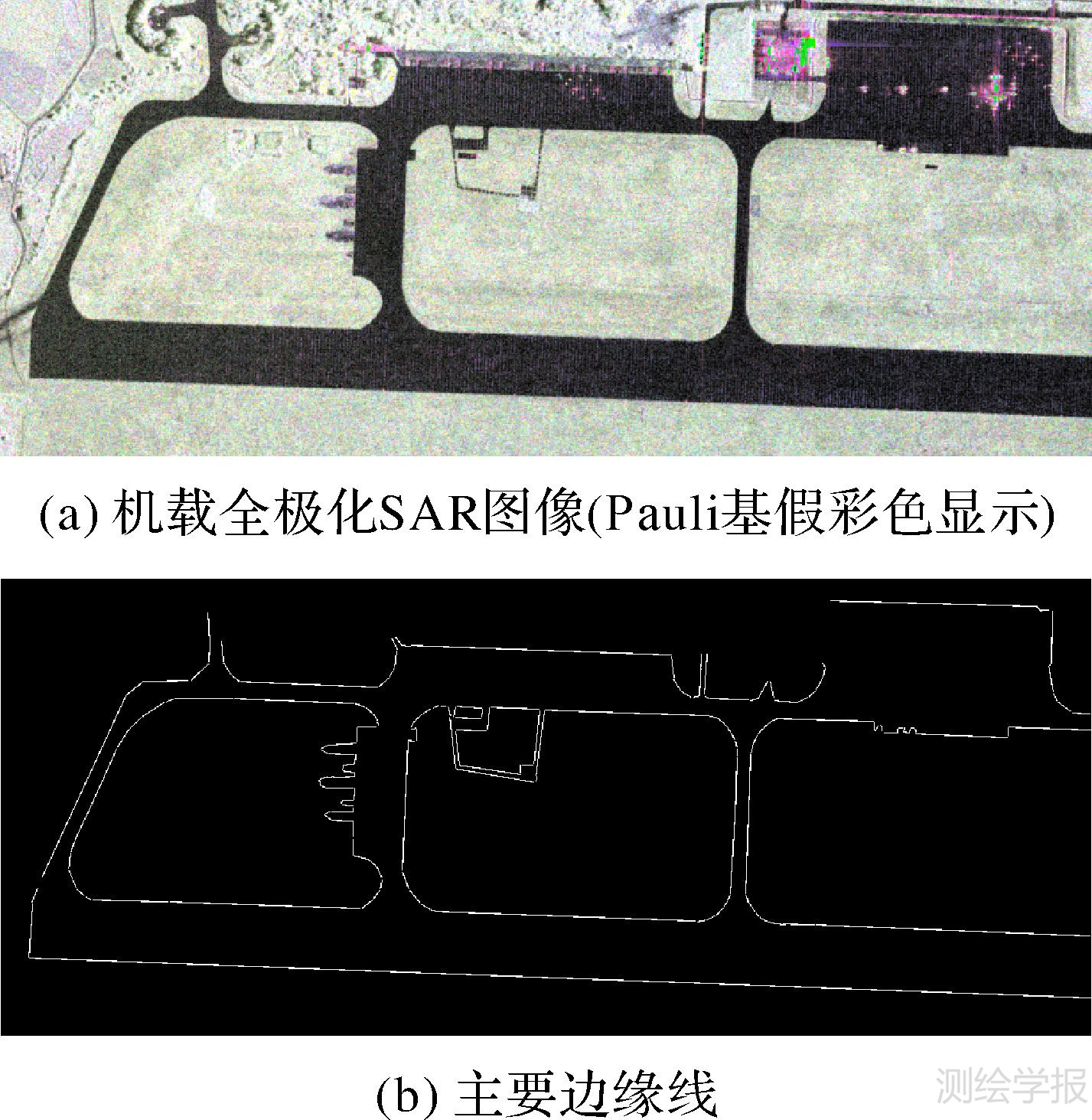
|
| 图 2 真实图像与主要边缘线参考图 Fig. 2 Real image and reference map of main edges |
为验证边缘定向的敏感度,分别获取草地和机场跑道的协方差矩阵期望值(C1和C2),并生成如图 3(a)5×5大小的PolSAR模拟图像,其边缘如图 3(b)所示。
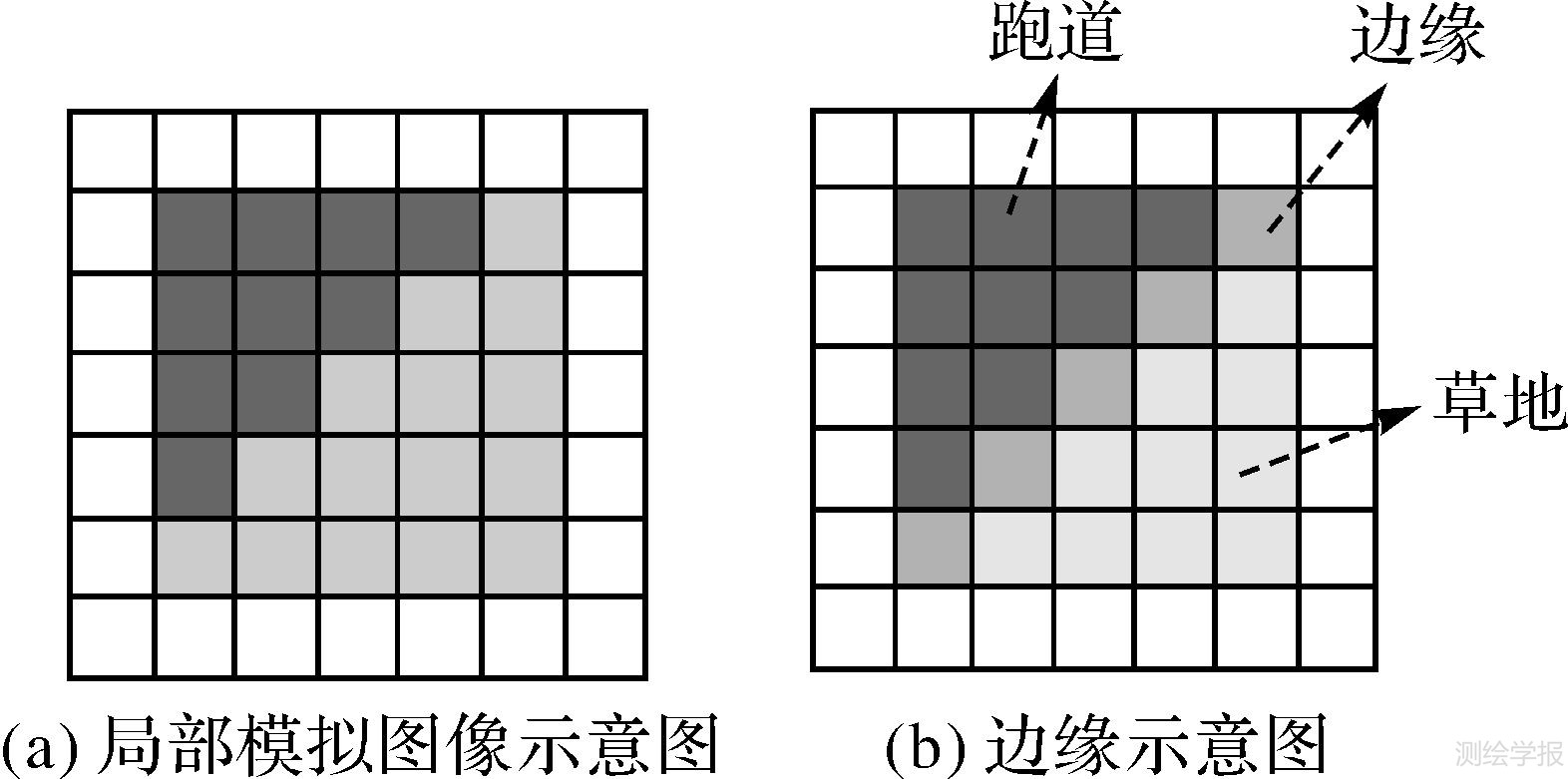
|
| 图 3 模拟图像与边缘线 Fig. 3 Simulated image and edge |
为便于可视化,设置草地的协方差矩阵期望值C1中的C11(434 979+X)项是变化的,X是从0~80 000,以2000为间隔递增。
草地

跑道

根据八方向检测窗口(图 1),计算8个边缘的KL距离与C11的变化关系(图 4)。由图 4可知,C11增大,其他项不变,说明边缘两侧的强度差异增大。以X=0为例,草地和跑道构成的正确边缘(边缘4)的KL距离最大(约为30),而其他7个边缘的KL距离均很小。图 3边缘两侧地物沿45°方向对称,因此边缘3、5、7的KL距离值理论上均应为0。边缘6和8形状更接近于边缘4,因此其相比边缘1和2,KL距离理论上应相对较大。特别是边缘8与边缘4仅有两个像素的差异,但其KL距离实际值却相差近20倍。由此可见,KL距离对边缘走向非常敏感,非常有利于准确的边缘定向和后续阈值分割边缘提取。另外,C11增大,边缘两侧对比度也增大。由图 4可见,边缘4对应的KL距离随C11的增大呈近似指数级增大,而其他7个边缘的KL距离基本不变,且很小。这说明,当类别差异增大时,边缘处对应的KL距离呈显著增大趋势,这使得后续阈值选择更加容易,虚警率更低。
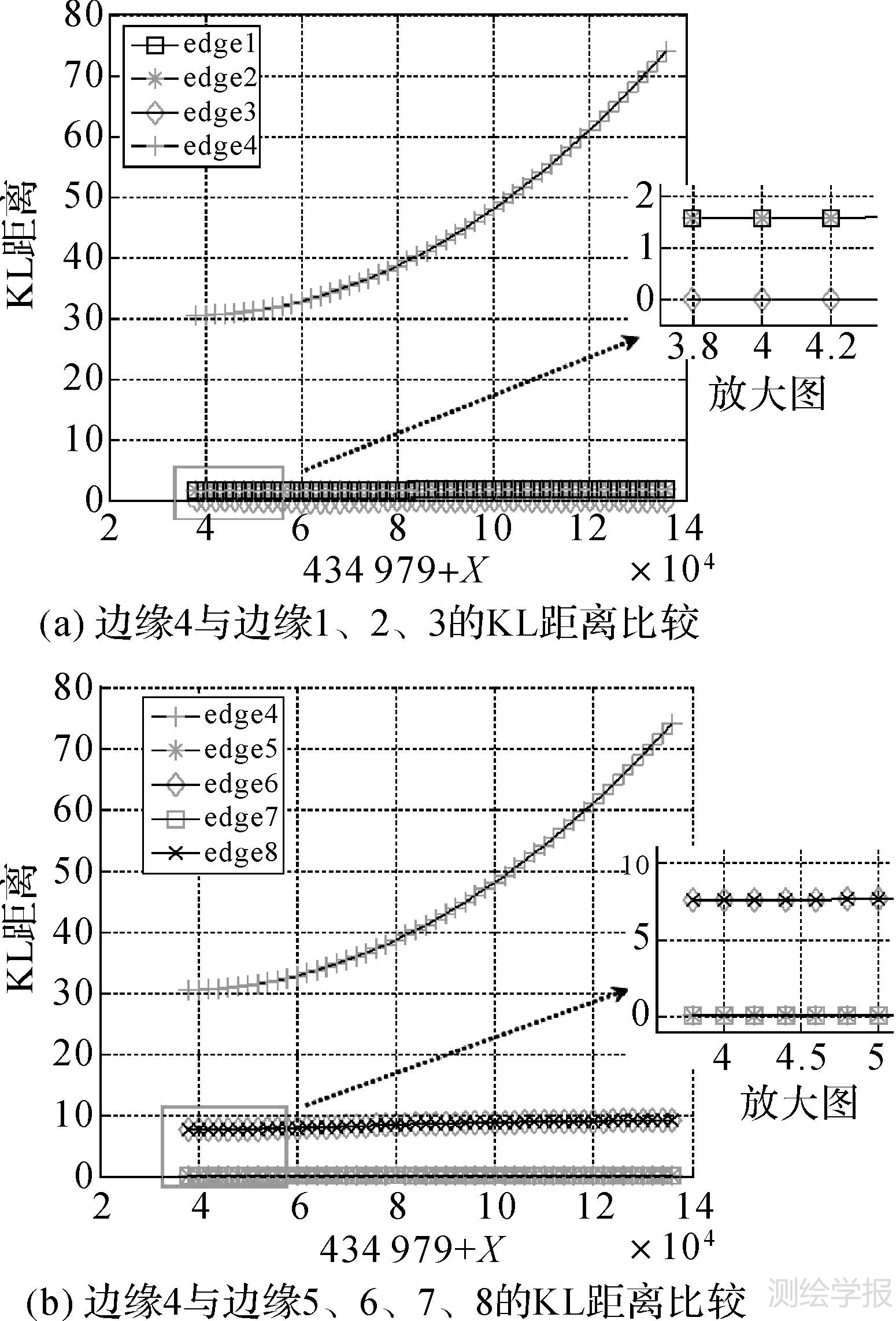
|
| 图 4 基于KL距离的边缘检测敏感度分析 Fig. 4 Sensitivity analysis of KL distance edge detection method |
为检验KL距离的边缘定位性能,以图 3为例,通过在边缘垂直方向(法线)上移动边缘4检测窗口来获得其KL距离与边缘中心位置的关系(图 5)。由图 5可知,随着距边缘中心距离的减小,KL距离显著增大。由图 5(a)可见,边缘恰好与检测窗口边缘吻合时KL距离最大,且远高于相邻边缘中心仅一个像素的KL距离,约为3倍。图 5(b)是由边缘两侧为相同协方差矩阵,且仅有一侧协方差矩阵的C11变化,而得到的KL距离与边缘中心的距离关系,X=0表示边缘两侧地物相同(无边缘)。随着X增大,边缘两侧对比度增大,边缘中心处的随机距离也增大,且增大幅度比邻近边缘的像素的KL距离大,这与图 5(a)中的放大图显示的增大趋势是一致的,且增大幅度近似指数级。显然,这非常有利于提高边缘定位精度。另外,若设检测窗口为5×5,检测阈值设为接近于0,所得初始边缘宽度为3个像素。而若选择适当阈值,也可得到1个像素宽度的初始边缘。由此可见,使用5×5检测窗口,边缘定位精度理论上小于或等于3个像素。此时,边缘重定位处理时只需选择垂直边缘方向3×1子窗口。
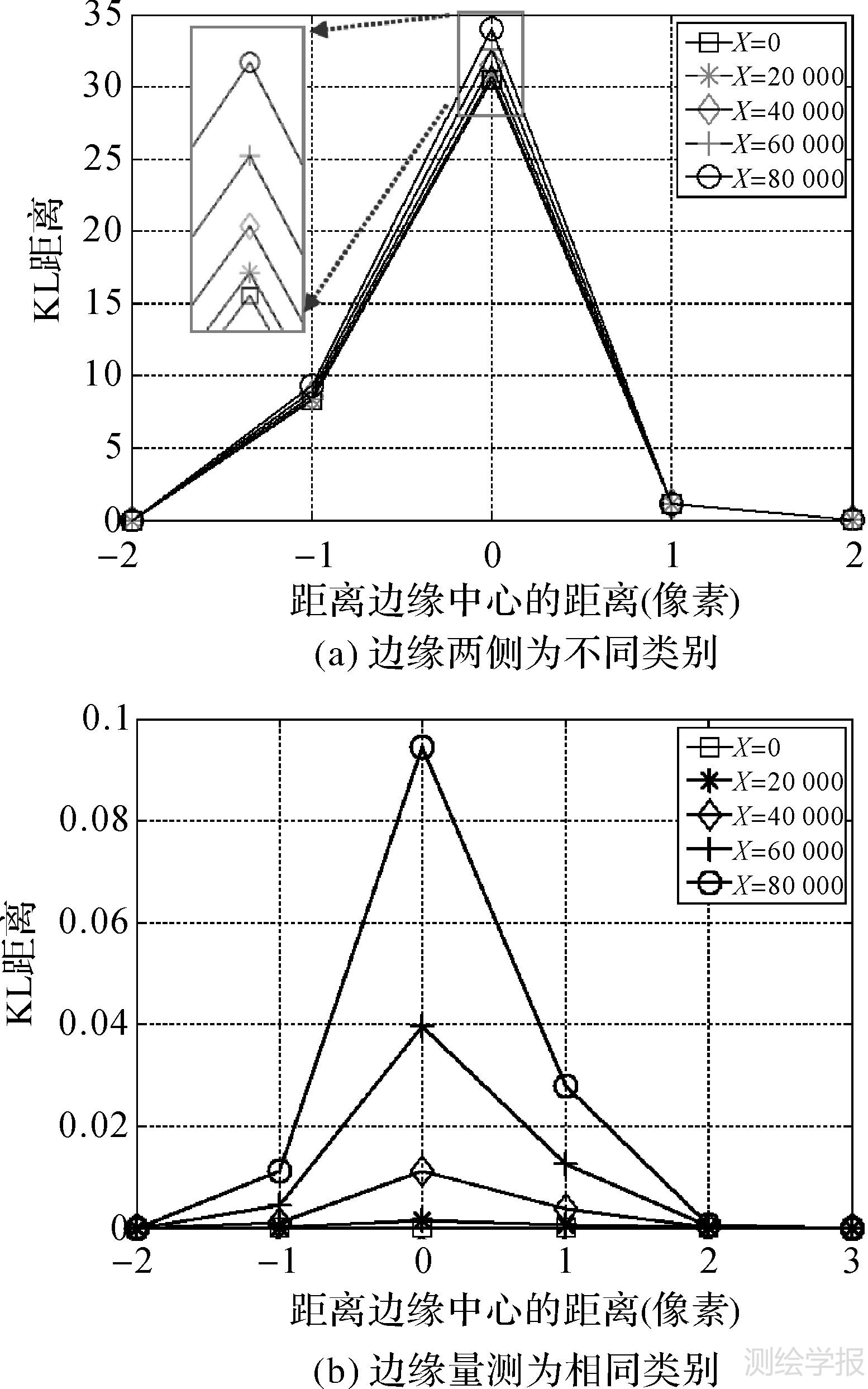
|
| 图 5 基于KL距离边缘检测的边缘定位精度分析 Fig. 5 Edge positioning accuracy analysis of KL distance detection method |
为对比KL距离与经典的复Wishart似然比方法[13, 14]对这种突变的敏感度,假设边缘两侧区域均为草地,其中一侧协方差为C1,且设置X=0,而另一侧协方差也为C1,但X是从0递增至434 979,使得协方差矩阵C11强度增大至两倍,得到边缘的KL距离与X的关系,如图 6(a)所示。根据文献[13]得到似然比与X的关系(归一化后)如图 6(b)。虽然两者边缘提取方法本质不同,但据图 6可知,随边缘两侧类别对比度的增大,KL距离呈指数增加趋势,而似然比变化呈增速放缓的趋势,且渐进地接近于2。很显然,当X较大即边缘两侧差别显著时,KL距离更有利于边缘的检测。当X较小时,边缘两侧差别较小,KL距离的增幅比似然比小,例如X从0增至1.0×105,即C11增大20%,其他协方差项不变,这在实际图像中很可能是由斑点噪声引起,所以该边缘可能不存在,而图 6显示该区间内KL距离的增大速率比似然比小,更符合实际情况。由此推断,KL距离检测边缘的抗斑点能力比Wishart似然比更强,边缘检测的准确率更高。
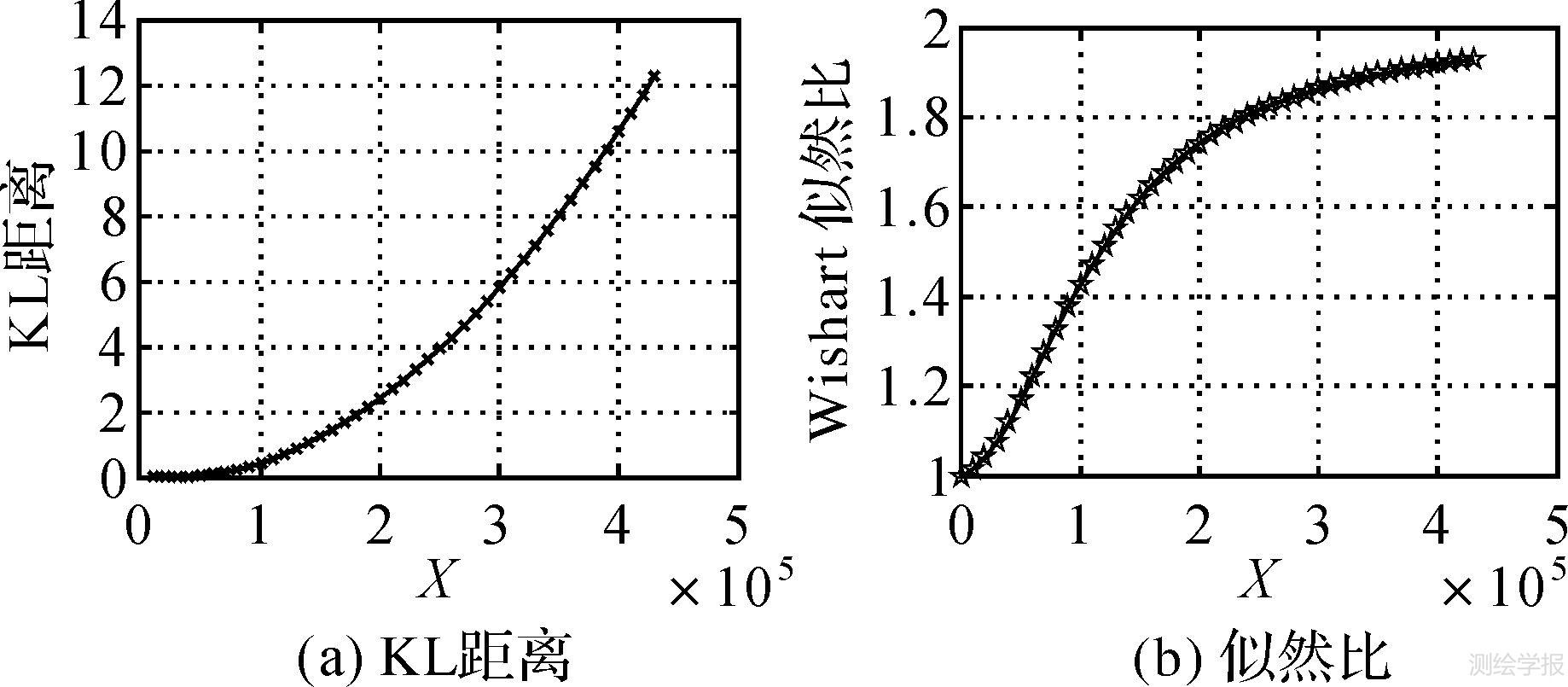
|
| 图 6 KL和似然比与X的关系 Fig. 6 The relationship of KL distance and Likelihood Ratio with X |
图 7(a)为模板图像。根据4类地物(1--草地、2--跑道、3--树林、4--建筑)协方差期望值,利用Wishart分布随机数生成随机协方差矩阵数据,并填充到图 7(a)各部分构建模拟PolSAR图像如图 7(b)所示。由式(4)得边缘强度图像(图 7(c)),为保证显示可见,其显示灰度范围在0~5,实际边缘的KL距离值远高于5,而非边缘区域的KL距离值远低于1。选择阈值2分割的初步检测结果如图 7(d)。后处理的单像素宽度的边缘如图 7(e)。将检测结果叠加至原始图像上如图 7(f),可见其与原始图像边缘非常吻合。利用Canny算子检测图 7(a)的真实边缘作为参考,并作叠加分析,统计错误定位点,其中有效检测边缘点数为2405,而真实边缘点数为2260,定位偏移1个像素的点有224个,约占9.3%;定位偏移错误超过两个及以上像素的点有78个,约占3.2%,漏检边缘像素为37个,约占1.5%。错误偏移和漏检边缘像素主要集中在图 7(a)中第3个图形的圆形拐角处(见文末)。

|
| 图 7 模拟PolSAR图像的边缘检测试验 Fig. 7 Edge detection experiment using simulated PolSAR image |
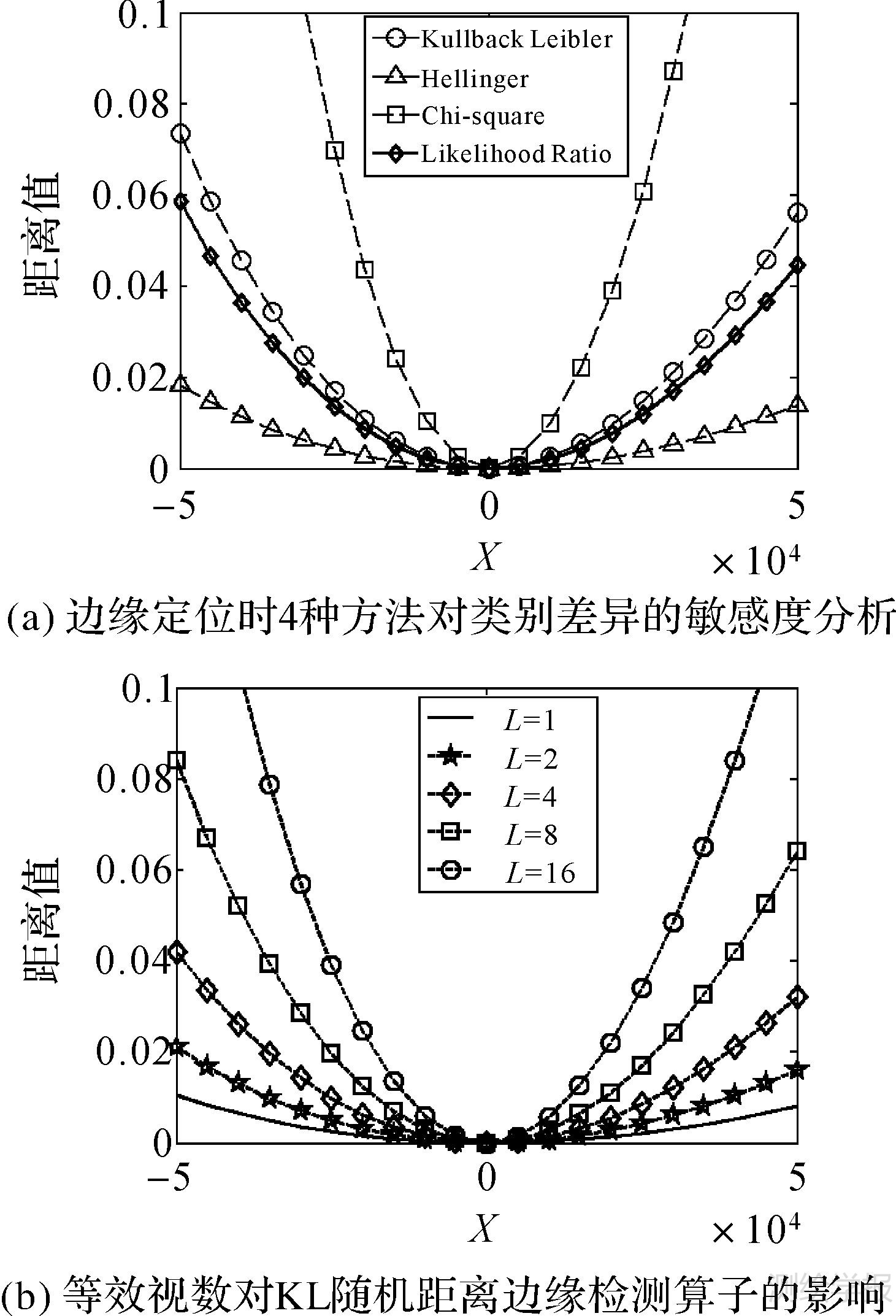
为比较上述3个随机距离的边缘检测灵敏度,试验选择草地协方差矩阵C1,通过改变其C11项来构造两类别,一类X从-50 000递增至50 000;另一类则X=0。两类的3个随机距离及似然比与X变量的关系如图 8(a),可见KL和Chi-square距离对X变化的敏感度高于似然比和Hellinger距离,即前两者反映边缘两侧的类别差异敏感度更高,更有利于边缘检测。为研究等效视数对边缘检测的影响,试验以KL随机距离为例给出等效视数与X的关系如图 8(b),L增大,KL距离值也增大,使得边缘检测更加敏感。
|
| 图 8 灵敏度分析 Fig. 8 Sensitivity analysis |
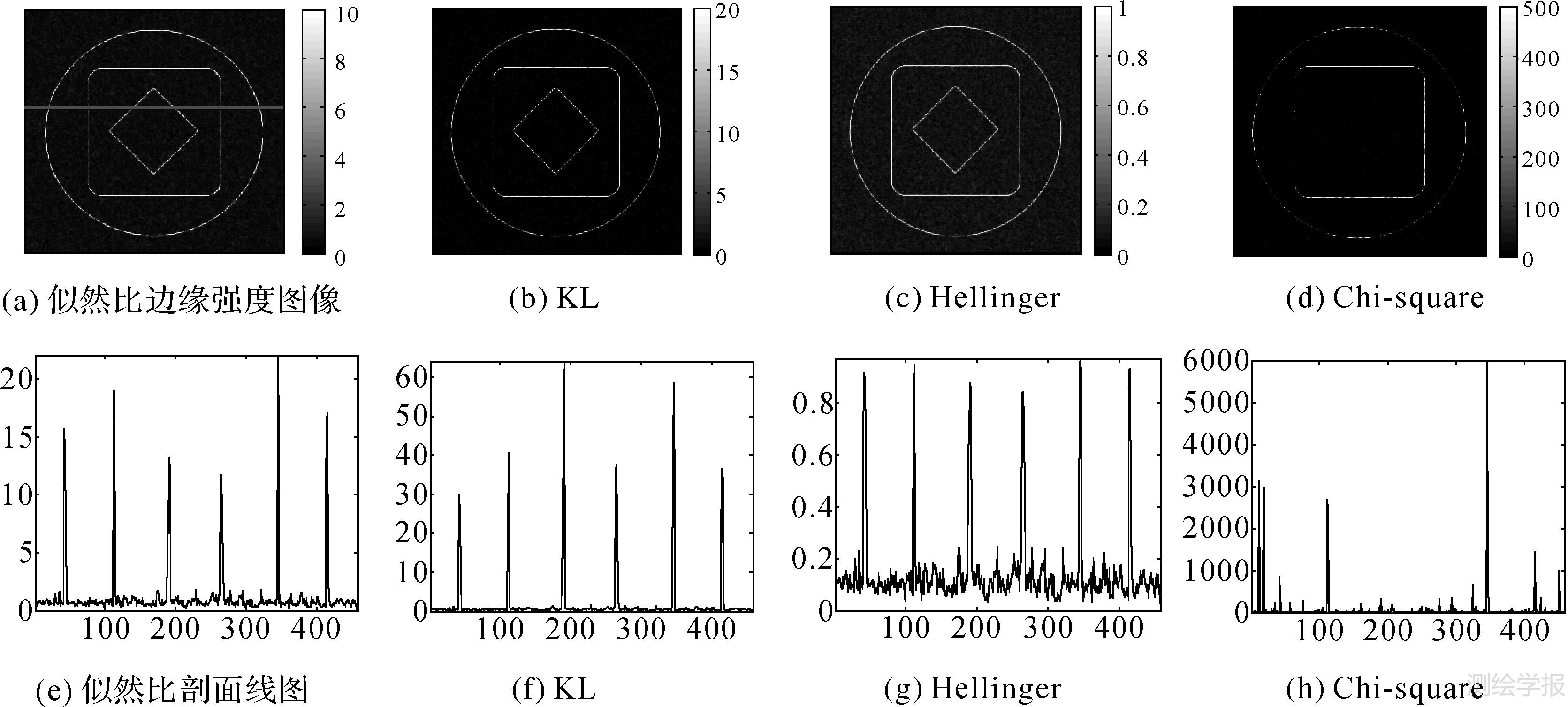
基于模拟极化SAR图像(图 7(b)),利用似然比和上述随机距离算子得到边缘强度图像分别如图 9(a)-图 9(d)。这些检测算子反映边缘强度的大小不同,显示色标取值范围也相差较大。为对比检测效果,选择一条剖面线如图 9(a)横线,得到各边缘强度图像剖面线如图 9(e)-图 9(h)。
|
| 图 9 4种方法边缘检测结果对比 Fig. 9 Comparison of edge detection results for four methods |
图 8(a)反映了各随机距离对边缘检测的敏感度关系: Chi-square>Kullback Leibler>Likelihood Ratio>Hellinger。可见,并不是所有随机距离的探测敏感度好于似然比距离。另外,图 9(d)和图 9(h)则反映Chi-square距离边缘检测效果受两侧类别差异影响较大。而图 9(c)和图 9(g)反映Hellinger距离边缘检测效果受两侧类别差异影响较小。对比图 9(a)-图 9(d),可见图 9(d)图的取值范围最大,图 9(c)图最小,且在0~1内。而图 9(a)和图 9(b)图取值范围适中,边缘处与非边缘处的差异较大,且均衡。因此,似然比和KL、Hellinger距离得到边缘强度图更适宜后期的阈值分割。对比图 9(e)-图 9(g)三剖面线的峰值(边缘处)与峰谷(非边缘处)的比值,可见图 9(f)的比值最大,其次是图 9(e),图 9(g)反映的比值最小,也就是说,KL距离检测边缘可以最强地凸现边缘,其次是似然比和Hellinger距离。由此可知,各随机距离应用于PolSAR图像边缘检测时对边缘的敏感度是不同的,其中KL距离检测效果最好,既突出边缘特征又抑制非边缘区斑点噪声的影响,而Chi-square对边缘两侧类别差异过于敏感,对于斑点较多的SAR图像,其边缘检测的虚警率会较高,Hellinger距离检测效果则一般,并不如似然比方法,但其优点是检测效果受边缘两侧类别差异影响最小。
4.3 真实PolSAR图像边缘检测试验采用八方向5×5检测窗口,利用KL距离对机载PolSAR图像进行边缘检测,得到KL距离强度图(图 10(a)),为了显示边缘与非边缘的KL距离值差异,灰色显示色表设为0~2。分别在图上选择3条跨越边缘的剖面线段(红线段1、2、3)和3条非边缘处的剖面线段(绿线段4、5、6),这6条线段对应的KL距离值如图 10(b)和图 10(c),横坐标是各线段的像素相对位置,纵坐标是KL距离值。线段1和2对应的KL距离在边缘处有明显的“脉冲”跳变,而线段3的跳变不是很显著,这是由于线段3所跨越的边缘相邻地物差异不很明显,尽管如此,线段3所横截的边缘对应KL距离仍然高于1。线段4、5、6表征了非边缘处的KL距离值变化情况,从图 10(c)可见,这些非边缘区域的KL距离值均很小,但有一定的浮动。理想情况下,线段4、5、6所对应的KL距离应等于零,由于相干斑,其实际取值为0~0.25,不过,其最大值也远小于边缘处的KL距离值。

|
| 图 10 KL距离边缘线剖面分析 Fig. 10 Profile analysis of edges detected by KL distance |
试验选择阈值为0.5,得到初始边缘如图 11(a),后处理的单像素宽度边缘如图 11(b)。图 11(c)和图 11(d)是似然比方法在相同阈值下得到的边缘检测结果。图 11(e)、图 11(f)为参考边缘细节图像,图 11(g)和图 11(h)分别为KL距离和似然比方法检测边缘细节图。对比可见,似然比方法检测结果中误判边缘点较多,其与KL距离的边缘检测结果精度分析如表 1所示。可见,相同分割阈值,KL距离检测边缘的误判率更低;若分割阈值更大,KL距离检测边缘的误判率比似然比方法更低。这与4.2节中基于模拟数据的理论分析是一致的,说明KL距离与似然比方法相比可以更好地抑制非边缘且突出边缘特征。

|
| 图 11 边缘检测结果与参考数据比较 Fig. 11 Comparison of edge detection results with reference data |
| 算 法 | 有效边缘检测点 | 准确边缘检测点 | 漏检边缘点 | 误判边缘点 |
| KL随机距离 | 8491 | 8164 | 125 | 202 |
| 似然比距离 | 8953 | 7988 | 301 | 664 |
本文引入统计学中的随机距离概念,给出了随机距离构建PolSAR图像边缘检测算子。通过模拟数据和真实数据的试验与分析,结果表明基于随机距离的边缘检测具有如下3个显著优点:①抑制斑点噪声的效果很好;②边缘方向检测的敏感度非常高;③边缘定位的精度高。
此外,参考复Wishart似然比方法,对比本文中的3个随机距离算子可以发现:①3个随机距离的取值范围不同,受边缘两侧类别强度变化的影响也不同,Hellinger距离受边缘两侧强度变化的影响最小,KL距离和似然比方法次之,而Chi-square距离最大;②边缘检测效果上,基于KL距离的边缘检测方法要优于似然比方法,而Hellinger和Chi-square距离则不如似然比方法。
总之,统计理论中随机距离概念应用于全极化SAR图像边缘检测是可行且有效的,可以根据应用需求选择适当的随机距离。
| [1] | TORRE V, POGGIO T A. On Edge Detection[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 1986, 8(2): 147-163. |
| [2] | DENG Shaoping, ZHANG Jixian, LI Pingxiang. Review of Edge Detection from Polarimetric SAR Imagery[J]. Computer Engineering and Application, 2011, 47(22): 1-5. (邓少平, 张继贤, 李平湘. 极化SAR影像边缘检测综述[J]. 计算机工程与应用, 2011, 47(22): 1-5). |
| [3] | ZHAO Lingjun, JIA Chengli, KUANG Gangyao. Overview of Edge Detection in SAR Images[J]. Journal of Image and Graphics, 2007, 12(12): 2042-2049. (赵凌君, 贾承丽, 匡纲要. SAR图像边缘检测方法综述[J]. 中国图象图形学报, 2007, 12(12): 2042-2049.) |
| [4] | TOUZI R, LOPES A, BOUSQUET P. A Statistical and Geometrical Edge Detector for SAR Images[J]. IEEE Transactions on Geoscience and Remote Sensing, 1988, 26(6): 764-773. |
| [5] | BOVIK A C. On Detecting Edges in Speckle Imagery[J]. IEEE Transactions on Acoustics, Speech and Signal Processing, 1988, 36(10): 1618-1627. |
| [6] | GANUGAPATI S S, MOLONEY C R. A Ratio Edge Detector for Speckled Images Based on Maximum Strength Edge Pruning[C]//IEEE International Conference on Image Processing. Washington, DC: IEEE, 1995, 2: 165-168. |
| [7] | FJORTOFT R, LOPES A, MARTHON P, et al. An Optimal Multiedge Detector for SAR Image Segmentation[J]. IEEE Transactions on Geoscience and Remote Sensing, 1998, 36(3): 793-802. |
| [8] | OLIVER C J, BLACKNELL D, WHITE R G. Optimum Edge Detection in SAR[J]. IEEE Proceedings on Radar, Sonar and Navigation, 1996, 143(1): 31-40. |
| [9] | LIU Junyi, LI Deren, LI Wei, et al. A Method for SAR Edge Detection Based on Ratio of Averages and Optimal Entropy[J]. Geomatics and Information Science of Wuhan University, 2007, 32(6): 494-497. (刘俊怡, 李德仁, 李微, 等. 一种基于均值比率和最佳熵的SAR影像边缘检测方法[J]. 武汉大学学报:信息科学版, 2007, 32(6): 494-497). |
| [10] | LI Pingxiang, DENG Shaoping, ZHANG Jixian, et al. An Edge Detector for Polarimetric SAR Images Based on Adaptive Optimal Polarimetric Contrast Enhancement[J]. Geomatics and Information Science of Wuhan University, 2012, 37(7): 789-793. (李平湘, 邓少平, 张继贤, 等. 利用自适应最优极化对比增强检测SAR影像边缘[J]. 武汉大学学报:信息科学版, 2012, 37(7): 789-793.) |
| [11] | LANG Fengkai, YANG Jie, ZHAO Lingli, et al. Polarimetric SAR Data Classification with Freeman Entropy and Anisotropy Analysis[J]. Acta Geodaetica et Cartographica Sinica, 2012, 41(4): 556-562. (郎丰铠, 杨杰, 赵伶俐, 等. 基于Freeman散射熵和各向异性度的极化SAR影像分类算法研究[J]. 测绘学报, 2012, 41(4): 556-562.) |
| [12] | WEI Jujie, LI Pingxiang, YANG Jie, et al. Removing the Effects of Azimuth Ambiguities on Ships Detection Based on Polarimetric SAR Data[J]. Acta Geodaetica et Cartographica Sinica, 2013, 42(4): 530-539. (魏钜杰, 李平湘, 杨杰, 等. 利用全极化SAR数据去方位向模糊的舰船目标检测方法[J]. 测绘学报, 2013, 42(4): 530-539.) |
| [13] | SCHOU J, SKRIVER H, NIELSEN A A, et al. CFAR Edge Detector for Polarimetric SAR Images[J]. IEEE Transactions on Geoscience and Remote Sensing, 2003, 41(1): 20-32. |
| [14] | CONRADSEN K, NIELSEN A A, SCHOU J, et al. A Test Statistic in the Complex Wishart Distribution and Its Application to Change Detection in Polarimetric SAR Data[J]. IEEE Transactions on Geoscience and Remote Sensing, 2003, 41(1): 4-19. |
| [15] | LEE J S, POTTIER E. Polarimetric Radar Imaging: From Basics to Applications[M]. Boca Raton: CRC Press, 2009: 138-139. |
| [16] | BORGHYS D, LACROIX V, PERNEEL C. Edge and Line Detection in Polarimetric SAR Images[C]//Proceedings of the 16th International Conference on Pattern Recognition. Quebec City, Quebec, Canada: IEEE, 2002(2): 921-924. |
| [17] | ZHOU G, CUI Y, CHEN Y, et al. Linear Feature Detection in Polarimetric SAR Images[J]. IEEE Transactions on Geoscience and Remote Sensing, 2011, 49(4): 1453-1463. |
| [18] | FRERY A C, NASCIMENTO A D C, CINTRA R J. Information Theory and Image Understanding: An Application to Polarimetric SAR Imagery[J]. Chilean Journal of Statistics, 2011, 2(2): 81-100. |
| [19] | FRERY A C, NASCIMENTO A D C, CINTRA R J. Analytic Expressions for Stochastic Distances between Relaxed Complex Wishart Distributions[J]. IEEE Transactions on Geoscience and Remote Sensing, 2014, 52(2): 1213-1226. |
| [20] | DOULGERIS A P, ANFINSEN S N, ELTOFT T. Automated Non-Gaussian Clustering of Polarimetric Synthetic Aperture Radar Images [J]. IEEE Transactions on Geoscience and Remote Sensing, 2011, 49(10): 3665-3676. |
| [21] | NASCIMENTO A D C, CINTRA R J, FRERY A C. Hypothesis Testing in Speckled Data with Stochastic Distances[J]. IEEE Transactions on Geoscience and Remote Sensing, 2010, 48(1): 373-385. |
| [22] | LEE J S. Refined Filtering of Image Noise Using Local Statistics[J]. Computer Graphics and Image Processing, 1981, 15(4): 380-389. |