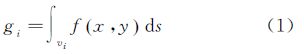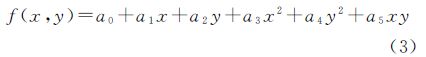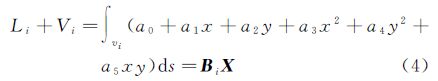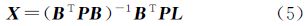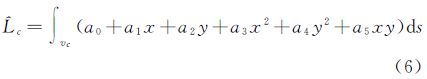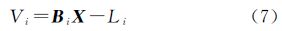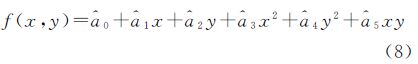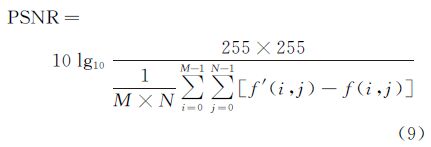1 引 言
目前的平差模型主要包含线性模型和非线性模型两种。线性模型中,观测值与平差参数之间是线性函数关系,例如经典平差中的条件平差模型和间接平差模型。而非线性平差模型中观测值与平差参数之间是一种非线性函数关系。传统的测量数据处理问题基本上都可以通过这两种模型来描述,例三角网、水准网、边角网、GPS网,摄影测量中的空三等,因而可用传统的测量数据处理理论来解决这些数据处理问题。由于技术的发展,数据采集的手段不断增多,现代测量数据处理中许多情况是不能简单地用线性平差模型或非线性平差模型来描述,例如极化干涉SAR中的复数问题、数字高程模型、图像处理等,在数字高程模型中,可以将每个格网的高程值看作地表函数在该格网范围内的一个积分。同样在图像处理时,也可以将每个像素值看作客体表面函数在该像元范围内的一个积分,当像素值已知,要利用不同像素值反求像元内客体表面函数时,那么观测的像素值与待求的函数之间就是一种积分关系,以这种积分关系建立起来的平差模型有两个特点:一是观测量与待求函数之间是一种积分关系;二是待求的是函数而不是参数。积分关系也是一种非线性关系,考虑到其特殊性,可称之为“积分型非线性平差模型”。积分型非线性平差模型实际在传统的大地测量中就出现并已经使用:传统大地测量中,重力测量值或者水准高差等于重力场的关系就是一种积分关系,当需要反求重力场时,建立的就是上述积分型非线性平差模型。传统大地测量中是用球谐函数将积分转换为求参数的平差模型。
图像超分辨率重建是指通过对多幅具有互补信息的低分辨率图像进行处理,重建一幅或多幅高分辨率图像的过程[1]。由于图像超分辨率重建能够突破硬件的限制来提高图像的分辨率,因而得到广泛的关注和推崇。最典型的应用是法国的SPOT 5卫星,该卫星通过获取两幅相互错位0.5像素的分辨率为5 m的图像,利用图像超分辨率重建技术,得到2.5 m分辨率图像,并向全球大量提供。目前图像超分辨率重建的算法大致可以分为两类:一是频率域算法[2, 3, 4, 5],即利用傅里叶变换将图像变换到频率域进行有关的重建计算;二是空域算法[6, 7, 8, 9, 10],即直接在空间域对图像灰度进行操作。频率域方法由于局限于全局平移运动和线性空间不变降质模型,且利用空域先验知识的能力有限,导致其适用范围非常有限;而空域算法,由于所采用的假设不同,不同的空域算法分别有不同的缺点[11, 12, 13, 14, 15]。本文的目的就是研究建立超分辨率重建的积分型非线性平差模型,用平差的方法解决超分辨率重建的问题。
为了评价该方法进行图像重建的效果,本文将利用传统的重建图像的评价指标进行定量评价。评价指标通常是采用PSNR和SSIM指数。PSNR指标用于衡量两幅图像之间的灰度相似性,而SSIM指标用于衡量两幅图像的结构相似性,本文将同时利用PSNR指数和SSIM指数对重建图像从灰度相似性和结构相似性方面进行综合评价[16]。
2 超分辨率重建的积分型非线性平差模型及其解算图像超分辨率重建过程就是对同一目标进行多次观测,获取多幅低分辨率影像,利用低分辨率影像求取目标的真实影像,即求取高分辨率影像的过程。这一过程与测绘领域中对同一对象进行观测,用测量平差求取对象最佳值的过程类似。如果用图像的灰度函数来表示图像的真实影像,任意像素值可以看作灰度函数在这个像素内的积分,那么低分辨率影像与真实影像之间的关系就可以通过一个积分来描述
式中,gi表示像素值;x、y是像素坐标;vi是像元范围;f(x,y)是客体表面灰度函数。当对同一目标进行多次观测时,获取多幅低分辨率图像时,可以构成观测方程 式中,观测值是像素值Li;Vi为改正值向量;待求的为灰度函数f(x,y)。每幅低分辨率图像的每个像素都可以建立一个如式(2)的方程,最后可根据需求组成一个观测方程组。与传统的测量平差模型不同的是,传统的测量平差待求量是参数,而式(2)的待求量是函数。依据上述观测方程求函数是一个值得深入研究的问题。重力测量中是用球谐函数将上述函数转换为参数,然后用最小二乘方法求解。对于图像,上述函数可以用傅里叶级数、小波函数来表示,本文尝试采用多项式,将其转换为参数估计的方法,即在图像上一个足够小的范围内,用二次多项式代替灰度函数 将式(3)代入式(2)得 式中,X=[a0 a1 a2 a3 a4 a5]T; Bi=[∫vids∫vixds ∫viyds ∫vix2ds ∫viy2ds ∫vixyds]。按最小二乘原理可解算出X
式中,P为观测值的权。对于上述图像超分辨率重建问题,如何选权也是一个值得研究的问题。实际上,上述像素值L所包含的误差可分为两个部分,一是图像本身的噪声,二是上述二次多项式替代过程中所带来的模型误差。而模型误差大小与像素距二次多项式曲面中心的远近有关,依据这一误差性质,本文按如下方案加权:选取参考图像中的任意像素L1(i,j),计算其周围8个像素中心与该像素的像素中心的距离。通过配准获得图像之间的空间转换参数后,将所有图像转换到参考图像相应的坐标系中,再计算其他图像对应的9个像素的像素中心与该像素中心的距离。取距离平方的反比对17个观测值定权,像素L1(i,j)本身也由像素的大小决定,即取像素半个像元宽度平方成反比。按式(5)解算出X,即可得到客体表面灰度函数。依据式(6)求解相应区域内的c个高分辨率像素值
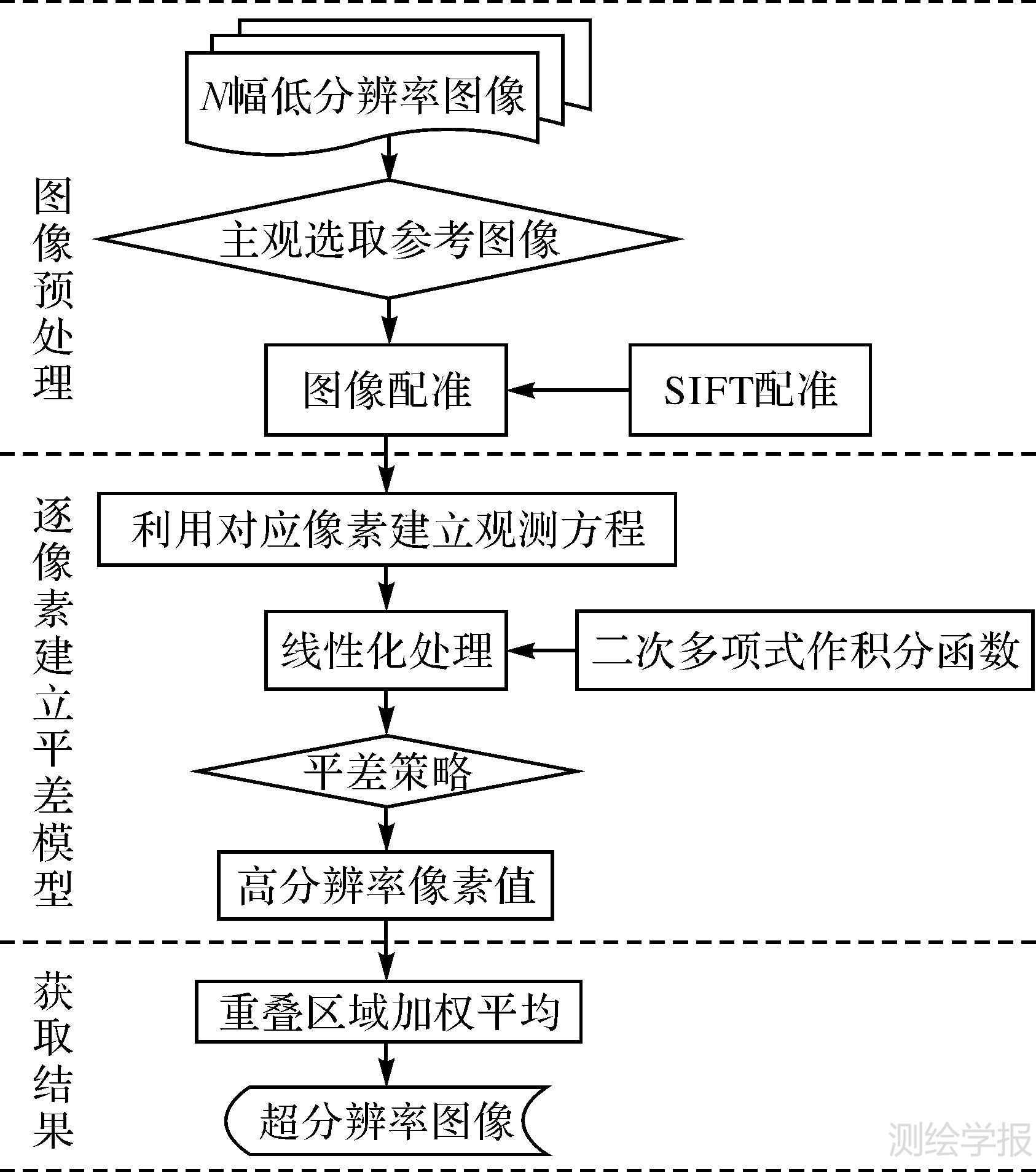
3 图像重建策略基于积分型非线性平差模型的重建方法流程如图 1所示,分为以下3步:
|
| 图 1 基于积分型非线性平差模型的重建方法流程图 Fig. 1 The flow chart of reconstruction method based on adjustment model of integral |
(1) 图像预处理:对低分辨率图像通过模糊估计和噪声估计获得模糊函数及噪声类型,在图像重建前先对低分辨率图像序列进行预处理,包括去模糊和去噪处理。选取参考图像L1,并定义参考图像的列为X轴,行为Y轴,X、Y坐标轴取值范围分别为0~N、0~M,N、M为参考图像的行列数。每个像元的坐标用像元中心的坐标值表示,也可以对坐标进行标准化处理:让X向和Y向像素之间的坐标间隔均为2/N,原点移至X轴的中央,此时X取值范围在-1~1变化,Y的取值范围在0~2M/N变化。然后采用SIFT特征配准方法计算获得其他各低分辨率图像序列与参考图像之间几何变换参数,包括平移和旋转,再根据变换参数,将图像序列变换到参考图像坐标系中。从参考图像中逐行依次选取像素L1(i,j)及周边8个像素点对应的像素值和坐标,再从其他序列图像中选取最靠近像素L1(i,j)的像素点Ln(k,r)及周边8个像素点对应的像素值及坐标。
(2) 超分辨率像素值的计算:在获得以上数据后,按照积分型非线性平差模型列出观测方程式(4)。每张图像有9个像素,如果有n张低分辨率图像,则有9n个方程,用矩阵形式,式(4)可表示为
式中的积分范围为各个低分辨率像素点所代表的区域。依据式(5)求取X,将求出的X代入式(3),得到L1(i,j)及相邻8个像素区域内的灰度函数
(3) 获得超分辨率图像:将式(8)代入式(6)就可以计算任意大小的高分辨率图像像素值,实际计算时,只计算与像素L1(i,j)重合的高分辨率图像像素的像素值及其周边的8个高分辨率像素值。如果低分辨率图像像素与高分辨率图像的像素大小比小于3,则求出的高分辨率像素值会存在重叠区域,如图 2所示,白色框为未重叠的高分辨率像素,格网框为重叠的高分辨率像素,对于该重叠区域,本文采用相邻像素点的高分辨率像素值取平均。

|
| 图 2 高分辨率像素值重叠区域示意图 Fig. 2 Schematic diagram of superposed high resolution pixel value |
为了研究对比平差方法的可行性并对其进行定量评价,本项目按如下思路展开模拟试验:从某个原始高分辨率图像,采样加噪获取系列低分辨率影像,再用采样获取的系列低分辨率影像重建与原始图像同一分辨率及大小的高分辨率图像,用重建的图像与原始图像比较,就可研究不同方法的效果。试验具体按获取低分辨率图像、图像配准、模糊函数及噪声估计、图像重建4个步骤进行。
4.1.1 获取低分辨率图像将一幅高分辨率图像经图像变换得到低分辨率序列,其中图像变换包括图像的平移和旋转、模糊化处理、降采样、加噪,详细过程可参考文献[17]。该方法获得的低分辨率图像序列完全能够满足超分辨率重建的试验要求。这里列出一张大小为800像素×600像素、灰度级为256的中南大学校园风景图进行试验,试验中首先利用模拟观测系统模拟出两幅具有亚像素位移的低分辨率图像,如图 3所示。

|
| 图 3 模拟低分辨率图像序列 Fig. 3 The low resolution images simulated |
图像配准就是选择其中一张LR图像作为参考帧,将其余LR图像在空间上与参考帧图像进行对准。多张LR图像经配准后为HR格网的非规则采样,常用的图像配准模型包括平移模型、仿射变换模型、双线性模型、投影模型与严格模型[11]。本文采用SIFT算法对低分辨率图像组进行亚像素级高精度配准,基于特征的图像配准一般可以分为3步:特征提取、特征描述、特征匹配[18]。
4.1.3 模糊度及噪声估计模糊函数描述了图像形成过程中受到模糊退化影响程度的大小,估计模糊函数的精度直接影响超分辨率重建图像的质量。本文试验采用模拟低分辨率图像序列,添加的模糊函数为高斯模糊函数,噪声为均值0、方差0.05的高斯噪声,在图像预处理阶段使用维纳滤波对低分辨图像序列进行去模糊处理和去噪处理。
4.1.4 图像重建用低分辨率图像序列分别用迭代反向投影法、凸集投影法、本文算法重建出一幅和原始图像大小相同的高分辨率图像,如图 4所示。通过对比可以看出,图 4(c)相对于其他算法,在主观视觉上最为模糊,而且可以清晰地看出,本文算法与其他方法相比较,重建图像的边缘效果处理得最为理想。

|
| 图 4 模拟影像重建结果 Fig. 4 Thereconstructionresultsofsimulatedimage |
对于图像重建的效果可用PSNR和SSIM图像评价指标进行客观评价。PSNR描述了以源图像为标准信号,重建图像的信噪比。PSNR越大,图像质量越好,其定义为
式中,M、N为图像大小;f′(i,j)、f(i,j)分别表示原始高分辨率图像和重建图像在(i,j)处的灰度值。SSIM是基于误差敏感的,这种评价方法将像素误差看作是质量的亏损,是一种充分考虑图像的结构信息和人类视觉特点的图像质量评价方法,并且其值越大,失真越小,图像质量越好。结果如表 1所示。通过与PSNR的对比,得出本文算法的峰值信噪比的PSNR值高于其他算法,说明本文重建图像与原高分辨率图像在灰度上相似性更高,虽然主观上看,图 4(b)比图 4(c)清晰,但是图 4(b)存在严重的波纹现象,影响了图像的纹理结构,从而使得PSNR值低于图 4(c)。通过对结构相似性指数SSIM的对比,得出本文重建算法与其他算法具有相同水平的结构相似性。
| 评价指标 | 迭代反向投影法 | 凸集投影法 | TV算法 | MRF-MAP | 本文算法 |
| PSNR/db | 74.637 1 | 75.035 4 | 75.300 | 74.831 0 | 75.783 6 |
| SSIM | 0.999 6 | 0.999 8 | 0.999 9 | 0.999 0 | 0.999 8 |
利用数码相机在不同位置、不同时刻对同一场景进行连续取景,在取景的过程中,相机与物体之间的水平距离保持不变,使得影像的空间分辨率不变,从而得到一组列相互错位的影像[19]。采用这种方法对实验室张贴的一幅上海地区遥感图像上的一处体育场进行拍摄取景,获取4幅分辨率为255像素×155像素的图像。选取其中一幅作为参考图像,利用SIFT算法对低分辨率图像序列进行配准,对图像序列进行重建。试验结果如图 5所示,图中5(a)为其中一幅低分辨率图像,通过图中体育场边界线可以看出,图 5(f)相对其他结果有着较好的视觉效果,图 5(b)、图 5(d)和图 5(e)存在明显的波纹,影响了图像的纹理结构,图 5(c)相对于其他结果较模糊,因此从主观视觉上,本文算法的结果较为理想。

|
| 图 5 真实影像重建结果 Fig. 5 The reconstruction results of real images |
超分辨率重建问题可以用平差的方法来解决。大量的试验证明,用二次多项式对超分辨率重建的积分型非线性平差模型在足够小的范围内进行参数化是可行的,试验结果显示,通过主观和客观的综合评价都表明采用平差方法解决图像超分辨重建问题能够得到较好的重建效果。
| [1] | SHEN Huanfeng, LI Pingxiang, ZHANG Liangpei, et al. Overview on Super Resolution Image Reconstruction[J]. Optical Technique, 2009, 35(2): 194-199. (沈焕锋, 李平湘, 张良培, 等. 图像超分辨率重建技术与方法综述[J]. 光学技术, 2009, 35(2): 194-199.) |
| [2] | TSAI R Y, HUANG T S. Multiframe Image Restoration and Registration[J]. Advances in Computer Vision and Image Processing, 1984(1): 101-106. |
| [3] | TEKALP A M, OZKAN M K, SEZAN M I. High Resolution Image Reconstruction from Lower Resolution Image Sequences and Spacevarying Image Restoration[C]//The IEEE International Conference on Acoustics, Speech and Signal Processing.San Francisco, CA: IEEE, 1992: 169-172. |
| [4] | DAVILA C E. An Efficient Recursive Total Least Squares Algorithms for FIR Adaptive Filtering[J]. IEEE Transactions on Signal Processing, 1994, 42(2): 268-280. |
| [5] | KALTENBACHER E, HARDIE R C. Highresolution Infrared Image Reconstruction Using Multiple, Low Resolution, Aliased Frames[C]//Proceedings of the IEEE 1996 National Aerospace Electronics Conference.Dayton, OH: IEEE, 1996: 702-709. |
| [6] | CLARK J J, PALMER M R, LAURENCE P D. A Transformation Method for the Reconstruction of Functions from Nonuniformly Spaced Samples[J]. IEEE Transactions on Acoustics, Speech and Signal Processing, 1985, 33(4): 1151-1165. |
| [7] | IRANI M, PELEG S. Improving Resolution by Image Registration[J]. Graphical Models and Image Processing, 1991, 53(3): 231-239. |
| [8] | STARK H, OSKOUI P. High-resolution Image Recovery from Image-plane Arrays, Using Convex Projections[J]. Journal of the Optical Society of America A, 1989, 6(11): 1715-1726. |
| [9] | SCHUULZ R R, STEVENSON R L. Extraction of High Resolution Frames from Video Sequences[J]. IEEE Transactions on Image Processing, 1996, 5(6): 996-1011. |
| [10] | ELAD M, FEUER A. Super Resolution Restoration of an Image Sequence: Adaptive Filtering Approach[J]. IEEE Transactions on Image Processing, 1999, 8(3): 387-395. |
| [11] | ZHANG Xinming, SHEN Lansun. The Development of Super-resolution Restoration from Image Sequences[J]. Measurement & Control Technology,2002,21(5): 33-35. (张新明, 沈兰荪. 超分辨率复原技术的发展[J]. 测控技术,2002,21(5): 33-35.) |
| [12] | FAN Chong, GONG Jianya, ZHU Jianjun. POCS Super-resolution Sequence Image Reconstruction Based on Image Registration Excluded Aliased Frequency Domain[J]. Acta Geodaetica et Cartographica Sinica,2006,35(4): 358-363. (范冲, 龚健雅, 朱建军. 一种基于去混叠影像配准方法的POCS超分辨率序列图像重建[J]. 测绘学报,2006,35(4): 358-363.) |
| [13] | SHEN Huanfeng, ZHANG Liangpei, HUANG Bo,et al. A Map Approach for Joint Motion Estimation, Segmentation, and Super Resolution[J]. IEEE Transactions on Image Processing, 2007, 16(2): 479-490. |
| [14] | RUDIN L I, OSHER S, FATEMI E. Nonlinear Total Variation Based Noise Removal Algorithms[J]. Physica D: Nonlinear Phenomena, 1992, 60(1-4): 259-268. |
| [15] | FARSIU S, Robinson M D. Fast and Robust Multi-frame Super Resolution[J]. IEEE Transactions on Image Processing, 2004, 13(10): 1327-1344. |
| [16] | ZHANG Liangpei, SHEN Huanfeng, ZHANG Hongyan, et al. Super Resolution Image Reconstruction[M]. Beijing: Science Press,2012. (张良培, 沈焕锋, 张洪艳, 等. 图像超分辨率重建[M]. 北京:科学出版社,2012.) |
| [17] | FAN Donghao, ZHU Jianjun, ZHOU Cui, et al. Designing and Implementation of the Simulation System of the Image Degradation[J]. Geotechnical Investigation & Surveying,2014,42(5): 75-79.(樊东昊, 朱建军, 周璀, 等. 图像退化仿真系统的设计与实现[J]. 工程勘察,2014,42(5): 75-79.) |
| [18] | KANG Yanni, HUANG Huan, ZHU Yuyan, et al. Super-resolution Image Registration Based on SIFT and Its Realization with Matlab[J]. Computer Knowledge and Technology,2009,5(28): 8031-8033. (康燕妮, 黄欢, 朱玉艳, 等. 基于SIFT的超分辨率图像配准及Matlab实现[J]. 电脑知识与技术,2009,5(28): 8031-8033.) |
| [19] | SHEN Huanfeng, LI Pingxiang, ZHANG Liangpei. Adaptive Regularized MAP Super-resolution Reconstruction Method[J]. Geomatics and Information Science of Wuhan University, 2006, 31(11): 949-952. (沈焕锋, 李平湘, 张良培. 一种自适应正则化MAP超分辨率重建方法[J]. 武汉大学学报:信息科学版,2006, 31(11): 949-952.) |
| [20] | SHEN Huangfeng, NGM K, LI Pingxiang,et al. Super-resolution Reconstruction Algorithm to MODIS Remote Sensing Images[J]. The Computer Journal, 2007, 52(1): 90-100. |
| [21] | PURKAIT P, CHANDA B. Morphologic Gain-controlled Regularization for Edge-preserving Super-resolution Image Reconstruction[J]. Signal, Image and Video Processing,2013,7(5): 925-938. |
| [22] | SHI Wenzhong, TIAN Yan, LIU Jian. A Fast Super-resolution Reconstruction from Image Sequence[J]. Wuhan University of Natural Sciences,2006,11(2): 399-404. |
| [23] | MA Jun, JING Weili, FAN Chong. Papoulis-gerchberg Super-resolution Reconstruction Based on Improvement Approach of Keren Registration Method[J]. Bulletin of Surveying and Mapping,2007(12): 14-17(马俊, 景维立, 范冲. 一种基于改进Keren空域配准方法的Papoulis-gerchberg超分辨率重建[J]. 测绘通报,2007(12): 14-17.) |
| [24] | WU Yan. One Improved Super-reconstruction Algorithm Based on IBP Theory[J]. Infrared,2009,30(12): 11-15. (吴艳. 一种改进的IBP超分辨率重构算法[J]. 红外,2009,30(12): 11-15.) |
| [25] | LUCCHESEL, CORTELAZZO GM. A Noise-robust Frequency Domain Technique for Estimating Planar Roto-translations[J]. IEEE Transactions on Signal Processing, 2000,48(6): 1769-1786. |