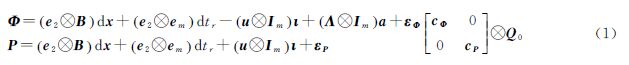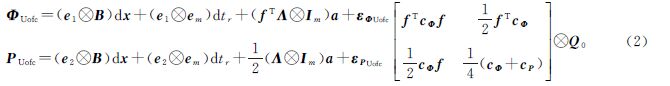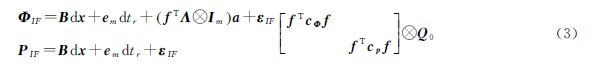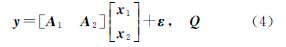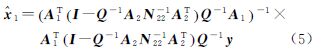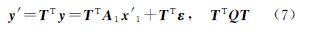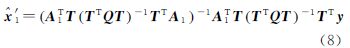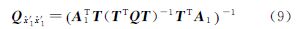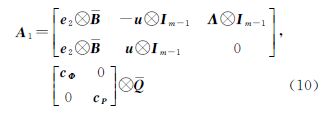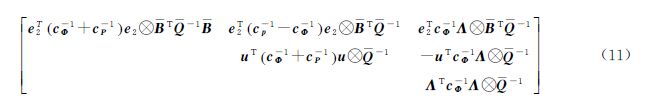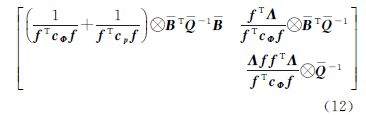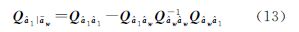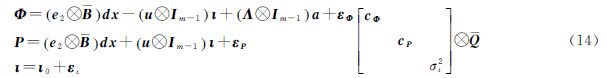1 引 言
GNSS精密单点定位(PPP)在近十年来得到了迅速发展。不同于传统的差分定位，精密单点定位只需要单台接收机，利用精密星历与精密钟差，就能实现厘米级精度的位置服务。对于海上、沙漠等不具备设置基站的地方的定位服务，具有重要的应用价值[1]。影响PPP定位精度的因素有多种，其中定位模型是重要因素之一，因此，有必要对PPP的定位模型进行深入分析。
常用的PPP模型有无电离层组合、Uofc和非组合3种模型。其中，无电离层组合模型是最常用的模型[2, 3, 4]，该模型通过双频相位和伪距之间分别组成消除电离层影响的组合，即得到两个无电离层组合观测量。由Calgary大学高扬教授提出的Uofc模型[5]同样是一种消除电离层影响的模型，与无电离层组合模型不同的是，除了采用两个频率相位观测值构成的无电离层组合外，还采用了各频率上的相位和伪距观测值组成的无电离层组合。相对于无电离层组合模型，Uofc模型得到3个无电离层组合观测量，保留了更多的信息，噪声也较伪距无电离层组合有大幅度减小。对于无电离层组合模型与Uofc模型，都通过对观测方程的组合消除电离层的影响，而实际应用中往往可以根据电离层模型及其物理特性来构造合理的电离层约束条件，从而增加观测模型强度，提高模糊度固定以及定位效果。显然在无电离层组合与Uofc模型中，由于电离层参数的消去使得无法对其施加约束条件。为了有效地利用电离层约束条件，近年来越来越多的学者建议采用基于原始观测值的非组合PPP模型[6, 7, 8, 9]，文献[7]比较了多种电离层模型对单频PPP解算的影响；文献[8]提出了利用电离层模型的先验信息及其时空变化特性合理地估计电离层延迟量的方法，提高单频PPP的解算效果；文献[9]参数化L1频率上的站星方向的电离层延迟，有效地避免了无电离层组合引起观测噪声放大的不利影响。目前，有研究人员基于L1和L2原始观测值，将斜向电离层延迟作为参数进行估计，顾及电离层时空约束并将实时电离层模型生成的电离层延迟量作为观测信息改善解算性能，能够大大提高模糊度首次收敛时间[10]。
在等价性研究方面，文献[11]利用空间和投影算子的概念证明了等价观测中的部分等价性定理。也有学者对GPS观测方程的不同差分方法和组合方法进行等价性研究[12, 13]，并对其算法进行改进。虽然近年来大量文献分析了在这3种模型下PPP的模糊度固定及定位效果，但未有文献对这3种模型从理论的角度做深入细致的比较分析。本文从模糊度固定的角度入手，采用模糊度精度因子详细论述了这3种模型的相互关系，证明了非组合模型与Uofc模型的等价性；并分析了它们较无电离层组合模型的优越性；此外，基于非组合模型，通过附加电离层约束条件引出了附电离层约束的非组合模型。最后，通过实例分析验证了本文理论推证的正确性。
2 3种PPP模型 2.1 非组合模型采用GPS双频接收机跟踪m颗卫星的单历元非组合观测方程如式(1)所示
式中，Ф和P为相位和伪距观测向量；dx包含坐标改正量以及对流层天顶湿延迟参数，B为其系数矩阵；dtr为接收机钟差；ι为电离层延迟参数，aT=[a1Ta2T]为模糊度参数，a1和a2分别为L1和L2频率的模糊度参数，对应波长矩阵Λ=diag(λ1，λ2)；εΦ和εP分别为相位和伪距观测噪声，对应方差因子矩阵为cΦ=diag(σΦ12，σΦ22)和cP=diag(σP12，σP22)，对应协因数矩阵为Q0=diag[(sinθ1)－2，(sinθ2)－2，…，(sinθm)－2][14]，其中θi为卫星高度角；e2=[11]T，u=[u1u2]T，μ1=1，u2=f12/f22，f1、f2表示双频的频率值；Im为m维单位阵；⊗表示克罗内克积。此外，此模型还需经过海潮、固体潮[15]等误差改正，卫星钟差从IGS提供的精密钟差文件中获得。 2.2 Uofc模型
Uofc模型由加拿大Calgary大学的高扬教授提出[5]，该模型也是一种无电离层组合模型，但它与传统的无电离层组合模型不同，该模型除了利用无电离层相位组合外，还分别采用了L1和L2频率上的码和相位平均形式的组合，即给非组合模型(1)两端左乘一个行满秩变换矩阵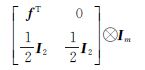
式中，fT=[f12－f22]/(f12－f22)则Uofc模型表示为
无电离层组合模型是最常用的PPP模型，它采用两个频率间的相位和伪距观测值分别构成无电离层组合，对应形式为
3 非组合与Uofc模型的等价性证明
为了证明非组合模型与Uofc模型的等价性，首先引出等价性原理。设有观测模型
式中，未知向量x1和x2分别包含n-t和t个参数。采用最小二乘准则推导得到x1的估值为
若存在转换矩阵TT，满足TTA2=0，且rank(T)=n-t，则
由此得
根据等价性原理，证明模型(4)和模型(7)求解参数x1的等价即要证明参数解等价及其对应的方差-协方差矩阵等价[16, 17]。根据TTA2=0且rank(T)=n-t，因此容易得出其投影变换等式为T(TTQT)－1TT=(I－Q－1A2N22－1A2T)Q－1[16]，由此可证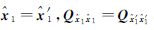
，故采用式(5)、式(6)和式(8)、式(9)求解得到的参数x1及其方差-协方差矩阵等价。
将等价性原理应用于非组合模型，将非组合模型改写为式(4)的形式，其中，A1=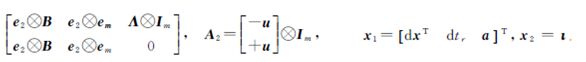
。对应转换矩阵
，满足TTA2=0，rank(T)=n-t，因此，可采用转换矩阵TT将非组合模型等价地变为Uofc模型。
由于非组合模型与Uofc模型等价，笔者从模糊度固定效率的角度比较非组合模型与无电离层组合模型。在非组合PPP模型中，其非差模糊度包含了接收机端和卫星端的偏差导致其不具有整数性。本文旨在比较3种PPP模型区别，重点通过分析模糊度的固定效果来分析3种模型的强度，因此，直接采用IGS发布的卫星差分码偏差产品和对应的UPD产品，并采用星间单差消除接收机端的偏差，从而实现PPP模糊度的整数固定。单历元非组合星间单差模型的设计矩阵及其对应的协方差矩阵为
式中，Dm－1=[－em－1Im－1]为单差算子；B=Dm－1B；Q=Dm－1Q0Dm－1T，为单差观测值协因数阵。值得说明的是，此时求解的电离层参数为星间单差电离层延迟；模糊度为经卫星端UPD产品改正后的星间单差模糊度，具有整数特性。推导得到对称的法方程系数矩阵如式(11)
根据法方程可导出非组合单差模型求解的模糊度方差-协方差矩阵，记为Qââ。
对于无电离层组合单差模型，也可类似导出相关法方程系数阵
由于行列式|ΛffTΛ|=0，说明无电离层组合模型无法同时求解两个频率的单差模糊度；而非组合单差模型中由于消除了接收机部分的误差，可以求解单差模糊度，因此，非组合模型要明显优于无电离层组合模型。
以上推导说明无电离层组合模型无法同时求解两个频率的单差模糊度，即使求解无电离层组合模糊度，由于无电离层组合模糊度的波长过短(约6mm)也无法恢复其整数特性。为了公平地定量比较两种模型求解模糊度的效果，笔者按照传统的做法，假设宽巷模糊度已经固定，比较两种模型固定窄巷模糊度的效果。令任一模型得到的模糊度方差-协方差矩阵有分块形式：Qââ=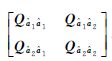
，类似于附约束条件平差，得到宽巷模糊度固定后的窄巷模糊度方差-协方差矩阵为[18]
；
。
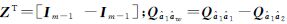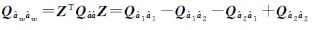5 附电离层约束的非组合模型通常PPP采用无电离层组合模型或Uofc模型消除电离层影响，研究表明电离层延迟是制约模糊度快速固定的主要因素，为了提高模糊度的固定效率，往往可以根据电离层的外界信息或者物理机制引入适当的电离层约束，从而提高模糊度的固定效率[19]。然而，在无电离层组合模糊度和Uofc模型中，电离层延迟项通过组合消除，从而无法施加外界电离层约束。而非组合模型将电离层延迟作为参数估计，尽管它与Uofc模型等价，但该模型可附加外界电离层约束从而得到“电离层加权模型”，其单历元星间单差模型如式(14)所示
式中，ι0为电离层延迟先验信息；σι为电离层延迟先验值信息的精度。由此得附约束条件的非组合单差模型的法方程系数阵与式(11)类似，只需把电离层参数所对应的系数矩阵uT(cΦ－1+cP－1)u⊗Q－1修改为[uT(cΦ－1+cP－1)u+σι－2]⊗Q－1。 6 试验分析
上文理论部分已经论证了3种PPP模型的优劣，证明了非组合模型与Uofc模型等价，且这两种模型都优于无电离层组合模型；此外，提出了附电离层约束的非组合模型，在给定适当的电离层先验信息时，该模型具有更好的模型强度。为验证理论的正确性，并定量分析各模型在固定模糊度方面的差别，使用24h采样间隔为30s的GPS双频观测数据，卫星截止高度角为10°(在固定模糊度时，卫星截止高度角取15°，即只有高度角大于15°的卫星才固定其模糊度)，取伪距和相位精度分别为10cm和1mm。
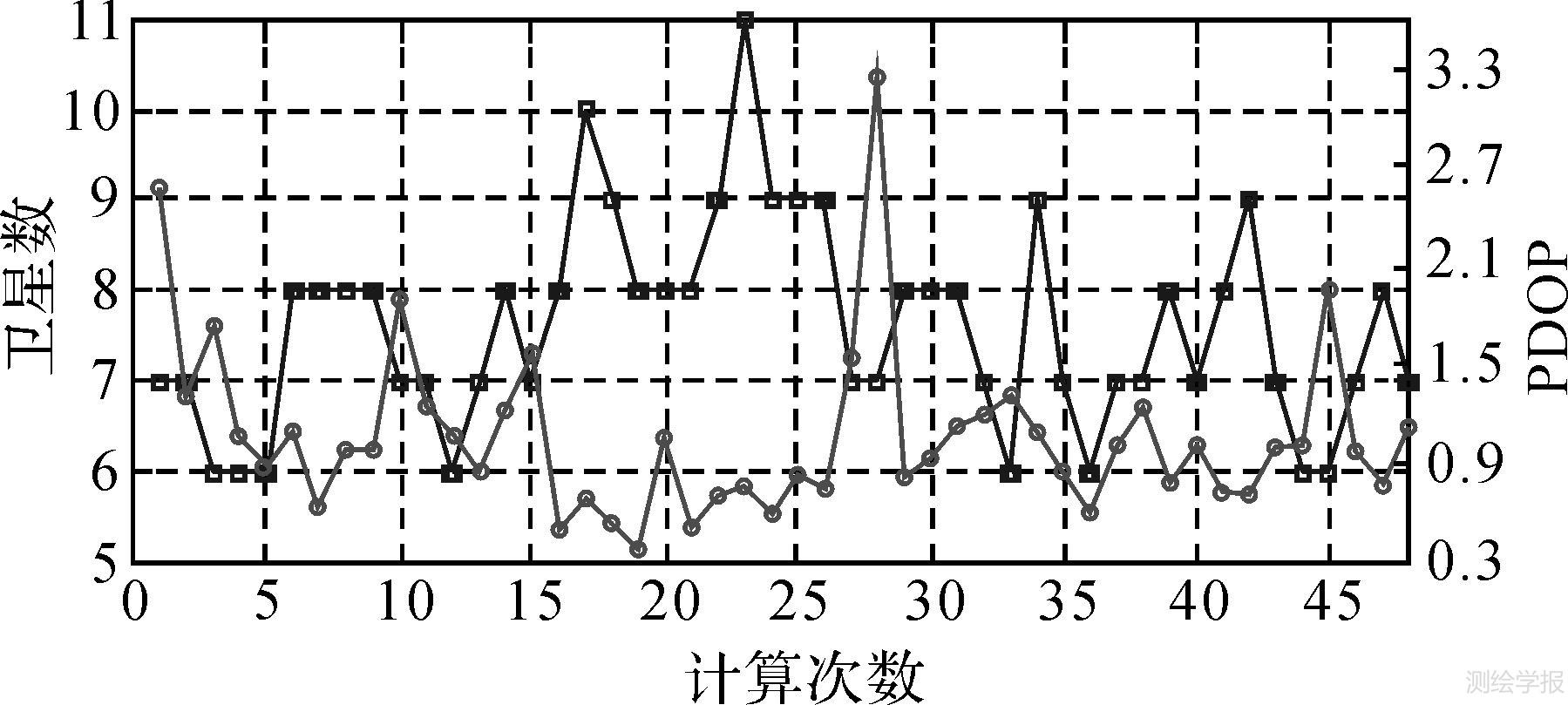
计算过程中，每隔60历元计算一次，24h总共计算48次，图 1给出了这48次计算对应的可用卫星数及相应的PDOP(position dilution of precision)值。每次计算采用不同的历元数(如10、20、40和60个历元)。由于试验旨在分析几种PPP模型固定模糊度的效率，在固定宽巷模糊度的基础上，分析几种PPP定位模型窄巷模糊度的固定效率。
|
| 图 1 24 h 48次试验对应的可用卫星数及相应PDOP值 Fig. 1 The number of availabl esatellites and PDOP for 48 experiments overtotal 24 h |
模糊度成功概率是模糊度固定效果的重要指标，反映了浮点模糊度质量及其对应数学模型的强度。由于模糊度成功概率的计算极其复杂，通常采用不同的成功概率上下界逼近[20]，其中模糊度精度因子(ambiguity dilution of precision，ADOP)因其计算简单且不随模糊度整数变换而改变的优点被广泛使用[21]。ADOP的定义为
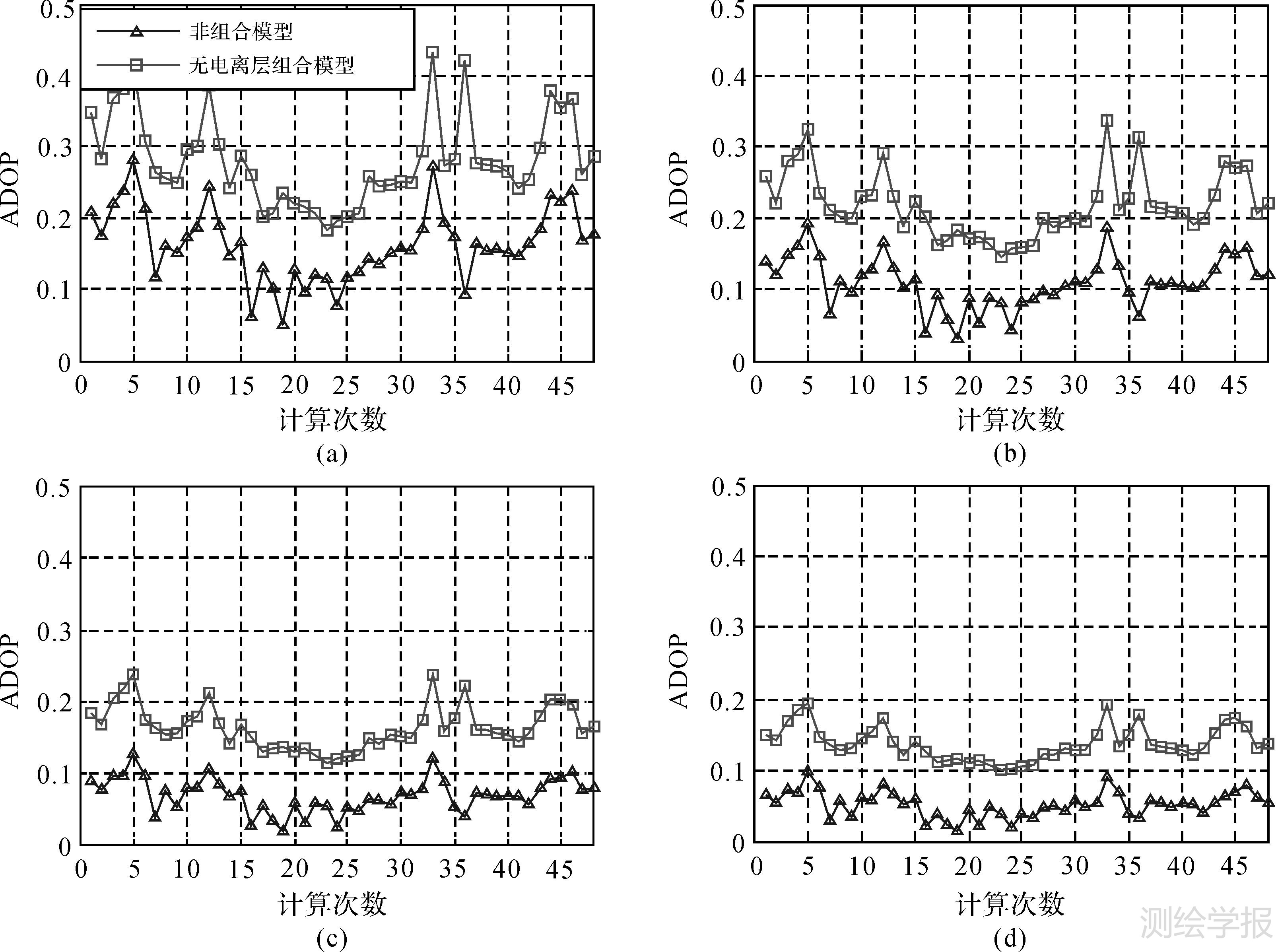
式中，|·|为求行列式算子，Qââ为模糊度浮点解的方差-协方差矩阵；n为模糊度向量维数。ADOP反映了整个浮点模糊度向量的几何平均精度，ADOP越小，模糊度成功固定概率越大，反之亦然。本文以ADOP为指标比较几种PPP模型的模糊度固定效果。
首先比较无电离层组合模型和非组合模型固定模糊度的效果，图 2给出了这两种模型采用不同历元数计算浮点模糊度，从而计算得到ADOP，图 2(a)-(d)分别为每次计算采用10、20、40和60个历元。分析图 2得出以下结论：首先，随着历元数由10增加至60，非组合模型和无电离层组合模型的ADOP值都明显地减小，这是由于随着观测数量的增多，两种模型的强度增强，求解的模糊度浮点解精度提高；其次，在采用相同历元数据时，无电离层组合模型的ADOP比非组合模型的ADOP大，即无电离层组合模型较非组合模型求解模糊度的效果差，这也印证了第4节的理论分析。注意到图 2中的ADOP变化并不平稳，某些ADOP值明显大于其他ADOP值，结合图 1分析得出引起ADOP变化特征的主要因素是跟踪卫星数目和PDOP的变化。随着卫星数目增多，无电离层组合模型和非组合模型的ADOP值都变小，说明卫星数目的增加导致模糊度固定效率的增加。通常情况下，卫星数目的增多可能会导致模糊度的数量增加，一定程度上导致固定所有模糊度的成功概率减小[22 ,23]。但另一方面，卫星数目的增多能改善定位模型的几何构型，从而提高模糊度的固定效率；由于本文计算时采用geometry-based模型，从图 1中可以看出，随着卫星数目的增加，PDOP值相应减小，说明卫星几何构型的改善能提高模糊度的固定效率，使得ADOP值随着卫星数目的增加而减小。
|
| 图 2 无电离层组合模型与非组合模型采用不同历元数计算得到的ADOP比较 Fig. 2 Comparison in ADOP between ionosphere-free model and uncombined model using different epochs |
最后，从图 2中可以看到，非组合模型与无电离层组合的ADOP曲线随着历元数增加有接近的趋势，因此，为了更加细致地比较无电离层组合模型和非组合模型随着历元数增加引起的模糊度固定效果，每次计算分别取10、15、20、…、60个历元，即每给定历元数，可计算得到48个ADOP值，对给定历元数得到的48个ADOP值取平均后将无电离层组合模型的平均ADOP与非组合模型的平均ADOP做差，结果如图 3所示。从图 3中可以看到，当观测历元数较少时，非组合模型的模糊度固定效率相对于无电离层组合模型有较大差距，随着观测历元数的增加，无电离层组合模型与非组合模型的模糊度固定效果的差距减小，这是由于随着观测量的累积，无电离层组合模型的浮点模糊度质量已经得到了很大的提高，使得非组合模型浮点模糊度较它差别较小。
|
| 图 3 无电离层组合与非组合模型在不同历元数下的平均ADOP之差 Fig. 3 Differences in average ADOP between uncombined model and ionosphere-fee model under different epochs |
为了比较非组合模型和附电离层约束的非组合模型的模糊度固定效果，以每次计算取60个历元为例，对附电离层约束的非组合模型，通过给定不同的电离层先验信息精度(σι=0.5、5、10cm和∞)来体现不同的电离层约束，比较不同电离层约束情况下的非组合模型的浮点模糊度ADOP值，结果如图 4所示。随着电离层约束的增强，附电离层约束的非组合模型的ADOP值逐渐减小，模糊度的固定效率逐渐提高。当对电离层的约束很弱时，附约束条件的非组合模型等价于非组合模型。为了更清晰地比较不同电离层约束情况下非组合模型的模糊度的固定效果，对不同电离层约束下的ADOP值取平均值，结果如图 5所示。从图 5中可以清楚看到，随着电离层的约束减弱，模糊度的固定效率逐渐降低，随着电离层的约束减弱到一定程度时，模糊度的固定效率变化缓慢，直至与非组合模型相同。所以，对于附电离层约束的非组合模型，考虑电离层信息对定位结果的影响，在具有合理的电离层先验信息的情况下，引入电离层约束，相比Uofc模型以及无电离层组合模型，能使精密单点定位的数学模型具有更好的模型强度。
|
| 图 4 不同电离层约束下的ADOP Fig. 4 ADOP under different ionospheric constraint |
|
| 图 5 同电离层约束下的平均ADOP Fig. 5 Mean ADOP under different ionospheric constraint |
精密单点定位技术中，数学模型一般为无电离层组合模型、Uofc模型以及非组合模型。针对未有文献对这3种模型从理论的角度做深入细致的比较分析，本文通过理论推导，详细论述了这3种模型的相互关系，并从模糊度固定效率的角度分析验证，得出以下结论。
(1) Uofc模型是在非组合模型的基础上在等式两边分别左乘一个行满秩矩阵而消除电离层信息，通过理论推导证明非组合模型等价于Uofc模型。
(2) 模糊度固定方面，若已知宽巷模糊度，非组合模型和Uofc模型的模糊度固定效率要高于无电离层组合模型，因此非组合模型和Uofc模型要优于无电离层组合模型。
(3) 非组合模型相比于Uofc模型和无电离层组合模型在处理电离层信息方面，能更方便地引入电离层约束，在有电离层先验信息的情况下，采用附电离层约束的非组合模型能改善模型强度，提高模糊度固定效率。
| [1] | COLOMBO O L, SUTTER A W, EVANS A G. Evaluation of Precise, Kinematic GPS Point Positioning[C]// Proceedings of ION GNSS. Long Beach, California: [s.n.], 2004: 21-24. |
| [2] | KOUBA J, HÉROUS P. Precise Point Positioning Using IGS Orbit and Clock Products[J]. GPS Solutions, 2001, 5(2): 12-28. |
| [3] | GE M, GENDT G, ROTHACHER M, et al. Resolution of GPS Carrier-phase Ambiguities in Precise Point Positioning(PPP) with Daily Observations[J]. Journal of Geodesy, 2008, 82(7): 389-399. |
| [4] | HAO Ming, WANG Qingliang, CUI Duxin. Study on Fast Convergence Method in Precise Point Positioning[J]. Journal of Geodesy and Geodynamics, 2009, 29(2): 88-91. (郝明, 王庆良, 崔笃信. GPS精密单点定位快速收敛方法研究[J]. 大地测量与地球动力学, 2009, 29(2): 88-91.) |
| [5] | GAO Y, SHEN X. Improving Ambiguity Convergence in Carrier Phase-based Precise Point Positioning[C]//Proceedings of ION GPS. Salt Lake City: [s.n.], 2001: 1532-1539. |
| [6] | ABDEL-SALAM M, GAO Y. Precise GPS Atmosphere Sensing Based on Un-differenced Observations[C] // Proceedings of ION GNSS. Long Beach: [s.n.], 2004: 933-940. |
| [7] | CHEN K, GAO Y. Real-time Precise Point Positioning Using Single Frequency Data[C]//Proceedings of ION GNSS. Long Beach: [s.n.], 2004: 1514-1523. |
| [8] | SHI C, GU S F, LOU Y D, et al. An Improved Approach to Model Ionospheric Delays for Single-frequency Precise Point Positioning[J]. Advances in Space Research, 2012, 49(12): 1698-1708. |
| [9] | ZHANG Baocheng, OU Jikun, YUAN Yunbin, et al. Precise Point Positioning Algorithm Based on Original Dual-frequency GPS Code and Carrier-phase Observations and Its Application[J]. Acta Geodaetica et Cartographica Sinica,2010, 39(5): 478-482. (张宝成, 欧吉坤, 袁运斌, 等. 基于GPS双频原始观测值的精密单点定位算法及应用[J]. 测绘学报, 2010, 39(5): 478-482.) |
| [10] | LI X X, GE M R, ZHANG H P, et al. A Method for Improving Uncalibrated Phase Delay Estimation and Ambiguity-fixing in Real-time Precise Point Positioning[J]. Journal of Geodesy, 2013, 87(5): 405-416. |
| [11] | SUN Xiaogong. Equal Observation and GPS Differencial Positioning[J]. Acta Geodaetica et Cartographica Sinica, 1992, 21(1): 50-56. (孙效功. 等价观测与GPS差分法定位[J]. 测绘学报, 1992, 21(1): 50-56.) |
| [12] | SHEN Y Z, XU G C. Simplified Equivalent Represtation of GPS Observation Equations[J]. GPS Solutions, 2007, 12(2): 99-108. |
| [13] | SHEN Y Z, LI B F, XU G C. Simplified Equivalent Multiple Baseline Solutions with Elevation-dependent Weights[J]. GPS Solutions, 2008, 13(3): 165-171. |
| [14] | LI B F, TEUNISSEN PJG. GNSS Antenna Array-aided CORS Ambiguity Resolution[J]. Journal of Geodesy, 2014, 88(4): 363-376. |
| [15] | WEI Ziqing, GE Maorong. Mathmatical Model of GPS Relative Positioning[M]. Beijing: Publishing House of Surveying and Mapping, 1998: 56-82. (魏子卿, 葛茂荣. GPS相对定位的数学模型[M]. 北京: 测绘出版社, 1998: 56-82.) |
| [16] | SCHAFFRIN B, GRAFAREND E. Generating Classes of Equivalent Linear Models by Nuisance Parameter Elimination[J]. Manuscripta Geodaetica, 1986, 11: 262-271. |
| [17] | XU G C. GPS Data Processing with Equivalent Observation Equations[J]. GPS Solutions, 2002, 6(1-2): 28-33. |
| [18] | LI B F, VERHAGEN S, TEUNISSEN PJG. Robustness of GNSS Integer Ambiguity Resolution in the Presence of Atmospheric Biases[J]. GPS Solutions, 2014, 18(2): 283-296. |
| [19] | LI B F, SHEN Y Z,FENG Y M, et al. GNSS Ambiguity Resolution with Controllable Failure Rate for Long Baseline Network RTK[J]. Journal of Geodesy, 2014, 88(2): 99-112. |
| [20] | LI B F, VERHAGEN S, TEUNISSEN PJG. GNSS Integer Ambiguity Estimation and Evaluation: LAMBDA and Ps-LAMBDA [C] //China Satellite Navigation Conference (CSNC) 2013 Proceedings.Wuhan: Springer, 2013: 291-301. |
| [21] | ODIJK D, Teunissen P J G. ADOP in Closed Form for a Hierarchy of Multi-frequency Single-baseline GNSS Models [J]. Journal of Geodesy, 2008, 82(8): 473-492. |
| [22] | VERHAGEN S, TEUNISSEN PJG,VAN DER MAREL H, et al. GNSS Ambiguity Resolution: Which Subset to Fix?[C]// Proceedings of IGNSS Symposium. Sydney, Australia: [s.n.], 2011. |
| [23] | TEUNISSEN PJG, JOOSTEN P,TIBERIUS C. Geometry-free Ambiguity Success Rates in Case of Partial Fixing[C]//Proceedings of ION-NTM. San Diego: [s.n.], 1999: 25-27. |