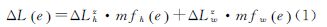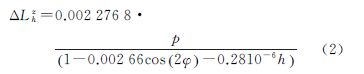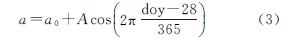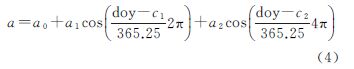2. 武汉大学地球空间环境与大地测量教育部重点实验室,湖北 武汉 430079
2. Key Laboratory of Geospace Environment and Geodesy, Ministry of Education, Wuhan University, Wuhan 430079, China
在GNSS(Global Navigation Satellite System)、VLBI(very long baseline interferometry)和DORIS(doppler orbitography by radiopositioning integrated on satellite)测量中,对流层斜路径延迟[1]是一个很重要的误差源,文献[2]提出高精度的适用于大区域的基于球冠谐分析的精密对流层延迟模型;文献[3]对GPS中性大气延迟量进行了研究,提出气压、气温、湿气压参数对延迟量的计算具有重要影响。在地基GPS水汽反演中,对流层延迟也是一个非常重要的参数,文献[4, 5]分别就香港和武汉地区的水汽反演进行相关研究;文献[6]对地基遥感大气水汽含量的误差进行了分析,提出由于地面气温和水汽压所引起的误差是非常重要的因素。对流层斜路径延迟包括干延迟和湿延迟[7]两个部分,即
式中,mfh(e)、mfw(e)分别为高度角为e处的干延迟和湿延迟的映射函数[8, 9, 10, 11];ΔLhz、ΔLwz分别为天顶方向干延迟和湿延迟。天顶方向湿延迟ΔLwz通常作为参数进行估计[12, 13, 14]。而天顶干延迟ΔLhz在静力学平衡条件下一般可用模型精确估计[15],常用的模型有萨氏(Saastamoinen)模型、霍氏(Hopfield)模型、布兰克(Black)模型,其中Saastamoinen模型最常用[16],表达式为
式中,p为地表总气压;φ为纬度;h为测站高程。文献[17]基于现有的萨氏模型、霍氏模型、布兰克模型3种干延迟模型,提出了修正模型。以上所有干延迟模型的表达式中均包含气压参数,试验证明,1hPa的气压精度可使干延迟的误差达2.3mm级。通过气象设备实测得到的气压具有很高的精度,但不是全球所有地方都有仪器测量实测气压,此时可以通过数值天气预报模型[18]NWMs产品获得气压,考虑到实测气压数据和NWMs产品都无法获取的情况,文献[19]建立了全球气温和气压经验模型GPT(global pressure and temperature),通过测站坐标和年积日即可提供全球范围的气温和气压。
尽管GPT模型使用方便,且全球适用,但是水平和时间分辨率较低,仅考虑年周期,建模理论不够完善,存在一定误差。文献[20]针对其部分不足之处作出改进和优化,构建了改进模型GPT2,但是目前尚未有文章专门对GPT2的精度进行检验分析,更未对其精度全球分布情况以及季节性差异作相关研究。
2 GPT与GPT2ECMWF (European Centre for Medium-Range Weather Forecasts)是一个旨在为用户提供全球数值天气预报的组织,可提供高精度ERA-Interim产品,在全球范围内包括南北极地区都具有很高的精度,常用于模型建立及检验。GPT采用ECMWF提供的40年的空间分辨率为15°×15°的全球气温和气压的月平均格网数据ERA40,基于9阶9次球谐函数建立。模型表达式如式(3)所示
式中,a0为平均值;A为年周期振幅;doy为年积日。GPT使用方便,只需输入测站坐标和年积日就能提供地球任一点的气温和气压,且全球适用,但是存在一些缺陷,例如,由于建模采用9阶9次球谐函数,导致模型水平分辨率为20°,相对比较粗糙;只考虑了平均周期和年周期,且初始相位固定为1月28日,导致时间精度较低;采用固定的气温随高程减小变化率,气压的减小率也是基于标准大气建立的,与实际情况相比具有一定的误差。
针对GPT的缺点,GPT2模型采用ECMWF提供的2001—2010年共10年的更高质量的ERA-37数据进行建模,同时在经验模型表达式中加入了半年周期项并估计了各个周期项的初相,并同时分别估计每个格网点上平均周期、年周期和半年周期的气温递减率,压强递减率也是基于每个格网点的实际气温得到的,整体精度有所提高。最后利用5°×5°的格网代替9阶9次球谐函数进行成果表达,提高了模型的空间分辨率。该模型可提供气温、气压、气温直减率、水汽压等对流层重要参数,模型表达式如式(4)所示
式中,a1为年周期振幅;c1为年周期初相;a2为半年周期项振幅;c2为半年周期项初相。 3 精度检验NOAA (National Oceanic and Atmospheric Administration)可通过全球不均匀分布的测站提供实测高精度气象数据,各个测站的时间分辨率不一致,但均不低于6h。本文利用ECWMF提供的2012年的时间分辨率为6h(UTC 0:00、6:00、12:00、18:00)、水平分辨率为2.5°×2.5°的ERA-Interim产品(包括地表气温、气压及水汽压),以及由NOAA提供的全球566个测站2012年的Hourly/Sub-Hourly气象数据,分别对GPT2模型提供的气温、气压和水汽压进行精度检验,分析GPT2精度的全球分布以及季节性特征。由于GPT2模型提供的模型参数水平分辨率为5°×5°,在检验过程中,采用内插的方法获得与检验数据同等时空分辨率的数据。
本文采用均方根误差(RMS)和偏差(Bias)作为精度评定标准来分析GPT2模型的精度和稳定性:RMS表示精度,用于衡量模型的可靠性和稳定性;Bias表示准确度,即模型与真值的偏离程度。
3.1 气 温首先分析利用ECMWF数据检验气温的结果,对全球10153个格网点上全年的检验结果进行统计。从表 1可以看出,Bias均值为-0.59°C,RMS均值也在5°C以内,说明GPT2气温模型整体精确度很高。从图 1(a)中可以看出,全球大部分格网点的Bias绝对值在均值附近,说明GPT2模型没有明显的系统差,在南极地区普遍出现较大的负偏差,最大正偏差和负偏差均分布在南极。从图 1(b)中可以发现,RMS分布具有显著的海陆差异,海洋地区RMS值基本为2°C左右,低于陆地区域,主要是由于陆地尤其是沙漠地区的昼夜温差相对海洋区域较大,气温的日波动比较明显,而GPT2模型并未考虑日周期特性;RMS最大值在南极地区。利用图 2NOAA提供的全球566个测站的全年气象数据进行检验,结果与ECMWF结果基本相同。
| 检验 数据 | Bias | RMS | |||||
| 平均值 | 最大值 | 最小值 | 平均值 | 最大值 | 最小值 | ||
| GPT2 (ECMWF) | -0.59 | 11.86 | -14.99 | 3.82 | 17.98 | 0.45 | |
| GPT2 (NOAA) | -0.70 | 8.17 | -7.09 | 5.09 | 12.38 | 0.77 | |

|
| 图 1 气温的Bias及RMS全球分布(ECMWF) Fig. 1 GlobaldistributionoftemperatureBiasandRMS(ECMWF |
|
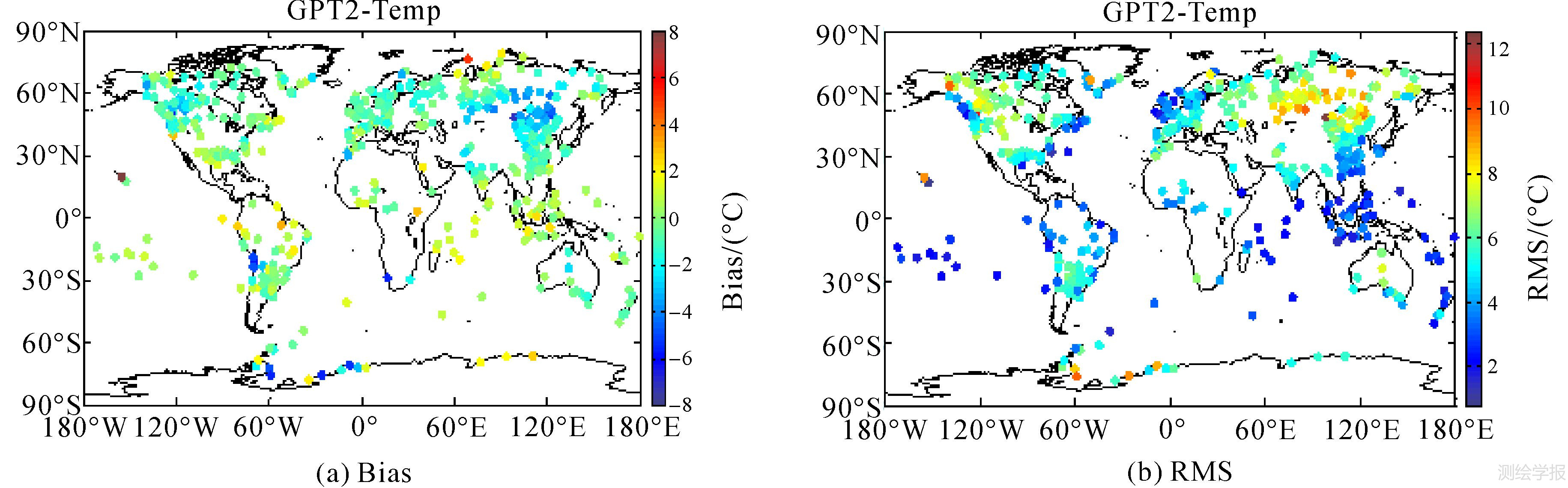
| 图 2 气温的Bias及RMS全球分布(NOAA) Fig. 2 GlobaldistributionoftemperatureBiasandRMS(NOAA) |
下面利用NOAA测站气象数据对GPT2气温模型的精度进行季节性分析。采用1月、4月、7月、10月这4个月作为季节代表。从表 2可以看出,不同月份的Bias及RMS差异较大,说明其具有明显的季节性。其中,7月份的Bias均值和RMS均值最小,分别为-0.20°C和4.44°C,4月份和10月份次之,1月份最大。从图 3(a)中可以发现,1月份位于北半球高纬度地区的奥廖克明斯克城市Bias出现负的最大值,正偏差最大值出现在北极附近的测站,7月份北半球高纬度地区的准确度明显提高,南极地区部分测站则出现了最大的负偏差,RMS和Bias结果基本一致,总体而言,北半球高纬度地区7月份气温最精确,1月最差,南极地区相反。
| 月份 | Bias | RMS | |||||
| 平均值 | 最大值 | 最小值 | 平均值 | 最大值 | 最小值 | ||
| 1月 | -1.32 | 9.75 | -21.99 | 5.50 | 22.67 | 0.76 | |
| 4月 | -0.22 | 9.54 | -14.49 | 4.80 | 16.18 | 0.92 | |
| 7月 | -0.20 | 9.82 | -12.11 | 4.44 | 14.01 | 0.71 | |
| 10月 | -0.73 | 9.92 | -7.27 | 4.45 | 10.79 | 0.63 | |
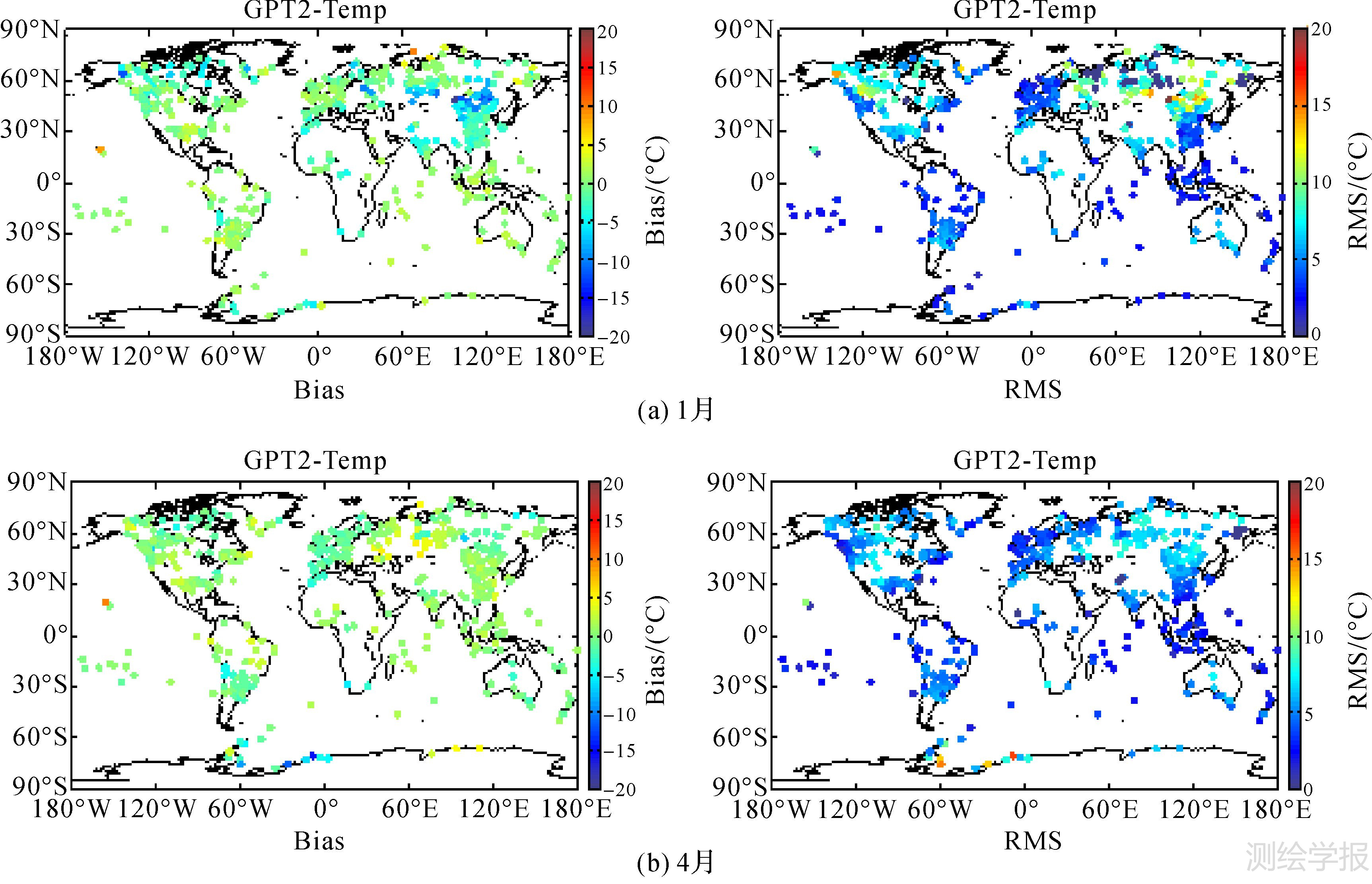
|
| 图 3 气温季节性精度检验全球分布 Fig. 3 Globaldistributionofseasonalaccuracytestoftemperature |
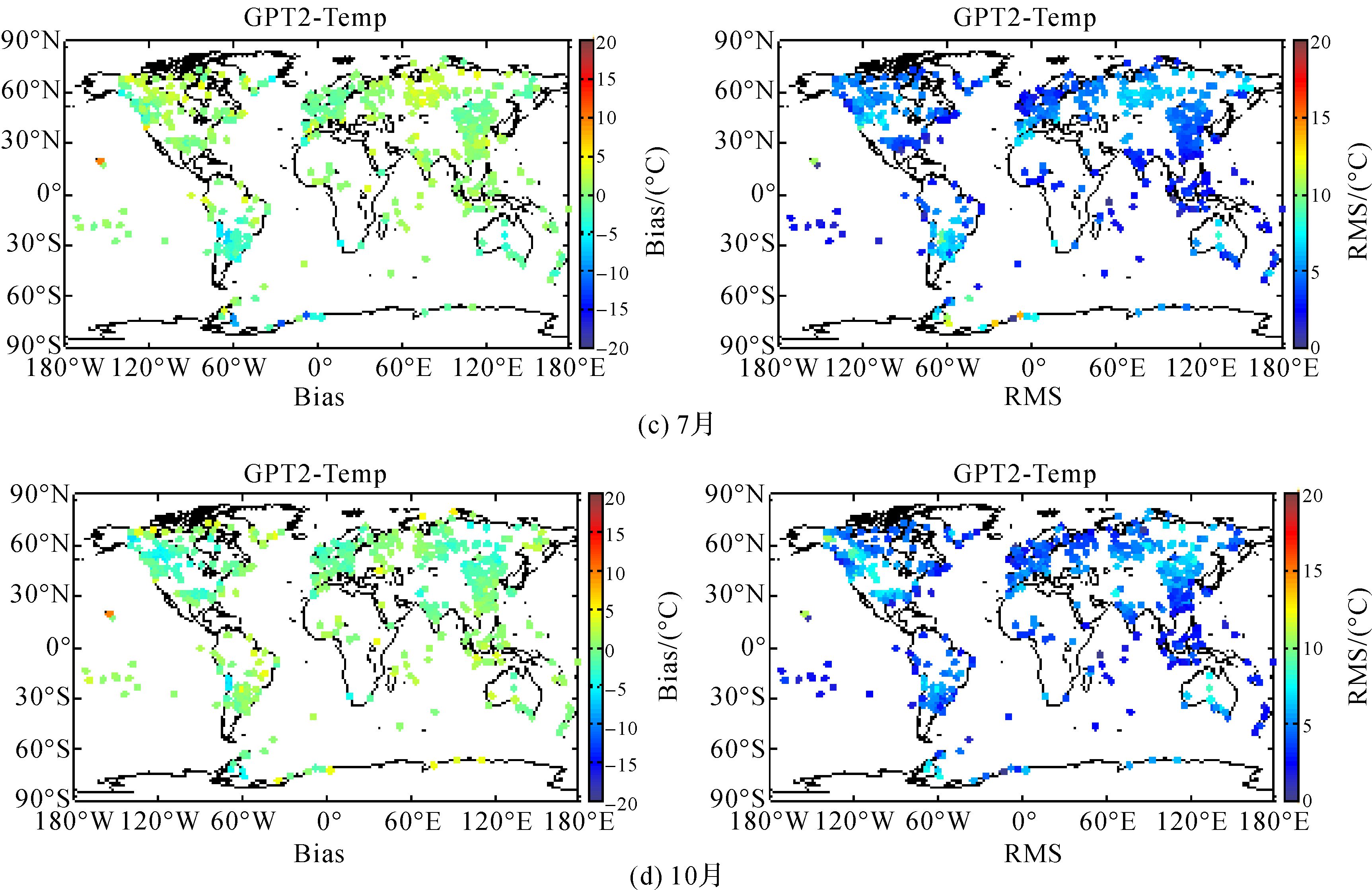
|
| 图 3 气温季节性精度检验全球分布 Fig. 3 Globaldistributionofseasonalaccuracytestoftemperature |
首先分析利用ECMWF数据检验气压的结果。从表 3中可以看出,Bias平均值为-0.26mb,RMS平均值为7.09mb,整体很精确。图 4(a)显示全球大部分格网点的Bias绝对值在2 mb以内,在青藏高原、喜马拉雅山脉、安第斯山脉以及南极洲部分沿海地区,负偏差较大,而在北欧地区出现正的最大偏差。从图 4(b)中可以看出,低纬度地区RMS小于高纬度地区,特别是在南纬60°以及北纬60°附近,主要是由于高纬度地区的气压变化较快而且复杂,因此气压的短时变化相比年际特征来说更为明显,而GPT2气压模型暂时还不能敏感到低于半年周期的短时变化特性。用NOAA提供气象数据对气压进行检验,结果与ECMWF所反映的结果基本相同。
| mb | |||||||
| 检验 数据 | Bias | RMS | |||||
| 平均值 | 最大值 | 最小值 | 平均值 | 最大值 | 最小值 | ||
| ECMWF | -0.26 | 4.56 | -14.99 | 7.09 | 16.32 | 0.97 | |
| NOAA | -0.31 | 4.93 | -8.96 | 6.91 | 14.60 | 1.51 | |
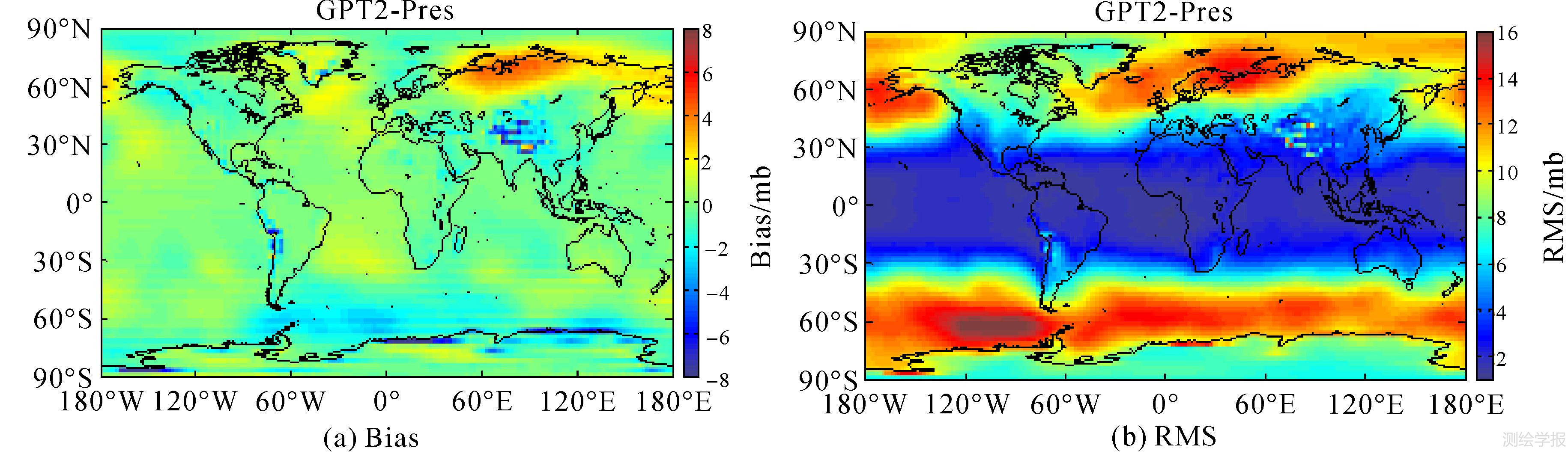
|
| 图 4 气压Bias及RMS全球分布(ECMWF) Fig. 4 GlobaldistributionofpressureBiasandRMS(ECMWF) |
GPT2气压模型精度的季节性统计结果见表 4。不同季节的GPT2气压精度差异较大。1月份Bias均值为0.66mb,而其他月份均为负值。7月的RMS最小。
| mb | |||||||
| 月份 | Bias | RMS | |||||
| 平均值 | 最大值 | 最小值 | 平均值 | 最大值 | 最小值 | ||
| 1月 | 0.66 | 30.87 | -18.94 | 8.03 | 31.14 | 1.24 | |
| 4月 | -3.36 | 8.44 | -30.57 | 7.93 | 32.56 | 1.35 | |
| 7月 | -2.79 | 7.19 | -40.59 | 6.42 | 40.93 | 1.31 | |
| 10月 | -1.80 | 13.49 | -33.70 | 7.78 | 34.31 | 1.37 | |
表 5为水汽压的年检验Bias及RMS统计结果,Bias平均值不足1mb,RMS平均值为2mb左右,说明GPT2水汽压模型整体很精确。图 5显示全球范围内Bias和RMS基本在均值附近,说明GPT2水汽压模型整体的精确度和稳定性相当高。Bias和RMS最大值均出现在红海及波斯湾地区。同时在低纬度地区,海洋地区精准度略高于陆地地区,沿海地区略差。
| mb | |||||||
| 检验 数据 | Bias | RMS | |||||
| 平均值 | 最大值 | 最小值 | 平均值 | 最大值 | 最小值 | ||
| ECMWF | 0.78 | 14.61 | -6.26 | 2.06 | 16.21 | 0.06 | |
| NOAA | 0.50 | 5.96 | -12.24 | 2.77 | 12.58 | 0.17 | |

|
| 图 5 水汽压的Bias及RMS全球分布(ECMWF) Fig. 5 GlobaldistributionofwatervaporpressureBiasandRMS(ECMWF) |
利用NOAA气象数据检验的结果与ECMWF基本一致。
表 6及图 6为季节性检验结果。从表 6可以发现,水汽压精度也存在较明显的季节性,1月的精度最高,Bias和RMS的平均值分别为0.02mb和2.22mb,4月和10月精度次之,7月的精度最差。图 6显示RMS的全球分布,可见各个测站的精度存在明显的季节差异。位于北半球中高纬度地区的测站的Bias和RMS在1月份明显小于7月份,显示出与温度的强相关性。整体分布规律与年检验结果基本一致。
| mb | |||||||
| 月份 | Bias | RMS | |||||
| 平均值 | 最大值 | 最小值 | 平均值 | 最大值 | 最小值 | ||
| 1月 | 0.02 | 6.15 | -11.67 | 2.22 | 12.06 | 0.33 | |
| 4月 | 0.68 | 8.08 | -9.63 | 2.61 | 9.80 | 0.39 | |
| 7月 | 0.96 | 6.63 | -11.26 | 3.06 | 11.54 | 0.35 | |
| 10月 | 0.36 | 8.34 | -10.65 | 2.76 | 11.09 | 0.40 | |

|
| 图 6 季节性精度检验 Fig. 6 Global distribution of seasonal accuracy test of water vapor pressure |
以上研究结果表明,GPT2模型精度和纬度与季节有较强的相关性。为此本文利用NOAA提供的2012年Hourly/Sub-Hourly气象数据,选取分别代表高纬度、中纬度、低纬度地区的AMDERMA(69.783°N,61.783°E)、CHAOYANG(41.55°N,120.45°E)、MIRI(4.333°N,113.983°E)3个测站进行残差时间序列分析。从表 7可以看出,MIRI测站的残差均值最小,AMDERMA测站残差最大。选取CHAOYANG测站4月份以及该月3d的残差分别进行月周期、日周期残差分析,结果如图 7所示。从图 7中可以看出,4月份的气温残差具有较明显的三角函数特征。3d的气温残差波动趋势基本一致,在相同的时间存在一个波峰。对MIRI、AMDERMA测站做相同的处理,除了残差的波动范围及程度不一样外,整体趋势一致。处于中高纬度地区的测站残差月波动、日波动相对于低纬度地区更明显,残差更大,且存在明显的三角函数特征,因此,在现有模型表达式的基础上,若增加月周期或者日周期项,可能会提高部分中高纬度地区的精度。
| 测站 | 平均值 | 最小值 | 最大值 |
| MIRI | 0.43 | -6.16 | 7.36 |
| CHAOYANG | -1.19 | -16.00 | 16.40 |
| AMDERMA | 1.74 | -16.05 | 18.61 |

|
| 图 7 月周期及日周期残差序列 Fig. 7 Time series of residual error for month and day |
通过ECMWF和NOAA提供的高精度数据分别对GPT2气温、气压和水汽压进行精度检验,结果表明,气温主要呈现为负偏差,海洋地区优于陆地地区,南极地区精度及准确度最差;气压在中低纬度地区全年精度都很高,在南北半球高纬度地区精确度较差且随季节波动较大;相对气温和气压来说,水汽压的整体Bias及RMS波动更小,高纬度地区精度优于低纬度地区,沿海地区精确度略差。三者均具有明显的季节性,且不同地区季节特性不一样。综合分析,GPT2模型提供的气温、气压和水汽压在全球范围内均具有很高的精确度和稳定性,可代替GPT广泛用于各种气象学研究中。但在南北极地区精度仍然较低,本文分别选取代表低纬度、中纬度、高纬度地区的3个NOAA测站进行残差时间序列分析,结果表明中高纬度测站残差值较大,具有更明显的短周期特征,在后面的研究中,可以根据精度检验结果以及月周期、日周期特征等,在现有模型表达式的基础上增加新的参数,并采用新的数据及方法精化模型、优化模型。
| [1] | SCHUELER T, HEIN G W, EISSFELLER B. A New Tropospheric Correction Model for GNSS Navigation[C]//Proceedings of GNSS. Sevilla, Spain: [s.n.], 2001: 8-11. |
| [2] | QIAN Chuang, HE Changyong, LIU Hui. Regional Precise Troposphere Delay Modeling Based on Spherical Cap Harmonic Analysis[J]. Acta Geodaetica et Cartographica Sinca, 2014, 43(3): 248-256. (钱闯, 何畅勇, 刘晖. 基于球冠谐分析的区域精密对流层建模[J]. 测绘学报, 2014, 43(3): 248-256.) |
| [3] | OU Jikun. Research on the Correction for the Neutral Atmospheric Delay in GPS Surveying [J]. Acta Geodaetica et Cartographica Sinica, 1998, 27(1): 31-36. (欧吉坤. GPS测量的中性大气折射改正的研究[J]. 测绘学报, 1998, 27(1): 31-36.) |
| [4] | CHEN Yongqi, LIU Yanxiong, WANG Xiaoya, et al. GPS Real-time Estimation of Precipitable Water Vapor——Hong Kong Experiences[J]. Acta Geodaetica et Cartographica Sinica, 2007, 36(1): 9-12. (陈永奇, 刘焱雄, 王晓亚, 等. 香港实时 GPS 水汽监测系统的若干关键技术[J]. 测绘学报, 2007, 36(1): 9-12.) |
| [5] | WANG Yong, LIU Lintao, HAO Xiaoguang, et al. The Application Study of the GPS Meteorology Network in Wuhan Region[J]. Acta Geodaetica et Cartographica Sinica, 2007, 36(2): 141-145. (王勇, 柳林涛, 郝晓光, 等. 武汉地区GPS气象网应用研究[J]. 测绘学报, 2007, 36(2): 141-145.) |
| [6] | CHEN Junyong. On the Error Analysis for the Remote Sensing of Atmospheric Water Vapor by Ground Based GPS[J]. Acta Geodaetica et Cartographica Sinica, 1998, 27(2): 113-118. (陈俊勇. 地基GPS遥感大气水汽含量的误差分析[J]. 测绘学报, 1998, 27(2): 113-118.) |
| [7] | DAVIS J L, HERRING T A, SHAPIRO I I, et al. Geodesy by Radio Interferometry: Effects of Atmospheric Modeling Errors on Estimates of Baseline Length[J]. Radio Science, 1985, 20(6): 1593-1607. |
| [8] | BOEHM J, NIELL A, TREGONING P, et al. Global Mapping Function (GMF): A New Empirical Mapping Function Based on Numerical Weather Model Data[J]. Geophysical Research Letters, 2006, 33(7). DOI: 10.1029/2005GL025546. |
| [9] | BOEHM J, WERL B, SCHUH H. Troposphere Mapping Functions for GPS and Very Long Baseline Interferometry from European Centre for Medium-range Weather Forecasts Operational Analysis Data[J]. Journal of Geophysical Research: Solid Earth (1978-2012), 2006, 111(B2). DOI: 10.1029/2005JB003629. |
| [10] | NIELL A E. Global Mapping Functions for the Atmosphere Delay at Radio Wavelengths[J]. Journal of Geophysical Research: Solid Earth (1978—2012), 1996, 101(B2): 3227-3246. |
| [11] | NIELL A E. Preliminary Evaluation of Atmospheric Mapping Functions Based on Numerical Weather Models[J]. Physics and Chemistry of the Earth, Part A: Solid Earth and Geodesy, 2001, 26(6-8): 475-480. |
| [12] | YAO Y B, XU C Q, ZHANG B, et al. GTm-Ⅲ: A New Global Empirical Model for Mapping Zenith Wet Delays onto Precipitable Water Vapour[J]. Geophysical Journal, 2014, 197(1): 202-212. |
| [13] | YAO Y B, ZHANG B, YUE S Q, et al. Global Empirical Model for Mapping Zenith Wet Delays onto Precipitable Water[J]. Journal of Geodesy, 2013, 87(5): 439-448. |
| [14] | YAO Y B, ZHU S, YUE S Q. A Globally Applicable, Season-specific Model for Estimating the Weighted Mean Temperature of the Atmosphere[J]. Journal of Geodesy, 2012, 86(12): 1125-1135. |
| [15] | YAO Y B, HE C Y, ZHANG B, et al. A New Global Zenith Tropospheric Delay Model GZTD[J]. Chinese Journal of Geophysics, 2013, 56(7): 2218-2227. |
| [16] | SAASTAMOINEN J H. Atmospheric Correction for the Troposphere and Stratosphere in Radio Ranging Satellites[M]//The Use of Artificial Satellites for Geodesy. Washington DC: American Geophysical Union, 1972: 247-251. |
| [17] | LIU Yanxiong, IZ H B, CHEN Yongqi. Precise Determination of Dry Zenith Delay for GPS Meteorology Applications[J]. Acta Geodaetica et Cartographica Sinica, 2000, 29(2): 172-180. (刘焱雄, IZ H B, 陈永奇. GPS 气象学中垂直干分量延时的精确确定[J]. 测绘学报, 2000, 29(2): 172-180.) |
| [18] | SCHUELER T, HEIN G W, EISSFELLER B. On the Use of Numerical Weather Fields for Troposphere Delay Estimation in Wide Area Augmentation Systems[C]//Proceedings of GNSS. Edinburgh, Scotland: [s.n.], 2000: 1-4. |
| [19] | BOEHM J, HEINKELMANN R, SCHUH H. Short Note: A Global Model of Pressure and Temperature for Geodetic Applications[J]. Journal of Geodesy, 2007, 81(10): 679-683. |
| [20] | LAGLER K, SCHINDELEGGER M, BÓHM J, et al. GPT2: Empirical Slant Delay Model for Radio Space Geodetic Techniques[J]. Geophysical Research Letters, 2013, 40(6): 1069-1073. |