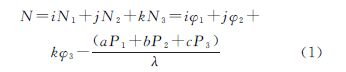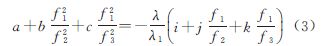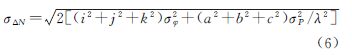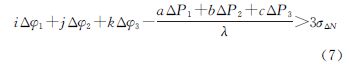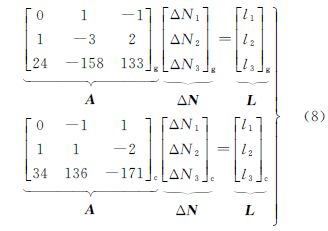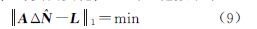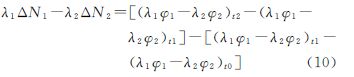2. 海洋测绘研究所,天津 300061;
3. 61618部队,北京 102102
2. Institute of Hydrographic Surveying and Charting, Tianjin 300061, China;
3. 61618 Troops, Beijing 102102, China
1 引 言
三频GNSS的发展,为提高GNSS导航定位精度和效率开辟了新途径[1],而高精度导航定位的前提是对周跳进行正确预处理。三频观测数据的出现,为周跳处理提供了更多具备噪声小、电离层延迟小、波长长的探测组合[2, 3, 4]。基于以上特性组合能实时实现周跳的探测与修复[5, 6, 7, 8, 9, 10]。常规条件下,无论是三频伪距/载波组合还是三频相位无几何组合周跳方法,均可忽略历元电离层残差组合,但当电离层活跃期(区)时,由于历元电离层延迟较大,为有效避免因电离层延迟造成的周跳探测误判,有必要考虑电离层延迟对周跳的影响。为此文献[11]开始研究电离层活跃条件下的周跳处理方法,文献[12]采用预先估计电离层延迟的方法来处理高电离层条件下的周跳,文献[13]则基于假设检验理论同时处理粗差、周跳和电离层异常。为简化周跳修复,文献[14—15]借鉴双频TurboEdit思想,分别提出了电离层延迟变化率+MW组合和两次历元差分后电离层残差组合+MW组合的方法进行周跳探测与修复。目前顾及高电离层延迟影响的三频周跳处理方法研究较少,鉴于三频组合观测值的灵活性,有必要研究一种更为简单可行的三频周跳处理方法以体现三频技术优势。
2 三频无几何无电离层组合
为保证周跳探测量不受站星距离、对流层延迟以及卫星、接收机钟差和电离层延迟一阶项的影响,且能保持模糊度整数特性,特借鉴双频MW组合特性,构造三频无几何无电离层组合作为三频周跳检验量
由于三频无几何无电离层组合因组合噪声绝大部分为伪距噪声[16],为此在筛选三频无几何无电离层超宽巷组合时应尽可能降低伪距组合系数。此时式(1)组合系数须满足
式(2)保证消除几何误差项;式(3)保证消除电离层延迟一阶项;式(4)保证伪距噪声影响最小。对于确定的载波组合系数(i,j,k),组合波长λ唯一确定,而伪距组合系数(a,b,c)的计算就是一个简单极小值求解问题。
设下一历元发生周跳,式(1)历元差分可得到三频无几何无电离层组合周跳探测方程
式(5)仅剩电离层二阶项和观测噪声。而在高电离层延迟(TEC=4.55e18/m2) 情况下,GPS原始观测值电离层延迟二阶项误差最大为0.19 m[17],而宽巷组合波长至少为0.75 m[18],为此最大二阶项误差也仅占1/4波长,并且观测值组合可进一步减弱电离层延迟二阶项影响,为此可忽略电离层延迟二阶项,仅考虑观测噪声影响[15],此时式(5)ΔN标准差为
以3σΔN(置信水平为99.7%)为探测阈值,满足式(7)的不等式即认为周跳发生
设GPS、BDS伪距噪声和载波噪声分别为0.3 m和0.01周,对三频无几何无电离层组合进行优化选取,并计算周跳探测检验量方差值,具体见表 1和表 2。由表 1和表 2第6列可知,虽然在组合成三频无几何无电离层组合时会放大观测噪声,但三频无几何无电离层组合更容易得到波长更长的宽巷或者超宽巷组合,除表 1中(24,-158,133)和表 2中(34,136,-171)组合以外,其他周跳探测组合(第8列所示)理论上均可实现对1周小周跳的探测,尤其GPS组合(0,1,-1)和BDS组合(0,-1,1),其阈值均不超过0.2周。三频观测组合的电离层延迟和观测噪声是一个不可调和的矛盾,即电离层延迟较小的组合往往观测噪声较大[3]。虽然式(7)忽略了电离层延迟二阶项,但其仍客观存在,如表 1、表 2中的第7列以周为单位的电离层延迟二阶项放大因子η所示。由于历元间隔越大历元间电离层延迟误差越大,为此在选择周跳探测时应选择具备较小电离层延迟放大因子的周跳探测组合。由表第9列可知,BDS和GPS两系统周跳探测阈值较小的组合其载波组合系数之和均为0,这与文献[4]结论一致。但任意3个组合系数为0的组合均线性相关,且均无法探测ΔN1=ΔN2=ΔN3这些特殊周跳。
| (i,j,k) | a | b | c | λ | η | σΔN | 3σΔN | i+j+k | |
| 1# | (0,1,-1) | 0.012 109 | 0.444 991 | 0.542 900 | 5.861 045 | 0.769 5 | 0.038 618 | 0.115 855 | 0 |
| 2# | (1,-3,2) | 0.842 594 | 0.156 314 | 0.001 092 | 1.221 051 | 1.893 7 | 0.213 848 | 0.641 544 | 0 |
| 3# | (1,-4,3) | 1.061 142 | 0.080 347 | -0.141 489 | 1.542 380 | 1.124 2 | 0.214 945 | 0.644 835 | 0 |
| 4# | (1,-2,1) | 0.699 407 | 0.206 086 | 0.094 507 | 1.010 525 | 2.197 3 | 0.219 644 | 0.658 931 | 0 |
| 5# | (1,-5,4) | 1.435 797 | -0.049 883 | -0.385 914 | 2.093 230 | 0.354 8 | 0.222 833 | 0.668 498 | 0 |
| 6# | (1,-6,5) | 2.226 735 | -0.324 813 | -0.901 922 | 3.256 136 | -0.414 7 | 0.236 834 | 0.710 502 | 0 |
| 7# | (1,-7,6) | 4.995 017 | -1.287 068 | -2.707 949 | 7.326 306 | -1.184 1 | 0.255 947 | 0.767 842 | 0 |
| 8# | (-1,8,-7) | -19.919 522 | 7.373 224 | 13.546 297 | 29.305 226 | 1.953 6 | 0.279 124 | 0.837 373 | 0 |
| 9# | (-1,9,-8) | -3.309 829 | 1.599 696 | 2.710133 | 4.884 204 | 2.723 0 | 0.305 442 | 0.916 325 | 0 |
| 10# | (24,-158,133) | -2.104 893 | 1.180 861 | 1.924 032 | 0.945 330 | -0.709 9 | 2.298 339 | 6.895 017 | -1 |
| (i,j,k) | a | b | c | λ | η | σΔN | 3σΔN | i+j+k | |
| 1# | (0,-1,1) | 0.019 945 | 0.552 577 | 0.427 478 | 4.884 204 | 0.823 1 | 0.063 920 | 0.191 760 | 0 |
| 2# | (1,1,-2) | 0.750 616 | 0.041 406 | 0.207 978 | 1.296 691 | 1.875 2 | 0.257 547 | 0.772 641 | 0 |
| 3# | (1,3,-4) | 1.577 791 | -0.537 279 | -0.040 512 | 2.764 644 | 0.229 0 | 0.265 826 | 0.797 477 | 0 |
| 4# | (1,0,-1) | 0.597 328 | 0.148 645 | 0.254 027 | 1.024 658 | 2.698 3 | 0.276 444 | 0.829 332 | 0 |
| 5# | (1,4,-5) | 3.609 763 | -1.958 831 | -0.650 933 | 6.370 701 | -0.594 1 | 0.291 697 | 0.875 090 | 0 |
| 6# | (-1,-5,6) | -11.775 173 | 8.804 347 | 3.970 826 | 20.932 304 | 1.417 2 | 0.328 150 | 0.984 449 | 0 |
| 7# | (34,136,-171) | -1.671 537 | 1.735 925 | 0.935 613 | 0.904 482 | -2.204 3 | 3.353 952 | 10.061 856 | -1 |
若选择3个线性无关无几何无电离层组合进行探测修复,至少应需选择一个i+j+k≠0的无几何无电离层组合。在i,j,k∈[-200,200]范围内,两系统满足条件的最优超宽巷组合分别为GPS组合(24,-158,133)和BDS组合(34,136,-171)。但两组合的周跳探测阈值较大,其能够探测的最小周跳分别为7周和11周,难以实现对小周跳的探测。并且由于这两组合载波系数i+j+k=-1,所以若两个系统的3个频点同时发生大小相同且分别小于7周和11周的周跳,则以上3个周跳探测检验量均无法探测到这些不敏感周跳。为减少不敏感周跳数目,可采用多项式拟合[19]或移动平滑窗口法对组合(24,-158,133)和(34,136,-171)的伪距噪声进行消噪处理,但这需要较长的观测历元,否则难以满足实时导航定位的需求。
3 周跳探测、修复与确认为简化周跳修复计算,借鉴三频伪距/载波组合算法思想,从表 1和表 2分别选择3个线性无关的周跳探测组合进行联合探测与修复,具体选择的组合为
式中,ΔNi和li(i=1,2,3)分别为周跳值和相应周跳探测检验量,下标g和c分别表示GPS和BDS系统。式(8)中,l1对应的周跳方差值σΔN1较小,可直接取整确定[20];而l2和l3由于周跳方差值较大,直接取整固定结果可能不正确,为此采取空间搜索方法[10],即分别以l2和l3为搜索中心,以组合探测阈值确定范围,搜索步长设为0.5周,对搜索范围内的每个可能整数周跳,利用式(8)进行解算。文献[9, 10]采用1范数最小原则确认周跳修复值,即正确的修复值与实测变化值L的1范数最小
由式(9)分析可知,不同搜索值解算的周跳值相差(1,1,1)的整数倍,由此式(9)中前两个组合1范数始终不变,而 (9)中三式的1范数只在不搜索时最小,为此1范数原则在此不适用。
为能检测到(1,1,1)这种特殊不敏感周跳,借鉴文献[15]选用两次历元差分后的电离层残差组合(1,-1,0)验证周跳修复值。由上可知,周跳修复不正确时,相当于存在一个(1,1,1)整数倍的周跳。由表 3可知,最不敏感周跳组合(1,1,1)引起的电离层残差组合(1,-1,0)变化量也达到0.053 9周;而为尽可能保证周跳检验准确性,选择4倍周跳方差值(置信区间为99.99%)为探测阈值,两次历元差分后的双频电离层残差值仍可实现对周跳(1,1,1)的探测。为此若式(10)所示的两次历元差分后的电离层残差组合未探测出周跳,则认为周跳修复正确,即
式中,λi(i=1,2,3)为i频点波长;t0、t1和t2表示先后连续的3个历元。| 探测量 | 差分次数 | 探测阈值 | (1,1,1)对应变化量 |
| GPS(1,-1,0) | 一次 | 0.017 6 | -0.053 9 |
| 两次 | 0.024 8 | ||
| BDS(1,-1,0) | 一次 | 0.017 7 | -0.056 3 |
| 两次 | 0.025 1 |
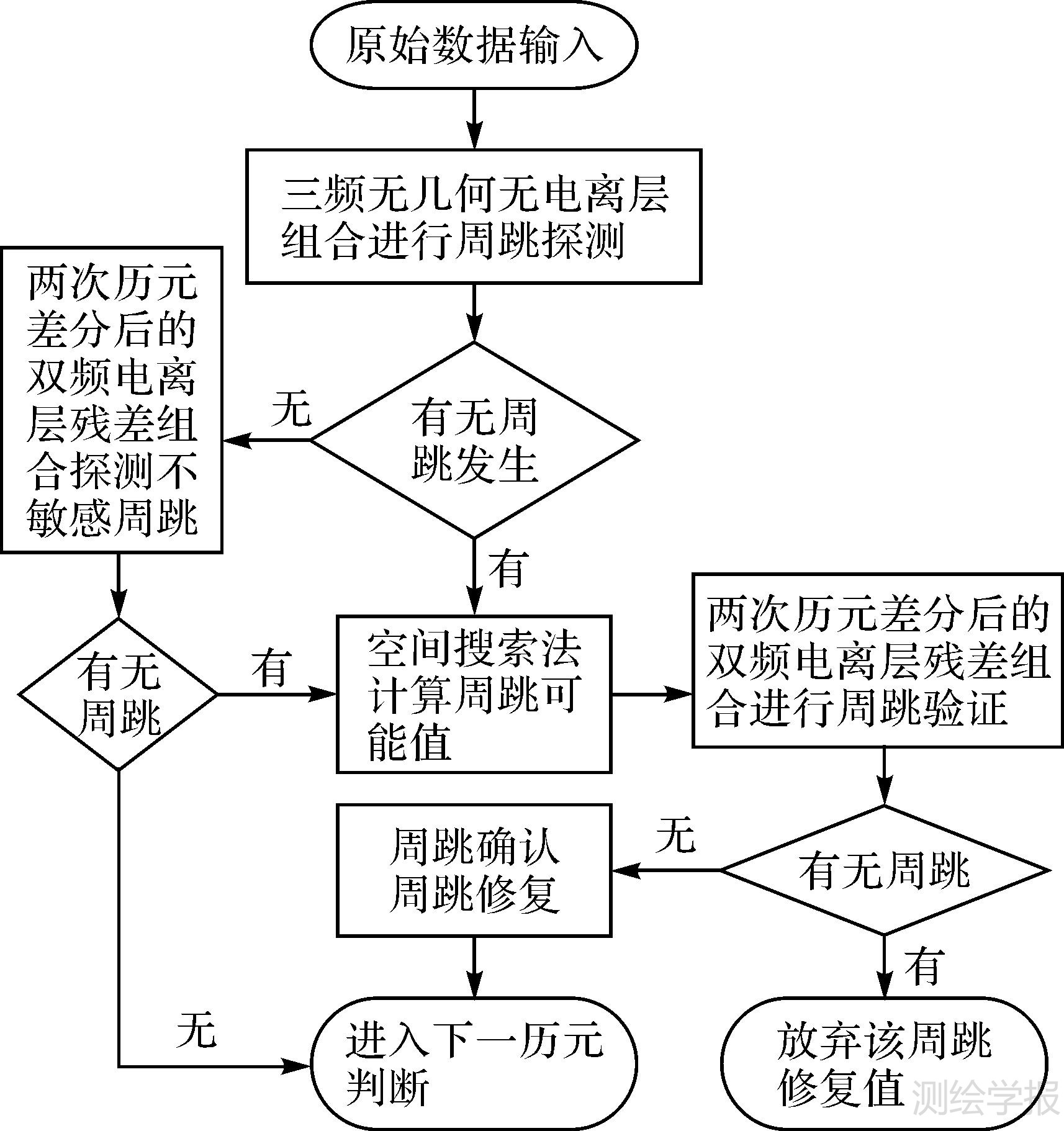
由表 2分析可知,式(9)三频无几何无电离层周跳探测组合仍存在(1,1,1)整数倍的小周跳组合,为此式(9)未探测到周跳,难以下“未发生周跳”的结论。而此时仍需利用式(10)进行验证,若未探测到周跳发生则认为无周跳。否则同样按照以上步骤进行周跳修复与确认。根据以上分析,基于三频无几何无电离层组合的周跳探测、修复与确认的处理流程如图 1所示。
|
| 图 1 算法示意图 Fig. 1 The sketch map of this method |
由文献[21]可知,2013年3月17日发生了大磁暴现象(磁暴指数<-100 nt),磁暴时变指数Dst峰值为-132 nt,如图 2所示,而参与IGS 多GNSS试验MGEX(multi-GNSS experiments)的站点JFNG(30.52°N,114.49°E)正好位于TEC变化显著区。为此选择该站点由Trimble NetR9观测到的BDS C02、C09和C12和GPS G25卫星三频数据进行分析,所有观测卫星的高度角均大于10°,采样间隔30 s,其中C02为MEO卫星,C09和C12为IGSO卫星。

|
| 图 2 2013年3磁暴时变指数 Fig. 2 Dst values of March 2013 |
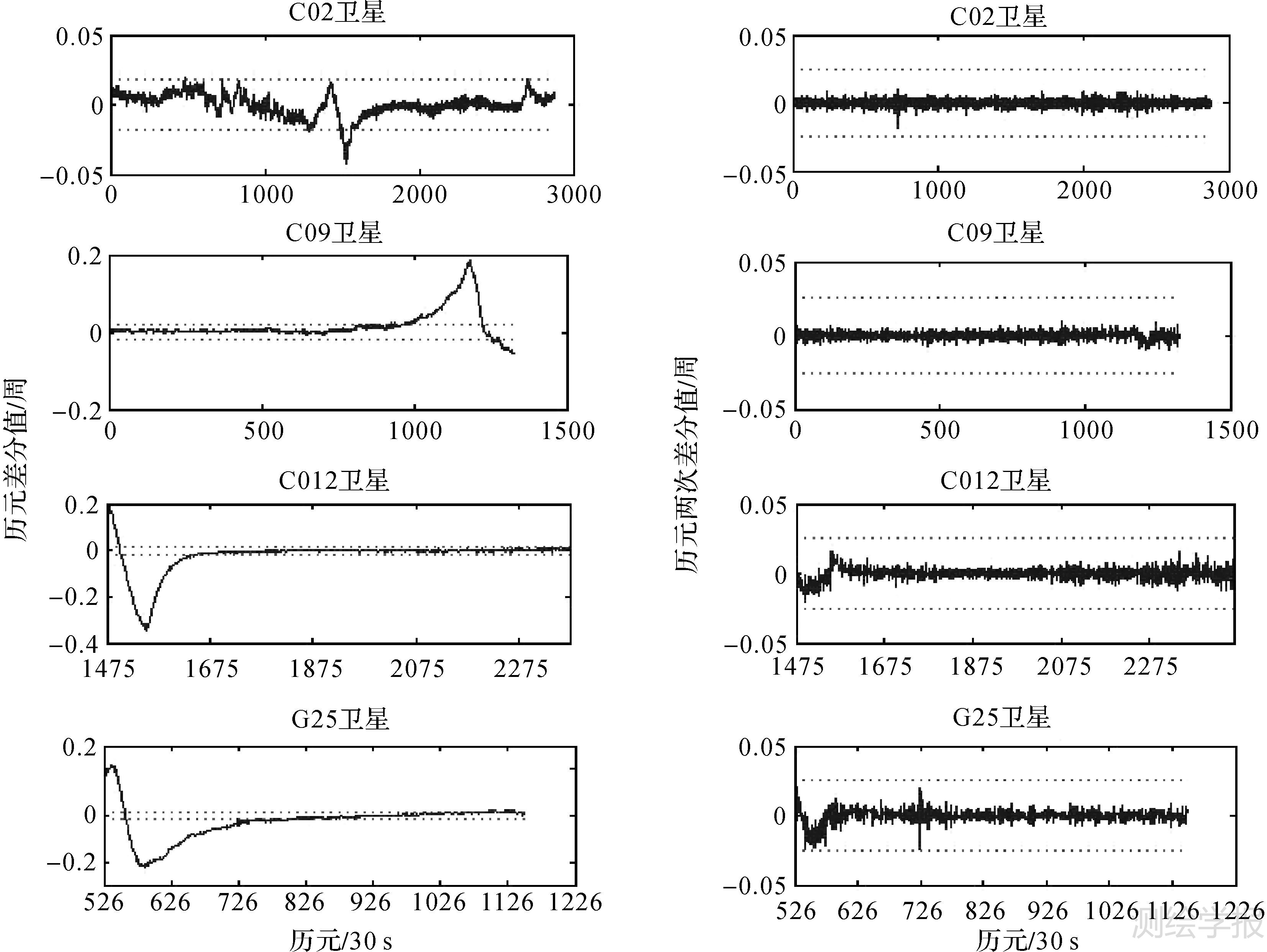
类似于文献[15],首先给出无周跳时GPS、BDS双频电离层残差组合历元差分和两次历元差分结果,以分析电离层活跃度(图 3),图 3中0历元对应00 h:00 min:00 s。由图 3左侧显示的双频电离层历元间差分值可知,双频电离层残差组合明显受到电离层延迟影响,其波动范围超出其周跳探测阈值,为此采用忽略电离层延迟影响的常规周跳探测方法难以准确探测。而图 3右侧所示的两次历元差分明显削弱了电离层延迟影响,其差分值均在探测阈值范围内,从而可对特殊不敏感周跳(1,1,1)进行验证。图 4给出了本文周跳探测组合无周跳情况下的历元差分效果图。由图 4可知,无几何无电离层组合能有效克服高电离层延迟影响,可用于高电离层延迟条件下的周跳探测与修复。
|
| 图 3 电离层残差组合差分值 Fig. 3 The differencing value of ionospheric residual combination |

|
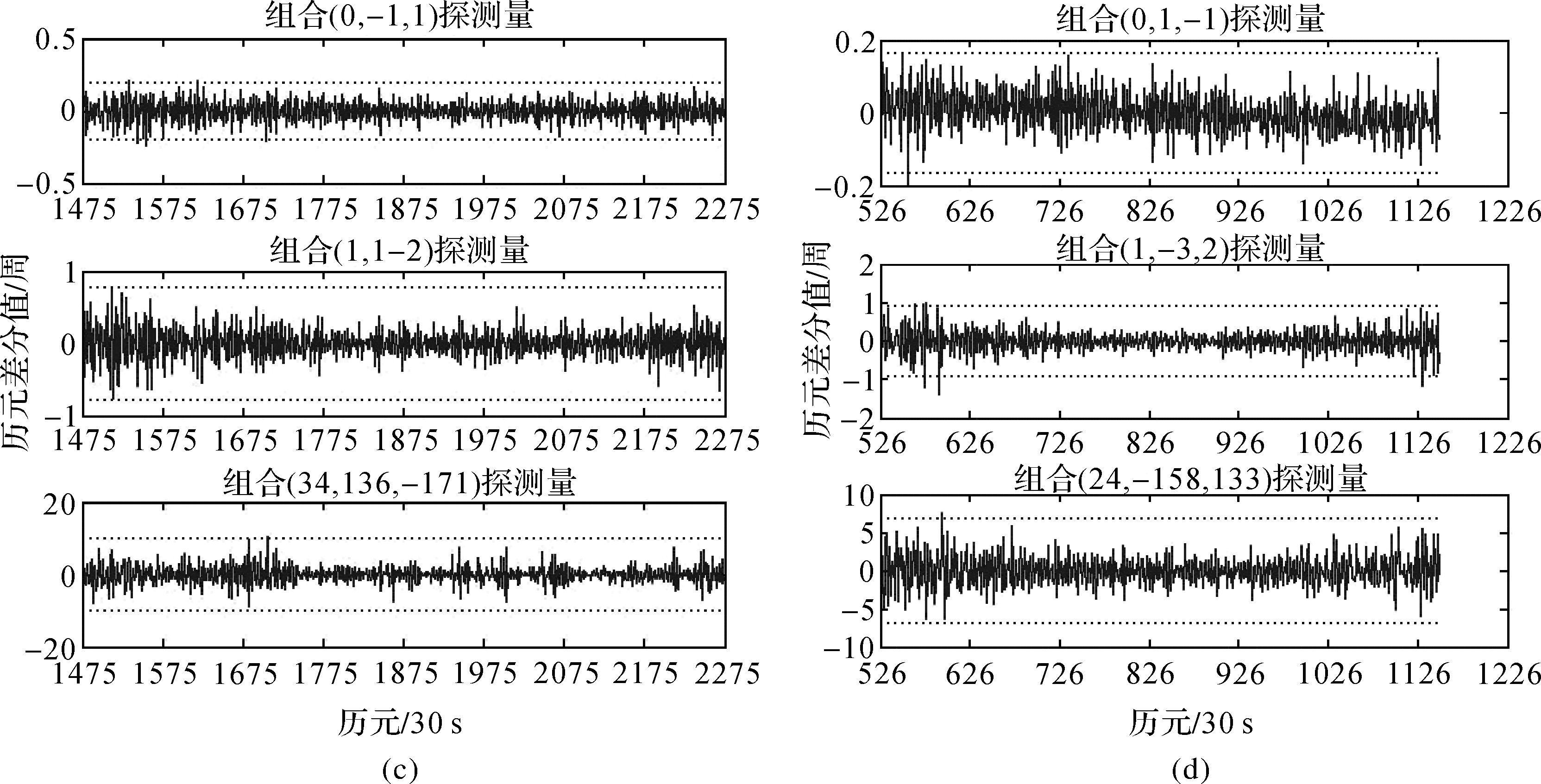
| 图 4 无几何无电离层周跳探测检验量 Fig. 4 The detection value of the GIF combination |
|
| 图 4 无几何无电离层周跳探测检验量 Fig. 4 The detection value of the GIF combination |
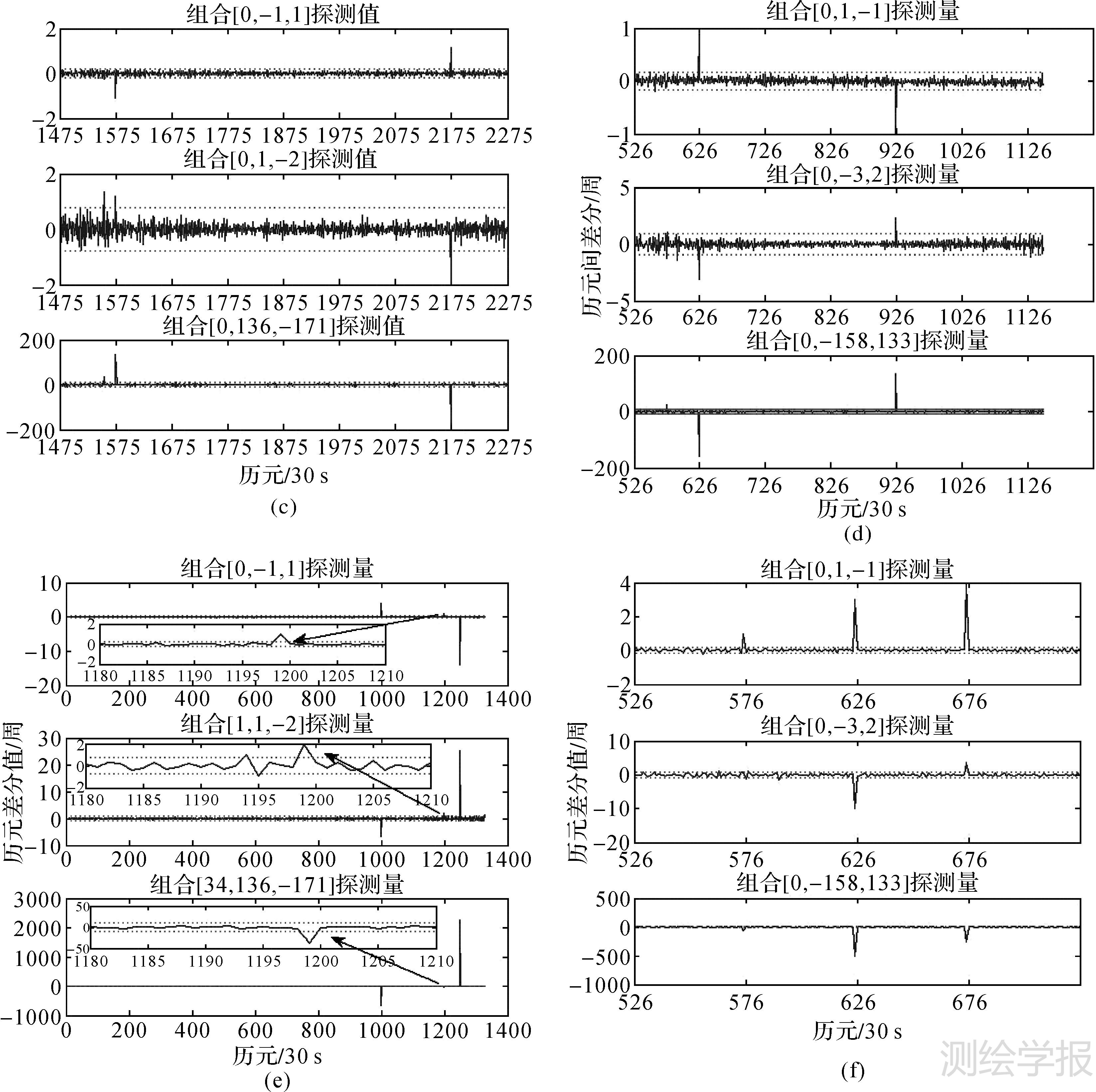
选择图 3中电离层延迟较大的历元,分别在4颗卫星的3个频点上依次加入1周小周跳,其周跳探测情况如图 5(a)-(d)所示;图 5(e)和图5(f)分别表示为C09卫星和G25卫星加入较大周跳的探测情况。由图 5(a)-(f)可以看出,该周跳探测能够探测并正确修复周跳,具体如表 4 第5列所示的周跳验证量均小于双频电离层延迟探测阈值,说明周跳修复检验正确。为验证对特殊不敏感周跳的探测检验效果,特对卫星C12和G25在电离层延迟变化较大历元加入最不敏感周跳(1,1,1)和临界不敏感周跳进行分析,具体加入大小如表 4所示。由图 5(g)和图 5(h)可知,GPS系统难以探测到周跳(1,1,1)和(6,6,6),BDS系统无法探测出周跳(1,1,1),而由BDS能够探测出理论上不敏感周跳值(10,10,10),说明实际BDS观测值误差比理论假设小。虽然对不敏感周跳(1,1,1)无法探测,但通过两次历元差分电离层残差组合的检验,可以实现对不感敏周跳的探测与确认。由此可以看出,当3个无几何无电离层组合未探测出周跳值,仍需进一步检验、确认,而额外的周跳检验、确认增加了一定计算量,但计算量非常小。进一步在C02和G25卫星3个连续历元加入不同周跳,并且G25卫星加入的周跳(7,5,3)还属于不敏感周跳,但由图 5(i)和图 5(j)可知,该算法同样能实现连续周跳的探测与修复。
|
| 图 5 周跳探测图 Fig. 5 The figure of cycle-slip detection |

|
| 图 5 周跳探测图 Fig. 5 The figure of cycle-slip detection |
| 卫星 图号 | 发生 历元 | 周跳大小 | 周跳探测检验量 | 周跳验证量 | 成功与否 |
| 5(a)/C02 | 1200 1500 2500 | (1,0,0) (0,1,0) (0,0,1) | (-0.03,0.87,33.16) (-0.95,0.94,135.93) (0.96,-1.82,-171.48) | 0.003 34 0.000 51 -0.001 07 | Yes Yes Yes |
| 5(b)/C09 | 1000 1100 1200 | (1,0,0) (0,1,0) (0,0,1) | (0.04,1.24,33.88) (-1.04,1.03,137.13) (1.00,-2.01,-172.63) | 0.000 68 0.001 46 -0.003 20 | Yes Yes Yes |
| 5(c)/C12 | 1555 1575 2175 | (1,0,0) (0,1,0) (0,0,1) | (-0.24,1.36,32.44) (-1.11,1.19,133.38) (1.14,-1.96,-170.72) | -0.011 91 0.002 40 0.007 05 | Yes Yes Yes |
| 5(d)/G25 | 576 626 926 | (1,0,0) (0,1,0) (0,0,1) | (-0.03,0.72,22.57) (1.00,-3.06,-157.93) (-0.99,2.28,133.31) | -0.021 28 0.003 36 0.003 33 | Yes Yes Yes |
| 5(e)/C09 | 1000 1200 1250 | (5,4,8) (6,2,3) (14,17,3) | (4.04,-6.76,-654.12) (1.00,1.99,-38.63) (-14.01,25.08,2272.28) | 0.000 68 -0.003 20 0.002 17 | Yes Yes Yes |
| 5(f)/G25 | 566 576 626 | (7,4,3) (5,9,3) (17,5,1) | (0.97,0.72,-66.43) (3.00,-10.06,-503.93) (3.98,3.76,-252.04) | -0.006 52 0.003 36 0.003 33 | Yes Yes Yes |
| 5(g)/C12 | 1555 1575 2175 | (10,10,10) (11,11,11) (1,1,1) | (-0.24,7.36,236.44) (-0.11,0.19,-13.62) (-0.04,-0.02,-1.26) | -0.011 90 0.002 40 0.007 06 | Yes Yes Yes |
| 5(h)/G25 | 586 626 926 | (1,1,1) (6,6,6) (8,8,8) | (-0.03,-0.28,-2.43) (0.00,-0.06,-5.93) (0.01,0.28,-7.69) | 0.001 00 0.003 36 0.003 33 | Yes Yes Yes |
| 5(i)/C02 | 1500 1501 1502 | (1,2,3) (3,4,5) (6,7,8) | (1.05,-3.06,-207.07) (0.99,-2.79,-210.40) (1.01,-3.02,-211.88) | 0.000 51 0.003 42 -0.001 25 | Yes Yes Yes |
| 5(j)/G25 | 586 587 588 | (7,5,3) (9,5,1) (4,8,2) | (1.96,-2.28,-224.43 ) (3.90,-5.19,-437.42 ) (0.16,-14.99,-908.37) | 0.000 996 0.005 98 -0.009 68 | Yes Yes Yes |
三频无几何无电离层组合消除了电离层延迟误差一阶项,可适用于高电离层延迟条件下的周跳探测与修复,但采用3个线性无关的三频无几何无电离层组合进行周跳的探测与修复仍会存在不敏感周跳。本文提出采用两次历元差分后的双频电离层残差组合对不敏感周跳进行验证的方法,能够保证对不敏感周跳探测与正确修复。由于不敏感周跳的存在,导致本文周跳探测需作进一步周跳验证与确认,增加了一定计算量,但这些计算量对于现有计算机运算能力可忽略不计。总之,本文算法能适用于高电离层延迟情况的三频周跳探测与修复,且适用于动态、非差连续的周跳探测与修复。收集更高电离层活跃期(区)的三频观测数据进行算法验证将是今后的一大工作。
| [1] | YANG Yuanxi. Progress, Contribution and Challenges of Compass/BeiDou Satellite Navigation System[J]. Acta Geodaetica et Cartographica Sinica, 2010, 39(1):1-6. (杨元喜. 北斗卫星导航系统的进展、贡献与挑战[J]. 测绘学报, 2010, 39(1):1-6.) |
| [2] | WANG Zemin, LIU Jingbin. Model of Inter-frequency Combinations of Galileo GNSS[J]. Geomatics and Information Science of Wuhan University, 2006, 28(6):723-727. (王泽民, 刘景斌. 卫星定位系统相位组合观测值的模型研究[J]. 武汉大学学报: 信息科学版, 2006, 28(6):723-727. ) |
| [3] | COCARD M, BOURGON S, KAMALI O, et al. A Systematic Investigation of Optimal Carrier-phase Combinations for Modernized Triple-frequency GPS[J]. Journal of Geodesy, 2008, 82(9):555-564. |
| [4] | HUANG Lingyong, SONG Lijie, LIU Xiandong. Optimization and Selection of GPS Triple-carries Phase Combination Observations Based Self-adaptive Clustering Algorithm[J]. Journal of Geodesy and Geodynamics, 2011, 311(4):99-102. (黄令勇, 宋力杰, 刘先冬. 基于自适应聚类算法的 GPS三频载波相位组合观测值优化选取[J]. 大地测量与地球动力学, 2011, 311(4):99-102.) |
| [5] | LI Jinlong, YANG Yuanxi, XU Junyi, et al. Real-time Cycle-slip Detection and Repair Based on Code-phase Combinations for GNSS Triple-frequency Undifferenced Observations[J]. Acta Geodaetica et Cartographica Sinica, 2011, 40(6):717-722. (李金龙, 杨元喜, 徐君毅, 等. 基于伪距相位组合实时探测与修复三频GNSS非差观测数据周跳[J]. 测绘学报, 2011, 40(6):717-722.) |
| [6] | HUANG Lingyong, SONG Lijie, WANG Yan et al. BeiDou Triple-frequency Geometry-free Phase Combination for Cycle-slip Detection and Correction[J]. Acta Geodaetica et Cartographica Sinica, 2012, 41(5):763-768. (黄令勇, 宋力杰, 王琰, 等.北斗三频无几何相位组合周跳探测与修复[J]. 测绘学报, 2012, 41(5) :763-768.) |
| [7] | CAO Xinyun, WANG Jian. Cycle-slip Detection and Repair Using GPS Triple-frequency Un-different Observations[J]. Geomatics and Information Science of Wuhan University, 2014, 39(4):450-456. (曹新运, 王坚. GPS三频非差观测值探测与修复周跳[J]. 武汉大学学报: 信息科学版, 2014, 39(4):450-456.) |
| [8] | DAI Z, KNEDLIK S, LOFFELD O. Instantaneous Triple-Frequency GPS Cycle-slip Detection and Repair[J]. International Journal of Navigation and Observation, 2009, 23(1):28-43. DOI: 10.1155/2009/407231. |
| [9] | DE-LACY M C, REGUZZONI M, SANSÓF. Real-time Cycle Slip Detection in Triple-frequency GNSS[J]. GPS Solutions, 2012, 16(3):353-362. |
| [10] | YU Xingwang. Multi-frequency GNSS Precise Positioning Theory and Method Research[D]. Wuhan: Wuhan University, 2011. (于兴旺. 多频GNSS精密定位理论与方法研究[D]. 武汉:武汉大学, 2011.) |
| [11] | BANVILLE S, LANGLEY R B, SAITO S, et al. Handling Cycle Slips in GPS Data during Ionospheric Plasma Bubble Events[J]. Radio Science, 2010, 45(6):15-31. |
| [12] | BANVILLE S, LANGLEY R B. Mitigating the Impact of Ionospheric Cycle Slips in GNSS Observations[J]. Journal of Geodesy, 2013, 87(2):179-193. |
| [13] | TEUNISSEN P J G, DE BAKKER P F. Single-receiver Single-channel Multi-frequency GNSS Integrity: Outliers, Slips and Ionospheric Disturbances[J]. Journal of Geodesy, 2013, 87(2): 161-177. |
| [14] | LIU Zhizhao. A New Automated Cycle Slip Detection and Repair Method for a Single Dual-frequency GPS Receiver[J]. Journal of Geodesy, 2011, 85(3):171-183. |
| [15] | CAI Changsheng, LIU Zhizhao, XIA Pengfei, et al. Cycle Slip Detection and Repair for Undifferenced GPS Observations under High Ionospheric Activity[J]. GPS Solutions, 2013, 17(2):247-260. |
| [16] | LIU Changjian. Study on Modeling Method and Model Quality Control of Ionosphere Based on GNSS[D]. Zhengzhou:Information Engineering University, 2011.(刘长建.GNSS电离层建模方法与质量控制研究[D]. 郑州:信息工程大学, 2011.) |
| [17] | WU Yue. The Theory and Applieationon Multi-frequency Data Proeessing of GNSS2[D]. Wuhan: Wuhan University, 2005. (伍岳.第二代导航卫星系统多频数据处理理论及应用[D]. 武汉:武汉大学, 2005.) |
| [18] | FENG Yanming. GNSS Three Carrier Ambiguity Resolution Using Ionosphere-reduced Virtual Signals[J]. Journal of Geodesy, 2008, 82(12):847-862. |
| [19] | BLEWITT G.An Automatic Editing Algorithm for GPS Data[J].Research Letters, 1990, 17(3):199-202. |
| [20] | HUANG Lingyong. Research on the Algorithms and Theory of GNSS Multi-frequency Data Processing[D]. Zhengzhou: Information Engineering University, 2012. (黄令勇. GNSS多频数据处理理论与方法研究[D]. 郑州:信息工程大学, 2012.) |
| [21] | JIN Rui, JIN Shuanggen, TAO Xuelin. Ionospheric Anomalies during the March 2013 Geomagnetic Storm from BeiDou Navigation Satellite System (BDS) Observations[C]//SUN J D, JIAO W H, WU H T, et al. China Satellite Navigation Conference (CSNC) 2014 Proceedings: Volume I. Heidelberg: Springer, 2014: 97-104. |