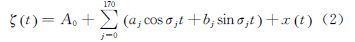2. 西安测绘研究所,陕西 西安 710054
2. Xi'an Research Institute of Surveying and Mapping, Xi'an 710054, China
1 引 言
高程基准是高程测量的起算依据,是大地测量基准的重要组成部分[1, 2]。青岛大港验潮站处于东部黄海沿岸,在我国海岸线的中部,1957年确定为我国基本验潮站。世界各地区的高程基准一般通过沿岸验潮站的平均海面高实现,我国将大港验潮站的平均海水面定义为我国高程基准的起算面。我国目前采用的“1985国家高程基准”,是由大港验潮站1952—1979年验潮数据确定的。计算时以19年为周期,滑动步长为1年,得到10组平均海面值,取其平均值242.89 cm作为当地黄海平均海面高,然后将这个平均海面作为我国的高程基准面,从而求出国家水准原点的高程值为72.260 m[2, 3, 4, 5]。
海水受到月球和太阳等天体的引潮力作用产生规律性的海洋潮汐运动,研究验潮站处的潮汐变化规律对于确定国家高程基准具有理论和实际意义[6, 7]。18世纪80年代达尔文对引潮位进行了近似调和展开,得到了60多个主要分潮的频率和平均振幅[4]。19世纪20年代杜德森引用月球运动的Brown系数和Newcomb表对引潮位进行了纯调和展开,获得400多个分潮的频率和振幅[8, 9, 10]。文献[11, 12]采用更新的天文变量按照杜德森方法将引潮位展开至3000多个分潮。这些分潮对解释潮汐现象起到了很大作用,但是这些展开的分潮振幅和相位并不能表征实际海域的分潮特征,因此需要采用大量潮汐观测数据进行潮汐调和分析来解释更符合实际的潮汐现象、分析平均海水面变化以及进行潮汐预报。大港验潮站自1952年至今已有60多年的观测数据,这对进一步分析我国高程基准面的变化具有重要作用。
另外,温室效应造成的冰川消融、局部地区地下水的开采以及海底地形的变迁等,都会引起海水面的升降变化[13]。实际计算1985国家高程基准时,受当时数据限制,并未考虑这种变化。随着大地测量精度的提高,国家高程基准如同坐标基准一样,应该考虑各种影响因素,以便保持现势性[14, 15, 16],因此对国家高程基准面最近60年的变化进行研究也有积极的意义。
为了分析和研究大港验潮站处潮汐的特征以及国家高程基准面在60年中的变化,本文首先采用1980—2011年每小时潮汐数据和1952—2011年月平均数据进行频谱分析获得影响大港验潮站处平均海水面的主要分潮;然后采用最小二乘调和分析对每小时潮汐数据进行逐年分析获得主要分潮的振幅和变化;并采用调和分析和18.61年移动平均对60年间国家高程基准面的变化进行计算和分析;最后给出关于我国国家高程基准定义的建议。
2 采用的数据数据1:大港验潮站1980—2011年共计11 688 d的每小时潮位数据,对其中缺少的72 h数据(1985-06-01、2001-04-02、2002-03-02各24 h),首先采用间隔25 h和50 h的数据平滑内插进行填补,之后采用3节调和分析的结果进行填补。
数据2:大港验潮站(1952—2007年)月均潮位数据,每月一个数据,共计672个数据。
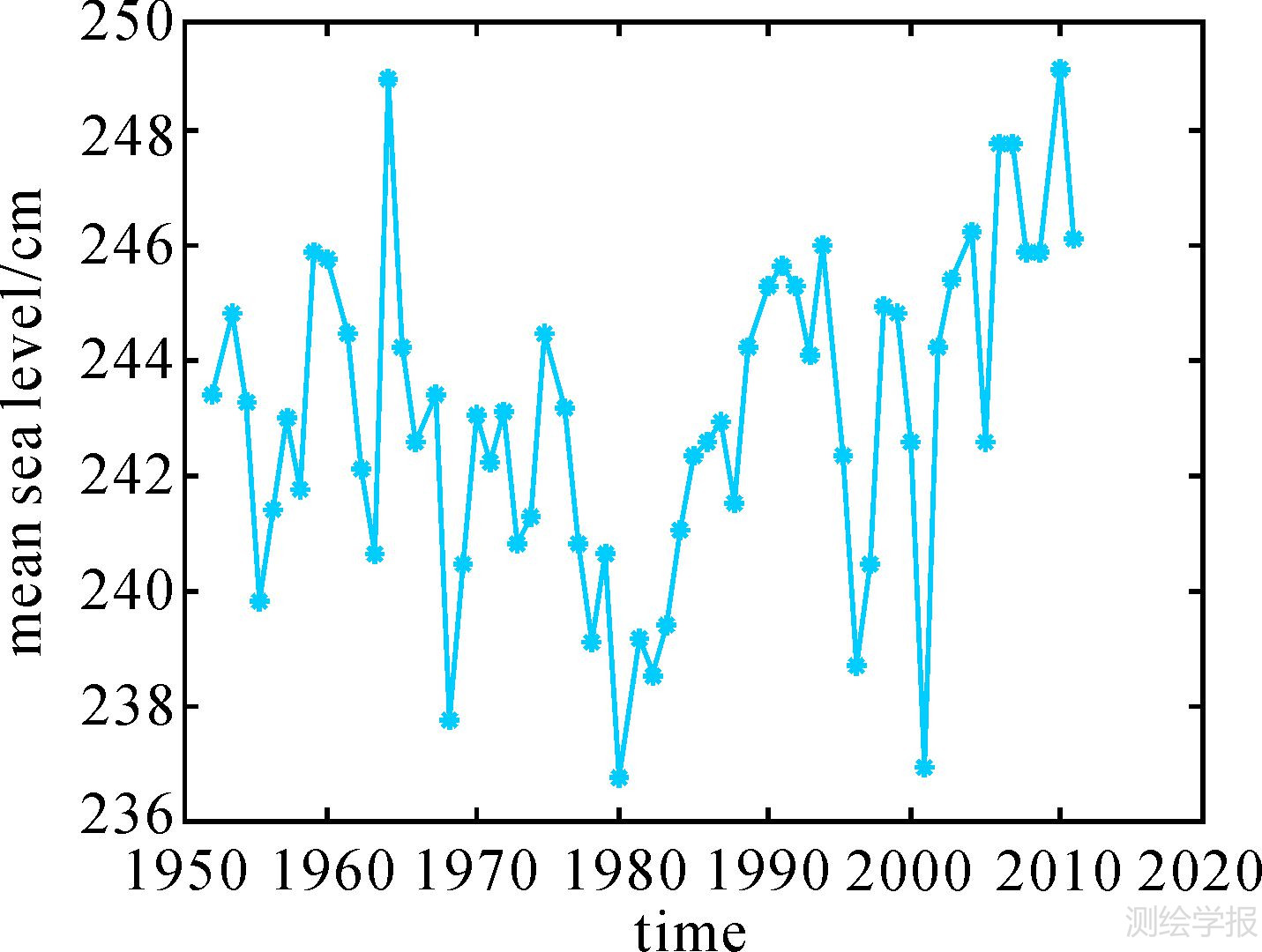
对这两组数据共有年份(1980—2007年)的年平均数据进行比较(如图 1,蓝色为第1组数据,红色为第2组数据),发现这两组数据在1995年之前相差较小,最大差距为0.34 cm;1995年之后相差较大,最大差距在2006年,为3.45 cm。考虑到每小时潮位资料的原始性和真实性,认为第1组数据是可靠的,因此用第1组数据代替第2组数据中从1980年之后部分的月平均和年平均数据,从而获得1952—2011年的月平均和年平均潮位数据(图 2)。

|
| 图 1 两组数据的比较 Fig. 1 Comparison of two sets of data |
|
| 图 2 1952—2011年年平均潮位数据 Fig. 2 Mean tidal data from 1952 to 2011 |
根据奈魁斯特定律,小时潮汐数据频谱分析可以获得最高频率为2 h的高频分潮。频谱分析的结果如图 3所示。

|
| 图 3 每小时潮汐数据频谱图 Fig. 3 Energy-frequency for hourly tidal data |
图 3中可见6处分潮集中频段。第1处是长周期分潮,主要表征周期大于半个月的分潮,其中可清晰判别年周期分潮Sa,半年周期分潮Ssa,月周期分潮Msm、Mm等;第2处是日周期分潮,主要表征周期在24 h左右的分潮,比较有代表性的有K1、O1、P1、Q1、S1、ψ1等;第3处是半日分潮,如M2、S2、N2、K2、T2、R2等;第4处是8 h左右分潮,如MO3、MK3等;第5处是6 h左右分潮,如M4、MS4、S4等;第6处是4 h分潮,如2MN6、M6、2MS6等。比较明显的分潮远不止这些,将其中振幅较大(大于数值0.45 cm)、周期在一年内的分潮选出,共计有180个,基本包含第3节调和分析的170个分潮。受篇幅限制,各分潮不详细列出。
3.2 月平均和年平均潮汐数据频谱分析理论上,海洋潮汐除了包括上述年周期以下的分潮外,还包含更长周期的分潮,如交点潮(周期18.61年)、太阳黑子潮(周期11.13年)、近点潮(周期8.85年)、3.57年周期潮汐和极潮(周期1.19年)等。2.1节中的小时潮汐数据长度较短,只有32年,对于交点潮不到两个周期,对于太阳黑子潮不到3个周期,不适合长周期潮汐分析,因此采用合并之后的60年月平均潮汐数据进行频谱分析,结果如图 4所示。

|
| 图 4 月平均潮汐数据频谱图 Fig. 4 Energy-frequency for monthly tidal data |
从图 4可以清晰地看出两处峰值,第1处是年周期分潮,第2处是半年周期分潮。由于离散化原因导致频谱分析获得的周期与相应的天文分潮周期不一致,如交点潮周期实际为18.61年,但分析出来为20年,见图 5。

|
| 图 5 年平均潮汐数据频谱图 Fig. 5 Energy-frequency for yearly tidal data |
实际上,以30 d或31 d为周期平均是不合理的,因为影响最大的月分潮周期是27.554个太阳日,因此又利用年平均潮汐数据进行频谱分析,如图 5所示。表 1给出主要分潮的周期和振幅。
| 频率/(1/a) | 分潮周期/a | 振幅/cm | 接近的天文分潮 |
| 0.050 | 20.000 | 1.295 | MN(交点潮) |
| 0.083 | 12.000 | 0.629 | 太阳黑子潮 |
| 0.117 | 8.571 | 0.358 | 近点潮 |
| 0.150 | 6.667 | 0.494 | |
| 0.183 | 5.455 | 0.380 | |
| 0.200 | 5.000 | 0.314 | |
| 0.217 | 4.615 | 0.467 | |
| 0.250 | 4.000 | 0.327 | |
| 0.267 | 3.750 | 0.313 | 3.57年周期潮 |
| 0.367 | 2.727 | 0.319 | |
| 0.400 | 2.500 | 0.374 |
如果认为分析得到的潮波与天文分潮接近,就认为海面高受这种天文分潮影响,那么从图 4和表 2可看出,大港验潮站处海水面受到交点潮的显著影响。综合表 1和表 2,大港验潮站海水面受到交点潮、太阳黑子潮、6.667年、4.615年等的影响,近点潮和3.57年分潮影响不明显,其中6.667年和4.615年分潮没有找到与之对应的分潮。
| 年份 | 参考 历元 | 平均海面 /cm | 上升速率 /(cm/a) | 交点潮 振幅/cm | 太阳黑子潮 振幅/cm | 近点潮 振幅/cm | 3.57年分潮 振幅/cm | 极潮 振幅/cm |
| 1952—1980年 | 1966.0 | 242.67 | -0.107 | 0.300 | 1.829 | 0.133 | 1.224 | 0.955 |
| 1980—2011年 | 1996.0 | 243.23 | 0.159 | 2.000 | 1.117 | 0.493 | 0.581 | 1.025 |
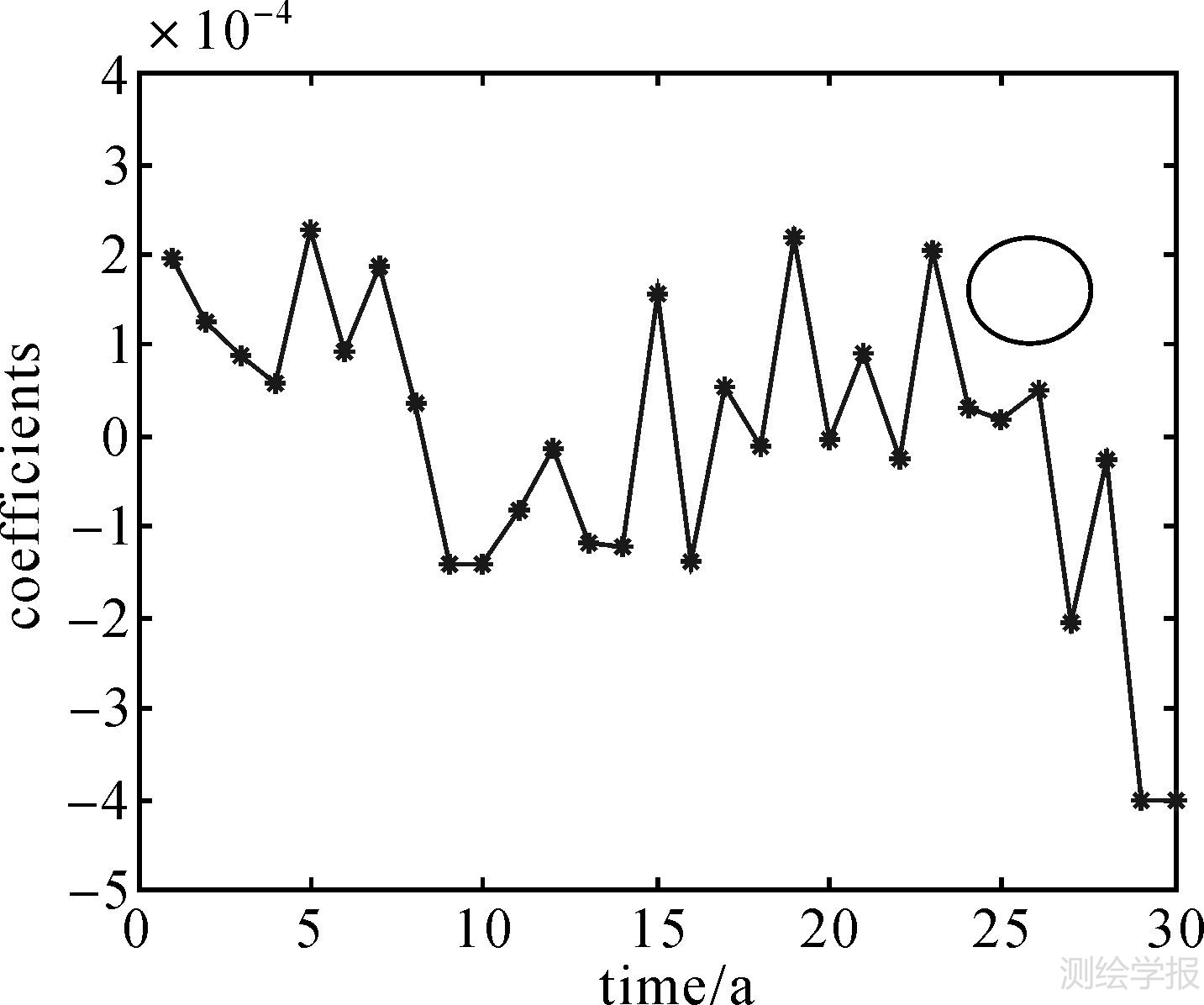
对月平均数据进行自相关分析,如图 6所示,受年周期分潮影响,其自相关值表现出很强的年周期特性,其他分潮影响被掩盖。如果认为在整年处自相关值受周年分潮影响相同,那么自相关值表现出来的不一致性可以认为是由附近的分潮引起的,为此给出整年处的自相关值,如图 7所示。从图 7可以清晰地看出,在19年处自相关值最大,可以认为是由交点潮引起的[17, 18, 19],另外在5年、7年、12年、15年和23年处自相关值也较大。5年、7年、12年与前面分析获得的4.615年、6.667年、12年一致,同样这里也没有分析得到近点潮。另外,尚不清楚15年和23年的影响原因,需要累积更多的数据或者寻找更合适的方法来分析。
|
| 图 6 月平均潮汐数据频自相关图 Fig. 6 Autocorrelation for monthly tidal data |
|
| 图 7 月平均潮汐数据频自相关图(整年部分) Fig. 7 Autocorrelation for monthly tidal data(full year) |
潮汐的引潮位理论只能给出海洋潮汐变化的基本规律和特点,并不能完全解释潮汐的各种现象。通过引潮位推导获得的潮汐振幅与某一海域潮汐的真实振幅也不一样,若想准确了解其大小及变化规律,必须通过实际观测进行潮汐分析和计算。潮汐调和分析可以根据潮汐观测数据计算各个分潮的调和常数,以了解该海区的潮汐特点、分析平均海水面变化机制,同时还可进行潮汐预报。目前,潮汐调和分析最常用的方法是最小二乘估计法[8, 20]。潮汐调和分析既适用于短时段的潮汐数据分析也适用于长时段数据分析。短时段分析是一种准调和分析,估计的分潮种类少、精度低,不需要考虑海面升降速率(每年1~2 mm的升降速率在短时间内可以忽略);长时段调和分析,估计的分潮种类多,待估参数也多,例如19年潮汐数据参数多达800多个至几千个,还需要考虑海面升降速率。这里对1980—2011年的潮汐数据逐年进行年潮汐调和分析,不考虑海面升降速率,可计算170个分潮[8],基本包含2.2节分析得到的大部分分潮。
设大港验潮站t时刻的潮高为
式中,A0为年平均海水面高;Rj、σj、θj分别为第j个分潮的振幅、频率和初相角;x(t)为随机误差。
取aj=Rjcos(θj),bj=Rjsin(θj),Rj= ,θ=arctan b/a,那么式(1)可表示为
,θ=arctan b/a,那么式(1)可表示为
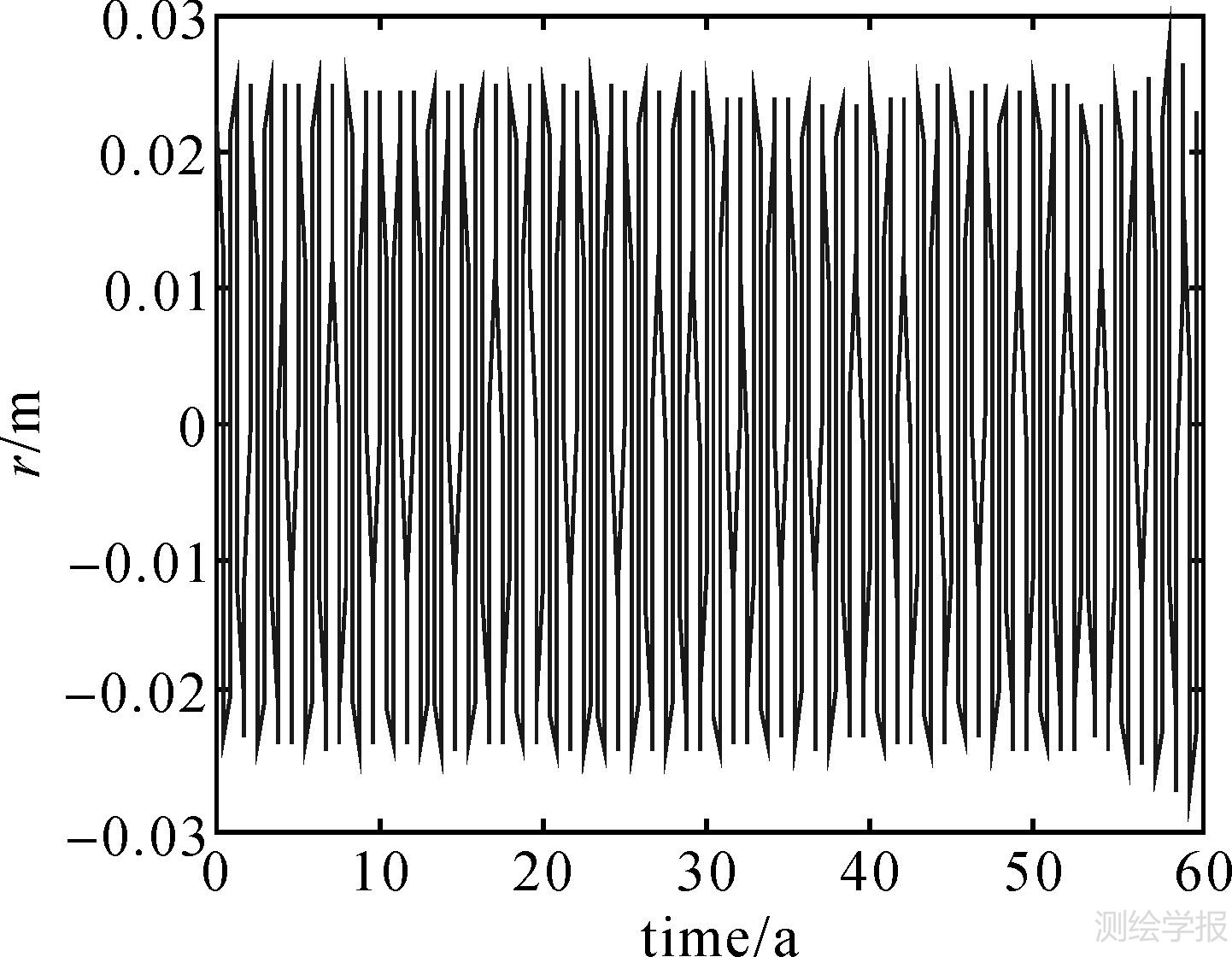
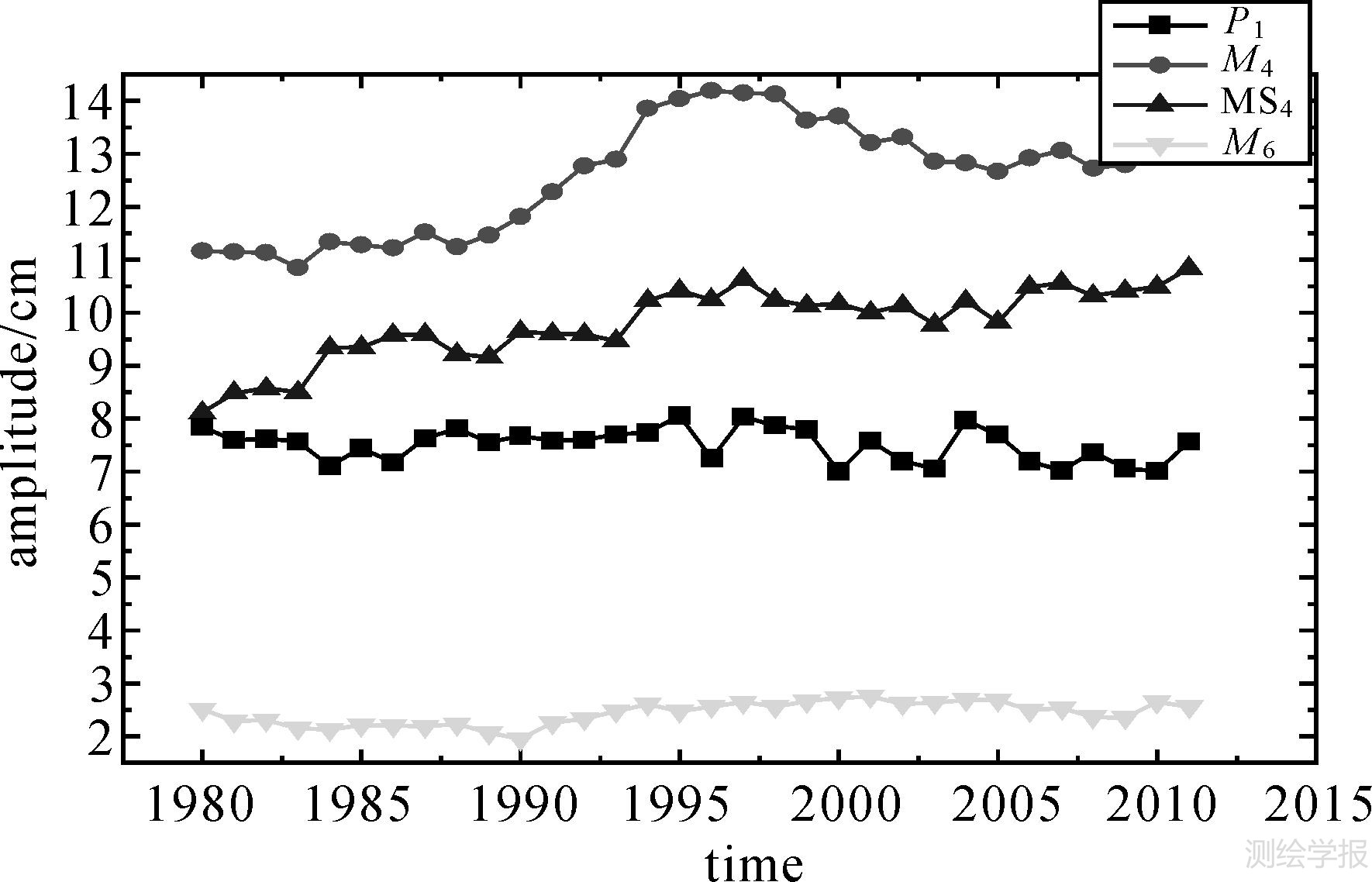
为显示验潮站处海水面的变化规律,作出了主要分潮在这32年间的振幅变化图,图 8是Q1、O1、K1、K2的振幅变化,图 9是M2振幅的变化,图 10是Sa、N2、S2振幅的变化,图 11是P1、M4、MS4、M6振幅的变化。可以看出,M2是影响大港海面高变化的主要分潮,其振幅最大达136cm,其次是S2、N2、K1、Sa等,其振幅分别达到40 cm、25 cm、25 cm、20 cm等。其他没有列出的分潮振幅很小,在1 cm量级甚至更小。

|
| 图 8 Q1、O1、K1、K2振幅的变化 Fig. 8 Changes of amplitudes of Q1、O1、K1、K2 |

|
| 图 9 M2振幅的变化 Fig. 9 Changes of amplitudes of M2 |

|
| 图 10 Sa、N2、S2振幅的变化 Fig. 10 Changes of amplitudes of Sa、N2、S2 |
|
| 图 11 P1、M4、MS4、M6振幅的变化 Fig. 11 Changes of amplitudes of P1、M4、MS4、M6 |
从图 8可看出,Q1、O1、K1、K2的振幅具有非常明显的约19年周期变化;M2尽管具有19年周期变化,但高点与低点的振幅不一致;其他分潮的周期变化不显著。应该指出,一年潮汐数据的最小二乘估计并不是完全的调和分析,估计获得的分潮的振幅和相位并不仅代表本身的振幅,还受一部分长周期分潮的影响,因此具有长周期变化。在潮汐学中,还需要通过交点因子对各个分潮的振幅进行订正获得分潮的平均振幅,来分析海域的潮汐变化,但在这里意义并不大。
式(2)中的A0代表大港从1980—2011年的年平均海面。为了检验这一结果的正确性,将该算法获得的年平均海面高与直接平均获得的年平均海面高进行比较,如图 12所示。最大差值在1.5 mm,平均值是0.071 mm,标准差是0.66 mm,可知通过最小二乘调和分析获得的年平均海面高是可信的。

|
| 图 12 A0与直接平均获得的年平均海面高的差值 Fig. 12 Difference of A0 and mean sea level |
国家高程基准由青岛大港多年平均海水面定义。温室效应造成的冰川融化、局部海底地形变迁等使得国家高程基准面产生变化。由图 2可看出,大体说来,1952—1980年平均海水面处于下降期,1980—2011年处于上升期。
国家高程基准面的变化包含两部分,一部分是长期性变化,另一部分是周期性变化。研究高程基准主要关心平均海面高和长期变化,应尽可能减小周期性变化的影响。下面通过两种方法研究高程基准面的变化。
5.1 最小二乘调和分析以年平均海面高为基础数据,在估计升降变化率k时,同时考虑交点潮(周期18.61年)、太阳黑子潮(周期11.13年)、近点潮(周期8.85年)、极潮(周期1.19年)以及具有3.57年周期的分潮。这里没有考虑2.2节中分析出的6.67年、4.62年、15年和23年周期分潮的影响,因为这些分潮尚没有找到与之对应的天文分潮,它们在频谱分析中的形成机制并不清楚,并且分析出的周期也不一定正确。
这样,年平均海面高可表达成[21]
式中,A′0为t0时的平均海水面高。图 13给出1952—1980年拟合的曲线与实际海水面图,图 14给出1980—2007年拟合的曲线与实际海水面图,表 2给出这两个时段分别计算的平均海面高、 海水面上升速率以及各分潮的振幅。

|
| 图 13 1952—1980年拟合曲线与实际海水面 Fig. 13 Fitting curving line and actual sea level for 1952 to 1980 |

|
| 图 1 1980—2011年拟合曲线与实际海水面 Fig. 1 Fitting curving line and actual sea level for 1980 to 2011 |
从表 2中可知,在1952—1980年期间太阳黑子潮、3.57年分潮和极潮对大港验潮站海面影响较大,在1980—2011年期间交点潮、太阳黑子潮、极潮对其影响较大。大港验潮站海水面在1952—1980年下降速率为1.07 mm/a,在1980—2007年期间上升速率为1.59 mm/a。
5.2 18.61年移动平均在4.1节中,仅考虑了5种分潮的影响,这是不符合实际情况的,剩余的分潮势必会影响海面升降速率和t0时的平均海水面高的计算。在计算1985国家高程基准时采用的是19年移动平均法,这里考虑采用交点潮周期18.61年(224个月)移动平均估计国家高程基准面的变化,其主要目的是尽最大可能来削弱交点潮的影响,同时减小周期小于18.61年的分潮影响。
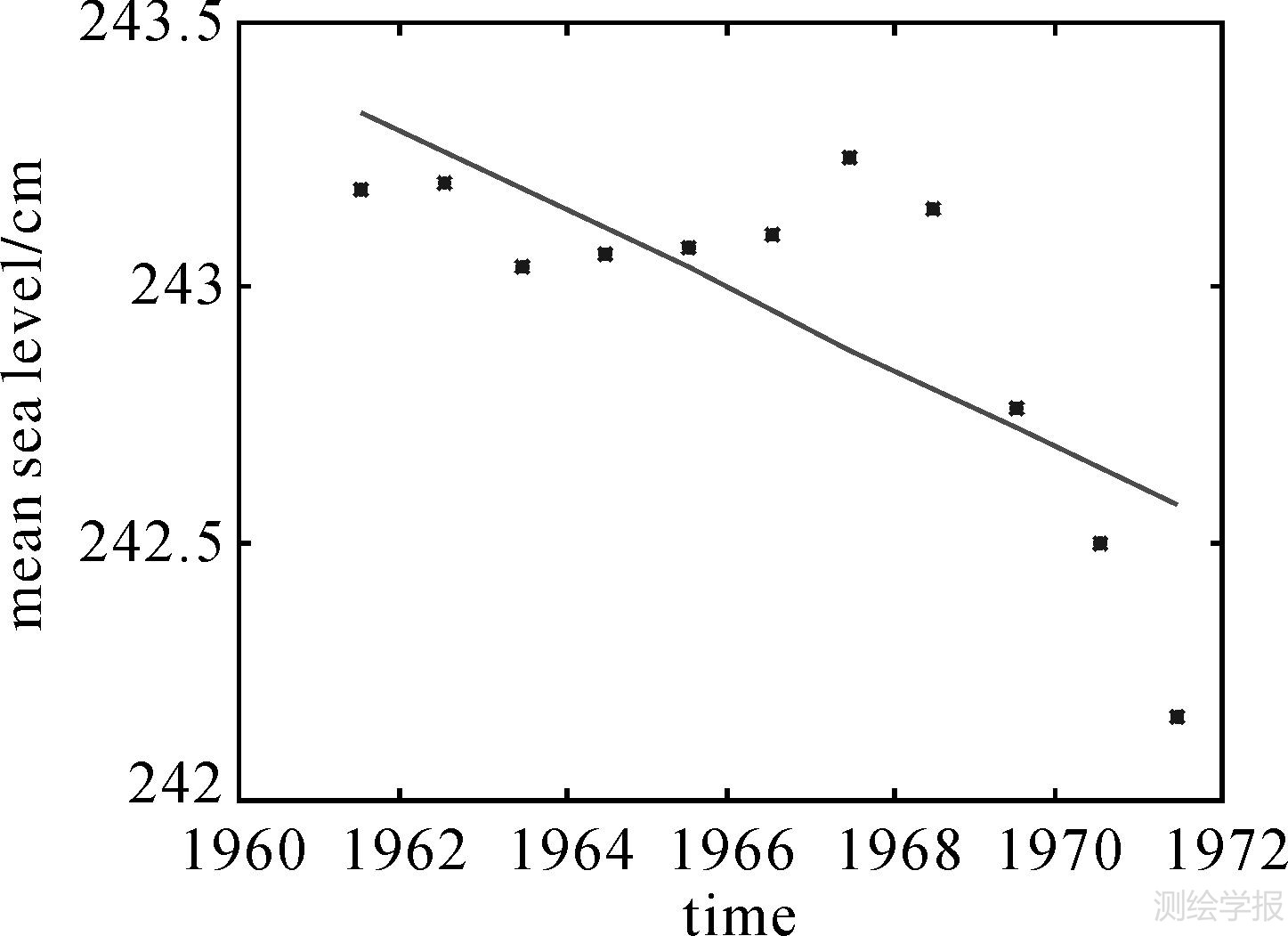
这样,在19年中(228个月)必然有4个月的数据不需要使用,为了充分利用数据,在19年中以224个月为周期进行移动平均,获得5个均值,再取其均值作为这19年的平均海面。将1952—1980年和1980—2011年的数据分别进行处理,在1952—1980年期间获得11个移动平均值,1980—2011年期间获得14个移动平均值,然后以这些移动平均值为观测值,进行一元线性回归,获得这两个时段的海面升降速率以及对应历元的平均海面高,见图 15和图 16及表 3。
|
| 图 15 1952—1980年拟合直线与平均海面 Fig. 15 Fitting line and actual sea level for 1952 to 1980 |

|
| 图 16 1980—2011年拟合直线与平均海面 Fig. 16 Fitting line and actual sea level for 1980 to 2011 |
| 年份 | 参考历元 | 平均海面 /cm | 上升速率 /(cm/a) |
| 1952—1980年 | 1966.0 | 242.98 | -0.076 |
| 1980—2011年 | 1996.0 | 243.72 | 0.162 |
由18.61年移动平均获得大港验潮站海水面在1952—1980年期间下降速率为0.76 mm/a,在1980—2007年期间上升速率为1.62 mm/a。与最小二乘调和分析相比,在1952—1980年差异较大,在1980—2007年差异不大。
5.3 比较与分析从以上分析可以看出:
(1) 最小二乘调和分析和18.61年移动平均都能够削弱一些主要分潮的影响,最小二乘调和分析能够削除交点潮、太阳黑子潮、近点潮、极潮和3.57年周期分潮的影响,也能削弱部分其他分潮的影响,18.61年移动平均能够消除交点潮和以18.61年为公倍数的分潮影响(如半日潮、日潮等),也能够削弱其他分潮的影响,但这两种方法都不能消除所有分潮的影响。
(2) 最小二乘调和分析法可以同时估计出海面升降以及某些分潮的振幅,但在同时估算时,分潮的周期性变化会影响升降速率的计算。
(3) 18.61年移动平均采用先平均削弱分潮影响后估计升降速率,分潮对速率计算影响较小,但这种方法会重复使用数据,一旦某一时段数据出现问题会放大影响面,如1952—1956年之间的数据观测精度较低且是经过修补的,是否存在问题是值得怀疑的,在最小二乘调和分析中这段数据只使用了1次,对整个计算影响较小,但在18.61年移动平均中,这段数据影响了半数左右的平均海面的计算,这也是在1952—1980年两种方法估计速率差异较大的部分原因。
(4) 相比而言,在潮位数据不存在问题的前提下,例如1980—2011年,18.61年移动平均比最小二乘调和分析法要稳定、可靠。
6 1985高程基准的检核利用18.61年移动平均对1985国家高程基准加以检核是有意义的。定义1985国家高程基准时,没有考虑海面升降的因素,采用1952—1979年10组19年周期的移动平均值的均值242.89 cm作为基准。这里笔者利用18.61年移动平均对1952—1979年潮位数据进行处理,得到平均海面高为243.03 cm,与1985国家高程基准相差0.14 cm。这说明18.61年移动平均相比于19年移动平均是有差别的,但差别不大,也说明18.61年移动平均用于计算国家高程基准是可行的。
7 结 论本文利用青岛大港1980—2011年每小时潮汐数据和1952—2007年月平均数据对大港验潮站海洋潮汐进行分析、对国家高程基准进行研究,得出如下结论:
(1) 通过每小时潮汐数据、月平均以及年平均潮汐数据的频谱分析,获知大港海水面主要受到6个长周期和180个较短周期分潮的影响,其中包括交点潮、太阳黑子潮、近点潮、极潮、年周期分潮Sa,半年周期分潮Ssa,月周期分潮Msm、Mm等,日周期分潮K1、O1、P1、Q1、S1、ψ1等,半日分潮M2、S2、N2、K2、T2、R2,8 h分潮MO3、MK3等,6 h分潮M4、MS4、S4等,4 h分潮2MN6、M6、2MS6等。
(2) 通过对每小时潮汐数据的调和分析,获知M2是影响大港海面高变化的主要分潮,其振幅达到130 cm,其次是S2、N2、K1、Sa等,其振幅分别达到40 cm、25 cm、25 cm、20 cm等,并且M2、Q1、O1、K1、K2的振幅具有非常明显的19年周期变化。
(3) 通过数据分析发现,国家高程基准面在1952—1980年呈下降趋势,在1980—2011年呈上升趋势;利用最小二乘调和分析和18.61年移动平均分别计算出相应历元的平均海面高和升降速率,并对这两种方法进行了比较。
(4)利用18.61年移动平均对1952—1979年潮位数据进行处理,得到平均海面高为243.03 cm,与1985国家高程基准相差0.14 cm。
致谢:感谢验潮部门提供潮汐数据及有关方面对使用数据提供的方便。
| [1] | GUO Hairong, JIAO Wenhai, YANG Yuanxi, et al. Systematic Error of the 1985 National Height Datum[J]. Geomatics and Information Science of Wuhan University, 2004, 29(8): 715-719. (郭海荣, 焦文海, 杨元喜, 等. 1985国家高程基准的系统差[J]. 武汉大学学报: 信息科学版, 2004, 29(8): 715-719.) |
| [2] | YANG Y X, WEN Y N, XIONG J, et al. Robust Estimation for a Dynamical Model of Sea Surface[J]. Survey Review, 1999, 35(271): 2-10. |
| [3] | CHEN Zongyong. The Method of Calculating the Mean Sea Level [J]. Journal of Ocean Institute of Shandong, 1960(1): 65-73. (陈宗镛. 计算平均海面的方法[J]. 山东海洋学院学报, 1960(1): 65-73.) |
| [4] | CHEN Zongyong. Tide[M]. Beijing: Science Press, 1980. (陈宗镛. 潮汐学[M]. 北京: 科学出版社, 1980.) |
| [5] | CHEN Zongyong, ZHOU Tianhua, YU Yifa, et al. A Study on the 1985 National Datum Level of Altitude[J]. Journal of Ocean University of Qingdao, 1988, 18(1): 9-14. (陈宗镛, 周天华, 于宜法, 等. 1985国家高程基准的研究[J]. 青岛海洋大学学报, 1988, 18(1): 9-14.) |
| [6] | WEI Ziqing. On the Permanent Tide in Geodesy [J]. Acta Geodaetica et Cartographica Sinica, 2012, 41(4): 475-482. (魏子卿. 大地测量中的永久潮汐问题[J]. 测绘学报, 2012, 41(4): 475-482.) |
| [7] | CHEN Junyong. Permanent Tides and Geodetic Datum[J]. Acta Geodaetica et Cartographica Sinica, 2000, 29(1): 12-16. (陈俊勇. 永久性潮汐与大地测量基准[J]. 测绘学报, 2000, 29(1): 12-16.) |
| [8] | HUANG Zuke, HUANG Lei. Tidal Principles and Calculation [M]. Beijing: Chinese Ocean University Press, 2005. (黄祖柯, 黄磊. 潮汐原理与计算[M]. 北京: 中国海洋大学出版社, 2005.) |
| [9] | DOODSON A T. The Harmonic Development of the Tide-Generating Potential [J]. Proceedings of the Royal Society of London, 1921, 100(704): 305-329. |
| [10] | DOODSON A T. The Analysis of Tidal Observations[J]. Philosophical Transactions of the Royal Society of London, 1928, 227: 223-279. |
| [11] | XI Qinwen, HOU Tianhang. A New Complete Development of the Tide-generating Potential for the Epoch J2000. 0[J]. Acta Geophysica Sinica, 1987, 30(4): 349-362. (郗钦文, 侯天航. 新的引潮位完全展开[J]. 地球物理学报, 1987, 30(4): 349-362.) |
| [12] | XI Qinwen. The Evaluation of the Precision of the Development of the Tidal Generation Potential[J]. Acta Geophysica Sinica, 1992, 35(2): 150-153. (郗钦文. 精密引潮位展开的精度评定[J]. 地球物理学报, 1992, 35(2): 150-153.) |
| [13] | HUANG Zuke, CHEN Zongyong, SI Hongye, et al. Analysis of 19 Year Tidal Data[J]. Science in China (Series D), 1997, 27(2): 174-179. (黄祖柯, 陈宗镛, 司鸿业, 等. 我国沿海若干验潮站的19年潮汐分析[J]. 中国科学: D辑, 1997, 27(2): 174-179.) |
| [14] | CHEN Junyong. Thinking on the Establishment of Modern Geodetic Datum of China[J]. Geomatics and Information Science of Wuhan University, 2003, 28(S): 1-6. (陈俊勇. 建设我国现代大地测量基准的思考[J]. 武汉大学学报: 信息科学版, 2003, 28(S): 1-6.) |
| [15] | CHEN Junyong. On the Chinese Modern Geodetic Coordinate System and Height System [J]. Bulletin of Surveying and Mapping, 2002(8): 1-5. (陈俊勇. 对我国建立现代大地坐标系统和高程系统的建议[J]. 测绘通报, 2002(8): 1-5.) |
| [16] | WEN Yuanlan, YANG Yuanxi. Research on Sea Level and Rising Trend of Coastal Waters in China[J]. Geomatics and Information Science of Wuhan University, 2001, 26(2): 127-131. (文援兰, 杨元喜. 我国近海平均海面及其变化的研究[J]. 武汉大学学报: 信息科学版, 2001, 26(2): 127-131. |
| [17] | QIAO Jianrong. Mean Sea Level Changes on the Yellow Sea for 60 Years[J]. Coastal Engineering, 1985, 4(2): 83-88. (乔建荣. 六十年来黄海平均海平面的变化[J]. 海岸工程, 1985, 4(2): 83-88.) |
| [18] | YU Ling, FANG Guohong. Tidal Harmonic Analysis for Long Term Sea Level Data of Tidal Gauge Stations in Seas Adjacent to China[J]. Advances in Marine Science, 2010, 28(2): 133-141. (于玲, 方国洪. 中国近海验潮站长期观测资料的潮汐调和分析[J]. 海洋科学进展, 2010, 28(2): 133-141.) |
| [19] | ZHENG Wenzhen. Distribution of Annual Rates of Sea Level and Variation of Long-period Constituents in China[J]. Marine Science Bulletin, 1999, 18(4): 1-10. (郑文振. 我国海平面年速率的分布和长周期分潮的变化[J]. 海洋通报, 1999, 18(4): 1-10.) |
| [20] | VAN ETTE A C M, SCHOEMAKER H J. Harmonic Analyses of Tides Essential Features and Disturbing Influences[M]. [S.l.]: Netherland Hydrographer, 1966: 79-107. |
| [21] | TIAN Hui, CHEN Zongyong. Stochastic Dynamical Analyses for Monthly Mean Sea Level along the Coast of China[J]. Acta Oceanologica Sinica, 1988, 28(4): 9-15. (田晖, 陈宗镛. 中国沿岸近期多年月平均海面随机动态分析[J]. 海洋学报, 1988, 28(4): 9-15.) |