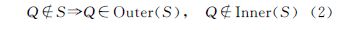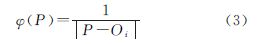1 引 言
Delaunay三角网(Delaunay triangulated irregular network,Delaunay-TIN)的构建通常有两种方法:一是根据其几何特性给出的依据“任意四点不共圆”特性[1]的构建法;二是基于Voronoi图衍生定义的生成法。
相较于Delaunay三角网来自Voronoi图的定义而言,构建法因为直接面向点集数据构模,在国内外研究应用更多,文献[2]给出了学术上认可的Delaunay三角网构TIN的主流方法,包括插入法、生长法及分治-综合方法,其中逐点插入法[3]因为简单稳定而被广泛应用,但由于插入法的效率会随着三角网数量的增加急剧下降,不适合大规模点集构TIN;生长算法[4]因为确立生成点困难且效率不占优势因而应用受限;分治-综合法[5,6,7]通常以插入法实现子网格内部建模后再进行子网的整合,但整合的过程相对比较复杂耗时。文献[8, 9]分别给出了两种基于Voronoi图的生成算法,生成法需要首先构建Voronoi图,构建的方法多种多样,效率上不能简单与直接构建法相比。
三角网构建算法从构TIN形式上讲分为完全Delaunay三角网与受限Delaunay三角网(constrained Delaunay triangulation,CDT),文献[10]就是为保障诸如道路、河沟等表达而在前者基础上进行约束的构TIN方法。绝大部分三角网的生成算法是构建于欧氏空间的,文献[11]基于应用的需要从球空间角度论述了一种立面构TIN方法,而文献[12]基于数据来源的不同研究了在栅格空间中进行构TIN的不同实现。
插入法构TIN的基本方法就是在已知网上确立插入点的影响域[13],通过插入点与影响域的边界重构替代原来的域内三角形,外接圆的判断方法虽然简单,但如何快速从大量急剧增加的三角形中查找到域内三角形,成为海量空间点构TIN的重要瓶颈。分治-综合建模方法就是采取化整为零、分大为小的方法实现对大空间的网格分割后在较小的网格中按插入法各自构TIN得到各个网格的子三角网,然后再实现各个子网的合并。其困难是子网综合的复杂性既影响了构TIN的稳定性,也增加了额外的时间消耗,同时递归的处理方式也不能达到并行处理的效果。
在这3种传统算法之上,文献[13, 14]还给出了一种利用良好的数据组织形式或虚拟网格结构从逻辑上区域化记录一个搜索起始三角形,显著提高插入点影响域搜索效率的方法,是一种逻辑上区域化的改进型插入法,没有复杂的子网合并过程。
在应用层面,随着大数据时代的到来,各种并行构TIN[15]、多核异构并行构TIN[16]或是流式构TIN[17]应对大数据高效需求的算法研究成为热点。本文结合对空间的物理分割,借鉴分治-综合法的局部处理策略,融合生长法的膨胀思维,逆向思维,采取相反的先分后总、由外而内的收缩建模方法,避免了网格之间复杂的综合过程,是一种新型的总分式空间建模方法。与分治方法相同的是,其根本实现构TIN的手段也是插入法构TIN。通过基于LOD概念的层次网格划分,实现了由整体到局部、先总后分的构TIN实现,并运用多线程技术高效地实现了各个子网格的并行构TIN。
2 基本原理
设海量点云数据N在投影空间上构成的最小外接矩形区域为S,算法的核心思想是:对大空间S细分为{S0,S1,S2,…,Sm}个子空间,使得任意两个子空间Si,Sj有Si∩Sj=ø,且有S= =Si。
=Si。
与传统的分治-综合法相比,为了让网格间的综合变得相对简单,通常采用四叉树的均分网格形式[18]进行空间划分,即相同层级的网格其空间大小是相同的,但本文算法中,由于没有后期复杂的网格拓扑综合过程,对网格的划分完全可以根据点群的局部密集度来进行。其划分原则是假定点是均匀分布的,按照总共需要的子网块数及空间的纵横比来确立。如以规模上限LN=200为例,当一个网格里的点数大于200时,该网格需要平均地分为C×R个子网格,结合网格的空间大小(设网格空间长WG、HG)与网格内点的数量N,C与R的计算规则如下
按式(1)对整个大区域进行递归逻辑空间分割后,点云与网格的映射关系如图 1所示。
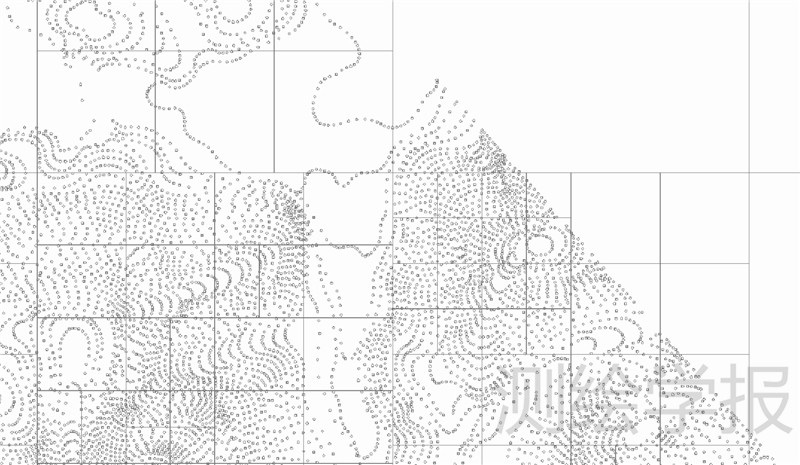
|
| 图 1 自适应网格划分图 Fig. 1 Self-adaptive grid division |
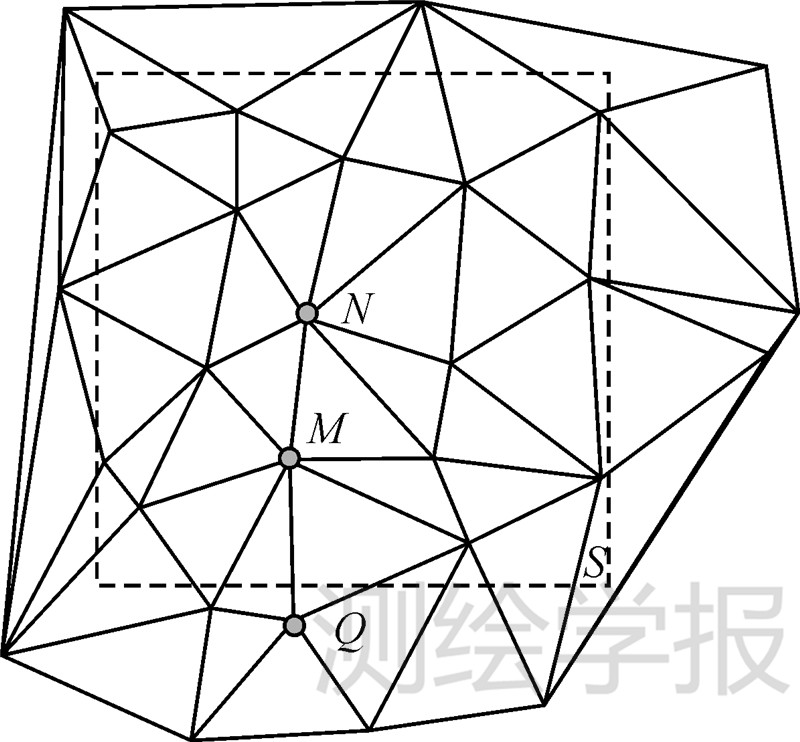
定义:对给定的Delaunay三角网,顶点P及网格S,如果顶点P的所有三角形均包含于网格S内部,则称点P为网格S中的逻辑内部点,P∈Inner{S};否则称P为逻辑外部点,P∈Outer{S},如图 2所示。
|
| 图 2 网格的逻辑内部点定义 Fig. 2 Definition of grid logical interior points |
图 2中对给定的网格S,M、N均为网格中的顶点,物理划分上
N∈S, M∈S
逻辑划分上
N∈Inner(S),M∈Outer(S)
很显然有
由式(2)可见物理划分与逻辑划分上的不同特性,上述判断的依据是根据已经存在的Delaunay三角网。三角网的构建实质是建立点与点之间的拓扑逻辑关系,根据Delaunay三角网的构建特性,对给定的点集,其Delaunay三角网是唯一确定的[19],与建模的过程无关。
对给定的点云集N及给定的网格区域S,无论是否已对点云构建Delaunay三角网,S中的任意点P其归属于Inner{S}还是归属于Outer{S}是确定的。这一认识对总分并行式构建三角网思想提供了根本的理论支持:对每一个子网格Si中的所有点再进行逻辑划分,预先形成网格内部Inner{Si}与网格外部Outer{Si}的集合。首先从总体布局上对每一个网格逻辑外部点Outer{Si}利用传统的Delaunay插入法建立全局三角网,然后分别对各个网格的逻辑内部点Inner{Si}进行构TIN,由前述定义可知,Inner{Si}中的点拓扑三角形都会局限于网格内部,有益于各网格并行构TIN的实施。
困难的是,在未建立完整的三角网之前,虽然点P与网格Si的内外部关系是确定的,但是却难以确立,从而导致上述思想的实施困难。但可以依据空间点的邻近关系对Si中每一个点P建立其对网格Si的影响力因子公式,定义为
式中,Oi为网格Si的中心点,即网格中的点离网格中心距离越近,对网格中心的影响力越大,越有可能是属于Inner{Si},反之则越有可能属于Outer{Si},如图 3所示,设ξ为某一方向上的界定逻辑内外部点的影响因子阈值,则有
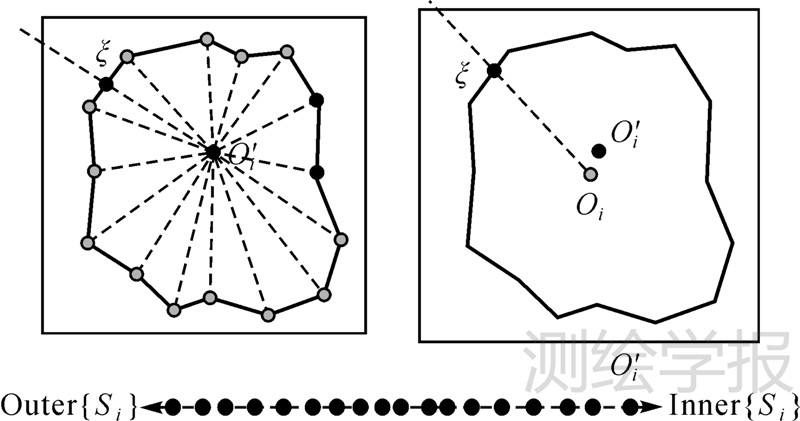
|
| 图 3 基于方位划分的网格逻辑内外部界定 Fig. 3 Definition of grid logical interior points |
Inner(Si)={P|P∈Si,φ(P)>ξ}
Outer(Si)={P|P∈Si,φ(P)≤ξ}
可见存在方向与分割阈值ξ界定的困难,但如果将网格Si中的所有点按到中心Oi的距离从大到小进行排序,则队列前面的点比队列后面的点更有可能属于Outer{Si}。
在此基础上要界定方向与分割阈值ξ,首先要确立一个方向原点,由于网格中心Oi并不真实地存在于网格Si中,为避免方向判断上的困难,选取离中心最近的队列尾结点作为方向的原点。
定义:在网格Si的所有顶点集中,定义最靠近网格中心的顶点为网格的参考中心点,记为O′i。
为了建立各网格的方向三角形,对Si顶点队列进行微调整,将O′i置首,优先构建起网格的方向三角形及网格间的均衡三角网。如此对方向的确立可以按与O′i关联的方向三角形来进行判断,n个关联三角形就可以将周围360°方向角划分为n个具体的区域方位。
定义:在总分式网格建模过程中,网格Si中以O′i为顶点的所有三角形称为方向三角形。由方向三角形所覆盖的区域称为网格的闭包区域DT。闭包区域上所有边界顶点均位于网格Si的内部时,称为物理闭包区域DTP;同样可以定义与闭包区域边界直接关联的外部顶点均为网格逻辑内部点的区域为逻辑闭包区域DTT。
从算法目的上,前面所有定义的目的就是为了在适当情形下启用网格的分化并行建模,如图 4所示。
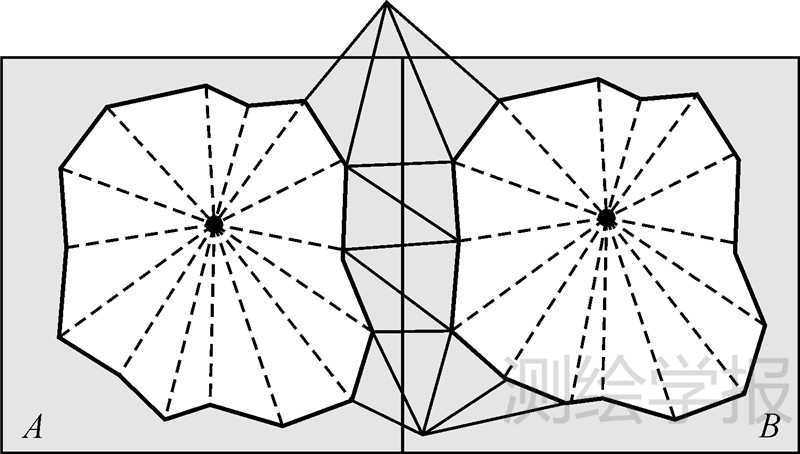
|
| 图 4 网格的逻辑内部点定义 Fig. 4 Definition of grid logical interior points |
对两个相邻网格A、B,如果分别启用一个独立线程进行建模,由于拓扑关系的存在,两个闭包之外的三角形就有可能同时被两个线程同时进行访问修改,从而引发线程间的并发冲突,虽然从并发程序上可以通过锁存控制来让某一个线程进行等待来保障程序进行下去,但过于频繁的并发冲突处理将会严重地影响到算法的效率,因此,从算法思维上减少并发访问冲突是非常必要的。
DT、DTP、DTT给出的定义也都是针对方向三角形的建模过程的,理论上讲,DTT区域由于外围顶点也是网格自身的内部资源,不会与相邻网格存在并发冲突,但DTT在建模过程中是难以确立的。但可以根据对DT的初步判断来尽可能地减少冲突,推迟甚至避免性能不高的线程启用。判断条件逐步检测如下:
(1) 网格建模的初期,属于自己内部的三角形数量相对较少,网格间共享的三角形比较多,因此可以从实现周期上进行控制,对网格的前若干个插入点建模时不作多线程检测及启用多线程;实践经验是前200个顶点免检基本可以达到稳定的并行处理效果。
(2) 如果DT不是DTP,则DT一定也不是DTT区域。这时冲突会大量存在,达不到进行网格独立建模的基本条件,不能采用多线程进行。
(3) 对DT边界的外围关联三角形的顶点进行判断,相当于沿DT向外作了一个三角形的缓冲拓展得到一个新的闭合区域DT′。对DT′进行类似步骤(2)的判断,当DT′为网格的物理闭包区域时,再启用多线程进行建模,可以极大地减少并发冲突的发生。
对步骤(3)的检测实施需要求取闭包区域的外围缓冲区域,也需要消耗较多的计算时间,如果直接利用拓扑关系,使用方向三角形的邻接三角形顶点来进行判断,可以简化检测过程同时能够起到如完全缓冲检测相接近的冲突减少效果,如图 5中所示。从理论技术上,现在还无法确切地在建模过程中区分出内外部逻辑点及逻辑闭包区域,要做的工作就是尽量减少并发冲突发生的可能性,无法避免的冲突再交由线程的安全访问机制进行解决,但这些概念的提出,却有助于总分式并行构TIN算法的提出与技术实施。
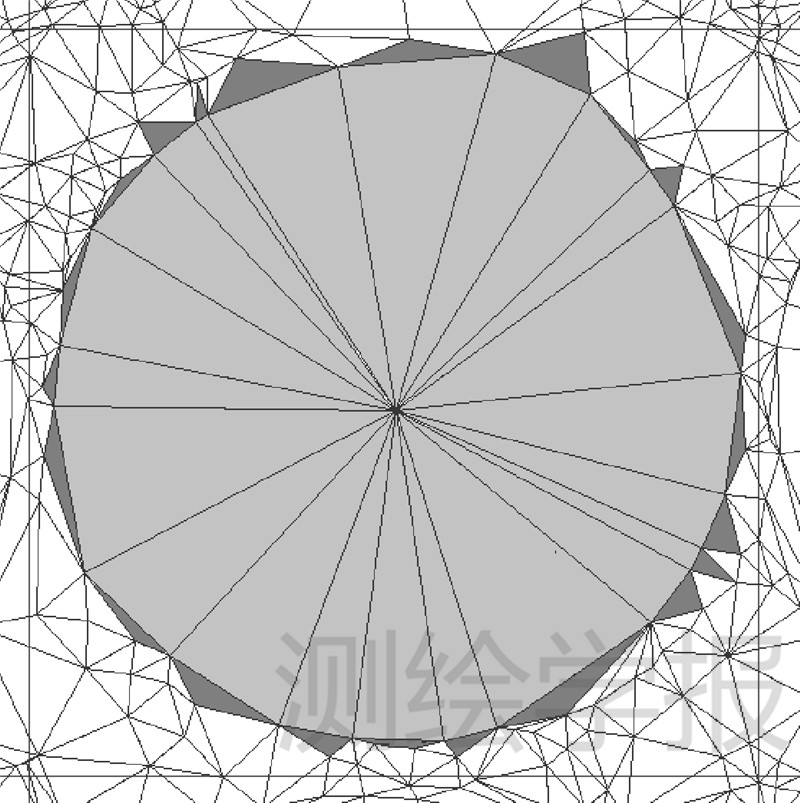
|
| 图 5 网格检索封闭闭包区域 Fig. 5 Grid enclosed area searching |
在前面的网格划分及网格内的数据进行排序等预处理后,可以利用传统的插入构TIN法来逐步构建三角网。插入构TIN法是一种性能非常稳定的构TIN方法,根据检索定位插值点所在的三角形的方法,可以分为查找插入法和拓扑插入法。查找插入法需要对每一个生成的三角形进行逐一搜索并判断插入点是否在三角形中,随着三角形数据的急剧增加,查找效率会急剧下降,对海量点云数据构TIN不可接受,但其不依赖拓扑关系,无先决条件要求。拓扑插入法通常是通过指定的起始三角形依据拓扑关系通过方向搜索[13]的方式沿路径找到插入点所在的三角形,比查找插入法有更高的效率,但与起始三角形的维系和搜索路径长度有关。
本文充分发挥两者的各自优势并综合运用,实现建立三角网的全过程。总分式构建三角网的方法是基于每一个网格Si的循环处理。对每一个网格Si(0≤i≤m)的一次处理过程定义为一个处理周期,为描述方便,记网格Si中点的最大个数为LN,实际点数为Ni(0<Ni≤LN),网格的第k(0<k≤LN)个处理周期插入点为Pik,构成的三角网记为DTS(k),则第k周期构TIN结束后,参与构建的三角网的顶点数可记为
在不同的处理周期中,可以采用不同的方法建立三角网:
(1) k=1时,三角网为空,无初始条件且三角形数量较少,采用查找插入法对每一个网格的O′i构建起始的均匀三角网。
一个处理周期后就可以确立方向三角形,建立三角形之间的拓扑关系及指定用于方向拓扑搜索的起始三角形。但考虑到此时三角形数量并不多,且DT(Si)具有明显的外部三角形特征,查找插入效率与方向搜索插入效率相比不会有太大的劣势,故还可以再多执行几个周期,如k→K,K=2,3,4,5,6…,通常可执行到k=5,此时不仅三角网的数量已显著增加,除O′i外的Pi2、Pi3、Pi4、Pi5 4个插入点,按点集均匀分布特征评估将分别位于网格Si的四角点附近,可以初步形成网格内的闭包区域,有助于后续方向搜索与逻辑内部点的判断。
K个周期执行完成后,将采用方向拓扑搜索法插入构TIN,需要指定起始三角形,自外而内的插入法有一个显著的特征是,每一个周期完成后插入点所构成的新三角形中,均至少存在一个与O′i顶点关联的三角形,指定其中一个三角形为网格Si的起始三角形,为下一个周期的顶点插入构TIN提供检索条件。与文献[13]确立的起始三角形相比,这种绑定网格中心的指定具有非常短的搜索路径,对Si的n个方向三角形而言,其搜索长度不大于n/2个三角形。
(2) 对k=K+1至LN个执行周期,采用方向拓扑搜索插入法依次对各个网格进行建模并更新网格关联的起始三角形。若网格Si中待插入点Ni-k≤0,则表明该网格已经提前完成建模,不再对其进行处理。
按上述步骤,完成LN个周期后,能够保障所有网格中的所有点均已构建到三角网中,不需要引入并行线程就可以完成三角网的整体建模。由于更临近的起始三角形指定及更高效的方向搜索方式,其效率已明显优于分治-综合方法给出效率值,在普通PC机上,处理212 459个点建模时,效率可达9.23 s。图 6展示了不同周期时三角网的构成结构。

|
| 图 6 三角网建模插值到k个采样点时效果图 Fig. 6 Interpolation of the k-th sampling points to the triangulation model |
从图 6可以看出,与传统的插入法相比,由于插点排序的存在,在总体构TIN过程中会优先在网格间的外围区域形成稳定的Delaunay三角形,构成计算机内存中的静态数据,不仅有效地提高了后续构TIN的访问效率,更可以在大规模构TIN过程中逐步输出这些成果并从内存中释放空间。
为了更加高效地提高建模效率,可以在上一步的每一个周期末对网格待插入点集进行逻辑内部点的判断,然后运用计算机多线程并行技术独立运用拓扑插入法对余下的点集进行建模。检测方法前面已经给出,但检测与多线程开启也是有系统额外开销的,可以对具备较大访问冲突的前若干个周期(如k<200)不进行检测,或对网格中剩余插值点数小于一定数量的网格不进行检测与独立线程的启用,如Ni-k<200,因为这种情形启用一个新线程的时间资源开销可能比直接在主线程中完成的开销更大或相当,并行线程在大量点集下启用更具规模优势。
4 试验分析除了点云总数量SN、网格规模限定LN、查找插入点数K等控制参数对算法效率有直接影响外,插入法构TIN都会涉及频繁地大量删除影响域内的三角形。经过试验表明,批量进行三角形队列删除整理比针对每一个插入采样点进行即时删除具备更高的效率,这样可以通过标记无效来排除三角形,等到无效三角形的个数达到给定规模数DTN时再从队列由后向前地进行一次性删除。
试验结果如图 7所示,当DTN=5000时,具备最优的队列重整效果。
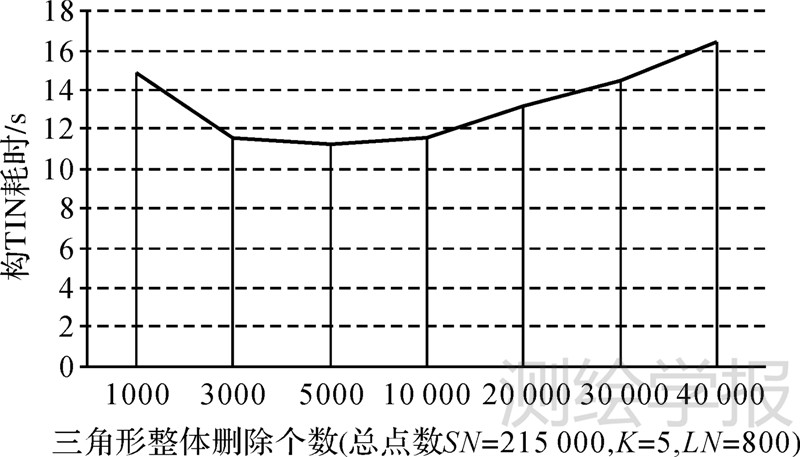
|
| 图 7 三角形统一删除个数与构TIN效率关系图 Fig. 7 Relationship between deleted number of triangle and modeling efficiency |
通过引入多线程并行构TIN机制后,有效地提高了整体空间构TIN的效率,同等测试条件下构TIN的时间由先前的9.23 s减少为5.76 s,同时当网格中限制点数LN趋大时,构TIN的时间消耗依然保持了稳中有降的规模优势,如图 8所示。
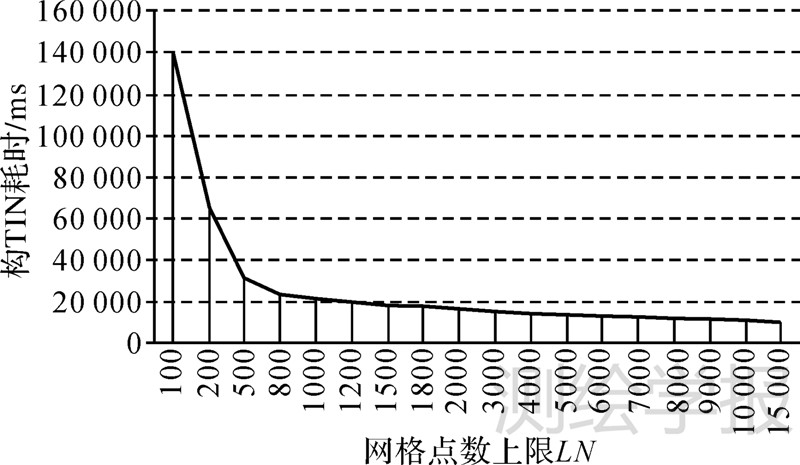
|
| 图 8 网格最大点数上限与构TIN效率关系图 Fig. 8 Relationship between the max number of grid points and modeling efficiency |
经过综合测试,当DTN=10 000时,各项指标与构TIN的效率如表 1所示。
| 总点数SN | LN | k | 三角形数 | 耗时/s |
| 209 396 | 800 | 5 | 316 182 | 12.968 75 |
| 212 459 | 800 | 3 | 313 992 | 12.421 87 |
| 212 459 | 800 | 2 | 303 908 | 11.609 37 |
| 27 342 | 2000 | 5 | 21 275 | 0.281 25 |
| 297 785 | 5000 | 5 | 458 363 | 13.437 5 |
| 297 785 | 15 000 | 5 | 442 703 | 10.328 12 |
| 70 656 | 2000 | 5 | 76 653 | 1.218 75 |
| 137 631 | 2000 | 5 | 163 523 | 3.437 5 |
| 137 631 | 1000 | 5 | 169 366 | 4.390 62 |
| 137 631 | 200 | 5 | 203 336 | 12.062 5 |
| 212 459 | 2000 | 5 | 316 183 | 9.484 37 |
| 212 459 | 10 000 | 5 | 316 183 | 5.765 62 |
通过试验结果可以进一步看出:当点云规模相当,网格限定一致的情形下,网格内查找插入法使用点数k越多,耗时越多,这与顺序查找插入法的特性相吻合的;但同时,k越大,生成的有效三角形数越多,这同样表明查找插入法具有局部拓扑插入法不可比拟的全面覆盖特性。因此,保持适当规模的查找插入数量是非常必要的。
5 结论与展望本文提出的总分式并行构TIN技术通过算法与编程技术的综合应用,能够显著提升传统地形数据建模的吞吐量,有利于实现更大区域的实时整体建模,有利于实现更精细数据的细节建模。算法实现简单、运行稳定,能够为数字区域、数字城市、数字地球提供强有力的数据整合建模,对大型工程的数字化实现提供了非常现实的实现手段。下一步将研究明确界定网格内外部的先前判定理论来替代逐步检测机制、开展更大点云规模的构TIN测试以更全面量化统计多线程的冲突数、不同参数条件下的算法效率统计与优化外,同时将针对网络传输下的空间大数据流式建模展开应用研究,以更好地满足网络环境下大区域地形的实时建模表达。
| [1] | DELAUNAY B. Sur la sphère vide, Izvestia Akademii Nauk SSSR[J]. Otdelenie Matematicheskikh i Estestven-nykh Nauk, 1934(7): 793-800. |
| [2] | WU Xiaobo, WANG Shixin, XIAO Chunsheng. A New Study of Delaunay Triangulation Creation[J]. Acta Geodaetica et Cartographica Sinica, 1999, 28(1): 28-35. (武晓波, 王世新, 肖春生. Delaunay三角网的生成算法研究[J]. 测绘学报, 1999, 28(1): 28-35.) |
| [3] | LEWIS B A, ROBINSON J S. Triangulation of Planar Regions with Applications[J]. The Computer Journal, 1978, 21(4): 324-332. |
| [4] | GREEN P J, SIBSON R. Computing Dirichlet Tesselations in the Plane[J]. The Computer Journal, 1978, 21(2): 168-173. |
| [5] | LEE D T, SCHACHTER B J. Two Algorithms for Constructing a Delaunay Triangulation[J]. International Journal of Computer & Information Sciences, 1980, 9(3): 219-242. |
| [6] | HU Jinxing, MA Zhaoting, WU Huanping, et al. Massive Data Delaunay Triangulation Based on Grid Partition Method[J]. Acta Geodaetica et Cartographica Sinica, 2004, 33(2): 163-167. (胡金星, 马照亭, 吴焕萍, 等. 基于格网划分的海量数据Delaunay三角剖分[J]. 测绘学报, 2004, 33(2): 163-167.) |
| [7] | RUI Yikang, WANG Jiechen. A New Study of Compound Algorithm Based on Sweepline and Divide-and-conquer Algorithms for Constructing Delaunay Triangulation[J]. Acta Geodaetica et Cartographica Sinica, 2007, 33(2): 163-167. (芮一康, 王结臣. Delaunay三角形构网的分治扫描线算法[J]. 测绘学报, 2007, 33(2): 163-167.) |
| [8] | DWYER R A. A Faster Divide-and-conquer Algorithm for Constructing Delaunay Triangulations[J]. Algorithmica, 1987, 2(1-4): 137-151. |
| [9] | MOSTAFAVI M A, GOLD C M, DAKOWICZ M. Delete and Insert Operations in Voronoi/Delaunay Methods and Applications[J]. Computers & Geosciences, 2003, 29(4): 523-530. |
| [10] | CHEN Chujiang, WANG Defeng. CDT Fast Generation from Mass Geographic Data and Real Time Updating[J]. Acta Geodaetica et Cartographica Sinica, 2002, 31(8): 262-265. (陈楚江, 王德峰. 海量数据CDT快速建立及其实时更新[J]. 测绘学报, 2002, 31(8): 262-265.) |
| [11] | ZHANG Fan, HUANG Xianfeng, LI Deren. Spherical Projection Based Triangulation for One Station Terrestrial Laser Scanning Point Cloud[J]. Acta Geodaetica et Cartographica Sinica, 2009, 38(1): 48-54. (张帆, 黄先锋, 李德仁. 基于球面投影的单站地面激光扫描点云构网方法[J]. 测绘学报, 2009, 38(1): 48-54.) |
| [12] | CUI Xueseng, YANG Shenglong, FAN Wei. Grid Based Local Subdivision Algorithms for Constructing Triangulated Irregular Network under Restriction Conditions[J]. Acta Geodaetica et Cartographica Sinica, 2008, 37(2): 196-199. (崔雪森, 杨胜龙, 樊伟. 基于栅格局部细分的带约束条件的不规则三角网生成算法[J]. 测绘学报, 2008, 37(2): 196-199.) |
| [13] | PU Hao, SONG Zhanfeng, ZHAN Zhenyan. On the Method for Fast Constructing Delaunay Triangulation DTM[J]. China Railway Science, 2001, 22(6): 100-105. (蒲浩, 宋占峰, 詹振炎. 快速构建三角网数字地形模型方法的研究[J]. 中国铁道科学, 2001, 22(6): 100-105.) |
| [14] | XIA Shaofang, CHEN Lichao, LIU Jia. High Efficient Algorithm for Building Delaunay Triangulation Based on Virtual Grid[J]. Computer Engineering and Design, 2009, 30(1): 238-240. (夏少芳, 陈立潮, 刘佳. 基于虚拟网格的高效Delaunay三角网生成算法研究[J]. 计算机工程与设计, 2009, 30(1): 238-240.) |
| [15] | LI Jian, LI Deren, SHAO Zhenfeng. A Streaming Data Delaunay Triangulation Algorithm Based on Parallel Computing[J]. Geomatics and Information Science of Wuhan University, 2013. 7, 38(7): 794-798. (李坚, 李德仁, 邵振峰. 一种并行计算的流数据Delaunay构网算法[J]. 武汉大学学报: 信息科学版, 2013, 38(7): 794-798.) |
| [16] | WU H Y, GUAN X F, GONG J Y. Para Stream: A Parallel Streaming Delaunay Triangulation Algorithm for LiDAR Points on Multicore Architectures[J]. Computers & Geosciences, 2011, 37(9): 1355-1363. |
| [17] | ISENBURG M, LIU Y X, SHEWCHUK J, et al. Streaming Computation of Delaunay Triangulations[J]. ACM Transactions on Graphics, 2006, 25(3): 1049-1056. |
| [18] | SONG Zhanfeng, PU Hao, ZHAN Zhenyan. Study on an Algorithm for Fast Constructing Delaunay Triangulation[J]. Journal of the China Railway Society, 2001, 23(5): 85-91. (宋占峰, 蒲浩, 詹振炎. 快速构建Delaunay 三角网算法研究[J]. 铁道学报, 2001, 23(5): 85-91.) |
| [19] | MILES R E. Solution to Problem 67-15 (Probability Distribution of a Network of Triangles)[J]. Society for Industrial and Applied Mathematics, 1969, 11(3): 399-402. |