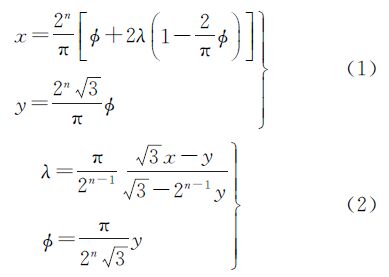2. 河南省测绘地理信息局，河南 郑州 450003
2. Henan Administration of Surveying,Mapping & Geo-information,Zhengzhou 450003,China
1 引 言
地球是一个普通的天体，整个地球重力场是一个以地球质心为中心、具有多圈层结构的流形空间[1]。数字地球则是一个技术概念，即一种基于当代信息技术、可以嵌入海量地理数据的、多分辨率的和三维的地球表示，是把地理空间信息按照地理位置进行无缝集成而形成的一个球状模型[2, 3]。数字地球第一次把人类的视角抬升到了高空，并对地表进行多尺度建模与表达，可以认为是继语言文字、地图和地理信息系统(GIS)之后的第4代地学语言。随着信息和航天技术的发展，人们利用全球分布的大量服务器系统和高效的空间数据传输与三维可视化技术，将大量覆盖全球的高分辨率影像数据组织成逻辑上的数字地球平台，使任何人在任何时候都可以查询到全球任何地方的地理空间信息[4]。本世纪以来，以Google Earth为代表，人们业已建立了50余种数字地球平台[5]，成为当代地理信息技术的重要标志[4]。
与基于欧氏投影模型的地图和GIS不同，数字地球平台采用了非欧流形的空间数据模型——全球离散网格体系(discrete global grid systems，DGGS)[6]。它是一套覆盖整个球面的网格集合，每个网格单元(瓦片)与其内的一个单独点相关联[7]，具有层次性和全球连续性特征，可以以一定的精度对多分辨率的空间数据进行规范表达、组织、分析和计算，有望从根本上解决平面模型在全球多分辨率空间数据管理上的断裂、变形和拓扑不一致等问题[8, 9, 10]。从传统经纬网格到正多面体网格，有超过15种的球面网格剖分方案被提出，我国学者还将其推广到了椭球[11]。上述第一代数字地球模型，利用球面剖分瓦片，构建了2.5维的地球表面，第一次恢复了地表的流形性质，实现了多源多尺度空间数据的无缝集成、共享与可视化，可以进行查询、浏览、标注、量算和线路规划等简单的空间地理计算。然而，数字地球仪模型本质上是静态的表面建模，基本不涉及地表上下的空间，无法实现天地一体化的地理空间大数据的有机整合，不支持面向大区域和全球尺度的、综合的大型地理计算，尤其是不能基于社会与环境过程模型模拟地球将来的状态[12]。因而，研究真三维数字地球模型，构建面向地理空间过程的动力学计算平台，十分重要和必要，是数字地球发展的必然趋势。
真三维数字地球平台必须建立在球体三维剖分的基础上。全球三维体剖分(Earth system spatial grid,ESSG)[1]与二维球面剖分(DGGS)的研究基本上是并行发展的。球体剖分主要有球体经纬网格、球面三角网径向延伸网格[13]、cubed-sphere网格[14]、阴阳网格[15]、基于球面三角网和径向不连续面划分的网格[16]、适应性细分网格[17]、退化八叉树网格(spheroid degenerated octree grid,SDOG)[18]、地球圈层网格(sphere shell space grid，S3G)[19]和大圆弧QTM八叉树网格(sphere geodesic octree grid,SGOG)[20, 21]等9种。全球三维离散网格考虑了地表之下的空间剖分，尤其是后3种方案实现了整个重力场的剖分，彻底恢复了地理空间的流形性质。然而，作为地理信息科学空间数据模型的ESSG，必须具备整体性、系统性、基准性的特征，也就是说面向地理信息科学应用的剖分网格体系必须具备紧致(没有重叠)、递归(剖分)、(形状与粒度相对)均匀、(编码、拓扑关系)一致、(与传统坐标系对应)整齐等基本要求[1, 20, 22]。对照这些要求，会发现上面列举的9种方案中，前6种模型除经纬网格外都是针对某一领域或某种应用而设计的“一次性”网格系统，都较为严重地违背了这些标准的主旨(包括经纬网格)，不适宜作为地理信息科学的空间数据模型。只有后3种模型基本符合这些标准，可以作为面向地球系统复杂地理计算的空间数据模型。
上述3种网格又各有特点。SDOG是球面退化四叉树网格向球体的推广，通过变经纬剖分的方法达到整个网格体系的相对均匀，具有非收敛、非叠置、正交、经纬一致性的特点，但其实质是球面变经纬网格的扩展，仍存在网格体系及其空间关系复杂、网格单元的形状和粒度变化较大的问题[19, 21]。S3G基于地球的圈层结构，分别在中纬度和两极地区，采用不同的剖分规则，实现对地球的近似均匀剖分。理论上更为精确，有多种自由度，两极单独处理，避免了极点的奇异化，大部分是经纬正交网格。但剖分规则多样，剖分体系复杂，体元变形较大，几何特征模糊。尤其是这两种网格均属于经纬网格范畴，不能推广到椭球(定义大地纬度的椭球法线一般不通过椭球中心)，无法实现基于椭球流形的地理空间精准建模。本文基于QTM瓦块构建了真三维的数字地球模型，并实现了地表、地下和空中空间实体的建模与可视化。
2 球体大圆弧QTM八叉树剖分(SGOG)的理论体系
全球离散剖分体系的网格是构建数字地球平台的砖和瓦[12]。完整的全球离散网格理论体系包括以下主要内容：剖分原理、网格几何特征分析、编解码方法及其应用等。
2.1 剖分原理
在DGGS领域，QTM网格具有定位明确、结构相对简单、变形适中的特点，是所有离散网格中研究最多、应用最广的离散网格模型[23]。SGOG剖分的基本原理为：把地球近似视为球体，首先用0°~180°首子午圈、东西经90°子午圈和赤道把球体八等分；然后，对每一个八分体的球面和径向进行递归剖分。对球面而言，把每个球面三角形3个边的中点以大圆弧连接，进行QTM递归四叉树剖分，同时在径向上，以等长半径的球面进行二叉树递归剖分，或者以不等长半径的球面进行二叉树递归剖分，剖分的层次n依据具体的应用而定。这样，就可以把球体分割为整齐一致的球面三棱台(上下底面为球面，侧面为平面)和三棱锥(球心处)。这些棱锥和棱台统称为网格体元，以其几何中心为参考点。把包括大气层在内的整个重力场看作一个球，依据以上方法便可实现对整个重力场的剖分[20, 21]。其中径向不等长剖分也叫变长八叉树剖分，可以起到调节体元粒度的作用。比如以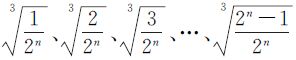
的比例剖分，可以实现径向所有网格的体积相等[21]。
2.2 网格几何特征分析
SGOG大圆弧网格体系，形状简单，排列规整，空间拓扑关系一致。网格体元瓦块的几何特征明晰，均可用精确的数学公式表示(表 1)。
| 几何特征 | 数学公式 | 备注 |
| 中心点坐标 | 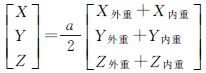 | 重——三角形的重心坐标(平面三角形，为三个顶点坐标的算术平均数)；内、外为网格内、外三角底面；a为放大系数，即把欧氏三棱柱上下底面中心连线的中点“放大”(投影)到球面上，其半径为：R=R内+(R外-R内)/2；α为球面三角形三顶点矢量所夹的圆心角的度数(正数)；R为(地)球半径；n为剖分层次；A、B、C为球面三角形的三个内角(可通过网格三个侧面所夹的二面角求得)；θ为球面三角形的内角和；球心处三棱锥的内半径为0。 |
| 上下底面边长 | L上=|α|R外 L下=|α|R内 | |
| 径向棱长 |  | |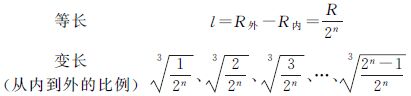
| 上下底面面积 | S上=(A+B+C-π)R外2=(θ-π)R外2 S下=(A+B+C-π)R内2=(θ-π)R内2 | |
| 侧面积 |  | |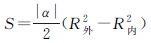
| 体积 | V=(A+B+C-π)(R外3-R内3)/3=(θ-π)(R外3-R内3)/3 |
根据以上原理，很容易实现基于体元的空间定量计算。例如编码为11A0101B2015-6-694的瓦块，其中心点的坐标(m)为：(5038019.000，5038019.000，5038019.000)，表面积约为7.955×106km2，体积约为1.240×109km3(本文除特殊说明外，地球半径取6371km)。
随着剖分层次的增加，同层QTM球面瓦片的最大最小边长和面积的比率收敛于2[24]，退化八叉树瓦片的最大最小面积比收敛于2.22[18]，同层QTM八叉树瓦块最大最小体积比也收敛于2[21]；径向上，等长八叉树瓦块的体积比不收敛，变长八叉树瓦块收敛于2[21]，退化八叉树瓦块收敛于8.89[18]。
2.3 编解码方法
与传统连续坐标空间不同，离散网格通过离散的网格编码来标识网格空间位置。网格编码是一个将多维离散空间映射到一维离散空间的过程，蕴含着网格的位置、尺度和空间关系，通过对编码的简单代数运算，可以实现对空间实体的定位、检索、空间量算与空间关系分析，是网格具有多分辨率空间数据组织能力的重要体现[25]。因而，编码是全球离散网格的核心。
2.3.1 SGOG方案的编码模型在重力场中，从地心到磁层，16倍的地球半径就可以满足包含地球系统所有圈层、基本覆盖人类活动空间的要求[1]。考虑到网格定位及计算的方便，SGOG网格采用以下编码模型：圈层码(十六进制)+八分体标识码(八进制)+球面位置编码(四进制)+径向深度码(二进制)。这里的圈层，不是严格意义上的地球圈层，而是以整数倍地球半径表示的从地心和磁层的距离。八分体标识码表示网格所在的八分体的位置，从0°开始，沿经度增加的方向，按每90°为一个卦限，北半球分为0~3、南半球分为4~7共8个卦限。球面QTM四叉树网格已有很多种成熟的编码方案，如固定方向编码[26]、ZOT编码[27]和LS编码[24]等。本研究采用固定方向编码，径向深度采用二叉树编码(靠近球心的位置取0)[21]。
2.3.2 八叉树编码到经纬度和深度的相互转换所谓离散网格编码到经纬度的相互转换是指：已知网格的编码，求网格体元中心点的经纬度；或者反过来，给定某点的经纬度求该点所在某层次(或满足某种精度)网格的体元编码。本研究以一倍的地球半径为例，并将网格的定位分为球面四叉树经纬度求解和径向二叉树深度(离地心的距离)求解两个步骤。
方向四叉树编码到经纬度相互转换原理参见文献[26, 28]。该方法的核心是将八面体按等边三角形投影(equal-triangles projection，ETP)，把经纬度转换为笛卡尔直角坐标，并以其为桥梁，实现从地址码到经纬度的相互变换。其主要数学模型如式(1)和式(2)所示[26]
式中，λ、ø为经纬度；x、y为ETP投影坐标。
径向二叉树编码的实质就是以某层次的网格棱长去度量地球的半径。其编解码的方法详见文献[21]。变长八叉树的编解码方法与等长在原理上是一样的，仅剖分的比例不同。将变长比例代入相应的解码公式即可。
基于以上原理，实现了四叉树码到经纬度和二叉树到深度的相互转换。以剖分15层为例，E30.456°、N50.454°所在瓦块的四叉树编码为：123023011223202；二叉树编码为0010011111 11111的瓦块距地心的距离为995.274km。
2.3.3 八叉树编码到空间直角坐标的相互转换这里网格编码到空间直角坐标的转换是指由网格的编码求网格单元各顶点的空间直角坐标(进而根据表 1可以求得网格中心点坐标)，而空间直角坐标到网格编码的转换是指已知某点的空间直角坐标和剖分层次，求其所在网格单元的编码。由于SGOG采用了大圆弧中分的剖分规则，所以整个网格体系与空间直角坐标对应十分整齐。下层网格瓦块新增顶点与上层瓦块的顶点之间存在着简单的中分关系。通过求出弦的中点，将其投影到相应的剖分球面上即可。在可视化时，用多段的弦来逼近弧。
本研究在算法设计时，对上面的编码模型做了一些变动：将整个码用标示符A和B分为3个码段。A之前的为圈层码，由0~n个1构成。若没有1，则表示是固体地球本身(即1倍的地球半径)，每多一个1，球的半径就乘以2，依此类推。A和B之间的二叉树码表示网格体元瓦块的径向位置。B之后的第一位八进制码为瓦块所在的八分体标识码，其余的四进制码表示瓦块在球面的横向位置。根据以上编码和剖分规则，给定初始条件，设计八叉树编码与空间直角坐标转换的算法思路如图 1所示。图 1(a)为编码到空间直角坐标，图 1(b)为空间直角坐标到编码(算法默认点所在的圈层为剖分时的最外层)。
|
| 图 1 八叉树编码到空间直角坐标的算法思路 Fig. 1 Conversion algorithm between octree code and 3D coordinates |
例如：编码为11A001B0000的瓦块，其外半径为1(将地球视作单位球)，外层3个顶点坐标分别为：(0.640，0.640，0.426)、(0.640，0.4260，0.640)、(0.4260，0.640，0.640)；内半径为0.5，内层3个顶点坐标分别为：(0.320，0.320，0.213)、(0.320，0.213，0.320)、(0.213，0.320，0.320)。点(0.500,0.600,0.700)在第4层剖分所在的瓦块编码是1A1000B00013；点(1.100,1.200,1.300)在第6层剖分所在的瓦块编码为11A100001B0000320。
3 基于瓦块的真三维地理实体构建从上面论述可知，SGOG网格的编码与空间直角坐标的转换简单直接，通过编码可直接对瓦块进行操作，因而很容易利用瓦块构建真三维的空间地理实体模型，除地表实体外，还包括地下和空中的实体目标。这些都是目前流行的数字地球仪做不到的。
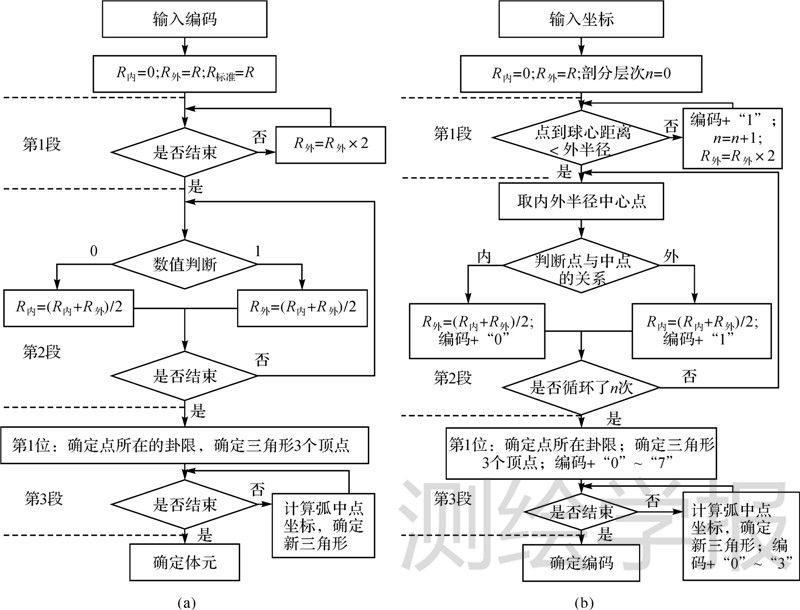
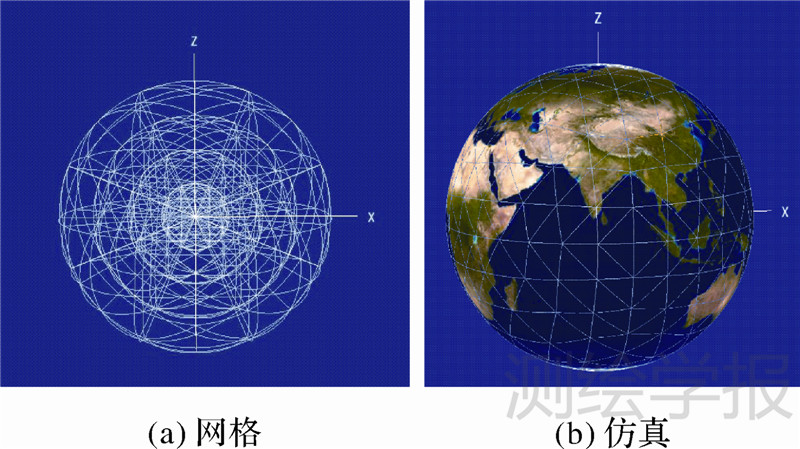
3.1 真三维球体及其分割依据给定层次的完全八叉树，就可以实现真三维的数字地球(图 2)。通过对体元瓦块的操作，可以实现基于瓦块的球体任意分割(图 3)。
|
| 图 2 真3维数字地球 Fig. 2 True three-dimensional digital Earth based on voxel bricks |
|
| 图 3 真3维数字地球的分割 Fig. 3 Arbitrarily divided of true three-dimensional digital Earth based on voxel bricks |
3.2 地表大尺度DEM建模
考虑到大范围的DEM数据和高层次的剖分数据都是海量数据，利用单机进行计算和显示比较困难，选择中国大陆地区作为显示范围。从共享网站(http://srtm.csi.cgiar.org/)上下载了覆盖中国大陆地区的1144幅90m分辨率的DEM数据。基本参数：投影UTM/WGS-84，GeoTIF格式，3601像素×3601像素。基于第9层QTM网格(网格球面边长约为19.5km)建模。通过经纬度坐标实现网格节点与DEM行列号的匹配，然后进行高程采样，最终实现DEM的可视化。图 4表示的是高程放大30倍后的效果。在此基础上，根据地形起伏的实际情况，分别以第3、6、9层网格进行了DEM自适应可视化(图 5)。
|
| 图 4 大区域DEM可视化效果 Fig. 4 Large area DEM visualization |
|
| 图 5 大区域DEM的自适应可视化 Fig. 5 Large area DEM adaptive visualization |
利用瓦块构建地下和空中实体的步骤如下：①根据地理实体尺寸和表达精度，确定体元的大小，进而确定递归剖分的层次；②根据实体外围特征点的坐标，计算对应体元的网格编码，进而确定对应的网格特征与位置；③展绘实体区域对应的所有网格(可以通过网格编码，对相邻网格进行高层次的合并)，即可实现实体的三维模型可视化。图 6为台风建模示意图，图 7则实现了天地一体化的地理空间实体建模(假设数据)，包括地下矿体、空中的卫星轨道和台风。
|
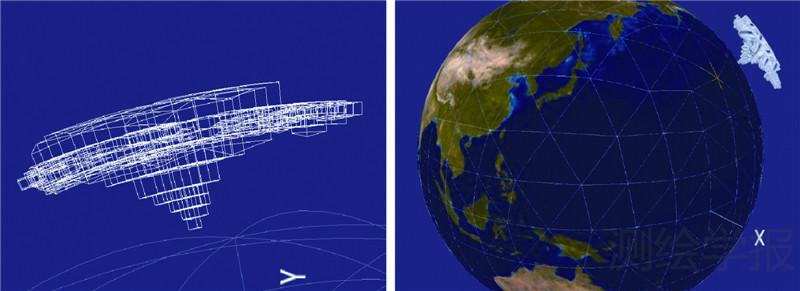
| 图 6 台风建模 Fig. 6 A typhoon model |
|
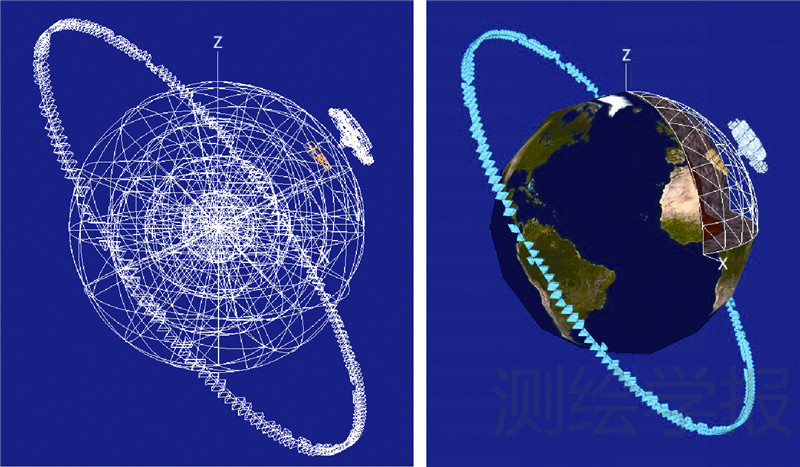
| 图 7 天地一体化地理实体建模 Fig. 7 The integrative geographic entity modeling |
本文详细论述了SGOG网格的理论体系及其在任意地理空间实体建模中的应用。研究表明，SGOG模型具有以下优点：
(1) 网格体系简单。其充分利用了圆心与大圆弧的特性，规则简单，体元瓦块相对于地心呈放射状对称分布，与空间直角坐标对应整齐，适合作为全球框架的坐标基准。
(2) 体元瓦块的几何特征明晰，均可用精确的数学公式表示。由编码可以直接得到瓦块精确的几何特征值，对于空间度量和空间计算意义重大。
(3) 在横向上，同层网格的几何特征变形小，利于横向尤其是地表地理过程的动态模拟。
(4) 由于大圆弧与椭球上的测地线具有类似的性质，所以SGOG网格完全可以推广到椭球。
综上，SGOG方案在空间数据的组织与管理、地理空间实体建模与可视化、三维空间地理度量与计算、浅表地理过程动态模拟以及基于椭球流形的地理空间建模拓展等方面具有一定优势。
众所周知，球面和平面不同胚[24]。用二维(经纬线)和三维(三维直角坐标)正交基去度量球面和球体，必然产生两极和球心收敛，这是基本的数学事实。无论怎样地均衡和拼凑，这种趋势永远不会消失，而且会因此产生相应的代价。无论哪一种球面和球体剖分方案，都不可能像欧式平面网格和立方体网格那样“完美无缺”，满足所有应用需求。应根据实际的应用目标，在网格几何均匀性和体系复杂性之间取得一定的平衡。对于地理信息科学的空间数据模型而言，其普适性是比较重要的。正如文献[12]所言，剖分单元几何特征的均匀性固然是离散剖分的一个重要因素，但是包括计算性能在内的其他许多因素都影响一种离散剖分方案的适用性。测地线是流形空间的“直线”，三角形是最简单的多边形，所以基于测地线和三角形的剖分计算是最简单的计算，适用性最强。SGOG网格虽然具有上述各种优点，但其同时存在大圆弧与经纬度对应不直接、径向体元变形较大(等长剖分体积变形大，变长剖分形状变形大)等缺点，与人们传统的地理空间认知习惯有一定差异，在与传统基于地理坐标的计算体系的衔接以及垂向上大尺度地理过程的动态模拟等方面具有一定的局限性。
基于瓦块的地理空间建模是全球三维离散网格最直接、最基础的应用。其他如大场景、精细模型构建以及动态模拟仿真，空间大数据的融合与集成，基于瓦块的空间信息服务，大尺度和全球尺度专业模型的建立与推演以及椭球测地线三维剖分拓展等，都是进一步研究的方向。
| [1] | WU Lixin, Yu Jieqing. Global 3D Grid Based on Sphere Degenerated Octree and Its Distortion Features[J]. Geography and Geo-Information Science, 2012, 28(1): 7-13. (吴立新, 余接情. 地球系统空间格网及其应用模式[J]. 地理与地理信息科学, 2012, 28(1): 7-13.) |
| [2] | LI Deren. NII, NSDI and Digital Earth[J]. Acta Geodaetica et Cartographica Sinica, 1999, 28(1): 1-5. (李德仁. 信息高速公路、空间信息基础设施与数字地球. 测绘学报[J]. 1999, 28(1): 1-5.) |
| [3] | LI Deren, GONG Jianya, SHAO Zhenfeng. From Digital Earth to Smart Earth[J]. Geomatics and Information Science of Wuhan University, 2010, 35(2): 127-132. (李德仁,龚健雅,邵振峰. 从数字地球到智慧地球[J]. 武汉大学学报: 信息科学版,2010,35(2):127-132.) |
| [4] | GONG Jianya. The Development and Application of 3-D Virtual Earth Technology[J]. Geomatic World, 2011, 9(2): 15-17. (龚健雅. 3维虚拟地球发展及应用[J]. 地理信息世界. 2011,9(2):15-17.) |
| [5] | PANG Xinhua, SHI Juncheng. Review and Prospect of the Development of 3D Virtual Earth[J]. Bulletin of Surveying and Mapping, 2010(sup): 441-444. (庞新华,石俊成. 三维虚拟地球发展回顾与展望[J]. 测绘通报,2010(增刊):441-444.) |
| [6] | SAHR K, WHITE D. Discrete Global Grids Systems[C]//Computing Science and Statistics: 30: Proceedings of the 30th Symposium on the Interface, Computing Science and Statistics. Minnepolis: Interface Foundation of North America, 1998:269-278. |
| [7] | SAHR K, WHITE D. Geodesic Discrete Global Grid Systems[J]. Cartography and Geographic Information Science, 2003, 30(2): 121-134. |
| [8] | DUTTON G. A Hierarchical Coordinate System for Geoprocessing and Cartography: Lecture Notes in Earth Sciences[M]. Berlin: Springer-Verlag, 1999. |
| [9] | GOLD C M, MOSTASAVI M. Towards the Global GIS[J]. ISPRS Journal of Photogrammetry and Remote Sensing, 2000, 55(3): 150-153. |
| [10] | LUKATELA H. Ellipsoidal Area Computations of Large Terrestrial Objects[C]//Proceedings of the 1st International Conference on Discrete Grids’ 2000. Santa Barbara: Geodesy Limited, 2000. |
| [11] | BAI Jianjun, SUN Wenbin, ZHAO Xuesheng. Character Analysis and Hierarchical Partition of WGS-84 Ellipsoidal Facet Based on QTM[J]. Acta Geodaetica et Cartographica Sinica, 2011, 40(2): 243-248. (白建军,孙文彬,赵学胜. 基于QTM的WGS-84椭球面层次剖分及其特点分析[J]. 测绘学报, 2011, 40(2): 243-248.) |
| [12] | GOODCHILD M F. Discrete Global Grids: Retrospect and Prospect[J]. Geography and Geo-Information Science, 2012, 28(1): 1-6. (迈克尔F·古德切尔德. 全球离散格网:回顾与展望[J]. 地理与地理信息科学,2012, 28(1): 1-6.) |
| [13] | BAUMGARDNER J R. Three-dimensional Treatment of Convective Flow in the Earth’s Mantle[J]. Statistical Physics, 1985, 39(5): 501-511. |
| [14] | TUSBOI S, KOMATITSCH D, JI C. et al. Computations of Global Seismic Wave Propagation in Three Dimensional Earth Mode[C]//High-performance Computing. New York: Springer, 2008: 434-443. |
| [15] | KAGEYAMA A, SATO T. The “ Yin-Yang Grid”: An Overset Grid in Spherical Geometry[J]. Geochemistry Geophysics Geosystem, 2004, 5(9): 1-15. |
| [16] | BALLARD S, HIPP J R, YOUNG C J. Efficient and Accurate Calculation of Ray Theory Seismic Travel Time through Variable Resolution 3D Earth Models[J]. Seismological Research Letters, 2009, 80(6): 989-999. |
| [17] | STADLLER G, GURNIS C, BURSTEDDE C. The Dynamics of Plate Tectonics and Mantle Flow: From Local to Global Scales[J]. Science, 2010, 329(5995):1033-1038. |
| [18] | WU Lixin, YU Jieqing. Global 3D Grid Based on Sphere Degenerated Octree and Its Distortion Features[J]. Geography and Geo-Information Science, 2009, 25(1): 1-4. (吴立新,余接情. 基于球体退化八叉树的全球三维网格与变形特征.地理与地理信息科学[J]. 2009, 25(1): 1-4.) |
| [19] | CAO Xuefeng. Research on Earth Sphere Shell Space Grid: Theory and Algorithms[D]. Zhengzhou: Information Engineering University, 2012. (曹雪峰. 地球圈层空间网格理论与算法研究[D]. 郑州:信息工程大学,2012.) |
| [20] | WANG Jinxin, LU Fengnian, CHEN Jie. Comparison of Surface and Solid Discrete Global Grids[J]. Science of Surveying and Mapping, 2012, 37(6): 34-36. (王金鑫,禄丰年,陈杰. 球面离散网格与球体离散网格的比较研究[J]. 测绘科学,2012,37(6):34-36.) |
| [21] | WANG Jinxin, LU Fengnian, GUO Tongde, et al. Global 3D-grids Based on Great Circle Arc QTM Sphere Octree and Unequal Octree[J]. Geomatics and Information Science of Wuhan University, 2013, 38(3): 344-348. (王金鑫,禄丰年,郭同德,陈杰. 球体大圆弧QTM八叉树剖分[J]. 武汉大学学报: 信息科学版, 2013, 38(3): 344-348.) |
| [22] | GOODCHILG M F. Criteria for Evaluation of Global Grid Models for Environmental Monitoring and Analysis[EB/OL]. Buffalo: NCGIA, 2000. [2014-01-12]. http://www.ncgia. ucsb. edu/pubs/pubslist.html. |
| [23] | ZHAO X S, CHEN J, LI Z L. A QTM-based Algorithm for the Generation of Voronoi Diagram on Sphere[M]. Advances in Spatial Data Handling. Berlin: Springer-Verlag, 2002: 269-284. |
| [24] | ZHAO Xuesheng, HOU Miaole, BAI Jianjun. Spatial Digital Modeling of the Global Discrete Grids[M]. Beijing: Surveying and Mapping Press, 2007. (赵学胜,侯妙乐,白建军. 全球离散网格的空间数字建模[M]. 北京:测绘出版社,2007.) |
| [25] | YU Jieqing, WU Lixin. On Coding and Decoding for Sphere Degenerated: Octree Grid[J]. Geography and Geo-Information Science, 2012, 28(1): 14-18. (余接情,吴立新. 球体退化八叉树网格编码与解码研究[J]. 地理与地理信息科学, 2012, 28(1): 14-18.) |
| [26] | GOODCHILD M F, YANG S. A Hierarchical Data Structure for Global Geographic Information Systems[J]. Computer Vision and Geographic Image Processing, 1992, 54(1): 31-34. |
| [27] | DUTTON G. Modeling Location Uncertainly via Hierarchical Tessellation[C]//Accuracy of Spatial Database. London: Taylor and Francis, 1989: 125-140. |
| [28] | ZHAO Xuesheng, CHEN Jun. Fast Translating Algorithm between QTM Code and Longitude/Latitude Coordination[J]. Acta Geodaetica et Cartographica Sinica, 2003, 32(3): 272-277. (赵学胜,陈军. QTM地址码与经纬度坐标的快速转换算法[J]. 测绘学报,2003,32(3):272-277.) |