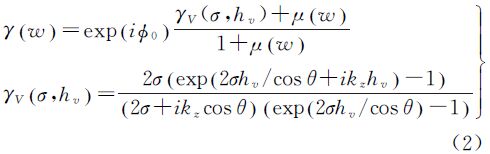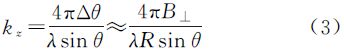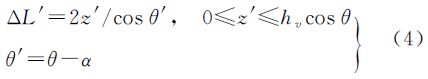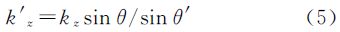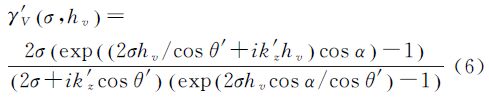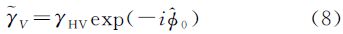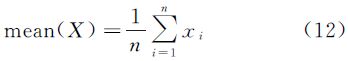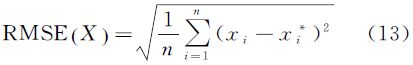1 引 言
森林覆盖了地球陆地30%左右的面积[1]。由于植被覆盖的影响，目前传统的测绘遥感手段获取的数字地形模型存在一个植被高偏差[2]，因此如何快速、精确、大范围地获取植被高度是获取森林覆盖区高精度数字地形模型的关键。极化干涉合成孔径雷达(polarimetric SAR interferometry,PolInSAR)技术综合了PolSAR技术对分辨单元内散射体特性敏感的优势和InSAR技术对散射体高度敏感的特点[3, 4, 5, 6]，具有监测植被高度的能力，已经在微波遥感领域中得到广泛应用。
目前PolInSAR植被高度反演方法主要可分为两大类：①基于RVOG(random volume over ground)模型的物理观测方法，如三阶段算法[7, 8]、六维非线性迭代算法[9]、复数域平差算法[10]；②基于相位作差的几何观测方法，均是用于提取冠层相位和地表相位，如物理先验信息方法[11 ,12]、ESPRIT算法[13, 14, 15]、相干最优算法[3, 16, 17, 18, 19]。经过大量试验验证，基于RVOG模型的三阶段算法是目前最为广泛使用的方法[20 ,21]，其反演结果质量容易受到地形相位估计误差和纯体相干性估计误差的影响。此外，RVOG模型建立时没有考虑植被层下地表的地形变化影响，目前发表的试验研究也主要集中在地表相对平坦的区域，对于地形起伏较大的区域忽略地形影响显然会导致最终植被高度估计出现偏差，这将会严重限制PolInSAR植被高度监测技术走向实用化。针对PolInSAR植被高反演中的地形影响，2013年，文献[21]将RVOG模型进行扩展，提出一种考虑地形坡度的S-RVOG(slope-RVOG)模型。然而，一方面从模型角度上，没有给出坡度对基于传统RVOG模型植被高度反演的影响规律，以及采用S-RVOG模型对不同坡度水平情况进行地形改正的有效性情况；另一方面从反演算法角度，经典的三阶段算法存在着地表相位估计和纯体去相干性估计不准确两方面的问题，没有尝试采用一些方法来有效地削弱这两部分误差。此外，这个模型只是用了模拟数据验证，还未在真实场景进行试验，特别是对于已知植被高度和坡度区域的实例验证。因此，针对三阶段算法中的两类误差影响问题和RVOG模型中的坡度影响，本文提出一种反演思路，即采用考虑地形因素的S-RVOG模型作为反演模型用于校正地形影响，同时引入PD (phase diversity)相干最优算法用于改善三阶段算法中直线拟合地表相位估计和纯体相干性估计精度，分析并试图揭示其中的一些内在规律。为了分析地形对植被高度反演的影响规律，需要排除时间去相干、大气影响等其他因素干扰，故本文采用欧空局提供的PolSARpro软件模拟不同地形坡度水平的PolInSAR数据，通过模型和反演方法选择不同构建4种策略进行植被高度反演。为了进一步验证反演思路的可靠性和实用价值，利用德国宇航局E-SAR系统获取的两景植被覆盖区全极化影像开展真实场景试验验证，并对最终反演结果进行定性和定量分析。
2 PolInSAR植被高反演方法 2.1 反演模型 2.1.1 RVOG模型RVOG模型即随机地体二层相干散射模型，是目前PolInSAR植被高反演中应用最广泛的散射模型。如图 1中(a)和(b)所示，假设植被场景散射由地面和厚度为hv的随机方向粒子组成的植被体两层构成。该模型从复相干性出发，假定植被层中散射能量随着高度增加呈指数变化且地面不可穿透。图 1(c)所示为不考虑地形坡度时InSAR获取几何关系图，从图中可以看出z轴方向上不同位置散射体对应的雷达波在植被层中的消光路径ΔL为
式中，z为雷达波在植被层传播的垂直路径长度；θ为雷达入射角。在忽略时间去相干、大气影响和配准处理误差并进行距离向频谱滤波消除基线几何去相干后的复相干性可以表示为[9] 式中，w为单位复数矢量，代表某一种物理散射机制；hv为植被高度；Φ0为植被下的地表相位；μ(w)为地体幅度比；消光系数σ用来描述植被层粒子对入射波的吸收和散射过程；γV表示只由植被层产生的纯体相干性；kz表示有效垂直波数，依赖于成像几何(垂直基线B⊥，斜距R和入射角θ)和雷达波长λ，其一般表达式为[9]
|
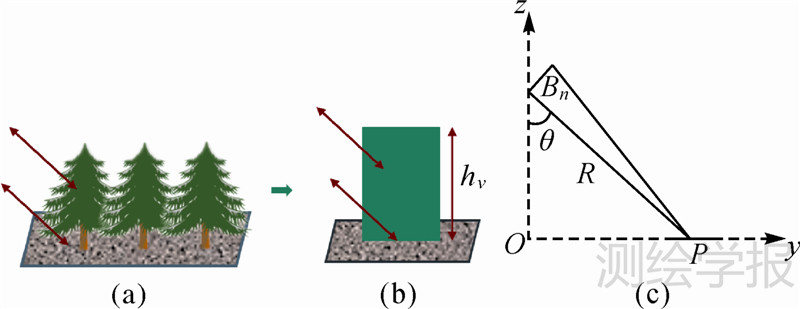
| 图 1 RVOG模型示意图 Fig. 1 Illustration of RVOG model |
如图 2中(a)和(b)所示，当地面存在一定坡度时，雷达波在植被层中的消光路径发生了变化，显然按照RVOG模型进行反演肯定会引入误差。2013年，文献[21]针对地形坡度影响，将RVOG模型进行了扩展，首次提出了考虑地形坡度的散射模型，即S-RVOG模型。如图 2(c)所示为考虑地形坡度时InSAR获取几何关系图。从图中可以看出S-RVOG模型假设距离向上存在一个坡度角α，由于地面散射体沿着斜坡分布，沿着z轴描述其能量变化比沿着z′轴要更加复杂，故该模型是在沿斜坡方向和垂直斜坡方向的坐标系y′O′z′中建模。经过坐标系统转换后，考虑地形坡度的模型建立方式与RVOG模型类似，但由于引入坡度角，S-RVOG模型相比RVOG模型有以下变化：
(1) 消光路径ΔL发生变化。此时在z′轴方向上不同位置散射体对应的雷达波在植被层中的消光路径为
(2) 有效垂直波数kz发生变化
(3) 仅由植被体引起的纯体相干性发生变化，建立二维查找表时计算公式做相应变化如下
|
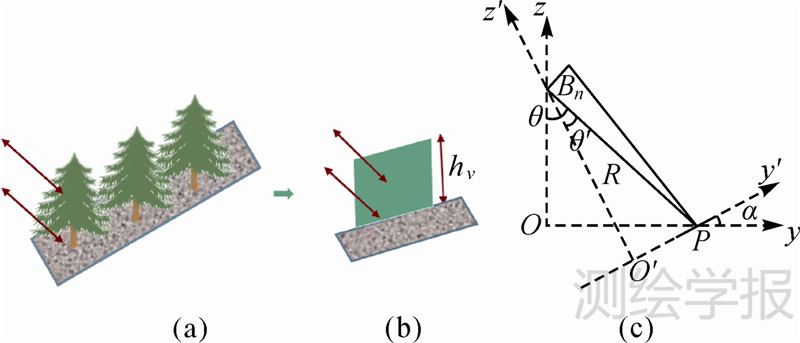
| 图 2 S-RVOG模型示意图 Fig. 2 Illustration of S-RVOG model |
文献[5]提出三阶段算法是一种目前最常用的基于RVOG模型的PolInSAR植被高度反演方法。它的反演过程主要包括以下几个步骤：
(1) 不同极化状态对应的复相干性在复平面上进行直线拟合。该方法首先将RVOG模型改写成如下线性模型
由式(7)可以看出，该模型为一复线性模型，不同极化状态的复相干性在复平面上理论上呈直线分布。
(2) 地表相位Φ0估计。由复线性模型表达式可以看出，拟合的直线与复平面上的单位圆有两个交点，分别对应L=1、μ=±∞两种情况。根据相干性排序规则，可以从两个交点中选择μ=+∞的那一个交点，其对应的相位即为地表相位的估计值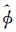
0。
(3) 植被高度hv估计。假设HV极化通道仅有植被层散射体贡献其散射能量，其地体幅度比为0，即μHV=0，则纯体相干性γV的估计值为
为了减少运算时间，故采用数值计算方法，事先给定植被高hv和消光系数σ合理的取值范围，根据式(1)建立γV关于这两个参数的二维查找表，然后通过比较估计值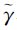
V和查找表中计算的理论值，找出差异最小的那一组值，从而求得植被高度hv。相应的约束条件如下
由三阶段算法反演过程看，其反演精度依赖于直线拟合精度和纯体相干性γV的估计精度。在文献[7]提出的经典三阶段算法中，直线拟合选取的是线极化和Pauli基极化方式，即HH、VV、HV、HH+VV、HH-VV 5个极化通道，纯体相干性估计时选择HV极化通道认为其地体幅度比为0。然而，大量试验结果表明，这5个极化通道对应的复相干性在复平面上分布的较为密集，从而导致较大的直线拟合误差。此外，HV极化通道中仍残留着较大的地面散射贡献，从而会污染纯体相干性估计。基于这两点，本文考虑引入文献[17]提出的PD相干最优化算法来削弱这两部分影响。
2.2.2 PD相干最优化算法根据雷达极化理论，任意极化基下的雷达回波能量可以由单个极化基(如HV极化基)下观测的回波能量的线性组合获得[22]。之后，许多学者将这一思想推广到极化干涉SAR领域，其目的是在极化空间内寻求最优极化方式使得其对应的复相干性满足某种限定条件，这些研究工作即为极化相干最优化算法研究。PD相干最优化算法作为此类算法的代表性之一，其主要目的是为了在极化空间内寻找两种极化状态，使得其对应的复相干性在复平面上表现为相位差异最大。该算法首先引入一个约束条件，即要求对于主辅影像，其对应的最优极化散射矢量相同，表现为同一种物理散射机制。然后，该算法可以转换为寻找复相干性相位角有最大的余切的组合，进而可以转换为一个特征值求解问题[17]
式中，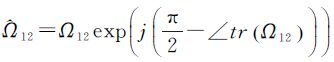
。
式中，Spq(p,q=H或V)表示HV极化基下采用p极化方式发射，q极化方式接收的复散射系数。通过特征值求解可以得到最大特征值和最小特征值对应的两个特征向量wPDhigh和wPDlow，对应相位差异最大的两种散射机制。然后，根据相干性的计算公式可以求得这两种极化方式对应的复相干性观测值γPDhigh和γPDlow。
由于理论上PD相干最优化算法得到的复相干性观测相位差异大，故考虑引入这两个极化方式的复相干性参与三阶段算法中的直线拟合阶段，使得复相干平面上点分布更为分散，更加有利于直线拟合，从而提高地表相位估计精度。此外，由于最大特征值对应的γPDhigh的相位中心在物理上解释为极化空间内位置较高的相位中心，相比HV极化通道离地表相位中心更远，残留的地表散射分量更少，相应的地体幅度比更小，更接近于三阶段算法中第3步中的假设条件，从而可以有效提高纯体相干性γV的估计精度。因此，理论上引入PD相干最优化算法可以削弱三阶段算法中的两类误差影响，从而提高最终植被高度估计的精度。
2.2.3 4种植被高度反演策略为了清晰地分析反演模型和反演算法两部分影响因素，本文分别采用4种植被高度反演策略开展试验，即：
(1) 经典的RVOG模型+三阶段算法，其详细解算流程如2.2.1小节。
(2) 经典的RVOG模型+改进的三阶段算法(引入PD相干最优)。关键在于三阶段算法直线拟合阶段加入这两种极化方式对应的复相干性观测值γPDhigh和γPDlow，植被高度hv估计阶段假设PDhigh极化仅有植被体散射贡献。
(3) 考虑地形的S-RVOG模型+三阶段算法。关键在于植被高度hv估计阶段采用考虑了地形坡度角的式(6)计算查找表。
(4) 考虑地形的S-RVOG模型+改进的三阶段算法，即同时考虑了模型因素和反演算法误差，将其解算过程同时采用了策略(2)和策略(3)中的关键设置。
3 试验结果与分析 3.1 仿真试验3.1.1 试验数据介绍
为了排除时间去相干、大气影响等其他因素干扰，专门分析坡度影响对基于现有反演模型的植被高度估计的影响规律以及采用新模型校正坡度影响的稳健性。试验数据采用欧空局提供的极化雷达遥感领域公认的算法测试软件PolSARpro中的森林模块模拟多组不同坡度水平的极化干涉SAR数据来验证算法的有效性。其模拟参数如表 1。
| 平台高度/m | 中心频率/GHz | 入射角 | 垂直基线/m | 水平基线/m | 方位向分辨率/m | 地距向分辨率/m | 植被类型 | 植被高度/m |
| 3000 | 1.3 | 45° | -6.01 | 6.01 | 1.5 | 1.5 | 针叶林 | 10 |
为了验证算法的稳健性，本文试验设计时，在数据模拟阶段将距离向坡度水平参数设置为0%、5%、10%、15%、20%、25%、30%、35%、40%，其对应的坡度角0°、2.86°、5.71°、8.53°、11.31°、14.04°、16.70°、19.30°、21.80°。图 3为坡度为0%条件下植被场景的Pauli基合成影像图。
|
| 图 3 坡度为0%条件下植被场景的Pauli基合成图 Fig. 3 The Pauli decomposition image of the simulated forest scene with slope of 0% |
图 4表示的是针对9组不同坡度水平(0%～40%)极化干涉SAR数据，由式(12)计算得到的4种策略反演得到的植被高结果对应图 3中方框区域内的统计均值，从图 4中可以直观地看出：
|
| 图 4 植被高度反演结果均值对比 Fig. 4 Comparison of mean of forest height inversion results |
(1) 从反演模型角度来看，当反演模型不考虑坡度因素时，即采用传统的RVOG模型作为反演模型，反演方法无论是采用传统三阶段算法(策略(1)，红线)，还是改进的三阶段算法(策略(2)，绿线)，其植被高反演结果随着地形的增加逐渐增高。然而，当反演模型顾及地形因素时，即采用S-RVOG模型作为反演模型，两种反演方法反演的植被高结果随着地形的增加基本保持稳定，如图 4中蓝线和黑线所示。这表明地形坡度为正时，地形影响会造成反演结果出现高估现象，这与文献[21]中的采用常规三阶段算法针对地形坡度水平为35%的数据试验出现高估现象的结果一致。然而，采用顾及地形因素的S-RVOG模型可以对地形影响进行有效校正。
(2) 从反演方法角度来看，不考虑地形因素，即在没有坡度影响(slope=0%)时，传统的三阶段算法得到的植被高度出现低估现象(红色正方形)，而引入PD相干最优后得到的结果基本处于10m位置(绿色上三角形)，与植被高真值十分吻合。这表明PD相干最优可以对三阶段算法中的直线拟合精度和纯体相干性γV的估计精度进行有效补偿，从而可以改善三阶段算法自身存在的低估偏差。
(3) 在没有坡度影响时(slope=0%)，采用顾及地形因素的S-RVOG模型得到的植被高反演结果和RVOG模型得到的反演结果一致，这表明RVOG模型只是S-RVOG模型的一种特殊情况，顾及地形的S-RVOG模型具有统一性。
(4) 随着坡度的增加，常规的三阶段算法的反演结果会受到两方面的影响，地形引起的高估影响和自身低估的误差影响。其反演结果是两方面误差综合作用的结果，需要对两方面影响进行校正和补偿。
当坡度较小(如图 4中slope＜10%)时，地形影响较小，自身低估的误差占主导作用，此时常规三阶段算法出现低估现象。若反演模型采用RVOG模型，即不进行地形影响校正，只考虑引入PD相干最优进行自身低估补偿(策略(2)，绿线)，其得到的反演结果要优于三阶段算法(策略(1)，红线)，反演精度仍然较高。
当地形坡度较大(如图 4中slope>10%)时，地形影响导致的高估作用占主导地位，抵消了常规三阶段算法自身低估的影响，使得策略(1)(红线)反演的植被高度逐渐增高，其反演结果逐渐逼近于真值。随着坡度的逐渐增加，当地形坡度增加到20%左右时，其结果甚至出现与植被高真值一致的现象，之后坡度继续增加，高估现象逐渐严重。若此时采用策略(2)(绿线)只进行自身低估影响补偿，由于地形高估的影响，其反演精度甚至低于常规三阶段算法。同样，若此时只采用策略(3)(蓝线)进行地形高估影响校正，但由于三阶段算法自身低估的影响，其反演结果在不同坡度水平都出现低估现象。
采用本文提出的策略(4)，既对地形高估影响进行校正，同时补偿三阶段算法自身低估影响，且S-RVOG模型对地形影响的校正随着坡度的增加，校正程度越大。其反演结果随着坡度增加，基本保持稳定，且维持在植被高真值10m附近，说明策略(4)反演精度高，可靠性强且比较稳健。
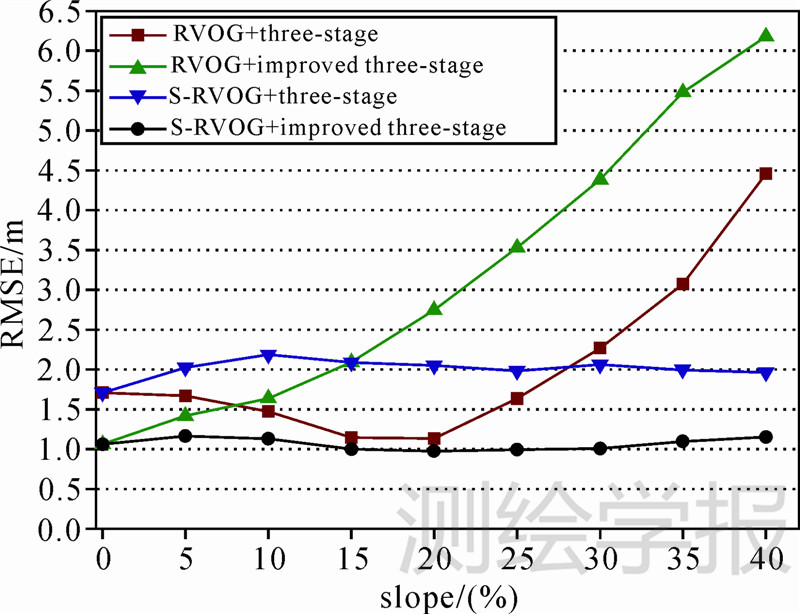
由于植被高度真值10m已知，根据式(13)统计对应相同区域统计的均方根误差(RMSE)，如图 5所示。由图 5可以看出，4种策略中，采用考虑了地形的S-RVOG模型和PD相干最优算法在不同坡度水平上得到的植被反演结果精度最高。三阶段算法随着坡度的增加，其RMSE先降低后增加，其原因是地形影响使得其结果先逼近与真值10m，然后远离真值10m。在较低坡度水平下，策略(2)(绿线)引入PD算法也能得到较高精度的反演结果。
|
| 图 5 植被高度反演结果均方根误差对比 Fig. 5 Comparison of root mean square error of forest height inversion results |
此外，为了对比算法的时间效率，在对影像进行配准、去平地相位和相干性估计获得不同极化方式的复相干性观测数据后，在CPU为intel-i7、4核、8GB内存配置的电脑上，利用matlab R2011b软件平台对4种试验策略进行程序测试并统计运行时间。经过统计，对于试验采用的9组不同坡度水平的数据，其单个影像大小均为147行和167列，采用策略(1)和策略(2)平均用时6.0s，而策略(3)和策略(4)平均用时6.2s。这表明几种试验策略的植被高度反演精度各有不同，但计算时间基本相当。
试验结果的精度评价采用统计均值和均方根误差两种指标描述。对于一组样本数量为n的观测序列X，xi*表示第i个观测样本xi对应的真值，则其对应的均值和均方根误差计算公式如下：
均值
均方根误差
3.2 真实试验 3.2.1 试验数据介绍
为了更为有效地检验算法的可靠性，采用德国宇航局E-SAR机载系统获取的两景P波段全极化影像开展植被高度提取试验，影像主要参数如表 2。由表 2可以看出两景影像间的时间间隔约半小时左右，故时间去相干影响基本可以忽略。影像覆盖区域是瑞典北部的Krycklan地区，该地区属于典型的北方森林地带，树种以挪威云杉和欧洲赤松等针叶林为主。为了研究植被高反演中的地形影响并评定精度，收集了该地区分辨率为1m×1m的DEM用于获取地形坡度信息，同时获取了该地区2个典型样地的地面实测植被参数数据(断面积加权的平均植被高度、植被密度、胸高断面积等)用于分析和评估植被高度反演精度。图 6为试验区Pauli基分解图及两个林分样地的位置。
| 影像 | 极化方式 | 获取时间 | 垂直基线 | 水平基线 | 方位向分辨率 | 斜距向分辨率 |
| 主影像 | 全极化 | 2008-10-14T 11:42:03 | -1.324 | -16.673 | 1.60 | 2.12 |
| 辅影像 | 全极化 | 2008-10-14T 12:15:19 |
|
| 图 6 试验区的Pauli基分解图及覆盖区内的2个典型林分样地矢量边界 Fig. 6 Pauli decomposition RGB image of the test site overlaid by 2 forest stands vector boundary |
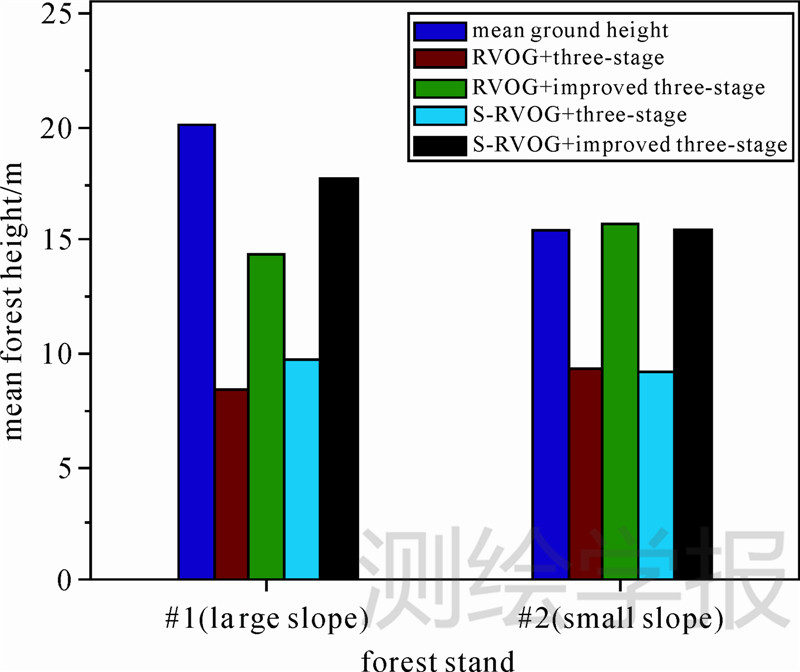
与仿真模拟数据一样，采取4种策略开展植被高度反演试验，获取了整个试验区的植被高度结果。其中真实数据试验中的坡度信息是通过将DEM地理编码到SAR坐标系后计算获得，并规定坡面朝向雷达视线方向坡度角为正，背向雷达视线方向为负。经过计算，林分#1的平均坡度为-8.24°(14.48%)，方差为3.5°(6.12%)，属于地形起伏较大的区域；林分#2的平均坡度为1.59°(2.78%)，方差为2.5°(4.37%)，属于地形起伏较小的区域。利用式(12)分别统计4种策略得到的2个样地的平均植被高度值，其结果如图 7所示。从图 7可以看出：
|
| 图 7 4种反演策略在2个林分样地上估计的平均植被高度对比 Fig. 7 Comparison of mean forest height results based 4 inversion strategies in 2 forest stands |
(1) 在两块林分样地上，采用策略(4)考虑地形的S-RVOG模型+改进的三阶段算法反演的植被高度精度最高，最接近于地面实测值。引入PD相干最优算法的反演策略得到的结果比借鉴传统三阶段算法的反演策略的结果精度更高。
(2) 对于地形起伏较大的林分#1，地形校正程度更大；对于地形起伏较小的林分#2，地形校正程度较小。
(3) 林分#1经过地形校正和算法补偿后其反演结果仍然出现低估，其原因主要由于植被密度引起的。根据实地调查资料，林分#1的植被密度分别是1174.56 stems/ha，树木分布相对较为密集，植被冠层散射贡献较大，选用的几个极化通道之间相位中心相对集中，会导致地表相位估计不准确，其相位中心相对偏高，从而导致最后估计出的植被高度偏低。
为了对比算法的计算效率，在同样的计算机平台上测试，发现4种反演策略的计算效率基本相当。从反演结果来看，真实场景的试验结果基本上与模拟试验得出的规律一致，本文算法在坡度较大的区域优势明显，在坡度较小的区域也具有良好的适用性。
4 结 论本文提出了一种极化干涉SAR植被高度反演方法，通过模拟的不同坡度水平下的极化SAR数据以及真实场景的机载全极化SAR数据进行试验验证，结果表明：
(1) 引入PD相干最优算法能够有效改善三阶段算法中直线拟合估计地表相位的精度和纯体相干性估计精度，补偿三阶段算法自身存在的误差影响。
(2) 当地形坡度为正时，地形对植被高度反演存在高估影响。采用考虑地形因素的S-RVOG模型作为反演模型可以有效地校正植被高度反演中的地形影响，且校正程度随着坡度的增加逐渐增加。
(3) 该方法融合了S-RVOG模型校正地形影响的优点，以及引入PD相干最优补偿三阶段算法自身误差的优势，在不同坡度水平下均能得到较好的估计结果，具有适用性强、稳健性强的特点。
(4) 本文提出的方法原理清晰，易于理解，反演精度更高，计算效率相当，给极化干涉SAR技术监测地形起伏地区植被高度提供了一种新思路。但由于该方法需要输入地形坡度信息，现有的DEM获取地形坡度存在误差，因此分析坡度误差对该方法的影响，建立经验或理论模型，指导其实际应用是下一步要研究的方向。此外，植被密度也是植被高度反演中的重要影响因素，如何削弱或补偿这部分影响也需要进一步研究。
致谢：项目数据来自欧空局数据合作计划(NO.14751)的支持，感谢德国宇航局(DLR)提供的E-SAR数据，瑞典农业科技大学(SLU)提供的地面实测林业数据。
| [1] | FAO. Global Forest Resources Assessment 2005[R]. [S.l.]: FAO Forestry Paper, 2005: 147. |
| [2] | LOPEZ-MARTINEZ C, PAPATHANASSIOU K P. Cancellation of Scattering Mechanisms in PolInSAR: Application to Underlying Topography Estimation[J]. IEEE Transactions on Geoscience and Remote Sensing, 2013, 51(2): 953-965. |
| [3] | CLOUDE S R, PAPATHANASSIOU K P. Polarimetric SAR Interferometry[J]. IEEE Transactions on Geoscience and Remote Sensing, 1998, 36(5): 1551-1565. |
| [4] | WU Yirong, HONG Wen, WANG Yanping. The Current Status and Implications of Polarimetric SAR Interferometry[J]. Journal of Electronics & Information Technology, 2007, 29(5): 1258-1262. (吴一戎, 洪文, 王彦平. 极化干涉SAR的研究现状与启示[J]. 电子信息学报, 2007, 29(5): 1258-1262.) |
| [5] | LI Tingwei, LIANG Diannong, ZHU Jubo. A Review of Inversion of the Forest Height by Polarimetric Interferometric SAR[J]. Remote Sensing Information, 2009(3): 85-90. (李廷伟, 梁甸农, 朱炬波. 极化干涉SAR森林高度反演综述[J]. 遥感信息, 2009(3): 85-90.) |
| [6] | LUO Huanmin. Models and Methods of Extracting Forest Structure Information by Polarimetric SAR Interferometry[D]. Chengdu: University of Electronic Science and Technology of China, 2011. (罗环敏. 基于极化干涉SAR的森林结构信息提取模型与方法[D]. 成都: 电子科技大学, 2011.) |
| [7] | CLOUDE S R, PAPATHANASSIOU K P. Three-stage Inversion Process for Polarimetric SAR Interferometry[J]. IEEE Proceedings: Radar, Sonar and Navigation, 2003, 150(3): 125-134. |
| [8] | TAN Lulu, CHEN Bing, YANG Ruliang. Improved Three-stage Algorithm of Tree Height Retrieval with PolInSAR Data[J]. Journal of System Simulation, 2010, 22(4): 996-999. (谈璐璐, 陈兵, 杨汝良. 利用PolInSAR数据反演植被高度的改进三阶段算法[J]. 系统仿真学报, 2010, 22(4): 996-999.) |
| [9] | PAPATHANASSIOU K P, CLOUDE S R. Single-baseline Polarimetric SAR Interferometry[J]. IEEE Transactions on Geoscience and Remote Sensing, 2001, 39(11): 2352-2363. |
| [10] | ZHU Jianjun, XIE Qinghua, ZUO Tingying, et al. Criterion of Complex Least Squares Adjustment and Its Application in Tree Height Inversion with PolInSAR Data[J]. Acta Geodaetica et Cartographica Sinica, 2014, 43(1): 45-51. (朱建军, 解清华, 左廷英, 等. 复数域最小二乘平差及其在PolInSAR植被高反演中的应用[J]. 测绘学报, 2014, 43(1): 45-51.) |
| [11] | FREEMAN A, DURDEN S L. A Three-component Scattering Model for Polarimetric SAR Data[J]. IEEE Transactions on Geoscience and Remote Sensing, 1998, 36(3): 963-972. |
| [12] | BALLESTER-BERMAN J D, LOPEZ-SANCHEZ J M. Applying the Freeman-Durden Decomposition Concept to Polarimetric SAR Interferometry[J]. IEEE Transactions on Geoscience and Remote Sensing, 2010, 48(1): 466-478. |
| [13] | RODRIGUEZ E, YAMADA H, YAMAGUCHI Y, et al. Polarimetric SAR Interferometry for Forest Analysis Based on the ESPRIT Algorithm[J]. IEICE Transactions on Electronics, 2001, 84(12): 1917-1924. |
| [14] | TAN Lulu, YANG Libo, YANG Ruliang. Investigation of Tree Height Retrieval with Polarimetric SAR Interferometry Based on ESPRIT Algorithm[J]. Acta Geodaetica et Cartographica Sinica, 2011, 40(3): 296-300. (谈璐璐, 杨立波, 杨汝良. 基于ESPRIT算法的极化干涉SAR植被高度反演研究[J]. 测绘学报, 2011, 40(3): 296-300.) |
| [15] | YANG Lei, ZHAO Yongjun, WANG Zhigang. Polarimetric Interferometric SAR Data Analysis Based on TLS-ESPRIT of Joint Estimation of Phase and Power[J]. Acta Geodaetica et Cartographica Sinica, 2007, 36(2): 163-168. (杨磊, 赵拥军, 王志刚. 基于功率和相位联合估计TLS-ESPRIT算法的极化干涉SAR数据分析[J]. 测绘学报, 2007, 36(2): 163-168.) |
| [16] | SAGUES L, LOPEZ-SANCHEZ J M, FORTUNY J, et al. Indoor Experiments on Polarimetric SAR Interferometry[J]. IEEE Transactions on Geoscience and Remote Sensing, 2000, 38(2): 671-684. |
| [17] | TABB M, ORREY J, FLYNN T, et al. Phase Diversity: A Decomposition for Vegetation Parameter Estimation Using Polarimetric SAR Interferometry[C]//Proceedings of 4th European Synthetic Aperture Radar Conference (EUSAR 2002). Cologne, Germany: [s.n.], 2002: 721-724. |
| [18] | GOMEZ-DANS J L, QUEGAN S. Constraining Coherence Optimisation in Polarimetric Interferometry of Layered Targets[C]//Proceedings of the 2nd ESA Workshop on Applications of SAR Polarimetry Interferometry, POLINSAR 2005. Frascati, Italy: ESA, 2005: 65-72. |
| [19] | [JP+2]COLIN E, TITIN-SCHNAIDER C, TABBARA W. An Interferometric Coherence Optimization Method in Radar Polarimetry for High-resolution Imagery[J]. IEEE Transactions on Geoscience and Remote Sensing, 2006, 44(1): 167-175. |
| [20] | PAPATHANASSIOU K P, CLOUDE S R, LISENO A, et al. Forest Height Estimation by Means of Polarimetric SAR Interferometry: Actual Status and Perspectives[C]//Proceedings of the 2nd ESA PolInSAR Workshop. Frascati, Italy: [s.n.], 2005: 152-162. |
| [21] | LU X Y, SUO Z Y, GUO R, et al. S-RVoG Model for Forest Parameters Inversion over Underlying Topography[J]. Electronics Letters, 2013, 49(9): 618-620. |
| [22] | VAN ZYL J J, ZEBKER H A, ELACHI C. Imaging Radar Polarization Signatures: Theory and Applications[J]. Radio Science, 1987, 22(4): 529-543. |