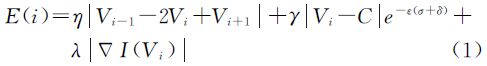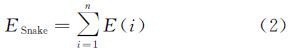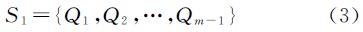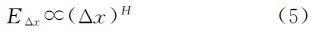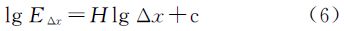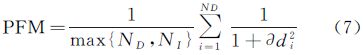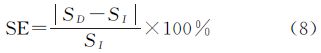1 引 言
遥感影像水体提取在水资源调查和洪涝灾害监测中发挥着重要作用,目前有水体指数法[1]、谱间关系法[2]和面向对象分类[3]等多种方法,但是要获取准确而连续的水体边界依然需要进一步的处理。文献[4]提出的主动轮廓搜索模型(Snake)能直接获取目标连续性轮廓,在道路提取[5]和GIS矢量边界更新[6]中得到了成熟应用。文献[7]利用Snake模型提取了双线型河流,文献[8]利用掩膜Snake模型获取了密云水库面积。但Snake模型对凹边界提取效果不佳,对复杂拓扑结构的处理能力较弱。文献[9]提出的GVF Snake模型改进了Snake模型的外部力,对浅凹边界具有更强的收敛性能。文献[10, 11]分别利用GVF Snake模型提取了多光谱影像和SAR影像中的海陆边界,文献[12]研究了GVF Snake的初始轮廓对边界提取结果的影响,并提取了遥感影像中不规则水域边界。但该模型同样需手工获取靠近边缘的初始轮廓,并且也存在对噪声敏感、无拓扑变换能力等不足之处,难以提取有深凹边界和复杂拓扑结构(如包含河中岛)的复杂河流边界。
文献[13]提出的拓扑自适应动态轮廓(topology adaptive Snake,T-Snake)模型是对Snake模型的另一种改进,用三角网格划分图像,通过判断和处理三角网格与Snake曲线的空间关系来实现拓扑变形,成功应用在医学影像边缘提取中。针对该模型需计算节点移动方向和位置的缺点,文献[14]用正交网格代替三角网格,省略对节点移动方向的判断,在大脑皮层重建和细胞提取中取得了良好效果。文献[15, 16, 17]进一步将节点约束在网格顶点,成功提取了血管影像边缘。文献[18]将T-Snake模型与同态滤波技术相结合,文献[19]改进了T-Snake模型的外部能量,这些改进均降低了图像斑点噪声对T-Snake边缘提取精度的影响。文献[20]在T-Snake模型中增加了自适应性强的膨胀力和区域能量,使之有效提取图像的弱边界和不连续边界。但这些文献均未考虑Snake曲线在遇到目标内部岛状空洞时的拓扑冲突问题,而这一点却是遥感影像河中岛边界提取时需要考虑的重点。另外,这些研究均采取手动方式进行T-Snake模型初始化,自动化程度不高。
正交T-Snake模型在目标边缘处能够自适应地改变轮廓曲线的拓扑结构,对于有复杂拓扑结构边界的提取能力较强,目前尚未有学者将其应用在遥感影像地物提取中。本文以复杂水体边界自动提取为目标,引入正交T-Snake模型并加以改进,针对包含河中岛的河流边界提取会产生的拓扑冲突,提出了一种检测和处理机制,并依据遥感影像分形特征,提出了水体初始轮廓自动生成方法。
2 正交T-Snake模型 2.1 Snake曲线的运动和拓扑变形正交T-Snake模型采用一定大小的正交网格划分影像,并用顺序相连的网格顶点所构成的闭合轮廓来表示某一时刻的Snake曲线,如图 1(a)所示,实心点为曲线的内部点,空心点为曲线的节点和外部点,箭头表示节点方向。正交T-Snake模型中对节点有两个约束条件:一是节点必须沿网格线移动,二是节点必须位于网格顶点处。因此,曲线节点总是沿网格线从一个网格顶点移动到下一个网格顶点。
|
| 图 1 Snake曲线的运动与拓扑变形 Fig. 1 Movement and topology deformation of Snake curve |
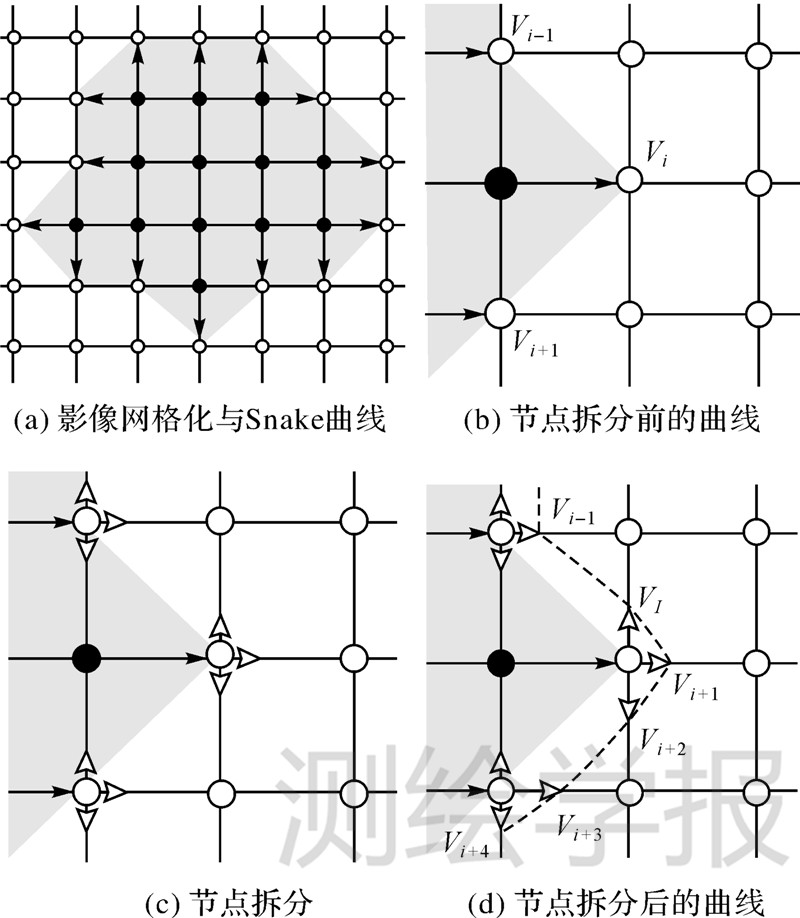
在曲线每次变形前先进行节点拆分。如图 1(b)-(d)所示,对每一个节点,除了其来源方向之外,在剩余的3个方向上各生成一个新节点,新节点在影像上的位置坐标均与原节点相同,不同的是各自的移动方向;若新节点的方向指向曲线内部则弃之,并将剩余节点按顺序插入原曲线节点序列中去,此时这部分曲线的拓扑结构就发生了改变。
2.2 能量函数
能量函数的内部能量由弹力和张力组成,弹力可避免曲线出现曲率过大的部分,张力可使曲线相邻节点间的距离趋于相同。由于正交T-Snake模型的节点约束在网格顶点,节点间距固定为k或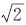 k(k为网格边长),因此本文忽略张力。为保证曲线向外膨胀变形,添加一个膨胀力。外部能量主要指图像力,可保证Snake曲线停留在梯度极大值处(目标边缘)。因此,节点Vi的局部能量由弹力、膨胀力和图像力组成,函数表达式为
k(k为网格边长),因此本文忽略张力。为保证曲线向外膨胀变形,添加一个膨胀力。外部能量主要指图像力,可保证Snake曲线停留在梯度极大值处(目标边缘)。因此,节点Vi的局部能量由弹力、膨胀力和图像力组成,函数表达式为
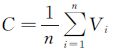 是曲线几何中心;e-ε(σ+▽)是膨胀力衰减系数;ε∈[0, 1]是衰减速度;σ和▽是节点邻域的灰度标准差和极差;|▽I(Vi)|是节点Vi处的灰度梯度值。整条Snake曲线的能量函数为
式中,n为曲线节点数。
是曲线几何中心;e-ε(σ+▽)是膨胀力衰减系数;ε∈[0, 1]是衰减速度;σ和▽是节点邻域的灰度标准差和极差;|▽I(Vi)|是节点Vi处的灰度梯度值。整条Snake曲线的能量函数为
式中,n为曲线节点数。
以这样一个由弹力、膨胀力和图像力组成的能量函数为原则,引导Snake曲线检测目标边界的过程是:①当节点在河流内部并远离边缘时,|▽I(Vi)|较小而e-ε(σ+▽)值较大,此时膨胀力占主导作用。随着曲线向外扩张,节点与曲线几何中心的距离|Vi-C|逐渐变大导致膨胀力逐渐变小,因而能量函数值逐渐变小,使曲线继续变形以追求能量函数最小值;②当节点在河流边缘时,e-ε(σ+▽)的值迅速衰减至零而|▽I(Vi)|突然变大,此时图像力占主导作用,能量函数值将不再继续减小,促使曲线停止运动,从而停留在该处。
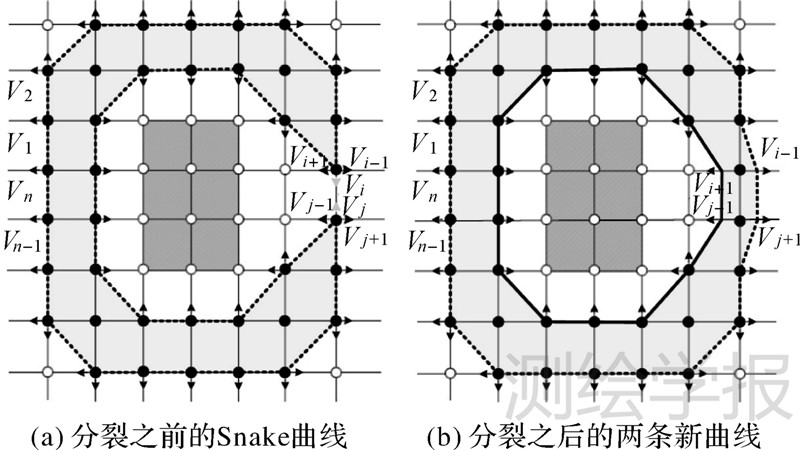
3 复杂水体边界提取 3.1 岛状空洞拓扑冲突的检测和处理当要提取的目标边界由两个轮廓曲线组成,且其中一个轮廓曲线在另一个的内部时,将内部轮廓所构成的区域称为岛。在河流影像上常常出现这种情况,例如河中岛或沙洲等。这种情况下Snake曲线一定会在某个地方发生自相交,如图 2(a)所示,节点Vi与Vj将在曲线下一次变形中发生重合,从而发生自相交拓扑冲突。解决办法是将Vi的前一节点与Vj的后一节点相连,Vi的后一节点与Vj的前一节点相连,然后将Vi、Vj抛弃,如图 2(b)所示。这样原曲线分裂为两条新曲线,内部曲线将检测内部岛屿边界,外部曲线将检测目标边界。
|
| 图 2 岛状空洞拓扑冲突的处理 Fig. 2 Handling for topological conflict caused by island shaped hollow |
假设当前Snake曲线是S={V1,V2,…,Vn},节点个数是n。对于当前要移动的节点Vi,如果它的目标位置是曲线上另一节点Vj,而j-i=m(即Vi、Vj之间的节点个数为m-1),那么进行以下操作:从节点Vi、Vj处将曲线S分裂成两条新闭合曲线S1、S2,其中,S1是内部曲线,由Vi和Vj之间的节点序列构成,节点个数是m-1;S2是外部曲线,由V1到Vi-1、和Vj+1到Vn两个节点序列合并构成,节点个数是n-m-1。曲线S1构造为
式中,令Q1=Vi+1,Q2=Vi+2,…,Qm-1=Vi+m-1(即:Qm-1=Vj-1)。曲线S2构造为
式中,令P1=V1,P2=V2,…,Pi-1=Vi-1,Pi=Vj+1,Pi+1=Vj+2,…,Pi+(n-j-1)=Vj+(n-j)(即:Pn-m=Vn)。外部曲线继续向外扩张变形,最终停留位置就是河流自身边界,内部曲线向内运动变形,最终停留位置就是河中岛的边界。
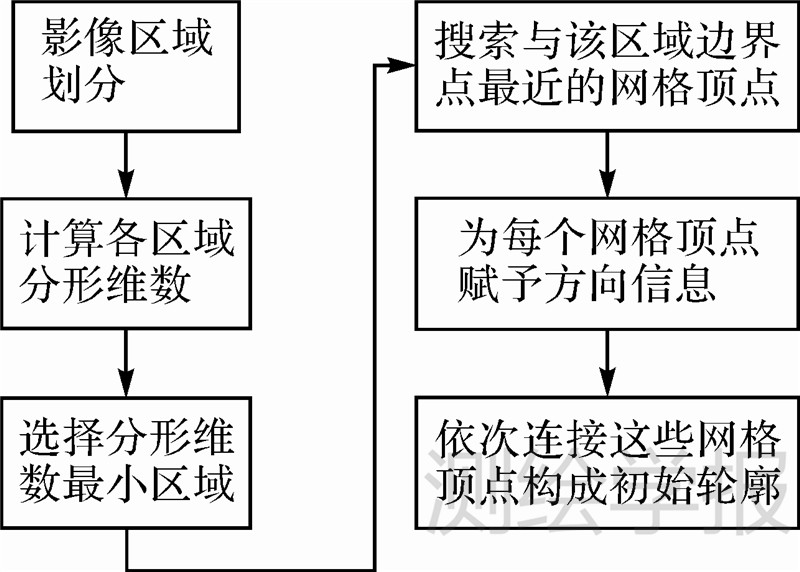
3.2 基于分形维数的水体轮廓初始化正交T-Snake模型只要求初始轮廓是目标内部一条闭合曲线,无形状和大小限制,一般手工选取目标内任一点,将距该点最近的网格顶点依次相连作为初始轮廓。文献[21]分析了遥感影像中自然地物纹理的分形特征,用分形维数(fractal dimension,FD)度量,认为水体的分形维数是最低的。据此,本文提出水体轮廓自动初始化方法,如图 3所示。
|
| 图 3 轮廓初始化流程 Fig. 3 Flowchart of contour initialization |
首先,将影像划分成一系列的影像块,计算每块影像的分形维数;其次,选择分形维数最小的影像块作为水体内部区域,若多个区域同时拥有最小值,则随机选择其中一个;然后,对该区域的每一个边界点,搜索与它距离最近的T-Snake模型网格顶点,根据网格顶点与该点之间的位置关系,为网格顶点赋予方向属性:若网格顶点在相应边界点的上方,则网格顶点的方向是“向上”,同理,可判断方向为“向下”“向左”或“向右”的网格顶点;最后,将这些网格顶点按顺时针顺序依次相连,所构成的闭合曲线作为水体初始轮廓。
每个影像块的分形维数采用分形布朗运动模型[22]计算,该模型将图像的灰度值当作是随机游走的结果:对于任一点x,其邻域(x+△x)内各像素灰度对应的空间曲面可以用一个分形布朗曲面f(x)来拟合。f(x)具有一个基本性质,即
式中,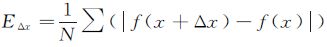 代表影像中所有相距为△x的两个像素的灰度值之差的期望;N是相距为△x的像素对的总数;H∈(0,1)是一个常数。
代表影像中所有相距为△x的两个像素的灰度值之差的期望;N是相距为△x的像素对的总数;H∈(0,1)是一个常数。
根据H可以计算分形维数FD=3-H。求H值的方法是对式(5)取对数,有
式中,c是常数。变换不同的△x值(尺度),求出一组E△x值,对(lg△x,lgE△x)采用最小二乘法进行线性拟合,得到的直线斜率即为H。然后,计算分形维数值FD=3-H。 3.3 水体边界提取水体边界提取是初始轮廓随着能量函数最小化而逐渐优化的过程,算法如下:
(1) 模型初始化。初始化网格大小r;用3.2节方法初始化水体轮廓,记录各节点为(x,y,O),其中,(x,y)是节点坐标,O={‘up’,‘down’,‘left’,‘right’}是节点方向;计算初始轮廓的能量Ebefore。
(2) 节点拆分,并记录新的节点序列中各点的坐标和方向。
(3) 遍历节点序列,对节点Vi(xi,yi,Oi)进行以下操作:①判断Vi的目标位置V′i,若Oi=‘up’,则 V′i(xi,yi-r,‘up’);若Oi=‘down’,则V′i(xi,yi+r,‘down’);若Oi=‘left’,则V′i(xi-r,yi,‘left’);若Oi=‘right’,则V′i(xi+r,yi,‘right’)。②检测岛状空洞拓扑冲突,若存在一个曲线节点Vj,坐标上满足Vj=V′i,则说明发生拓扑冲突,执行③;若不存在,则执行④。③按照3.1节方法将原曲线分裂成为两条新曲线S1和S2,然后对S1和S2分别执行(2)。④计算Vi、V′i的局部能量Ei、E′i,并比较大小:若E′i<Ei,则令Vi=V′i,Ei=E′i。
(4)计算新曲线的能量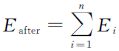 。比较曲线变形前后的能量大小:若Eafter<Ebefore,则令Ebefore=Eafter,继续执行(2);否则,输出Snake曲线的节点坐标序列。最终输出的一条或多条Snake曲线就是提取到的水体边界。
。比较曲线变形前后的能量大小:若Eafter<Ebefore,则令Ebefore=Eafter,继续执行(2);否则,输出Snake曲线的节点坐标序列。最终输出的一条或多条Snake曲线就是提取到的水体边界。
试验数据为国产GF-1卫星PMS相机近红外波段的一幅湖泊影像(1100像素×1100像素),如图 4(a)所示,和一幅包含河中岛的长江某段影像(2244像素×1339像素),如图 6(a)所示,空间分辨率为8m。采取改进的正交T-Snake模型进行水体边界提取:正交网格大小r=2;弹力的权重系数η=0.1;膨胀力的权重系数γ=-0.2,膨胀力的衰减速度ε=2,在膨胀力中计算节点邻域灰度标准差和极差的邻域大小k=2;图像力的权重系数λ=0.4。

|
| 图 4 3种模型提取的湖泊边界 Fig. 4 The lake boundary extracted by three models |
|
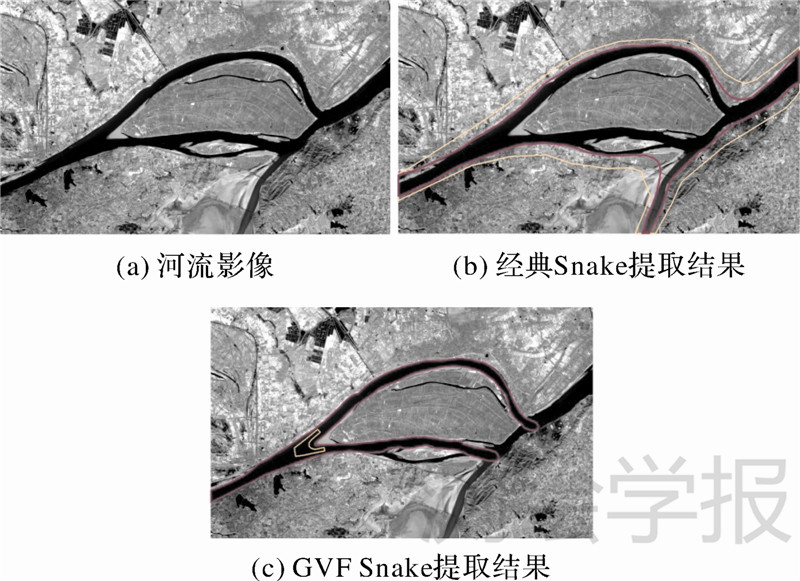
| 图 6 经典Snake模型和GVF Snake模型的河流边界提取结果 Fig. 6 The results of the river boundary extraction based on classic Snake model and GVF Snake model |
采用经典Snake模型[7]和GVF Snake模型[12]的提取结果进行对比,考虑到它们对初始轮廓的敏感性,试验中保证初始轮廓尽量贴近水体边缘,且几何形状尽量与水体边界形状一致。试验在Intel酷睿i5、CPU主频2.27GHz、内存4GB的计算机上,eclipse+pydev编译环境下用Python编程实现。
4.2 结果分析 4.2.1 水体边界提取结果第1幅影像的湖泊边缘有多处深凹边界,如图 4(a)所示。图 4(b)、(c)分别为传统Snake和GVF Snake的提取结果,黄色曲线是初始轮廓,红色曲线是检测的湖泊边界。图 4(d)为本文方法的提取结果,黄色区域是自动获取的分形维数最小区域,红色曲线是检测的湖泊边界。
|
| 图 5 不同的曲线变形方式 Fig. 5 Different curves deformation mode |
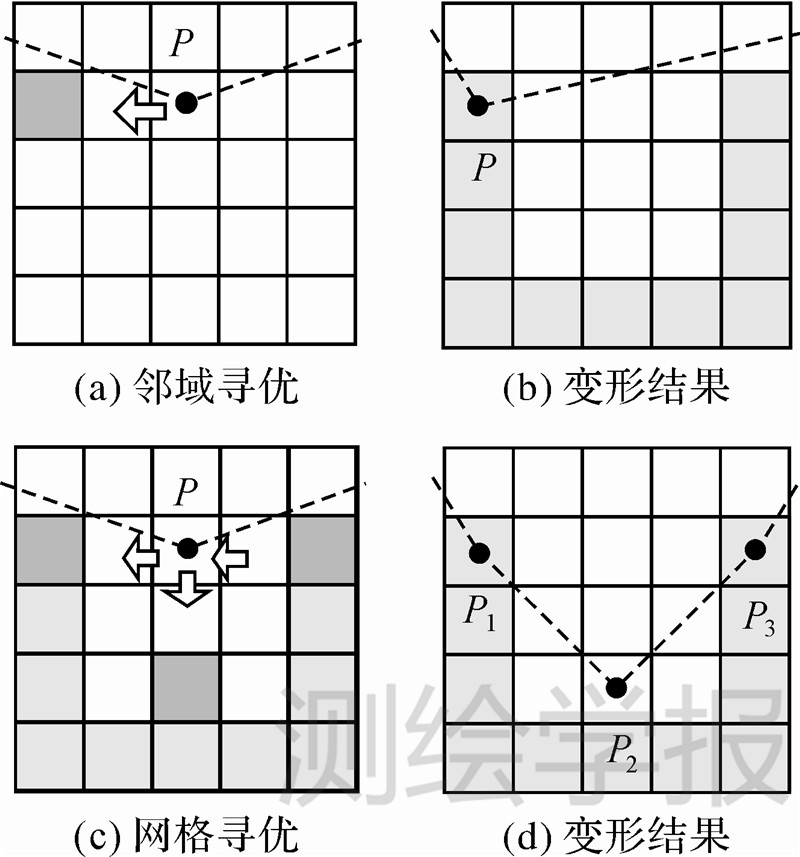
从图 4可以看出,传统Snake和GVF Snake的边界提取效果均不如改进正交T-Snake模型,表现为对凹状边界的收敛效果不佳。因为它们是通过搜索邻域能量最小点作为节点新位置,如图 5(a)、(b)所示,阴影区域为点P的5×5邻域的局部最优点,在狭长凹区域会导致节点易在局部能量极小值的作用下停留在凹区域内某一侧方边界上,这将使得Snake曲线不能收敛到凹区域真正边界。GVF Snake由于采取GVF场作为外部力,扩大了节点搜索范围,故对浅凹边界的检测效果优于传统Snake,但对于狭长深凹边界依然会出现跟传统Snake一样的缺点。改进的正交T-Snake模型由于通过节点拆分和搜索最优的网格顶点来实现曲线变形,故不会陷入局部极小值,如图 5(c)、(d)所示,所以能够很好地收敛到各深凹区域的边缘。
第2幅影像中河流内有两个河中岛,对于传统Snake和GVF Snake,如图 6所示,考虑到它们对于初始轮廓的敏感性,传统Snake的初始轮廓完全包裹影像中整个河流,GVF Snake模型的初始轮廓尽量与河流形状相似,但即便如此,这两种模型均不能获取完整而精确的河流边界:传统Snake模型不能检测到河流内部河中岛的边界,GVF Snake模型无法提取河流的所有支流边界。特别是GVF Snake模型,受其曲线变形方式的局限性,容易出现局部极小值,因检测不到岛区域背面边界,曲线在继续变形过程中会不断演变成U型,因此无法提取完整的岛区域边界。
改进正交T-Snake模型提取河流边界的过程如图 7所示,图 7(a)是用23×23的窗口计算分形维数,并均衡化拉伸到0-255区间后得到的分形维数分布图。可以看到,纹理光滑平坦的河流内部分形维数偏低,表现为连续均匀的暗区域,其中黄色区域为计算得到的一个分形维数最小的区域,可以看到该区域位于河流的内部某一处。从图 7(b)-(e)可以看出,Snake曲线在能量函数的作用下不断地膨胀和向河流边缘运动,在此过程中,其形状也在不断地发生改变;在遇到河中岛时,由于设计了合理的拓扑冲突检测机制和处理办法,Snake曲线的两端在河中岛边界某处融合,并且整体分裂为两条曲线,其中内部曲线停留在该处从而获取了河中岛的边界,而外部曲线则继续运动检测到河流自身边界。这说明本文方法在提取含河中岛河流时是有效的。
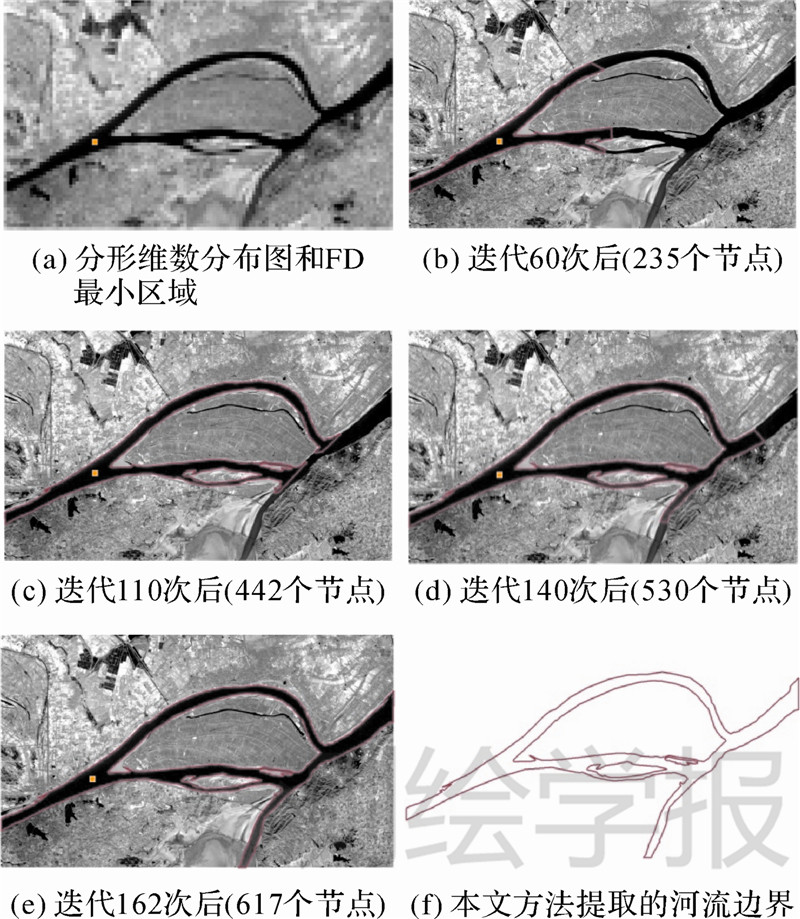
|
| 图 7 基于改进正交T-Snake模型的河流边界提取结果 Fig. 7 The results of the river boundary extraction based on improved orthogonal T-Snake model |
采用Pratt品质因数(Pratt’s figure of merit,PFM)[23]和形状误差[6]相结合的方式对3种模型的水体边界提取精度进行客观评价。
Pratt品质因数可评价边界的定位精度,计算公式为
式中,ND是检测到的边缘像素的个数;Ni是理想的边缘像素的个数;∂是常数(取∂=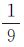 );di是检测到的第i个边缘点与真实边缘点的距离。PFM值越高,则边界提取的定位精度越高。形状误差可评价边界的形状准确度,本文利用曲线长度、最小外接矩形面积、长度和宽度的均值作为特征值。对于河流影像,将外部河流边界和内部岛屿边界的形状特征值相加,作为河流边界的形状特征值,计算公式为
式中,SD是提取到边界的形状特征值;Si是理想边界的形状特征值。SE越小,则形状准确度越高。
);di是检测到的第i个边缘点与真实边缘点的距离。PFM值越高,则边界提取的定位精度越高。形状误差可评价边界的形状准确度,本文利用曲线长度、最小外接矩形面积、长度和宽度的均值作为特征值。对于河流影像,将外部河流边界和内部岛屿边界的形状特征值相加,作为河流边界的形状特征值,计算公式为
式中,SD是提取到边界的形状特征值;Si是理想边界的形状特征值。SE越小,则形状准确度越高。
在湖泊影像和河流影像上手动提取湖泊边界和河流边界,将它们作为各自的理想边界,然后利用式(7)或式(8)分别计算经典Snake模型、GVF Snake模型和本文方法的Pratt品质因数(PFM)和形状误差(SE)。另外统计了3种模型在两个案例中的时间开销。精度和效率的统计结果如表 1所示。
| 湖泊影像 | 河流影像 | ||||||
| Pratt品质因数(PFM) | 形状误差(SE)/(%) | 耗时/s | Pratt品质因数(PFM) | 形状误差(SE)/(%) | 耗时/s | ||
| 经典Snake模型 | 0.729236 | 24.4166 | 147 | 0.194168 | 46.1901 | 184 | |
| GVF Snake模型 | 0.875142 | 11.7906 | 152 | 0.210091 | 57.2118 | 201 | |
| 改进正交T-Snake模型 | 0.942279 | 3.5283 | 49 | 0.938064 | 4.7874 | 58 | |
从表 1可以看出,两个案例中正交T-Snake模型的PFM最高、SE最低,说明正交T-Snake模型所提取的水体边界在定位精度和形状准确度上都是最佳的。GVF Snake的湖泊边界提取精度优于传统Snake,是因为它能够检测到部分浅凹边界,但它们均遗漏掉很大一部分河流边界,因此在河流案例中的精度都非常低。该结果亦验证了4.2.1 节的定性分析。从表 1中还可以看出,改进正交T-Snake模型的耗时最少,计算效率最高,这是因为:①本文方法实现了轮廓自动初始化因而在构造初始轮廓上耗时最少;②另两种模型需对节点邻域的所有像素都计算一次能量函数,若邻域大小M×M,节点数n,则一次迭代的时间复杂度是O(n×M2),而本文方法的每个节点最多计算3个方向的能量函数,一次迭代的时间复杂度小于O(3n);③曲线两次变形之间,另两种模型需进行的节点内插操作也增加了时间开销,而本文方法无需此项操作。
4.2.3 正交T-Snake模型的网格大小图 8统计了当网格宽度分别为1、2、3、4、5个像素时的两幅影像的水体提取效率和精度。总体上,随着网格大小的增加,水体提取的时间效率有所提高,而水体提取精度则会下降(Pratt品质因数降低,形状误差变大)。其中,当网格宽度大于2时,随着网格宽度变大,Pratt品质因数明显降低,形状误差大幅增加,而耗时的变化比较缓慢。因此,本试验的网格大小设置为2×2,此时基于改进正交T-Snake模型的水体提取精度较好,计算效率也较高。
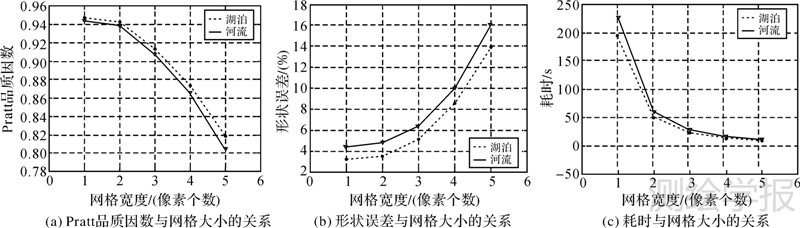
|
| 图 8 改进正交T-Snake模型的网格大小对精度和耗时的影响 Fig. 8 The grid size of the T-snake model impact on accuracy and time cost |
(1) 本文提出了一种可自动提取复杂水体边界的改进正交T-Snake模型,在国产GF-1卫星数据的水体边界提取中取得了不错的效果。试验证明,该模型所提取的水体边界的Pratt品质因数超过93%、形状误差在5%以下,定位精度和形状准确度很高,对于深凹边界的提取效果优于传统Snake和GVF Snake模型。
(2) 改进正交T-Snake模型特别针对河中岛现象设计了曲线变形冲突检测与处理算法,使遥感影像中包含沙洲或岛屿的水域边界的直接提取变得简单化,且可以直接得到连续的水体边界线。
(3) 改进正交T-Snake模型无需手动设置初始轮廓,自动化程度高;曲线变形过程简单使得模型计算效率较高。
(4) 在改进正交T-Snake模型中,划分影像的网格尺寸越大,边界提取的效率越高而精度越低,因为一些小于网格大小的影像特征易被忽略。实际应用中需灵活设置网格大小,在边界提取精度和模型计算效率两者之间取得平衡。
综上所述,本文改进的正交T-Snake模型具有自动化程度高、拓扑变形能力强、深凹边界收敛性能好、可检测含岛目标和计算效率高等特点,能够对包含河中岛的拓扑结构极其复杂的河流边界进行精确提取,亦可在其他地物边界提取中推广应用,如海上岛屿提取和道路网提取等。
| [1] | JIANG H, FENG M, ZHU Y, et al. An Automated Method for Extracting Rivers and Lakes from LandSat Imagery[J]. Remote Sensing, 2014, 6(6): 5067-5089. |
| [2] | YANG Shuwen, XUE Chongsheng, LIU Tao, et al. A Method of Small Water Information Automatic Extraction from TM Remote Sensing Images[J]. Acta Geodaetica et Cartographica Sinica, 2010, 39(6): 611-617. (杨树文, 薛重生, 刘涛, 等. 一种利用TM影像自动提取细小水体的方法[J]. 测绘学报, 2010, 39(6): 611-617.) |
| [3] | SHEN Li, TANG Hong, WANG Shidong, et al. River Extraction from the High Resolution Remote Sensing Image Based on Spatially Correlated Pixels Template and Adaboost Algorithm[J]. Acta Geodaetica et Cartographica Sinica, 2013, 42(3): 344-350. (慎利, 唐宏, 王世东, 等. 结合空间像素模板和Adaboost算法的高分辨率遥感影像河流提取[J]. 测绘学报, 2013, 42(3): 344-350.) |
| [4] | KASS M, WITKIN A, TERZOPOULOS D. Snakes: Active Contour Models[J]. International Journal of Computer Vision, 1988, 1(4): 321-331. |
| [5] | WU Liang, HU Yun'an. Balloon Snake with Adjustable Expansion Coefficient in Road Contour Extraction[J]. Acta Geodaetica et Cartographica Sinica, 2011, 40(1): 71-77. (吴亮, 胡云安. 膨胀系数可调的Balloon Snake方法在道路轮廓提取中的应用[J]. 测绘学报, 2011, 40(1): 71-77.) |
| [6] | HAN Min, SUN Yang. A Method of Vector Edge Updating Based on Grouping Snake Model in GIS[J]. Acta Geodaetica et Cartographica Sinica, 2009, 38(2): 168-174. (韩敏, 孙杨. 一种基于分组式蛇模型的GIS矢量边界更新方法[J]. 测绘学报, 2009, 38(2): 168-174.) |
| [7] | DILLABAUGH C R, NIEMANN K O, RICHARDSON D E. Semi-Automated Extraction of Rivers from Digital Imagery[J]. GeoInformatica, 2002, 6(3): 263-284. |
| [8] | MIAO Lixin, TANG Shouzheng, LI Xia, et al. Extract Reservoir Water Area Automatically Using Masked Active Contour Model from Multispectral Remote Sensing Images[J]. Research of Soil and Water Conservation, 2010, 17(5): 7-11. (苗立新, 唐守正, 李霞,等. 利用掩膜主动轮廓模型提取水库水面面积[J]. 水土保持研究, 2010, 17(5): 7-11.) |
| [9] | XU C Y, PRINCE J L. Snakes, Shapes, and Gradient Vector Flow[J]. IEEE Transactions on Image Processing, 1998, 7(3): 359-369. |
| [10] | HU Qian, ZHANG Feng, LIU Renyi, et al. Land-sea Boundary Extraction Based on Gradient Vector Flow and Active Contour Model[J]. Journal of Zhejiang University: Science Edition, 2013, 40(6): 698-704. (胡倩, 张丰, 刘仁义,等. 基于梯度矢量流和主动轮廓模型的海陆边界提取[J]. 浙江大学学报: 理学版, 2013, 40(6): 698-704.) |
| [11] | SHENG G F, YANG W, DENG X P, et al. Coastline Detection in Synthetic Aperture Radar (SAR) Images by Integrating Watershed Transformation and Controllable Gradient Vector Flow (GVF) Snake Model[J]. IEEE Journal of Oceanic Engineering, 2012, 37(3): 375-383. |
| [12] | ZHU Shulong, MENG Weichan, ZHU Baoshan. Irregular Water Boundary Extraction Using GVF Snake[J]. Journal of Remote Sensing, 2013, 17(4): 742-758. (朱述龙, 孟伟灿, 朱宝山. 运用GVF Snake算法提取水域的不规则边界[J]. 遥感学报, 2013, 17(4): 742-758.) |
| [13] | MCLNERNEY T, TERZOPOULOS D. T-Snakes: Topology Adaptive Snakes[J]. Medical Image Analysis, 2000, 4(2): 73-91. |
| [14] | BISCHOFF S, KOBBELT L P. Snakes with Topology Control [J]. The Visual Computer, 2004, 20(4): 217-228. |
| [15] | SUN Zheng. Coronary Vessel Detection and Motion Tracking Based on T-Snake Model[J]. Journal of Optoelectronics·Laser, 2007, 18(10): 1260-1264. (孙正. 基于T-snake模型的冠状动脉血管提取和运动跟踪[J]. 光电子·激光, 2007, 18(10): 1260-1264.) |
| [16] | ZHOU Jie, JIANG Xiaohua, CHENG Liuquan, et al. Coronary Artery Edge Detection Based on an Orthogonal T-Snake Model[J]. Journal of Tsinghua University: Science and Technology, 2009, 49(1): 41-44. (周洁, 蒋晓华, 程流泉,等. 基于正交T-Snake模型的冠状动脉边缘检测[J]. 清华大学学报: 自然科学版, 2009, 49(1): 41-44.) |
| [17] | ZHENG S. An Intensive Restraint Topology Adaptive Snake Model and Its Application in Tracking Dynamic Image Sequence[J]. Information Sciences, 2010, 180(16): 2940-2959. |
| [18] | SUN F R, LIU Z, LI Y L, et al. Improved T-Snake Model Based Edge Detection of the Coronary Arterial Walls in Intravascular Ultrasound Images[C]//Proceedings of the 3rd International Conference on Bioinformatics and Biomedical Engineering. Beijing, China: IEEE, 2009: 1-4. |
| [19] | DIAO X F, ZHANG X Y, WANG T F, et al. Robust Topology-adaptive Snakes for Medical Ultrasonic Image Segmentation[C]//Proceedings of the 3rd International Conference on Biomedical Engineering and Informatics. Yantai, China: IEEE, 2010: 527-530. |
| [20] | YUAN Yanhong, NI Dong. Segmentation of the Left Ventricle Myocardium in Echocardiography Based on T-Snake Model[J]. Journal of Biomedical Engineering Research, 2013, 32(1): 7-11, 21. (袁艳红, 倪东. 基于T-Snake模型的超声左心室心肌分割方法的研究[J]. 生物医学工程研究, 2013, 32(1): 7-11, 21.) |
| [21] | LIANG B Q, WENG Q H, TONG X H. An Evaluation of Fractal Characteristics of Urban Landscape in Indianapolis, USA, Using Multi-sensor Satellite Images[J]. International Journal of Remote Sensing, 2013, 34(3): 804-823. |
| [22] | YU Zifan, LIN Zongjian. Arithmetic Research of Fractal Dimension with Image Face Based on Fractional Brownian Motion[J]. Geomatics and Information Science of Wuhan University, 2005, 30(2): 161-165. (于子凡, 林宗坚. 基于图像表面积的分形布朗运动分数维算法研究[J]. 武汉大学学报: 信息科学版, 2005, 30(2): 161-165.) |
| [23] | GONZALEZ RC, WOODS RE. Digital Image Processing[M]. New York: John Wiley and Song, 1991. |