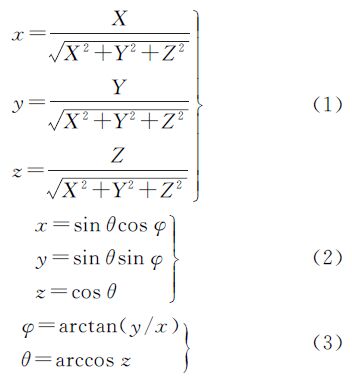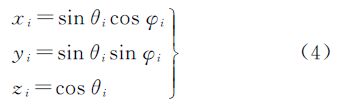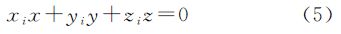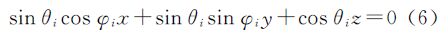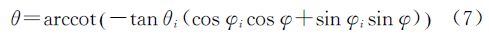2. 武汉大学遥感信息工程学院,湖北 武汉 430079
2. School of Remote Sensing and Information Engineering,Wuhan University,Wuhan 430079,China
1 引 言
地面激光扫描(terrestrial laser scanning)系统能够快速获取目标表面精确而密集的点集,是一种高效的数据获取模式。激光扫描数据由密集而离散的三维点构成,又被称作激光点云。三维激光点云的直线段提取是数据配准、对象识别和三维重建方法的基础步骤。然而,目前较成熟的直线提取方法,如霍夫变换、启发式连接、层次记号编组等[1]都只适用于二维图像,无法直接应用于三维激光点云的直线段提取。
三维激光点云的直线提取,有两大类方法:直接法和降维法。直接法是在点云数据三维计算和分析的基础上提取直线,最常见的是平面相交法[2, 3]。常见的直接法之一是将三维点云分割为不同的平面,拟合平面参数,通过相邻且有一定夹角的平面相交提取直线。此方法提取直线精度较高,在机载点云的建筑物重建中应用较多,但因地面激光扫描数据分辨率高、邻接关系复杂,该方法往往需要大量人工交互操作。另一类常见的直接法首先构建三维激光点云之间的邻接关系或将点云拟合为参数表面,然后通过邻近点或参数表面形成的面状特征进行直线或曲线的提取[4, 5, 6]。这类方法适用于小型零件结构特征的精确提取,在逆向工程和计算机辅助设计方面应用广泛,但复杂场景地面激光点云拟合表面本身就是一个较复杂的问题,因而,此类方法适用性较差。
地面激光点云数据量大、缺乏拓扑邻接关系,直接法的三维计算需要消耗非常多的计算资源。因此,许多研究者提出将三维点云降维处理后进行特征检测和直线提取,将三维激光扫描数据按扫描线进行分解,每条扫描线就是一个二维点集,以减少计算量。这类降维法大多用于面片提取[7, 8]或移动机器人导航[9, 10, 11],无法提取整站地面激光点云中的直线特征。另一类常用的降维法是投影法,将点云以平行投影[12, 13, 14, 15]或中心投影[16, 17, 18]的方式投影到对应的光学图像上,利用图像处理的方法检测特征并提取直线段,再将二维图像的直线段提取结果反投影到三维空间获得三维直线段提取结果。这类方法在处理机载点云数据和地面激光扫描视场角较小的情况下能得到较好的结果,但激光扫描视场角较大(如超过180°)或场景较复杂时,通过这些投影方式必然会造成点的重叠或遮挡等问题,从而导致信息缺失或提取错误。更重要的是,这种投影很难保证点云中的三维点与投影后的二维点一一对应,因而,在反投影过程中容易出现错误。
为了克服投影法在投影过程中的重叠或遮挡等问题,文献[19]将单站激光点云投影到以激光中心为球心的球面上进行分析计算从而构建三角网。因此,本文选择这种球面投影的方法将单站激光扫描数据进行投影,并利用球面霍夫变换方法[20]提取球面投影后的三维直线段特征,最后利用稳健的三维空间直线拟合方法计算激光点云中的三维直线段。
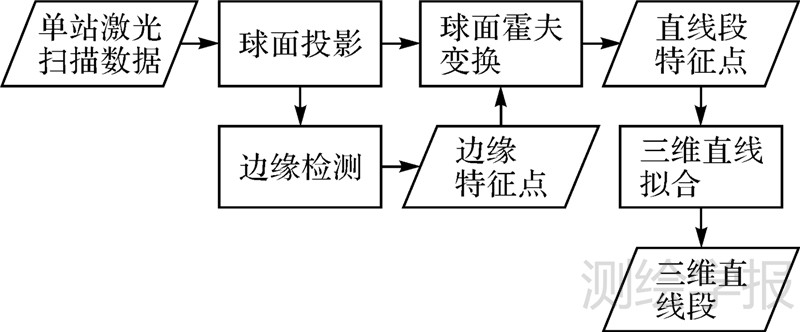
2 方 法基于球面投影的单站地面激光扫描数据直线段提取方法流程如图 1所示,大体上分为球面投影、边缘检测、球面霍夫变换及三维直线拟合4个步骤:
|
| 图 1 球面投影直线段提取方法流程 Fig. 1 Flow chart of proposed method |
(1) 球面投影。将单站激光扫描数据进行球面投影,计算每个激光点对应球面坐标的两个角度值,并利用这两个角度值和激光点云强度信息生成全景图,由于单站激光扫描角度间隔固定,所以全景图的像素与点云中的激光点一一对应。
(2) 边缘检测。利用数字图像边缘检测方法对全景图进行边缘检测,获得全景图上的边缘点,这些边缘点包含了组成直线段的特征点。
(3) 球面霍夫变换。由于三维空间中的直线段经过球面投影后成为球面大圆的弧,球面霍夫变换在二维球面坐标空间中检测边缘点中的大圆,即可提取三维空间中的直线段特征点。
(4) 三维直线拟合。由于投影及边缘检测带来的错误,球面霍夫变换检测的大圆可能包含错误点,利用稳健的三维直线拟合方法剔除粗差,并拟合出精确的三维直线段,完成三维直线段提取。
本节将对算法涉及的理论和实施步骤进行详细描述。
地面激光扫描仪的扫描方式是底座水平放置,激光脉冲发射方向随着扫描头在垂直方向上下摆动或连续转动,同时扫描底座在水平方向缓慢自转,扫描仪通过记录激光脉冲的方向和经目标表面反射后返回的时间(或相位差)来计算目标表面三维坐标。因此,可将单站激光扫描数据中的扫描点无重叠的投影到以激光发射中心点为球心的球面上,通过由三维球坐标系降维简化的二维球面坐标系来描述激光扫描数据。
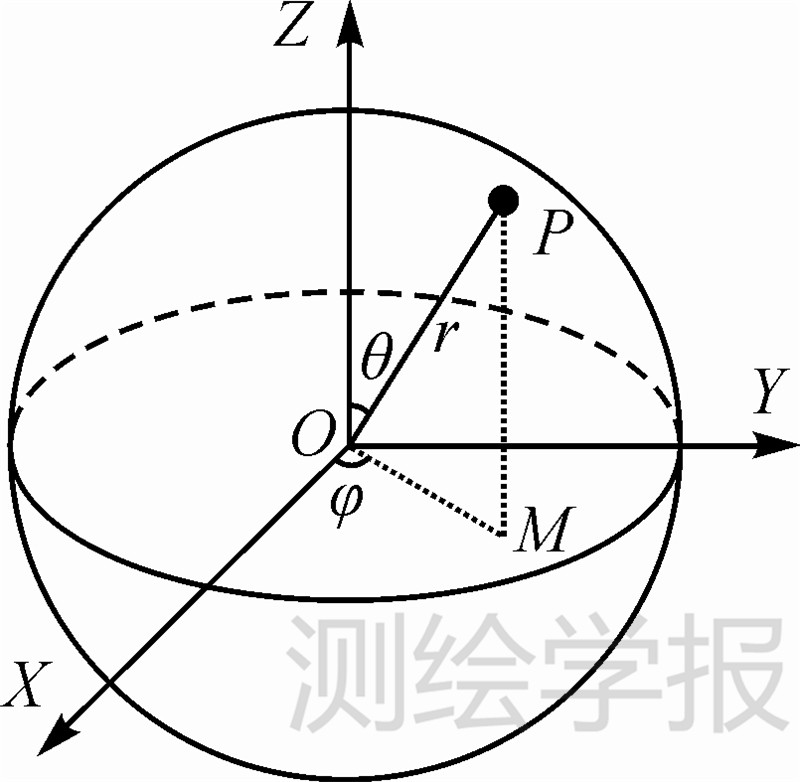
球坐标系是利用球坐标(r,θ,φ)表示一个点P空间位置的三维正交坐标系[21]。图 2示意了球坐标的几何意义:原点与点P之间的径向距离r,原点到点P的连线与正Z轴之间的天顶角θ,以及原点到点P的连线在XOY平面的投影线MO与X轴之间的方位角φ。本文定义的球面坐标系是设径向距离r为单位常量1的球坐标系,即,将三维球坐标系(r,θ,φ)简化为二维球面坐标系(θ,φ)。
|
| 图 2 球坐标系 Fig. 2 Spherical coordinates |
记空间中的一点P的三维坐标为(X,Y,Z),该点投影到半径为1的单位球面后的点p的球面坐标为(φ,θ)、三维坐标为(x,y,z),则有
式中,φ和θ即为获取该点时激光脉冲的水平角和垂直角。因单站激光扫描中,激光器水平和垂直方向的角分辨率是固定的,则点云在球坐标系下的φ和θ的间隔也是固定的,因此,对投影后的点云可以用二维栅格进行索引,某一点在栅格中的二维坐标由φ和θ确定。栅格中存放的是点云的三维坐标、深度和强度等信息,每个三维激光点都有唯一的二维栅格与之对应[22]。如果将二维栅格表示为图像,则该图像为全景图,图像的像素灰度值可由其对应点云的深度或强度等信息决定。图 3用不同方式表现了单站地面激光扫描数据,像素的灰度值由点云回波强度决定。图 3(a)为点云的三维透视图,其经过球面投影后如图 3(b)所示,将其展开为全景图如图 3(c)所示。

|
| 图 3 按强度赋色的激光点云不同表现形式的图像 Fig. 3 Different view types of point cloud colored according to intensity |
点云的深度是被测点与扫描仪中心的距离,强度表示激光脚点经由目标表面反射后激光器接收激光信号的强弱。通常情况下,深度的阶跃会导致强度的阶跃变化。除此之外,颜色、材质、角度的变化也会导致强度的变化,因此,许多深度变化不明显的地方,如建筑物的拐角处、不同颜色的装饰处等在强度中的变化十分明显。可见,强度包含了十分丰富的信息,利于激光扫描数据的分析与计算,本文选取由强度信息生成的全景图进行进一步的特征提取。
2.2 边缘检测与球面霍夫变换全景图与普通图像一样,可以用图像处理的方法进行边缘提取。Edison算子[23]将像素的嵌入置信度贯穿到Canny算子中,满足最佳边缘提取算子的3个准则:高信噪比、精确定位和单边缘响应[24]。因此,本文选用了Edison算子进行边缘检测。
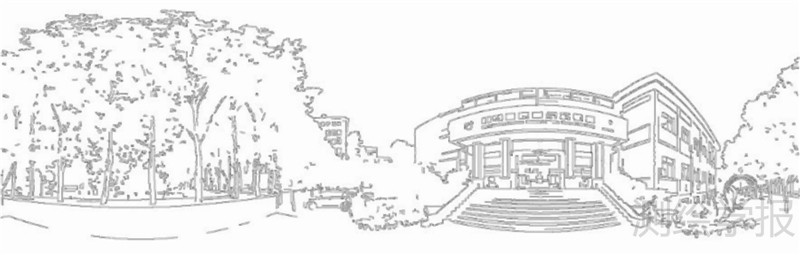
对图 3(c)的强度全景图边缘检测结果如图 4所示。可以看出,利用Edison算子可以较好地检测出强度全景图中的边缘特征。然而,三维空间中的直线在球面投影与展开后的全景图中变成了曲线,无法用传统霍夫变换提取这些直线。由立体几何知识可知,三维空间中的直线段投影到球面上是一个大圆弧,而球面上大圆的轨迹可以用一系列的球面坐标(θi,φi)表示,而且这些二维坐标也能在球面坐标φ-θ空间中累积形成峰值。文献[20]利用球面霍夫变换准确估计三维点云中圆柱的方向,基于类似原理,本文利用球面霍夫变换检测球面空间的大圆。
|
| 图 4 强度全景图的边缘检测结果 Fig. 4 Edge detection results of intensity panoramic image |
球面上某一点Pi(θi,φi),记其对应的三维空间坐标为(xi,yi,zi),由式(2)可知
由立体几何知识可知,一个球有且仅有一条直径与球面上某一已知圆垂直,球面三角中将这条垂直直径的两个端点定义为该已知圆的极。因此,球面上一个大圆有且仅有两个极,反之,以球面上一个点为极的大圆也是唯一的。
由极的定义可知,以Pi为极的大圆所在的平面垂直于线段OPi(O为球心),即该平面的法向为(xi,yi,zi),且该平面过原点,则该平面方程为
将式(4)代入式(5)得该平面与球面相交形成的大圆(即以Pi为极的大圆)的三维直角坐标系方程为
将式(2)代入式(6)可得该大圆的球面坐标系方程为
由极的定义可得到以下两个有关极和大圆之间关系的推论,推论和证明如下:
推论1:经过球面上某一已知点的所有大圆的极形成的轨迹是球面上以该已知点为极的大圆。
证明:如图 5(a)所示,球面上某一已知点M,记经过点M的大圆直径的另一端点为M′,那么经过点M的所有大圆Ci都会以MM′为直径。根据极的定义,大圆Ci的极Ni和Ni′的连线NiNi′是与大圆Ci垂直的直径,显然直径NiN′i垂直于直径MM′。由此推断,所有的点Ni和点N′i都在过圆心且垂直于直径MM′的平面与球面的交线上,即为一个大圆,且该大圆的极为M和M′。
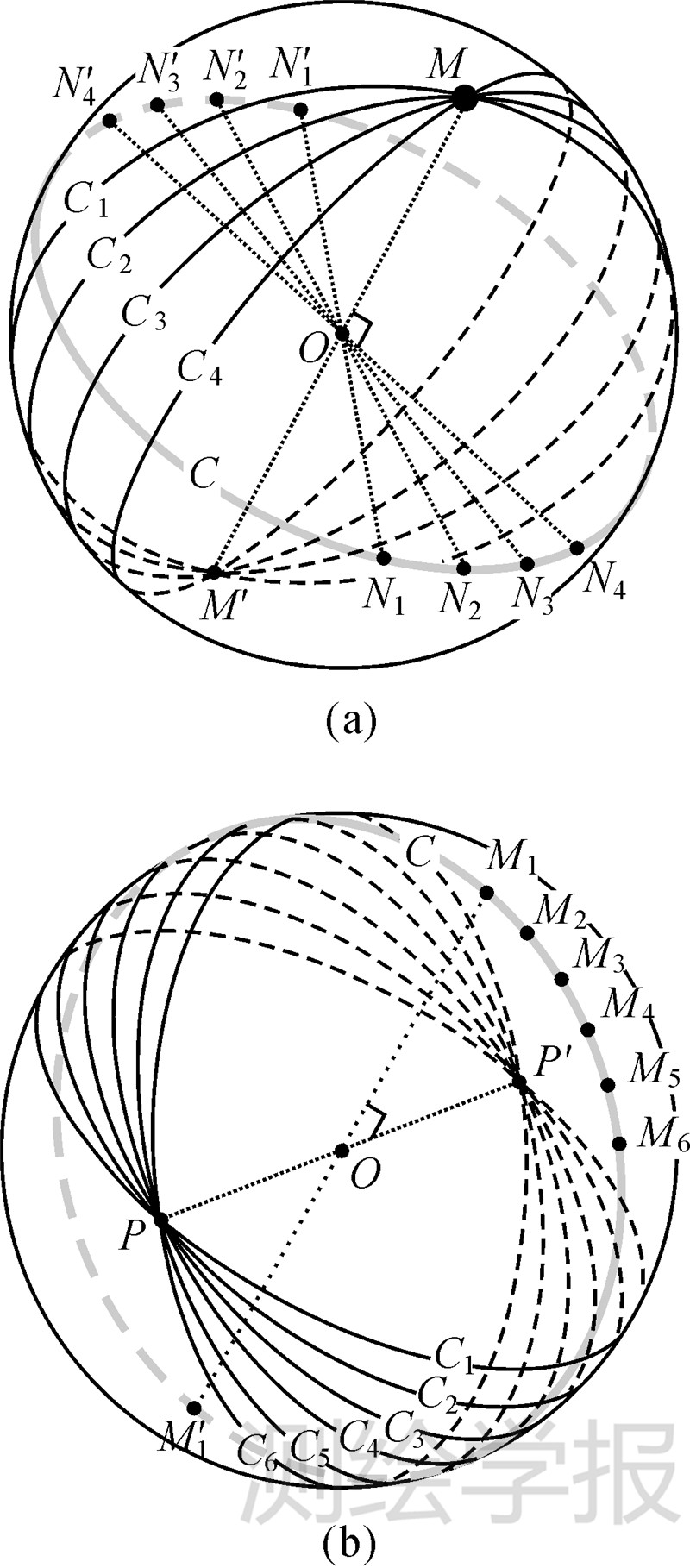
|
| 图 5 球面上极和大圆的关系 Fig. 5 Relationships between spherical poles and great circles |
推论2:以球面上某一已知大圆上的所有点为极的大圆交汇于该已知大圆的极。
证明:如图 5(b)所示,记已知大圆C上的任一点为Mi,过Mi的大圆直径的另一端点为M′i,过圆心且与直径MiM′i垂直的平面与球面相交的大圆为Ci。由极的定义可知,大圆Ci的极为Mi和M′i。由于大圆Ci与大圆C的直径MiM′i垂直,所以大圆Ci与大圆C垂直。记大圆C的极为P和P′,由于大圆Ci和直径PP′均与大圆C垂直,且均过圆心O,因此,直径PP′与大圆Ci共面,即球面上所有大圆Ci都交汇于点P和P′。
由上述推论可知,球面上一个点有且仅有唯一的大圆以该点为极,本文称该大圆为“该点对应的大圆”。同时,由式(7)可知大圆轨迹可以在一个有限的φ-θ二维空间表现为一条曲线。利用霍夫变换原理,如果将一段大圆弧上所有点对应的大圆轨迹在这个φ-θ二维参数空间进行累积,则φ-θ二维参数空间中在该大圆弧的两个极会形成峰值,通过峰值的φ-θ坐标即可求得大圆方程。
为避免霍夫变换全局投票给较短的特征线段带来漏检测或检测不准确的影响,本文采用局部霍夫变换[25]的方法进行大圆检测:首先,将边缘点按邻接关系分成若干的边缘组;再以边缘组为单位进行球面霍夫变换,单独解算某条边缘中包含大圆的参数;最后按照大圆参数和端点距离合并大圆弧段。
图 6为图 4通过球面霍夫变换检测大圆弧段的结果,这些大圆弧段即对应三维点云中的直线段特征点集。
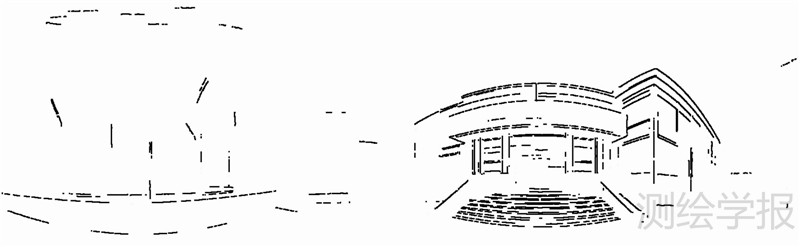
|
| 图 6 球面霍夫变换直线段提取结果 Fig. 6 Spherical Hough transform results of straight line segment extraction |
由于边缘提取误差、球面投影带来的空间歧义以及激光扫描系统本身在边缘处的噪声,导致球面霍夫变换提取的三维点云直线段特征点中除了真正的直线段特征点外,往往还包含一些噪声点。激光扫描数据中比较理想的是脊状边缘上的直线段特征,如图 7(a)所示,对其提取到的三维直线段特征点如图 7(b)所示,这类特征比较理想,无噪声点。然而,激光扫描数据中还存在大量如图 7(c)所示的由阶跃引起的边缘,由于激光光斑有一定的大小,在边缘处的激光点会包含一些噪声,如图 7(d)所示;此外,如图 7(e)所示直线段边缘处有植被等其他对象干扰时也会在三维直线段特征点中引入一些噪声点,如图 7(f)所示。对于存在噪声点的直线段特征点集,如果仅用最小二乘法无法准确解算三维空间的直线段参数,本文用RANSAC[26]的方法剔除直线段特征中的粗差点,稳健的拟合三维直线。这种方法与文献[16]中的类似,本文不再详细讨论。通过稳健的三维直线拟合得到的最终直线段提取结果如图 8所示。
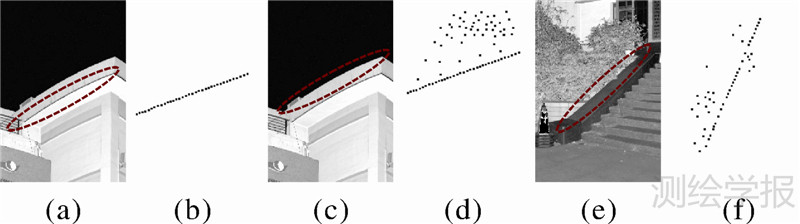
|
| 图 7 几种典型的直线边缘及对应的三维直线段特征点集 Fig. 7 Several typical straight line edges and corresponding 3D point sets |

|
| 图 8 三维直线段提取结果 Fig. 8 Results of 3D straight line segment extraction |
记单站激光点云中包含的激光点Pi的三维空间坐标为(Xi,Yi,Zi),归一化强度值为Ii。该站激光扫描水平与垂直角度范围为H和V,角分辨率为RH和RV。本方法实施步骤如下:
2.4.1 球面投影及三维点索引
根据(Xi,Yi,Zi),利用式(1)和式(3)计算每个点Pi的球面坐标(θi,φi)。
根据H、V、RH和RV利用式(8)计算球面投影后的二维栅格大小M×N。
根据θi、φi、RH和RV利用式(9)计算点Pi在二维栅格中的存放位置ri和ci,并将点Pi的三维空间坐标(Xi,Yi,Zi)及归一化强度Ii存入ri行ci列的栅格中。
建立一张M×N的图像,图像像素值设置为栅格中对应位置激光点的强度Ii×255,生成强度全景图,对应栅格中没有激光点的像素(如天空等无回波对象)像素值设置为0。
2.4.2 边缘检测与球面霍夫变换利用Edison算子对步骤(1)生成的强度全景图进行边缘检测,利用8连通将检测到的边缘点分组,以组为单位进行球面霍夫变换。
球面φ-θ参数空间中,完整球面的参数范围是φ∈[0,2π),θ∈[0,π)。球面霍夫变换是累积大圆极的轨迹,一个大圆对应的两个极在球面呈中心对称,因此,只需半球的参数空间φ∈[0,π),θ∈[0,π)即可。参数空间量化间距大小取角度分辨率,从而,累积矩阵大小为:π/RV行,π/RH列。
利用式(7)计算该组内每个边缘点对应的大圆轨迹,并计入累积矩阵。累积完成后,选取累积峰值及其对应的边缘点。
所有边缘组大圆检测完成后,按大圆参数排序,合并大圆参数相同且弧段端点在一定阈值内的大圆弧。
2.4.3 三维直线拟合步骤(2)中检测出的大圆弧对应的是全景图上的一系列边缘点,每个边缘点对应二维栅格中存储的一个三维激光点。取出每个大圆弧对应的一系列三维激光点,通过稳健的三维直线拟合方法拟合三维直线方程,通过边缘点的范围计算三维直线段的两个顶点,完成三维直线段提取。
3 试验与分析 3.1 直线段提取试验本文选择了建筑物室外和室内两站地面激光扫描数据进行直线段提取试验。试验数据的采集仪器为Z+F Imager5006型三维激光扫描仪。该扫描仪25m处测距中误差为1.5mm,试验数据采集的水平角度范围为360°,垂直角度范围为310°,角分辨率为0.018°。
对建筑物室外场景的激光扫描数据已经在第2节的方法描述中进行了试验说明,提取直线段结果如图 8所示,建筑物上的主要直线段特征都被正确提取,但仍存在一些特征被遗漏,以及少量树上干扰特征的过检测。
建筑物室内激光扫描试验数据集及中间步骤结果如图 9所示。其中,图 9(a)为点云三维透视视图,图 9(b)为球面投影后展开的强度全景图,由于建筑物内部的主要直线段特征在扫描仪中构象的水平角度范围大,因此,直线段特征呈现出更明显的弯曲。利用Edison算子的边缘提取结果如图 9(c)所示,边缘检测结果中除了场景的直线段特征外,还存在大量的干扰特征。通过球面霍夫变换大圆检测后,得到的大圆弧中保留了大部分主要特征,剔除了大部分干扰特征,如图 9(d)所示。通过直线拟合后的三维直线段提取结果如 图 10所示。建筑物内部的主要直线段特征都被正确提取。

|
| 图 9 室内点云试验数据及中间步骤结果 Fig. 9 The data set of indoor scene and the interim results |

|
| 图 10 室内场景三维直线段提取结果 Fig. 10 Results of straight line segment extraction of indoor scene |
以上室内和室外场景两组试验都验证了本文提出的直线段提取方法的正确性,虽然本方法存在少量直线段特征的过检测和漏检测,但目前其他文献的方法从理论上,都无法自动完成此类全站激光扫描数据的直线段提取。
3.2 对比与分析本文首先选择了商业软件Geomagic Studio进行对比试验,并在精度上与文献[15, 17]中的直线段提取方法进行比较。
商业软件Geomagic Studio的直线段提取采用的是平面相交法,具体步骤为:首先自动将待提取点云构建三角网,然后在三角网中自动提取平面,再通过人工交互选取相邻且有一定夹角的平面相交提取直线段,最后人工交互合并邻近且共线的直线段。
Geomagic Studio对数据量的限制及其方法需要大量人机交互操作,因此,对比试验选取室外场景的台阶部分进行,此部分数据直线段特征集中,适合试验分析。Geomagic Studio与本文方法的直线段提取结果对比如图 11所示。

|
| 图 11 Geomagic Studio与本方法的直接提取结果对比 Fig. 11 Comparison of straight line segment extraction results of Geomagic Studio and proposed method |
效率方面。Geomagic Studio提取直线段过程较复杂,且需大量人工交互操作,而本方法为自动提取,效率高于Geomagic Studio软件。
直线段提取完整性方面。Geomagic Studio的直线段提取依赖于平面特征检测的结果,平面检测的遗漏会导致直线段检测的遗漏及长度完整性不够。由图 11的对比结果可知,本方法提取的直线段也存在遗漏,但在直线段的长度完整性方面优于Geomagic Studio。
直线段提取精度方面。由激光扫描原理可知,激光扫描点云拟合的平面精度高,因而Geomagic Studio的平面相交法提取的直线段精度较高。本文统计本方法与Geomagic Studio提取的16条同名直线段之间的夹角和距离,对本方法提取直线段的精度进行间接验证,统计结果如表 1所示。从统计数据看,夹角平均值为0.153°,距离平均值为0.0033m。本文方法的距离平均值大幅度优于文献[17]中的结合影像与点云自动直线特征提取方法结果的0.0096m,同时,本方法与文献[15]中的霍夫变换与最小二乘提取直线的误差统计结果相比也有较大的优势。
| 直线段编号 | 4/89 | 8/97 | 8/77 | 3/76 | 2/73 | 16/75 | 15/61 | 14/62 |
| 夹角/(°) | 0.1172 | 0.3362 | 0.2896 | 0.0973 | 0.0435 | 0.2028 | 0.0429 | 0.1441 |
| 距离/m | 0.0071 | 0.0185 | 0.0026 | 0.0065 | 0.0006 | 0.0023 | 0.0024 | 0.0004 |
| 直线段编号 | 7/60 | 13/59 | 12/57 | 1/56 | 0/54 | 11/55 | 10/94 | 17/49 |
| 夹角/(°) | 0.5281 | 0.0745 | 0.1216 | 0.0417 | 0.1406 | 0.0641 | 0.1772 | 0.0262 |
| 距离/m | 0.0037 | 0.0005 | 0.0001 | 0.0007 | 0.0012 | 0.0024 | 0.0001 | 0.0030 |
| 夹角平均值:0.153° | 距离平均值: 0.0033m | |||||||
本文提出了一种基于球面投影的单站三维激光点云直线段提取方法,其核心思路是将单站激光扫描数据进行球面投影,不仅能用二维的规则格网对三维激光扫描数据索引,简化计算和分析,更能避免其他投影方法引起的重叠或遮挡等问题。而在以强度信息为依据生成的影像上进行计算,不仅能检测出几何的直线段特征,也能检测出纹理的直线段特征。
如何有效融合包括深度、强度甚至可见光影像的数据进行更稳健的直线段提取,弥补单一强度信息特征提取的不足,是本文进一步的研究方向。此外,将直线段提取结果用于数据配准、对象识别和三维建模等方面,也将是下一步的研究方向。
| [1] | WEN Gongjian, WANG Runsheng. A Robust Approach to Extracting Straight Lines[J]. Journal of Software, 2001, 12(11): 1660-1666. (文贡坚, 王润生. 一种稳健的直线提取算法[J]. 软件学报, 2001, 12(11): 1660-1666.) |
| [2] | HABIB A, GHANMA M, MORGAN M, et al. Photogrammetric and LiDAR Data Registration Using Linear Features[J]. Photogrammetric Engineering and Remote Sensing, 2005, 71(6): 699-707. |
| [3] | HUANG Xianfeng. Research on 3D Building Model Extraction from Airborne LIDAR Data[D]. Wuhan: Wuhan University, 2006. (黄先锋. 利用机载LIDAR数据重建3D建筑物模型的关键技术研究[D]. 武汉: 武汉大学, 2006.) |
| [4] | DANIELS J, HA L K, OCHOTTA T, et al. Robust Smooth Feature Extraction from Point Clouds[C]//Proceedings of the IEEE International Conference on Shape Modeling and Applications. Lyon: IEEE,2007: 123-136. |
| [5] | MEHDI-SOUZANI C, DIGNE J, AUDFRAY N, et al. Feature Extraction from High-density Point Clouds: Toward Automation of an Intelligent 3D Contactless Digitizing Strategy[J]. Computer-aided Design and Applications, 2010, 7(6): 863-874. |
| [6] | WEBER C, HAHMANN S, HAGEN H. Methods for Feature Detection in Point Clouds[C]//Visualization of Large and Unstructured Data Sets: Applications in Geospatial Planning, Modeling and Engineering. Bodega Bay, CA: Schloss Dagstuhl-Leibniz-Zentrum fuer Informatik, 2011: 90-99. |
| [7] | SURMANN H, LINGEMANN K, NVCHTER A, et al. A 3D Laser Range Finder for Autonomous Mobile Robots[C]//Proceedings of the 32nd International Symposium on Robotics. [S. l.]: ISR, 2001: 153-158. |
| [8] | PAN Guorong, GU Chuan, WANG Suihui, et al. Research on Fitting Line Automatic Extraction Algorithm of 3D Laser Scanning[J]. Journal of Geodesy and Geodynamics, 2009, 29(1): 57-63. (潘国荣, 谷川, 王穗辉, 等. 三维激光扫描拟合直线自动提取算法研究[J]. 大地测量与地球动力学, 2009, 29(1): 57-63.) |
| [9] | FERNNDEZ C, MORENO V, CURTO B, et al. Clustering and Line Detection in Laser Range Measurements[J]. Robotics and Autonomous Systems, 2010, 58(5): 720-726. |
| [10] | MOVAFAGHPOUR M A, MASEHIAN E. Poly Line Map Extraction in Sensor-based Mobile Robot Navigation Using a Consecutive Clustering Algorithm[J]. Robotics and Autonomous Systems, 2012, 60(8): 1078-1092. |
| [11] | NOROUZI M, YAGHOBI M, SIBONI M R, et al. Recursive Line Extraction Algorithm from 2D Laser Scanner Applied to Navigation a Mobile Robot[C]//Proceedings of the IEEE International Conference on Robotics and Biomimetics. Bangkok: IEEE, 2009: 2127-2132. |
| [12] | SUI L C. Processing of Laser Scanner Data and Extraction of Structure Lines Using Methods of the Image Processing[J]. Acta Geodaetica et Cartographica Sinica, 2004, 33(1): 63-70. |
| [13] | JIANG X, BUNKE H. Edge Detection in Range Images Based on Scan Line Approximation[J]. Computer Vision and Image Understanding, 1999, 73(2): 183-199. |
| [14] | DENG Fei. Research on LiDAR and Digital Images Registration and Objects Extraction[D]. Wuhan: Wuhan University, 2006. (邓非. LiDAR数据与数字影像的配准和地物提取研究 [D]. 武汉: 武汉大学, 2006.) |
| [15] | ZHAN Qingming, ZHOU Xingang, XIAO Yinghui, et al. Comparison of Linear and Circular Feature Extraction Methods Based on Laser Point Clouds of an Ancient Architecture[J]. Geomatics and Information Science of Wuhan University, 2011, 36(6): 674-677.(詹庆明, 周新刚, 肖映辉, 等. 从激光点云中提取古建筑线性和圆形特征的比较[J]. 武汉大学学报: 信息科学版, 2011, 36(6): 674-677.) |
| [16] | LU Z J, BAEK S, LEE S. Robust 3D Line Extraction from Stereo Point Clouds[C]//Proceedings of the IEEE Conference on Robotics, Automation and Mechatronics. Chengdu: IEEE, 2008: 1-5. |
| [17] | MEIERHOLD N, SCHMICH A. Referencing of Images to Laser Scanner Data Using Linear Features Extracted from Digital Images and Range Images[C]//Proceedings of the ISPRS Workshop Laser Scanning 2009. [S. l.]: ISPRS, 2010: 210-219. |
| [18] | LEE S, KIM E, PARK Y. 3D Object Recognition Using Multiple Features for Robotic Manipulation[C]//Proceedings of the 2006 IEEE International Conference on Robotics and Automation. Orlando, Florida: IEEE , 2006: 3768-3774. |
| [19] | ZHANG Fan, HUANG Xianfeng, LI Deren. Spherical Projection Based Triangulation for One Station Terrestrial Laser Scanning Point Cloud[J]. Acta Geodaetica et Cartographica Sinica, 2009, 38(1): 48-54. (张帆, 黄先锋, 李德仁. 基于球面投影的单站地面激光扫描点云构网方法 [J]. 测绘学报, 2009, 38(1): 48-54.) |
| [20] | SHAH T R. Automatic Reconstruction of Industrial Installations Using Point Clouds and Images[D]. Delft: Technische Universiteit Delft, 2006. |
| [21] | ARFKEN G B. Mathematical Methods for Physicists[M]. 6th ed. Orlando, FL: Academic Press, 2005. |
| [22] | BRIESE C. Structure Line Modelling Based on Terrestrial Laser Scanner Data[C]//Proceedings of the ISPRS Symposium on Image Engineering and Vision Metrology. Dresden: ISPRS, 2006: 129-136. |
| [23] | MEER P, GEORGESCU B. Edge Detection with Embedded Confidence[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2001, 23(12): 1351-1365. |
| [24] | CANNY J. A Computational Approach to Edge Detection[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 1986, 8(6): 679-698. |
| [25] | ZHANG F, HUANG X F, CHENG X G, et al. Edge Extraction Algorithm Based on Linear Perception Enhancement[C]//Proceedings of the International Archives of the Photogrammetry, Remote Sensing and Spatial Information Sciences. Beijing: ISPRS, 2008: 497-502. |
| [26] | FISCHLER M A, BOLLES R C. Random Sample Consensus: A Paradigm for Model Fitting with Applications to Image Analysis and Automated Cartography[J]. Communications of the ACM, 1981, 24(6): 381-395. |