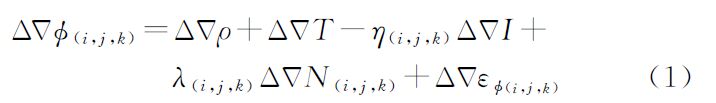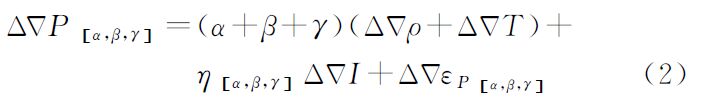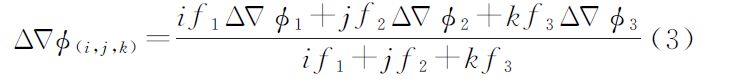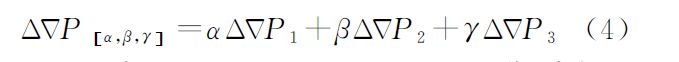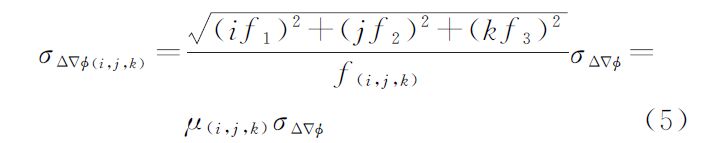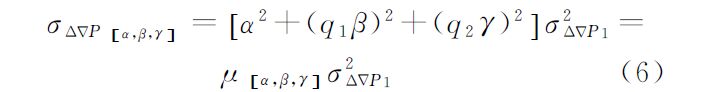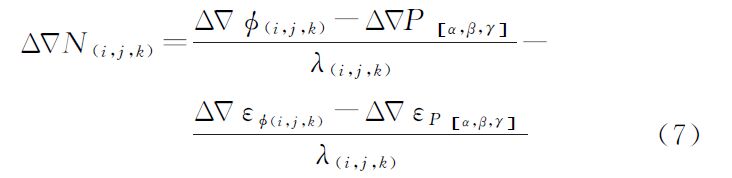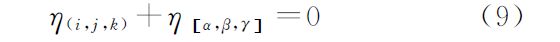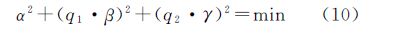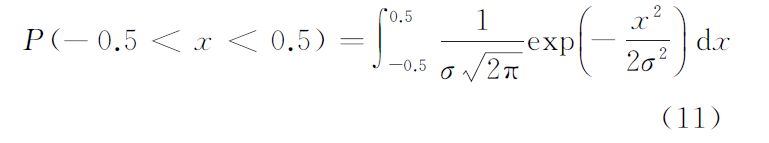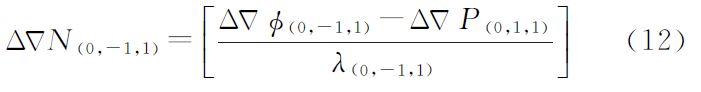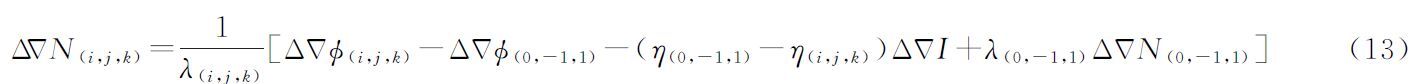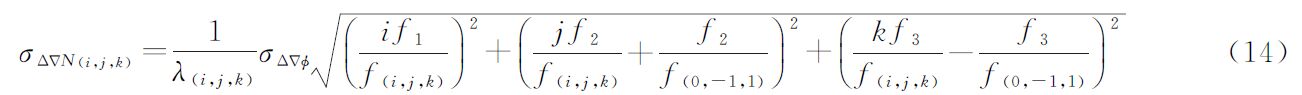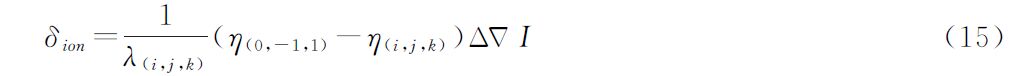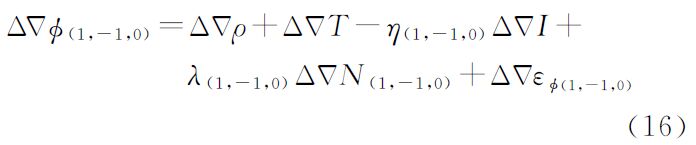2. 东南大学仪器科学与工程学院,江苏 南京 210096;
3. 安徽理工大学测绘学院,安徽 淮南 232001
2. School of Instrument Science and Engineering,Southeast University,Nanjing 210096,China;
3. School of Surveying and Mapping Engineering,Anhui University of Science & Technology,Huainan 232001,China
1 引 言
网络RTK技术是目前应用范围最广的GNSS精密定位技术之一,它能够让用户便捷地在较大空间范围内实时地获得均匀、高精度的定位结果,已广泛应用于测绘、精密导航等诸多领域[1, 2, 3]。目前网络RTK的定位精度约为平面1~2cm,高程3~5cm[4, 5]。模糊度的快速可靠固定是获得实时高精度定位结果的前提。目前在网络RTK定位中,用户端大多是基于解算L1或L2基础模糊度,以GPS为例,其波长分别约为19cm和24cm,受基站间距离、大气误差内插精度以及用户站观测环境等因素的影响,短时间内模糊度解算的成功率较低,仍然存在初始化时间过长(如大于1min)甚至长时间无法固定的情况[3, 5, 6],且在卫星信号失锁或网络差分信号中断后,需要重新初始化;同时,定位结果的可靠性也因模糊度成功率较低而无法得到保障[7]。
为了提高模糊度解算的成功率、可靠性和缩短定位初始化时间,文献[8]曾提出利用宽巷的长波长特性,优先固定宽巷模糊度的部分模糊度固定方法;文献[9]也提出了一种利用三频宽巷组合观测值结合利用宽巷观测值反算的电离层信息进行长距离实时精密导航的方法,通过1~2min的平滑可得到平面厘米级的定位精度。事实上,在中等比例尺测图、精密交通导航、水深测量平面定位等测量作业中,用户对定位时效性和连续性有较高的要求,而可接受目前网络RTK定位精度的适度降低。在网络RTK中直接使用模糊度固定的宽巷观测值,并在差分改正信息的支持下进行定位,虽然一定程度上放大了载波观测噪声,但理论上仍可实现厘米级定位精度并满足很多场合下的应用需求。
对宽巷模糊度的解算有两种情况,一是在目前双频系统条件下,依靠载波和伪距组合基于无几何或几何模式进行解算[10, 11, 12]。但两种模式下伪距观测噪声的影响均较大,单历元固定的可靠性不高,仍然需要一定的初始化时间,且基于几何模式的解法也受观测条件的影响,在遮挡等环境下成功率降低;二是使用三频系统,利用三频观测值可组成一系列具有长波长的宽巷或超宽巷组合,能够很好地削弱大气误差和观测噪声的影响从而提高模糊度固定的成功率[13, 14, 15, 16, 17]。2012年底,我国自主建设的北斗系统完成区域组网,正式提供亚太地区的导航定位服务,且全系统卫星均播发三频信号。在这一条件下,本文研究在网络RTK中利用北斗三频观测值进行超宽巷和宽巷模糊度的单历元可靠解算方法,并直接使用模糊度固定的宽巷观测值和差分改正信息进行单历元定位,也通过实测北斗三频数据对模糊度解算时效性和定位解的精度进行了分析验证。
2 北斗观测值及其线性组合顾及双差对流层和电离层一阶项的影响,以距离为单位的北斗双差载波和伪距观测方程可分别表示为式(1)和式(2)[16, 18]
其中组合的双差载波和伪距观测值为
式(1)—(4)中,△▽φ(i,j,k)和△▽P[α,β,γ]分别为组合的载波和伪距观测值;i、j、k为任意整数;△▽φi为第i个频率上的双差载波观测值;α、β、γ为任意实数;△▽Pi为第i个频率上的双差伪距观测值;f1、f2、f3分别为北斗系统的3个载波频率;△▽ρ、△▽T、△▽I分别为双差站星距离、双差对流层延迟值、北斗B1频点上的双差电离层延迟值。组合观测值的模糊度△▽N(i,j,k)、频率f(i,j,k)和波长λ(i,j,k)的定义可参见文献[16];η(i,j,k)、η[α,β,γ]、△▽εφ(i,j,k)和△▽εP[α,β,γ]分别为组合双差载波、伪距观测值的电离层延迟因子和观测噪声,具体表达式可参考文献[16]和文献[18]。一般认为3个频点上的载波观测值等精度,即
| 组合 序号 | 组合系数 (i,j,k) | 波长 λ(i,j,k)/m | 电离层因子 η(i,j,k) | 噪声放大因子 μ(i,j,k) |
| 1 | (0,-1,1) | 4.8842 | -1.5915 | 28.5287 |
| 2 | (1,4,-5) | 6.3707 | 0.6521 | 172.6135 |
| 3 | (1,3,-4) | 2.7646 | -0.6179 | 59.2629 |
| 4 | (1,2,-3) | 1.7654 | -0.9698 | 28.0859 |
| 5 | (1,1,-2) | 1.2967 | -1.1348 | 13.9022 |
| 6 | (-1,-5,6) | 20.9323 | -8.9631 | 686.9493 |
| 7 | (1,-1,0) | 0.8470 | -1.2932 | 5.5752 |
| 8 | (1,0,-1) | 1.0247 | -1.2306 | 6.8751 |
采用载波和伪距组合的无几何无电离层(GIF)模型[20, 21]求解超宽巷或宽巷模糊度如式(7)所示
式(7)需满足以下两个条件 式(8)保证了伪距和载波组合观测值中的几何项相同,从而能消除站星距离、对流层延迟、轨道误差等其他几何相关项的影响;式(9)保证了两者的电离层延迟大小相等,从而能够消除电离层延迟的影响。从式(7)可以看出,GIF模型求解宽巷模糊度受载波和伪距观测值噪声的影响,与基线距离无关。当给定载波组合系数时,通过使伪距观测值噪声最小即可获得最优组合,其等价于式(10)所示条件 联立式(8)—式(10)采用最小范数法即可求解最优的伪距组合系数[18]。顾及不同接收机性能,假设载波噪声σ△▽φ为0.5cm和1cm两种情况,伪距噪声σ△▽P为0.3m、0.6m和1m3种情况[15, 18],组成如表 2所示的6种噪声组合情况。同时根据文献[18, 19],取q1=1、q2=0.2和q1=1、q2=1两种情况。| 组合号 | 噪声组合 |
| 1 | σ△▽φ=0.5cm,σ△▽P=0.3m |
| 2 | σ△▽φ=0.5cm,σ△▽P=0.6m |
| 3 | σ△▽φ=0.5cm,σ△▽P=1m |
| 4 | σ△▽φ=1cm,σ△▽P=0.3m |
| 5 | σ△▽φ=1cm,σ△▽P=0.6m |
| 6 | σ△▽φ=1cm,σ△▽P=1m |
根据式(8)—式(10)所示原则,求解GIF模型在不同观测值噪声情况下模糊度解算精度,按式(11)计算成功率[22]
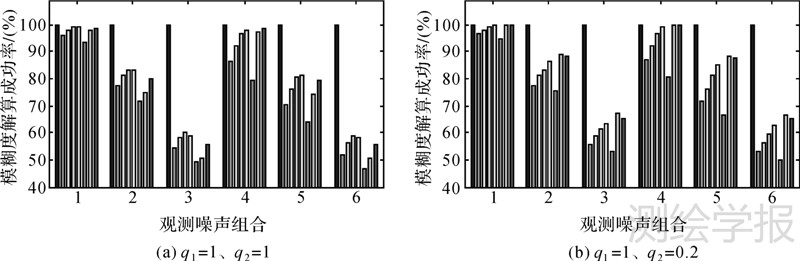
式中,σ为观测值噪声造成的随机性偏差。结果如图 1所示。图 1中对应每种噪声组合,从左至右依次为表 1中所示的8种观测值组合。
|
| 图 1 不同噪声情况下使用GIF模型模糊度解算成功率 Fig. 1 Success rate of AR with GIF model in different noise combinations |
从图 1中可以看出,使用GIF模型求解宽巷模糊度,(0,-1,1)组合在不同噪声情况下解算成功率均接近100%,而其他组合受伪距噪声影响明显,当伪距噪声较大时,模糊度解算成功率显著下降。对比图 1(a)和(b)可以看出,当北斗B3频点伪距精度较高时,使用GIF模型求解模糊度成功率得到一定提高。
从表 1中可以看出(0,-1,1)组合观测值噪声较大,无法直接用于定位解算,因此需要求解第2个宽巷或超宽巷模糊度,以组合得到观测噪声和大气延迟影响较弱的宽巷或超宽巷组合。
上述无电离层无几何方法中模糊度求解精度受伪距噪声影响明显,且在伪距噪声比值系数不同的时候,按式(8)—(10)所示原则求取的伪距组合系数也存在较大的差异,实际应用中伪距的噪声比值系数是难以准确获得的,因此GIF模型实用价值有限。实际应用中,(0,-1,1)组合模糊度一般按式(12)进行求解[15, 16]
式中,△▽P(0,1,1)表示以周为单位组合的(0,1,1)伪距观测值,形式与式(3)相同。式(12)同样消除了电离层延迟、几何相关项等的影响,在表 2所示几种噪声情况下模糊度解算中误差和成功率如表 3所示。| 噪声组合号 | 解算中误差/周 | 成功率/(%) |
| 1 | 0.052 | 100.00 |
| 2 | 0.092 | 100.00 |
| 3 | 0.148 | 99.93 |
| 4 | 0.073 | 100.00 |
| 5 | 0.105 | 100.00 |
| 6 | 0.156 | 99.86 |
从表 3中可以看出,(0,-1,1)组合模糊度在所示几种噪声情况下解算成功率几乎均为100%,单历元即可可靠固定。
利用式(12)所示模型能单历元可靠固定(0,-1,1)组合模糊度的优势,可采用分步固定思想的TCAR方法[13, 14],即将模糊度已固定的(0,-1,1)宽巷组合观测值作为一个较高精度的观测量,与第2个宽巷/超宽巷观测值组成无几何模型,以辅助解算第2个超宽巷/宽巷模糊度,如式(13)。按照式(13)求解的模糊度噪声及电离层影响δion分别如式(14)和式(15)所示
从式(13)—(15)中可以看出TCAR方法消除了对流层误差、轨道误差等与频率无关的误差,且避免了伪距噪声的影响,只受载波噪声和残余的电离层延迟项的影响,两种影响因素的影响程度如表 4所示。
| 组合 | 电离层延迟影响 系数(η(0,1,-1)- η(i,j,k))/λ(i,j,k) | 载波噪声影响 /周(σ△▽φ= 0.5cm) | 载波噪声 影响/周 (σ△▽φ=1cm) |
| (1,4,-5) | -0.352 | 0.157 | 0.315 |
| (1,3,-4) | -0.352 | 0.157 | 0.315 |
| (1,2,-3) | -0.352 | 0.157 | 0.315 |
| (1,1,-2) | -0.352 | 0.157 | 0.315 |
| (1,5,-6) | -0.352 | 0.157 | 0.315 |
| (1,-1,0) | -0.352 | 0.157 | 0.315 |
| (1,0,-1) | -0.352 | 0.157 | 0.315 |
从表 4中可以看出每种宽巷组合使用TCAR方法求解模糊度时受电离层延迟和载波观测值噪声的影响是相同的,同时可以看出模糊度解算受电离层延迟(以m为单位)的影响系数为-0.352,敏感程度较小,例如当大气误差建模后残余的电离层达到20cm时,其造成的系统性偏差也仅为0.07周,在两种载波噪声情况下的模糊度解算成功率分别可达到99.67%和87.88%。对于网络RTK用户站,通过区域大气误差建模改正后残余的电离层误差一般都小于20cm,因此在载波观测值精度较好的情况下,使用TCAR方法求解第2个超宽巷或宽巷模糊度基本可以实现单历元准确固定。
3.2 基于宽巷组合的坐标解算当表 1中任意两个超宽巷或宽巷模糊度解算完成之后,即可通过整数组合得到任一组合系数之和为0的宽巷模糊度。选择其中观测值噪声和电离层延迟综合影响最小的组合观测值进行坐标解算,顾及电离层延迟通过区域建模可改正其大部分,因此选择表 1中的(1,-1,0)组合观测值作为坐标解算的观测值,定位解算的方程如式(16)所示
式(16)中,双差对流层和电离层延迟通过网络RTK区域建模内插得到,对于不同卫星采用基于卫星高度角的定权方式进行定权[23]。
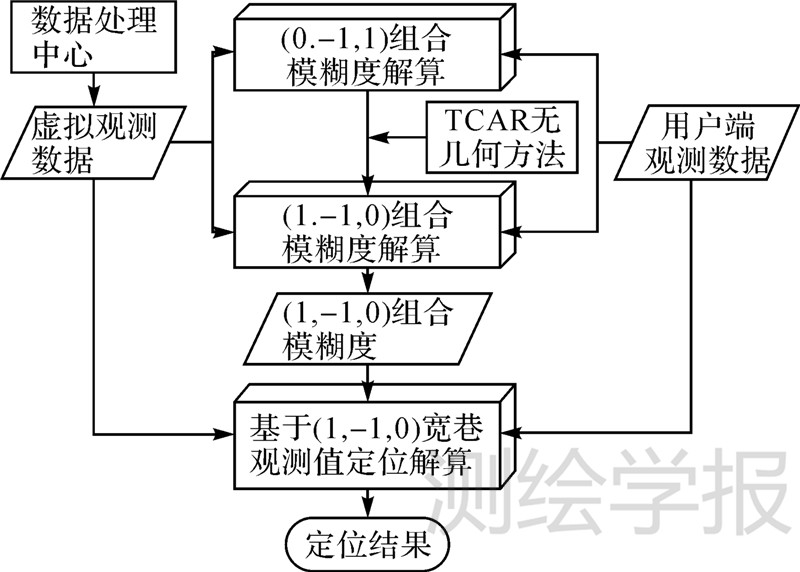
与常规网络RTK相比,式(16)所示的观测值噪声约为L1或L2观测值的5.58倍,因此定位的精度略低于常规网络RTK。但其优势在于宽巷模糊度可基于单历元、单个卫星对(非参考星和参考星组成)解算,除共有参考星之外,卫星对之间不相互影响,能够有效避免局部观测值粗差、卫星观测结构等的影响,这对于一些严重遮挡环境下的应用具有较大意义。综合3.1节和3.2节所述的单历元定位方法流程如图 2所示。
|
| 图 2 基于三频宽巷单历元定位方法流程 Fig. 2 Flowchart of single-epoch positioning method based on triple-frequency widelane combination |
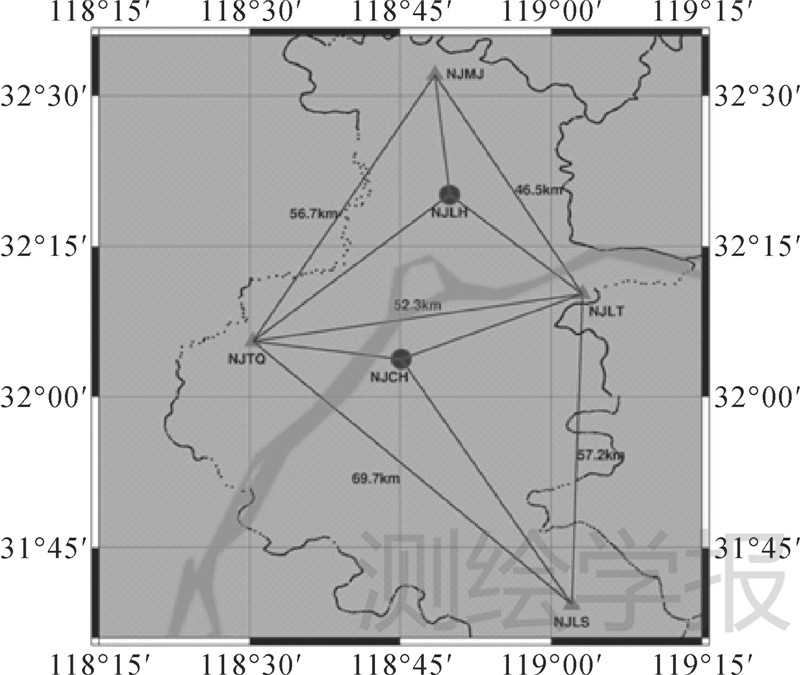
本文采用江苏省北斗地基增强系统一期工程中的6个参考站(参考站分布如图 3所示)于2014年5月6日UTC时0:00—16:00共16h的观测数据进行试验解算,6个参考站均包含BDS 3个频点数据,解算所用数据的采样间隔为5s。试验解算中,以NJMJ、NJTQ、NJLS和NJLT 4个站为参考站,组成两个三角形解算单元,以NJLH和NJCH两个站为用户站点,进行动态解算试验,试验采用网络RTK技术中常用的VRS模式。
|
| 图 3 试验所用站点分布图 Fig. 3 Distribution of the experimental stations |
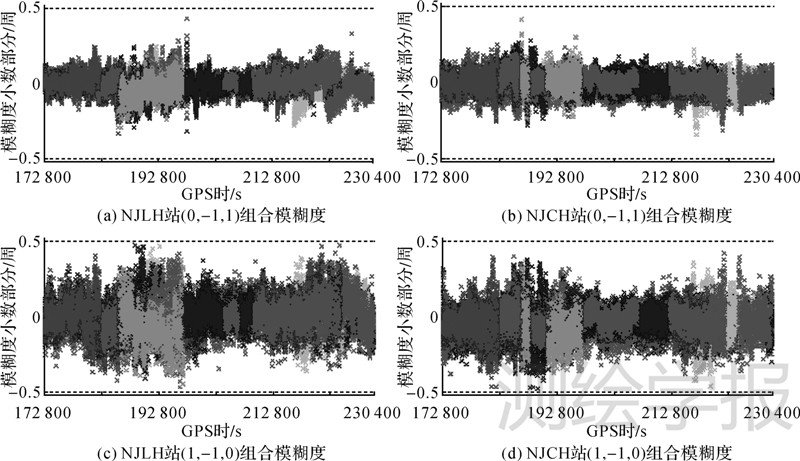
采用式(12)所示模型,分别以NJMJ和NJTQ为主参考站单历元求解与两个用户站间的(0,-1,1)组合超宽巷模糊度,解算时段内所有卫星的模糊度解算中误差和准确率如表 5所示(模糊度准确值由多历元平滑获得);浮点解四舍五入取整可准确固定的模糊度其单历元小数部分(即模糊度偏差)如图 4(a)和图 4(b)所示。
|
| 图 4 (0,-1,1)和(1,-1,0)单历元模糊度偏差 Fig. 4 Single-epoch biases of (0,-1,1)and (1,-1,0)combination AR |
从表 5可以看出,两个用户站单历元解算(0,-1,1)组合模糊度准确率均为100%,且解算中误差均在±0.1周之内,这也验证了式(12)所示模型单历元解算(0,-1,1)组合模糊度的可靠性;同时从图 4(a)和4(b)中也可以看出浮点解小数基本上都分布在-0.2~0.2周范围之内。
| 站名 | 卫星 | C01 | C02 | C03 | C04 | C06 | C07 | C08 | C09 | C10 | C11 | C14 |
| NJLH站 |
|
| NJCH站 |
|
在(0,-1,1)组合模糊度解算完成之后,即可按照式(13)所示模型直接求解(1,-1,0)组合模糊度,此时需利用内插的电离层延迟改正以削弱电离层误差的影响(差分改正信息的获得需固定基站间窄巷模糊度,算例中通过事后解获得,由于不是本文重点,本文不详细展开)。过低高度角卫星大气误差建模精度较低且将直接影响到其后的用户站坐标解算结果,因此本文设置用户站使用卫星的截止高度角为15°。试验数据所用的可视卫星中,大气延迟建模误差95%以上在±5cm内(篇幅所限,不再详细给出)。解算时段内所用卫星的(1,-1,0)组合模糊度解算中误差和准确率如表 6所示;单历元模糊度偏差如图 4(c)和4(d)所示。
| 站名 | 卫星 | C01 | C02 | C03 | C04 | C06 | C07 | C08 | C09 | C10 | C11 | C14 |
| CJLH 站 |
|
| NJCH 站 |
|
从表 6可以看出,两个用户站单历元解算(1,-1,0)组合模糊度准确率均高于99.9%,且解算中误差也均在±0.16周之内,这也表明使用TCAR方法单历元求解用户站(1,-1,0)组合模糊度也是准确可靠的;从图 4(c)和4(d)可以看出浮点解小数在0附近分布的密集程度小于(0,-1,1),但大部分分布在-0.3~0.3周之内,这与随机误差概率分布特性也是相一致的。
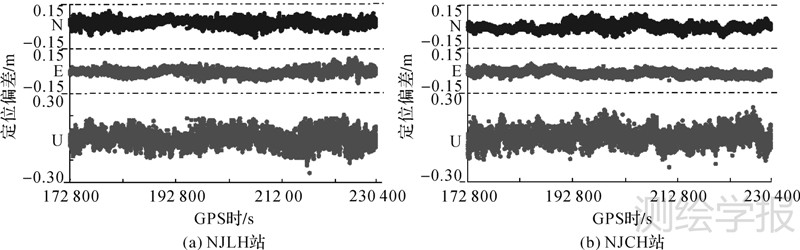
4.2 用户站定位解算在(1,-1,0)组合模糊度解算完成之后,用户站即可利用已固定模糊度的(1,-1,0)组合观测值和数据处理中心实时播发的大气延迟信息进行单历元定位解算。两个模拟用户站点NJLH和NJCH的单历元坐标解算偏差分别如图 5(a)和图 5(b)所示。
|
| 图 5 用户站单历元定位解算偏差结果 Fig. 5 Positioning biases with single epoch at user stations |
图 5所示两个用户站定位N/E/U 3个方向中误差分别为3.4/2.0/5.0cm和2.2/2.0/4.8cm。应该注意的是统计的中误差体现了解算时段内整体的误差水平,局部时间的解算结果仍有偏差较大的情况,如高程方向上仍有误差超出10cm的情况,这主要是由于宽巷观测值放大噪声以及卫星几何分布不均匀所导致的。从图 5中也可以看出,E方向定位精度略高于N方向,这主要是由于目前的北斗卫星整体上南北方向分布均匀性相比东西方向较差,在我国大部分地区尤其是北方地区,可视的北斗卫星大多分布在测站天顶方向的南侧,南北方向上定位的几何强度较弱;而高程方向上由于受大气建模误差以及低高度角卫星较少(高程方向定位几何强度较弱)的影响,偏差波动范围大于平面方向。
5 结 论本文提出的基于北斗三频宽巷组合的网络RTK单历元定位方法使用载波、伪距组合以及分步解算的TCAR方法单个历元即可完成模糊度解算,模糊度解算准确率高于99.9%。模糊度解算过程中对大气误差的敏感性较小;且基于单个卫星对解算,能够有效避免局部观测值粗差或卫星观测环境对模糊度解算的影响。通过基于实测北斗三频数据的用户站动态解算试验得出:平面定位中误差为3~4cm,高程方向约为5cm。高精度的单历元定位特性对于中等比例尺测图、精密交通导航、水深测量平面定位等对定位时效性和连续性有较高要求的作业方式具有重要意义。需要说明的是,该方法中虽然宽巷模糊度的解算对大气误差的敏感性较小,但定位精度依然受差分改正信息的影响,因此如何更快速、准确地实时解算参考站长基线模糊度以生成可靠的大气改正信息需要进一步深入研究。
| [1] | LIU Jingnan, LIU Hui. Continuous Operational Reference System: Infrastructure of Urban Spatial Data[J]. Geomatics and Information Science of Wuhan University, 2003, 28(3): 259-264. (刘经南, 刘晖. 连续运行卫星定位服务系统: 城市空间数据的基础设施[J]. 武汉大学学报: 信息科学版, 2003, 28(3): 259-264.) |
| [2] | LI Bofeng, SHEN Yunzhong, FENG Yanming, et al. GNSS Ambiguity Resolution with Controllable Failure Rate for Long Baseline Network RTK[J]. Journal of Geodesy, 2014, 88(2): 99-112. |
| [3] | LANDAU L, VOLLATH U, CHEN X M. Virtual Reference Station System[J]. Journal of Global Positioning Systems, 2002, 1(2): 137-143. |
| [4] | HUANG Dingfa, ZHOU Letao, LI Chenggang, et al. Strategy and Experimental Results of Augmentation Reference Station Network RTK Positioning[J]. Geomatics and Information Science of Wuhan University, 2009, 34(11): 1344-1349. (黄丁发, 周乐韬, 李成钢, 等. 增强参考站网络 RTK 算法模型及其实验研究[J]. 武汉大学学报: 信息科学版, 2009, 34(11): 1344-1349.) |
| [5] | YANG Yang, PAN Shuguo, WANG Denghui, et al. Software of BeiDou Ground Based Augmentation System (Earth Net 2.0) and Its Application[J]. Bulletin of Surveying and Mapping, 2014(10): 46-49. (杨徉, 潘树国, 汪登辉, 等. 北斗地基增强系统软件(Earth Net 2.0)及其应用[J]. 测绘通报, 2014(10): 46-49.) |
| [6] | HU G R, KHOO H S, GOH P C, et al. Development and Assessment of GPS Virtual Reference Stations for RTK Positioning[J]. Journal of Geodesy, 2003, 77(5-6): 292-302. |
| [7] | WANG C, FENG Y M, HIGGINS M, et al. Assessment of Commercial Network RTK User Positioning Performance over Long Inter-station Distances[J]. Journal of Global Positioning Systems, 2010, 9(1): 78-89. |
| [8] | LI J L, YANG Y X, XU J Y, et al. GNSS Multi-carrier Fast Partial Ambiguity Resolution Strategy Tested with Real BDS/GPS Dual and Triple-frequency Observations[J]. GPS Solutions, 2015, 19(1): 5-13. |
| [9] | LI Bofeng, SHEN Yunzhong, FENG Yanming. Long-range Real-time Precise Navigation with Three Frequency GNSS[J]. Geomatics and Information Science of Wuhan University, 2009, 34(7): 782-786. (李博峰, 沈云中, 冯延明. 利用三频GNSS进行长距离实时精密导航[J]. 武汉大学学报:信息科学版, 2009, 34(7): 782-786.) |
| [10] | MELBOURNE W G. The Case for Ranging in GPS-based Geodetic Systems[C]//Proceedings of the 1st International Symposium on Precise Positioning with the Global Positioning System. Rockville, Maryland: [s.n.], 1985: 373-386. |
| [11] | WUBBENA G. Software Developments for Geodetic Positioning with GPS Using TI-4100 Code and Carrier Measurements[C]//GOAD C C. Proceedings of the First International Symposium on Precise Positioning with the Global Positioning System. Rockville, Maryland: [s.n.], 1985: 403-412. |
| [12] | DAI L W. Dual-frequency GPS/GLONASS Real-time Ambiguity Resolution for Medium-range Kinematic Positioning[C]//Proceedings of the 13th International Technical Meeting of the Satellite Division of the US Institute of Navigation. Salt Lake City, Utah: [s.n.], 2000: 19-22. |
| [13] | FORSSELL B, MARTíN-NEIRA M, HARRISZ R A. Carrier Phase Ambiguity Resolution in GNSS-2[C]//Proceedings of the 10th International Technical Meeting of the Satellite Division of the Institute of Navigation (ION GPS 1997). [S.l.]: ION,1997: 1727-1736. |
| [14] | JUNG J, ENGE P, PERVAN B. Optimization of Cascade Integer Resolution with Three Civil GPS Frequencies[C]//Proceedings of the ION GPS 2000. Salt Lake City: ION, 2000: 2191-2200. |
| [15] | FENG Y M. GNSS Three Carrier Ambiguity Resolution Using Ionosphere-reduced Virtual Signals[J]. Journal of Geodesy, 2008, 82(12): 847-862. |
| [16] | LI Bofeng, SHEN Yunzhong, ZHOU Zebo. A New Method for Medium and Long Range Three Frequency GNSS Rapid Ambiguity Resolution[J]. Acta Geodaetica et Cartographica Sinica, 2009, 38(4): 296-301. (李博峰, 沈云中, 周泽波. 中长基线三频 GNSS 模糊度的快速算法[J]. 测绘学报, 2009, 38(4): 296-301.) |
| [17] | LI Jinlong, YANG Yuanxi, HE Haibo, et al. Optimal Carrier-phase Combination for Triple-frequency GNSS Derived from an Analytical Method[J]. Acta Geodaetica et Cartographica Sinica, 2012, 41(6): 797-803. (李金龙, 杨元喜, 何海波, 等. 函数极值法求解三频GNSS最优载波相位组合观测量[J]. 测绘学报, 2012, 41(6): 797-803.) |
| [18] | LI Jinlong. Researches on the Algorithms of GNSS Triple Frequency Precise Positioning[D]. Zhengzhou: The PLA Information Engineering University, 2011. (李金龙. GNSS 三频精密定位数据处理方法研究[D]. 郑州: 解放军信息工程大学, 2011.) |
| [19] | TANG W M, DENG C L, SHI C, et al. Triple-frequency Carrier Ambiguity Resolution for Beidou Navigation Satellite System[J]. GPS Solutions, 2014, 18(3): 335-344. |
| [20] | LI Bofeng, FENG Yanming, SHEN Yunzhong. Three Carrier Ambiguity Resolution: Distance-independent Performance Demonstrated Using Semi-generated Triple Frequency GPS Signals[J]. GPS Solutions, 2010, 14(2): 177-184. |
| [21] | WANG K, ROTHACHER M. Ambiguity Resolution for Triple-frequency Geometry-free and Ionosphere-free Combination Tested with Real Data[J]. Journal of Geodesy, 2013, 87(6): 539-553. |
| [22] | TEUNISSEN P J G. Influence of Ambiguity Precision on the Success Rate of GNSS Integer Ambiguity Bootstrapping[J]. Journal of Geodesy, 2007, 81(5): 351-358. |
| [23] | GAO Chengfa, ZHAO Yi, WAN Dejun. The Weight Determination of the Double Difference Observation in GPS Carrier Phase Positioning[J]. Science of Surveying and Mapping, 2005, 30(3): 28-32. (高成发, 赵毅, 万德钧. GPS 载波定位中双差观测值权的合理确定[J]. 测绘科学, 2005, 30(3): 28-32.) |