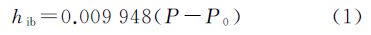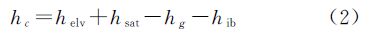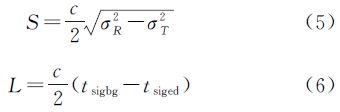1 引 言
北冰洋水文的最大特点是海面上的浮冰,即使在夏季,这些海冰的平均覆盖面积也占北冰洋面积的一半以上[1]。海冰产生和融化的过程对于北冰洋海水温度和盐度的变化具有重要作用,并且海冰的覆盖也阻隔了海水和大气间热量、动量和水汽的交换[2],海冰的变化不仅对北极地区的气候产生巨大影响,对全球气候以及海洋系统能量交换也有很大影响。近年来,北冰洋海冰呈现明显的减少趋势,仅仅通过卫星遥感影像获取的海冰覆盖面积已经无法满足海冰研究的需要,根据海冰出水高度反演海冰厚度成为亟待解决的问题[3]。此外,海冰出水高度的确定也是利用卫星测高确定北冰洋海面高的关键步骤,对于北冰洋海面高、海面动力地形以及北极地区大地水准面的研究具有重要意义[4, 5, 6]。测高卫星的出现使得人们能够对海冰出水高度开展大范围的研究,2003年,文献[7]根据ERS卫星的雷达测高数据首次得到了北冰洋海冰出水高度的模型。携带了地学激光测高系统GLAS(geoscience laser altimeter system)的ICESat(ice,cloud and land elevation satellite) 卫星是一颗轨道倾角94°的近极轨卫星,由于激光具有光斑小、不穿透雪层的特点,非常适合用于海冰出水高度的观测。在其6年的运行周期内,所提供的海冰测高数据为两极海冰的研究起到了重要作用。2005年,文献[4]利用GRACE数据改进后的ArcGP北极大地水准面模型作为基准,根据“最低面滤波法”,利用 ICESat测高数据获得了北冰洋海冰出水高度模型。2007年,文献[8]提出了根据海平面高与海冰表面高程变化的线性关系以及ICESat激光反射率确定海面高的方法,先后获得了2003-2008年北冰洋海冰出水高度和厚度模型[9, 10]。2008年,文献[11]将沿轨50 km范围内ICESat测高数据中最低的2%的点作为海面高观测值,研究了南极威德尔海的海冰出水高度及厚度变化。2009年,文献[12]则提出了根据ICESat回波波形参数识别海面测高数据的方法,并分析了2003-2009年北冰洋海冰出水高度的变化。国内目前利用ICESat数据进行的研究主要集中在南北两极的冰盖[13, 14, 15, 16]及在海冰的应用方面。文献[17]探讨了联合重力数据和ICESat数据获取海冰出水高度的可能性;文献[18]利用ICESat数据反演了南极罗斯海的海冰厚度;文献[19]利用ICESat数据获得的海冰出水高度对北冰洋海冰厚度变化进行了研究;文献[20]利用EnviSat研究了两极海冰的分布特性。
目前,文献[6, 18, 21, 22, 23, 24]提出的最低点法被认为是计算海冰出水高度最简单、有效的方法,得到了广泛的应用。但由于目前对北冰洋海冰的了解太少,无法确定2%的最低点是否能够很好地代表海面高,因此这种方法效果并不理想。本文提出利用ICESat波形参数,结合高程特征确定海冰出水高度的方法,并与最低点法进行比较,对两种方法的误差进行了分析,进而计算了2005-2006年北冰洋海冰出水高度。
2 数据描述及预处理ICESat/GLAS每年只观测2~3个周期,每个周期为期大约33 d,观测时间选在每年的2-3月、5-6月以及10-11月。本文选取了2005 -2006年ICESat在北极的6个任务周期的观测数据,任务期编号为L3b-L3g(见表 1)。数据是由美国冰雪中心(NSIDC)提供的ICESat GLA05和GLA13数据集,版本为目前最新的Release 633。
| 名称 | 观测时间 | 季节 | 有效观测 数量/万次 |
| L3b | 2005-02-17-2005-03-24 | 冬季 | 583 |
| L3c | 2005-05-20-2005-06-23 | 夏季 | 238 |
| L3d | 2005-10-21-2005-11-24 | 秋季 | 307 |
| L3e | 2006-02-22-2006-03-28 | 冬季 | 574 |
| L3f | 2006-05-24-2006-06-26 | 夏季 | 86 |
| L3g | 2006-10-25-2006-11-27 | 秋季 | 202 |
ICESat测高数据主要有两个误差源,一是大气前向散射,二是由于回波能量超过接收器接收能力造成的波形饱和,两者都会延长激光传播时间,从而造成测高数据偏低。因此,为保证数据质量,须对数据进行预处理。本文综合了文献[8, 11, 12]的预处理方法,具体数据编辑准则包括:①剔除反射率>1的数据,过大的反射率是由于严重的波形饱和造成的;②剔除接收回波拟合残差V>60的数据,过大的回波拟合残差意味着波形被严重的扭曲,因而数据精度较差;③剔除接收机增益大于30的数据,较高的接收机增益表示激光在传播过程中能量衰减严重,信噪比较差;④剔除反射率小于0.05以及波形展宽大于0.8 m的数据,这些数据受大气前向散射影响的可能性较高[11]。此外,为避免无冰区域对计算的影响,根据AMSR-E 12.5 km分辨率的海冰密集度数据[25]剔除了海冰密集度低于35%的区域。各任务期用于出水高度计算的观测值数量如表 1所示。
GLA13中提供的高程数据(helv)是基于TOPEX/Poseidon(T/P)卫星所采用的椭球,并经过了潮汐和对流层延迟改正的大地高。首先对helv进行波形饱和改正hsat、大地水准面改正hg和逆气压改正hib,其中hsat 由GLA13数据提供,大地水准面模型为EGM2008(归算至T/P卫星椭球),hib则由下式计算[26]
式中,P为观测时的海面气压;P0为标准大气压。经各项改正后,获得的初始高程序列hc为
由于模型的误差,hc存在约±1 m的波动,将hc移去25 km滑动平均值hm25来获得一个零均值的高程序列hr(如图 1)
25 km的滑动窗口不仅可以去除模型化残差的长波变化,而且可以有效地区分海面和海冰高程变化的波长[8],同时也可减小ICESat的空间分辨率对出水高度计算造成的影响[27]。
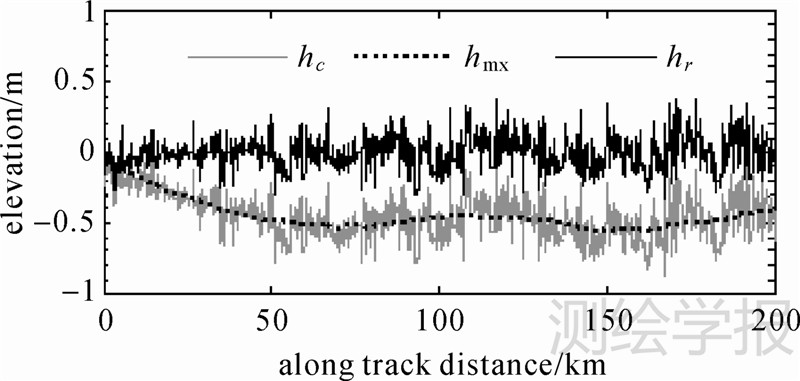
|
| 图 1 ICESat高程序列 Fig. 1 ICESat derived elevation series |
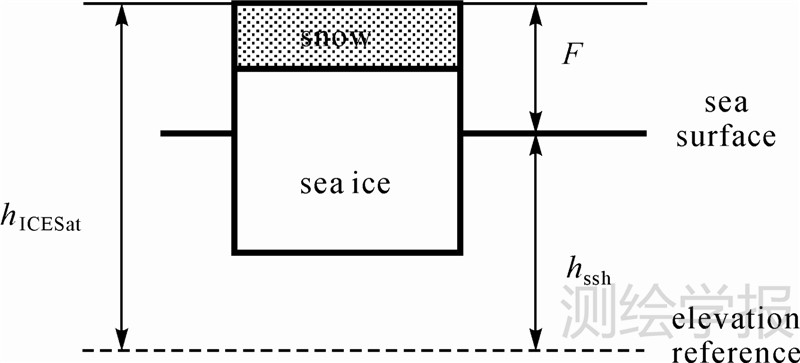
海冰出水高度(F),或称为海冰干舷高[17],是指海冰露出海平面的高度。对于ICESat来说,由于激光无法穿透海冰表面的雪层,因此,得到的出水高度是海冰露出海水的高度加上雪层的厚度,如图 2所示。故出水高度就是ICESat测得的高度与海面高之差
但是,即使使用最精确的大地水准面、海面动力地形和潮汐模型来计算海面高也会产生一定的误差[11],因此,不能通过模型化的方法来计算hssh。由于海冰的水平运动,有时在海冰之间会产生一些裂缝而露出海面,称为冰间水道(open lead),利用ICESat在这些水道表面的观测值可以确定海平面。
|
| 图 2 ICESat海冰出水高度示意图 Fig. 2 Illustration of ICESat freeboard |
由于表面特性的不同,ICESat发射的激光在水面和覆盖着雪层的海冰表面的回波具有不同的性质,在不受严重的波形饱和或大气前向散射影响时,可以通过回波的特征参数将海面的观测值区分出来。这些参数包括反射率R、波形展宽S、波形长度L和回波拟合残差V。反射率R完全取决于反射面的物理性质,通常,水面的反射率约为0.25,雪的反射率约为0.7[9]。V是回波脉冲拟合为高斯波形的残差,光滑的表面对波形造成的扭曲较小,回波形状更接近标准的高斯波形,所以水面观测值的V一般较小。这两个参数在GLA13数据产品中已直接给出。波形展宽S是ICESat发射光波和回波的脉冲宽度之差[11],而波形长度L是脉冲回波信号持续的长度,这两个参数的计算如下
式中,σT、σR分别表示ICESat发射和接收的激光脉冲的脉冲宽度;tsigbg、tsiged则分别表示接收信号有效信号的起止时间[28];c是光速。反射面越粗糙,波形展宽越严重,脉冲持续的长度也越长,因此S和L在一定程度上代表了ICESat光斑内地形的起伏。对于冰间水道这样的平静表面,这两个参数的值通常比较小。图 3所示的是2005年10月20日ICESat在85°N、156.8°W附近的一段数据,从中可以看出选用的参数和高程变化之间的关系:高程较低的海面点,4个参数的数值都比较小。对大量类似图 3的数据进行波形特征统计,并参考ICESat在水面上的波形特征[28],可以认为海面观测值一般应满足以下波形条件:R≤0.45,S≤0.30 m,L≤5.25 m,V≤15 mV,如图 3(b)-图 3(e) 所示。

|
| 图 3 IceSat海冰观测示例 Fig. 3 Example of ICESat sea ice observation |
由于ICESat波形很容易受到波形饱和、大气状况以及反射面的倾斜度等的影响,回波参数并不十分稳定,仅仅依靠波形特征判断海面观测值有可能会产生误判,因此有必要对海面高程的变化特征进行一定的了解,通过高程的变化进一步进行判断。在海冰出水高度较大的区域,根据高程的明显区别以及回波参数,可以比较容易地找出一些明显的海面观测值,以便对海面高程的变化进行分析。图 3(a)中圆点所示的就是明显的海面点。
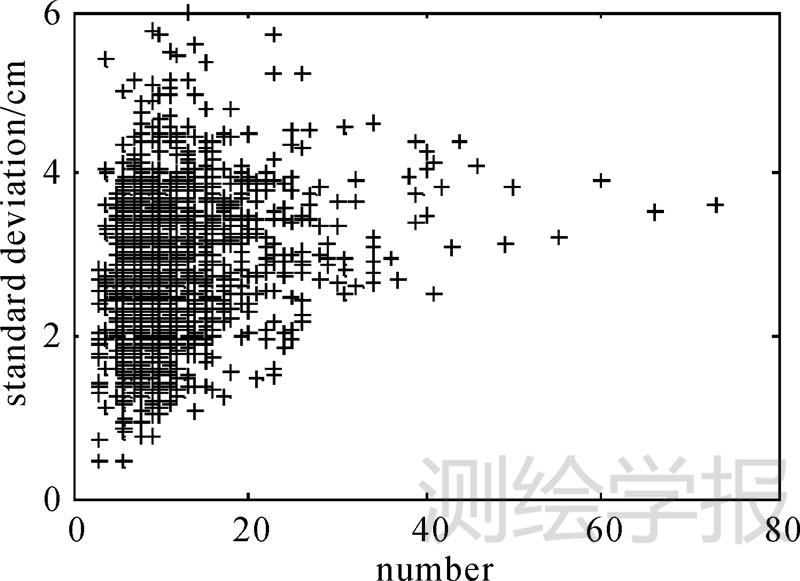
通过人工判断的方式,在L3b-L3g的6期数据中找出了16 535个明显的海面点,并按照25 km的间距分段,共1426段轨迹,对每个25 km长的轨迹内海平面高的标准差进行了统计,结果如图 4所示,其平均值为2.98 cm,标准差为±0.86 cm。这其中包括了水准面、潮汐等模型残差的短波误差,以及ICESat的观测误差。研究表明ICESat在平坦的冰盖表面的测高精度为2 cm(文献[29]),考虑到海面高观测值中还存在模型残差的影响,本文的统计结果与这个结果是基本一致的。
|
| 图 4 25 km海平面变化标准差统计 Fig. 4 Standard deviation of sea surface height within 25 km |
在本文统计的1426个25 km海面高标准差中,75%以上的数据均在3.5 cm以内,因此,在确定海平面高时,要求每个25 km轨迹中用于计算平均海面高的观测值的高程标准差不超过3.5 cm。标准差限值的主要作用是剔除一些粗差,因此限值大小的选择不会对结果产生太大的影响。对标准差限值的取值进行试验,结果表明将标准差限制在3~6 cm的范围对海冰出水高度平均值的影响不超过1 cm。
3.3 海冰出水高度的计算
显然,如果不考虑观测误差,则ICESat测得的最低点应该是来自海面或者出水高度最低的海冰表面的高程,因此,要求计算的海平面与25 km内最低点之间的高差在两者的1倍中误差以内,以进一步防止海面观测值的误判。海面高的中误差取3.2节中分析获得的3 cm,ICESat测高的中误差为14 cm(文献[30]),故计算的海面高不应高于最低点17 cm。在大多数情况下,这个条件不会影响海平面高的计算,以L3d为例,仅有8%的海面高在计算时受到了17 cm的高差限制。
计算出水高度的步骤如下:
(1) 对每个ICESat观测值,取沿轨前后各12.5 km内满足R≤0.45、S≤0.30 m、L≤5.25 m、V≤15 mV的观测值,计算高程标准差及平均值。
(2) 若上一步计算的高程标准差大于3.5 cm或平均值与最低点高差超过17 cm,则去掉其中高程最高的点,重新计算标准差和平均值,直至满足条件。
(3) 将满足上述条件的高程平均值作为该点处的海平面高,根据式(4)计算海冰出水高度。
在利用上述方法确定海面出水高度时,根据季节的不同,每个任务期用于确定海面高的观测值的比例约为3%~6%,这与北冰洋冰间水道的比例基本保持一致[7, 31]。然而由于冰间水道空间分布的不均匀,这种方法不能保证在每个25 km轨迹内都能确定海面高,由此产生的影响将在4.2节中讨论。
4 不同方法计算出水高度的比较 4.1 试验方案
最低点法的假设是海冰覆盖区冰间水道的比例不小于2%,但冰间水道的分布随季节和区域的变化较大,例如,文献[31]通过高分辨率辐射仪影像数据发现在北冰洋中心海域冰间水道的比例在冬季时为2%~3%,夏季为5%~7%,而冬季时外围海域冰间水道的比例则为6%~9%,文献[7]通过水下声呐数据计算的北冰洋冰间水道比例在10月份约为10%,3、4月份则约为3%。因此,2%的比例可能会使出水高度的计算产生误差。例如,文献[24]通过ICESat与空载电磁感应测深数据的对比发现,在南极麦克默多湾,5%的冰间水道比例更适合于出水高度的计算。
为对不同方法确定出水高度的结果进行比较,本文用5种方案计算了出水高度:方案1采用本文提出的方法;方案2-方案5均采用最低点法,冰间水道比例分别为2%、2%、5%和9%,其中方案2没有对出水高度计算的区域进行限制,方案3-方案5则将计算区域限定在与方案1相同的范围内(即只在方案1能够确定海面点的25 km轨迹分段内进行确定海冰出水高度的计算,若采用方案1的方法没有找到海面观测值,则不进行计算),以避免空间分布差异对结果的影响。此外,方案5还要求所选最低点的高程标准差不超过3.5 cm。不同方案计算的北冰洋海冰平均出水高度如表 2所示。
| L3b | L3c | L3d | L3e | L3f | L3g | |
| 方案1 | 35.03 | 29.67 | 25.00 | 31.86 | 31.57 | 24.90 |
| 方案2 | 38.50 | 36.04 | 27.21 | 33.48 | 38.36 | 27.18 |
| 方案3 | 35.03 | 32.51 | 25.30 | 32.08 | 33.43 | 25.35 |
| 方案4 | 31.97 | 28.05 | 22.50 | 29.23 | 28.72 | 22.68 |
| 方案5 | 34.68 | 31.45 | 24.49 | 30.97 | 33.04 | 24.40 |
| 最终结果 | 39.71 | 33.45 | 27.51 | 33.88 | 35.36 | 27.22 |
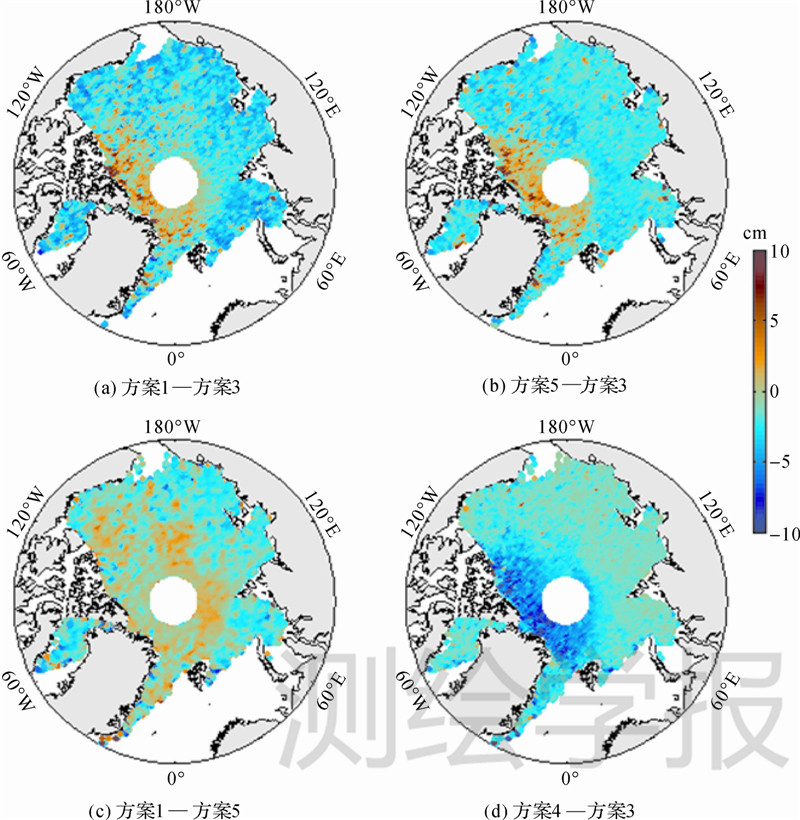
表 2的结果中,方案1与方案3的结果非常接近,特别是在观测质量较好的秋、冬季节,两者的差异不到0.5 cm,体现了很好的一致性。图 5(a)所示为方案1和方案3计算的L3d海平出水高度差异的分布。在格陵兰、加拿大群岛北部等海冰较厚的多年冰区,方案1计算的海冰出水高度明显高于方案3,这是由于在这些区域,冰间水道的实际比例还不到2%,最低点法在选取海面观测值时引入了冰面上的观测值,由此确定的海面高偏高。当通过在最低点法中加入3.5 cm的高程标准差限差来剔除来自冰面观测的粗差后(方案5),即使最低点的比例提高到9%,在厚冰区仍然得到了比方案3更高的结果(图 5(b)),并且与方案1的结果非常接近(图 5(c))。这表明本文方法计算厚冰区海冰出水高度的可靠性要明显优于最低点法。根据图 5(a),在海冰较薄的外围海域,方案1的结果明显低于方案3,这是由于10月份北冰洋外围海域冰间水道比例远远大于2%,在这样的情况下,2%的最低点显然低估了海平面,从而导致计算的出水高度偏高,当最低点的比例提高时,这种差距明显地减小了(如图 5(c))。此外,方案1与方案3的结果在两个夏季任务期L3c与L3f的差异约为2~3 cm,远远大于其他两个季节的任务期。由于冰雪的融化,夏季北极大气中的水汽成分明显增加,使得GLAS的激光脉冲受到更严重的大气前向散射影响,对于这个影响,目前既没有有效的改正方法,也无法准确地识别受影响的观测值[28],所以,即便对数据进行了严格的数据编辑,夏季的观测数据质量仍然比其他两个季节的观测质量要差。受到大气前向散射影响的ICESat观测值会偏低,因此最低点法对于大气前向散射的影响非常敏感,而本文的方法对波形进行了识别,不仅可以避免一些来自冰面上的受到大气前向散射影响的数据,而且波形识别的过程也对观测值的质量起到了一定的控制作用,相比之下具有更高的可靠性。
|
| 图 5 不同方法计算的L3d海冰出水高度差异 Fig. 5 Differences of freeboard of L3d estimated with different methods |
方案2和方案3采用了完全一样的计算方法,因此两种方案的差异完全是由两者计算区域的不同所导致的,其中方案3只在方案1能够找到海面观测值的区域计算海冰出水高度,而方案2则在所有有ICESat观测值的区域都进行了计算。对比两者的结果,方案2在6个任务期计算的平均出水高度均高于方案3。这种情况是由于冰间水道在空间分布上的不均匀造成的,在海面完全被海冰遮盖的区域,本文的方法无法确定海面高,也无法计算海冰出水高度。这样的区域在夏、秋、冬季分别约占50%、40%和60%,并且较多地集中在海冰较厚、出水高度较高的多年冰区,因此在这些区域获得的出水高度结果较少。这使得本文的方法估计的整个北冰洋海域的平均海冰出水高度偏低,在观测质量较好的秋、冬季,这个偏差大约为2~3 cm。
方案3和方案4均采用了最低点法,最低点比例分别为2%和5%,在秋、冬季,两者的差异均为3 cm左右,而夏季则超过4.5 cm。图 5(d)所示为方案4和方案3计算的L3d海冰出水高度的差异,在不同区域明显表现出不同的特性:在格陵兰和加拿大群岛北部的多年冰区,由于5%的比例引入了较多的冰面高程,两者的差异较大,局部地区可达到10 cm左右,而在亚欧大陆北侧的首年冰区,两种方案的差值接近于0,这些区域的冰间水道比例在5%以上,因此,两种方案的计算中都没有引入冰面上的高程,两者的差异是由于ICESat的观测误差以及海面的自然起伏引起的。这个结果说明最低点的比例大于冰间水道的实际比例时造成的误差比小于冰间水道实际比例时造成的误差要大得多。
5 2005-2006年北冰洋海冰出水高度
5.1 北冰洋海冰出水高度的计算
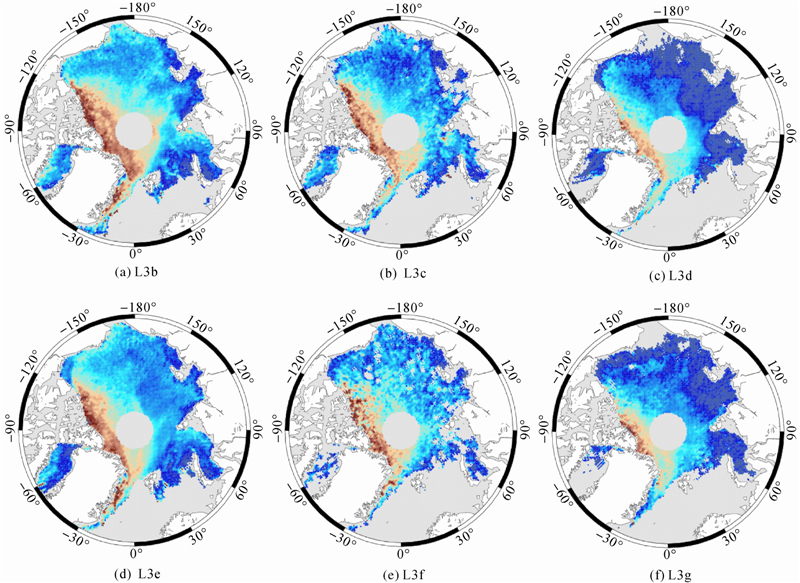
通过上面的讨论可知,本文的方法在局部区域具有比最低点法更高的可靠性,但由于空间分布的不均匀,平均出水高度的结果存在2~3 cm的偏差。最低点法虽然不存在空间分布不均的问题,但在出水高度的空间分布上存在系统性的误差,特别是在海冰较厚的多年冰区域。因此,为获得最优结果,将两种方法进行结合:对每个ICESat观测值,首先根据本文的方法判断该点处的瞬时海面高,如果这种方法找不到符合要求的观测值,则用加上3.5 cm高程标准差限制的最低点法确定海平面高。在对不同季节使用最低点法计算海面高时,采用了不同的冰间水道比例,秋、冬季节观测质量较好,不同方法间的结果较差较小,采用2%的最低点比例,而夏季糟糕的观测质量对最低点法的影响较大,则选择9%的冰间水道比例。这不仅更接近实际情况,而且较多的观测值也可以减小观测误差对结果的影响。最终获得的6个任务期的平均海冰出水高度如表 2最后一行所示。将计算结果在25 km×25 km格网内取平均后,得到了2005-2006年北冰洋海冰出水高度的空间分布,如图 6所示。

|
| 图 6 L3b-L3g北冰洋海冰出水高度分布 Fig. 6 Maps of Arctic freeboard for L3b-L3g |
从图 6可以看到,海冰出水高度的空间分布大致是从亚欧大陆沿岸向格陵兰岛、加拿大沿岸逐渐增加,最厚的区域在格陵兰岛和加拿大群岛的北侧,最大可达0.8 m。格陵兰岛东侧的法拉姆海峡是北冰洋海冰通向外海的主要出口,海冰在进入温暖的大西洋后迅速融化,海冰的分布在这里形成了一条长长的拖尾。在秋季(L3d、L3g)海冰出水高度的分布中,可以根据20 cm的出水高度分为明显的两个区域,其中低于20 cm的区域(图中深蓝色部分)主要是9月以后才逐渐形成的首年冰,这些区域的海冰在夏季时会融化,是季节性的海冰覆盖区。一部分首年冰在海流和风力作用下向北移动,在进入更寒冷的区域或经挤压后变得更厚,即使夏天也不会完全消融,形成了较厚的多年冰,即图中出水高度大于20 cm的区域。
海冰出水高度的季节性变化非常明显:冬季是海冰最厚的季节,而经过夏季的融化后,秋初时海冰出水高度达到一年中的最低值。尽管在图 7中,可以明显地看出夏季(L3c、L3f)海冰出水高度相比冬季(L3b、L3e)有所下降,但在表 2 的统计中,L3f海冰平均出水高度要大于L3e。可能的原因有两个:一是夏季糟糕的观测质量导致出水高度结果的不可靠;二是北极的降雪可以持续到5月,使得5、6月时海冰表面的雪层比冬季更厚,因此一些区域的海冰出水高度可能会比冬季更高。由表 2的数据可知,2005、2006两年,北冰洋海冰出水高度从3月至10月分别减少了12.2 cm和6.7 cm,两者几乎相差1倍。比较合理的解释是2005年夏季的北极气候异常,资料显示2005年9月北冰洋海冰的覆盖面积达到当时的历史新低[32]。
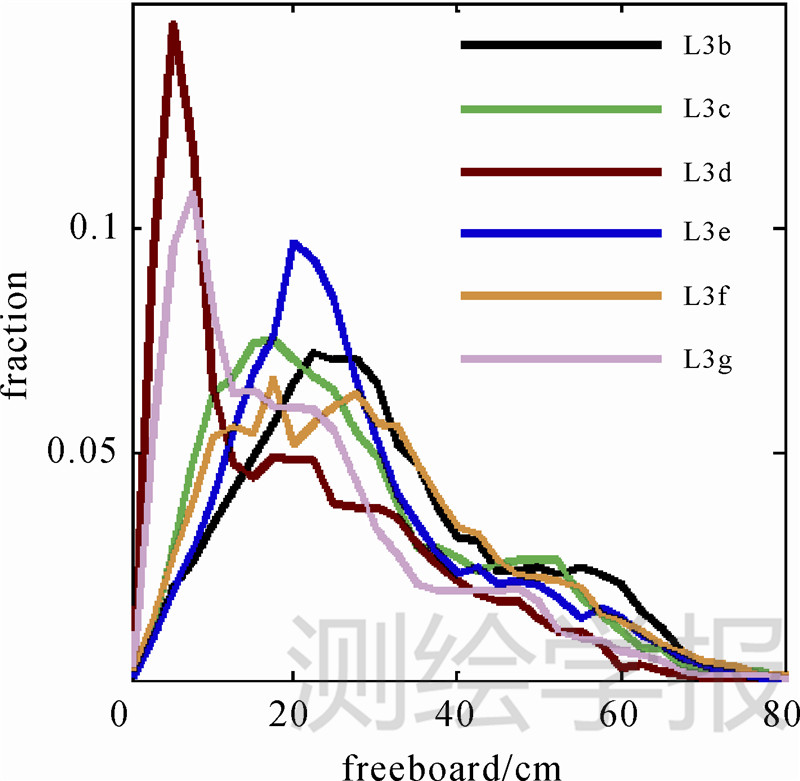
|
| 图 7 北冰洋海冰出水高度统计 Fig. 7 Distributions of Arctic freeboard |
图 7所示为各任务期海冰出水高度统计分布。由于首年冰和多年冰的明显区别,北冰洋海冰通常会呈现出双峰的分布特征[11]。例如在L3b和L3c的出水高度统计中,可以清楚地看到两个峰值,分别代表了首年冰(20~30 cm左右)和多年冰(50~60 cm左右)。而在L3d的分布中,尽管仍有两个波峰,但首年冰的峰值下降到不足10 cm,并且出水高度小于20 cm的首年冰的比例远远高于其他5个季度。此后,在L3e的出水高度分布中,已经看不到多年冰出水高度的峰值,出水高度在30 cm以上的统计曲线全部低于L3b,首年冰的比例则比L3b高出很多,首年冰出水高度的峰值相比L3b也有10 cm左右的下降。这些现象表明,在2005年夏季前后,北冰洋多年冰和首年冰的比例打破了原有的平衡,发生了巨大变化。这个影响一直持续到了2006年的夏季,直到2006年10月,才能再次在L3g的海冰出水高度分布中区分出首年冰和多年冰,但从两类冰所占的比重来看,也明显有别于L3b和L3c。海冰组成比例的变化也证明了2005年夏季的气候异常对北冰洋海冰带来的巨大影响。
6 结 论本文提出利用ICESat数据获取北冰洋海冰出水高度的新方法,主要是通过海冰覆盖区海面的起伏和ICESat回波特征识别海平面的测高数据,从而计算海冰出水高度。通过与最低点法的比较,表明本文提出的方法在观测质量不佳或冰间水道比例不满足假设条件时具有比最低点法更高的可靠性,但是在多年冰区域则有可能因找不到有效的海平面高而无法确定海冰出水高度。将两种方法进行结合,获得了2005-2006年的6个ICESat任务周期的北冰洋海冰出水高度,分析了两年间海冰出水高度的季节性变化。结果表明,受2005年夏季异常气候的影响,北冰洋海冰的厚度大大减少,组成比例也有所变化,由于首年冰和多年冰对于海洋及大气的影响作用不同,因此这种比例的变化可能会对北冰洋以及北极的气候产生深远的影响。
| [1] | POLYAK L, ALLEY R B, ANDREWS J T, et al. History of Sea Ice in the Arctic[J]. Quaternary Science Reviews, 2010, 29(15-16): 1757-1778. |
| [2] | SPREEN G. Satellite-based Estimates of Sea Ice Volume Flux: Applications to the Fram Strait Region[D]. Hamburg: Hamburg University, 2008. |
| [3] | RENGANATHAN V. Arctic Sea Ice Freeboard Heights from Satellite Altimetry[D]. Calgary: University of Calgary, 2010. |
| [4] | FORSBERG R, SKOURUP H. Arctic Ocean Gravity, Geoid and Sea-ice Freeboard Heights from ICESat and GRACE[J]. Geophysical Research Letters, 2005, 32(21): L21502. |
| [5] | KWOK R, MORISON J. Dynamic Topography of the Ice-covered Arctic Ocean from ICESat[J]. Geophysical Research Letters, 2011, 38(2): L02501. |
| [6] | FARRELL S L, MCADOO D C, LAXON S W, et al. Mean Dynamic Topography of the Arctic Ocean[J]. Geophysical Research Letters, 2012, 39(1): L01601. |
| [7] | LAXON S, PEACOCK N, SMITH D. High Interannual Variability of Sea Ice Thickness in the Arctic Region[J]. Nature, 2003, 425(6961): 947-950. |
| [8] | KWOK R, CUNNINGHAM G F, ZWALLY H J, et al. Ice, Cloud, and Land Elevation Satellite (ICESat) over Arctic Sea Ice: Retrieval of Freeboard[J]. Journal of Geophysical Research, 2007, 112(C12): 120-130. |
| [9] | KWOK R, CUNNINGHAM G F. ICESat over Arctic Sea Ice: Estimation of Snow Depth and Ice Thickness[J]. Journal of Geophysical Research, 2008, 113(C8): 10-18. |
| [10] | KWOK R, CUNNINGHAM G F, WENSNAHAN M, et al. Thinning and Volume Loss of the Arctic Ocean Sea Ice Cover: 2003—2008[J]. Journal of Geophysical Research, 2009, 114(C7): 75-86. |
| [11] | ZWALLY H J, YI D H, KWOK R, et al. ICESat Measurements of Sea Ice Freeboard and Estimates of Sea Ice Thickness in the Weddell Sea[J]. Journal of Geophysical Research, 2008, 113(C2): 215-228. |
| [12] | FARRELL S L, LAXON S W, MCADOO D C, et al. Five Years of Arctic Sea Ice Freeboard Measurements from the Ice, Cloud and Land Elevation Satellite[J]. Journal of Geophysical Research, 2009, 114(C4): 4008-4016. |
| [13] | LI Jiancheng, FAN Chunbo, CHU Yonghai, et al. Using ICESat Altimeter Data to Determine the Antarctic Ice Sheet Elevation Model[J]. Geomatics and Information Science of Wuhan University, 2008, 33(3): 226-228. (李建成, 范春波, 褚永海, 等. ICESAT卫星确定南极冰盖高程模型研究[J]. 武汉大学学报: 信息科学版, 2008, 33(3): 226-228.) |
| [14] | HUANG Hailan. Determination of Polar Ice Sheet Change form ICESat and GRACE Satellite[D]. Wuhan: Wuhan University, 2011. (黄海兰. 利用ICESat和GRACE卫星观测数据确定极地冰盖变化[D]. 武汉: 武汉大学, 2011.) |
| [15] | SHI Hongling, LU Yang, DU Zongliang, et al. Mass Change Detection in Antarctica Ice Sheet Using ICESat Block Analysis Techniques from 2003—2008[J]. Chinese Journal of Geophysics, 2011, 54(4): 958-965. (史红岭, 陆洋, 杜宗亮, 等. 基于ICESat块域分析法探测2003—2008年南极冰盖质量变化[J]. 地球物理学报, 2011, 54(4): 958-965.) |
| [16] | SHEN Qiang, CHEN Gang, E Dongchen, et al. Recent Elevation Changes on the Lambert-Amery System in East Antarctica from ICESat Crossover Analysis[J]. Chinese Journal of Geophysics, 2011, 54(8): 1983-1989. (沈强, 陈刚, 鄂栋臣, 等. 基于ICESat轨道交叉点分析的东南极Lambert-Amery系统当前高程变化特征分析[J]. 地球物理学报, 2011, 54(8): 1983-1989.) |
| [17] | FAN Chunbo. Theory and Application of Spaceborne Laser Altimeter[D]. Wuhan: Wuhan University, 2007. (范春波. 星载激光测高理论与应用[D]. 武汉: 武汉大学, 2007.) |
| [18] | WU Xiaodong. Variation of Sea Ice Thickness and Area in the Ross Sea[D]. Qingdao: Ocean University of China, 2012. (邬晓冬. 南极罗斯海海冰厚度和面积变化研究[D]. 青岛: 中国海洋大学, 2012.) |
| [19] | BI H B, HUANG H J, SU Q, et al. An Arctic Sea Ice Thickness Variability Revealed from Satellite Altimetric Measurements[J]. Acta Oceanologica Sinica, 2014, 33(11): 134-140. |
| [20] | YANG Lei, CHANG Xiaotao, GUO Jinyun, et al. Research on Distribution Characteristics of Polar Sea Ice by ENVISAT Altimetry Backscatter Coefficient[J]. Acta Geodaetica et Cartographica Sinica, 2013, 42(5): 676-681. (杨磊, 常晓涛, 郭金运, 等. ENVISAT雷达高度计后向散射系数的极区海冰分布特性[J]. 测绘学报, 2013, 42(5): 676-681.) |
| [21] | YI D H, ZWALLY H J, ROBBINS J W. ICESat Observations of Seasonal and Interannual Variations of Sea-ice Freeboard and Estimated Thickness in the Weddell Sea, Antarctica (2003-2009)[J]. Annals of Glaciology, 2011, 52(57): 43-51. |
| [22] | XIE H J, TEKELI A E, ACKLEY S F, et al. Sea Ice Thickness Estimations from ICESat Altimetry over the Bellingshausen and Amundsen Seas: 2003—2009[J]. Journal of Geophysical Research: Oceans, 2013, 118(5): 2438-2453. |
| [23] | MARKUS T, MASSOM R, WORBY A, et al. Freeboard, Snow Depth and Sea-ice Roughness in East Antarctica from in Situ and Multiple Satellite Data[J]. Annals of Glaciology, 2011, 52(57): 242-248. |
| [24] | PRICE D, RACK W, HAAS C, et al. Sea Ice Freeboard in McMurdo Sound, Antarctica, Derived by Surface-validated ICESat Laser Altimeter Data[J]. Journal of Geophysical Research: Oceans, 2013, 118(7): 3634-3650. |
| [25] | National Snow and Ice Data Center. AMSR-E/Aqua Daily L3 12.5 km Tb, Sea Ice Concentration, & Snow Depth Polar Grids: Version 3[EB/OL].[2014-05-20]. http://nsidc.org/data/AE_SI12. |
| [26] | DENG Xiaoli, CHAO Dingbo, CHEN Junyong. A Preliminary Process of TOPEX and Poseidon Data in the China Sea and Neighbour[J]. Acta Geodaetica et Cartographica Sinica, 1996, 25(3): 226-232. (邓晓丽, 晁定波, 陈俊勇. 中国近海TOPEX/Poseidon卫星测高数据处理的初步结果[J]. 测绘学报, 1996, 25(3): 226-232.) |
| [27] | WEISSLING B P, ACKLEY S F. Antarctic Sea-ice Altimetry: Scale and Resolution Effects on Derived Ice Thickness Distribution[J]. Annals of Glaciology, 2011, 52(57): 225-232. |
| [28] | WANG X W, CHENG X, LI Z, et al. Lake Water Footprint Identification from Time-series ICESat/GLAS Data[J]. IEEE Geoscience and Remote Sensing Letters, 2012, 9(3): 333-337. |
| [29] | KWOK R, ZWALLY H J, YI D H. ICESat Observations of Arctic Sea Ice: A First Look[J]. Geophysical Research Letters, 2004, 31(16): L16401. |
| [30] | ZWALLY H J, SCHUTZ B, ABDALATI W, et al. ICESat’s Laser Measurements of Polar Ice, Atmosphere, Ocean, and Land[J]. Journal of Geodynamics, 2002, 34(3-4): 405-445. |
| [31] | LINDSAY R W, ROTHROCK D A. Arctic Sea Ice Leads from Advanced very High Resolution Radiometer Images[J]. Journal of Geophysical Research, 1995, 100(C3): 4533-4544. |
| [32] | NATIONAL SNOW AND ICE DATA CENTER. Sea Ice Decline Intensifies[EB/OL].[2014-06-20]. http://nsidc.org/news/newsroom/archive/2005. |