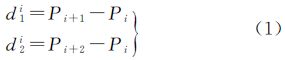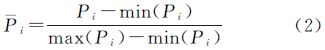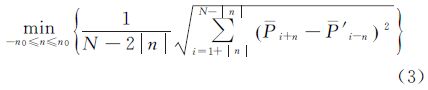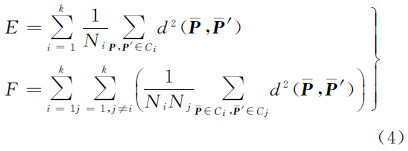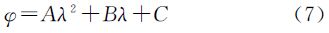2. 同济大学空间信息科学及可持续发展应用中心,上海 200092
2. Center for Spatial Information Science and Sustainable Development,Tongji University,Shanghai 200092,China
1 引 言
测高卫星技术能在全球海洋区域进行全天候的重复观测,为海平面变化的研究提供了高精度的海面高数据。然而在近岸海域,海面高数据的精度通常低于开阔海域。其主要原因,一方面是各项地球物理改正的精度较低,另一方面是测高波形受到不同反射面的影响,发生不同程度的变形,使得基于Brown模型的波形重构算法失效[1]。为提高近岸海域的海面高精度,不同学者提出了一系列的波形重构算法,有的是根据波形形状建立数学模型[2, 3],有的是采用经验统计算法[4, 5, 6, 7]。然而一种波形重构算法,只适用于重构一种反射面产生的测高波形,并不能重构所有的波形,因此将测高波形分成不同类别,按波形的类别分别采用相应的波形重构算法[8, 9]。
本文采用波形分类重构算法处理EnviSat卫星2003年至2010年的测高波形数据,提高了长江口近岸海域(28°N~32°E,120°N~125°E)的海面高精度。该区域的海况较为复杂,包括世界第三大河流长江的入海口、由长江三角洲不断延伸所形成的杭州湾以及中国第一大群岛舟山群岛,几乎囊括了近岸海域影响测高波形的各种因素,对于研究近岸海面高的可用性具有典型意义。通过对长江口近岸海域的EnviSat卫星测高波形进行分类,在该海域除占主导的海洋波形外,还有波形后缘前端出现峰值的波形、波形后缘后端出现峰值的波形、似镜面波形和复杂波形。利用基于波形分类的重构算法对测高波形进行重构,其中,海洋波形按EnviSat星载的Ocean波形重构算法进行重构;波形后缘前端出现峰值的波形、波形后缘后端出现峰值的波形和复杂波形采用按子波形算法,计算精确的海面高。
2 数据和研究区域EnviSat是继ERS-1和ERS-2之后欧空局发射的又一对地观测卫星,2002年3月1日发射升空,轨道高度800km,轨道倾角98.5°,重复周期为35d,一直工作到2012年4月8日。本次研究中采用2002年10月至2010年5月(cycles 10—90)的RA2_MWS_2P数据产品。该产品提供了地球物理数据(GDR)数据和波形(WAP)数据。研究区域为长江口近岸海域4条上升轨迹(P096、P139、P368、P411)和4条下降轨迹(P046、P089、P275、P318),如图 1所示。采用NGDC (national geophysical data center)提供的精度为1 ′的ETOPO1模型和GSSHS海岸线模型剔除陆地区的测高数据,采用EGM2008大地水准面模型分析重构前后的海面高的改善程度。
|
| 图 1 EnviSat卫星在长江口近岸海域星下点轨迹 Fig. 1 The ground tracks of EnviSat satellite around Yangtze estuary |
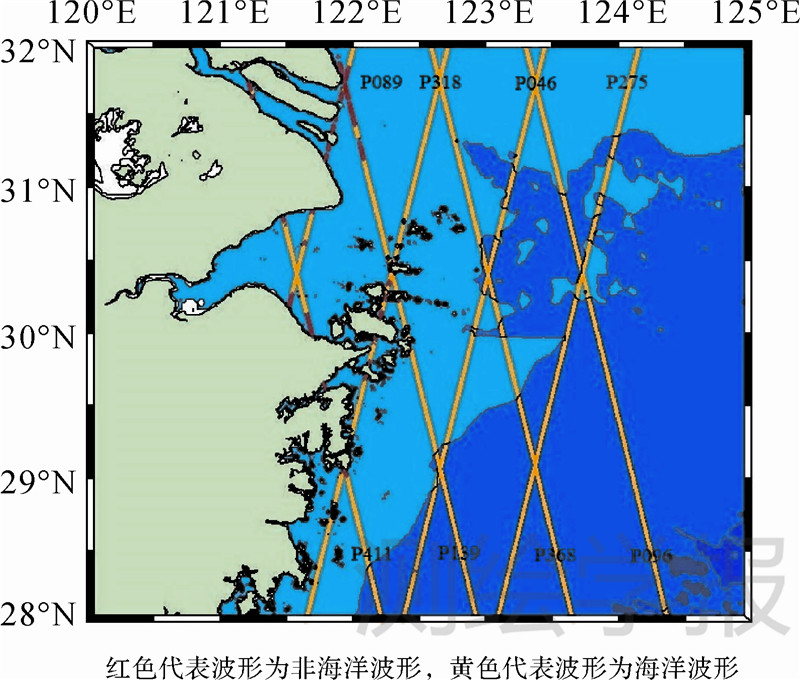
波形重构算法是一种针对波形数据的后处理方法,目的是计算测高波形实际前缘中点与预设的前缘中点之间的距离改正量。在近岸海域,星下点雷达脉冲照明区内反射面不一致,使得波形形状复杂多变(如图 2所示),因此需要采用不同的波形重构算法。其中,Ocean算法、β-参数算法、OCOG算法、Threshold算法较为常用,可参阅文献[10]。在此只简要介绍子波形算法。

|
| 图 2 cycle66 pass 139波形序列 Fig. 2 Waveform series along the pass 139 of cycle 66 |
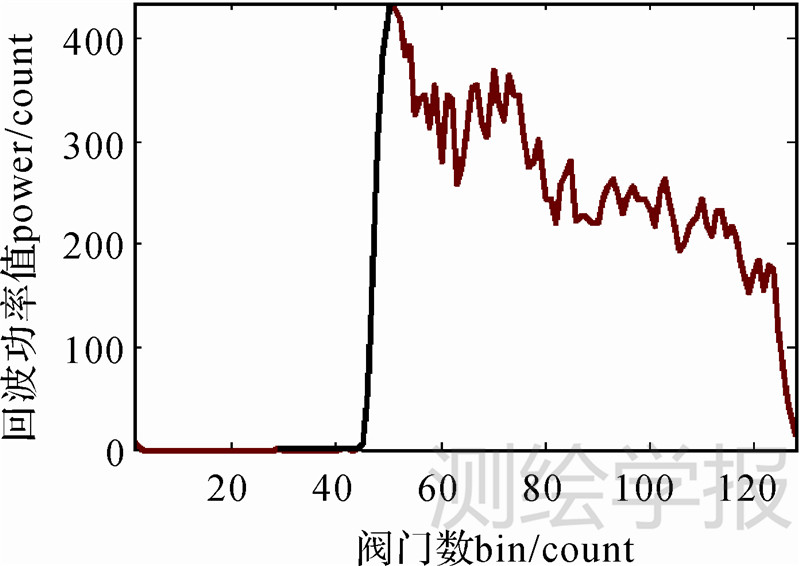
子波形算法先从完整的回波波形中提取出具有海洋回波特性的一段子波形(如图 3黑线所示的波形段),再用某个波形重构算法确定子波形的前缘中点,若子波形的数量不止一个,则要从多个前缘中点中选取最佳的前缘中点。
|
| 图 3 子波形示意图(黑色线段为子波形) Fig.3 The shape of sub-waveform (the black line denotes the sub-waveform) |
提取子波形的核心是找出子波形的起点和终点。如图 3所示,子波形起点的回波功率值最小,终点的回波功率值最大,因此式(1)求得的子波形相邻与相隔采样点回波功率的两类差值d1i、d2i应该大于0
根据这一性质,可以采用如下策略确定子波形的起、终点。因为波形前缘处的回波功率差值较大,先找出差值d2i最大的s点;再从s点开始,根据两类差值d1i、d2i向前搜索起点,该差值小于0的点为起点;然后从s点开始向后搜索终点,同样将两类差值小于0的点为终点。
在计算过程中,若是子波形起点的回波功率值大于整个波形回波功率的平均值,就认为这个子波形是无效的子波形。因为这种子波形通常出现在波形后缘,是由陆地回波引起的。提取出的子波形可以采用OCOG算法、Threshold算法、5-参数算法计算波形前缘中点。本文采用Threshold算法计算波形前缘中点。
4 波形分类及对应波形重构算法的选取 4.1 测高波形聚类分析聚类分析是把数据对象划分成不同类别子集的过程。测高波形的形状是测高波形的重要特征,因此利用波形形状来进行聚类分析。由于不同波形的振幅不同,在进行聚类分析前,先要对波形按式(2)进行归一化处理,得到归一化的波形Pi
式中,Pi表示波形P在第i个阀门处的回波功率值;min(Pi)和max(Pi)是波形P的最小回波功率值和最大回波功率值。根据式(3)可计算两个归一化波形间的距离d(P,P′)[9] 式中,P与P′表示两个不同的波形;Pi+n表示波形P在第i+n个阀门处的回波功率值;N为波形数据的总阀门数;n是平移参数;n0为n的取值范围。利用平移参数可以计算两个波形进行相应平移后的距离,从而降低波形前缘错位产生的影响。本文采用k-中心点算法,将归一化后的波形分成k个聚类中心所代表的波形类别。其k个初始聚类中心的确定方法如下:①按式(3)计算所有波形之间的距离,选取距离最大的两个波形分别作为第1类和第2类波形的聚类中心;②根据到这两个聚类中心最小距离的最大值为准则,确定第3类波形的聚类中心。同理,根据到前i个聚类中心最小距离的最大值为准则,确定第i+1类波形的聚类中心。依此类推,直至确定出k个聚类中心。确定初始聚类中心后,再按如下方法完成波形分类:①计算某个待分类波形到k个聚类中心距离,该波形加入到距离最小的聚类中心所代表的波形类别;②加入新波形后的波形类别,需要确定新的聚类中心,其准则是聚类中心到该波形类别中所有波形的距离之和最小;③重复步骤①和步骤②,直至完成所有波形的分类,同时确定了最终的k个聚类中心。
好的波形分类结果应该满足类内紧密度E(即同一类别波形间的距离之和)尽可能小,而类间分离度F(不同类别波形间的距离之和)尽可能大。类内紧密度E和类间分离度F的计算公式如下
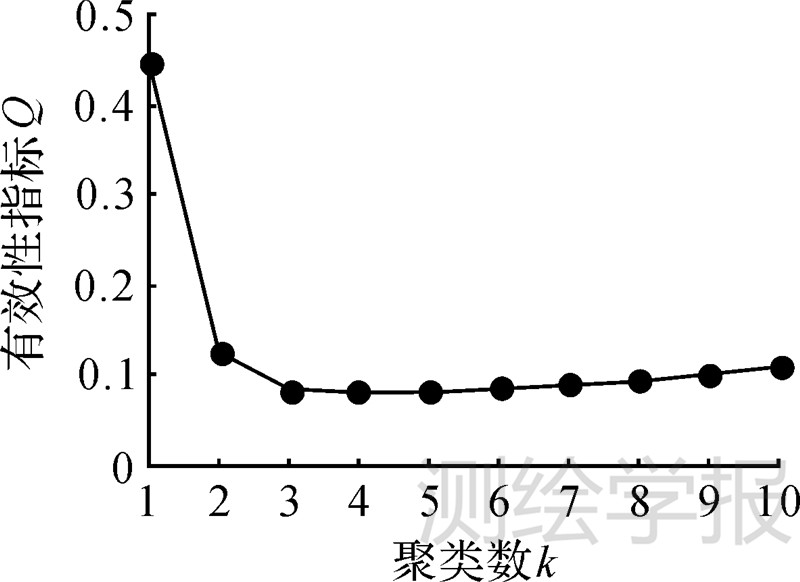
式中,Ci表示第i类波形;k为聚类数;Ni为第i类波形所包含的波形个数。将类内紧密度E与类间分离度F之和称为有效性指标Q,用于最佳的波形类别数,该指标越小,分类结果越好。因此,利用聚类分析将波形分成k个波形类别后,需要根据有效性指标进一步确定最佳的波形类别数。 4.2 分类结果分析按照上述方法,将波形类别数k依次定为1~10,分别计算不同波形类别数所对应的有效性指标,从而确定最佳的波形类别数,其结果如图 4所示。
|
| 图 4 有效性指标变化曲线图 Fig. 4 The curve graph of validity index and cluster number |
由图 4可见,当波形类别数k=4时,有效性指标取得最小值0.0825,这说明将波形数据分为4类最为合理。
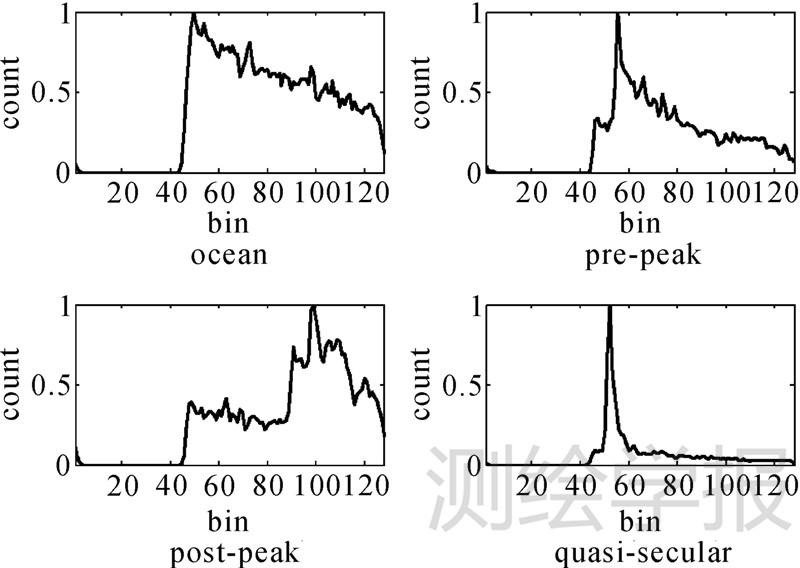
图 5给出了代表4类波形的4个聚类中心,第1类波形是海洋波形,该波形主要出现在开阔海域,采用Ocean算法对该类波形进行重构;第2类波形是波形后缘前段出现峰值的波形(pre-peak),第3类波形是波形后缘后端出现峰值的波形(post-peak),第2类和第3类波形采用子波形算法进行重构;第4类波形是似镜面波形(quasi-specular),这类波形采用OCOG算法、Threshold算法进行重构,该类波形受到陆地影响很大,重构效果明显不如前面3类波形,因此在计算海面高的时候,并未采用似镜面波形的海面高重构结果。
|
| 图 5 聚类中心波形图 Fig. 5 Cluster centers of waveforms around Yangtze estuary |
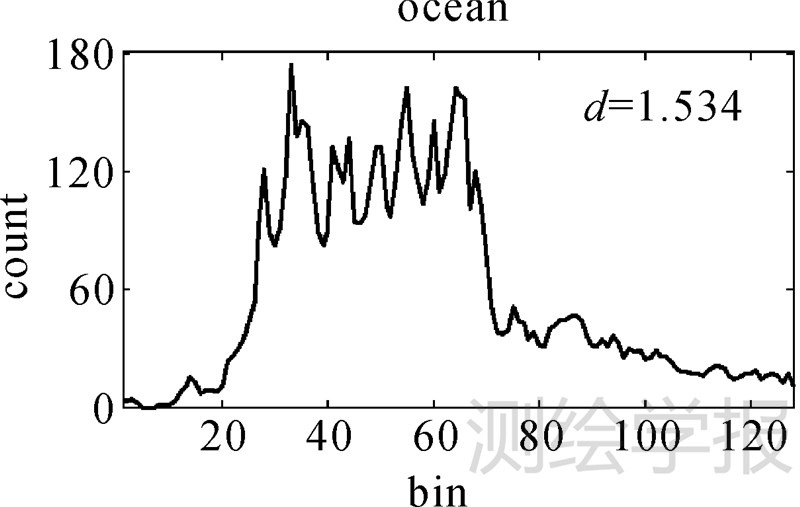
如图 6所示的波形在聚类分析时也被划分到海洋波形一类,但该波形与海洋波形有较大差异,称为复杂波形(complex)。通过统计分析,发现复杂波形与聚类中心的距离(简称为波形距离)都比较大。通过每类波形到其聚类中心的距离的均值m和标准差σ,将波形距离大于阈值m+2σ的波形划分为复杂波形。长江口近海EnviSat测高波形的最终分类结果如表 1所示。
|
| 图 6 复杂波形示意图 Fig. 6 The shape of complex waveform |
| 类别 | 阈值 | 个数 | 百分比(%) |
| ocean | 0.010 | 529230 | 89.03 |
| pre-peak | 0.016 | 17565 | 2.95 |
| post-peak | 0.019 | 2667 | 0.45 |
| quasi-specular | 0.012 | 19656 | 3.31 |
| complex | — | 25348 | 4.26 |
从表 1可以看出,海洋波形数量最多,占所有波形数据总量的89.03%;其次是似镜面波形,占3.31%;第2类和第3类波形共占3.40%,超出各类波形距离阈值的波形共占4.26%。分类的准确性对按波形类别进行重构非常重要,特别是Ocean算法和β-参数算法,错误的分类会导致重构后的海面高偏离正确值。因此,将与聚类中心距离大于阈值的波形提取出来,采用子波形算法进行重构,这样可避免采用不恰当的波形重构算法。
5 长江口近岸海域波形重构结果通过波形重构算法计算得到测高波形的前缘中点后,便可以按式(5)计算距离改正量R
式中,ΔR是测高波形相邻两个阀门所对应的距离,EnviSat卫星为0.4684m;g是计算得到的前缘中点;g0是预设的前缘中点,EnviSat卫星为46.5。为求得最终的海面高,还需要添加各项地球物理改正,包括干对流层改正、湿对流层改正、电离层改正、逆气压改正、海况偏差改正、海潮改正、固体潮改正、极潮改正。其中,干对流层改正和湿对流层改正采用欧洲中期天气预报中心(ECMWF)提供的数值预测模型计算得到,电离层改正采用美国喷气推进实验室(JPL)提供的GIM模型计算得到。采用模型改正值是因为在近岸海域,受到陆地反射面的影响,原本精度较高的雷达测高计的双频电离层改正和微波辐射计的湿对流改正反而产生较大误差。
5.1 阈值水平的选取Ocean算法和5-参数算法都是基于Brown模型的波形重构算法,采用迭代最小二乘算法计算前缘中点[8]。OCOG算法、Threshold算法和子波形算法在计算前缘中点时需要选取合适的阈值水平。文献[4]指出,使用Threshold算法时,阈值水平的选取和雷达脉冲的反射面有关。当反射面是大陆冰盖时,10%的阈值水平是最佳的;当反射面是海洋表面时,50%的阈值水平是最佳的。
由于本文研究区域属于温带气候,海面不会发生冻结,海洋表面反射的作用占主导地位,阈值水平应为50%左右。
进一步确定最佳的阈值水平时,注意到不同的波形重构算法之间存在偏差。同时,研究发现5-参数算法和Ocean算法之间的偏差是稳定的系统偏差,其偏差值为25.71cm,中误差为6.2mm(表 2),并计算了OCOG算法、Threshold算法和子波形算法计算得到的海面高与Ocean算法计算得到的海面高之间的系统偏差[11]。但是不同的阈值水平会得到不同的偏差值,因此,本文选取不同的阈值水平,从10%~75%,每次间隔1%,分别计算其对应的海面高,然后计算由OCOG算法、Threshold算法和子波形算法计算的海面高与Ocean算法计算的海面高的差值的均值和中误差,结果如图 7所示。显然,若以中误差最小为准则,OCOG算法、Threshold算法与子波形算法的最佳阈值水平分别是65%、45%与50%。这些波形重构算法与Ocean算法求得的海面高之间的差值均值和中误差如表 2所示。只要改正系统偏差,便可实现不同波形重构算法海面高的融合。
| 重构算法 | 偏差值均值 | 中误差 |
| 5-参数 | 25.71 | 0.62 |
| OCOG | 21.82 | 0.39 |
| Threshold | 23.27 | 0.40 |
| 子波形 | 21.60 | 0.44 |

|
| 图 7 阈值水平与海面高偏差值中误差变化曲线图 Fig. 7 The curve graph of threshold level and standard deviation of sea surface height |
波形分类重构算法,采用Ocean算法和子波形算法进行波形重构,充分发挥了这两种重构算法处理海洋波形和多前缘波形的优势。本文根据重构后海面高的IMP值以及波形重构恢复的数据量来评价重构的效果,IMP值的计算公式如下
式中,σraw是GDR文件给出的原始海面高与大地水准面高差值的标准差;σretracked是重构后的海面高与大地水准面高差值的标准差。图 8给出了Ocean算法、子波形算法和波形分类重构算法在研究区域内的每条轨迹的IMP值变化曲线,只有极少数周期的IMP值出现负值。从图中可以看出,离海岸线较远的4条轨迹(P046、P096、P275、P368),Ocean算法和波形分类重构算法的IMP值优于子波形的IMP值,但相差不是很大,说明子波形算法即使在开阔海域也能取得较好的精度。而离海岸线较近的4条轨迹(P089、P139、P318、P411),子波形算法和波形分类重构算法的IMP值明显优于Ocean算法的IMP值,说明在靠近海岸线的地方,子波形算法和波形分类重构算法能很好地改善海面高的精度。各轨迹不同周期IMP的平均值如表 3所示 (其中最大值用粗体表示),说明波形重构使每个轨迹的海面高精度均获得明显改善。

|
| 图 8 不同轨迹的IMP值变化曲线图 Fig. 8 The curve graph of IMP of different ground tracks |
| 轨迹 | 重构算法 | ||
| Ocean | 子波形 | 基于波形分类 | |
| P046 | 30.01 | 26.16 | 30.35 |
| P089 | 6.16 | 29.34 | 29.23 |
| P096 | 28.73 | 21.80 | 28.82 |
| P139 | 38.65 | 53.47 | 53.86 |
| P275 | 26.45 | 17.13 | 25.98 |
| P318 | 28.00 | 56.26 | 56.41 |
| P368 | 28.80 | 23.48 | 28.86 |
| P411 | 4.48 | 16.55 | 16.62 |
图 9显示了Ocean算法,子波形算法和波形分类重构算法在各条轨迹恢复海面高数据的百分比。在离海岸线较远的4条轨迹(P046、P096、P275和P368),3种重构方法恢复的海面高数据量都很接近,在94%~99%之间,波形分类重构算法恢复的海面高数据稍多一些。而离海岸线较近的4条轨迹(P089、P139、P318和P411),Ocean重构算法恢复的海面高数据量明显低于子波形算法和波形分类重构算法,只有70%左右,而波形分类重构算法能够恢复90%左右的海面高数据,即使在P089,数据质量很差的情况下,也能恢复70%的数据,远高于Ocean算法的45%。

|
| 图 9 不同轨迹重构恢复的海面高数据量对比图 Fig. 9 Percentages of sea surface heights recovered from different ground tracks by different retrackers |
交叉点是卫星上升轨迹和下降轨迹投影在海平面上的交点。交叉点的海面高在理论上是相等的,因此可以根据交叉点的海面高差值,分析波形重构后海面高精度的改善情况。在实际数据中,交叉点处几乎没有实际测高观测值,通常通过内插求取交叉点处的海面高。通常采用二次多项式求解交叉点的位置[15],假设卫星星下点的经纬度的关系如式(7),利用交叉点处经纬度相等的条件求解
式中,λ表示经度;φ表示纬度;A、B、C表示未知参数。本文通过共线平差求得各条轨迹的平均海面高,然后求解各条轨迹的交叉点差值。波形重构前后,研究区域交叉点海面高的差值如表 4所示,可见重构后的交叉点海面高差值明显小于重构前的差值。在波形重构之后,只有轨迹P411、P089相关的交叉点的海面高差值为25cm左右,其他交叉点的海面高差值只有2~6cm。这说明轨迹P411、P089的海面高数据质量低于其他轨迹,因此重构后轨迹P411与P089的交叉点海面高差23.9cm是可信的,尽管在重构前只有6.8cm。从图 1可以看出,与轨迹P411、P089形成的交叉点分别位于舟山群岛、杭州湾和崇明岛附近。其中,靠近舟山群岛和崇明岛的交叉点可能因为离岸太近,制约了波形重构的改善效果。而在杭州湾的交叉点虽然离岸距离较远,但轨迹两端都有陆地,且海面宽度较窄,其观测环境近似于内陆湖泊,因而海面高精度较差。
| 上升轨迹 | 下降轨迹 | 交叉点经度/(°) | 交叉点纬度/(°) | 重构前的差值/m | 重构后的差值/m |
| P096 | P046 | 31.72 | 123.37 | -0.055 | -0.023 |
| P096 | P275 | 30.42 | 123.73 | 0.029 | 0.026 |
| P139 | P046 | 29.10 | 122.66 | 0.143 | 0.050 |
| P139 | P089 | 31.75 | 121.94 | 1.052 | -0.244 |
| P139 | P318 | 30.45 | 122.29 | 0.461 | -0.061 |
| P368 | P046 | 30.41 | 123.01 | 0.041 | 0.026 |
| P368 | P275 | 29.08 | 123.37 | 0.057 | 0.033 |
| P368 | P318 | 31.73 | 122.64 | -0.032 | -0.023 |
| P411 | P089 | 30.42 | 121.57 | -0.068 | -0.239 |
| P411 | P318 | 29.10 | 121.93 | 1.761 | 0.255 |
本文利用聚类分析的方法把波形数据分成了4类,并利用波形距离优化了分类结果,得到海洋波形(89.03%)、波形后缘前端出现峰值的波形(2.95%)、波形后缘后端出现峰值的波形(0.45%)、似镜面波形(3.31%)以及复杂波形(4.26%)。
对由不同重构算法计算得到的海面高之间的偏差进行了分析。研究发现,Ocean算法和5-参数算法之间的偏差是稳定的系统偏差,其偏差值是25.71cm,中误差是0.62cm。根据这一性质,计算得到了OCOG的最优阈值水平是65%,Threshold的最优阈值水平是45%,子波形的最优阈值水平是50%,其相应的偏差值分别为21.82cm、23.27cm、21.60cm,中误差分别为0.39cm、0.40cm、0.44cm。
利用EGM2008大地水准面模型评定重构前后海面高的改善程度。研究表明,波形分类重构算法的海面高重构精度明显优于Ocean算法和子波形算法,其改善程度在16.62%~53.86%之间,并且其恢复的有效海面高数据也多于后两种算法。同时交叉点分析的结果也表明重构后的海面高精度较重构之前有明显提高。除了与轨迹P089、P411形成的交叉点的海面高差值在25cm左右外,其余交叉点的差值均在2~6cm,这与在开阔海域所得到的交叉点差值是一致的。同时,轨迹P089,P411的数据质量低于其他轨迹,在海湾和江河入海口处的海面高精度的提高有待进一步研究。
| [1] | DENG X. Improvement of Geodetic Parameter Estimation in Coastal Regions from Satellite Radar Altimetry[D]. Perth: Curtin University of Technology, 2004. |
| [2] | BROWN G S. The Average Impulse Response of a Surface and Its Applications[J]. IEEE Transactions on Antennas and Propagation, 1977, 25(1): 67-74. |
| [3] | MARTIN T V, ZWALLY H J, BRENNER A C, et al. Analysis and Retracking of Continental Ice Sheet Radar Altimeter Waveform[J]. Journal of Geophysical Research, 1983, 88(C3): 1608-1616. |
| [4] | DAVIS C H. A Robust Threshold Retracking Algorithm for Measuring Ice-sheet Surface Elevation Change from Satellite Radar Altimeters[J]. IEEE Transactions on Geoscience and Remote Sensing, 1997, 35(4): 974-979. |
| [5] | HWANG C, GUO J Y, DENG X X, et al. Coastal Gravity Anomalies from Retracked GeoSat/GM Altimetry: Improvement, Limitation and the Role of Airborne Gravity Data[J]. Journal of Geodesy, 2006, 80(4): 204-216. |
| [6] | LEE H, SHUM C K, YI Y C, et al. Laurentia Crustal Motion Observed Using TOPEX/Poseidon Radar Altimetry over Land[J]. Journal of Geodynamics, 2008, 46(3-5): 182-193. |
| [7] | WINGHAM D J, RAPLEY C G, GRIFFITHS H. New Techniques in Satellite Tracking Systems[C]//Proceedings of IGARSS’ 88 Symposium. [S.l.]: IEEE, 1988: 186-193. |
| [8] | DENG X, FEATHERSTONE W E. A Coastal Retracking System for Satellite Radar Altimeter Waveforms: Application to ERS-2 Around Australia[J]. Journal of Geophysical Research, 2006, 111(C6), doi: 10.1029/2005JC003039. |
| [9] | WANG Haihong, YUE Yingchun, ZOU Xiancai, et al. Classification of Radar Altimeter Waveforms Based on Cluster Analysis[J]. Geomatics and Information Science of Wuhan University, 2010, 35(7): 833-836. (汪海洪, 岳迎春, 邹贤才, 等. 基于聚类分析的卫星雷达测高波形分类研究[J]. 武汉大学学报: 信息科学版, 2012, 35(7): 833-836.) |
| [10] | GOMMENGINGER C, THIBAUT P, FENOGLIO-MARC L, et al. Retracking Altimeter Waveforms Near the Coasts[M]//VIGNUDELLI S, KOSTIANOY A G, CIPOLLINI P, et al. Coastal Altimetry. Berlin: Springer-Verlag, 2011: 61-101. |
| [11] | PENG Fukai, SHEN Yunzhong, ZHAO Jian. Analysis of Bias Characteristics in Different Waveform Retracking Methods of Satellite Altimetry[J]. Hydrographic Surveying and Charting, 2014, 34(3): 1-4. (彭福凯, 沈云中, 赵健. 卫星测高不同波形重构方法的偏差特性分析[J]. 海洋测绘, 2014, 34(3): 1-4.) |
| [12] | BRENNER A C, KOBLINSKY C J, BECKLEY B D. A Preliminary Estimate of Geoid-induced Variations in Repeat Orbit Satellite Altimeter Observations[J]. Journal of Geophysical Research, 1990, 95(C3): 3033-3040. |
| [13] | BROOMHEAD D S, KING G P. Extracting Qualitative Dynamics from Experimental Data[J]. Physica D: Nonlinear Phenomena, 1986, 20(2-3): 217-236. |
| [14] | DONG Xiaojun, HUANG Cheng. Monitoring Global Mean Sea Level Variation with TOPEX/Poseidon Altimetry[J]. Acta Geodaetica et Cartographica Sinica, 2000, 29(3): 266-272. (董晓军, 黄珹. 利用TOPEX/Poseidon卫星测高资料监测全球海平面变化[J]. 测绘学报, 2000, 29(3): 266-272.) |
| [15] | GMEZ-ENRI J, CIPOLLINI P, GOMMENGINGER C, et al. Improving Coastal Altimeter Products by A New Retracking Approach[C]//Remote Sensing of the Ocean, Sea Ice, and Large Water Regions 2009. Berlin: SPIE, 2009: 1-15. |
| [16] | GMEZ-ENRI J, VIGNUDELLI S, QUARTLY G D, et al. Modeling EnviSat RA-2 Waveforms in the Coastal Zone: Case Study of Calm Water Contamination[J]. IEEE Geoscience and Remote Sensing Letters, 2010, 7(3): 474-478. |
| [17] | GUO Jinyun, GAO Yonggang, CHANG Xiaotao, et al. Optimal Threshold Algorithm of EnviSat Waveform Retracking over Coastal Sea[J]. Chinese Journal of Geophysics, 2010, 53(4): 807-814. (郭金运, 高永刚, 常晓涛, 等. 近岸海域EnviSat卫星测高波形重定的Threshold 化法算法[J]. 地球物理学报, 2010, 53(4): 807-814.) |
| [18] | HASSANI H. Singular Spectrum Analysis: Methodology and Comparison[J]. Journal of Data Science, 2007, 5(2): 239-257. |
| [19] | IDRIS N H, DENG X. The Retracking Technique on Multi-peak and Quasi-specular Waveforms for Jason-1 and Jason-2 Missions near the Coast[J]. Marine Geodesy, 2012, 35(S1): 217-237. |
| [20] | JIANG Weiping. The Application of Satellite Altimetry in Geodesy[D]. Wuhan: Wuhan University, 2000. (姜卫平. 卫星测高技术在大地测量学中的应用[D]. 武汉: 武汉大学, 2000.) |
| [21] | TSENG K H, SHUM C K, YI Y C, et al. EnviSat Altimetry Radar Waveform Retracking of Quasi-specular Echoes over the Ice-covered Qinghai Lake[J]. Terrestrial, Atmospheric and Oceanic Sciences, 2013, 24(4): 615-627. |
| [22] | LEE H, SHUM C K, EMERY W, et al. Validation of Jason-2 Altimeter Data by Waveform Retracking over California Coastal Ocean[J]. Marine Geodesy, 2010, 33(S1): 304-316. |
| [23] | NEREM R S. Measuring Global Mean Sea Level Variations Using TOPEX/Poseidon Altimeter Data[J]. Journal of Geophysical Research, 1995, 100(C12): 25135-25151. |
| [24] | KNUDSEN P, BROVELLI M. Collinear and Cross-over Adjustment of GeoSat ERM and Seasat Altimeter Data in the Mediterranean Sea[J]. Surveys in Geophysics, 1993, 14(4-5): 449-459. |
| [25] | WANG Haihong, LUO Zhicai, YANG Yuande, et al. An Adaptive Retracking Method for Coastal Altimeter Data Based on Waveform Classification[J]. Acta Geodaetica et Cartographica Sinica, 2012, 41(5): 729-734. (汪海洪, 罗志才, 杨元德, 等. 基于波形分类的近海卫星测高数据自适应重跟踪方法[J]. 测绘学报, 2012, 41(5): 729-734.) |
| [26] | WANG Huizan, ZHANG Ren, LIU Wei, et al. Improved Interpolation Method Based on Singular Spectrum Analysis Iteration and Its Application in Missing Data Recovery[J]. Applied Mathematics and Mechanics, 2008, 29(10): 1227-1236. (王辉赞, 张韧, 刘巍, 等. 奇异谱迭代插补的改进算法及其在缺损数据恢复中的应用[J]. 应用数学和力学, 2008, 29(10): 1227-1236.) |
| [27] | YANG Yuande. The Determination of Marine Gravity Anomalies over Antarctic Oceans from Satellite Altimetry[D]. Wuhan: Wuhan University, 2010. (杨元德. 应用卫星测高技术确定南极海域重力场研究[D]. 武汉: 武汉大学, 2010.) |
| [28] | ZHAO Jian, SHEN Yunzhong. Assessment of Retracked EnviSat Altimetry Sea Surface Heights Near Hainan Coastal Ocean[J]. Journal of Tongji University: Natural Science, 2013, 41(11): 1726-1731. (赵健, 沈云中. 海南近海EnviSat测高波形重构海面高质量评价[J]. 同济大学学报: 自然科学版, 2013, 41(11): 1726-1731.) |
| [29] | ZHANG Chuanyin, GUO Chunxi, CHEN Junyong, et al. EGM2008 and Its Application in Chinese Mainland[J]. Acta Geodaetica et Cartographica Sinica, 2009, 38(4): 283-289. (章传银, 郭春喜, 陈俊勇, 等. EGM2008地球重力场模型在中国大陆的适用性分析[J]. 测绘学报, 2009, 38(4): 283-289.) |