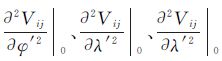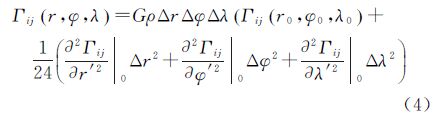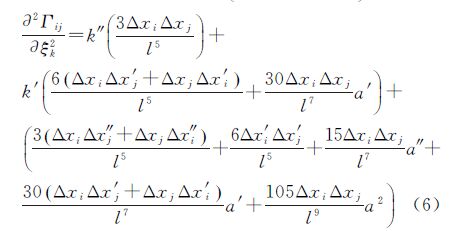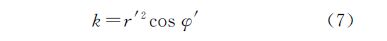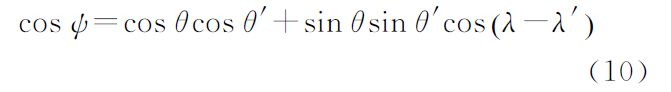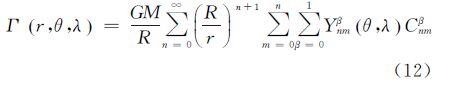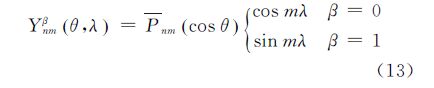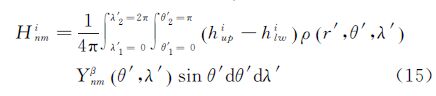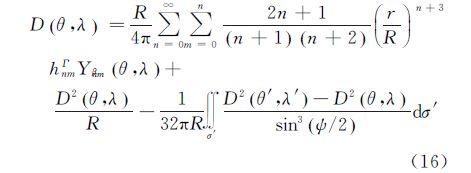1. 中国科学院大学,北京 100049;
2. 中国科学院测量与地球物理研究所大地测量与地球动力学国家重点实验室,湖北 武汉 430077;
3. 地理信息工程国家重点实验室,陕西 西安 710054
收稿日期:2014-01-16;修回日期:2015-03-15
基金项目:国家自然科学基金(41304023);国家重大科学仪器设备开发专项(2011YQ120045);地理信息工程国家重点实验室开放基金(SKLGIE2013-M-1-2);武汉大学地球空间环境与大地测量教育部重点实验室测绘基础研究基金(13-01-02).
第一作者简介:叶周润(1984—),男,博士生,研究方向为重力梯度。E-mail: yezhourun329@hotmail.com
The Signal Extraction of Gravity Gradient Disturbance on Moho
1. University of Chinese Academy of Sciences,Beijing 100049,China;
2. State Key Laboratory of Geodesy and Earth's Dynamics,Institute of Geodesy and Geophysics,CAS,Wuhan 430077,China;
3. State Key Laboratory of National Geographic Information Engineering,Xi'an 710054,China
First author: YEZhourun(1984),male,PhDcandidate,
majorsingravitygradient
E-mail: yezhourun329@hotmail.com
1 引 言
GOCE(Gravity Field and Steady-state Ocean Circulation Explorer)是一颗用于恢复地球重力场和探测静态洋流的重力梯度卫星,其优于100km的空间分辨率观测值能改善地球重力场的中高频信息,因此在精化全球大地水准面[1]的同时也可以为地球物理学研究带来更多信息。GOCE被认为可以捕捉到壳幔边界信号[2],对岩石圈的密度敏感[3],因此在盆地密度、地质构造、Moho面[4 ,5, 6]等具体研究中具有巨大潜力。
壳幔起伏和岩石圈密度是重要的地球内部结构研究,而Moho面的确定可以为地壳均衡和岩石圈有效弹性厚度研究提供相应依据[7],并且重点地区(如青藏高原等)的Moho面结构可以为此区域的地球动力学研究提供参考[8 ,9]。相对于地震方法,利用卫星重力确定地壳厚度可以弥补地面测量重力和地震资料的缺陷[10, 11, 12],尤其是重力梯度可以改善特定频段信号在地球物理应用中的精度[13],因此在GOCE卫星发射后非洲等地区成为研究热点[3]。另外重力测量值可以和地震资料进行联合反演,使解算结果相互约束从而提高反演精度。同时重力资料的分析方法可以用于其他星球,如月球等无地震数据的星球地壳厚度和地质构造研究[14]。本文的研究重点主要在于如何从GOCE观测值中提取出用于Moho面反演的初值。在理论上借鉴和改进了前人的研究思路:①伴随GPS定位技术发展,利用重力扰动(纯重力异常)分析扰动源更加方便[15],相对于重力异常,重力扰动用于Moho面反演也显现出更高精度[15, 16, 17, 18],因此本文研究中所提取的信号都是扰动重力梯度值;②比点质量模型正演精度更高的空间域Tesseroid单元体和频谱域球谐分析与综合方法被应用于重力梯度正演[19, 20, 21];③重力观测值结合地壳先验模型的逐步剥离方案被应用于重力梯度信号的提取中[22, 23],该处理策略减少了Moho面反演中由于地壳密度不均带来的误差影响。在具体计算中采用了最新CRUST1.0先验模型[24]。本文最后运用上述方法提取的扰动垂直重力梯度值,进行了全球Moho面的恢复工作,并与现有模型进行了对比验证。
2 方法介绍
2.1 Moho面信息提取策略
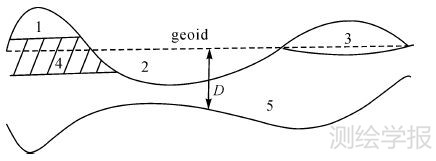
如图 1所示,Moho面以上的地球结构大体分层主要有陆地岩石(1)、海水(2)、冰层(3)、沉积层(4)和除上述之外的密度不均匀地壳(5)。
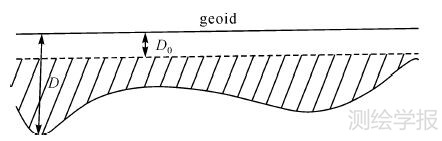
如果要用Vening Meinesz-Moritz[15, 16, 17 ,18]方法解算出地壳厚度,首先需要得到如图 2所示的一个单密度界面。
为此,本文采取结合地壳先验模型的逐步剥离方案,这种处理策略得到的最终结果被认为和由地震数据解算的Moho面具有很强的相关系数[22 ,23]。对于GOCE观测数据而言,则可采用式(1)进行有效信息逐步提取
式中,i,j∈1,2,3;Γ
ij表示梯度分量;δΓ
ij表示上地幔以上的扰动重力梯度;Γ
ijT、Γ
ijB、Γ
ijI、Γ
ijS、Γ
ijC分别表示由陆地地形产生的重力梯度及海水、冰层、沉积层和不均匀地壳相对于岩石密度产生的补偿重力梯度。
在壳幔信号分离中,依托于GOCE重力梯度模型,根据文献[25]结论在此扣除17阶以内主要存在于上地幔以下的长波信息。对于重力梯度正演部分,采用球坐标系下的空间域Tesseroid和频域球谐方法[19, 20, 21],以克服意大利GEMMA Moho团队的点质量模型计算误差[26]。在地壳信息校正部分,采用2013年7月最新发布的CRUST 1.0模型。该模型的陆地地形,海洋和冰层资料来自ETOPO1[27],同时沉积层和地壳密度的空间域分辨率也从2°提高到1°[24]。
2.2 GOCE模型计算扰动重力梯度值
从GOCE球谐位系数模型恢复扰动重力位信息可以采用式(2)的形式
式中,
r、
θ和
λ分别表示计算点的球心距离、地心纬度和经度;
GM代表万有引力常数和地球总质量的乘积(3.986005e14m
3/s
2);
R是地球平均半径(6371km);
Cnm和
Snm是GOCE模型位系数和正常位系数相减后得到的扰动位系数;
Pnm是完全正则化的连带勒让德函数;
Nmin和
Nmax分别为起始和最大阶数。
考虑到便于后续空间域和频谱域方法比较,这里选用当地右手坐标系LNOF(local north-oriented frame)。如果要转换到此坐标系,则可运用式(3)表述[28]
式(3)中对应的关于位的一阶和二阶导数详见文献
[28]。
2.3 空间域和频谱域正演扰动重力梯度
2.3.1 空间域Tesseroid单元体方法
在空间域计算中,笔者选取与地球表面地形非常吻合的Tesseroid单元体作为积分模型。根据文献[20]模拟试验结论,相对于点质量模型,Tesseroid单元体正演精度可以提高3个量级;另外文献[14]中试验表明0.25°的Tesseroid单元体对理论月球模型的拟合误差为0.001%,并且文献[19]和[20]中已经验证了该单元体用于扣除GOCE卫星扰动物质影响的可行性。
文中计算公式来自泰勒级数展开方法[19],若取Tesseroid单元体的中心点:r0=(r1+r2)/2,φ0=(φ1+φ2)/2,λ0=(λ1+λ2)/2,并展开到4阶无穷小,则经过相应数学计算,可以得到
式中,计算基准面为半径
R球面;
G表示万有引力常数;
ρ表示扰动物质密度; (
r,φ,λ)、(
r′,φ′,λ′)、(
r0,
φ0,
λ0)、(
r1,
φ1,
λ1)、(
r2,
φ2,
λ2)表示流动计算点、积分点、Tesseroid中心点、上限和下限点的球心距离、余纬和经度;Δ
r、Δ
φ、Δ
λ分别表示Tesseroid在球心、纬度和经度方向的间距;
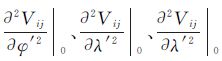
分别表示在球心、纬度和经度方向的Γij函数二阶导数位于Tesseroid中心点时的数值。o(Δ4)表示泰勒展开的截断误差。
由于从引力位表达式泰勒展开到二阶导数(引力梯度)比较繁琐,文献[19]将核函数分开求导,则有
式中,
φ表示纬度,且
φ=90°-
θ;
i,
j,
k∈{1,2,3};Δ
xi、Δ
xj、Δ
xk分别代表
x、
y、
z方向的间距;并且当
i=
j时,
δij=1;
i≠
j时,
δij=0。
式(6)中其他表达式有
(10)式(7)—式(10)中,l和
ψ分别表示积分点和计算点之间的球面距离和夹角;其他变量具体表达详见文献
[19]。
2.3.2 频谱域球谐分析与综合方法
设一物体的内部质点分布连续,则该物体外一点的引力位为
可将距离l函数进行球谐展开,然后对
r′进行积分,进行级数3次项展开,并假定用球面代替大地水准面,则经过运算后有如文献
[29]形式的表达
式中
式中,
i∈{1,2,3};
ρ表示地球平均密度(5500kg/m
3);
hup和
hlw分别表示积分体高程上下限,具体数值以球面(大地水准面)为基准,即球面以上为正,反之为负;
Hnmi表示球谐谱系数,可由式(15)计算得到,将
Hnmi代入式(14)即可得到最终计算需要谱系数。则上述就是由扰动物质通过球谐谱域计算扰动位的一般表达形式,之后的各重力梯度分量则可由式(3)得到。
2.4 Moho面恢复谱域计算公式
为了验证前述Moho面扰动重力梯度信息的提取结果,笔者利用Γzz分量进行了试验计算。从Γzz分量进行Moho面恢复的频谱域公式为
式中,d
σ′=sin
θ′d
θ′d
λ′;D(
θ,
λ)和D(
θ′,
λ′)分别为计算点和流动点的Moho面深度;
hnmΓ为频谱域的Moho面解算初值。
3 试验计算及其结果分析
本文试验原始重力梯度数据来源于GOCO03S模型,该模型在低阶以GRACE为主,高阶采用GOCE从2009年11月开始历时18个月的中高频数据[30]。在球谐合成时,正常重力场参考GRS80模型。选定GOCE轨道平均值255km为计算高度,并忽略空气微小值影响[21] 。岩石、海水和冰层密度分别取值2670kg/m3、1025kg/m3920kg/m3。沉积层和地壳密度数据全部来自CRUST1.0模型。综合GOCE观测数据的空间分辨率和地壳先验模型精度,文中计算结果分辨率设为1°×1°。考虑到空间域和球谐谱对应关系,式(2)和式(12)中n最大值取180。
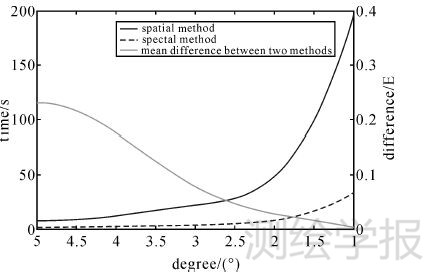
图 3表示以Γzz为例的空间域与频谱域方法在随网格分辨率改变时的计算所需时间和两者结果差异变化图(648个10°×10°等间距采样点)。左侧纵轴表示计算时间,右侧纵轴表示两种方法绝对值之差的平均值。如图 3所示,随着网格分辨率的加密,空间域方法时间需求远高于频谱域方法,并且两者的计算时间差异呈非线性增长的方式。同时,计算方法的差异表现出随格网分辨率加密而减少的趋势。当格网点加密到1°×1°时,采样点绝对值之差的平均值仅为0.0038E(1E=10-9/s2)。表 1所展示的是空间域Tesseroid和频谱域球谐分析与综合方法的结果比较。表 2所示为Moho面扰动重力梯度信息逐步提取的结果统计。表中T、B、I、SED(S)和CRD(C)分别代表陆地地形、海水、冰层、沉积层和不均匀地壳。GTBISC表示扣除长波影响后的扰动重力梯度(G)通过逐步剥离步骤得到的含Moho面信息的扰动重力梯度值。如表 1所示,两种方法的平均值差异在10-3量级左右。此外,笔者统计了表 1中的差异值对于最终扰动值(表 2中GTBISC项)的相对平均幅度,其结果是:2.2%(Γxx)、3.4%(Γyy)和1.3%(Γzz)。
表 1 空间域与频谱域方法结果比较
Tab. 1 Comparison between spatial and spectral methodology
| 10-9/s2 |
| Γxx |
| TBI | 0.0729 | -0.0409 | 1.1050e-3 | 0.0105
| | GTBISC | 0.0619 | -0.0880 | 2.0013e-4 | 0.0148 |
|
| Γyy |
| TBI | 0.0436 | -0.0442 | 8.3022e-4 | 0.0076
| | GTBISC | 0.0666 | -0.0564 | 9.9322e-5 | 0.0107 |
|
| Γzz |
| TBI | 0.0596 | -0.0904 | -1.9352e-3 | 0.0151
| | GTBISC | 0.1081 | -0.0924 | -2.9954e-4 | 0.0215 |
|
表 2 Moho面扰动重力梯度信息逐步提取结果统计
Tab. 2 Statistics of gravity gradient from Moho using step by step correction
| 10-9/s2 |
| Γxx |
| G | 1.2889 | -0.8819 | 0.0000 | 0.0973
| | GTBI | 4.7214 | -3.2956 | -0.3998 | 0.9526
| | GTBISC | 6.0803 | -3.7452 | -0.0567 | 1.3150 |
|
| Γyy |
| G | 0.7355 | -0.7673 | 0.0014 | 0.0942
| | GTBI | 5.6524 | -2.9044 | -0.3069 | 0.9229
| | GTBISC | 7.5100 | -3.7497 | 0.0351 | 1.3009 |
|
| Γzz |
| G | 1.1885 | -1.4776 | -0.0014 | 0.1591
| | GTBI | 4.5047 | -6.2266 | 0.7067 | 1.6560
| | GTBISC | 4.8844 | -8.6549 | 0.0215 | 2.2892 |
|
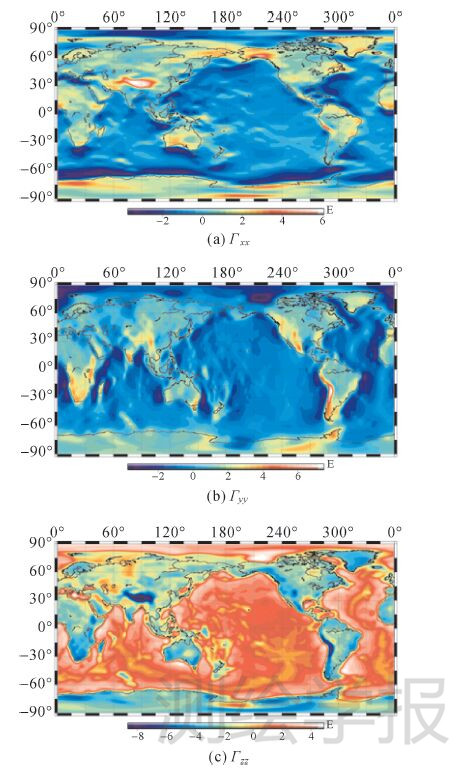
图 4表示在GOCE轨道平均高度扣除长波影响后的Γzz分量结果(1 E=10-9/s2)。如图 4所示,虽然在球谐合成时进行了长波信息滤除,但图 4中的扰动重力梯度图形轮廓变化依旧分明,尤其在青藏高原和安第斯山脉地区表现明显。这说明扰动信息的来源主要是陆地地形起伏,海水补偿密度和地幔及其上部的密度异常等。如表 2 所示,上面提及的扰动源造成的Γzz影响接近1.5E。
图 5反映的是经过陆地地形、海水和冰层校正后的结果。图形轮廓相对比图 4已然发生较大改变,这些显著变化表明陆地和海洋地形是大成分扰动源。其实在地壳厚度粗略估算中,一般也只扣除陆地和海洋地形影响。这些在表 2中也有所体现,Γzz GTBI项极值较于G项数值已扩大3倍以上。
图 6和图 7表现的是沉积层和地壳补偿密度的正演结果。表 3是相应的结果统计。如图 6所示,沉积层不仅在全球范围内分布广泛,而且极值区间也可达2E左右。这是由于虽然沉积层密度相对于岩石密度波动不大,但厚度可达数千米以上。所以该项改正不仅在地壳厚度研究中要加以重视,而且在地幔密度反演中也是一项重要研究。考虑到Moho面实质是同一密度单层厚度反演,地壳中残余密度差影响要尽量消除,而图 7计算就是为解决此问题。如图 7所示,以青藏高原为例,此区平均密度值明显小于正常岩石密度。如表 3所示,由于地壳密度残差造成全球重力梯度影响最大值达到近4E。
表 3 沉积层和地壳补偿密度正演结果统计
Tab. 3 Statistics of forward modelling from sediment and uneven density of crust
| 10-9/s2 |
| Γxx |
| SED | 0.4751 | -1.1635 | -0.0630 | 0.1875
| | CRD | 1.9764 | -0.8131 | 0.4061 | 0.4111 |
|
| Γyy |
| SED | 0.5415 | -0.9757 | -0.0729 | 0.1705
| | CRD | 2.1207 | -0.7716 | 0.4150 | 0.4168 |
|
| Γzz |
| SED | 1.6502 | -0.4457 | 0.1359 | 0.3052
| | CRD | 0.5296 | -3.8028 | -0.8211 | 0.7166 |
|
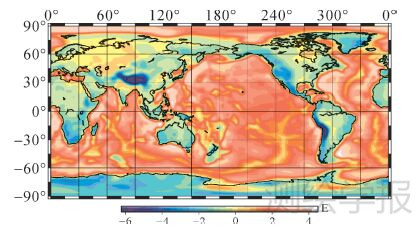
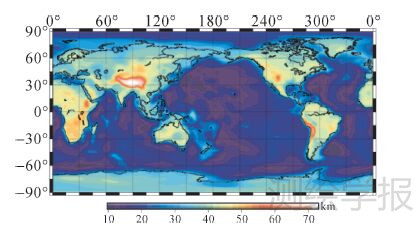
图 8所示是经过全部校正后的结果,也即笔者采用重力梯度测量值进行Moho面反演的初始值。如表 2 所示,在GOCE平均轨道高度最终Moho面信息Γzz分量位于区间[-8.7,4.9]E。图 9表现的是采用文中计算的初始值解算的全球Moho面。结果显示陆地地区Moho面Γzz扰动多为负值,解算的Moho面多大于正常地壳厚度,海洋地区则反之。其中青藏地区由于印度板块和欧亚板块的挤压,呈现明显的边缘浅,中部深的特点。这些结果符合均衡理论,使得Moho面的深度和地形负载呈现强相关性。
4 结 论
依据球坐标系的空间域和频谱域正演方法,结合地壳先验模型,本文讨论了从GOCE重力梯度模型提取Moho面扰动信息的步骤和方法,并提供了适合该层面反演的最终结果。从文中的讨论和数据分析可以得到如下结论:
(1) 在文中1°×1°空间分辨率下,空间域和频谱域方法结果接近,同时也验证了程序和计算的正确性,这两种方法除了适合本文信息提取工作,同时也适用于其他扰动源改正。
(2) 在Moho面扰动信息剥离过程中,陆地地形和海水的影响最大,并且沉积层和地壳密度差的校正不可忽略。
(3) 在通过频域公式恢复的Moho面结果与地震模型和基于GOCE数据已解算的Moho面结果的对比后验证了文中的扰动信息提取计算的可靠性。
致谢:感谢斯图加特大学F.Wild博士、中国地质大学杜劲松博士、米兰理工大学D. Sampietro博士、武汉大学Robert Tenzer教授和中科院测地所方剑教授等在该论文上的帮助。
参考文献
| [1] |
LUO Zhicai. The Theory and Method for the Determination of Earth Gravity Field from Satellite Gravity Gradient Data[D]. Wuhan: Wuhan Technical University of Surveying and Mapping, 1996. (罗志才. 利用卫星重力梯度数据确定地球重力场的理论和方法[D]. 武汉: 武汉测绘科技大学, 1996.)
|
|
| [2] |
HIRT C, KUHN M, FEATHERSTONE W E, et al. Topographic/Isostatic Evaluation of New-generation GOCE Gravity Field Models[J]. Journal of Geophysical Research: Solid Earth (1978-2012), 2012, 117(B5), DOI: 10.1029/2011JB008878.
|
|
| [3] |
EBBING J, BOUMAN J, FUCHS M, et al. Sensitivity of GOCE Gravity Gradients to Crustal Thickness and Density Variations: Case Study for the Northeast Atlantic Region[M]// MARTI U. Gravity, Geoid and Height Systems. Berlin: Springer, 2014: 291-298.
|
|
| [4] |
EVERTON P B. Ouso dos Dados da Missāo GOCE Para a Caracterizaçāo ea Investigaçāo das Implicaçoes na Estrutura de Densidade das Bacias Sedimentares do Amazonas e Solimoes, Brasil[D]. Sāo Paulo: Universidade de Sāo Paulo, 2012.
|
|
| [5] |
ÁLVAREZ O, GIMENEZ M, BRAITENBERG C, et al. GOCE Satellite Derived Gravity and Gravity Gradient Corrected for Topographic Effect in the South Central Andes Region[J]. Geophysical Journal International, 2012, 190(2): 941-959.
|
|
| [6] |
REGUZZONI M, SAMPIETRO D. Moho Estimation Using GOCE Data: A Numerical Simulation[M]// KENYON S, PACINO M C, MARTI U. Geodesy for Planet Earth. Berlin: Springer, 2012: 205-214.
|
|
| [7] |
YANG Ting, FU Rongshan, HUANG Jinshui. On the Inversion of Effective Elastic Thickness of the Lithosphere with Moho Relief and Topography Data[J]. Chinese Journal of Geophysics, 2012, 55(11): 3671-3680. (杨亭, 傅容珊, 黄金水. 利用 Moho 面起伏及地表地形数据反演岩石圈有效弹性厚度的莫霍地形导纳法 (MDDF)[J]. 地球物理学报, 2012, 55(11): 3671-3680.)
|
|
| [8] |
KE Xiaoping, WANG Yong, XU Houze. Moho Depths Inversion of Qinghai-Tibet Plateau with Variable Density Model[J]. Geomatics and Information Science of Wuhan University, 2006, 31(4): 289-292. (柯小平, 王勇, 许厚泽. 用变密度模型反演青藏高原的莫霍面深度[J]. 武汉大学学报: 信息科学版, 2006, 31(4): 289-292.)
|
|
| [9] |
XING Lelin, SUN Wenke, LI Hui, et al. Present-day Crust Thickness Increasing Beneath the Qinghai-Tibetan Plateau by Using Geodetic Data at Lhasa Station[J]. Acta Geodaetica et Cartographica Sinica, 2011, 40(1): 41-44. (邢乐林, 孙文科, 李辉, 等. 用拉萨点大地测量资料检测青藏高原地壳的增厚[J]. 测绘学报, 2011, 40(1): 41-44.)
|
|
| [10] |
ZHANG Chijun, REN Kang. The Undulation between Core and Mantle of Earth from Disturbing Potential[J]. Chinese Journal of Geophysics, 1994, 37(1): 115-119. (张赤军, 任康. 由扰动位确定核幔起伏[J]. 地球物理学报, 1994, 37(1): 115-119.)
|
|
| [11] |
FANG Jian. Global Crustal and Lithospheric Thickness Inversed by Using Satellite Gravity Data[J]. Crustal Deformation and Earthquake, 1999, 19(1): 26-31. (方剑. 利用卫星重力资料反演地壳及岩石圈厚度[J]. 地壳形变与地震, 1999, 19(1): 26-31.)
|
|
| [12] |
SHIN Y H, XU H Z, BRAITENBERG C, et al. Moho Undulations beneath Tibet from GRACE-integrated Gravity Data[J]. Geophysical Journal International, 2007, 170(3): 971-985.
|
|
| [13] |
HU Minzhang, LI Jiancheng, XING Lelin. Global Bathymetry Model Predicted from Vertical Gravity Gradient Anomalies[J]. Acta Geodaetica et Cartographica Sinica, 2014, 43(6): 558-574. (胡敏章, 李建成, 邢乐林. 由垂直重力梯度异常反演全球海底地形模型[J]. 测绘学报, 2014, 43(6): 558-574.)
|
|
| [14] |
LIANG Q, CHEN C, LI Y G. 3D Inversion of Gravity Data in Spherical Coordinates with Application to the GRAIL Data[J]. Journal of Geophysical Research: Planets, 2014, 119(6): 1359-1373.
|
|
| [15] |
TENZER R, BAGHERBANDI M. Reformulation of the Vening Meinesz-Moritz Inverse Problem of Isostasy for Isostatic Gravity Disturbances[J]. International Journal of Geosciences, 2012, 3(5A): 918-929.
|
|
| [16] |
WANG Hansheng, CHENXue, YANGHongzhi. An Iterative Method for Inversion of Deep Large-scale Single Density Interface by Using Gravity Anomaly Data[J]. Chinese Journal of Geophysics, 1993, 36(5): 643-650. (汪汉胜, 陈雪, 杨洪之. 深部大尺度单一密度界面重力异常迭代反演[J]. 地球物理学报, 1993, 36(5): 643-650.)
|
|
| [17] |
SJÖBERG L E. Solving Vening Meinesz-Moritz Inverse Problem in Isostasy[J]. Geophysical Journal International, 2009, 179(3): 1527-1536.
|
|
| [18] |
SJÖBERG L E. On the Isostatic Gravity Anomaly and Disturbance and Their Applications to Vening Meinesz-Moritz Gravimetric Inverse Problem[J]. Geophysical Journal International, 2013, 193(3): 1277-1282.
|
|
| [19] |
GROMBEIN T, SEITZ K, HECK B. Untersuchungen zur Effizienten Berechnung Topographischer Effekte auf den Gradiententensor am Fallbeispiel der Satellitengradiometriemission GOCE[M]. [S.l.]: KIT Scientific Publishing, 2010.
|
|
| [20] |
WILD F, HECK B. Topographic and Isostatic Reductions for Use in Satellite Gravity Gradiometry[C]// XU P L, LIU J N, DERMANIS A. VI Hotine-Marussi Symposium on Theoretical and Computational Geodesy. Berlin: Springer, 2008: 49-55.
|
|
| [21] |
NOVÁK P, GRAFAREND E W. The Effect of Topographical and Atmospheric Masses on Spaceborne Gravimetric and Radiometric Data[J]. Studia Geophysica et Geodaetica, 2006, 50(4): 549-582.
|
|
| [22] |
TENZER R, HAMAYUN K, VAJDA P. Global Maps of the CRUST 2.0 Crustal Components Stripped Gravity Disturbances[J]. Journal of Geophysical Research: Solid Earth (1978-2012), 2009, 114(B5), DOI: 10. 1029/2008 JB006016.
|
|
| [23] |
TENZER R, HAMAYUN, NOVÁK P, et al. Global Crust-Mantle Density Contrast Estimated from EGM2008, DTM2008, CRUST2. 0, and ICE-5G[J]. Pure and Applied Geophysics, 2012, 169(9): 1663-1678.
|
|
| [24] |
LASKE G, MASTERS G, MA Z T, et al. Update on CRUST1.0-A 1-degree Global Model of Earth’s Crust[C]// Proceedings of EGU General Assembly Conference Abstracts. Vienna, Austria: [s.n.], 2013: 15-26.
|
|
| [25] |
BAGHERBANDI M, SJBERG L E. Non-isostatic Effects on Crustal Thickness: A Study Using CRUST2.0 in Fennoscandia[J]. Physics of the Earth and Planetary Interiors, 2012, 200-201(1): 37-44.
|
|
| [26] |
REGUZZONI M, SAMPIETRO D. Moho Estimation Using GOCE Data: A Numerical Simulation[M]// KENYON S, PACINO M C, MARTI U. Geodesy for Planet Earth. Berlin: Springer, 2012: 205-214.
|
|
| [27] |
AMANTE C, EAKINS B W. ETOPO1 1 Arc-minute Global Relief Model: Procedures, Data Sources and Analysis[R]. National Geophysical Data Center. Washington D C: NOAA, 2009.
|
|
| [28] |
ZHU L Z. Gradient Modelling with Gravity and DEM[D]. Columbus, Ohio: The Ohio State University, 2007.
|
|
| [29] |
TSOULIS D. A Comparison between the Airy/Heiskanen and the Pratt/Hayford Isostatic Models for the Computation of Potential Harmonic Coefficients[J]. Journal of Geodesy, 2001, 74(9): 637-643.
|
|
| [30] |
MAYER-GVRR T, The GOCO Consortium: The New Combined Satellite only Model GOCO03s[J]. Journal of Geodesy, 2012,87(9): 843-867.
|
|
文章信息
- 叶周润,柳林涛,梁星辉
- YE Zhourun,LIU Lintao,LIANG Xinghui
- Moho面扰动重力梯度信息的提取
- The Signal Extraction of Gravity Gradient Disturbance on Moho
- 测绘学报,2015,44(6):609-615
- Acta Geodaeticaet Cartographica Sinica,2015,44(6): 609-615.
- http://dx.doi.org/10.11947/j.AGCS.2015.20140015
-
文章历史
- 收稿日期:2014-01-16
- 修回日期:2015-03-15
相关文章
工作空间