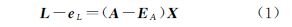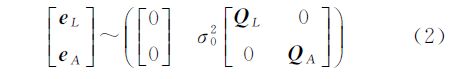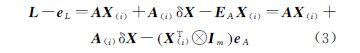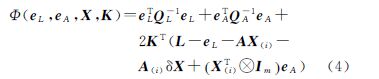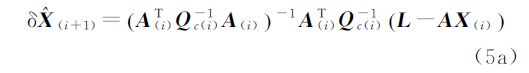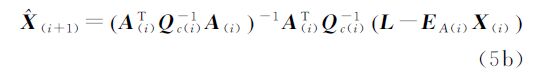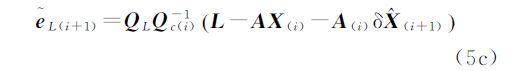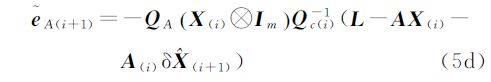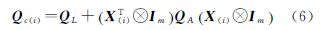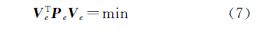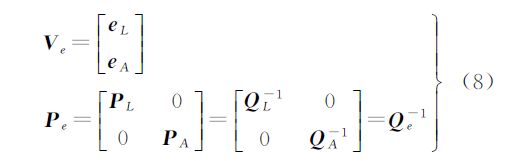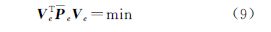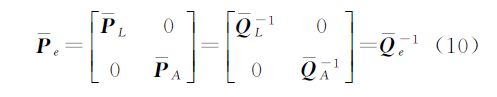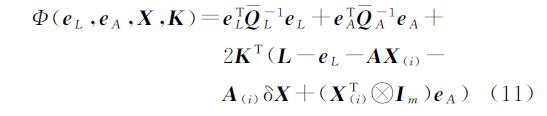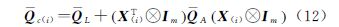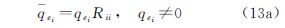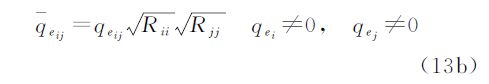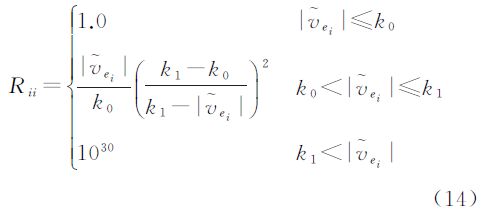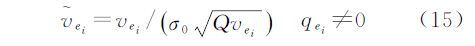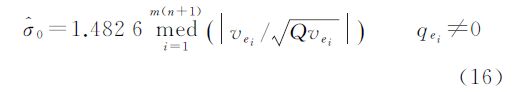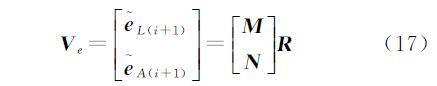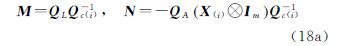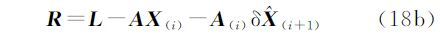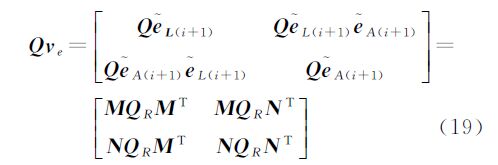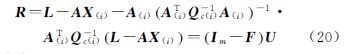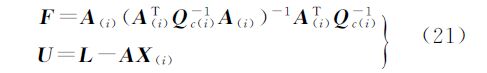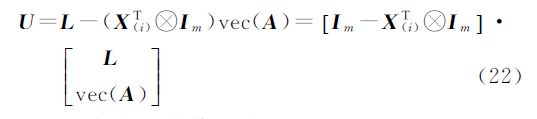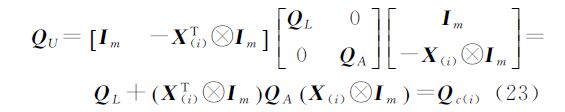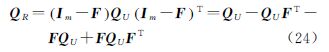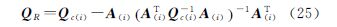2. 中国矿业大学环境与测绘学院，江苏 徐州 221116；
3. 安徽理工大学测绘学院，安徽 淮南 232001
2. School of Environment Science and Spatial Informatics,China University of Mining and Technology,Xuzhou 221116,China;
3. School of Geodesy and Geomatics,Anhui University of Science and Technology,Huainan 232001,China
1 引 言
整体最小二乘(TLS)方法可以有效解决系数矩阵含有误差的参数估计问题，得到了国内外学者的广泛关注，并取得了较为理想的结果[1, 2,3,4,5]。近几年，针对实践中观测值不等精度的问题，国内外学者对于加权整体最小二乘(WTLS)的算法及应用进行了深入研究。文献[6]将不等精度条件下的变量误差(EIV)模型的函数模型作为限制条件，通过构造拉格朗日函数的方式推导了WTLS的迭代算法，并应用到了线性回归中；文献[7]利用高斯-赫尔默特模型研究了WTLS的计算方法，并将其应用于平面坐标转换中；文献[8]引入非线性最小二乘的牛顿-高斯(Newton-Gauss)法，获得了WTLS的迭代算法；文献[9]也从非线性最小二乘的角度入手，研究了WTLS的解算方法并推广到了partial-EIV模型中，有效地减少了未知数的数量。
以上研究都是针对系数矩阵和观测向量中仅包含偶然误差的情况，当系数阵和观测向量受到粗差污染时，参数估值必将受到不利影响，有时甚至会严重失真。国内外对于经典最小二乘的粗差处理方法已经进行了深入研究，采用的方法大致可分为基于均值漂移的粗差探测[10, 11]和基于方差-协方差膨胀的抗差估计[12,13,14, 15,16,17]两大类。相对于粗差探测技术，抗差估计的实现通常更为简单，其关键是权因子函数的构造。一个合理的抗差方案应能同时顾及观测空间和结构空间抗差，为达到这一目的通常应采用标准化残差构造权因子函数[13]。
目前，关于整体最小二乘的粗差处理方法的研究还较少。文献[18—19]基于高斯-赫尔默特模型和Huber权函数提出了三维坐标转换的稳健WTLS方法。文献[20]对稳健混合TLS方法进行了研究。文献[21]将文献[18—19]中的Huber权函数替换成了IGG函数，并通过试验验证了该方法的优势。然而，上述关于WTLS的粗差处理方法存在着共同的问题：直接采用残差构造权因子函数，无法顾及结构空间的抗差性，模型不够合理，特别在非等精度的情况下抗差效果并不理想。本文基于WTLS的Newton-Gauss迭代算法[8]，借鉴一般抗差估计的等价权原理，提出一种抗差加权整体最小二乘(RWTLS)模型，采用标准化残差构造权因子函数，并利用中位数法获得具有抗差性的单位权中误差估值。在模型构建过程中，对权因子的计算和等价权的更新、系数阵固定元素的处理等关键问题进行了研究。为获得标准化残差，利用线性近似的协因数传播律推导了WTLS残差协因数阵的表达式，并给出了迭代计算方法。该算法在观测空间和结构空间均具有良好的抗差能力。
2 基于Newton-Gauss法的WTLS迭代算法EIV模型的函数模型为
式中，L为m×1维的观测向量; A为m×n维的系数矩阵，rank(A)=n＜m；eL是L的随机误差向量；EA为A的随机误差矩阵；X为n×1维的未知参数向量。
相应的随机模型为
式中，eA =vec(EA )，vec 表示矩阵的列向量化算子，是将矩阵的每一列按从左到右的顺序堆叠；QL和QA分别为eL和eA的协因数阵，其维数分别为m×m和mn×mn；σ0为单位权中误差。
设在第i次迭代计算后，获得的参数估值为X(i)，预测残差矩阵为EA(i)，将式(1)右端在(X(i),EA(i))处利用泰勒级数展开
式(3)省略了二阶以上的部分，仅保留一阶项。式中，δX为X(i)的微小改正值，且A(i)=A－EA(i);Im表示m阶单位阵。
结合EIV模型的参数估计准则，可构造出WTLS的拉格朗日目标函数[8]
利用Euler-Lagrange必要条件，对各变量求导并令导数为零可得
式中
将最小二乘的参数估值作为初值，按照式(5a)—式(5d)所描述的迭代过程进行计算，当满足||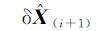
||＜ε0(ε0是给定的小正数)时停止迭代，即可获得参数的WTLS解。
3 基于Newton-Gauss法的RWTLS的基本原理和算法 3.1 RWTLS的基本原理
将EIV模型的参数估计准则写成式(7)的形式
式中
这与经典最小二乘估计准则的形式相同，当观测向量L和系数阵A含有粗差时，难以获得准确的参数解。为此，本文借鉴一般抗差估计的等价权原理，提出RWTLS模型，以式(9)作为估计准则
式中
式中，PL和PA分别是观测向量和系数阵的等价权阵;QL和QA可称为观测向量和系数阵的等价协因数阵。以此构造以下的拉格朗日目标函数
利用Euler-Lagrange必要条件可解出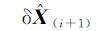、X(i+1)、
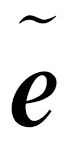L(i+1)和,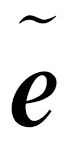A(i+1)，形式与式(5a)—式(5d)完全相同，只需将QL、QA和Qc(i)分别替换为QL、QA和Qc(i)，其中
在WTLS方法的迭代计算过程中，先验协因数阵QL和QA始终保持不变。RWTLS算法与之不同，为了达到抵抗粗差的效果，等价协因数阵QL和QA需要在迭代过程中不断更新。
根据等价权抗差原理，在迭代计算过程中需要利用权因子函数计算等价权阵Pe，而计算公式中需要的是等价协因数阵Qe(QL和QA)，为了方便计算，当观测值相互独立时，采用式(13)直接获得Qe
相关观测条件下，为保持观测值间的相关性不变，采用双因子模型[15, 16]的形式
式中，下标i和j表示观测值序号；qeij和qeij分别表示<Qe和Qe中对应位置的元素；Rii和Rjj为相应权因子的倒数，这里称之为协因数因子。式(13a)—(13b)两边同时乘以单位权方差因子就是异常观测方差膨胀模型，这与直接计算等价权阵e的方式是完全等价的[15]。需要注意的是，这里应加入i和j的限制条件为对应的先验协因数不为零，如果系数阵中含有固定元素，则对应位置的先验协因数为零，在平差后不参与误差分配，就不存在更新权的问题。
对于IGG Ⅲ的权因子函数，对其求倒数便可获得对应的协因数因子函数
由于IGG Ⅲ函数的第3段为0，对应协因数因子的理论值应为无穷，为了方便实际计算，用一个大数(1030)代替，这样在数值计算上完全能够满足要求。k0和k1为常数，实际中通常可分别取k0=2.0～3.0，k1=4.0～8.0。直接利用残差构造的权因子(或协因数因子)函数没有考虑结构空间的抗差性，难以保证良好的抗差性能，式(14)采用标准化残差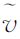
ei进行构造在理论上更加合理，而且不受先验单位权中误差取值的影响。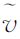ei的计算公式为<
式中，σ0为单位权中误差;υei表示残差向量Ve的第i个元素，在迭代计算过程中不断更新。在一般的标准化残差抗差估计模型中，是利用各最小二乘残差的协因数来计算标准化残差的，而这里的Qυei代表第i个WTLS残差的协因数。由于传统的计算公式获得的σ0估值受粗差的影响较大，本文引入一般抗差估计模型中采用的中位数法[12]获得具有抗差性的单位权中误差估值，计算公式为
需要注意的是,式(15)和式(16)都应加入i 的限制条件(qei ≠0).
3.2 WTLS残差协因数阵的推导在一般的抗差估计模型中，LS残差的协因数阵很容易获得。然而由于EIV模型的非线性特性以及WTLS算法本身的复杂性，相应协因数阵的获得较为困难。针对此问题，本文利用线性的近似协因数传播律推导残差协因数阵的表达式。
根据式(5c)、式(5d)，WTLS方法在第i+1次迭代计算后得到的残差向量Ve可表示为
式中
在Newton-Gauss法的第i+1次迭代计算过程中，A(i)、X(i)是作为固定值处理的，因此仅认为系数阵A和观测向量L有误差。根据协因数传播律可得
由式(19)可知求解Qνe要先获得QR。将式(5a)代入式(18b)，可得
式中
对U作如下变换
根据协因数传播律可得
又由式(20)可知
将式(21)和式(23)代入式(24)并整理可得
将式(25)代入式(19)便可获得残差协因数阵Qνe。由于计算标准化残差时只需要各残差的协因数，因此只需分别计算出QêL(i+1)和QêA(i+1)并取其对角线上的元素。
在一般的抗差估计模型中，最小二乘残差的协因数阵只与系数矩阵和观测向量的先验权阵(或协因数阵)有关，因此其在迭代过程中保持不变。然而上述推导获得的WTLS残差协因数阵不仅取决于先验协因数阵QL和QA，还与本次计算所代入的参数和系数阵残差的初值X(i)和EA(i)(A(i)由EA(i)计算所得)有关。因此RWTLS与一般抗差估计方法不同，在每迭代一次后计算标准化残差时，均应将先验协因数阵QL、QA以及本次迭代所代入的参数和系数阵残差的初值代入式(19)来更新WTLS方法对应的残差协因数阵。
3.3 RWTLS的迭代计算步骤将WTLS得到的参数估值和残差向量作为初值，按照以下步骤进行RWTLS迭代计算：
(1) 将第k次迭代中参数和系数阵残差的初值(第k-1次迭代计算的结果)以及先验协因数阵QL和QA代入式(25)和式(19)以更新相应的WTLS残差协因数阵。
(2) 将残差向量和步骤(1)获得的WTLS残差协因数代入式(16)和式(15)获得第k次迭代的标准化残差。
(3) 利用式(13)和式(14)更新QL和QA，进而获得第k+1次迭代的参数估值和残差向量。
p> 反复进行步骤(1)—步骤(3)，直到满足||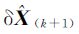
||＜ε0(ε0是给定的小正数)时停止迭代计算，此时便能获得参数的RWTLS解。
4 算例分析设一直线方程为y=4x+3，设待估参数分别为截距a和斜率b，则对应的真值分别为3和4。
在此直线上选取26个观测点，事先分别给定各点x和y坐标的标准差(非等精度)，每次模拟均根据相应的标准差产生模拟随机误差并加入到各点的坐标真值中。
指定粗差的位置随机产生(可能同时出现在某点的x和y坐标上)，其绝对值介于10～30倍的标准差之间，分别在粗差个数为1、2和3个时进行500次模拟，每次均加入到含有随机误差的观测数据中。先验单位权中误差σ0=0.2，设计的计算方案如下：加入粗差前进行WTLS估计(方案①)；加入粗差后，依次采用WTLS方法(方案②)、文献[21]的RWTLS-IGG方法(方案③)和本文提出的RWTLS方法处理(方案④)。
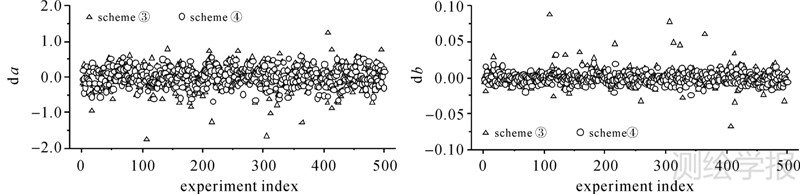
对各方案的计算结果进行统计分析，得到参数a和b的均方根误差及其与真值的最大偏差，见表 1。图 1,图 2,图 3为上述不同粗差个数情况下方案③和方案④的试验序列对比图，纵轴da和db分别表示参数估值a和b与其真值的偏差量。
| 粗差 个数 | 计算 方案 | RMSE (a) | a最大 偏差 | RMSE (b) | b最大 偏差 |
| 1 | ① | 0.238 7 | 0.690 5 | 0.006 5 | 0.019 8 |
| ② | 0.752 2 | 2.974 2 | 0.019 5 | 0.088 3 | |
| ③ | 0.325 7 | 1.761 1 | 0.011 5 | 0.088 4 | |
| ④ | 0.253 0 | 0.669 7 | 0.007 2 | 0.032 7 | |
| 2 | ① | 0.238 6 | 0.854 2 | 0.006 4 | 0.023 6 |
| ② | 0.995 6 | 3.787 9 | 0.026 7 | 0.103 6 | |
| ③ | 0.404 0 | 1.993 2 | 0.016 2 | 0.095 7 | |
| ④ | 0.268 8 | 0.979 6 | 0.007 8 | 0.037 6 | |
| 3 | ① | 0.243 4 | 0.787 9 | 0.006 7 | 0.020 6 |
| ② | 1.145 1 | 3.819 7 | 0.031 4 | 0.124 6 | |
| ③ | 0.496 3 | 2.046 8 | 0.020 4 | 0.097 5 | |
| ④ | 0.275 8 | 1.022 4 | 0.008 4 | 0.036 3 |
|
| 图 1 粗差个数为1时方案③和方案④的对比 Fig. 1 Comparison between schemes③ and ④ when there exists one gross error |
|
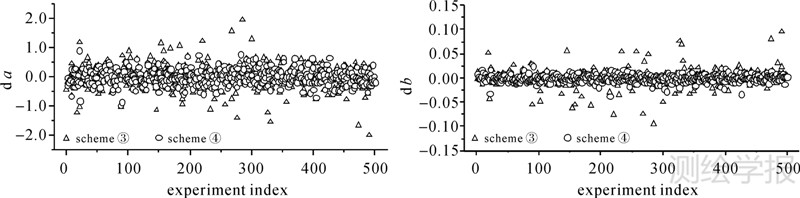
| 图 2 粗差个数为2时方案③和方案④的对比 Fig. 2 Comparison between schemes ③ and ④ when there exist two gross errors |
|
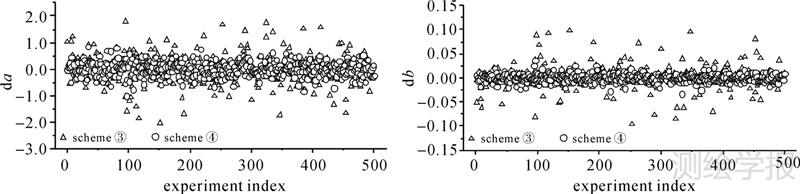
| 图 3 粗差个数为3时方案③和方案④的对比文标题 Fig. 3 Comparison between scheme ③ and ④ when there exist three gross errors |
根据表 1和图 1,图 2,图 3的结果可以得到以下结论：
(1) 无粗差时WTLS方法(方案①)的估计结果在4种计算方案中是最优的。然而当观测数据受到粗差污染时，WTLS方法(方案②)的参数估值受到了破坏性的影响，与真值产生了很大的偏差。
(2) 方案③和方案④的估计结果较方案②在整体上均有较大的改善，但方案④较方案③明显更优。当粗差个数分别为1、2和3个时，方案④所得参数a的均方根误差分别为方案③的77.6%、66.5%和55.6%，参数b的均方根误差分别为方案③的62.6%、48.1%和41.2%。不难发现，随着粗差个数的增多，方案③获得的各参数均方根误差显著增大，方案④较方案③的优势也更为明显。在500次的模拟过程中，方案③的参数估值多次与真值产生了较大的偏差，而方案④所获得的参数最大偏差值仍然较小。
(3) 方案④所得参数估值的准确度虽不及方案①，但总的来说差异并不显著，参数解仍然准确可靠。
得到上述结果的原因是：方案②的WTLS方法不具备抵抗粗差的能力；方案③的RWTLS-IGG方法虽然具有一定的抗差能力，但其直接采用残差构造的权因子函数无法顾及结构空间的抗差性，在理论上存在一定的缺陷；本文提出的RWTLS方法(方案④)采用标准化残差构造权因子函数，并由中位数法获得单位权中误差估值，在观测空间和结构空间均具有良好的抗差能力，在理论上较方案③更为合理。
表 2是500次模拟试验中方案③和方案④对粗差点的识别情况，分别统计了不同粗差个数条件下，粗差点识别正确(不存在漏判和误判)的次数和正确率。由表 2的结果可知：随着粗差个数的增加，方案③和方案④的粗差点识别正确率均有所降低，但在不同的粗差个数条件下，方案④的正确率始终显著高于方案③，从而进一步验证了方案④的优势。
| 粗差个数 | 计算方案 | 正确识别次数 | 正确率/(%) |
| 1 | ③ | 114 | 22.8 |
| ④ | 362 | 72.4 | |
| 2 | ③ | 95 | 19.0 |
| ④ | 315 | 63.0 | |
| 3 | ③ | 73 | 14.6 |
| ④ | 260 | 52.0 |
综上所述，在受到粗差污染的加权整体最小二乘问题中，本文提出的RWTLS模型的抗差性能优于文献[21]中的RWTLS-IGG方法。
5 结 语针对加权整体最小二乘的粗差处理问题，本文在WTLS的Newton-Gauss迭代法基础上，提出了一种抗差加权整体最小二乘模型。采用标准化残差构造权因子函数，并利用中位数法获得具有抗差性的单位权中误差估值。为获得标准化残差，利用线性近似的协因数传播律推导了WTLS残差协因数阵的表达式，并给出了迭代计算方法。得到结论：
(1) 由标准化残差构造的权因子函数同时实现了观测空间和结构空间抗差，利用中位数法获得的单位权中误差估值在迭代过程中具有更好的稳健性，较已有的稳健WTLS方法在理论上更加合理。
(2) 试验结果表明：当粗差个数分别为1、2和3个时，本文提出的RWTLS算法的粗差点识别正确率分别为文献[21]中RWTLS-IGG方法的3.2倍、3.3倍和3.6倍；所得参数a的均方根误差分别为该方法的77.6%、66.5%和55.6%，b的均方根误差分别为该方法的62.6%、48.1%和41.2%。粗差识别能力和参数估值的准确度均有显著改善。
| [1] | FELUS Y A. Application of Total Least Squares for Spatial Point Process Analysis[J]. Journal of Surveying Engineering, 2004, 130(3): 126-133. |
| [2] | SCHAFFRIN B, LEE I, FELUS Y, et al. Total Least-squares (TLS) for Geodetic Straight-line and Plane Adjustment[J]. Bollettino di Geodesia e Scienze Affini, 2006, 65(3): 141-168. |
| [3] | MARKOVSKY I, VAN HUFFEL S. Overview of Total Least Squares Methods[J]. Signal Processing, 2007, 87(10): 2283-2302. |
| [4] | SCHAFFRIN B, FELUS Y A. On the Multivariate Total Least-squares Approach to Empirical Coordinate Transformations: Three Algorithms[J]. Journal of Geodesy, 2008, 82(6): 373-383. |
| [5] | CHEN Yi, LU Jue, ZHENG Bo. Application of Total Least Squares to Space Resection[J]. Geomatics and Information Science of Wuhan University, 2008, 33(12): 1271-1274. (陈义, 陆珏, 郑波. 总体最小二乘方法在空间后方交会中的应用[J]. 武汉大学学报: 信息科学版, 2008, 33(12): 1271-1274.) |
| [6] | SCHAFFRIN B, WIESER A. On Weighted Total Least-squares Adjustment for Linear Regression[J]. Journal of Geodesy, 2008, 82(7): 415-421. |
| [7] | NEITZEL F. Generalization of Total Least-squares on Example of Unweighted and Weighted 2D Similarity Transformation[J]. Journal of Geodesy, 2010, 84(12): 751-762. |
| [8] | SHEN Y Z, LI B F, CHEN Y. An Iterative Solution of Weighted Total Least Squares Adjustment[J]. Journal of Geodesy, 2011, 85(4): 229-238. |
| [9] | XU P L, LIU J N, SHI C. Total Least Squares Adjustment in Partial Errors-in-variables Models: Algorithm and Statistical Analysis[J]. Journal of Geodesy, 2012, 86(8): 661-675. |
| [10] | BAARDA W. A Testing Procedure for Use in Geodetic Networks[J]. Netherlands Geodetic Commission Publication on Geodesy: New Series, 1968, 2(5): 45-53. |
| [11] | OU Jikun. A New Method to Detect Gross Errors—Quasi-accurate Detection Method[J]. Chinese Science Bulletin, 1999, 44(16): 1777-1781. (欧吉坤. 一种检测粗差的新方法——拟准检定法[J]. 科学通报, 1999, 44(16): 1777-1781.) |
| [12] | ROUSSEEUW P J, LEROY A M. Robust Regression and Outlier Detection[M]. New York: John Wiley and Sons, 1987. |
| [13] | ZHOU Jiangwen, HUANG Youcai, YANG Yuanxi, et al. Robust Least Squares Method[M]. Wuhan: Huazhong University of Science and Technology Press, 1997. (周江文, 黄幼才, 杨元喜, 等. 抗差最小二乘法[M]. 武汉: 华中理工大学出版社, 1997.) |
| [14] | YANG Y. Robust Estimation of Geodetic Datum Transformation[J]. Journal of Geodesy, 1999, 73(5): 268-274. |
| [15] | YANG Yuanxi, SONG Lijie, XU Tianhe. Robust Parameter Estimation for Geodetic Correlated Observations[J]. Acta Geodaetica et Cartographica Sinica, 2002, 31(2): 95-99. (杨元喜, 宋力杰, 徐天河. 大地测量相关观测抗差估计理论[J]. 测绘学报, 2002, 31(2): 95-99.) |
| [16] | YANG Y X, SONG L J, XU T H. Robust Estimator for Correlated Observations Based on Bifactor Equivalent Weights[J]. Journal of Geodesy, 2002, 76(6-7): 353-358. |
| [17] | XU P L. Sign-constrained Robust Least Squares, Subjective Breakdown Point and the Effect of Weights of Observations on Robustness[J]. Journal of Geodesy, 2005, 79(1-3): 146-159. |
| [18] | CHEN Yi, LU Jue. Performing 3D Similarity Transformation by Robust Total Least Squares[J]. Acta Geodaetica et Cartographica Sinica, 2012, 41(5): 715-722. (陈义, 陆珏. 以三维坐标转换为例解算稳健总体最小二乘方法[J]. 测绘学报, 2012, 41(5): 715-722.) |
| [19] | LU J, CHEN Y, LI B F, et al. Robust Total Least Squares with Reweighting Iteration for Three-dimensional Similarity Transformation[J]. Survey Review, 46(334): 28-36. |
| [20] | GONG Xunqiang, LI Zhilin. A Robust Mixed LS-TLS Based on IGGII Scheme[J]. Geomatics and Information Science of Wuhan University, 2014, 39(4): 462-466. (龚循强, 李志林. 一种利用IGG Ⅱ方案的稳健混合总体最小二乘方法[J]. 武汉大学学报: 信息科学版, 2014, 39(4): 462-466.) |
| [21] | GONG Xunqiang, LI Zhilin. A Robust Weighted Total Least Squares Method[J]. Acta Geodaetica et Cartographica Sinica, 2014, 43(9): 888-894. (龚循强, 李志林. 稳健加权总体最小二乘法[J]. 测绘学报, 2014, 43(9): 888-894.) |