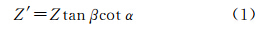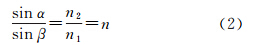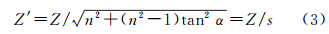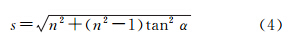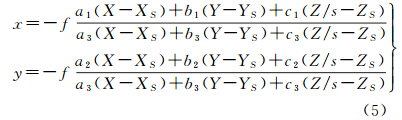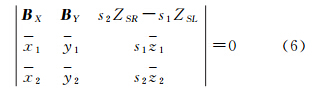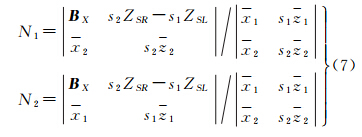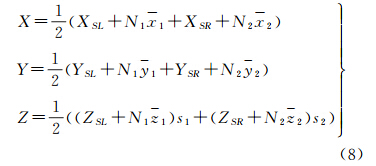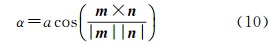2. 中测新图(北京)遥感技术有限责任公司,北京 100039;
3. 河南理工大学,河南 焦作 454000
2. China TopRS Technology Co.Ltd, Beijing 100039, China;
3. Henan Polytechnic University, Jiaozuo 454000, China
双介质摄影测量[1, 2]是指所摄物体同摄影机处于不同介质中,成像光线必须穿过两种不同的介质,利用物方空间和像方空间处在两种不同介质中拍摄的图像确定被摄目标几何特性的技术。其基本理论和方法在经典的摄影测量教科书中亦有系统介绍,在理论研究及实际应用中,又分为两种,一种是相机位于水中[3, 4, 5, 6](即近景摄影测量范畴),主要为水下考古、水生物学、探坝、水文学、核反应器探查和水下近景变形测量等学科提供测量手段;另一种是相机位于空中(即航空摄影测量范畴)。相对于水下双介质摄影测量,航空双介质摄影测量的实际应用并没有广泛开展,但在理论研究上并没有驻足:文献[7]推导了适于解析处理的双介质摄影测量基本公式;文献[8]进行了水下近景摄影测量的双介质多片空间后方交会及前方交会研究;文献[9]提出了双介质摄影测量相对定向的试验流程;文献[10]探究了基于POS数据的双介质相对定向和直接定向。美国海洋测量局于20世纪90年代就开始了近岸、海岛礁、浅滩等周边海域的航空摄影水下地形探测和水深测量工作,在当时的航空摄影技术和成像条件下,其测量深度可达到5.5 m,透明水域能达到20 m。
航空双介质摄影测量探测深度有限,探测精度相对较低,但其空间分辨率高,相对于其他水深测量技术(声呐、激光等),对描述海底地貌特征、建立三维景观模型具有突出优势。由于技术和条件的限制,开展双介质摄影测量研究相对较少。本文基于低空无人机航空影像,进行航空双介质水下礁盘深度测量试验研究。首先简单介绍了航空双介质摄影测量的基本原理;接着详述了试验流程、关键技术问题及试验结果与分析。
2 双介质摄影测量原理
2.1 双介质摄影测量基本公式
图 1为双介质摄影测量构像图,其中水下地形摄影测量物点A(X,Y,Z),像点a(x,y)及摄影中心S(XS,YS,ZS)。与传统摄影测量不同,双介质摄影测量的物点、像点、摄影中心不共线。取摄影测量坐标系的平面XOY与当地水平面平行,Z轴垂直于平面XOY,假设海面与当地水平面平行。图中水下点A(X,Y,Z)经过折射构象于a(x,y)。由折射原理知,对应像点a(x,y)在单介质下交会的点为A'(X,Y,Z'),其位于A(X,Y,Z)的垂直上方,平面坐标相等。
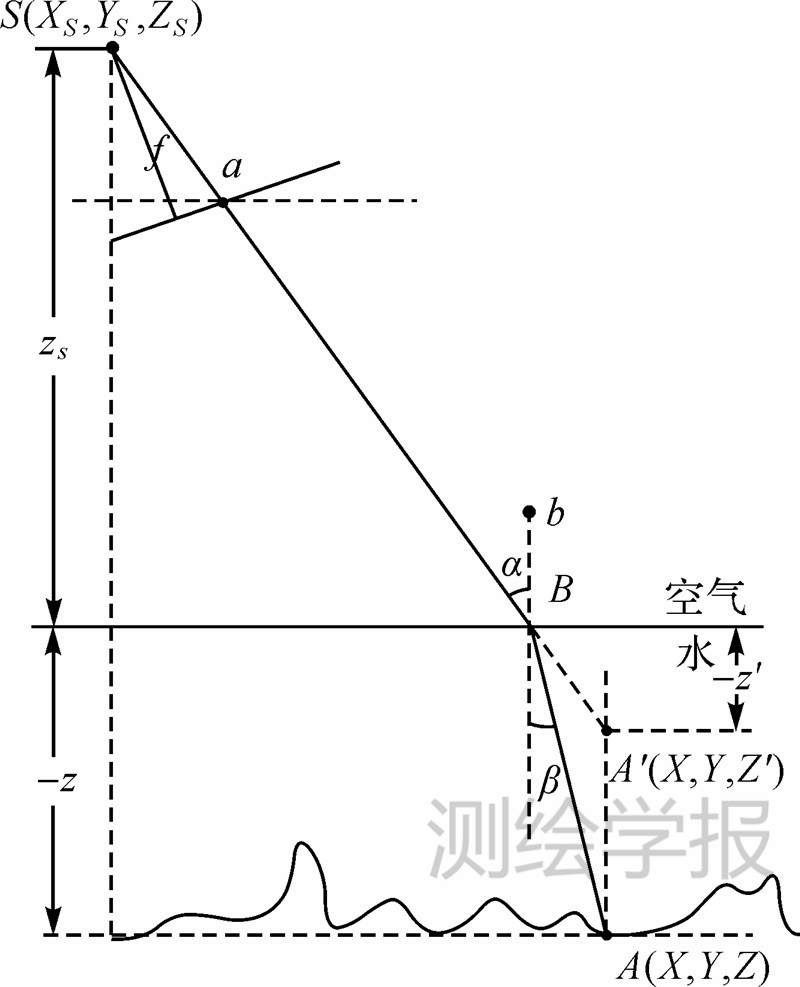 |
| 图 1 双介质摄影测量构象图Fig. 1 Constellation-diagram of two-media photogrammetry |
2.1.1 共线条件方程
由图 1可知
由折射定律知
式中,α为入射角;β为折射角;n1为第一介质折射率,n2为第二介质折射率;把空气的折射率视为1,n就为介质分界面之下介质的折射率。由式(1)、式(2)得
式中 式(3)和式(4)中,s为该点由折射引起的高程改正系数,它是相对折射率n和入射角α的函数,每个像点对应一个值。结合式(3)和传统共线条件方程可得双介质共线条件方程为2.1.2 共面条件方程
像空间辅助坐标系是以左摄影中心为坐标原点,地面摄测坐标系以平行于介质面某一点为坐标原点;(XSL,YSL,ZSL)、(XSR,YSR,ZSR)分别为左右摄影中心坐标;s1、s2分别为左右影像像点的高程改正系数;f为相机主距;(x1, y1, z1)、(x2, y2, z2)分别为左、右影像像点的像空间坐标系坐标;令BX=XSR-XSL、BY=YSR-YSL、BZ=ZSR-ZSL,则双介质摄影测量的共面条件方程为
2.1.3 左右影像同名像点的投影系数
由式(6),按照传统方法计算左右影像同名点投影系数,得
2.1.4 前方交会公式
2.2 对海水折射率的精度要求
由于本文是基于环海岛周边海域航空影像的试验,因此需要分析一下对式(2)中的第二介质即海水折射率的精度要求。
将式(3)对折射率微分,并转换为误差形式,得折射率误差对双介质摄影水深测量的影像关系如下[11, 12, 13]
式中,n=4/3。双介质摄影水深测量误差可用σZ′表示。由式(9)可知,当入射角和折射率误差一定时,水深测量误差与水深值随着水深值的增加而增长。取Z为双介质摄影测量最大探测理论的深度30 m,水深测量误差范围为0~0.45 m,并以0.05 m递增,入射角范围为0°~10°,同时限定水深测量误差和入射角,得出水深测量误差、入射角和折射率误差之间的关系,见图 2。从图中可以看出,入射角对水深测量误差基本上没有影响。利用式(9),入射角随意取0°~10°的某一个值,实测水深取30 m,折射率误差小于0.003和实测水深取10 m,折射率误差小于0.01时,双介质水深测量误差达到百分位,即实测水深的百分之几,可忽略不计。另外由于海水折射率会随海水温度、盐度、工作波段和压力等4个方面的影响,但对于航空双介质摄影测量所能探测的浅海海域而言,主要考虑海水温度和盐度两个因素,一般来说,准确计算海水折射率的话,会精确到千分位,甚至为万分位。
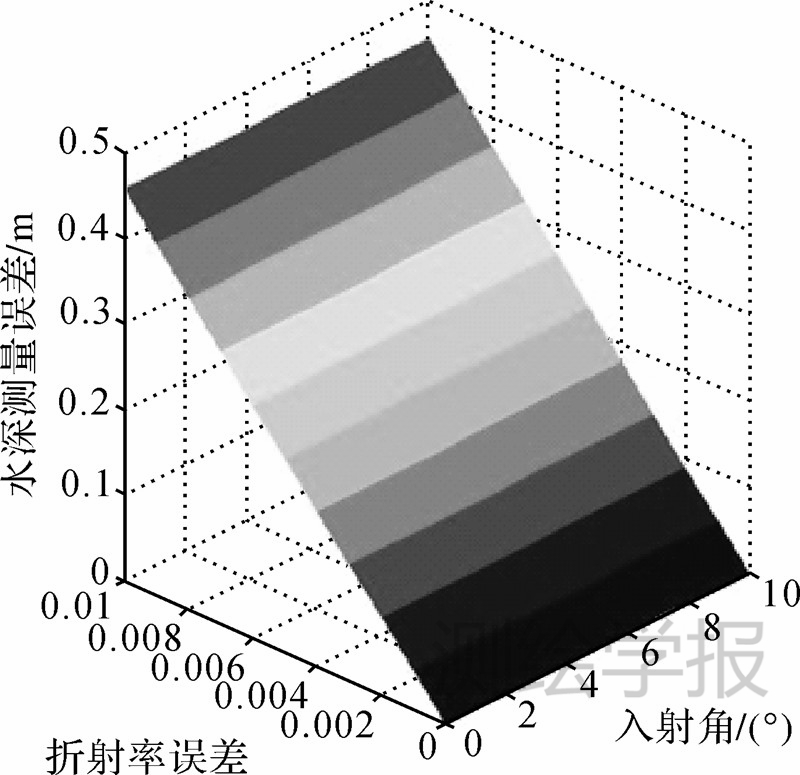 |
| 图 2 水深30 m时双介质水深测量误差随折射率误差和入射角变化的关系Fig. 2 Two-media water depth measurement error with the refractive index changes in the relationship between errors and the angle of incidence,when water depth is 30 m |
因此,海水折射率误差对双介质水深测量影响不大,取n=4/3基本能满足测量需求。
2.3 高程改正系数求解
由式(4)可知,高程改正系数是折射率n和入射角α的函数,由2.2节分析可知折射率取为4/3,故高程改正系数的求解就是对入射角α的求解。
由图 1可知入射角α是入射光线aB与垂直于介质面(空气和海水的分界线)bB的夹角,将aB与bB同置于像空间辅助坐标系下,并分别看作为向量,aB等同于Sa在像空间辅助坐标下的表示,记作m;bB等同于竖直方向的单位向量n(模为1)在像空间辅助坐标系下的表示,且方向都向下,借助求两向量夹角之间的公式得
式中,向量m可由像点a的像空间坐标与旋转矩阵相乘得到像点a在像空间辅助坐标系下的坐标,由于S为像空间辅助系的原点,故所求得像点a的坐标也是Sa在像空间辅助坐标下的向量表达,单位向量n为(0,0,-1)。利用式(10)求得入射角后,再将α代入式(4)中分别求得左右相片同名像点的高程改正系数值。由于基于同名像点的光线角度各不相同,按照上述原理分别求得相片同名点对应左右相片高程改正系统值。
由式(10)知,影响求取影像上某一点光线入射角精度因素的是对应像点坐标精度和影像获取时的姿态精度。对于海岛无人机航摄而言,这两个因素取决于整个测区稀少控制的空三精度。如果空三精度高,表明外方位元素精度高,而对于水下同名像点坐标的获取,也是基于空三成果构建的立体模型(下文会有详细介绍),然后对某些特征点进行采集,获取左右像点坐标。
3 试验与分析
3.1 试验数据
3.1.1 无人机航空影像
本试验采用的是环西沙群岛东部的某岛周边海域的无人机航空影像,地面分辨率为0.1 m,部分像对如图 3所示。
 |
| 图 3 环岛屿周边海域的无人机航空影像Fig. 3 UAV aerial images surrounding islands |
3.1.2 气象海况
航空双介质摄影测量水下成像对气象条件要求比较苛刻,要求航摄时风浪应小于1 m。测区的海岛位于南海中西部,影像获取于2011年5月13日,查阅资料获悉当日海况[14]:风向南风、风力4~5级、浪高1.5 m。可知,浪高超出了气象条件规定要求,由于试验数据有限,在此条件下进行了试验。
3.1.3 实测水深
测区内的实测水深数据,包括水下点平面坐标(高斯3°带投影)以及对应的基于水深基准面的水深值。
3.2 试验关键技术
航空双介质摄影测量试验流程图如图 4所示。试验基于航空数据空三加密成果,在立体环境中量测左右影像水下礁盘的同名像点坐标,将量测的同名像点坐标加入双介质摄影测量模型,进行双介质水深解算;利用潮汐推算模型完成水深成果到深度基准面的转换;实测的水深与双介质水深比较,进行精度评价,完成了水上水下一体化制图表达。
 |
| 图 4 航空双介质摄影测量试验流程Fig. 4 Flowchart of aerial two-media photogrammetry experiment |
3.2.1 水下同名像点坐标获取
受水质和深度的影响,光线在传输过程中发生衰减,成像时光线亮度发生变化,随之地物在影像中所表现的特征亮度也发生变化;当传感器从不同角度拍摄水下同一地物,由于受光线传播折射的影响,影像中的地物不能真实反映其几何特征。受以上两点限制,基于特征和灰度值的特征点匹配算法不能很好的应用于水下同名像点的获取[15]。
为了获取水下同名像点坐标,本试验避开了传统获取同名像点的特征点匹配思路,采用基于测区空三加密成果构建立体模型、进行水下像点立体采集,基本流程如下:
(1) 基于空三加密成果对整个测区的平均航向角θ、平均航高h、平均高程H进行概算,并在此基础上对原始影像进行像点重新排列和按一定比例缩放,得到用于构建立体的“理想影像”。
(2) 为了便于模型构建和后续坐标解算,将测区的所有摄影中心坐标平移到左下角影像的摄影中心,并将线元素的X元素旋转到平均航向角方向。
(3) 以像素为单位,计算航片地面覆盖范围,并将所有立体像对左片、右片进行连接生成。
(4) 对拼接线附近一定范围的影像按一定公式进行融合消除,最终得到整个测区的连续立体模型。
(5) 基于立体模型采用频闪或红绿模式进行立体采集,将采集得到的“理想影像”像点坐标转换到原始影像像素坐标,获取水下同名像点坐标。
在对整个测区立体构建过程中,相邻模型之间都有连接差:航带间方向和航带内方向,通过一定公式计算出两个方向的连接差,可以初步判断立体模型构建精度。另外在实际采集过程中某个特征点的上下视差也是立体模型构建质量直接反应,同时也是定性反应同名像点坐标精度。
3.2.2 确定介质面高程
由图 1可知,双介质摄影测量模型中,曝光点S高程坐标起算面是介质面(海水与空气的交界面),直接获取的高程值是基于某一高程基准面的。利用双介质摄影测量模型进行水下礁盘量测时,需要确定航摄时刻介质面在同一高程基准下的高程值,将曝光点S高程归算到以介质面为基准的表达值。
基于潮汐模型推算摄影时刻海岛周边的瞬时水位(介质面)高程为0.42 m(1985国家高程基准),根据气象海况观测,影像获取时刻测区有1.5 m高海浪,不可直接按理论推算出的0.42 m作为测区的瞬时水位高程进行解算。理论上可以通过基于摄影时刻的水位观测序列对理论瞬时水位高程面进行改正,获取精确的介质面高程。由于数据不完整,试验采用基于逐个像对量测一定数量可靠瞬时水边线点高程的方法,取其均值作为观测像对介质面的高程值。
3.2.3 高程基准换算
双介质摄影测量测得水下点的高程值是基于陆地高程基准起算的,海底水深是基于理论深度基准面表示的,两者的垂直参考面不一样。高程基准换算[16, 17],即某一陆地高程基准面和理论深度基准面之间的转换关系,其意义在于将双介质量测的水下点高程值转换到以深度基准面为起算面的水深值表达。海岛周边元素垂直基准面表达关系如图 5所示。
 |
| 图 5 海岛垂直基准面关系图Fig. 5 Vertical datum relations of islands |
试验直接获取的水下点高程是基于1985国家高程基准,要实现1985国家高程基准面与理论深度基准面的转换,先通过平均海面高度(大地高)数值模型,内插出某岛的平均海面在CGCS2000椭球下的高度为6.03 m(精度10 cm),此面是深度基准面的起算面;以平均海面为参考面,根据当地多年潮汐参数,结合潮汐模型推算,得到某岛的瞬时水位线、深度基准面在CGCS2000椭球下的高度分别为5.75 m、4.64 m;利用大地水准面精化技术得到某一水准面距地球椭球面的垂直偏差——高程异常,利用该模型推算得到某岛的1985高程基准面与CGCS2000椭球面的距离(即高程异常值)为5.33 m,瞬时水位线、深度基准面在1985高程基准面上高度分别为0.42 m、-0.69 m。
由图 6可知:某岛深度基准面在1985国家高程基准下高程为-0.69 m,水深值转换按3种情况进行计算:
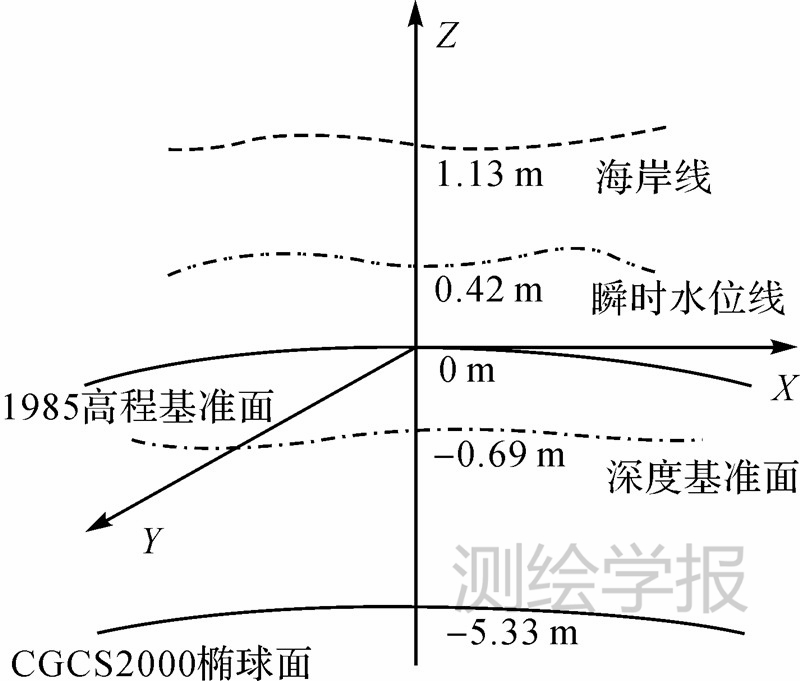 |
| 图 6 某岛垂直基准面间关系图Fig. 6 Vertical datum relations of island |
(1) 0.42 m>H85≥0 m:H深度基准=H85+0.69。
(2) 0 m>H85≥0.69 m:H深度基准=0.69-|H85|。
(3) -0.69 m>H85:H深度基准=H85+0.69。
3.2.4 双介质水深精度评价
与传统摄影测量不同,双介质摄影测量虽然能获取某些水下特征点的三维坐标,但水下对应特征点并没有精确三维坐标,不能采用传统精度评价方法来验证双介质摄影测量精度。由图 1可知,双介质摄影测量模型在量测水下点三维坐标的时候,其X、Y坐标和单介质交会的一样,在这里不作讨论。单从量测值Z出发,即双介质水深值精度评价[18, 19]出发,本试验成果为三维点坐标,与实测点不一一对应,类似LiDAR点云成果,精度评价借鉴LiDAR点云的高程精度评价方法:
(1) 对实测水深构建不规则三角网(TIN)(见图 7);
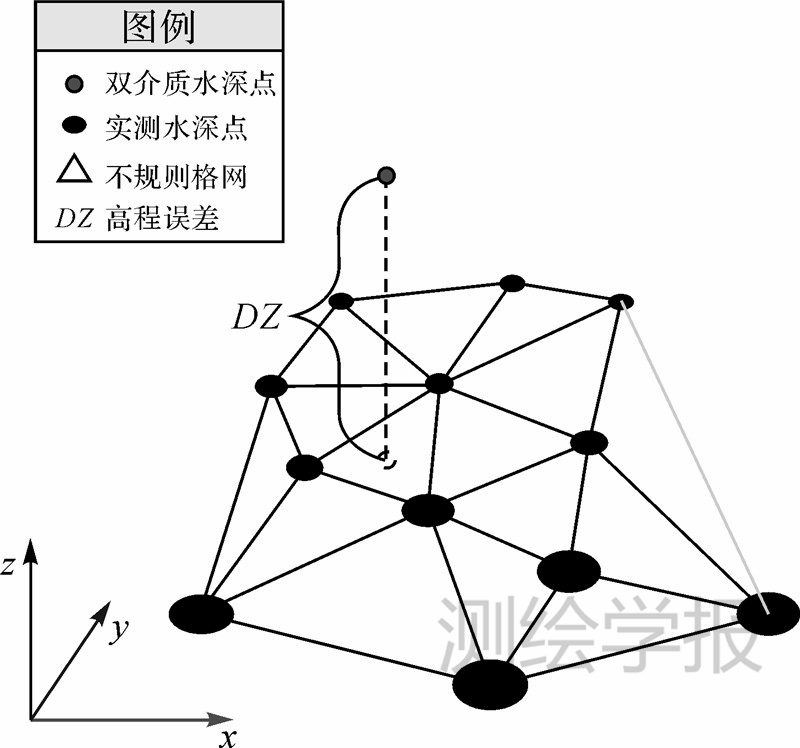 |
| 图 7 水深精度评价方法原理图Fig. 7 Depth accuracy assessment methods and principles |
(2) 判断检查点的位置并确定该检查点沿Z轴方向所投影到的三角形;
(3) 将检查点的X和Y值带入此三角形中,计算出投影到此三角形中的Z值,记作TZ,用TZ与Z作差得到高程误差DZ;
(4) 对所有的DZ进行最大值、均值、中误差等统计分析,以评定综合评定水深精度。
3.3 试验分析与成果
3.3.1 试验误差分析
此次试验环岛海域共采集了4520个水下点,其分布情况如图 8所示。
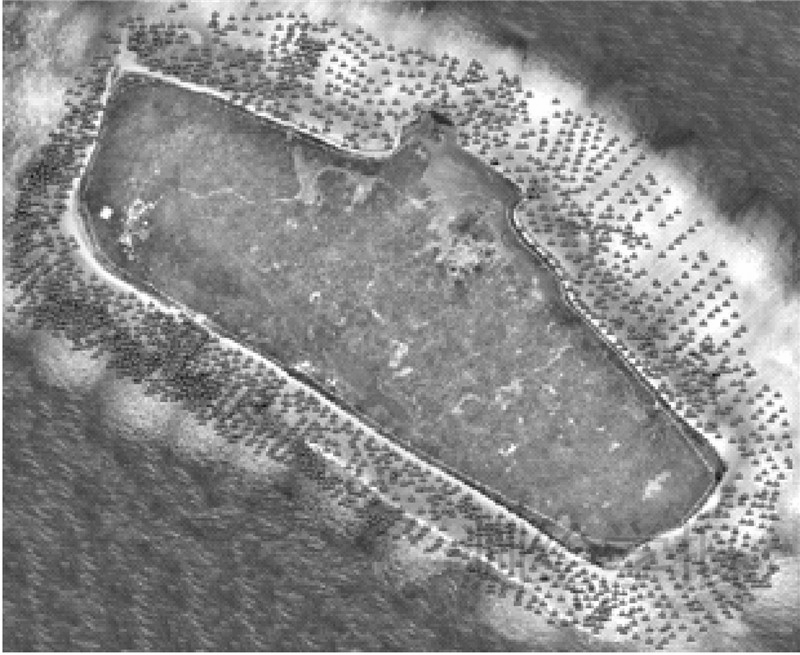 |
| 图 8 双介质水下点分布情况图Fig. 8 Two-media Underwater Points distribution |
将双介质摄影测量方法解算出的水下点高程转换到以理论深度基准面为起算面表达,利用3.2.4 节介绍的精度评定方法与实测水深进行比较。由于采集水下像点时,是基于单个立体模型即两张相邻影像构建的立体进行,所以对每个像对的双介质水深值也进行了误差分析。部分像对误差分析如表 1所示,整个测区误差分析如表 2所示。
| 像对号 | STDEV/m | RMS/m | AVE Dz/m |
| 378-376 | 0.10 | 0.09 | -0.80 |
| 386-384 | 0.48 | 0.47 | 0.27 |
| 390-388 | 0.78 | 0.77 | 1.97 |
| 394-392 | 0.57 | 0.56 | 0.74 |
| 402-400 | 0.53 | 0.52 | -0.32 |
| 594-596 | 0.46 | 0.46 | 0.07 |
| 598-600 | 0.57 | 0.56 | -0.66 |
| 679-677 | 0.49 | 0.49 | 0.01 |
| 404-402 | 1.18 | 1.18 | 0.20 |
| 点数/个 | 最深值/m | STDEV/m | RMS/m |
| 4520 | 6.2 | 0.61 | 0.68 |
由表 2部分像对误差结果来看,个别像对误差出现异常,这可能与像对之间的模型连接差以及航摄时气象海况对岛周边地势影响有关:如果像对模型连接差大表明外方位元素和像点坐标精度都不好,解算出的水下点坐标精度也比较差;风向对于海岛不同区域的瞬时水位影响不同,用求取部分点水边线高程平均值的方法来确定瞬时水位高程对于像对区域内瞬时海况变化比较大(如像对包含区域为迎风口)有一定的不可控性。
从总体精度分析表来看,其最深值(基于理论深度基准面)为6.2 m,测量深度不深,其主要受限于海浪、反光等客观条件的存在,无法看清水下立体,限制了双介质量测深度。中误差为0.61 m,相对于高精度船载多波束、机载激光水深测量手段,误差偏大。从整个试验流程看,误差可能受海浪超限、介质面高程推算及部分人为因素(如立体采集)等几方面的影响比较大。
3.3.2 水上水下一体化制图表达
双介质摄影测量水深成果和岛陆地上的DEM都是基于低空无人机航空影像制作的。因此,可以将双介质摄影测量水深成果和陆地上的DEM进行统一成图[20],实现水上水下一体化制图表达。
由于此次试验水下立体观测深度限制,加上影像有强反光、明显波纹等问题存在,造成水下立体环境采集的点密度不够、分布不均。水上水下一体化等高线制图效果如图 9所示,DEM晕渲效果图如图 10所示。
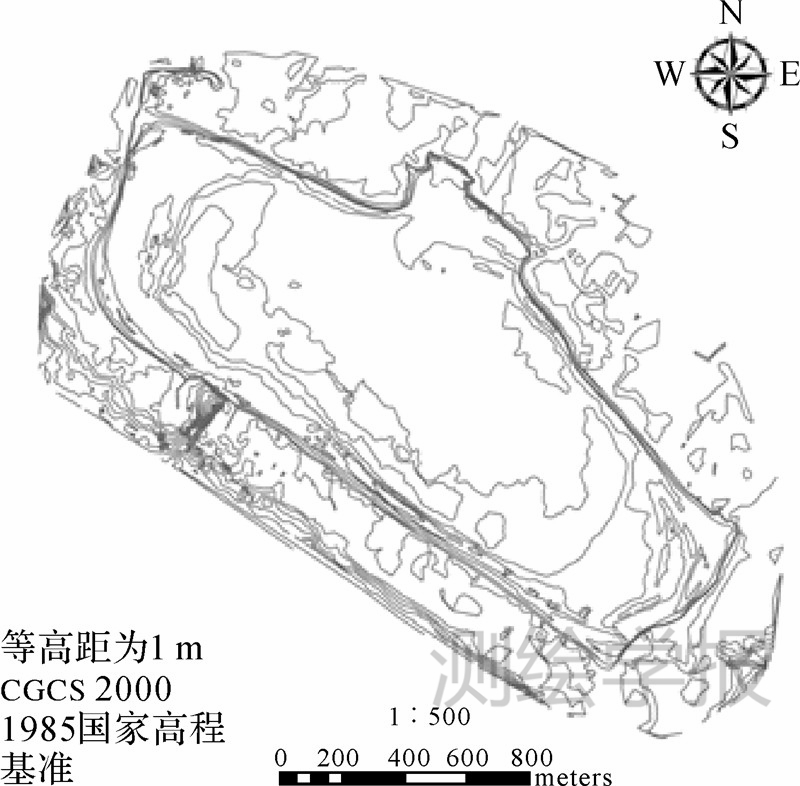 |
| 图 9 某岛及其周边海域等高线图Fig. 9 Island and its surrounding waters contour map |
 |
| 图 10 某岛及其周边海域DEM晕渲图Fig. 10 Island and its surrounding waters DEM shading map |
4 结束语
本文在对双介质摄影测量原理进行深入分析的基础上,利用环海岛的低空无人机航空影像开展了水下礁盘深度测量试验,并对试验成果进行精度评价,测量的最深水深值(基于深度基准面)为6.2 m。按照整个流程对另一个岛的周边海域水下礁盘也进行了测量试验,其当时航摄自然条件比较好,测量的最深处为21.6 m,由于没有实测水深值进行精度评价,故在本文中进行没有详细介绍。
本试验验证了航空双介质摄影测量在实际应用中的可行性,不足之处是在误差分析中,由于试验数据不完整,没有对误差因素进行定量分析。在以后的试验或应用过程中拟选择航摄自然条件较好、水质比较清澈的区域获取数据,克服影像的海浪、反光等问题;数据处理过程采用自动化操作,减少人为干涉因素;进一步改善数据处理方法,如基于余水位的潮汐模型优化改正,将其应用于海岛空三平差处理和瞬时水位高程推算。以上改进措施将大大提高量测精度。目前,国内先前的双介质摄影测量研究没有开展实际应用试验,此次试验为以后推广双介质摄影测量的应用提供了指导性建议。
| [1] | WANG Zhizhuo.Principles of Photogrammetry[M]. Beijing: Surveying and Mapping Press, 1979.(王之卓.摄影测量学原理[M].北京:测绘出版社,1979.) |
| [2] | CARLL, RUDOLPH B. Photogrammetry[M]. Beijing: Surveying and Mapping Press, 1979.(林纳卡尔,布尔哈特鲁道夫.摄影测量学[M].北京:测绘出版社,1979.) |
| [3] | MODUNCE L E.Underwater Photography[M]. ZHANG Wendi, trans.Beijing: Science Press, 1979.(莫顿斯L E.水中摄影学[M]. 张闻迪,译.北京:科学出版社,1979.) |
| [4] | LI R, LI H, ZOU W, et al.Quantitative Photogrammetric Analysis of Digital Underwater Video Imagery[J].IEEE Journal of Oceanic Engineering,1997, 22(2): 364-375. |
| [5] | MAAS H G. New Developments in Multimedia Photogrammetry[J].Optical 3D Measurement Techniques III, 1995. |
| [6] | GILI T, SAGI F. Photogrammetric Modeling of Underwater Environments[J]. ISPRS Journal of Photogrammetry and Remote Sensing,2010,65(5):433-444. |
| [7] | CHANG Benyi. Basic Formulas of Two-media Photogrammetry[J].Acta Geodaetica et Cartographica Sinica,1991,20(4):288-294.(常本义.双介质摄影测量基本公式[J].测绘学报,1991,20(4):288-294.) |
| [8] | WANG Younian, HAN Ling, WANG Yun. Experimental Research of Underwater Close-range Photogrammetry[J].Acta Geodaetica et Cartographica Sinica,1988, 17(3)217-224.(王有年,韩玲,王云.水下近景摄影试验研究[J].测绘学报,1988,17(3):217-224.) |
| [9] | SHAN Jie. Relative Orientation for Two-media Photogrammetry[J].Journal of Zhengzhou Institute of Surveying and Mapping,1993, 10(3):38-44.(单杰.双介质摄影测量的相对定向[J].解放军测绘学院学报,1993,10(3):38-44.) |
| [10] | [JP+3]LIU Shanlei,ZHAO Yindi,LI Yingcheng et al.Analysis at Underwater Topographic Two-media Photogrammetry with POS Data[J].Science of Surveying and Mapping,2011,36(6):42-45.(刘善磊,赵银娣,李英成,等.POS数据用于双介质水下地形摄影测量的研究[J].测绘科学,2011,36(6):42-45.) |
| [11] | DANG Yamin,CHENG Pengfei,ZHANG Chuanyin et al.Sea Reefs Mapping Technology and Methods[M].Beijing:Surveying and Mapping Press,2012.(党亚民,程鹏飞,章传银等.海岛礁测绘技术与方法[M].北京:测绘出版社,2012.) |
| [12] | QUAN X,FRYE S. Empirical Equation for the Index of Refraction of Seawater[J].Applied Optics,1995,34(18). |
| [13] | [JP+2]JIANG Liangguang,SUN Peng.Models of the Wavelength Dependence for the Index of Refraction of Water[J].Chinese Journal of Spectroscopy Laboratory,2002,19(4):554-556.(姜良广,孙鹏.水的折射率与波长间函数关系的模型[J].光谱试验室,2002,19(4):554-556.) |
| [14] | Lianyungang Maritime Safety Administration. (2011-03-15)[2014-01-30].http://www.lygmsa.gov.cn/.(连云港海事局网站.(2011-03-15)[2014-01-30].http://www.lygmsa.gov.cn/.) |
| [15] | ZHANG Zuxun, ZHANG Jianqing.Digital Photogrammetry[M]. Wuhan: Wuhan University Press.2012.(张祖勋,张剑清.数字摄影测量[M].武汉:武汉大学出版社.2012.) |
| [16] | SHEN Jiashuang. Research on Technology of Equal Waterline Information Extraction and Vertical Datum Transformation in Coastal Zone[D].Zhengzhou:Information Engineering University,2011.(申家双.海岸带等水位线信息提取与垂直基准转换技术研究[D].郑州:信息工程大学,2011.) |
| [17] | BAO Jingyang, ZHANG Chuanyin.On the Sea and Ocean Vertical Datum[J].Bulletin of Surveying and Mapping,2010,(6):10-11,26.(暴景阳,章传银.关于海洋垂直基准的讨论[J].测绘通报,2010(6):10-11,26.) |
| [18] | [JP+6]LI Tao.Construction and Visualization Methods and Implementation for Delaunay Triangulation[D].Nanchang:East China Institute of Technology,2012.(李涛.Delaunay 三角网构建及可视化方法与实现[D].南昌:东华理工大学,2012.) |
| [19] | XU Duowen.Construction and Application of TIN[D].Ganzhou: Jianxi University of Science and Technology,2010.(许多文.不规则三角网(TIN)的构建及应用[D].赣州:江西理工大学,2010.) |
| [20] | SHEN Jiashuang, ZHAI Jingsheng, ZHAI Guojun et al.The Research on the Coastal Topographic Map and Its Surveying Method[J].Bulletin of Surveying and Mapping,2007(8):29-32.(申家双,翟京生,翟国君,等.海岸带地形图及其测量方法研究[J].测绘通报,2007(8):29-32.) |