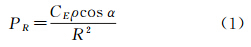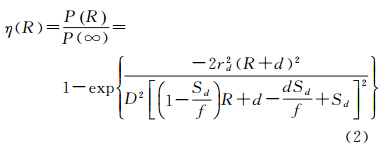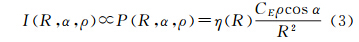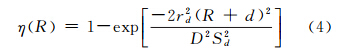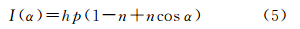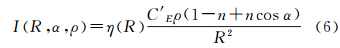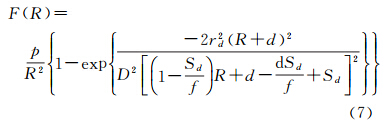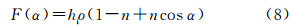石窟和壁画是大量存在于我国中西部地区的佛教文化遗产,由于受到自然变化和人类行为的影响,正在快速退化,因此建立高精度数字化壁画档案已经迫在眉睫。地面三维激光扫描(terrestrial laser scanning,TLS)因其能快速获取高精度密集表面点云数据,近年来在考古和文化遗产数字化领域得到大量使用。三维激光扫描不仅能获取目标表面几何信息,还能够记录激光回波强度,这种同时具备表面空间位置和光谱信息的属性使得激光扫描数据常常作为壁画影像和三维空间的媒介,用于壁画影像的正射纠正和纹理映射。
现有的石窟建模过程中,一种主要的方法就是利用激光扫描建立洞窟的三维模型,并将纹理映射到三维模型上[1],然后通过对映射后的纹理进行投影和内插就可以实现壁画纠正,这需要充分利用几何特征点和强度特征点来实现控制点关联[2]。虽然在大多数的应用中强度信号的价值常常被忽视,但实际上,强度在高精度的壁画精确纠正中具有不可替代的作用[3, 4]。由于洞窟墙壁平坦,单独利用几何形状难以建立几何-纹理之间的映射关系,利用TLS点云强度数据作为配准参考,则可以实现高精度壁画影像在三维空间中的几何纠正。
TLS强度信号除了受到噪音、目标材质和表面色彩以及大气环境的影响之外,还受到测量距离和入射角变化的影响,如图 1所示,这种影响导致强度影像“曝光”不均匀,给壁画定位时的特征点特征提取带来很大的影响,需要通过后处理方法来提高强度数据的质量。为了提高点云强度的质量,文献[5]采用三维扩散滤波方法实现了TLS的强度噪音的有效抑制,由于TLS扫描距离较近,大气环境对其回波强度的影响可以忽略不计,至于材质和表面色彩则是目标表面固定属性,不需要对其进行校正,因此,距离和入射角度是TLS强度校正研究的重点。
 |
| 图 1 莫高窟单站激光点云原始强度全景影像Fig. 1 Original panorama image of single station TLS data of a cave in Mogao Grottoes,Dunhuang |
作为一种主动测量手段,TLS强度理论上与距离的平方成反比,其关系可以描述为K/R2,其中K是常数,R是扫描距离[6]。但在近距离时,实际数据并不满足这种关系。文献[7, 8, 9, 10]虽然注意到了这种近距离强度反常现象,并提出了多种假设,但是缺乏系统的解释和校正方法。文献[11]认为近距离反常现象的产生是由于激光束和接收器之间的不完全重叠,但只能解释旁轴激光扫描系统,同轴系统并没有这种不完全重叠结构。文献[7]认为近距离效应是由保护传感器的自动减光系统(automatic brightness reducer,ABR)引起的。然而TLS(尤其是相位式)采集数据速度非常快(每秒高达一百万点),使得ABR几乎没有时间对光强变化作出反应。文献[12]认为近距离效应产生的原因是由于接收器光学系统的散焦,并且存在于旁轴和同轴系统中,但是对于TLS却没有提出系统的校正方案。
对于入射角因素,双向反射分布函数(bilateral reflectance distribution function,BRDF)是描述入射光束与物体表面[13]之间相互作用最全面的模型,然而这种模型非常复杂,在实际应用中需要目标表面的先验信息(粗糙度、介电常数等)。为了避免这种情况,文献[14]对TLS的强度和入射角之间的关系进行了直接研究。定性研究发现,当目标表面不规则时,TLS的强度和入射角无关[15]。因此,在对TLS强度数据进行入射角校正时,为了得到正确的纠正结果,通常会考虑目标表面的粗糙度[16]。
本文针对激光扫描强度数据用于壁画纠正的实际需求,研究了激光点云强度影像“曝光”不均匀现象产生的原因,并建立了顾及接收光学系统散焦效应的TLS激光强度理论模型,在此基础上设计了试验来估计模型中各个参数。最后用估计得到的参数对敦煌莫高窟壁画点云强度进行了校正,并将强度校正方法与数字图像处理方法进行了对比,以证明强度校正对壁画纠正的意义。
2 顾及接收光学系统散焦效应的TLS强度模型[17] 2.1 TLS强度的理想模型
TLS强度值是数字化表示的激光回波能量,它与入射到探测器上的光子数量成正比[18]。大多数扫描仪通过反射式或者透镜型接收望远镜将回波激光信号聚焦在光探测器上,从而实现距离计算和强度记录。激光雷达方程可以表示TLS的回波强度,它是一个通用模型,描述了接收激光功率和发射激光功率之间的关系[6]。由于扫描仪获得的强度值正比于总接收激光功率,所以通过对激光雷达方程进行简化[5],激光扫描仪的总接收功率可以表示为
式中,CE是一个常数;PR和强度成正比。由于激光扫描仪在记录目标距离R的同时还记录激光强度,而入射角α则可以通过法线拟合计算出来,这样,对于给定材质的表面(反射率ρ恒定),可以通过估计其上的TLS点云样本数据来得到CE。另外,从式(1)中能够看出,距离和入射角对激光强度的作用在理论上是互相独立的,可以分开处理。2.2 接收光学系统散焦效应
式(1)是一个理论模型,它假设激光发射器接收器为理想配置,然而在近距离时,实际测量中TLS收集的数据通常表现出与式(1)截然不同结果[8, 19]。对这种TLS在近距离时异常的问题,现有研究仍缺少合理的解释,更没有理论性的推导。通过研究各种TLS硬件结构原理,笔者发现接收光学系统中使用凸透镜或凹面镜把返回的激光聚焦到探测器(如图 2所示):当目标距离过近时,像平面后移,从而可能导致探测器平面上激光光斑面积大于探测器的现象,这就是接收光学系统的散焦效应。部分激光扫描仪内部使用凹面镜而不是凸透镜,其功能与凸透镜相同,考虑到行文简洁,均以凸透镜代替。
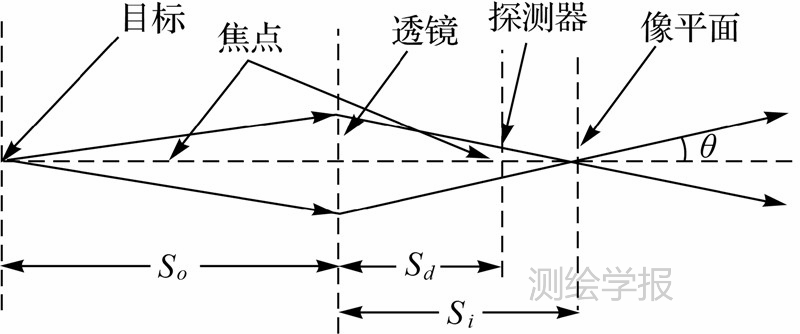 |
| 图 2 近物距下的透镜成像示意图Fig. 2 The illustration of lens focusing with close object distance |
TLS强度的散焦效应可以描述为从有限和无限距离返回的激光信号被探测器捕获的功率之比,如式(2)所示,其中p、rd、d、D、Sd、f为激光扫描仪相关参数[20]
因此,结合式(1),考虑TLS近距离效应的强度值可以表示为
如果探测器放在透镜焦点位置(Sd=f),则式(2)可写为
这是一个典型的倒置正态分布:在较近的距离内,η(R)随着距离迅速增大;在远距离,η(R)几乎保持在1.0不变,而I(R,α,ρ)的形状与K/R2相似。
2.3 TLS强度的入射角效应
入射角效应和观测角、入射角以及它们之间的方位角、表面特性(反射率、粗糙度等)等观测几何因素相关[12]。本文对同轴TLS进行校正,因此只需要考虑入射角和表面特性。在文献[7]中,同轴TLS入射角对强度的影响可以简化为
式中,h和目标表面反射率ρ相关,因为式(3)中已经考虑到反射率,因此h可以看作一个常数;参数n与粗糙度正相关。最后,结合式(3),式(5)变为 式中,C′E=hCE为常数。式(6)是激光雷达方程与考虑近距离效应和入射角的改进,在本文中被称为TLS的强度模型。3 TLS强度模型参数估计与点云强度校正
式(6)中的各参数与特定激光扫描系统有密切关系,因此需要通过实测数据来获得这些参数,从而进行强度校正,如:探测器尺寸、接收器光学元件的焦距。本文通过实测数据来估计公式中的各个参数。试验中,把式(6)看作是待估计参数和它们的组合构成的目标函数。由于距离和入射角对强度的影响相互独立,可以把参数估计的目标函数分为两个部分,即“强度-距离”和“强度-入射角”函数。在估计强度-距离函数时,入射角为常数;而估计强度-入射角函数时,距离应保持不变。点云强度校正流程如图 3所示。
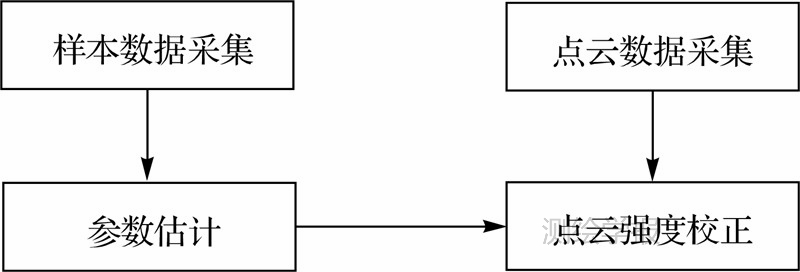 |
| 图 3 点云强度校正流程Fig. 3 Flow chart of TLS intensity correction |
3.1 校正距离影响 3.1.1 样本数据采集
为了估计强度-距离函数,笔者设计了一组试验,让TLS在相同的入射角下采集同种材质目标表面上的多个距离-强度样本数据。试验中,选择白色打印纸作为测量不同距离强度样本数据的标靶材质。为了尽可能减少环境光变化和扫描仪的热积累对激光强度的影响,设计的试验需要在很短时间内完成。试验中让标靶沿着二维螺旋线放置,螺旋线的中心与激光扫描仪的旋转中心重合(如图 4所示)。标靶放置于平坦地面,其平面垂直于上述螺旋线的半径(入射激光束),从而保证每个标靶上有垂直入射的激光点。
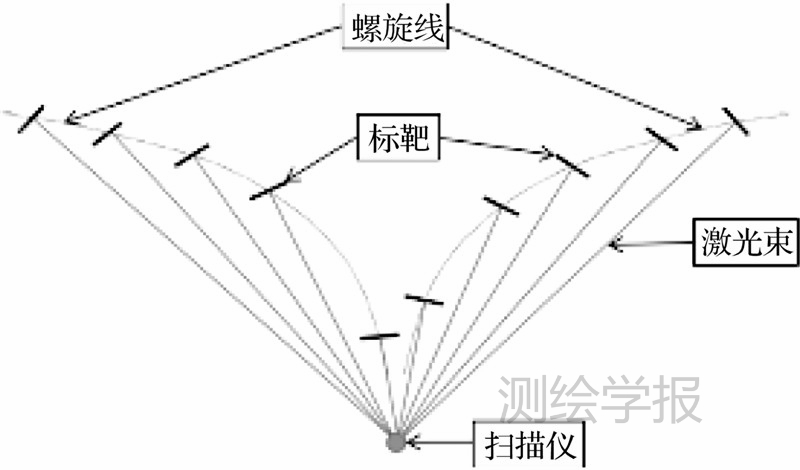 |
| 图 4 标靶和扫描仪分布Fig. 4 Positions of scanner and targets |
如图 5中的点所示,从白纸标靶上收集到的数据结果表明,随着距离增大,强度变得接近激光雷达方程所表示的K/R2函数。然而随着距离减小,出现了明显的激光近距离强度异常,实际上这是接收光学器件散焦效应的影响,强度偏离K/R2曲线。
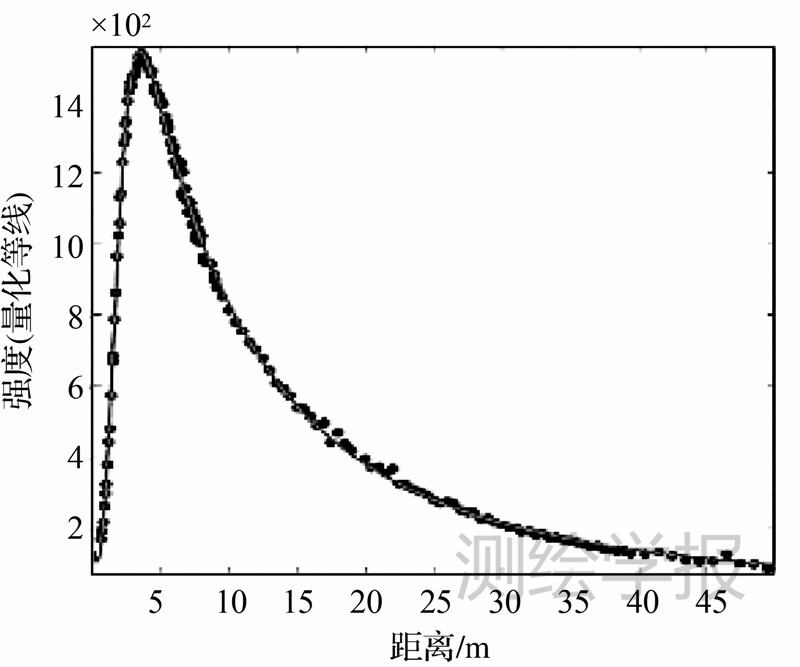 |
| 图 5 样本数据和式(7)的拟合结果Fig. 5 Sample data and fitting result of Equation (7) |
3.1.2 参数估计
试验中的同材质白纸反射率恒定,而入射角是零,则p=C′Eρ(1-n+ncos α)=hCEρ是一个常数。因此,强度-距离函数可以从式(6)中简化为
由于参数E=(p,rd,d,D,Sd,f)具有物理意义并且它们的初值和变化范围可以通过观察预测,利用这些初值和样本数据,通过曲线拟合,可以更快地得到更准确的参数估计结果。拟合结果如图 5曲线所示,可以看到在0~4 m的距离范围内,强度随着距离增加而快速增强;而在4 m距离以后,强度则开始随距离增大而衰减,拟合曲线与试验数据完美重合。
3.1.3 距离校正
根据式(6)可知,如果距离、入射角为常量,激光回波强度仅仅与目标的表面属性相关,这个不受其他外界因素影响的反射率就是校正后的强度。换句话说,从不同反射率的表面得到的强度-距离曲线具有相同的形状。因此,将测得的强度比上相同距离的白纸强度,即可得到相对反射率,从而实现强度对距离的相对校正。
3.2 入射角影响校正
3.2.1 样本数据采集
由于入射角的影响依赖于物体的表面特性,与角度相关的模型参数的估计需要实测才能获得。为此,笔者进行了第2组试验,通过将标靶设置为与激光光束存在一定夹角的位置上进行试验,从而验证角度对强度的影响,图 6为验证试验设计示意图,其中所有标靶中心与扫描仪距离相等,标靶与其所在圆周点对应半径成不同的夹角。
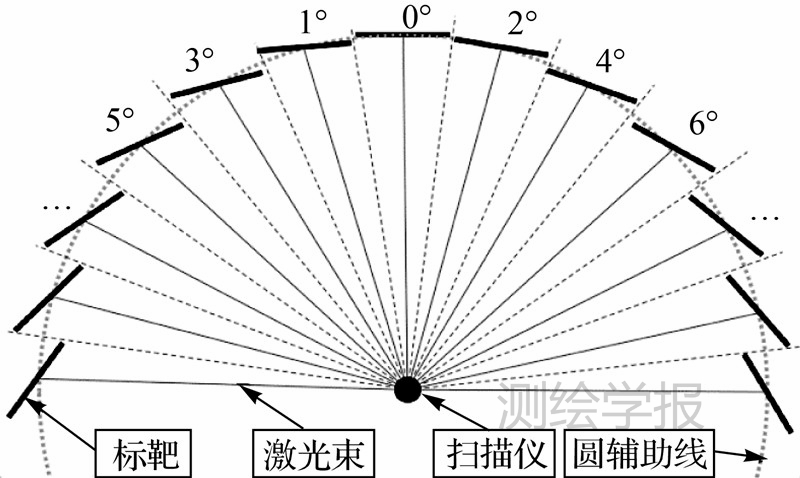 |
| 图 6 入射角数据采集实验标靶和扫描仪分布示意图Fig. 6 Positions of scanner and targets for incidence angle sample data collection |
根据式(6),在距离和表面反射率不变的情况下,入射角效应估计函数可以写成
通过拟合球形邻域内的点,可以计算相应的入射角。为了确保精确的估计,球形邻域的直径定义为两倍的测距精度。如图 7所示,在试验中总共选取了160个样本点数据,其中入射角的变化范围从1°~80.5°,通过曲线拟合方程(8)得到的估计结果如图 7中的曲线所示。
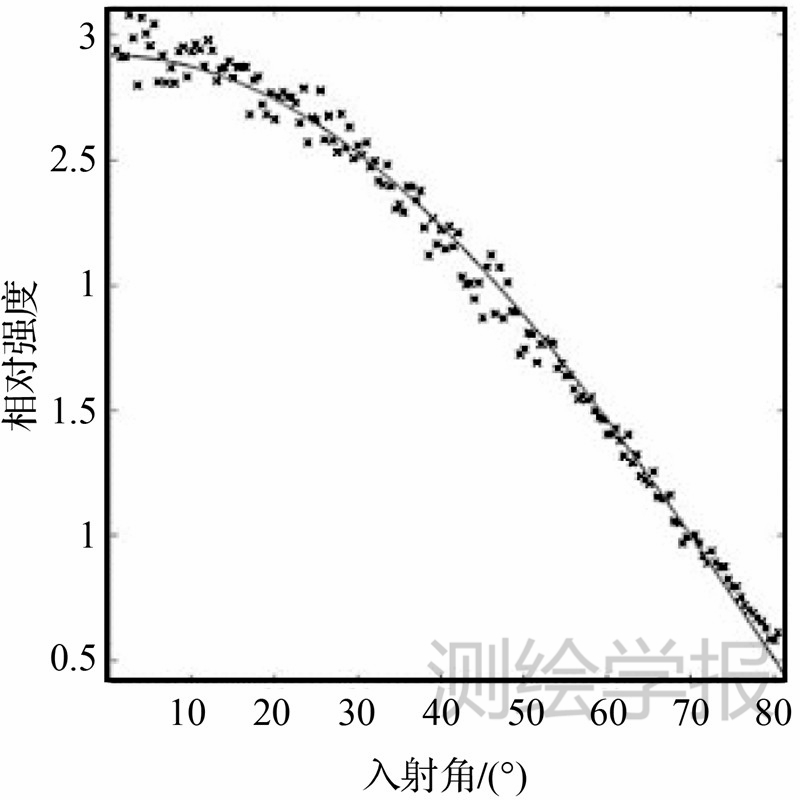 |
| 图 7 从距离校正后的墙面数据中选取的样本点和入射角-强度曲线拟合结果Fig. 7 The estimation results of the intensity-incidence angle function |
3.2.3 入射角校正
根据式(8),入射角对强度的影响依赖于被扫描表面的粗糙度,因此假定待校正后的数据来自粗糙度均匀的表面,将强度乘以对应入射角和距离下式(8)的倒数值,就可以消除入射角影响。
4 基于点云强度校正的壁画纠正试验
壁画纠正的主要过程是利用激光点云生成壁画的强度影像,然后,寻找点云强度影像和壁画影像之间的同名特征点,为壁画控制点赋予三维坐标。而强度校正能够对消除强度影像存在的“曝光”不均匀现象,提高强度影像和壁画影像间同名特征点数量和分布均匀性,从而优化壁画纠正结果。
4.1 试验环境
试验采用的扫描仪为Z+F Imager5006i,其测量点云密度可以高达25点/cm2(根据Z+F提供参数,其点间距可以达2 mm),试验中对莫高窟322窟采集了一站共1.7亿个点。扫描得到的强度全景展开图如图 1所示,可以看到明显的近距离反常效应,强度在近距离低于远距离区域。试验壁画采用敦煌研究院提供的整幅322洞窟东壁影像,由佳能1D MarksⅢ相机采集的196张影像拼接而成,分辨率可达300 DPI。
4.2 壁画纠正试验
试验软件用笔者自主开发的面向TLS的纹理处理软件ModelPainter完成,其在VS2010平台下用C++语言编写完成,硬件环境为Intel 2.3 GHz 4核处理器、8 GB内存。点云强度影像的生成需要先人工在壁面点云上选取投影面,然后将点云强度投影到该平面上并进行内插。强度影像和壁画影像的配准采用SIFT算子提取特征点,并分别利用SIFT特征的距离尺度和互信息作为粗匹配和精匹配的策略。图 8所示为Model-Painter点云强度影像和壁画影像匹配界面,针对SIFT特征点不精确的地方,软件支持人工检查和微调以确保配准和纠正精度。
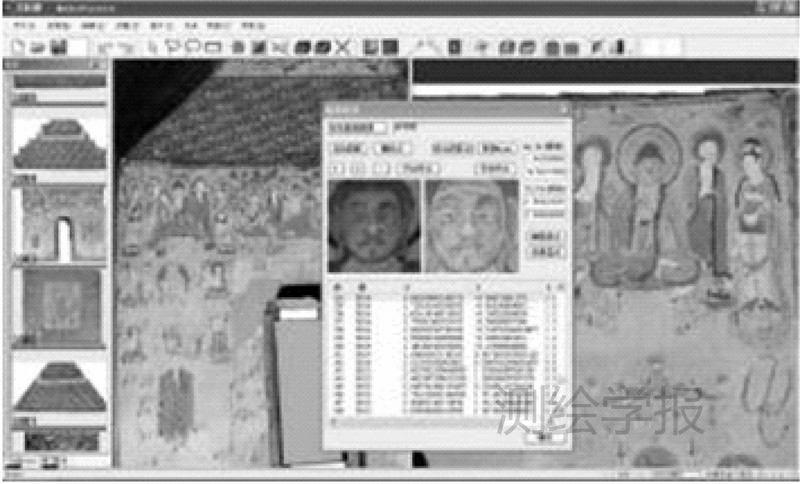 |
| 图 8 在ModelPainter软件中实现基于激光点云强度的壁画纠正Fig. 8 TLS intensity-based mural image rectification in ModelPainter |
4.3 强度校正试验和分析
在进行特征提取之前,先利用第2节中强度校正方法和参数对322洞窟的强度数据进行校正。如图 9所示:(a)为强度数据距离校正后的结果,(b)为强度数据入射角校正后的结果。对比图 1的原始强度影像可以看到强度得到有效校正,特别在距离校正以后,入射角对强度的影响开始变得明显(见图 9(a)矩形区域)。由于激光在几何结构复杂区域(如墙角)存在多路径效应,部分墙角区域在入射角校正后产生了过度增强的地方(图 9(b)中的箭头所指区域),这需要更深入的研究。
 |
| 图 9 莫高窟322激光点云强度校正前后对比Fig. 9 Comparison of the intensity images of the Mogao Grottoes before and after corrections |
为了验证强度校正对于壁画纠正的必要性,笔者对比了SIFT算法在提取校正前后影像特征点的数量和分布;同时,利用图像处理中的自动色阶对比度调整强度影像,然后对比了调整前后SIFT特征点的数量和分布,结果如表 1和图 10所示。
 |
| 图 10 强度影像校正前后以及数字图像处理后SIFT特征点分布对比Fig. 10 Comparison of intensity image SIFT features before and after correction and digital image processing |
| 处理方法 | 特征点数(校正前) | 特征点数(校正后) |
| 未处理 | 15 996 | 72 904 |
| 自动色阶对比度 | 43 835 | 126 309 |
进行SIFT特征提取时,先将强度数据内插为图像,根据点云密度设定分辨率为3578×3776。从表 1和图 10(a)、图 10(b)的对比可以看到,强度校正后特征点数量明显增多,特征点分布更均匀。未校正的强度影像经过自动色阶处理后,特征点数量也可以明显提高,但分布仍然非常不均匀(图 10(c)),这容易导致壁画纠正精度的空间分布不均。通过对校正后的强度影像进行图像自动优化不仅能提高特征点数量,还能保持特征分布的均匀性,这种优势是仅用数字图像处理方法无法替代的。
5 结 论
壁画数字化工作是敦煌莫高窟数字化保护的重要内容和基础工作,而壁画纠正能够减少或消除壁画数字化过程中因镜头畸变、壁面起伏和后处理等造成的壁画扭曲、变形、拉伸等几何失真,通过正射投影生成的壁面正射影像可以给壁画提供精确的位置信息,从而有效地辅助海量壁画的快速采集、有序存储、高效管理和多元应用。从强度数据中提取关键点进行壁画纠正则要求极高的点云密度,因此需要进行近距离扫描,而此时TLS点云强度受反常效应的严重影响。本文通过分析激光强度产生的机理,提出的强度校正方法能有效消除近距离反常效应,从根本上改善激光强度影像特征点分布不均匀和数量不足的问题,使得强度影像和壁画影像能够有效配准。本文的研究进一步揭示了激光数据的产生过程。此外,由于受多种因素的影像,入射角效应的校正在角度较大的地方并不彻底,这需要深入研究更严格的激光反射模型的应用。
致谢:特别感谢祝波提出的对扫描仪结构的启发性建议,感谢张振宇、雍小龙、张飞、屈孝志、王健、杨冲、付正文、姜福泉等在试验数据采集中予以的帮助,同时也感谢审稿人对本文提出的宝贵修改意见。
| [1] | HU Shaoxing, ZHA Hongbin, ZHANG Aiwu. Modeling Method for Large-scale Cultural Heritage Sites and Objects Using Real Geometric Data and Real Texture Data[J]. Journal of System Simulation, 2006, 18(4):951-963.(胡少兴,查红彬,张爱武.大型古文物真三维数字化方法[J]. 系统仿真学报, 2006, 18(4):951-963.) |
| [2] | ZHANG Fan, HUANG Xianfeng, LI Deren. A Review of Registration of Laser Scanner Data and Optical Image[J]. Bulletin of Surveying and Mapping,2008(2):7-10. (张帆,黄先锋,李德仁. 激光扫描与光学影像数据配准的研究进展[J].测绘通报, 2008(2):7-10.) |
| [3] | ZHANG Fan, HUANG Xianfeng, FANG Wei, et al. Non-rigid Registration of Mural Images and Laser Scanning Data Based on the Optimization of the Edges of Interest[J]. Science China Information Sciences, 2013, 56(6): 1-10. |
| [4] | DIAS Paulo, SEQUEIRA Vítor, GONALVES Joao GM, et al. Automatic Registration of Laser Reflectance and Colour Intensity Images for 3D Reconstruction[J]. Robotics and Autonomous Systems, 2002, 39(3): 157-168. |
| [5] | ZHANG Yi, YAN Li. 3D Diffusion Filtering Method of Intensity Noise for Terrestrial Laser Scanning Point Cloud[J]. Acta Geodaetica et Cartographica Sinica, 2013,42(4):568-573. (张毅,闫利. 地面激光点云强度噪声的三维扩散滤波方法[J].测绘学报, 2013,42(4):568-573.) |
| [6] | JELALIAN A. Laser Radar Systems[M]. Boston: Artech House, 1992. |
| [7] | KAASALAINEN S,KUKKO A, LINDROOS T, et al. Brightness Measurements and Correction with Airborne and Terrestrial Laser Scanners[J]. IEEE Transactions on Geoscience and Remote Sensing, 2008, 46(2): 528-534. |
| [8] | KAASALAINEN S, JAAKKOLA A, KAASALAINEN M,et al. Analysis of Incidence Angle and Distance Effects on Terrestrial Laser Scanner Intensity: Search for Correction Methods[J]. Remote Sensing, 2011, 3(10): 2207-2221. |
| [9] | HÖFLE B,PFEIFER N. Correction of Laser Scanning Intensity Data: Data and Model-driven Approaches[J]. ISPRS Journal of Photogrammetry and Remote Sensing, 2007, 62(6): 415-433. |
| [10] | JUTZI B, GROSS H. Normalization of Lidar Intensity Data Based on Range and Surface Incidence Angle[J].International Archives of the Photogrammetry,Remote Sensing and Spatial Information Science 2009(38):213-218. |
| [11] | STELMASZCZYK K, DELL'AGLIO M, CHUDZYNSKI S, et al. Analytical Function for Lidar Geometrical Compression Form-factor Calculations[J]. Applied Optics,2005,44(7): 1323-1331. |
| [12] | BIAVATI G, DONFRANCESCO G D, CAIRO F, et al. Correction Scheme for Close Range Lidar Returns[J]. Applied Optics, 2011, 50(30):5872-5882. |
| [13] | TORRANCE K E,SPARROW E M. Theory for Off-specular Reflection from Roughened Surfaces[J].Journal of the Optical Society of America,1967, 57(9): 1105-1112. |
| [14] | KUKKO A, KAASALAINEN S, LITKEY P. Effect of Incidence Angle on Laser Scanner Intensity and Surface Data[J]. Applied Optics, 2008, 47(7): 986-992. |
| [15] | PESCI A,TEZA G. Effects of Surface Irregularities on Intensity Data from Laser Scanning: an Experimental Approach[J]. Annals of Geophysics, 2008, 51(5-6):839-848. |
| [16] | KAASALAINEN S,KROOKS A, KUKKO A, et al. Radiometric Correction of Terrestrial Laser Scanners with External Reference Targets[J]. Remote Sensing, 2009, 1(3): 144-158. |
| [17] | FANG Wei, HUANG Xianfeng, ZHANG Fan, et al. Intensity Correction of Terrestrial Laser Scanning Data by Estimating Laser Transmission Function[J]. IEEE Transactions on Geoscience and Remote Sensing, 2015, 53(2): 942-951. |
| [18] | COREN F,STERZAI P. Radiometric Correction in Laser Scanning[J]. International Journal of Remote Sensing, 2006, 27(15): 3097-3104. |
| [19] | PFEIFER N, HÖFLE B, BRIESE C, et al. Analysis of the Backscattered Energy in Terrestrial Laser Scanning Data[J].International Archives of the Photogrammetry, Remote Sensing and Spatial Information Science, 2008(37):1045-1052. |
| [20] | SELF S A. Focusing of Spherical Gaussian Beams[J]. Applied Optics,1983,22(5):658-661. |