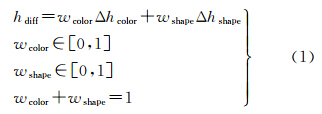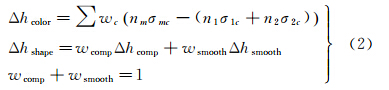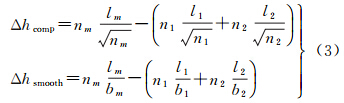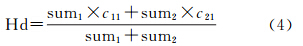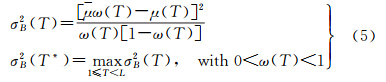2. 中国科学院电子学研究所空间信息处理与应用系统技术重点实验室，北京 100190；
3. 河北省制图院, 河北 石家庄 050031
2. Key Laboratory of Technology in Geo-spatial Information Processing and Application System, Institute of Electronics, Chinese Academy of Sciences, Beijing 100190, China;
3. Hebei Provincial Institute of Cartography, Shijiazhuang 050031, China
随着遥感技术的发展，高分辨率影像能够提供越来越详尽的地面特征，既有如水体、农田等大尺度地物，又有如汽车、交通标记等小尺度地物，多尺度特征表现得更加明显。单个像元已经很难表达一个地物目标并且基于像元的分割结果往往不连续，而面向对象的分割方法可以克服这些缺点，随之应运而生。伴随着多尺度特征的凸显，于21世纪初多尺度概念在图像分割领域得到了广泛应用。多尺度分水岭(watersheds)算法[1, 2]、均值漂移算法(mean shift)[3]、统计区域合并算法[4]、小波域HMT模型[5]、基于图的分割算法[6]以及分形网络演化方法(fractal net evolution approach，FNEA)[7]等都是多尺度分割领域典型的算法。这类方法通常试图采用特定的最优尺度阈值参数来控制分割过程，以使地物高水平对象特征得到更好地表达[8]。目前最优分割尺度的选择方法可以归为定性和定量两种。定性方法主要是“试错法”[9]，即根据研究者的需求通过反复试验分割尺度，目视确定其值。这种方法具有一定的主观性，受工作人员专业水平和感官差异的限制，很难得到最优分割结果。另有一些研究者设计各种模型或算法来定量确定不同地物的最佳分割尺度，以增强对目标物的检测与识别能力,如影像方差和空间自相关法[8]、局部方差法[10]、最大面积法[11]、矢量距离指数[12]以及建立图斑显著性变化曲线[13]，对最优尺度的确定进行试验，也取得了一定的成效。然而这些方法往往只针对某种特定地物类型，这时获得的最佳分割尺度并非每种地物的最佳分割尺度。因为在一幅遥感图像中，对于不同的地物，其适宜的分割尺度可能不同，如水体和汽车所需的分割尺度就不一样。研究表明小的尺度阈值会得到详尽的较小区域，大的尺度阈值产生较大的影像区域从而反映特征显著的对象。这样往往导致大尺度地物适合时，小尺度地物欠分割；小尺度地物适合时，大尺度地物过分割，很难得到一个满足不同尺度地物需求的结果。
鉴于此，本文提出一种k均值聚类引导的多尺度分割优化方法，该方法降低了对尺度参数的依赖，可以同时获得适应不同地物类型的分割结果，下面以FNEA方法为例来说明该优化方法的原理与流程。
2 基于FNEA的影像初分割FNEA是文献[7]在2000年提出的一种面向对象的多尺度图像分割方法，通过设置不同的尺度参数，并基于自下而上信息进行区域合并，最终得到对象的层次结构。这种面向对象的思想综合考虑对象的光谱特征和形状特征等优点，使得其优于其他的多尺度分割算法。
该方法的依据为合并前后单元的异质度变化程度，合并规则要求合并前后对象的异质度变化最小，合并后异质度的增加量hdiff表示为
式中，Δhcolor为光谱异质度增量，权重为wcolor；Δhshape为形状异质度增量，权重为wshape。Δhshape由紧致度增量Δhcomp和光滑度增量Δhsmooth两部分组成，权重分别为wcomp和wsmooth，计算公式如式(2) 式中 式中，wc表示每个波段c的权值；n1、n2、σ1c、σ2c、l1、l2、b1、b2分别为要合并的两个对象的像素个数、方差、周长和最小外包矩形的周长；nm、σmc、lm、bm分别为合并后的对象的像素个数、方差、周长和最小外包矩形的周长。
FNEA方法采用局部最优合并策略，与全局最优策略相比，能够顾及更多的细节和低对比度区域，而且执行效率更高。FNEA对象的合并是一个迭代的过程，在每一次迭代中，若该对象与其邻域对象的最小异质度增量小于阈值，则将它与该邻域对象合并成新的对象，否则不进行任何操作。迭代终止的条件是在该次迭代中所有的对象都没有与其邻域对象进行合并，即该次迭代过程中异质度的增加量超出了阈值。
在本文中，FNEA作为初分割，设置较小的尺度参数得到较小的分割对象，以便作为后续基于k均值聚类引导优化合并过程的基础。
3 k均值聚类引导的多尺度分割优化方法3.1 k均值聚类引导的优化策略
k均值聚类[14]是一种非监督分类方法，易于实现且效率较高，在所有聚类算法中应用最为广泛。它以距离为相似性准则，认为两个对象的距离越近，其相似度越大。利用k均值聚类对原始数据进行分类，能够得到适合大尺度地物较好的分类结果。
将k均值聚类结果应用于初分割后的小尺度对象合并过程，包括以下3个步骤：
(1) 判断对象层中每个对象和其邻域对象的类别。结合k均值聚类的结果，统计FNEA小尺度分割结果每个对象的类别直方图。判定标准：如果该对象中绝大多数像素即第一主类的百分比大于k均值聚类影响控制因子α，则定义该对象为第一主类所属类别；反之则不对该影像进行处理。
(2) 计算当前对象与类别相同的邻域对象的类别同质度Hd，并得到最大的类别同质度Hdmax。
(3) 该对象与类别同质度最大的邻域对象合并。
算法的具体流程参见图 1。
 |
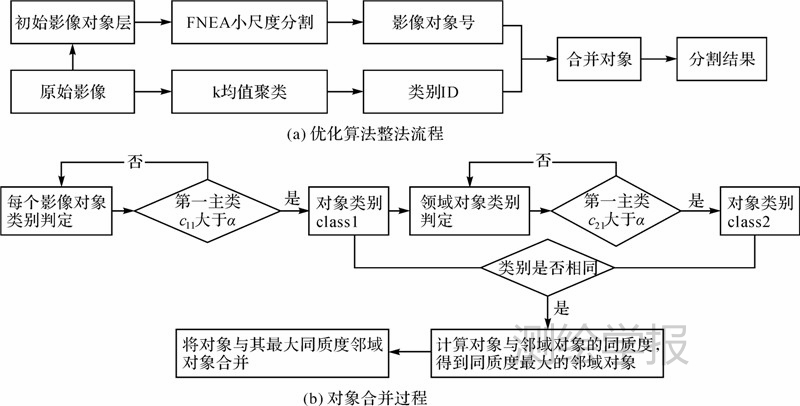| 图 1 k均值聚类引导多尺度分割算法流程Fig. 1 The flowchart of k-means clustering guiding multi-scale segmentation |
这里合并中所用类别同质度的定义为
式中，sum1和c11分别为当前处理对象像素数和第一主类百分比；sum2和c21分别为邻域对象的像素数和第一主类百分比。 3.2 基于Otsu自动阈值的k均值聚类影响控制因子α的确定
从图 1 k均值聚类引导优化流程可以看出，控制因子α的确定至关重要。为了保证该因子能够自动的适应不同影像的需要，提出一种基于Otsu自动阈值选择的确定方法。Otsu阈值选择法[15]是一种比较流行的自动阈值选择方法。该方法将阈值选择看作一种二类分割问题，基于直方图统计理论寻找类内方差最小或类间方差最大的值。在分割合并过程中，k均值聚类结果的影响无非是判断该对象类别的单纯性和主导性，进而判断是否要进行后面的引导处理，本质上也是一种二类问题，所以在此应用二类分割方法来自动获取控制因子是可行的。Otsu自动阈值分割方法的目标函数可以用类间方差最大求解，其形式为
式中，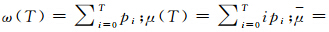
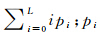表示值为i的像素出现的概率；T*表示满足目标函数的最优阈值；L为影像的灰度水平。首先将原始影像的每个像素的波段值进行平方和相加再开平方获得每个像素的亮度值，然后利用Otsu方法对亮度值影像按照式(5)进行二类分割获得阈值T*，求取T*所对应的累积概率值，该值即为所求取的控制因子α。
4 试验结果与分析为了验证本文方法的有效性，采用模拟影像和GeoEye-1遥感影像两组数据进行试验，如图 2所示。利用FNEA不同分割尺度与本文方法进行对比试验，运用对象一致性误差[16, 17](object-level consistency error，OCE)，变化信息(variation of information，VI)[18]作为分割结果整体评价的定量评价指标。为了更好地体现面向对象的思想，同时利用形状指数(shape index，SI)[19]、完整性(completeness，CPS)和正确性(correctness，CRS)[20]来对分割结果进行对象级别的定量评价。
 |
| 图 2 试验数据Fig. 2 The images of experiments |
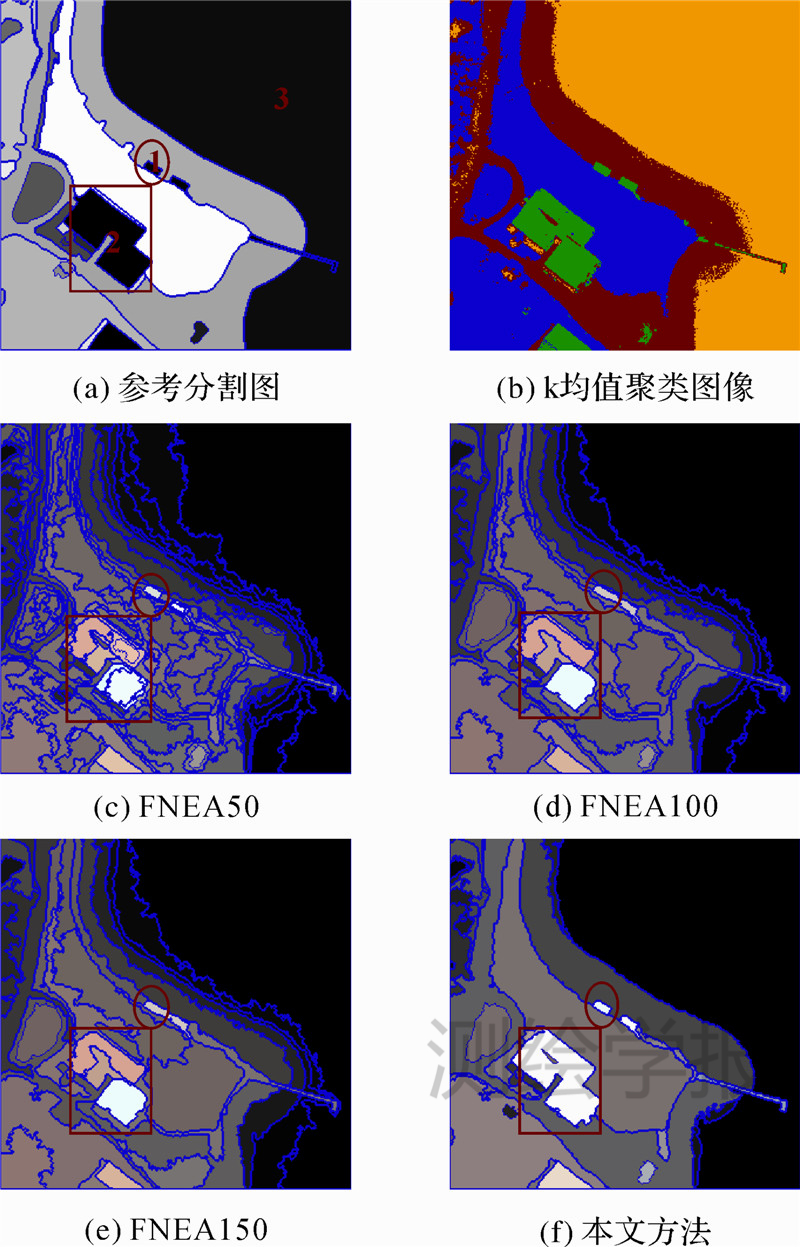
第1组试验数据是从GeoEye-1遥感影像中提取的样本数据而组合的图像，影像左上角为草地、右上角为森林、左下角为水体、右下角为耕地，在草地和林地中还零星有一些大小和颜色不同的房子，大小为512像素×512像素，如图 2(a)所示。图 3(a)是用来评价的参考分割图像，分别选取3个不同尺度的对象(对象1、对象2和对象3)区域作定量评价。图 3(b)是经k均值聚类得到的分类图。利用FNEA不同尺度参数50、100、150以及本文方法(初分割尺度50)对图 2(a)进行分割，分割结果分别见图 3(c)、图 3(d)、图 3(e)、图 3(f)，定量评价见表 1、表 2、表 3。
 |
| 图 3 模拟影像分割结果Fig. 3 Segmentation results of the simulated image |
从图 3分割结果可以看出FNEA方法在较小尺度时存在过分割现象，如图 3(c)对象1区域内的房子、对象2区域的房子和右下角耕地区域，而在较大尺度时误分割严重，如图 3(e)中圆形区域内小房子没有被分割出来。主要原因在于FNEA分割过程中过度依赖尺度参数，尺度阈值越大，分割结果合并越严重，容易产生欠分割现象；反之则存在过分割现象。与FNEA各个尺度分割结果相比，本文方法分割结果能够较好地满足各种尺度地物的分割需要，分割效果均有很大提高。
定量评价指标中，VI是由实际分割结果的熵、参考分割图像的熵以及实际分割结果与参考分割图像的联合熵这3个分量计算得出，用以衡量实际分割结果相对参考分割图像的信息变化量，VI值越小分割效果越好。OCE综合考虑对象的形状和大小，能量化同一对象级别的分割图像与地面真实图像之间的差异，数值越小分割质量越好。这两个指标是分别从熵和对象的角度对整幅图像进行评价。由表 1可知，在模拟影像试验中，与FNEA不同尺度参数分割结果相比，本文方法的VI值为0.063、OCE值为0.159，均最小，表明了本文方法得到的分割结果最接近参考分割图像。
| 评价方法 | 试验方法 | |||
| FNEA 50 | FNEA 100 | FNEA 150 | 本文方法 | |
| VI | 0.706 | 0.147 | 0.143 | 0.063 |
| OCE | 0.394 | 0.219 | 0.219 | 0.159 |
CPS和CRS越接近1，表明其分割结果与参考分割图像越接近；分割对象的SI值与参考对象的SI值越接近，表明分割边界越正确，区域一致性越好，分割效果越佳。由于篇幅限制，这里只展示了有代表性的3个不同尺度对象区域定量评价结果。从表 2中可以看出，随着分割尺度参数的增加，图 3(c)—图 3(e)中对象1的分割结果逐渐变好，尺度参数为50时得到6个子对象，尺度参数为150时得到3个子对象，其SI值也越来越接近参考分割图像的SI值。结合图 3(c)、图 3(d)、图 3(e)可知，随着分割尺度的增加，小尺度地物对象2消失了，存在严重的欠分割现象。相比之下，在本文方法的分割结果图 3(f)中对象1的SI值与参考分割图像的SI值最接近，分割对象数目也相同。结合CPS和CRS可知，本文方法得到了较好的分割结果。为了验证不同尺度地物的情况，选取对象1、对象2和对象3的平均情况来进行评价，如表 3所示。从表 3中可以看出，传统FNEA不同尺度参数分割结果存在不同程度的过分割和欠分割现象，它们的SI值与参考分割图像差异较大，相比之下本文方法得到的分割结果克服了过分割和欠分割问题，SI值与参考分割图像SI值的差异最小。综上所述，本文方法能够较好地解决传统FNEA分割结果过度依赖尺度参数的问题，能够较快速得到一种适合多种尺度地物的分割结果。
| 评价指标 | 对象1 | FNEA 50 | FNEA 100 | FNEA 150 | 本文方法 |
| CPS | 1.00 | 0.440 | 0.497 | 0.509 | 0.998 |
| CRS | 1.00 | 0.434 | 0.489 | 0.501 | 0.984 |
| SI | 1.035 | 6.009 | 4.401 | 3.630 | 1.044 |
| difference /(%) | 480.580 | 325.217 | 250.725 | 0.870 | |
| 评价指标 | FNEA 50 | FNEA 100 | FNEA 150 | 本文方法 |
| 参考对象个数 | 3 | 3 | 3 | 3 |
| SI平均差异[%] | 224.795 | 99.736 | 74.906 | -0.142 |
| 对象平均分割数目 | 4.667 | 2 | 1.667 | 1 |
4.2 真实GeoEye-1遥感图像分割试验
第2组试验数据是澳大利亚塔斯马尼亚州的首府霍巴特港口区域分辨率为0.5 m的GeoEye-1影像,图中主要有植被、水体、房屋和不透水层4类地物，为了清楚的展示结果，笔者选取大小为300像素×300像素局部影像块。图 2(b)是待分割的影像，图 4(a)是参考分割图，分别选取3个有代表性的对象(对象1、对象2和对象3)区域作定量码评价，图 4(b)为图 2(b)经k均值聚类得到的分类图。同样，作者采用传统的FNEA不同尺度参数50、100、150与本文方法(初分割尺度50)进行对比，分割结果分别见图 4(c)、图 4(d)、图 4(e)、图 4(f)。定量评价见表 4、表 5、表 6。
 |
| 图 4 真实GeoEye-1影像分割结果Fig. 4 Segmentation results of the real GeoEye-1 image |
| 评价方法 | 试验方法 | |||
| FNEA 50 | FNEA 100 | FNEA 150 | 本文方法 | |
| VI | 2.187 | 1.427 | 1.296 | 0.497 |
| OCE | 0.807 | 0.685 | 0.676 | 0.635 |
| 评价指标 | 对象1 | FNEA 50 | FNEA 100 | FNEA 150 | 本文方法 |
| CPS | 1.000 | 0.234 | 0.398 | 0.398 | 0.952 |
| CRS | 1.000 | 0.225 | 0.392 | 0.427 | 0.880 |
| SI | 1.042 | 0.992 | 0 | 0 | 0.992 |
| difference /(%) | -4.798 | -100 | -100 | -4.798 | |
| 注：-100%表示对象没有被分割出来。 | |||||
| 评价指标 | FNEA 50 | FNEA 100 | FNEA 150 | 本文方法 |
| 参考对象个数 | 3 | 3 | 3 | 3 |
| SI平均差异/(%) | 233.360 | 97.158 | 74.787 | 21.135 |
| 对象平均分割数目 | 8.667 | 3 | 2.33 | 2 |
从图 4分割结果可以看出，FNEA方法在各种尺度下都存在明显的误分割现象，在较小分割尺度，存在明显的过分割现象，如图 4中对象2区域内的房子。随着尺度参数的增加，房子分割效果明显变好，但是较小尺度地物如图 4中对象1区域内房子却没有分割出来，即存在欠分割现象。本文方法不仅纠正了误分割现象，解决了FNEA小尺度参数的过分割现象和大尺度参数的欠分割现象，而且很大程度上保留了分割对象边界的细节信息，分割精度得到了较大的提高。
在定量评价上，采取与模拟影像试验一样的评价策略。整体评价指标中，本文方法的VI值为0.497，低于FNEA各个尺度参数分割结果的最小值1.296，表明本文方法所得分割结果与理想分割结果相比，信息变化量较少。本文方法的OCE值为0.635，小于FNEA各个尺度参数分割结果的最小值0.676，表明本文方法所得分割结果与参考分割结果最为一致。表 5是图 4中对象1(红色圆形内)各种分割方法的定量评价，显然FNEA在尺度参数为50的时候，能够将该对象较好地分割出来，但是对于其他大尺度地物来说，却存在明显的过分割现象(如水体和植被)。随着分割尺度的增加，在尺度参数为100和150的时候，过分割现象逐渐减小，但是小尺度地物却存在欠分割现象如对象1没有被分割出来。表 6是选取3个有代表性的对象区域的平均情况进行定量评价结果，可以看出本文方法的SI值平均差异为21.135%，较FNEA各个尺度参数分割结果74.787%更接近0，同时各个对象平均分割数目是2也相对较好，不存在明显的过分割现象。综上可知，本文方法在FNEA小尺度分割结果的基础上再进行一次对象合并，能较好地保持小尺度分割结果中的细节，如尺寸很小的房子(对象1)，同时也得到了更加完整、规则的较大尺度地物，如水体、植被等。
5 结 论
针对传统多尺度分割方法过分依赖尺度参数，大尺度地物和小尺度地物分割难以得到权衡的问题，本文提出一种k均值聚类引导的多尺度分割优化方法。模拟影像和真实遥感影像的试验结果表明与传统FNEA方法相比，本文方法在分割精度和细节方面有较大的提高，能够得到适合多种尺度地物较好的分割结果，无需进行多次尝试得到最优尺度参数，基本解决了传统FNEA方法的分割结果对尺度参数过度依赖的问题。
本文仅以FNEA这种多尺度分割方法为例，下一步工作是将这种优化策略扩展到其他的多尺度分割方法中，并利用其他更优的非监督分类算法进行引导，从而得到适应不同尺度地物的最优分割结果。
致谢：感谢张靖博士在论文前期工作中给予的支持。
| [1] | VANHAMEL I, PRATIKAKIS I, SAHLI H. Multiscale Gradient Watersheds of Color Images[J]. IEEE Transactions on Image Processing, 2003, 12(6): 617-626. |
| [2] | XIAO Pengfeng, FENG Xuezhi, ZHAO Shuhe, et al. Segmentation of High Resolution Remotely Sensed Imagery Based on Phase Congruency[J]. Acta Geodaetica et Cartographica Sinica, 2007, 36(2): 146-151. (肖鹏峰, 冯学智, 赵书河, 等. 基于相位一致的高分辨率遥感图像分割方法[J]. 测绘学报, 2007, 36(2): 146-151.) |
| [3] | COMANICIU D, MEER P. Mean Shift: A Robust Approach toward Feature Space Analysis[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2002, 24(5): 603-619. |
| [4] | NOCK R, NIELSEN F. Statistical Region Merging[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2004, 26(11): 1452-1458. |
| [5] | HAN Bing, ZHAO Yindi, GE Lele. Wavelet-domain in HMT Model Based on Iterative Context Fusion for Remote Sensing Image Segmentation[J]. Acta Geodaetica et Cartographica Sinica, 2013, 42(2): 233-237. (韩冰, 赵银娣, 戈乐乐. 遥感图像分割的迭代上下文融合小波域HMT模型[J]. 测绘学报, 2013, 42(2): 233-237.) |
| [6] | FELZENSZWALB P F, HUTTENLOCHER D P. Efficient Graph-based Image Segmentation[J]. International Journal of Computer Vision, 2004, 59(2): 167-181. |
| [7] | BAATZ M, SCHPE A. Multiresolution Segmentation: An Optimization Approach for High Quality Multi-scale Image Segmentation[C]//Angewandte Geographische Informationsverarbeitung XII: Beitrge zum AGIT-Symposium. Salzburg: Herbert Wichmann Verlag, 2000: 12-23. |
| [8] | IKOKOU G B, SMIT J. A Technique for Optimal Selection of Segmentation Scale Parameters for Object-oriented Classification of Urban Scenes[J]. South African Journal of Geomatics, 2013, 2(4): 358-369. |
| [9] | LI Qin, GAO Xizhang, ZHANG Tao, et al. Optimal Segmentation Scale Selection and Evaluation for Multi-layer Image Recognition and Classification[J]. Journal of Geo-Information Science, 2011, 13(3): 409-417. (李秦, 高锡章, 张涛, 等. 最优分割尺度下的多层次遥感地物分类实验分析[J]. 地球信息科学学报, 2011, 13(3): 409-417.) |
| [10] | KIM M, MADDEN M, WARNER T. Estimation of Optimal Image Object Size for the Segmentation of Forest Stands with Multispectral IKONOS Imagery[M]//Object-based Image Analysis. Berlin: Springer, 2008: 291-307. |
| [11] | HUANG Huiping. The Scale of the Problem of Object-oriented Image Analysis[D]. Beijing: Institute of Remote Sensing and Digital Earth Chinese Academy of Sciences, 2003, 124-126. (黄慧萍. 面向对象影像分析中的尺度问题研究[D]. 北京: 中国科学院遥感应用研究所, 2003, 124-126.) |
| [12] | YU Huan, ZHANG Shuqing, KONG Bo, et al. Selection of the Optimal Segmentation Scale in Object-oriented Remote Sensing Image Classification[J]. Journal of Image and Graphics, 2010, 15(2): 352-360. (于欢, 张树清, 孔博, 等. 面向对象遥感影像分类的最优分割尺度选择研究[J]. 中国图象图形学报, 2010, 15(2): 352-360.) |
| [13] | CHEN Jianyu, PAN Delu, MAO Zhihua. High-resolution Remote Sensing Images Coastal Optimal Partition of Simple Objects-scale Problems[J]. Scientia Sinica Terrae, 2006, 36(11): 1044-1051. (陈建裕, 潘德炉, 毛志华. 高分辨率海岸带遥感影像中简单地物的最优分割尺度问题[J]. 中国科学: 地球科学, 2006, 36(11): 1044-1051.) |
| [14] | WANG Xiaojun, LEESER M. K-means Clustering for Multispectral Images Using Floating-point Divide[C]//Proceedings of the 15th Annual IEEE Symposium on Field-programmable Custom Computing Machines. Napa, CA: IEEE, 2007: 151-162. |
| [15] | OTSU N. A Threshold Selection Method from Gray-level Histograms[J]. IEEE Transactions on Systems, Man and Cybernetics, 1979, 9(1): 62-66. |
| [16] | POLAK M, ZHANG Hong, PI Minghong. An Evaluation Metric for Image Segmentation of Multiple Objects[J]. Image and Vision Computing, 2009, 27(8): 1223-1227. |
| [17] | ZHOU Jiaxiang. Study on Mean Shift Segmentation and Application of Remotely Sensed Imagery[D]. Changsha: Central South University, 2012. (周家香. Mean Shift 遥感图像分割方法与应用研究[D]. 长沙: 中南大学, 2012.) |
| [18] | MEILA M. Comparing Clusterings: An Information Based Distance[J]. Journal of Multivariate Analysis, 2007, 98(5): 873-895. |
| [19] | NEUBERT M, MEINEL G. Evaluation of Segmentation Programs for High Resolution Remote Sensing Applications[C]//Proceedings of the Joint ISPRS/EARSel Workshop:High Resolution Mapping from Space. Hannover, Germany: [s.n.], 2003. |
| [20] | ROTTENSTEINER F, TRINDER J, CLODE S, et al. Using the Dempster-shafer Method for the Fusion of LiDAR Data and Multi-spectral Images for Building Detection[J]. Information Fusion, 2005, 6(4): 283-300. |