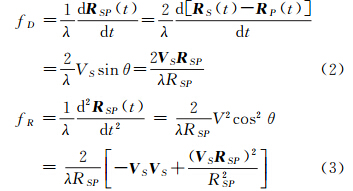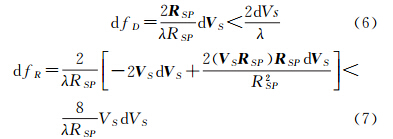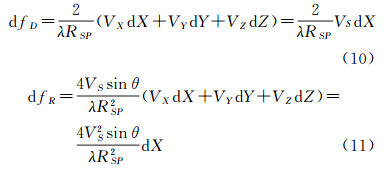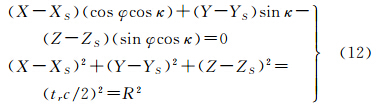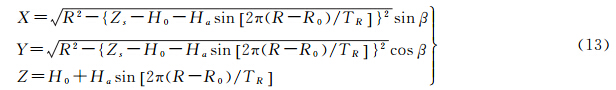2. 武汉大学测绘遥感信息工程国家重点实验室, 湖北 武汉 430079
2. State Key Laboratory of Information Engineering in Surveying, Mapping and Remote Sensing, Wuhan University, Wuhan 430079, China
1 引 言
SAR成像涉及两种多普勒参数,一种是SAR信号的多普勒,它是成像处理的输入参数,不同信号单元间的多普勒值规律性较差;另一种是成像处理后的输出多普勒参数,用于SAR影像几何处理,不同像点间多普勒参数值规律性强。SAR多普勒参数估计是对输入多普勒中心频率fD和调频率fR的估计,其估计误差不仅会导致噪声和模糊度的增高,降低信噪比,影响到图像的清晰度[1],也影响输出多普勒精度,影响到SAR成像形变和影像的目标对地定位[2]。当输出多普勒存在误差时,其对影像几何定位的影响为[3]
式中,R为斜距; Ma为影像成像分辨率; V为速率; x为方位向影像坐标。式(1)表明,每单位多普勒误差对SAR影像目标几何定位的影响可达到像素级。SAR多普勒中心频率估计方法有多种,如频谱分析法通过最小熵、能量平衡、压缩信号幅度[4, 5]等实现多普勒中心估计。矢量法可以通过测量目标与传感器的相对关系和速度计 算[6, 7],在星载SAR多普勒参数的估计中得到较广泛的应用,一些文献也考虑了姿态对星载SAR多普勒的影响[8]。由于飞机在飞行的过程中受到大气和其他干扰因素,传感器的位置、速度、姿态变化较快,稳定性差,加上航高较低,地形变化对多普勒参数的影响明显,给矢量法估计多普勒参数带来很大困难,以致目前在机载SAR多普勒参数估计中仍缺少有效的矢量法。对于大斜视角及复杂飞行条件下的机载SAR,距离徙动严重,导致多普勒参数估计性能下降,传统方法也遇到挑战[9]。
POS(GPS+IMU)是目前航空摄影测量重要的辅助设备,用于传感器位置和姿态的精确测量与控制。POS辅助光学影像和激光雷达(LiDAR)的直接对地定位精度可以达到米级[10, 11],表 1所列出Applanix公司产品POSAV510、AV610按不同处理方式获得的精度[12]。同时,SAR和InSAR的传感器检校技术,为获得高精度几何定标参数提供了日益成熟的方法[13]。国内1∶5万DEM已实现全覆盖,公开的全球数字高程模型(DEM)精度也在不断提升,如当前ASTER G-DEM分辨率达到30m,高程标称精度20m。这些已有的辅助数据,为使用矢量法进行复杂条件下的机载SAR高精度多普勒中心估计提供了可能。
| POS AV510 | POS AV610 | ||||||
| C/A GPS | DGPS | post | SPS | DGPS | XP3 | post | |
| position/m | 4.0~6.0 | 0.5~2.0 | 0.05~0.3 | 1.5~3 | 0.5~2 | 0.1~0.5 | 0.05~0.3 |
| velocity/(m/s) | 0.05 | 0.05 | 0.005 | 0.03 | 0.02 | 0.01 | 0.005 |
| roll & pitch/(°) | 0.008 | 0.008 | 0.005 | 0.005 | 0.005 | 0.005 | 0.002 5 |
| true yaw/(°) | 0.070 | 0.050 | 0.008 | 0.030 | 0.030 | 0.020 | 0.005 |
多普勒参数与信号的波长λ、传感器状态参数(位置向量OS和速度VS)及地面目标位置向量OP有关,fD与fR的计算式为[14]
式中,RSP、VS分别为方位向t时刻地面目标点P到传感器天线中心S的相对位置矢量及传感器速度;RSP为天线中心S到地面点P的距离;VS为传感器速率;θ为斜视角,该角与波束指向(姿态)和目标斜距相关[14](图 1)。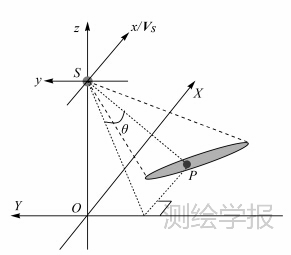 |
| 图 1 姿态对多普勒参数影响示意图 Fig. 1 Influence of attitude to Doppler centroid |
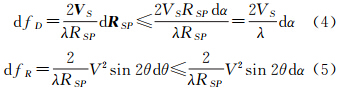
式(2)、式(3)中虽没有姿态参数,但当存在俯仰角φ或偏航角κ时,则会改变当前SAR信号的斜视角θ和目标被照射时的距离(图 1),故φ角和κ的改变会使fD和fR发生改变。欧拉姿态角有多种转角顺序,文献[15]表明,三轴均有旋转,且仅滚动角转序置于最后时,才不会影响目标被照射时与传感器间的相对关系,不改变信号的多普勒参数。
姿态会导致不同距离端照射目标的改变,设传感器绕通过自身轴旋转的小角度dα导致斜距为RSP的新目标位置偏移为dRSP,则有
假设,载机的速度为150m/s,斜距长度为7000m,当λ波长为0.03m,θ=10°时,可得由AV610姿态误差0.005°导致的fD和fR误差分别小于0.87Hz和0.0064Hz/s,AV510姿态误差0.008°导致的fD和fR的误差分别小于1.00Hz和0.01Hz/s。
2.2 POS速度及其误差对多普勒参数的影响
式(2)、式(3)分别对速度微分,有
POS AV510和AV610速度测量后处理精度为0.005m/s,由其导致的fD和fR精度损失不大于0.33Hz和0.025Hz/s。 2.3 DEM及其误差对多普勒参数的影响
传感器或地面点位置的变化均会引起传感器至地面目标矢量RSP的改变,式(2)、式(3)分别对向量RSP微分,有
高程发生变化时,距离单元信号反射体理论位置沿着波束面内的等距离圆移动,影响到地面坐标的计算。设地面坐标增量为(dX,dY,dZ),并考虑到速度与X方向一致,由式(8)、式(9)得
高程变化对dX的影响与传感器姿态、地面入射角密切相关。在φ或κ非0情况下,根据成像几何,高程误差dH对dX的影响分别为dHtanφ和dHcotαsinκ(α为入射角)。在φ或κ角为10°、RSF=7km时,20m高程误差对dX值的影响可达3.52m,对fD和fR的影响最大达到4.19Hz和0.02Hz/s,且随高程误差和姿态角的减小、斜距的增大而降低。
以上理论分析表明,传感器状态矢量、姿态和地形参数对多普勒参数的影响均不能忽略,但在POS和合适精度DEM的支持下,可将其精度控制在理想的范围内。
3 POS与DEM支持的SAR瞬时多普勒中心计算
为了计算多普勒参数,传感器状态和地面点坐标应归算到一个统一的坐标系中,这个统一的坐标系可以是地心直角坐标系,也可以在DEM数据所在的投影(UTM或高斯)坐标系中进行。当采用DEM数据所在的参考坐标系作为物方坐标系时,能够方便后继多普勒参数的处理。本文采用投影系,在处理前将POS测量得到的传感器位置和姿态数据进行了转换,其中姿态采用文献 [16]提出的导航坐标系到投影坐标系转换方法进行转换。
不同方位和距离向信号单元的瞬时多普勒参数是不同的[17],矢量法多普勒参数的计算需要确定信号反射体的地理位置,距离-共面方程以传感器位置和姿态作为参数,能够建立起当前快、慢时间传感器状态与信号反射体间的关系[14]
式中,R=trc/2;tr为SAR信号距离向当前快时间;c为光速;(XS,YS,ZS,φ,κ)为当前慢时间对应的传感器位置和姿态(φ,κ)。式(12)表明,根据投影坐标系中SAR传感器的位置和姿态后,如果知道信号反射目标的地面高程Z,根据式(12),可以计算当前快时间信号反射体地面坐标(X,Y,Z)。在已知目标的位置后,根据传感器的位置速度状态矢量,即可计算多普勒参数。传感器状态姿态参数可由POS获取,虽然提供了DEM数据获取,但需要已知平面坐标的情况下,相应点的高程才可从DEM数据中提取,这与距离-共面方程首先需要知道高程才能计算平面坐标的方法相矛盾。本文借鉴遥感影像的纠正方法,通过迭代计算信号反射体的位置。即根据信号单元的快慢时间计算投影坐标系传感器状态矢量、姿态和斜距,设置高程迭代初值Z=Zi,根据式(12) 计算目标点平面坐标为(Xi,Yi),从DEM中提取平面坐标(Xi,Yi)处的高程值Zi+1;若Zi和Zi+1之差的绝对值小于给定的阈值δ,即|Zi+1-Zi|<δ,则求得的(Xi,Yi,Zi)即为SAR信号反射体目标的坐标,否则将高程参数重新赋值为Z=Zi+1,重新迭代计算反射体平面坐标,直到满足高程限差条件。获得地面点坐标后,利用式(2)、式(3)计算相应方位向和距离向时刻信号的多普勒参数。
由于信号是连续的过程,无法全部计算。本文在有效方位向时间和有效斜距范围内,以一定的方位向时间间隔和斜距距离间隔构建二维格网,根据各格网点的方位和距离向时间(或斜距),按上述步骤计算各格网点的多普勒参数,而任意方位向时刻和斜距信号的多普勒参数,以格网点的多普勒参数为基础,通过拟合与插值得到。其中格网大小可根据插值精度需求确定,计算也可以通过当前的多核GPU和CPU加速技术实现。
4 仿真与分析
本文试验分两部分,一是在模拟的传感器姿态和地形参数基础上进行,重点考察姿态和地形对机载SAR多普勒参数的影响;另一是以真实的复杂地形DEM和真实POS数据为基础,进行大斜视角和复杂地形条件下的波束中心多普勒参数提取试验。
4.1 姿态和地形对多普勒参数的影响仿真 4.1.1 模拟地形
为了考察不同姿态条件下地形对某一束波多普勒参数的影响,设计如下模拟地形,该模拟地形为斜距R和地面目标方位角β的函数
式中,H0为高程均值;Ha为地形的振幅;TR为地形随斜距方向的变化周期;Zs为载机的飞行高度;R为斜距。
本文令地面平均高程H0=1000m,高程变化幅度 Ha=1000,高程变化范围为0~2000m,取高程沿斜距向变化周期TR=2.4km。地形如图 2所示。该模拟地形有两个特点:①地形是同心圆正弦波形函数,高程随斜距的变化作周期性变化;②将雷达波的发射源设置在Z轴上,无论姿态角怎么变化,对于任意快时间(斜距)信号的地面反射点,高程不会出现变化。上述两点表明,任意姿态下SAR波束中心照射到的是一个形状相同的正弦波地形,有利于在不受地形干扰的情况下分析姿态对多普勒参数的影响,同时,随着斜距的不同,高程呈周期性变化,多普勒值随着高程的变化而变化能考察高程对多普勒参数的影响。
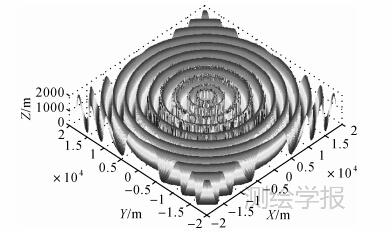 |
| 图 2 图 2模拟地形 Fig. 2 Topography simulation |
本文分别模拟φ、κ角以及φ和κ组合对多普勒参数影响。仿真采用速度为125m/s,方向与X轴相同,SAR信号的波长为0.03m,初始斜距R0=7km,远距端斜距为Rn=19km,载机飞行的航高为6.0km,相对地面平均高程的航高为5.0km,右侧视。为了考察不同地形对多普勒参数的影响,有效斜距范围划分为5个地形变化周期对多普勒值进行考察。 4.1.2 姿态和地形对目标反射信号多普勒参数的影响
(1) κ为0°,φ角-20°~20°范围内以5°作为采样间隔,斜距7~19km范围内分别以100m作为采样间隔,计算并绘制各采样点对应的fD(图 3(a),即Doppler,下同)和fR(图 3(d),即DopplerRate,下同)。
(2) φ为0°,κ角-20°~20°范围内以5°作为采样间隔,斜距7~19km范围内分别以100m作为采样间隔,计算采样点的多普勒参数,绘制fD(图 3(b))和fR(图 3(e))。
(3) 给定斜距R=7000m,分别在φ角-20°~20°、κ角-20°~20°范围内各以1°作为间隔,计算各采样点的多普勒参数,绘制fD(图 3(c))和fR(图 3(f))曲线。
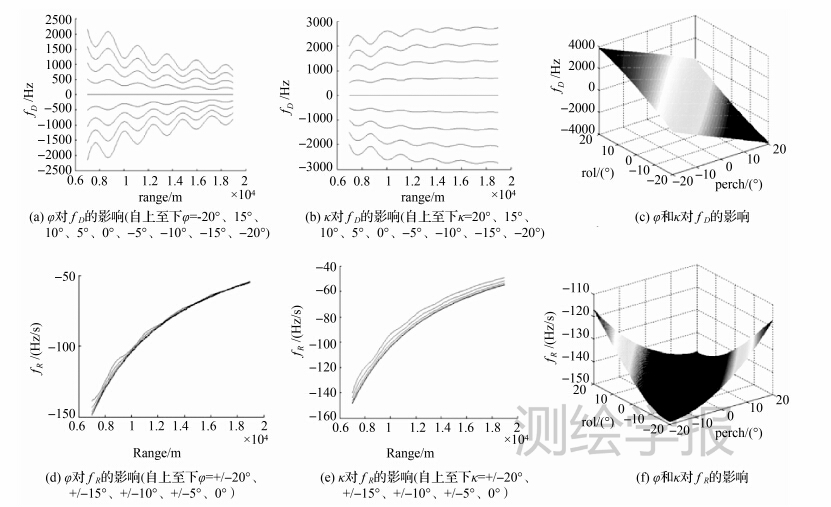 |
| 图 3 图 3姿态角对多普勒参数的影响 Fig. 3 Influence of attitudes to Doppler parameters |
在4.1.2试验1的基础上,分别以①φ各加上0.005°;②高程增加20m作为误差,重新计算距离单元反射体位置和多普勒中心值,获得高程误差导致的多普勒参数误差,绘制fD增量(图 4(a)、图 4(c))和fR增量曲线(图 4(e)、图 4(g))。在4.1.2试验2的基础上,分别以①κ角各加上0.005°;②高程增加20m作为误差,同样计算高程误差导致的多普勒参数误差,绘制fD增量(图 4(b)、图 4(d))和fR增量曲线(图 4(f)、图 4(h))。
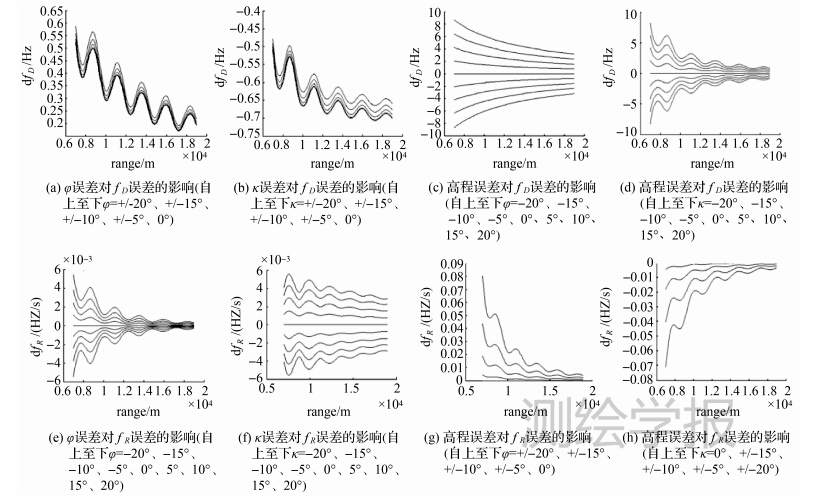 |
| 图 4 姿态误差和高程误差对多普勒参数误差的影响 Fig. 4 Influence of attitude and height errors to Doppler parameter errors |
从以上fD、fR走势图中,可以得出姿态、斜距及高程对多普勒参数(绝对值)的影响规律:
(1) 从图 3(a)、图 3(e)可以看出,φ越大,fD越大,fR越小,fD受φ的影响比fR更明显;κ角为0且φ非0时,斜距越大,fD和fR越小。
(2) 从图 3(b)、图 3(f)可以看出,κ越大,fD越大,fR越小,fD受κ的影响比fR更明显;斜距越大,fD越大,fR越小。
(3) 从图 3(a)、图 3(e)、图 3(b)、图 3(f)可以看出,fD和fR受地形的影响近距端值大于远距端值,大姿态角时值大于小姿态角时值。
(4) 从图 3(c)、图 3(g)可以看出,κ和φ对斜距信号fD的影响呈近似线性关系,φ或κ角度达到20°时,fD将近2000Hz,均达到20°时,fD最大达到3800>Hz;姿态对fR的影响相对较小,当两种姿态角取值相近时,fR的数值较大,互为相反数时,它们对fR的影响有抵消作用。
(5) 图 4表明,姿态误差和高程误差对fD的影响大于对fR的影响,在POS测量精度下,姿态误差对fD和fR的影响分别小于0.6Hz和0.006Hz/s;较大姿态角时高程误差对多普勒参数的影响也较大,姿态角达到10°时,20m高程误差导致fD和fR误差可达4.20Hz和0.02Hz/s;姿态和高程误差导致的多普勒估计值近距端误差大于远距端误差。
以上理论和试验表明,即使在全球SRTM支持下,实际应用中大多数情况下多普勒估计能获得理想的精度,表明本文方法对外部辅助DEM要求的精度远低于的当前机载InSAR DEM产品精度(国内外均可优于1m[18, 19])。同时由于多普勒估计误差与雷达波长成反比、与高程误差成正比,在国内1∶5万DEM已全覆盖、1∶1万DEM也普遍存在情况下,特殊条件下fD和fR最大误差可控制在1Hz和0.005Hz/s;对于常用的Ku~P波段,雷达波长在0.02~1.30m,大多数情况下会高于本文0.03m波长SAR数据精度。
4.2 山区DEM与POS结合的多普勒参数提取
地形数据取自我国西部山区ASTER G-DEM数据,区域中心地理坐标为(32.36°N,103.75°E),该区域高程范围为2500~4500m,地形复杂。采用2006年异地飞行的机载POSAV510数据,平移到该DEM数据区域,设计航高为9700m,相对于地面平均高程的航高约为6000m,载机的飞行速度约为135m/s北向飞行。试验时假设SAR天线安装时俯仰向偏置角为0°,天线安装偏航角分别设计为0°和10°。图 5显示了UTM投影坐标系(X轴朝东,Y轴朝北)中POS姿态和速度测量值。方位向采样间隔为5m,距离向采样间隔为10m,SAR的波长设计为X波段的0.03m。得到所有采样点的瞬时多普勒参数值并对相邻采样点间差异值进行了统计,结果填于表 2中。图 6和图 7分别显示了偏置角为10°时各采样点对应的高程、fD和fR走势。
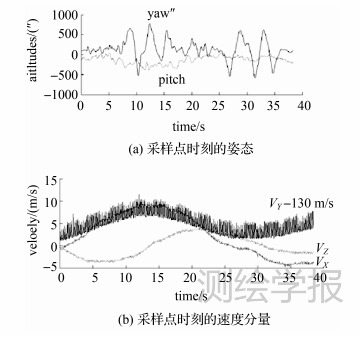 |
| 图 5 转换后的UTM坐标系POS数据 Fig. 5 POS in UTM coordinate system |
| 安装偏航角 | 特征值(绝对值) | 所有采样点 | 相邻点fD差异/Hz | 相邻点fR差异/(Hz/s) | |||
| 频率/Hz | 调频率/(Hz/s) | 方位向 | 距离向 | 方位向 | 距离向 | ||
| 0° | 最大值 | 618.58 | 166.81 | 63.21 | 58.95 | 9.92 | 0.32 |
| 最小值 | 0.000 | 63.78 | 0.000 | 0.000 | 0.000 | 0.03 | |
| 平均值 | 246.7 | 98.33 | 10.92 | 0.16 | 1.75 | 0.08 | |
| 10° | 最大值 | 2119.83 | 164.33 | 193.30 | 165.01 | 9.82 | 0.98 |
| 最小值 | 470.28 | 62.16 | 0.000 | 0.000 | 0.000 | 0.03 | |
| 平均值 | 1373.16 | 96.16 | 16.33 | 0.80 | 1.72 | 0.08 | |
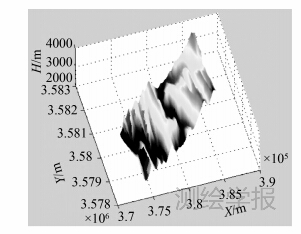 |
| 图 6 每个采样点对应的高程 Fig. 6 Sampling point elevation on different azimuths time and slope distance |
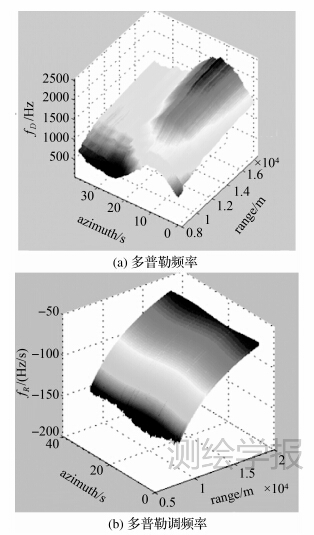 |
| 图 7 采样点多普勒频率和调频率 Fig. 7 Doppler frequency and Doppler rate of sampling points |
作为比较,本文计算了不考虑POS和DEM数据(将载机航线作为匀速直线处理,姿态按线性变化拟合插值,地面高程不变并取地面平均高程值3200m)、考虑POS但不考虑DEM数据的多普勒参数,分别计算天线安装相对于正侧视条件下偏航偏置角为0°和10°的各采样点多普勒参数值fDm和fRm。将考虑POS与DEM的数据与不考虑或不完全考虑POS与DEM的相应采样点值fDn和fRn相比,按公式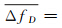
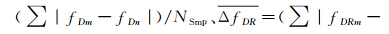
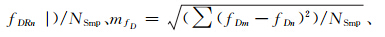
 计算相对均误差和相对中误差(NSmp为采用点总数) ,即为考虑POS与DEM数据的估计方法相对于未考虑相关参数估计精度的提高量,所得结果统计于表 3。
计算相对均误差和相对中误差(NSmp为采用点总数) ,即为考虑POS与DEM数据的估计方法相对于未考虑相关参数估计精度的提高量,所得结果统计于表 3。
| 比较内容 | 0°时fD/Hz | 0°时fR/(Hz/s) | 10°时fD/Hz | 10°时fR/(Hz/s) | ||||
| 均误差 | 中误差 | 均误差 | 中误差 | 均误差 | 中误差 | 均误差 | 中误差 | |
| 与有POS无DEM比较 | 8.87 | 13.74 | 0.02 | 0.03 | 41.56 | 65.13 | 0.14 | 0.23 |
| 与无POS无DEM比较 | 249.23 | 294.54 | 2.83 | 3.51 | 258.84 | 301.34 | 2.34 | 2.96 |
(1) 图 5和图 7可以看出,虽然POS测量速度误差对多普勒参数估计误差影响不大,但有较大偏航角情况下,速度对fD的影响是最明显的。
(2) 从表 2和图 7可以看出,在天线安装偏航偏置角达到10°时,复杂地形条件下fD变化区间为470~2120Hz,fR变化区间为62~164Hz/s,相邻点fD和fR差异分别为10.92Hz和1.75Hz/s,距离向相邻采样点多普勒参数间的差异要小于方位向相邻点多普勒差异,表明还可以通过增大距离向采样间隔、减小方位向的采样间隔来进一步平衡计算效率与估计精度的关系。
(3) 距离向相邻两点间多普勒参数值的差异主要由高程引起,方位向相邻采样点间的多普勒参数值差异与采样点处的姿态、速度、高程差异紧密相关。表 2中偏航偏置角10°时距离向fD差值最大值达到193.30Hz时,追踪相应的相邻采样点对应地面的高程分别为2562m和3033m,高差达到471m,表明陡峭地形对侧视雷达瞬时信号的多普勒中心频率有很大的影响。
(4) 从表 3可知,试验区考虑POS和DEM数据估计的多普勒参数与不考虑POS和DEM数据的值相比,0°和10°偏航偏置角条件下fD精度分别提高了294Hz和301Hz,fR分别提高了3.51Hz/s和2.96Hz/s,表明考虑POS和DEM数据的方法在复杂条件下获取的SAR数据多普勒参数估计中能显著提高精度。
5 结 论
本文分析了POS和地形误差对多普勒参数的影响,针对载机飞行不稳定的特点,利用POS数据和DEM数据,高精度估计多普勒中心值。即以POS数据获取的传感器状态矢量、姿态数据为基础,结合DEM数据,根据严密几何解算出信号反射体的位置,以传感器位置、速度和地面点位置计算多普勒参数。通过计算方位向时间和距离向快时间格网上的多普勒参数,拟合插值任意方位和距离向时刻信号的fD和fR值。本文提出的机载多普勒参数估计方法不仅考虑了传统的传感器位置和速度因素,也考虑了传感器的姿态和地形参数。理论和仿真表明,在POS和DEM支持下,本文矢量法也可以用于机载SAR多普勒中心估计,并能大幅提高斜视、非稳定飞行及复杂地形条件下的机载SAR多普勒参数估计精度,将误差控制在理想的范围内。
| [1] | LI Wenchao, YANG Jianyu, WU Junjie, et al. A Geometry-based Doppler Centroid Estimator for Bistatic Forward-looking SAR[J]. Geoscience and Remote Sensing Letters, 2012, 9(3): 388-392. |
| [2] | KONG Y K, CHO B L, KIM Y S. Ambiguity-free Doppler Centroid Estimation Technique for Airborne SAR Using the Radon Transform[J]. IEEE Transactions on Geoscience and Remote Sensing, 2005, 43(4): 715-721. |
| [3] | CHENG Chunquan, ZHANG Jixian, HUANG Guoman, et al. Range-cocone Equation with Doppler Parameter for SAR Imagery Positioning[J]. Journal of Remote Sensing, 2013,17(6):1444-1458. (程春泉, 张继贤,黄国满, 等. 考虑多普勒参数的SAR影像距离: 共面方程及其定位[J]. 遥感学报, 2013, 17(5): 1444-1458.) |
| [4] | LONG T, LU Z, DING Z G, et al. A DBS Doppler Centroid Estimation Algorithm Based on Entropy Minimization[J]. IEEE Transactions on Geoscience and Remote Sensing, 2011, 49(10): 3703-3712. |
| [5] | ZHU S, LIAO G, QU Y, et al. Unambiguous Doppler Centroid Estimation Approach for Synthetic Aperture Radar Data Based upon Compressed Signal Magnitude[J]. Radar, Sonar & Navigation, 2011, 5(3): 341-348. |
| [6] | RANEY R K. A Comment on Doppler FM Rate[J].International Journal of Remote Sensing, 1987, 8(7): 786-799. |
| [7] | BAMLER R. Doppler Frequency Estimation and the Cramer-Rao Bound[J]. IEEE Transactions on GRS, 1991, 29(3): 385-389. |
| [8] | ZHAO Bingji, QI Xiangyang, SONG Hongjun, et al. Accurate Doppler Parameters Estimation of Geo-SAR Based on Elliptical Orbit[J]. Journal of Electronics & Information Technology, 2012, 34(11): 2642-2647. (赵秉吉,齐向阳,宋红军, 等. 基于椭圆轨道的Geo-SAR 精确多普勒参数解析计算方法[J]. 电子与信息学报, 2012, 34(11): 2642-2647.) |
| [9] | YU Mingcheng, XU Jia, PENG Yingning, et al. Estimation of Doppler Parameters for Large Squint SAR[J]. Modern Radar. 2008, 30(2): 44-48. (于明成, 许稼, 彭应宁, 等. 大斜视SAR的多普勒参数估计[J]. 现代雷达, 2008, 30(2): 44-48.) |
| [10] | MOSTAFA M M R, HUTTON J. Direct Positioning and Orientation Systems: How Do They Work? What is the Attainable Accuracy?[C]//Proceedings of American Society of Photogrammetry and Remote Sensing (ASPRS) Annual Meeting. ST Louis: ASPRS, 2001: 18-27. |
| [11] | ZHAO Lijian, CHENG Xinwen, LI Yingcheng, et al. Accuracy Check and Analysis of LiDAR Elevation Data[J]. Geospatial Information, 2009, 7(1): 58-60. (赵礼剑, 程新文, 李英成, 等. 机载LiDAR点云高程数据精度检核及误差来源分析[J]. 地理空间信息, 2009, 7(1): 58-60.) |
| [12] | APPLANIX. POSAV Specification[EB/OL]. 2012[2013-11-21]. http://www.applanix.com/media/downloads/ products/specs/ POSAVSPECS0812. pdf. |
| [13] | JIN Guowang, ZHANG Wei, XIANG Maosheng, et al. A New Calibration Algorithm of Interferometric Parameters for Dual Antenna Airborne InSAR[J]. Acta Geodaetica et Cartographica Sinica. 2010, 39(1): 76-81. (靳国旺, 张薇, 向茂生, 等. 一种机载双天线InSAR干涉参数定标新方法[J]. 测绘学报, 2010, 39(1): 76-81.) |
| [14] | CUMMING I G, WONG F H. 2005. Digital Processing of Synthetic Aperture Radar Data: Algorithm and Implementatoin. Boston: Artech House Publishers. |
| [15] | CHENG Chunquan, ZHANG Jixian, DENG Kazhong, et al. Range-coplanarity Equation for Radar Geometric Imaging[J]. Journal of Remote Sensing, 2012, 16(1): 38-49. (程春泉, 张继贤, 邓喀中, 等. 雷达影像几何构像距离-共面方程[J]. 遥感学报, 2012, 16(1): 38-49.) |
| [16] | YUAN Xiuxiao, ZHANG Xueping, FU Jianhong. Transformation of Angular Elements Obtained via a Position and Orientation System in Gauss-Kruger Projection Coordinate System[J]. Acta Geodaetica et Cartographica Sinica, 2011, 40(3): 338-344. (袁修孝, 张雪萍, 付建红. 高斯-克吕格投影坐标系下POS角元素的转换方法[J]. 测绘学报, 2011, 40(3): 338-344.) |
| [17] | LIU Guangyan, HUANG Shunji. New Applications of Doppler Frequency in Squint SAR Imaging Processing[J]. Acta Electronica Sinica, 2003, 31(6): 829-832. (刘光炎, 黄顺吉. 斜视成像处理中多普勒频率的新应用[J]. 电子学报, 2003, 31(6): 829-832.) |
| [18] | MERCER B. National and Regional Scale DEMs Created from Airborne InSAR[C]//Proceedings of International Archives of Photogrammetry, Remote Sensing and Spacial Information Sciences: Photogrammetic Image Analysis. Munich: [s.n.], 2007: 49-56. |
| [19] | ZHANG Yanbin, GUO Huadong, HAN Chunming. High Precision DEM Generation Using Airborne Dual-antenna InSAR Data: A Case Study of Large Hilly Areas[J]. Remote Sensing for Land and Resources, 2014, 26(1): 97-102. (张延冰, 郭华东, 韩春明. 利用机载双天线InSAR数据生成高精度DEM的试验研究: 以大面积丘陵地区为例[J]. 国土资源遥感, 2014, 26(1): 97-102.)" |