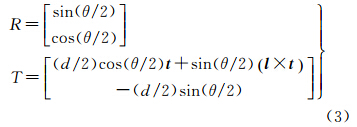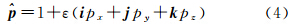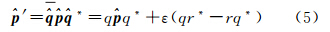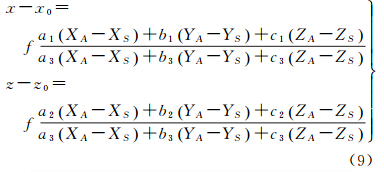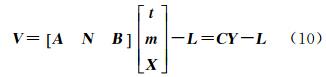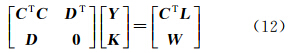1 引 言
近景摄影测量系统已广泛应用于机械制造、航空航天技术、城市区域规划和古文物研究等国民经济领域[1, 2, 3, 4]。近景摄影测量的重要研究内容是解算影像的方位元素和模型点的物方坐标。直接线性变换(direct linear transformation,DLT)与空中三角测量是近景摄影测量最常用的两种解析手段。DLT模型对控制点个数和分布要求高,易出现病态解,从而影响模型点的物方求解效率和精度,而且该模型只能独立处理单个模型,模型与模型之间不能整体平差,需要大量的外业控制点,因此在实际工程应用中工作效率低、劳动强度大且测量精度低[5]。空中三角测量是基于严密公式的解析方法,可解算影像的内、外方位元素和模型点坐标,平差精度稳定,控制点数量要求低,且深度方向的相对精度是DLT模型的4.5倍,因此在工程应用中,空中三角测量的精度最高、效率最高[6]。但传统近景影像空中三角测量需要构建测区自由网为平差提供初值,初值的好坏影响平差迭代的次数和最终的平差精度,而近距离摄影时相机抖动、平台不稳定导致近景影像姿态角大、方向无规律,易造成传统空中三角测量迭代不收敛[7]。
几何代数学中的对偶四元数能将转动和平移统一考虑,实现坐标系的空间螺旋运动[8, 9, 10]。在计算机视觉等领域,对偶四元数特别适用于分析几何投影问题[11],是描述螺旋运动的最简洁和最有效的方法[12]。在摄影测量领域,对偶四元数航空影像空间后方交会,算法的稳定性与可靠性不依赖于影像位置与姿态的初始值,并且具有迭代次数少和定向精度高等优点[13]。对偶四元数线阵CCD遥感影像几何定位能够克服成像几何参数之间的强相关性,减小位姿间的耦合误差,提高定位精度[14]。单位对偶四元数航空影像区域网平差精度与常规的区域网平差方法相当,但仅适用于姿态角小的航空影像,没有针对轻小平台影像进行处理[15]。此外,与航空摄影不同,近景摄影时,相机镜头在拆卸和重新安装过程中会引起相机内方位元素的变化,特别是像主点变化较大,可达到10个像素,严重影响了测量精度[16]。本文根据近景影像间的约束关系,建立对偶四元数近景影像空中三角测量模型,同时解算影像内、外方位元素。
2 对偶四元数近景影像空中三角测量模型 2.1 对偶四元数表示的坐标系螺旋运动
对偶四元数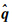 是由两个四元数q和r组成的对偶数[17]
是由两个四元数q和r组成的对偶数[17]
由Euler定理知,任意定点刚体运动可以等价为绕过该定点的轴的转动[11]。类似的,由Chasles定理知,任意刚体运动可以通过绕某个轴的旋转和沿相同轴的平移实现[18],即单位对偶四元数 的矢量形式可以完整并简洁地表示这种螺旋运动
的矢量形式可以完整并简洁地表示这种螺旋运动
 和
和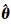 分别是螺旋轴和对偶角,
分别是螺旋轴和对偶角, =l+εp×l,
=l+εp×l,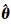 =θ+εd;单位矢量l是旋转轴的方向;矢量p是l上的点p的位置矢量;θ是绕l旋转的角度;螺距d是沿着l的方向平移的距离。利用
=θ+εd;单位矢量l是旋转轴的方向;矢量p是l上的点p的位置矢量;θ是绕l旋转的角度;螺距d是沿着l的方向平移的距离。利用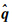 表示的坐标系的螺旋运动如图 1所示。
表示的坐标系的螺旋运动如图 1所示。
 |
| 图 1 坐标系的螺旋运动 Fig. 1 Skew motion of coordination |
坐标系S1-X1Y1Z1沿l旋转θ角度,再沿着l的方向平移距离d,可得到坐标系S2-X2Y2Z2。其中,S1在l上的投影点为p,且点矢量p=(t-dl+cot(θ/2)l×t)/2,而d=tl,则旋转矩阵和平移向量可用式(3)表示
设点p的对偶四元数形式为[19]
由图 1所示的螺旋运动可知,点p可变换到点p′,即
式中,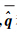 和
和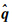 *分别是的对偶共轭和共轭。
*分别是的对偶共轭和共轭。根据式(4),点p的齐次坐标为p=(1,px,py,pz),则式(5)变为
式中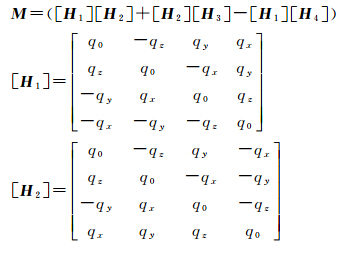

由于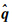 在描述螺旋运动时有8个元素,即l、θ、d和t,而描述p到p′变换过程的独立变量是6个,这意味着
在描述螺旋运动时有8个元素,即l、θ、d和t,而描述p到p′变换过程的独立变量是6个,这意味着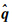 中的8个元素有两个不是独立的,应满足两个限制条件
中的8个元素有两个不是独立的,应满足两个限制条件

式中,R为利用对偶四元数实部表达的旋转矩阵[20, 21],也是摄影测量中常用的旋转矩阵;T为由对偶四元数的实部和对偶部共同表达的平移矩阵,描述了空间刚体变换中的平移变换,用来求解影像的线元素。
2.2 对偶四元数与序列影像的几何关系
对偶四元数空中三角测量模型通过对偶四元数统一表示不同拍摄时刻的光线束在空间的旋转和平移,克服了传统方法中旋转和平移分而治之引起的耦合误差,从而获得高精度的影像外方位元素和模型点的物方坐标。同时,分析不同姿态角情况下的精度,明确了对偶四元数用于近景影像空中三角测量平差解算的潜力。坐标系间的对偶四元数描述如图 2所示。区域网内有3张影像,点S1、S2、S3分别表示摄站位置,S1A、S2A、S3A为同名光线。利用形如式(2)的3个单位对偶四元数,分别将同名光线绕l旋转θ角度,再沿着l的方向平移距离d,使各影像同名光线最佳地交会于点A,整体区域网最佳地纳入物方坐标系中,获得影像外方位元素和模型点物方坐标。
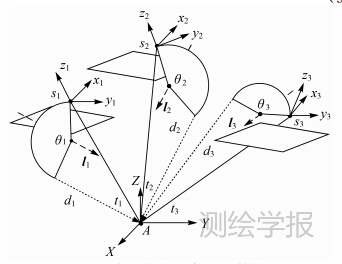 |
| 图 2 坐标系间的对偶四元数描述 Fig. 2 Coordinate transformation based on dual quaternion |
近景摄影测量时,由于相机主光轴由航空摄影时的铅垂方向变为水平方向,则坐标y和z、轴Y与Z均需互换,因此焦距f在坐标系中为正值,x、z为像点坐标观测值,x0、z0和f为影像内方位元素,且ai、bi、ci的排列与航空摄影测量不同,近景影像的共线条件方程为[22]
区域内每张近景影像外方位元素可以用式(1)进行描述,其矩阵形式为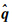 =[q0qxqyqz]T+εr0rxryrzT,由其构成的旋转矩阵与平移矩阵如式(8)所示。
=[q0qxqyqz]T+εr0rxryrzT,由其构成的旋转矩阵与平移矩阵如式(8)所示。
2.4 平差模型及其解算
考虑到相机拆装对相机内方位元素的影响,线性化方案是x0、z0和f一起进行偏导数计算,将式(8)代入式(9)中,按照泰勒公式展开至一次项,得线性化的观测方程为
式中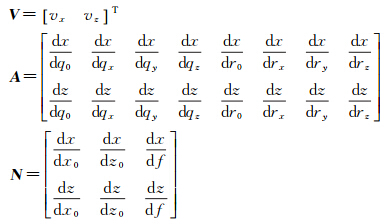
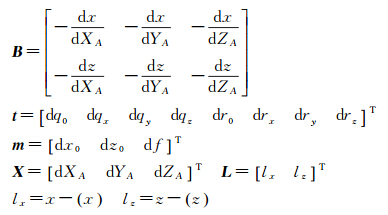
(x)和(z)是用各待定值的近似值代入式(9)求出的。
将式(4)线性化得限制条件方程
式中
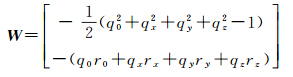
利用带条件的间接平差法建立法方程式为
式中,K为过渡性数值[23]。2.5 算法流程
算法的主要流程如下。
(1) 确定区域网内n张影像对偶四元数法各元素的初始值:q00i=1,q0xi=q0yi=q0zi= r00i=r0xi=r0yi=r0zi=0(i=0,1,…,n)。
(2) 由于未知数的近似值非常粗糙,因此计算需要通过逐次趋近方法,每次趋近时需要重新计算新的常数项,>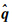 i的改正数给予限值10-6,x0i、z0i和fi的改正数给予限值10-8,当各改正数均小于限值时,趋近结束。
i的改正数给予限值10-6,x0i、z0i和fi的改正数给予限值10-8,当各改正数均小于限值时,趋近结束。
(3) 单位权中误差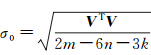 ,其中,m是控制点的像点坐标观测值个数;n是区域内影像个数;k是待求的模型点个数。在评定精度估值时,用各未知数平差值代入式(9)求出(x)和(z),得V=-lx-lzT。
,其中,m是控制点的像点坐标观测值个数;n是区域内影像个数;k是待求的模型点个数。在评定精度估值时,用各未知数平差值代入式(9)求出(x)和(z),得V=-lx-lzT。
3 试验结果及分析 3.1 真实影像试验
试验采用检校场和歼-5飞机两个不同摄影比例尺的近景目标,其主要参数如表 1所示,控制点和检查点分布分别如图 3和图 4所示(三角形为控制点、圆圈为检查点),试验区域控制点的物方坐标由摄影全站仪测量得到,对偶四元数误差方程式为 。改进的对偶四元数方法平差模型为式(12),各种方法的试验结果见表 2。
。改进的对偶四元数方法平差模型为式(12),各种方法的试验结果见表 2。
 |
| 图 3 检校场的控制点和检查点分布 Fig. 3 Distribution of control points and check points of calibration field |
| 参数 | 检校场 | 歼-5飞机 |
| 相机 | Canon EOS 5D | kodak DCS Pro-14n |
| 成像类型 | 框幅式 | 框幅式 |
| 航线/条 | 1 | 1 |
| 影像数 | 3 | 6 |
| 摄影距离/m | 40 | 5 |
| 像素大小/mm | 0.0064 | 0.008 |
| 影像分辨率 | 3732×4684 | 3000×4500 |
| x0/mm | 0 | -0.027 |
| z0/mm | 0 | 0 |
| f/mm | 51.803 | 24.138 |
| 控制点个数 | 9 | 8 |
| 检查点个数 | 6 | 11 |
| mm | |||
| 影像 | x0 | z0 | f |
| 检校场 | 0.2212 | -0.0472 | 51.782 |
| 飞机 | -0.012 | -0.0763 | 24.123 |
表 2和3结果表明,两种对偶四元数方法精度高于旋转矩阵和四元数法,这是由于近景摄影时,平台的位置和姿态会随着时间一起发生变化,旋转矩阵和四元数法通常对其采取分而治之的处理方法,破坏了运动学问题的完整性,导致转动和平移的耦合误差,而对偶四元数能够同时处理转动和平移向量,利用对偶四元数统一描述角元素和线元素,不仅构像的几何意义更加明确,而且降低了问题处理的复杂度,从而提高了平差精度。由于考虑了相机拆装后内方位元素的变化,因此改进的对偶四元数方法检查点实际深度方向精度高于其他方法,提高了测量精度。
| 平差方法 | 影像 | σ0/μm | 中误差/m | 最大残差/m | ||
| XZ | Y | XZ | Y | |||
| 旋转矩阵 | 检校场 | 9 | 0.08 | 1.02 | 0.13 | 1.98 |
| 飞机 | 2.5 | 0.004 | 0.045 | 0.006 | 0.053 | |
| 四元数 | 检校场 | 7 | 0.07 | 0.95 | 0.11 | 1.72 |
| 飞机 | 2.1 | 0.003 | 0.031 | 0.005 | 0.042 | |
| 对偶四元数 | 检校场 | 6.3 | 0.05 | 0.75 | 0.09 | 1.43 |
| 飞机 | 1.8 | 0.002 | 0.019 | 0.003 | 0.021 | |
| 改进的对偶四元数 | 检校场 | 6.1 | 0.05 | 0.56 | 0.09 | 1.12 |
| 飞机 | 1.7 | 0.002 | 0.017 | 0.003 | 0.019 | |
为了进一步验证本文方法用于一般近景影像的正确性和可靠性,本文模拟相机的拍摄状态按照不同的姿态角模拟生成了大姿态角近景影像,1个条带3张影像,外方位元素设置如表 4,像元大小为8μm,内方位元素初始值x0=z0=0mm,f=25mm,影像大小为1024像素×1280像素。采用9个控制点和133个检查点,控制点和检查点分布如图 5所示。
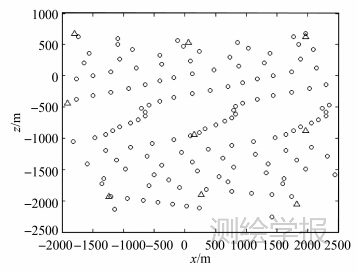 |
| 图 5 模拟影像的控制点和检查点分布图 Fig. 5 Distribution of control points and check points in the simulated images |
| 影像 | Ψ/° | ω/° | κ/° | XS/m | YS/m | ZS/m |
| 0 | 15 | -10 | -20 | 0 | -925 | 1000 |
| 1 | 20 | -25 | 30 | 200 | -925 | 1000 |
| 2 | 5 | 20 | -25 | 400 | -925 | 1000 |
针对表 4中的大姿态角近景区域网模拟影像,传统旋转矩阵法不能求解,原因是最小二乘法对法方程的性质十分依赖,当影像姿态角过大时,初值设置的不合理会造成法方程产生病态[16],导致迭代无法收敛。四元数、两种对偶四元数方法的平差结果见表 5。改进的对偶四元数方法检查点X、Z和Y方向的精度如图 6所示。
| 平差方法 | σ0/μm | 理论精度/cm | 实际精度/cm | 最大残差/cm | |||
| XZ | Y | XZ | Y | XZ | Y | ||
| 四元数 | 1.2 | 0.7 | 40.2 | 0.7 | 39.3 | 11.0 | 140.2 |
| 对偶四元数 | 1 | 0.5 | 37.8 | 0.5 | 36.2 | 10.6 | 134.1 |
| 改进的对偶四元数 | 0.9 | 0.5 | 36.5 | 0.5 | 35.3 | 10.5 | 129.4 |
表 5结果表明,四元数和两种对偶四元数法都能够进行大姿态角近景影像的空中三角测量处理,获得的单位权中误差分别为1.2μm、1μm和0.9μm。由于统一解算影像方位元素,因此改进对偶四元数法精度高于其他方法。
从图 6可以看出:
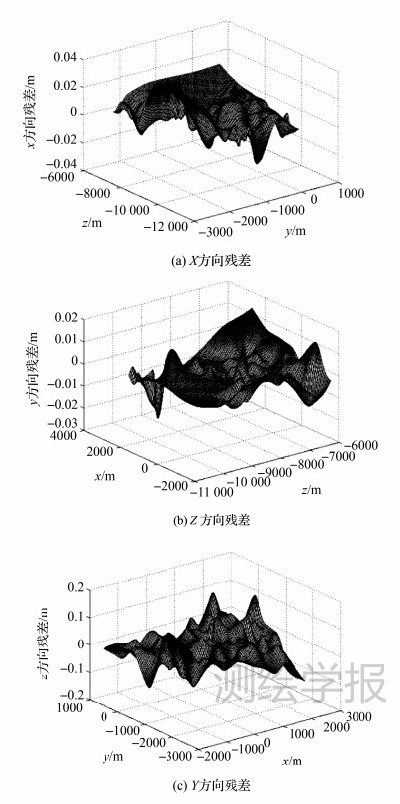 |
| 图 6 模拟影像的检查点残差图 Fig. 6 Error of check points in the simulated images |
(1) 改进的对偶四元数方法平面、深度方向实际精度分别为0.5cm和35.3cm,最大误差分别为10.5cm和129.4cm,由于该方法对初值保持了独立性,并且在平差过程中避免了频繁的三角函数运算,因此适用于姿态角较大的近景影像。
(2) 改进的对偶四元数方法平面、深度方向理论精度分别为0.5cm和36.5cm,空中三角测量平差的实际精度与理论精度相吻合,这表明模拟的控制点和像点误差非常小,此外,模拟影像相邻模型中,80%的模型点为3°重叠,因此,区域网本身的构网强度高,这从理论上保证了区域网平差的高精度。
(3) 检查点的残差分布基本符合正态随机分布,这说明这些点评定该区域网的空中三角测量加密精度是可靠的。
(4) 理论精度在深度方向明显低于平面方向,这是由于区域网内影像数量少,平差几何条件差,未知数之间的相关性影响了法方程系数矩阵的状态。由于实际精度和理论精度基本相符,因此实际深度方向精度同样明显低于平面方向。一般具有较强约束条件的一定数量的控制点不会显著影响整体平差结果,因此下一步的研究目标是分析区域网影像的数量和同名像点的交会摄影情况等对深度方向精度的影响。
4 结 论
本文提出了一种改进的对偶四元数近景影像空中三角测量模型,获得了方位元素和模型点物方坐标。结果表明由于对偶四元数统一表示了近景区域网中所有光线束的位置与姿态,因此克服了传统方法中旋转和平移分而治之引起的耦合误差,提高了解算精度。该模型不仅适用于较小姿态角的近景影像,而且由于在迭代过程中对初值无依赖,因此对于较大姿态角的近景影像,也可以得到可靠的平差结果。考虑了相机拆装对相机内方位元素的影响,能同时解算影像的内、外方位元素,因此该模型更加严密和实用,在空中三角测量结果经常不稳定的近景摄影测量中有较大的应用价值。
| [1] | XIE Yilin, YAO Lianbi, JI Huili. Approach of Sea Piling Positioning Based on Close-range Photogrammetry[J]. Acta Geodaetica et Cartographica Sinica, 2010,39(3): 238-244. (谢义林, 姚连璧, 季惠丽. 基于近景摄影测量的海上打桩定位方法研究[J]. 测绘学报, 2010,39(3): 238-244.) |
| [2] | JIA Shengju, YU Jingtao. Application of Digital Close-range Photogrammetry to Inspection of Machine Parts[J]. Acta Geodaetica et Cartographica Sinica, 2002,31:61-65. (贾盛举, 于晶涛. 数字近景摄影测量在工业检测中的应用[J]. )测绘学报, 2002,31:61-65. |
| [3] | JI Zheng. Research on Automation Technique for Close-range Object's 3D Reconstruction[D]. Wuhan:Wuhan University, 2007. (季铮. 近景目标三维重建自动化关键技术研究[D].武汉:武汉大学,2007.) |
| [4] | JI Shunping, SHI Yun. Image Matching and Bundle Adjustment Using Vehicle-based Panoramic Camera[J]. Acta Geodaetica et Cartographica Sinica, 2013,41(1):94-101. (季顺平, 史云. 车载全景相机的影像匹配和光束法平差[J]. 测绘学报, 2013,41(1):94-101.) |
| [5] | ZHANG Yongjun, ZHANG Zuxun, ZHANG Jianqing. Camera Calibration Using 2D_DLT and Bundle Adjustment with Planar Scenes[J]. Geomatics and Information Science of Wuhan University, 2002,27(6):566-571. (张永军, 张祖勋, 张剑清. 利用二维DLT及光束法平差进行数字摄像机标定[J].武汉大学学报:信息科学版, 2002,27(6):566-571.) |
| [6] | KE Tao, ZHANG Zuxun, ZHANG Jianqing. Panning and Multi-baseline Digital Close-range Photogrammetry[J]. Geomatics and Information Science of Wuhan University, 2009,34(1):44-51.(柯涛, 张祖勋, 张剑清. 旋转多基线数字近景摄影测量[J]. 武汉大学学报:信息科学版, 2009,34(1):44-51.) |
| [7] | JIANG Gangwu, JIANG Ting, DING Jing, et al. Principle and Method of Space Resection Using Orientation Matrix[J]. Journal of Geomatics Science and Technology,2009,26(1):15-19.(江刚武,姜挺,丁静,等.直接利用旋转矩阵进行空间后方交会的原理和方法[J].测绘科学技术学报, 2009,26(1):15-19.) |
| [8] | CLITFORD W. Preliminary Sketch of Biquaternions[J].Proceedings of the London Mathematical Society,1871(S1-4):381-395. |
| [9] | BI Q Z, WANG Y H, ZHU L M, et al. An Algorithm to Generate Compact Dual NURBS Tool Path with Equal Distance 5-axis NC Matching[J]. Intelligent Robotics and Applications, 2010,64(25):553-564. |
| [10] | CHIANG Y T, CHUNG Y H. Computing Location and Orientation from 2-D Line Correspondence Using Dual Quaternion[J].International Journal of Industrial Mechatronics and Automation,2010,10(6):303-306. |
| [11] | DANIILIDIS K. Hand-eye Calibration Using Dual Quaternions[J]. International Journal of Robotics Research, 1999,18:286-298. |
| [12] | STUDY E. Geometrie der Dynamen[M]. Leipzig: Nabu Press,1901. |
| [13] | JI Ting, SHENG Qinghong, WANG Huinan, et al. Dual Quaternion of Space Resection with Single-image[J]. Journal of Image and Graphics, 2012,4(17):494-503. (姬亭,盛庆红,王惠南,等.对偶四元数单片空间后方交会算法[J].中国图象图形学报, 2012,4(17):494-503.) |
| [14] | SHENG Qinghong, JI Ting, LIU Weiwei, et al. Geo-positioning Line-array CCD Images with Dual Quaternion[J]. Journal of Image and Graphics, 2012,10(17):1319-1326. (盛庆红,姬亭,刘微微,等.对偶四元数线阵遥感影像几何定位[J]. 中国图象图形学报, 2012,10(17): 1319-1326.) |
| [15] | GONG Hui, JIANG Ting, JIANG Gangwu, et al. Bundle Block Adjustment of Aerial Imagery Based on Unit Dual Quaternion[J]. Geomatics and Information Science of Wuhan University, 2012,2(37):154-159.(龚辉,姜挺,江刚武,等.利用单位对偶四元数进行航空影像区域网平差解算[J]. 武汉大学学报:信息科学版, 2012,2(37):154-159.) |
| [16] | JIANG Wensong, ZHANG Qingling, DAI Yongshu. Effects of Atmospheric Pressure on the Interior Orientation Elements about Aerial Survey Camera[J]. Acta Geodaetica et Cartographica Sinica, 1993, 22(1): 51-55.(蒋文松, 张庆令, 戴勇书. 环境压力对相机内方位元素的影响[J]. 测绘学报, 1993,22(1):51-55.) |
| [17] | ROONEY J. A Comparison of Representation of General Spatial Screw Displacement[J]. Environment and Planning B,1978,5:45-88. |
| [18] | AKYAR B. Dual Quaternions in Spatial Kinematics in an Algebraic Sense[J]. Turkish Journal of Mathematics, 2008, 32:373-391. |
| [19] | BI Q Z, WANG Y H, ZHU L M, et al.Intelligent Robotics and Applications[M]. Heidelberg:Springer, 2010: 553-564. |
| [20] | GONG Hui, JIANG Ting, JIANG Gangwu, et al. A Globally Convergent Algorithm of Space Resection Based on Quaternion[J]. Acta Geodaetica et Cartographica Sinica, 2011,40(5):639-645,654. (龚辉,姜挺,江刚武,等.一种基于四元数的空间后方交会全局收敛算法[J]. 测绘学报, 2011,40(5):639-645,654.) |
| [21] | GONG Hui, JIANG Ting, JIANG Gangwu, et al. Solution of Exterior Orientation Parameters for High-resolution Satellite Imagery Based on Quaternion Differential Equation[J]. Acta Geodaetica et Cartographica Sinica, 2012,41(3):409-415. (龚辉, 姜挺, 江刚武,等.四元数微分方程的高分辨率卫星遥感影像外方位元素求解[J]. 测绘学报, 2012,41(3):409-415.) |
| [22] | LI Deren, JIN Weixian, YOU Jianshan, et al. Basic Photogrammetry[M]. Beijing: Surveying and Mapping Press, 1992. (李德仁,金为铣, 尤兼善,等.基础摄影测量学[M].北京:测绘出版社,1992.) |
| [23] | YU Zongtao, YU Zhenglin. Survey Adjustment[M]. Wuhan: Wuhan Technical University of Surveying and Mapping Press,1990.(於宗涛,于正林.测量平差[M].武汉:武汉测量科技大学出版社,1990.) |
| [24] | JI Ting.Research of Geo-positioning High Resolution Satellite Imagery Based on Dual Quaternion[D].Nanjing:Nanjing University of Aeronautics and Astronautics,2012.(姬亭.基于对偶四元数的高分辨率卫星遥感影像几何定位研究[D].南京:南京航空航天大学,2012.)" |