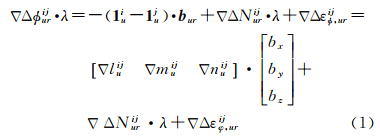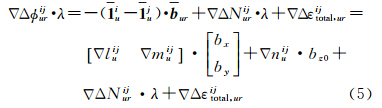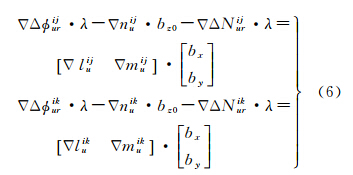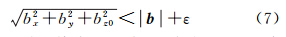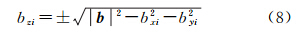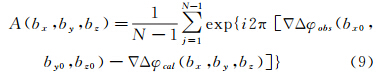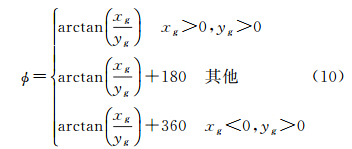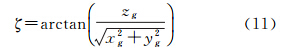2. 中国科学院大学,北京 100094
2. University of Chinese Academy of Sciences, Beijing 100094, China
1 引 言
由于具有精度高、无累积误差、成本低等优势,利用卫星导航系统进行载体定向测量已成为卫星导航高精度应用的一个重要方面[1]。2012年12月27日,北斗区域卫星导航系统正式投入运行[2],在各GNSS系统竞相发展的态势下,深入探索基于北斗系统的高精度解算技术具有重要意义,本文的目的就是研究针对北斗载波相位的高精度定向算法。
载体定向需要实时动态地确定接收机天线的相对位置。在使用卫星导航系统进行载体定向解算时,通常采用载波相位差分技术来求得载体的航向解。其中,整周模糊度的实时动态求解是关键问题。针对模糊度的解算问题,目前使用最广泛的是Teunissen提出的LAMBDA算法[3]以及学者们在此基础上提出的很多改进算法[4, 5, 6, 7, 8]。这类算法基于整数最小二乘搜索理论,在初始解算时需要较长的初始化时间,而且对周跳比较敏感。另一方面,这些算法是针对GPS提出的,在应用于北斗系统时未考虑其特殊性。北斗系统区别于其他GNSS的特点之一是其星座构型。目前,北斗系统的星座配置为5GEO+5IGSO+4MEO。通常情况下,在我国境内有8~12颗卫星同时可见,其中包含3~5颗GEO卫星。基于整数最小二乘搜索的解算方法依赖于卫星几何构型的变化,但对于北斗系统来说,所有GEO卫星处于赤道上空同一轨道面,空间位置相对固定,短时间内相对几何构型变化小。北斗GEO卫星的这种特性造成平差矩阵具有严重的病态性,给参数的求解带来很大的不稳定性,不利于实时动态模糊度解算[9, 10]。因此,传统的模糊度解算方法应用于北斗系统具有一定的不适应性,必须探索针对北斗系统的整周模糊度确定方法。
本文分析了北斗系统星座的特点,避开其GEO卫星三维几何构型不好且变化率小,不利于整周模糊度固定的劣势,充分利用北斗系统GEO卫星东西向几何构型好的特点,提出了一种针对北斗系统的降维快速高精度定向算法。
2 常规载体定向解算方法
载体定向是求解短基线下接收机天线相对位置的问题,基线长度一般在100m以内。对于这种超短基线来说,双差后电离层延迟和对流层延迟都基本消除[11]。因此,在载体定向测量中,载波相位双差观测模型为[12]
式中,ΔΔφijur为双差载波相位模糊度测量值;λ为载波波长;1iu、1ju分别为测量天线指向卫星i、j的单位矢量;bur=(bx,by,bz)为基线向量;ΔΔNijur为双差模糊度值;ΔΔεijε,ur为双差载波相位测量噪声;Δliju、Δmiju、Δniju为三维方向上的差分方向余弦系数,表示为 式中,(xu,yu,zu)为接收天线的位置;(xi,yi,zi)和(xj,yj,zj)表示卫星i和卫星j的三维位置,表示为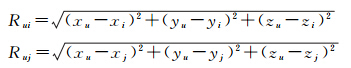
载体定向的关键技术是模糊度解算。常规算法通常采用无周跳的几个历元的数据组成如式(1)的观测方程,并联立形成方程组进行解算。解算时首先不考虑模糊度N的整数要求,直接求模糊度的浮点最小二乘解,然后在一定的搜索空间内进行整周模糊度搜索。常规算法需要进行周跳的检测和修复,并且依赖于卫星几何构型随时间的变化。对于北斗系统,由于GEO卫星静止不动导致几何构型变化小,不利于模糊度求解。
3 针对北斗系统的降维定向算法 3.1 北斗系统星座特性分析
目前,北斗系统星座构型为5GEO+5IGSO+4MEO混合星座。其中GEO卫星为地球静止轨道卫星,位于赤道平面上。根据式(2)—式(4)计算GEO卫星的三维差分方向余弦系数可知,相对于式(2)和式(3),式(4)的分子远小于分母,即z轴的方向余弦系数Δniju远小于x、y轴的方向余弦系数Δliju、Δmiju。如果忽略z轴的影响,那么立体空间内的三维解算就可以映射到二维空间内的平面解算,可将用户和卫星放在共面空间内解算。显然纬度越高,近似平面解算所带来的误差越大。图 1是在50°N地区(亚太地区内效果最差地区)对G3和G4星的三维差分方向余弦系数随经度变化的结果。由图 1可以看出,即使在亚太地区效果最差的地区,GEO卫星的z轴方向余弦系数也远小于x、y轴。式(1)中,Δniju接近于0,当bz变化较小时对式(1)其余未知参数的计算结果影响很小。
 |
| 图 1 50°N地区(效果最差地区)GEO双差方向余弦系数分析结果 Fig. 1 Coefficient value analysis results at 50°N (the least effective area) |
根据GEO卫星特性,在初始定位误差较小的情况下,可以忽略z轴误差带来的影响。对于式(1)中的Δniju·bz,解算时可直接代入初步解算的基线向量z轴分量bz0来计算其余未知参量。即式(1)可简化为
式(5)即为GEO卫星的降维双差模型。本文将北斗系统的这种特性称为GEO卫星的降维解算特性。
3.3 模糊度解算方法
针对北斗的星座特性,本文提出的针对北斗系统的定向解算方法如下:首先,利用双差伪距计算模糊度的初始值;然后,选择3颗GEO卫星组成两个降维双差观测方程,由初始伪距测量精度可以确定一组双差整周模糊度范围(±N1,±N2),根据式(5)对每一组模糊度解得一组对应的基线向量解(bx,by);利用基线长度约束计算出每一组解析解(bx,by)对应的bz,再利用所有卫星的双频观测量和模糊度函数判决准则找到最佳基线向量(bx,by,bz)并计算相应的整周模糊度,最终完成载体定向。
载体定向测量大多使用双频接收机,两个频率的观测量可以形成宽巷虚拟观测值。在双频模糊度解算时,为了提高模糊度解算的效率和成功率,通常先解宽巷模糊度,再求解原始频点模糊度[13, 14, 15]。北斗民用用户可以接收到B1、B2 两个频率的信号,这两个频率可以形成宽巷组合B1-B2。该组合在短基线下具有波长长、组合噪声小的良好性能[16]。利用组合信号先求解宽巷(B1-B2)模糊度,再用宽巷求解所得的结果作为初始基线向量求解B1频点模糊度可以减少计算量,提高解算效率。采用虚拟宽巷组合观测值对搜索点数的减小示意图如图 2所示,上半部分为直接解算B1频点模糊度所需的搜索点数,下半部分为先解算宽巷组合的模糊度,再解算B1频点模糊度所需的搜索点数。下半部分中大网格为宽巷搜索的点数,网格为在宽巷搜索的基础上进行B1频点搜索的点数。从图 2可以看出,采用虚拟组合观测值之后,搜索量大幅减小。
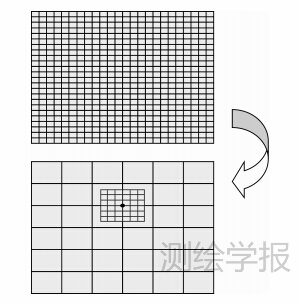 |
| 图 2 采用组合观测值带来的搜索量的减小 Fig. 2 The reduction of the amount of search using combined observations |
本节对提出的针对北斗系统的定向算法实施步骤进行具体描述。算法流程图如图 3所示。具体的算法实施步骤如下:
第1步:利用B1和B2频点上的观测量形成宽巷组合B1-B2,组合频率为353.958MHz,波长λML为0.874m。根据初始伪距值计算宽巷模糊度初始值ΔΔNij0。
第2步:利用GEO卫星的降维双差模型解算出一组基线向量候选值。
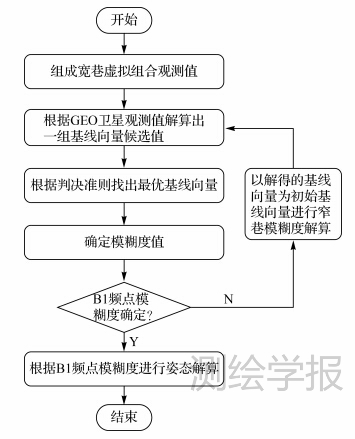 |
| 图 3 定向解算算法流程 Fig. 3 Flow chart of the new orientation algorithm |
选择3颗二维几何构型较好的GEO卫星组成两个双差观测方程,根据式(5)可得到方程组
根据初始伪距测量误差,确定ΔΔNijur、ΔΔNikur的取值范围。假设初始测量误差范围为±lm,则ΔΔNikur的取值范围为ΔΔNij0±round(l/λML)。假设有n组(ΔΔNijur,ΔΔNikur),对应于每一组(ΔΔNijur,ΔΔNikur),求解式(6)可得到一组对应的(bx,by)。根据基线长度约束
剔除部分粗差点(其中ε根据基线向量误差确定),得到l个解,表示为(bx1,by1)、(bx2,by2)、…、(bxl,byl)。对于每一组(bxi,byi),i=1,2,…,l,根据基线长度约束计算对应的bzi的值
根据式(8)得到l个基线解,表示为(bx1,by1,bz1)、(bx2,by2,by2)、…、(bxl,byl,bzl)。此时,可以将bzi代入式(6)再次计算对应的(bxi,byi)值,再计算式(8),可进一步削弱bz0误差所带来的影响。
这一步需要考虑卫星的选择,应尽量选择几何构型较好的卫星,以保证测量误差可以较少地传递到解算结果中去。将(bx,by)的解算方程简写成矩阵形式为bxby=A·δρijδρik,则各种残余误差通过矩阵A传递到解算结果(bx,by)中去,称矩阵A为误差传递矩阵。在解算时,应当选择使误差传递矩阵A的各元素较小的卫星组合,保证(bx,by)误差较小。
第3步:根据判决准则找出最优基线向量(bx,by,bz)。
在第2步所得的l个解中,只有一个解最接近基线向量的真实值,称其为最优解。这一步通过适当的判决准则来找出最优解。本文的判决准则采用模糊度函数,模糊度函数定义为[17]
式中,N表示每个历元同步观测的卫星数;ΔΔφobs(bx0,by0,bz0)为真实基线向量(bx0,by0,bz0)对应的双差载波相位观测值;ΔΔφcal(bx,by,bz)为由待检测基线向量(bx,by,bz)反算的双差载波相位值。当(ΔΔφobs-ΔΔφcal)为整数时,模糊度函数具有最大值1。显然,当基线向量最接近真值时,模糊度函数A(bx,by,bz)具有最大值。将所有可观测卫星的宽巷双差载波相位观测值和l个基线解代入式(9),利用max(A(bxi,byi,bzi))得到最优基线向量并计算相应的宽巷模糊度。
第4步:B1频点模糊度求解。通过第3步的计算得到了较为精确的基线向量,以该基线向量为初始基线向量。类似于第2步,利用B1频点观测值形成两个双差观测方程。利用宽巷模糊度计算B1频点的模糊度初始值,并确定B1频点的模糊度范围,对每一组模糊度再解算出基线向量候选值。并利用B1和B2频点的所有观测值代入模糊度函数对候选值进行判断,得到精确的B1频点的模糊度。
第5步:利用已知模糊度的高精度载波相位测量值进行定向解算。
对于双天线航向测量系统,基线与载体纵轴平行。航向角与俯仰角的计算公式为[18]
航向角(0°~360°)
俯仰角(-90°~90°)
5 仿真和结果
本文利用北斗的实际星历,在5m基线下仿真了由两个接收机天线构成的双天线定向系统。假设基线与载体纵轴平行,计算载体的航向角和俯仰角。仿真采用的测站位置为:40.07°N,116.27°S,高度85.01m。星历数据为2013-11-22 11:08:00到2013-11-23 11:08:00的北斗实际星历数据,设σφ=0.005m,σp=0.8m[19, 20],采样间隔为30s。仿真观测时间段内卫星可见性情况如图 4(b)所示,5颗GEO卫星全部可见,可见卫星总数为8~12颗。
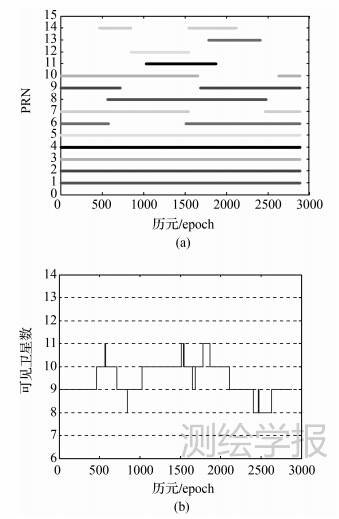 |
| 图 4 卫星可见情况 Fig. 4 Visible satellites |
利用本文提出的方法对基线向量进行单历元模糊度解算和姿态角解算。利用组合观测值进行宽巷解算的结果如图 5所示。其中图 5(a)为3轴方向上的向量误差,其中z轴误差在0.3m以内,表明下一步窄巷解算时忽略z轴带来的影响为毫米量级,保证了下一步的可行性。图 5(b)为三维误差,误差在0.5m以内,可用来确定窄巷的初始模糊度范围及搜索范围。这一步宽巷模糊度解算成功率为99.54%。
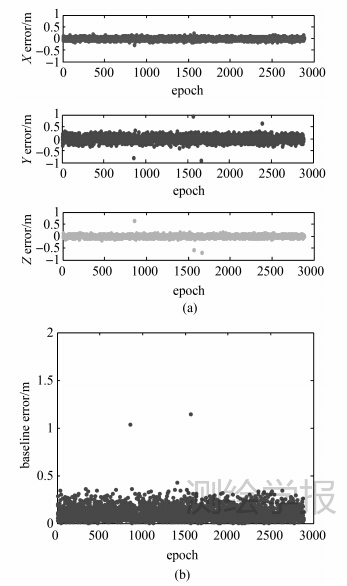 |
| 图 5 宽巷求解后所得的基线误差 Fig. 5 Baseline error after solving the wide lane |
将宽巷解算的结果作为初始基线向量值解算B1频点模糊度所得的解算误差如图 6所示。其中图 6(a)分别为3轴方向上的误差,图 6(b)为三维误差。这一步B1频点模糊度解算成功率为99.31%。
 |
| 图 6 窄巷求解后所得的基线误差 Fig. 6 Baseline error after solving the narrow lane |
利用B1频点解算结果进行载体定向解算结果如图 7所示。俯仰角的标准差为0.07°,航向角的标准差为0.13°。
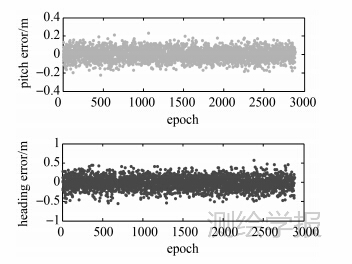 |
| 图 7 定向解算误差 Fig. 7 Orientation result error |
本文通过挖掘北斗卫星导航系统的特殊星座构型所带来的优势,提出了一种适用于北斗系统的单历元快速定向算法。该方法利用降维解算方法将模糊度搜索范围局限到几个分散的点,再利用模糊度函数法作为判决准则确定整周模糊度,并采用了先求宽巷模糊度再求解窄巷模糊度的思想,进一步减少了计算量。最后,采用仿真数据验证了新方法的有效性,得出以下结论:
(1) GEO卫星的特殊轨道特性可以使得三维解算转化为二维解算,减小模糊度搜索空间。
(2) 候选值的判断准则采用模糊度函数法,是一种简便高效的判决准则。
(3) 定向解算为短基线下的接收机天线相对位置问题,本文方法采用双差观测量,可以忽略空间误差影响,其模糊度解算成功率高(99.31%)。
(4) 采用双频观测量组成宽巷虚拟观测值,解算时先求宽巷模糊度,再求B1频点模糊度,可以提高解算效率。
(5) 本方法采用单历元数据解算,能够满足实时动态定向解算的需求。定向解算结果精度高(俯仰角的标准差为0.07°,航向角的标准差为0.13°)。
| [1] | WANG Y, ZHAN X, ZHANG Y. Improved Ambiguity Function Method Based on Analytical Resolution for GPS Attitude Determination[J]. Measurement Science and Technology, 2007, 18(9): 2985. |
| [2] | YANG Yuanxi, LI Jinlong, WANG Aibing, et al. 2014.Preliminary Assessment of the Navigation and Positioning Performance of BeiDou Regional Navigation Satellite System[J]. Science China: Earth Sciences,2014,44:72-81.(杨元喜, 李金龙, 王爱兵, 等. 2014. 北斗区域卫星导航系统基本导航定位性能初步评估[J]. 中国科学: 地球科学,2014,44: 72-81.) |
| [3] | TEUNISSEN P J G.The Least-squares Ambiguity Decorrelation Adjustment:A Method for Fast GPS Integer Ambiguity Estimation[J]. Journal of Geodesy,1995,70(1): 65-82. |
| [4] | MONIKES R, WENDEL J,TROMMER G F. A Modified Lambda Method for Ambiguity Resolution in the Presence of Position Domain Constraint[C]//Proceedings of the 18th International Technical Meeting of the Satellite Division of the Institute of Navigation. Long Beach:[s.n.],2005:81-87. |
| [5] | PETER B. The Baseline Constrained LAMBDA Method for Single Epoch,Single Frequency Attitude Determination Application[C]//Proceedings of the 20th International Technical Meeting of the Satellite Division of the Institute of Navigation. [S.l.]: ION, 2007:2962-2973. |
| [6] | GIORGI G, TEUNISSEN P J G, ODIJK D, et al. Enhancing the Time-to-fix for the Unaided Single-frequency Integer Ambiguity Resolution in GNSS Attitude Determination Applications[C]//Position Location and Navigation Symposium.[S.l.]:IEEE, 2010: 236-244. |
| [7] | GIORGI G, TEUNISSEN P J G. Low-complexity Instantaneous Ambiguity Resolution with the Affine-Constrained GNSS Attitude Model[J]. IEEE Transactions on Aerospace and Electronic Systems, 2013, 49(3): 1745-1759. |
| [8] | TANG W, DENG C, SHI C, et al. Triple-frequency Carrier Ambiguity Resolution for BeiDou Navigation Satellite System[J]. GPS Solutions, 2013: 1-10. |
| [9] | GAO W, GAO C, PAN S, et al. The Analysis of Ill Posedness in GNSS High-precision Differential Positioning[C]//Proceedings of China Satellite Navigation Conference.Heidelberg:Springer, 2013: 311-321. |
| [10] | WANG Shengli, WANG Qing, GAO Wang, et al.Analysis and Valuation of Ill-condition in Baseline Solution of GNSS Multi-system[J].Journal of Southeast University, 2013, 43(4): 753-757.(王胜利, 王庆, 高旺, 等. GNSS 多系统基线解算中的病态性分析与评价[J]. 东南大学学报: 自然科学版, 2013, 43(4): 753-757.) |
| [11] | XIE Gang. Principles of GPS and Receiver Design[M].Beijing: Publishing House of Electronics Industry,2009.(谢钢. GPS 原理与接收机设计[M]. 北京:电子工业出版社, 2009.) |
| [12] | PRATAP M, PER E.Global Positioning System: Signals, Measurements, and Performance[M]. Beijing:Publishing House of Electronics Industry, 2008:188-192. |
| [13] | QU J, YUAN H, ZHANG X, et al. Single-epoch COMPASS Carrier-phase Ambiguous Resolution Using Three Civil Frequencies and Special Constellations[C]//Proceedings of the ION GNSS. Nashville:[s.n.],2012. |
| [14] | ZHU Huizhong, LIU Jingnan, TANG Weiming. et al.The Algorithm of Single-epoch Integer Ambiguity Resolution between Long-range Network RTK Base Stations[J]. Acta Geodaetica et Cartographica Sinica,2012, 41(3): 359-365.(祝会忠, 刘经南, 唐卫明, 等. 长距离网络 RTK 基准站间整周模糊度单历元确定方法[J]. 测绘学报, 2012, 41(3): 359-365.) |
| [15] | WANG Lei, LIANG Kailong. Application of GPS Dual Frequency Observation in Attitude Determination[J]. Bulletin of Surveying and Mapping,2005(2): 32-35.(王磊, 梁开龙. 姿态测量中 GPS 双频观测的应用[J]. 测绘通报, 2005(2): 32-35.) |
| [16] | YAN Mingfeng.GNSS Three Carrier Ambiguity Resolution Using Ionosphere-reduced Virtual Signals[J]. Journal of Geodesy,2008, 82:847-862. |
| [17] | SHAO Weihan,RIZOS C. Improving the Computational Efficiency of the Ambiguity Function Algorithm[J], Journal of Geodesy, 1996,70:330-341. |
| [18] | CHEN Yulin. Study on Attitude Determination of Kinematical Carrier Using Carrier Phase of GPS System[D]. Nanjing: Nanjing University of Aeronautics and Astronautics,2005.(陈玉林. 利用 GPS 载波相位信号确定载体姿态研究 [D]. 南京:南京航空航天大学, 2005.) |
| [19] | MONTENBRUCK O, HAUSCHILD A, STEIGENBERGER P, et al. Initial Assessment of the COMPASS/BeiDou-2 Regional Navigation Satellite System[J]. GPS Solutions, 2013, 17(2): 211-222. |
| [20] | GUO Q. COMPASS Three Carrier Ambiguity Resolution[C]//China Satellite Navigation Conference (CSNC) 2013 Proceedings: Satellite Navigation Signal System, Compatibility & Interoperability: Augmentation & Integrity Monitoring—Models & Methods.[S.l.]:Springer, 2013, 244: 441. |