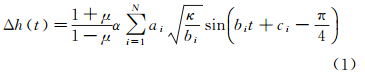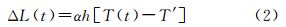2. 武汉大学测绘学院, 湖北 武汉 430079;
3. 卢森堡大学科学技术与通信系, 卢森堡
2. School of Geodesy and Geomatics, Wuhan University, Wuhan 430079, China;
JIANG Weiping(1972—),male,PhD,professor,PhD supervisor,majors in satellite geodesy and geodynamics. E-mail: wpjiang@whu.edu.cn
1 引 言
目前,坐标时间序列分析是解决高精度全球/区域坐标参考框架维持中关键问题的有效途径。GNSS基准站坐标时间序列中包含显著的线性趋势和非线性变化。其中,地表质量负载、GNSS技术类系统误差以及温度变化引起的热效应,可以解释测站高程方向的部分季节性变化[1, 2, 3, 4, 5, 6, 7]。热效应的影响主要包括地面天线观测墩的热胀冷缩,以及台站基岩热效应造成的测站水平和垂直方向的位移变化[2, 3, 4, 5, 8, 9]。
文献[10]给出一种计算不同深度基岩温度的模型,文献[1]在此基础上提出了基岩热膨胀造成的垂直方向位移变化的数学模型,估计高程方向周年变化的振幅不会超过0.56 mm。文献[2]利用文献[11]提出的简单线性模型,分别估计了地面和地下观测墩热膨胀造成的高程位移,其中地下部分引入尺度因子,利用测站附近同等深度的井水温度年变化值作为观测墩基岩温度的年变化值,结果显示地面和地下部分的振幅分别为0.2 mm和0.7 mm。文献[3]通过研究南加州GPS站坐标时间序列,发现热弹性应力可以解释水平坐标时间序列中的大部分周年变化。文献[1]提出的温度拟合模型仅考虑了谐波数为1的情形,仅估计了热膨胀造成的高程变化的最大振幅;文献[2]采用的线性模型不能精确计算地下基岩部分造成的高程位移,且无法很好地解释时间序列中的季节性变化。文献[4]在上述学者的基础上,利用改进的温度拟合模型和精化的基岩热膨胀模型,计算了全球86个IGS基准站热膨胀效应造成的高程方向变化,并讨论了泊松比的取值对基岩热膨胀周年振幅的影响,结果显示周年振幅最大可达1.3 mm,半周年振幅只占周年振幅的不到20%,且纬度越高周年振幅越大。文献[5]计算了中国区域地壳运动观测网中23个GPS台站的高程方向位移,发现温度变化影响的周年振幅最大可达2.8 mm,且有13个站的周年振幅大于1 mm。文献[12]处理了西龙池水库GPS短基线观测数据,认为部分测站时间序列中的周年运动可能是由所处基岩的热膨胀效应导致。
本文首先提出了一种计算热膨胀效应导致的基准站垂向位移的改进方法;然后,选择了有代表性的9个IGS基准站,利用基岩热膨胀模型计算了基岩热膨胀导致的基准站垂向位移,同时考虑基准站天线观测墩的热效应,计算出温度变化造成的测站垂直方向的总影响。最后,对热膨胀引起的GNSS测站垂直方向总位移进行最小二乘拟合,得出不同纬度测站的周期及相应的振幅和相位。同时,分析了仅顾及周年影响和顾及周年、半周年影响这两种拟合方法对拟合结果的影响。此外,基于上述方法,选取全球107个IGS站,计算了各测站热膨胀造成的垂向位移周年振幅及其相位。
2 拟合模型与采用的数据
首先,对原始温度数据进行建模,包括4个步骤[1, 2, 3, 4, 5, 8, 9]:①建立测站地表温度时间序列的拟合模型;②建立测站地表下不同深度基岩的温度模型;③建立基岩及观测墩热效应造成的垂直方向位移的数学模型;④得到热膨胀效应对垂直的总位移影响后对其进行最小二乘拟合的建模。
2.1 热膨胀造成的垂向总位移与拟合模型
通常情况下,温度变化对测站垂直位移的影响分为地上和地下两个部分[2, 3, 4, 5]。地上部分主要是由于放置天线的观测墩或金属杆热胀冷缩造成的长度变化,从而引起垂直位移;地下部分为地下基岩热应力造成的线性形变。
由于地表温度随季节的变化会通过热传导的方式向GPS台站的地下基岩传导热量,GPS台站基岩的不同深度对应的温度也不同,最终导致GPS台站的地表垂直位移[4, 5, 8, 9]。文献[1, 2, 3, 4]对不同的温度拟合模型进行了深入研究。根据广义胡克定律及文献[1,4—5]提出的公式,得到基岩热膨胀造成的测站垂直方向位移模型为
式中,μ为弹性体的泊松比;α为线性膨胀系数(1/℃)。
热膨胀效应的地面部分影响模型为
式中,h为天线水泥墩或金属杆的高度;T(t)为t时刻测站地表的空气温度;T′为平均温度。式(1)、式(2)相加即可得到热膨胀效应造成的地面部分和地下基岩部分垂直方向变化量的总影响。
得到总影响时间序列后,利用傅里叶变换和频谱分析法对所有9个测站序列中存在的周期项进行分析。由于篇幅关系,只列出了WILL测站的频率谱,如图 1所示。频谱分析的结果表明,在热膨胀效应造成的测站垂向位移总影响时间序列中,所有测站均存在周年周期,大部分测站存在半周年周期,这也与后文表 2中的拟合结果一致。
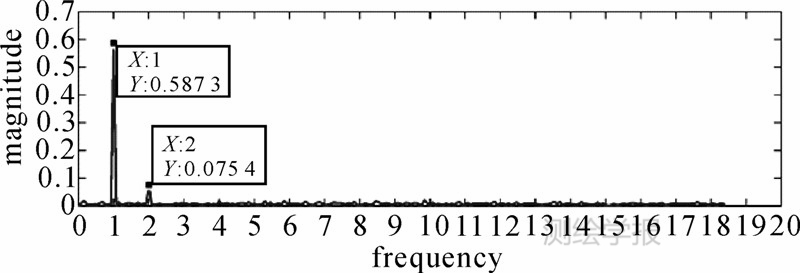 |
| 图 1 WILL站垂直方向总位移的频率谱 Fig. 1 Frequency spectrum of vertical variation(station WILL) |
为了进一步验证周年和半周年周期的存在,根据式(3)对总影响进行最小二乘拟合
式中,yt表示垂直方向总位移;A1、ω1、φ1和A2、ω2、φ2分别为周年、半周年的振幅、角频率及相位;a和b分别为斜率和截距;εt为随机噪声。文献[5]在进行最小二乘拟合时只考虑了周年周期的影响,本文对其拟合模型进行了扩展,同时考虑周年和半周年周期影响。在确定存在两个周期项后,本文将两个角频率作为未知参数,和其余参数一起进行最小二乘拟合,更为严谨地证明了热膨胀造成的测站垂向位移时间序列中,存在着周年、半周年周期。
2.2 采用的数据与原则
本文的GNSS基准站温度时间序列,是通过内插NCEP再分析数据集提供的全球地表附近空气温度格网数据获得的,时间跨度为1998年至2011年。基准站观测墩高度及基岩类型信息来自JPL网站提供的测站信息文件station_log。各测站坐标时间序列的周年及半周年周期振幅来自SOPAC提供的去除趋势项的全球测站坐标时间序列文件。
由于测站附近地表的年温差和测站纬度关系密切,同时考虑到IGS提供的station_log文件中部分测站观测墩高度信息缺失,因此本文选取了位于低(MANA、IISC、KOKB)、中(STR1、GRAZ、WILL)、高(KELY、MAW1、NYA1)纬度地区的9个GNSS基准站,着重研究基岩热膨胀和热效应对各测站垂向位移的影响量、热膨胀对垂向位移影响量的最小二乘拟合及不同方法的比较、热膨胀对坐标时间序列垂直方向周年及半周年振幅的贡献量以及加入热膨胀改正后坐标时间序列垂直方向RMS值的变化量等。各基准站详细信息统计结果见表 1。
| 测站 | 纬度 | 观测墩高度/m | 材质 | 泊松比 | 热膨胀系数 | 基岩类型 | |
| MANA | 12°08′56.8″N | 2.02 | 混凝土 | 0.17 | 1.2×10-5 | 沉积岩 | |
| 低纬 | IISC | 13°01′16.2″N | 1.60 | 混凝土 | 0.17 | 1.2×10-5 | 火成岩 |
| KOKB | 22°07′34.5″N | 4.00 | 混凝土 | 0.17 | 1.2×10-5 | 火成岩 | |
| STR1 | 35°18′55.9″S | 3.00 | 混凝土 | 0.17 | 1.2×10-5 | 火成岩 | |
| 中纬 | GRAZ | 47°04′1.60″N | 1.90 | 钢架 | 0.27 | 1.3×10-5 | 沉积岩 |
| WILL | 52°14′12.8″N | 2.30 | 混凝土 | 0.17 | 1.2×10-5 | 火山砾岩 | |
| KELY | 66°59′14.7″N | 1.50 | 混凝土 | 0.17 | 1.2×10-5 | 沉积岩 | |
| 高纬 | MAW1 | 67°36′17.3″S | 1.50 | 混凝土 | 0.17 | 1.2×10-5 | 火成岩 |
| NYA1 | 78°55′46.4″N | 5.50 | 钢桅杆 | 0.27 | 1.3×10-5 | 沉积岩 | |
| 注:表中热扩散系数的值同文献[1, 4, 5]一致,均取1 mm2/s。 | |||||||
根据式(1)得到基岩热膨胀造成的测站垂直方向的位移时间序列。同时,根据式(2)计算热效应造成的天线观测墩垂直方向上的位移量,二者相加得到地上部分和基岩的热膨胀效应对垂直方向位移的总影响,结果见图 2。
 |
| 图 2 热效应造成的测站垂直方向位移变化时间序列 Fig. 2 Vertical variation time series caused by thermal expansion |
图 2中黑线为热效应在垂直方向位移的总影响,红线为基岩热效应对垂直方向位移的贡献。低、中、高纬度测站高程方向的平均年变化量分别为0.43 mm、1.73 mm和1.72 mm,中高纬度测站变化量明显高于低纬度测站,在年温差较大的NYA1站甚至可以达到2.6 mm。低、中、高纬地区基岩热膨胀造成的测站垂直方向位移的量级分别约占总影响的37%、48%和45%。这说明,天线观测墩热效应所造成的垂直方向位移影响略高于基岩热效应造成的影响,尤其是在中、高纬度区域,很容易出现极端寒冷天气,对垂直方向的位移影响更大。同时,部分测站天线观测墩较高(如NYA1站高5.5 m),观测墩热效应造成的测站垂直方向位移对总位移影响(如NYA1站为71%)明显高于同纬度的其他测站(KELY站为42%,MAW1站为38%)。
利用式(3)给出的拟合模型,顾及周年及半周年周期,分别对9个测站的垂直方向位移总影响进行最小二乘拟合。同时为了对比不同模型的拟合效果,对测站分别进行了仅顾及周年影响的最小二乘拟合。两种模型的对比结果见图 3,参数统计结果见表 2、表 3。
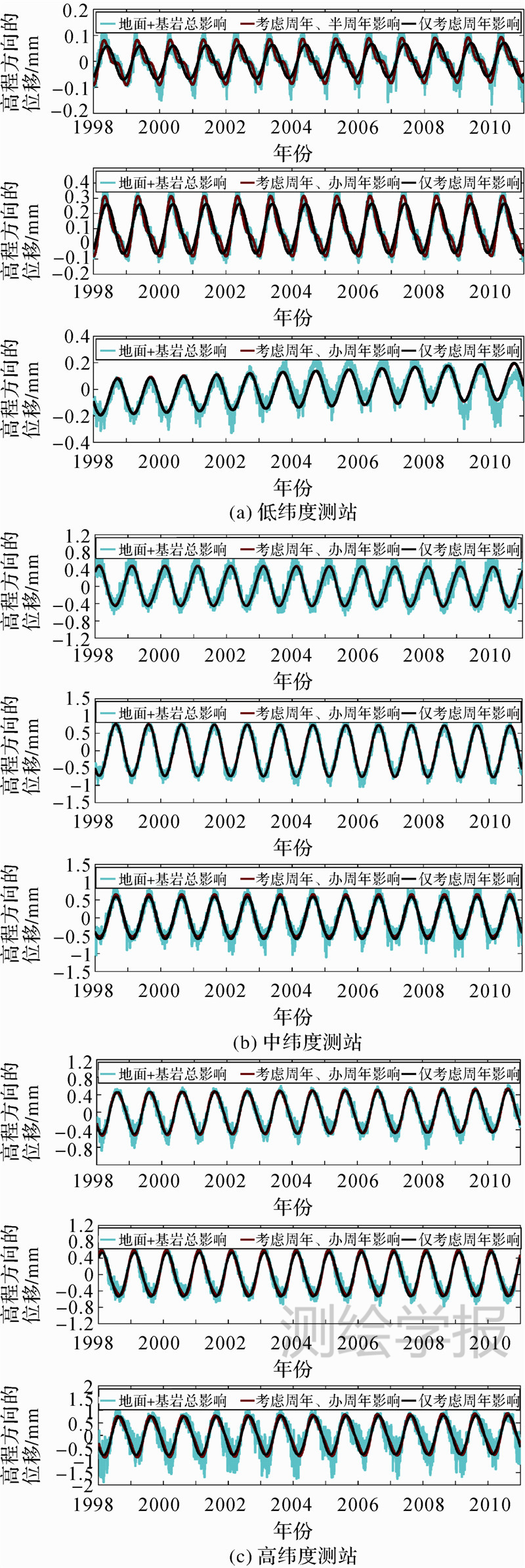 |
| 图 3 热膨胀造成的测站垂直方向位移及拟合方法对比 Fig. 3 Vertical variation time series caused by thermal expansion and comparison of fitting methods |
| 站点 | a/(mm/a) | b/mm | A1/mm | w1/d | φ1 | A2/mm | w2/d | φ2 | RMS | |
| 低纬 | MANA | 0.001 0 | -2.019 2 | 0.064 6 | 364.7 | 320.8° | 0.035 6 | 182.5 | 18.2° | 1.835 7 |
| IISC | 0.000 2 | -0.311 2 | 0.163 1 | 365.4 | 25.3° | 0.068 3 | 182.6 | 19.4° | 2.881 4 | |
| KOKB | 0.009 9 | -19.919 2 | 0.134 9 | 364.5 | 162.9° | 0.007 0 | 183.9 | 243.6° | 12.729 8 | |
| 中纬 | STR1 | 0.000 1 | -0.205 5 | 0.459 7 | 364.6 | 49.9° | 0.027 7 | 184.0 | 53.5° | 58.543 4 |
| GRAZ | -0.003 0 | 5.984 9 | 0.745 0 | 365.3 | 54.6° | 0.009 7 | 182.8 | 329.7° | 51.028 0 | |
| WILL | 0.000 6 | -1.135 3 | 0.587 3 | 364.8 | 284.7° | 0.075 3 | 182.7 | 73.9° | 73.177 9 | |
| 高纬 | KELY | 0.002 8 | -5.607 9 | 0.483 1 | 364.0 | 336.4° | 0.054 8 | 183.4 | 18.0° | 32.413 3 |
| MAW1 | 0.000 8 | -1.656 1 | 0.535 5 | 365.5 | 3.0° | 0.084 9 | 181.6 | 66.5° | 29.941 8 | |
| NYA1 | 0.003 9 | -7.855 6 | 0.780 5 | 363.7 | 322.2° | 0.158 9 | 183.8 | 32.8° | 459.843 6 | |
| 注:表中测站按纬度由低到高顺序排列。 | ||||||||||
| 站点 | a/(mm/a) | b/mm | A1/mm | w1/d | φ1 | RMS | |
| 低纬 | MANA | 0.001 1 | -2.165 3 | 0.064 6 | 364.9 | 128.5° | 4.841 4 |
| IISC | 0.000 4 | -0.895 3 | 0.163 1 | 365.4 | 288.4° | 13.950 6 | |
| KOKB | 0.010 0 | -19.966 7 | 0.134 8 | 364.5 | 217.3° | 12.844 7 | |
| 中纬 | STR1 | 0.000 05 | -0.090 6 | 0.459 9 | 364.6 | 46.7° | 60.354 2 |
| GRAZ | -0.003 0 | 5.984 9 | 0.745 0 | 365.1 | 54.6° | 50.806 8 | |
| WILL | 0.000 2 | -0.301 1 | 0.587 5 | 364.8 | 141.3° | 86.619 4 | |
| 高纬 | KELY | 0.002 7 | -5.438 1 | 0.483 8 | 364.7 | 246.5° | 39.503 6 |
| MAW1 | 0.000 6 | -1.167 8 | 0.535 8 | 365.1 | 184.0° | 47.026 3 | |
| NYA1 | 0.003 7 | -7.430 8 | 0.781 4 | 364.6 | 2.735 2° | 519.649 | |
| 注:表中测站按纬度由低到高顺序排列。 | |||||||
图 3中蓝线为垂直方向位移的总影响,红线为考虑周年、半周年周期影响的拟合曲线,黑线为仅考虑周年影响的拟合曲线。图 4和表 2的结果表明,低纬度地区测站的拟合结果普遍较好,中、高纬度测站由于低温天气多且温差较大,拟合后的RMS值稍大。需要说明的是,虽然拟合考虑了周年及半周年周期,但实际计算中是把两个角频率(w1、w2)作为未知量进行估算。
 |
| 图 4 热膨胀效应造成的全球各GNSS测站垂向位移周年振幅大小 Fig. 4 Annual amplitude of vertical variations caused by thermal expansion at each GNSS reference station |
从拟合的结果看,w1的值均非常接近365 d,w2的值均非常接近183 d,这也从理论上更严密地验证了热膨胀效应造成的垂直方向位移变化具有周年及半周年周期的影响。
根据表 2、表 3和图 3的结果,低、中、高纬地区测站半周年周期影响的振幅平均分别占周年影响的34.1%、6.7%和15.9%,从拟合结果看,二者的振幅相差较大,尤其是在中纬和高纬度地区。亦即,考虑半周年影响的拟合模型能适当提高拟合精度,但其对垂直方向位移的影响最大值仅为0.16 mm(NYA1站),因此在当前的观测精度要求下可以忽略不计。这与文献[2]得到的结论一致。
得到各测站由热膨胀效应引起的周年、半周年振幅后,利用SOPAC提供的全球测站坐标时间序列,计算了热效应造成的周年、半周年振幅对测站季节性变化的贡献,结果见表 4。
| 站点 | 最大偏移 /mm | 周年振幅 /mm | 热周年振幅 /mm | 贡献 /(%) | 半周年振幅 /mm | 热半周年振幅 /mm | 贡献 /(%) | |
| 低纬 | MANA | 0.14 | 3.37 | 0.03 | 0.9 | 0.32 | 0.02 | 5.3 |
| IISC | 0.19 | 6.82 | 0.08 | 1.2 | 0.45 | 0.05 | 11.1 | |
| KOKB | 0.35 | 0.93 | 0.15 | 16.2 | 0.92 | 0.01 | 1.3 | |
| 中纬 | STR1 | 0.81 | 2.62 | 0.46 | 17.6 | 0.46 | 0.03 | 6.1 |
| GRAZ | 0.58 | 6.7 | 0.37 | 5.5 | 0.31 | 0.01 | 3.2 | |
| WILL | 1.16 | 6.89 | 0.67 | 9.7 | 1.59 | 0.08 | 5.0 | |
| 高纬 | KELY | 0.50 | 5.07 | 0.26 | 5.2 | 2.42 | 0.02 | 1.0 |
| MAW1 | 0.42 | 1.51 | 0.13 | 8.8 | 0.36 | 0.03 | 8.6 | |
| NYA1 | 1.37 | 4.76 | 0.32 | 6.8 | 2.11 | 0.08 | 3.6 | |
| 注:表中最大偏移为热效应总影响造成的测站垂向位移最大偏移量。 | ||||||||
从表 4可以看出,在所选取的9个站点中,热膨胀效应造成的测站垂直方向的季节性位移变化,是造成测站高程方向季节性变化的因素之一。同时,在中、高纬度地区,热效应周年振幅对测站垂直方向周年变化的贡献普遍高于半周年振幅对测站垂直方向半周年变化的贡献。
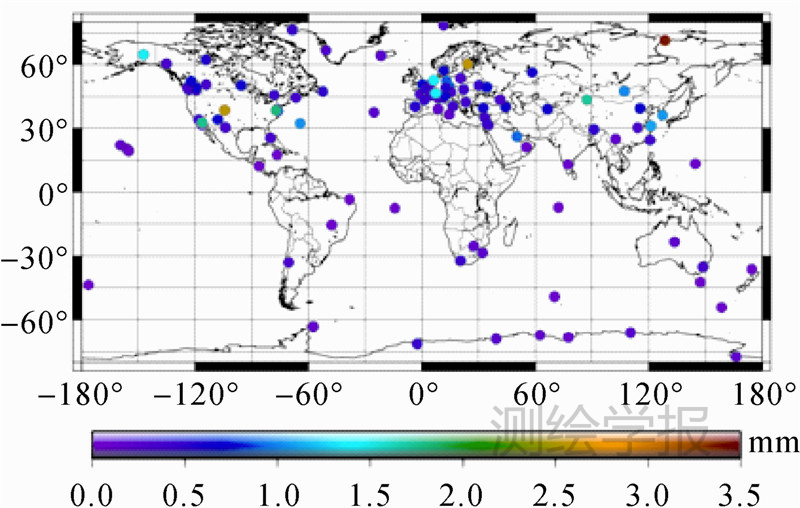
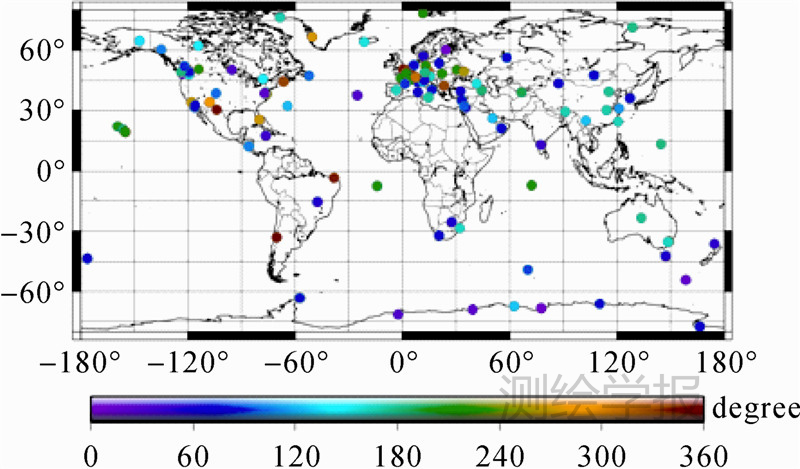
在此基础上,本文选取了全球107个IGS站,利用本文的方法,计算了热膨胀造成的各测站垂向位移周年振幅及其相位结果,如图 4、图 5所示。
 |
| 图 5 热膨胀效应造成的全球各GNSS测站垂向位移周年相位大小 Fig. 5 Annual phase of vertical variations caused by thermal expansion at each GNSS reference station |
从图 4、图 5中可以看出,热膨胀造成的测站垂向位移周年振幅最大可以达到3.3 mm,其大小和测站纬度具有比较明显的相关性,即中、高纬度地区测站的热膨胀影响明显高于低纬度测站。同时,热膨胀效应影响较大的测站大都分布在北纬40°以上的区域,而南半球的测站影响明显较小,测站周年相位则无明显规律。 3.2 其他异常周期影响
在研究其他站点(例如GLSV站,位于中纬度地区)时,发现除了周年影响外,还存在长度为51 d的小周期影响。表 5为该测站热膨胀造成的垂向位移总影响的最小二乘拟合结果。
| 站点 | a/(mm/a) | b/mm | A1/mm | w1/d | φ1 | A2/mm | w2/d | φ2 | RMS |
| GLSV | 0.002 3 | -4.622 5 | 0.996 0 | 6.275 9 | -0.288 1° | 0.042 4 | 45.002 8 | 3.424 2° | 115.111 5 |
可以看出,除了周年影响以外,序列中还可能存在着角频率为45.002 8(换算成周期为51 d)的谐波,振幅为周年振幅的4.3%。该周期产生的地球物理原因还有待研究,可能与其所处纬度及当地气候条件有关。
4 结 论
本文提出了计算基岩热膨胀导致测站垂直位移变化的改进模型,通过分析热膨胀效应对GNSS基准站垂直方向位移变化的影响,得到以下结论:
(1) 热膨胀效应会造成测站垂直方向的位移变化。中、高纬地区测站的年温度变化明显,造成的垂向位移振幅最大可达到1.8 mm(NYA1站),而低纬度测站平均振幅只有0.16 mm。低、中、高纬地区基岩热膨胀造成的测站垂直方向位移的量级分别约占总影响的37%、48%和45%,说明其不可忽视。
(2) 热膨胀效应造成的测站垂直方向位移时间序列存在明显的周年和半周年周期特性。低、中、高纬度测站平均周年振幅分别为0.12 mm、0.60 mm、0.60 mm,半周年振幅分别为0.04 mm、0.04 mm和0.10 mm。周年、半周年振幅在中、高纬度测站明显高于低纬度测站,同一测站的半周年振幅普遍小于周年振幅。
(3) 热膨胀效应造成的测站垂直方向的季节性位移变化,是造成测站高程方向季节性变化的因素之一。其中,周年、半周年影响平均可以解释11.2%、3.3%的测站坐标时间序列U方向的季节性变化。
(4) 对垂向位移时间序列分别进行仅顾及周年、同时顾及周年和半周年影响的最小二乘拟合,两种方法得到的RMS值和周年振幅相差很小。因此认为,半周年振幅在现有观测精度要求下基本可以忽略,但不排除在某些中、高纬度测站的影响较大。
(5) 部分测站(如GLSV站)除了周年影响外,发现了可能存在周期为51 d的小周期影响,振幅约为0.04 mm。虽然远小于周年影响(振幅为1.00 mm),但是其产生原理及存在的地球物理机制还有待研究。
| [1] | DONG D, FANG P, BOCK Y, et al. Anatomy of Apparent Seasonal Variations from GPS-derived Site Position Time Series[J]. Journal of Geophysical Research, 2002, 107(B4): ETG9-1-ETG9-16. |
| [2] | ROMAGNOLI C, ZERBINI S, LAGO L, et al. Influence of Soil Consolidation and Thermal Expansion Effects on Height and Gravity Variations[J]. Journal of Geodynamics, 2003, 35(4): 521-539. |
| [3] | PRAWIRODIRDJO L, BEN-ZION Y, BOCK Y. Observation and Modeling of Thermoelastic Strain in Southern California Integrated GPS Network Daily Position Time Series[J]. Journal of Geophysical Research: Solid Earth, 2006, 111(B2): B02408. |
| [4] | YAN Haoming, CHEN Wu, ZHU Yaozhong, et al. Contributions of Thermal Expansion of Monuments and Nearby Bedrock to Observed GPS Height Changes[J]. Geophysical Research Letters, 2009, 36(13): L13301. |
| [5] | YAN Haoming, CHEN Wu, ZHU Yaozhong, et al. Thermal Effects on Vertical Displacement of GPS Stations in China[J]. Chinese Journal of Geophysics, 2010, 53(4): 825-832. (闫昊明, 陈武, 朱耀仲, 等. 温度变化对我国GPS台站垂直位移的影响[J]. 地球物理学报, 2010, 53(4): 825-832.) |
| [6] | WANG Min, SHEN Zhengkang, DONG Danan. Effects of Non-tectonic Crustal Deformation on Continuous GPS Position Time Series and Correction to Them[J]. Chinese Journal of Geophysics, 2005, 48(5): 1045-1052. (王敏, 沈正康, 董大南. 非构造形变对GPS连续站位置时间序列的影响和修正[J]. 地球物理学报, 2005, 48(5): 1045-1052.) |
| [7] | MAO Ailin, HARRISON C G A, DIXON T H. Noise in GPS Coordinate Time Series[J]. Journal of Geophysical Research: Solid Earth(1978-2012),1999, 104(B2): 2797-2816. |
| [8] | LI Zhao. Research on the Non-linear Variation of GPS Coordinate Time Series[D]. Wuhan: Wuhan University, 2012. (李昭. GPS坐标时间序列的非线性变化研究[D]. 武汉: 武汉大学, 2012.) |
| [9] | WANG Yankai. Research on Geophysical Effect on GPS Height Coordinate Time Series[D]. Wuhan: Wuhan University, 2012. (王琰开. 地球物理效应对GPS高程坐标时间序列的影响研究[D]. 武汉: 武汉大学, 2012.) |
| [10] | TURCOTTE D L, SCHUBERT G. Geodynamics: Application of Continuum Physics to Geological Problems[M]. New York: John Wiley, 1982:450. |
| [11] | WEAST R C, ASTLE M J, et al. CRC Handbook of Chemistry and Physics[M]. Boca Raton, FL, USA: CRC Press, 1982. |
| [12] | JIANG Weiping, LIU Hongfei, ZHOU Xiaohui, et al. Analysis of Long-term Deformation of Reservoir Using Continuous GPS Observations[J]. Acta Geodaetica et Cartographica Sinica, 2012, 41(5): 682-689. (姜卫平, 刘鸿飞, 周晓慧, 等. 利用连续GPS观测数据分析水库长期变形[J]. 测绘学报, 2012, 41(5): 682-689.) |
| [13] | JIANG Weiping, LI Zhao, LIU Wanke, et al. Some Thoughts on Establishment and Maintenance of Terrestrial Reference Frame Considering Non-linear Variation[J]. Geomatics and Information Science of Wuhan University, 2010, 35(6): 665-669. (姜卫平, 李昭, 刘万科, 等. 顾及非线性变化的地球参考框架建立与维持的思考[J]. 武汉大学学报: 信息科学版, 2010, 35(6): 665-669.) |
| [14] | LI Zhao, JIANG Weiping, LIU Hongfei, et al. Noise Model Establishment and Analysis of IGS Reference Station Coordinate Time Series inside China[J]. Acta Geodaetica et Cartographica Sinica, 2012, 41(4): 496-503. (李昭, 姜卫平, 刘鸿飞, 等. 中国区域IGS基准站坐标时间序列噪声模型建立与分析[J]. 测绘学报, 2012, 41(4): 496-503.) |
| [15] | YUAN Linguo, DING Xiaoli, CHEN Wu, et al. Characteristics of Daily Position Time Series from the Hong Kong GPS Fiducial Network[J]. Chinese Journal of Geophysics, 2008, 51(5): 1372-1384. (袁林果, 丁晓利, 陈武, 等. 香港GPS基准站坐标序列特征分析[J]. 地球物理学报, 2008, 51(5): 1372-1384.) |
| [16] | FU Yang. Present-day Crustal Deformation in China and GPS-derived Coordinate Time Series Analysis[D]. Beijing: Graduate University of Chinese Academy of Sciences, 2002. (符养. 中国大陆现今地壳形变与GPS坐标时间序列分析[D].) |
| [17] | HUANG Liren. Noise Properties in Time Series of Coordinate Component at GPS Fiducial Stations[J]. Journal of Geodesy and Geodynamics, 2006, 26(2): 31-33, 38. (黄立人. GPS 基准站坐标分量时间序列的噪声特性分析[J]. 大地测量与地球动力学,2006, 26(2): 31-33, 38.) |
| [18] | VERHOEF A, VAN DEN HURK B J, JACOBS A F, et al. Thermal Soil Properties for Vineyard (EFEDA-I) and Savanna (HAPEX-Sahel) Sites[J]. Agricultural and Forest Meteorology,1996, 78(1): 1-18. |
| [19] | ZHANG Jie, BOCK Y, JOHNSON H, et al. Southern California Permanent GPS Geodetic Array: Error Analysis of Daily Position Estimates and Site Velocities[J]. Journal of Geophysical Research,1997, 102(B8): 18018-18035. |
| [20] | JIANG Zhihao, ZHANG Peng, BEI Jinzhong, et al. Velocity Estimation on the Colored Noise Properties of CORS Network in China Based on the CGCS2000 Frame[J]. Acta Geodaetica et Cartographica Sinica, 2010, 39(4): 355-363. (蒋志浩, 张鹏, 秘金钟, 等. 顾及有色噪声影响的CGCS2000下我国CORS站速度估计[J]. 测绘学报, 2010, 39(4): 355-363.) |
| [21] | JIANG Zhihao, ZHANG Peng, MI Jinzhong, et al. The Model of Crustal Horizontal Movement Based on CGCS2000 Frame[J]. Acta Geodaetica et Cartographica Sinica, 2009, 38(6): 471-476. (蒋志浩, 张鹏, 秘金钟, 等. 基于CGCS2000的中国地壳水平运动速度场模型研究[J]. )测绘学报, 2009, 38(6): 471-476. |
| [22] | ZHU Wenyao, FU Yang, LI Yan. Global Height Vibration and Its Seasonal Variation Induced by GPS Height[J]. Science in China: Series D, 2003, 33(5): 470-481. (朱文耀, 符养, 李彦. GPS高程导出的全球高程振荡运动及季节性变化[J]. 中国科学: D辑, 2003, 33(5): 470-481.) |